FREIRE, Amanda Freitas [1], RODRIGUES, Fabiana Soares [2], AQUINO, Maria Rosane Souza [3], SOARES, Maria Vanessa [4], GOIS, David Denis Pires de [5], VIANA, José Damião [6]
FREIRE, Amanda Freitas; et.al. O Uso do Geoplano no Ensino de Geometria: Cálculo de Área e Perímetro. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 06, Vol. 03, pp. 119-135, Junho de 2018. ISSN:2448-0959
Resumo
Esta pesquisa traz como tema central o ensino do cálculo de área e perímetro de figuras na Geometria Plana, utilizando como recurso o Geoplano. Defende-se, neste artigo, a ideia que através do uso de materiais manipuláveis existe a possibilidade de facilitar o ensino/aprendizagem do conteúdo, do mesmo modo desenvolver o raciocínio e o interesse dos discentes na resolução de problemas. Neste artigo será apresentada uma pesquisa de campo de caráter qualitativo, ocorrida nas séries finais do ensino fundamental, realizada no 8º ano “C” da escola Estadual Jornalista Edson Régis, localizada no bairro São Cristóvão na cidade de Arcoverde-PE, uma oficina realizada através do Programa Institucional de Bolsas de Iniciação à Docência (PIBID). Durante a oficina notou-se uma participação efetiva da turma e também uma melhoria no desempenho dos alunos.
Palavras-chaves: Ensino de Matemática, Geometria Plana, Geoplano.
Introdução
Na atualidade, vivemos em um meio que esta cada vez mais centrado nos avanços tecnológicos, o saber e o conhecer se fazem necessários para as diversas ações humanas desde coisas simples à complexas. O conhecimento matemático é de extrema importância para que o indivíduo se relacione com a sociedade e o meio em que vive. Esse conhecimento nos dias atuais não se faz presente no cotidiano de muitos alunos, por apresentarem dificuldades em estabelecer relações do que aprendeu com situações do dia a dia. O BNCC (Base Nacional Comum Curricular) relata sobre essa conexão que o alunado tem que estabelecer dos conhecimentos adquiridos com acontecimentos diários, e descreve o seguinte:
É importante destacar que essa associação entre o mundo físico que nos rodeia e o mundo desconhecido da matemática pode ser relacionado a uma mão de via dupla. Por exemplo, ao mesmo tempo em que um paralelepípedo retângulo funciona como um modelo abstrato para o objeto físico caixa de sapato, para o modelo abstrato da figura geométrica espacial esfera, podemos associar o objeto do mundo físico bola de futebol (BRASIL, 2015).
O objetivo desta pesquisa é ressaltar a importância do uso de recursos didáticos na aprendizagem de Matemática e no ensino de geometria plana, especificamente no cálculo de área e perímetro. Sendo assim seja no mundo físico ou imaterial a matemática se faz presente em tudo o que nos cerca, dessa forma é importante o seu conhecimento. Em sala de aula a complexidade em associar a Matemática com o dia a dia, torna-se mais presente, uma vez que os problemas e questionamentos apresentados não são representados de uma maneira em que o aluno possa apalpar e representar com algo físico. Esses problemas são apresentados de uma forma apenas imaginária. Então quando existe algum recurso que permita que o professor possa expor em sua forma física a dúvida, o impasse e os questionamentos levantados, o ensino torna-se mais atrativo e de fácil compreensão para o aluno.
Partindo dessas dificuldades apresentadas surgem alguns questionamentos: Como tornar o ensino de Matemática mais atraente para o aluno? O uso do Geoplano como ferramenta de ensino facilitaria a aprendizagem dos alunos? De que forma nós como educadores podemos tornar o ensino/aprendizagem mais versátil? É fundamental que o docente faça uso dos conhecimentos que o aluno já possui e partindo desse ponto pode ser feita conexões desse saber com a Matemática do dia a dia. Nada é mais proveitoso que usar as instruções aprendidas em problemas que surgem diante a sociedade. Com isso elaboramos essa pesquisa por meio do Programa Institucional de Bolsas de Iniciação a Docência[7] (PIBID) da Autarquia de Ensino Superiro de Arcoverde (AESA), com o intuito de apresentar ao aluno uma Matemática trabalhada com recursos didáticos. Sugerimos o Geoplano como ferramenta para o ensino/aprendizagem do cálculo de área e perímetro de figuras planas, para alunos das séries finais do Ensino Fundamental II, especificamente o 8º ano da Escola Jornalista Edson Régis situada na cidade e Arcoverde-PE. Uma vez que com esse recurso podemos explorar conceitos básicos da Geometria Plana ou Euclidiana tais como: o ponto, a reta e o plano.
As primeiras ideias geométricas se originaram com a capacidade humana de buscar alternativas para resolver problemas de ordem prática:
Buscando a origem do desenvolvimento da geometria nos primórdios, com o homem primitivo, podemos imaginar que o conhecimento das configurações do espaço, formas e tamanhos tenham se originado, possivelmente, com a capacidade humana de observar e refletir sobre os deslocamentos, com a construção de estratégias de caça e colheita de alimentos, com a criação de ferramentas e utensílios, visando satisfazer suas necessidades básicas. Ao fixar moradia, com a divisão do trabalho, outras necessidades foram surgindo e a produção do conhecimento geométrico se ampliando. A necessidade de fazer construções, delimitar a terra levou à noção de figuras e curvas e de posições como vertical, perpendicular, paralela (GRANDO, 2008, p. 7).
Metodologia
Trata-se de uma pesquisa com abordagem qualitativa, na qual foi utilizada uma técnica da pesquisa de campo. Como instrumento de coleta de dados foram utilizados questionários, entrevistas e a observação dirigida.
Em busca de respostas para às perguntas apresentadas na introdução, realizamos diferentes atividades como entrevistas com docentes e discentes, e uma oficina utilizando o Geoplano. A principio, foi entrevistado o professor regente do 8º ano “C”, e logo após o professor da série que antecede, foi elaborado um questionário contendo cinco perguntas: Você conhece o Geoplano? Você utiliza algum tipo de recurso para o ensino de Geometria? Quais as dificuldades encontradas durante essas aulas? Durante as aulas, você já apresentou as principais figuras geométricas planas? Como você ensina o cálculo de áreas e perímetros?
No que diz respeito aos discentes, aplicou-se um questionário para trinta alunos com cinco perguntas, algumas delas são: você conhece o Geoplano? Nas aulas de geometria o professor já utilizou algum tipo de material manipulável? Você sabe o que é perímetro? E área? Você sabe como calcular o perímetro e a área dessas figuras?
Ao analisar as respostas, percebe-se a grande dificuldade no conteúdo, a carência em conhecer o Geoplano e algumas figuras planas. Baseando-se nas respostas realizou-se uma oficina utilizando o Geoplano, abordando o cálculo de área e perímetro.
Após a aplicação da oficina, realizou-se entrevista com os alunos para avaliar o desempenho, contendo três perguntas: O Geoplano poderia ser utilizado nas aulas de geometria? Esse recurso facilitou o cálculo de área e o perímetro? Houve dificuldade no manuseio do Geoplano?
Pretende-se com este estudo, encontrar respostas para as questões enunciadas e verificar a importância do Geoplano como facilitador do ensino-aprendizagem do cálculo de área e perímetro.
Ensino da matemática
Os futuros docentes em Matemática deparam-se com situações preocupantes no processo de ensino-aprendizagem. Em sala de aula o professor deve ensinar uma vasta quantidade de conteúdos em pouco tempo, deve-se transmitir esses conhecimentos que demoravam centenas de anos de aperfeiçoamento em algumas horas de aula, sendo esses passados na maioria das vezes de uma forma abrupta e abstrata o que dificulta e causa bloqueios no entendimento dos alunos.
Esquecemos também que objetivo do processo educacional é que os alunos possam ter o maior aproveitamento possível, porém essa meta fica longe de ser atingida, pois muitos docentes preocupam-se mais com a quantidade de conteúdo aplicada do que a quantidade que esse conhecimento é receptivo pelo aluno.
A construção do conhecimento matemático depende muito da maneira em que são abordados, os conceitos devem ser repassados de uma forma mais próxima da realidade física, trazendo exemplos do cotidiano, e também utilizando os saberes já adquiridos pelo discente fora do campo escolar. Aos docentes ficaria a responsabilidade de planejar a sua aula com antecedência, baseando-se nas necessidades e dificuldades do seu aluno, na qual seu objetivo seja suprir a carência do seu alunado.
Santo Junior (2011), afirma que:
O Ensino de matemática precisa ser pensado como um processo mais amplo de construção, no qual é necessário se ter um planejamento para suprir as dificuldades apresentadas, e que seja possível atingir os objetivos propostos de uma maneira não mecânica.
A matemática na atualidade
Sabe-se que a Matemática surgiu a partir do momento que o homem necessitou fazer contagem. Desde esse momento o homem foi criando estratégias para contar até conseguir criar os primeiros símbolos matemáticos com o passar do tempo, as quantidades foram representadas por expressões, gestos, palavras e símbolos, sendo que cada povo tinha a sua maneira de representação.
A Matemática ao longo da história foi sofrendo diversas evoluções até chegar ao que conhecemos nos dias de hoje. Atualmente essa disciplina desempenha um papel essencial na vida do homem, seu uso é diário e o conhecimento nessa área proporciona ao indivíduo a oportunidade de construir um futuro significativamente melhor. A falta desse conhecimento restringe o ser humano de resolver problemas do cotidiano, de se inserir no mercado de trabalho e de adquirir novos conhecimentos em diversas áreas que utiliza a Matemática como uma disciplina indispensável.
Esse contexto nos permite analisar esta disciplina em diversos aspectos, trazendo para a sala de aula, iremos analisar as dificuldades em aprendizagens encontradas por alguns alunos.
Dentro deste campo existem diferentes conteúdos abordados em que são encontradas diversas dificuldades de aprendizagem, uma das disciplinas da Matemática em que se encontram grandes dificuldades é a Geometria.
Geometria plana ou Euclidiana
Euclides em sua obra “Os Elemento” dividido em 13 volumes, onde 10 desse ele se dedicou a sua criação e 03 a teoria dos números, buscou-se em três entes Geométricos, são eles:
- O Ponto (É tudo aquilo que não tem partes)
- A Reta (Comprimento sem espessura)
- O Plano (É tudo aquilo que tem comprimento e largura)
Esses entes são tidos como sem definição, pois são palavras primitivas.

No contexto de geometria plana vamos estudar os polígonos e as figuras planas, tais como: retângulo, quadrado, paralelogramo, triângulo, trapézio entre outros.
Polígono é um plano limitado por seguimentos de retas, partindo disso, encontramos dois tipos: Os regulares, com lados e ângulos congruentes e os irregulares, com lados e ângulos não congruentes, nesse estudo podemos encontrar conceitos primitivos da geometria plana, que é o cálculo de área e perímetro, o cálculo do perímetro de figuras planas é feita pela soma de seus lados. Sabemos que um quadrado possui quatro lados medindo ?, logo temos a seguinte expressão: , onde é o perímetro e ? é o lado do quadrado, ou seja, o perímetro é o contorno de uma superfície dada, seja ela regular ou não.
A área de um polígono já é um pouco mais complicada, pois não será o contorno da figura, mas sim o número que ela ocupa no plano, a área é geralmente dada pela letra pode ser determinada com uma expressão que vai de acordo com a figura que ele representa, vejamos agora algumas figuras e como calcular suas respectivas áreas e perímetros.
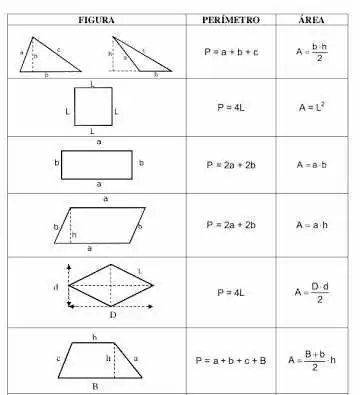
Exemplos:
Calcule as áreas das figuras abaixo:
Partindo desse ponto podemos constatar que a realidade do aluno está repleta de figuras planas geométricas, então esse aluno encontrará problemas de diversas complexidades, sendo assim o conhecimento geométrico torna-se importante para a formação intelectual do aluno, pois irá lhe proporcionar competências e habilidades que o ajudarão a se situar e solucionar determinados problemas no meio em que está inserido.
Segundo os Parâmetros Curriculares Nacionais – PCN’s (BRASIL, 1998), os conceitos geométricos constituem parte importante do currículo de Matemática no Ensino Fundamental, pois por meio deste o aluno desenvolve um tipo especial de pensamento que lhe permite compreender e representar o mundo em que vive. Este saber, se trabalhado a partir do mundo físico, permite ao aluno fazer conexões entre a Matemática e outras áreas de conhecimento.
Compreende-se que de acordo com os PCN’s a aprendizagem de Geometria é de suma importância em todos os níveis de ensino. Contudo os docentes por diversos motivos não se preocupam com o ensino da Geometria e tão pouco em pesquisar recursos que facilitem o ensino-aprendizagem e que torne essa aprendizagem mais dinâmica, sem desviar-se do contexto. Observando-se que alguns autores ao elaborarem seus livros didáticos colocam esse conteúdo nos últimos capítulos, dificultando assim o cumprimento traçado pelos educadores.
GEOPLANO
O nome Geoplano vem da junção Geo, que significa geometria e Plano, que significa superfície plana, portanto, Geoplano. Consta-se que ele foi utilizado pela primeira vez em 1961, pelo professor Caleb Gattegno, do Instituto de Educação da Universidade de Londres (KNIJNIK, BASSO; KLÜSENER, 1996; MENEZES, 2008).

O Geoplano é um pedaço de madeira de superfície plana com pregos batidos a mesma distância um dos outros. Existem alguns tipos de Geoplano: O Quadrado, O Circular, o Trelissado, e o Oval. O quadrado é o mais utilizado, composto superfície de madeira quadrada dividida de forma quadriculada por pregos equidistantes. É um recurso de simples confecção, que ajuda os alunos a superar suas dificuldades e ao mesmo tempo aprende a manipulá-lo, ele pode também ser utilizado como um jogo matemático que facilita a compreensão do aluno em relação lúdica. Esse recurso permite que o discente adquira novas experiências e também torna-se possível sua forma física, saindo assim do modo abstrato do imaginário, através de construção de figuras e tem um artifício adicional, baseando-se na contagem de pinos da esquerda para a direita, linhas e colunas, dentro e fora das figuras possibilitando trabalhar de forma mais dinâmica, pois ao contrário dos outros jogos o Geoplano tem flexibilidade, assim o discente pode fazer e desfazer sempre que desejar com o seu professor.
De acordo com Souza (2009, p. 8) destaca que:
No jogo pode-se correr risco, experimentar, tentar, inventar, tudo isso livre do fantasma de uma avaliação punitiva e castradora. O professor que utiliza o jogo tem o papel de organizar e sistematizar essas atividades para que elas possibilitem aos alunos caminhar em busca de novos conhecimentos (…).
No entanto percebe-se que com a introdução do Geoplano, pode-se promover ao ensino da Geometria Plana uma maneira diferente de abordar e representar de forma física diversos conteúdos, tais como: cálculo de área e perímetro dos polígonos.
Pesquisa de campo
Após a identificação do Geoplano como um recurso manipulável e capaz de promover uma aprendizagem significativa, realizou-se três questionários, dois foram para a coleta de dados e outro para coleta de resultados.
Segundo o questionário o atual docente respondeu que nunca utilizou nenhum recurso didático manipulável e desconhece o Geoplano. Já o da série anterior em seu relato afirma que fazia uso de outros materiais manipuláveis, inclusive o Geoplano. Estas trouxeram controversas, pois segundo a entrevista com os alunos, os mesmos alegaram desconhecer o material.
Os conteúdos trabalhados, foram cálculos de áreas e perímetros de figuras planas, antes de aplicarmos a oficina realizamos também uma entrevista com a turma, detectamos uma grande dificuldade por parte deles em reconhecer o Geoplano, alguns polígonos, calcular áreas e perímetros, como mostram os resultados a seguir.
1º) VOCÊ CONHECE O GEOPLANO?
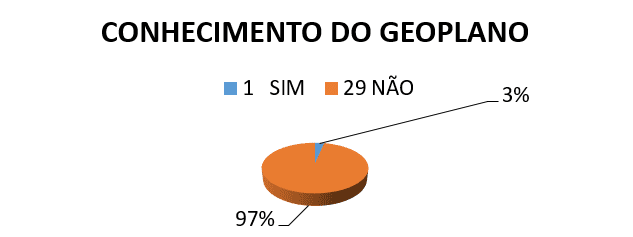
2º) NAS AULAS DE GEOMETRIA O PROFESSOR JÁ UTILIZOU ALGUM TIPO DE MATERIAL MANIPULÁVEL?
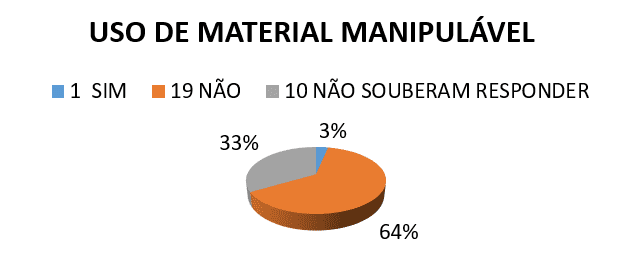
3º) VOCÊ SABE O QUE É PERÍMETRO OU ÁREA?

4º) QUAIS FIGURAS ABAIXO VOCÊ CONHECE?
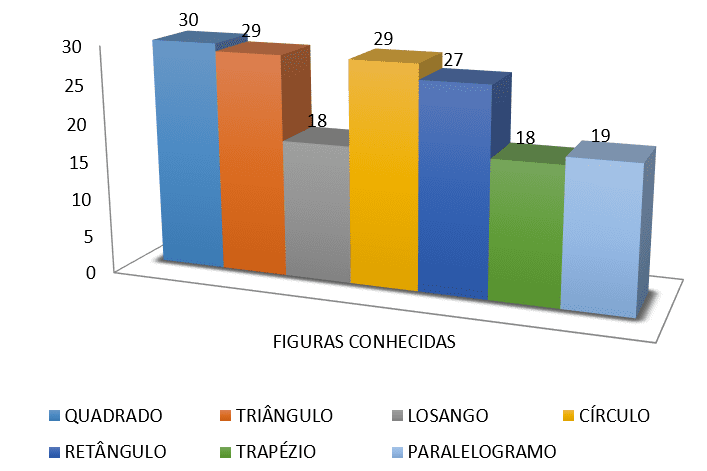
5º) VOCÊ SABE CALCULAR O PERÍMETRO OU A ÁREA DE ALGUMAS DESSAS FIGURAS?

Ao analisar os dados obtidos, percebeu-se a necessidade de realizar uma oficina, na qual o Geoplano foi apresentado como um recurso para o ensino e aprendizagem. Através desta oficina buscamos demonstrar de forma versátil como manusear esse recurso.
Dividiu-se a sala em cinco grupos de seis alunos, cada grupo recebeu dois Geoplanos, um quadrado, um circular e uma certa quantidade de elásticos. Em um primeiro momento após serem entregues os Geoplanos aos alunos, eles tiveram por um tempo a liberdade de manusear e construir figuras de acordo com a imaginação de cada um.
Com a utilização de slides, houve uma abordagem apresentando os principais polígonos regulares. Logo após, desafiou-se os discentes a realizar cálculos de perímetros e áreas de polígonos diversos, utilizando o Geoplano e a malha quadriculada. Este desafio trouxe uma movimentação participativa por parte dos alunos, tratando-se de algo diferente do seu cotidiano. O Geoplano quando utilizado encanta, desperta interesse e trás versatilidade para a aula.
Smole, Diniz e Cândido destacam que:
Uma das grandes vantagens do geoplano é que, ao contrário da folha de papel, ele tem mobilidade, é “dinâmico”, e a flexibilidade com que se pode fazer e desfazer construções permite que a criança habitue-se a ver figuras em diversas posições, perceber se uma determinada hipótese que fez para a solução de um problema é adequada e corrigi-la imediatamente se necessário. (2003, p. 112).
Durante a oficina através de observações, notou-se que ocorreu uma melhoria no desempenho dos alunos ao realizar os cálculos propostos, também uma participação efetiva da turma.



Como avaliação da aprendizagem houve a necessidade de realizar outro questionário com os discentes para a confirmação dos resultados obtidos como mostra os gráficos.
1º) O GEOPLANO PODERIA SER UTILIZADO NAS AULAS DE GEOMETRIA?

2º) ESSE RECURSO FACILITOU O CÁLCULO DE ÁREA E PERÍMETRO?

3º) CLASSIFIQUE SEU DESEMPENHO NO MANUSEIO DO GEOPLANO?
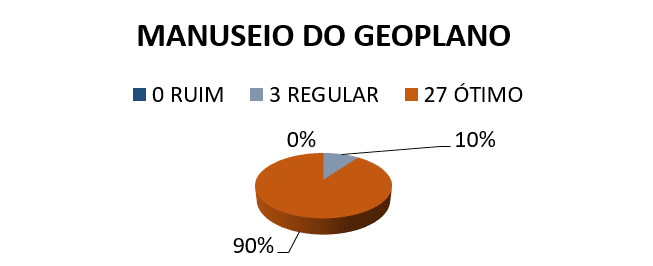
De acordo com os resultados obtidos através do questionário realizado com os discentes após a oficina, percebeu-se que houve uma concordância efetiva por parte dos discentes para alguns resultados. O primeiro e o segundo gráfico mostra que cem por cento dos alunos concordam com o uso do Geoplano nas aulas de geometria, uma vez que esse recurso facilitou o cálculo de área e perímetro. Ainda analisando os resultados é possível notar que esse recurso é de fácil manuseio, pois o terceiro gráfico apresenta uma boa classificação em relação à atuação dos alunos ao manusear o Geoplano, dez por cento dos alunos acharam seu desempenho no manuseio regular e noventa por cento ótimos.
Portanto a aprendizagem do aluno foi significativa durante a execução da oficina, os mesmos mostraram entusiasmo, participação, curiosidade e dedicação, o resolver os desafios propostos utilizando o Geoplano e a malha quadriculada.
Considerações finais
Os recursos, quando bem planejados, propiciam para os alunos a construção do conhecimento Matemático, por isso nesse trabalho resolvemos escolher o Geoplano, pois será a partir de um conhecimento prévio dessa ferramenta por parte do educador que podemos oferecer para o educando uma maneira diferente para ampliar o seu desenvolvimento cognitivo, proporcionando situações sistematizadas e concretas.
Portanto, esse recurso será utilizado como um método de ensino no qual os alunos podem vivenciar situações diferenciadas, aprendendo a trabalhar símbolos, resolver problemas envolvendo área e perímetro de polígonos, em que eles poderão fazer uma análise real daquilo que está sendo vivenciado. Desse modo, o Geoplano, escolhido para tal se encaixa com perfeição nessas atividades, pois segundo os Parâmetros Curriculares Nacionais, os jogos de um modo em geral são portadores de um relevante aspecto, que é um desafio que provoque o aluno, ou seja, é uma grande maneira de encorajá-lo a encarar novas situações onde possam colocar em prática seus aprendizados, perdendo o medo de aprender Matemática.
De acordo com Rêgo & Rêgo (2013).
…Por meio de experiências realizadas com material concreto, o aluno desenvolve o gosto pelo prazer da descoberta, para enfrentar desafios e vencê-los, desenvolvendo hábitos e costumes que podem conduzi-lo mais tarde a ser um individuo autônomo e capacitado a agir.
Pode-se concluir que através de jogos, recursos didáticos e ferramentas facilitadoras de ensino/aprendizagem é possível que os educadores tornem as aulas de matemática mais versátil, atrativa para o alunado.
Referências
BRASIL.Ministério de Educação. Base Comum Curricular: Matemática: MEC, 2015,p.116.
BRASIL.Secretaria da Educação Fundamental. Parâmetro Curricular Nacional: Matemática. Brasília:MEC/SEF,1998.
GRANDO, Cláudia Maria. Geometria: espaço e forma. Chapecó: Unochapecó; Coordenadoria de Educação a Distância, 2008.
MENEZES, J. E. (org.). Conhecimento, interdisciplinaridade e atividades de ensino com jogos matemáticos: uma proposta metodológica. Recife: UFRPE, 2008. (Série Contexto Matemático)
RÊGO, R. G; RÊGO. R. M. Matematicativa. 4. Ed. Ver.Campinas-SP 2013 (coleção formação de professores)P.25
SANTOS JUNIOR, V. B. D. A Mobilização de Conteúdos Matemáticos em Atividades Práticas em Contexto de Jogo com Licenciandos de Matemática. Dissertação (Mestrado em Ensino das Ciências e Matemática) – Programa de Pós-Graduação em Ensino das Ciências e Matemática, Departamento de Educação, Universidade Federal Rural de Pernambuco. Recife, 2011. P. 22-36
SOUZA, Mônica Menezes. A atividade lúdica na sala de aula de matemática: ação e reflexão. Disponível em <http://sbem.com.br/files/ix/enem/minicurso/trabalhos>. Acesso em 20 de outubro de 2009.
SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez de Souza Vieira; CÂNDIDO, Patrícia Terezinha. Figuras e formas. Porto Alegre: Artmed, 2003. (Coleção Matemática de 0 a 6, v. 3).
[1] Graduando no curso de licenciatura em Matemática do CESA.
[2] Graduando no curso de licenciatura em Matemática do CESA.
[3] Graduando no curso de licenciatura em Matemática do CESA.
[4] Graduando no curso de licenciatura em Matemática do CESA.
[5] Graduando no curso de Licenciatura em Matemática do CESA.
[6] Orientador. Professor do CESA.
[7] O PIBID é um programa do Governo Federal que quer incentivar a formação dos Docentes em nível superior para a educação básica, contribuindo para a valorização do magistério. Mais informações acessar: <HTTP://www.capes.gov.br/educacao-basica/capespibid>
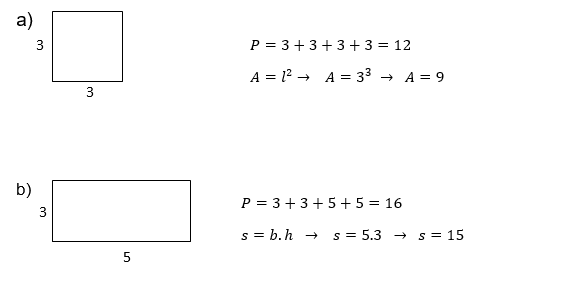
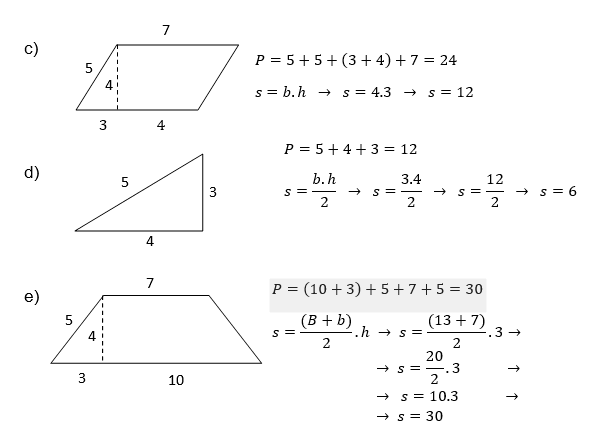


Uma resposta
Amei muito ,quero reproduzir a oficina em minha escola ,pois percebo a dificuldade dos alunos em abstrair esses conceitos matemáticos,e a dificuldade do professor em realizar atividades diversificadas com os alunos