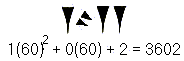ARTIGO ORIGINAL
BOMFIM, Jailto Francisco [1]
BOMFIM, Jailto Francisco. A Construção Do Número Na Educação Infantil. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 01, Vol. 01, pp. 47 – 76 . Janeiro de 2019. ISSN:2448-0959
RESUMO
O ensino do componente curricular de matemática promove uma melhor compreensão dos assuntos em estudo a serem abordados. A construção do número na educação infantil é um processo eficiente que favorece o desenvolvimento do raciocínio lógico, além de despertar a curiosidade dos educandos e professores, através de problemas e desafios. Neste contexto, o objetivo do aludido trabalho é analisar a importância da construção do número na educação infantil. Para desenvolvimento do mesmo foi utilizada a pesquisa qualitativa, descritiva, explicativa, exploratória e bibliográfica. Deste modo, pode-se concluir que, os pontos primordiais para o aprimoramento do ensino da matemática são: os conteúdos matemáticos a serem trabalhados, a prática pedagógica do docente e o relacionamento afetivo entre aluno e professor. A partir destes itens é possível oferecer um ensino da matemática de qualidade, no qual o processo de ensino-aprendizagem se desenvolva da melhor maneira.
Palavras-chave: Matemática, Número, Construção, Educação infantil.
INTRODUÇÃO
a Matemática está presente no cotidiano do homem, dificilmente se conseguiria passar um dia sem ter contato com pelo menos um conceito da área, mesmo sem que se perceba são realizadas atividades com conjuntos e formas geométricas, por exemplo, quase que naturalmente.
Apesar disso, paira no senso comum um conceito de poucos conseguirem aprender a disciplina em sala de aula, cultivando crenças e preconceitos de que a Matemática é para poucos.
Essas crenças e preconceitos cultivados parecem ser trazidos pelos alunos para a sala de aula desde as séries iniciais, o que lhe fecha para o processo de ensino e aprendizagem, podendo serem considerados como condicionantes desse processo.
De acordo com Oliveira, Negreiros e Neves (2015), o ser humano possui o sentido inato de número, sem precisar de qualquer intervenção direta uma criança pode ser capaz de contar e realizar operações matemáticas básicas, porém, quando esses conceitos são trazidos e aprofundados nas aulas, passam a ser considerados como complexos e de difícil aprendizagem.
Os autores justificam afirmando que o sentido inato de número está diretamente relacionado às necessidades de sobrevivência do homem, enquanto a Matemática enquanto disciplina é considerada como abstrata (OLIVEIRA, NEGREIROS; NEVES, 2015).
Assim, para que se possa aprimorar o processo de ensino e aprendizagem dos conteúdos matemáticas se faz importante considerar os fatores condicionantes desse processo, tanto internos quanto externos.
Muito embora tenham ocorrido avanços para o desenvolvimento da educação e a melhoria do ensino nas escolas por intermédio dos investimentos do Governo Federal, observa-se, ainda, a baixa qualidade do ensino, mesmo com a melhoria dos índices de aprovação e a contenção da evasão escolar, nos diversos níveis e graus de ensino, especialmente nas séries iniciais do ensino fundamental.
Tais resultados são muitas vezes refletidos por fatores internos da própria sala de aula, como aulas monótonas, conteúdos desinteressantes, ausência de leitura, despreparo dos professores e também a ausência de acompanhamento e controle, tanto da instituição escolar quanto da família, fatores estes que levam o educando a perder a motivação pelos estudos (GELATTI; MARQUEZAN, 2013).
A rotina escolar, a metodologia utilizada em sala de aula é fator primordial para despertar a atenção dos alunos. O aluno não se interessa mais pelo recurso da transmissão de conhecimento entre professor e aluno.
Aristóteles foi o ícone das representações poéticas e considerava que nada há na natureza tão significante que não valha a pena ser estudado, já que em todos os casos o verdadeiro objeto da pesquisa é a substância das coisas (OLIVEIRA, 2012). Assim, pode-se dizer que aprender envolve a vivência, a percepção e a reflexão, encaminhando-as para níveis cada vez mais elaborados.
Inúmeros são os estudos que estão sendo realizados na área da Matemática em busca de tornar seu processo de ensino e aprendizagem mais fácil, tendo em vista adotar recursos didáticos e ferramentas que proporcionem melhor transmissão, sistematização e assimilação dos conhecimentos.
Na pesquisa realizada por Souza (2010) foi verificado que o uso de recursos didáticos nas aulas de Matemática, principalmente, quando envolvem atividades lúdicas, tornam o processo de ensino e aprendizagem da disciplina mais atrativo e efetivo, contudo, também verificaram o pouco preparado dos professores para lidar com alunos de Ensino Fundamental.
De acordo com Cruz (2015), o ser humano pode aprender de diferentes maneiras, seja pela visão ao observar um comportamento, pela audição, ao ouvir um áudio, por exemplo, pelo olfato ao sentir o cheiro de algo, pelo paladar ao provar algo e pelo tato ao sentir, seja com mãos, pés ou qualquer parte da pele, podendo apresentar, ainda, um conhecimento cinestésico, ou seja, a partir do movimento do corpo em conjunto com a percepção de seus sentidos. O autor destaca, com base em especialistas da área, que uma aula com estímulos sensoriais pode se apresentar muito mais proveitosa.
Para a tradição aristotélica a ação humana orientada a um objeto final, sendo inerente a própria conduta ou animais, exige um projeto de elucidação teleológica para que se considerem as intenções situadas no futuro, onde qualquer circunstância envolvendo o movimento é fundamental o conceito do motor, levando a sua definição de que se a alma é o motor dos seres vivos, o movimento é a ação contínua do motor, onde só desaparece com o repouso do corpo (OLIVEIRA, 2012).
Nesse sentido o movimento se faz a partir da hora que se levanta da cama até o momento que volta pra ela. Nessa perspectiva, considera-se o movimento imprescindível à construção biológica, psicológica, social, cultural e evolutiva do homem, desde que é através de movimentos que o mesmo interage com o meio ambiente, expressando e compondo as múltiplas e complexas formas de vida do homem.
Paixão et al. (2015) destacam as potencialidades de explorar os sentidos dos alunos de séries iniciais no processo de ensino e aprendizagem. Em sua pesquisa, os autores levaram alunos de Ensino Fundamental para um horto, desenvolvendo atividades sensoriais com os alunos em contato com as plantas, percebendo em seus resultados que a percepção de um aluno não é a mesma do outro, além disso, perceberam maior atenção e interesse dos mesmos em relação ao conteúdo ministrado.
2. REFERENCIAL TEÓRICO
2.1 A HISTÓRIA DA MATEMÁTICA
A história da matemática vem desde os tempos da pré-história (hominídeos até 4.000 a.C) onde surgiu o cultivo de plantas e criação de animais, com agricultura e pastoreio. Nessa época os pastores de ovelhas precisavam controlar seus rebanhos para saber se não estava faltando ovelhas.
Os homens começaram a pensar: De que forma podemos controlar ovelhas? Através da matemática mesmo sem saber do que se tratava. De acordo com Eves (2004), ao soltar as ovelhas, o pastor separava uma pedra para cada animal que passava, e ao voltarem ele retirava do monte, a pedra de cada ovelha. Se não sobrassem pedras, significava que o rebanho estava completo.
Segundo Oliveira (2003), durante toda a história da humanidade pode-se perceber a evolução da matemática. No período do paleolítico o homem com o surgimento das necessidades do cotidiano, como administrar os alimentos que caçavam, teve de ter noções de matemática para se organizar.
No neolítico ocorre uma revolução agropastoril multiplicando a população cerca de 20 vezes em relação ao período paleolítico, dando início a uma série de inovações como o estoque de alimentos, o uso da roda, divisão de trabalho social, que requeriam cálculos para evitar desperdícios.
Com a chegada da Idade Antiga (4.000 a.C até 476 D.C) os babilônicos utilizavam sistema de numeração cuneiforme, ou seja, os números tinham forma de cunha.
De acordo com Oliveira (2003, p. 5):
Os babilônios empregaram sistemas decimais e frações sexagesimais, os mais usados nas tabelas para calcular peso e volumes. São conhecidos vários documentos que contém tábuas de multiplicação, de divisão, de quadrados e raízes quadradas, de cubos, de progressões aritméticas e geométricas e algumas tabelas particulares provavelmente empregadas em cálculos especiais. O sistema de frações sexagesimais foi transferido à Grécia e posteriormente para a Europa, sendo até hoje clara a sua influência, que se perpetuou através do hábito de medir o tempo e os ângulos.
No Egito as regras matemáticas eram utilizadas para resolver problemas aritméticos e algébricos enquanto os babilônicos e assírios utilizavam cálculos para verificar áreas de triângulos e quadriláteros, volumes de prismas e de pirâmides. (EVES, 2004).
Figura 1 – Sala de aula na Antiguidade.

Os babilônicos desenvolveram um sistema simbólico, eram pequenos objetos em argila com diferentes formas geométricas que utilizavam para fazer o registro de seus bens e comércio. Shen et. al. (1999, p. 21) elucida que “um cilindro de argila podia representar um animal, duas esferas dois bushel (medida de capacidade) de cereal.”
Oliveira (2003, p. 2) destaca que “(…) a criação dos símbolos foi um passo muito importante para o desenvolvimento da matemática. Na Pré–História, o homem juntava 3 bastões com 5 bastões para obter 8 bastões. Hoje sabemos representar está operação por meio de símbolos. 3+5=8”.
Por volta de 3.000 a.C os Sumérios se desenvolveram na Mesopotâmia por ter uma organização social e econômica complexa e juntamente o sistema numérico evolui para uma forma de sistema sexagesimal. Os registros escritos eram feitos em pequenas placas de argila, com estiletes de metal, osso ou marfim, que depois colocavam a secar ao sol. (OLIVEIRA, 2003).
De 2100 a.C a 2004 a.C os sumérios consolidaram o sistema jurídico, o calendário, o sistema meteorológico, além de construírem templos. Durante cerca de um século entre 2100 a.C. e 2004 a.C., os Sumérios viveram um período de grande prosperidade, tendo-se consolidado o sistema jurídico, revisto o calendário, o sistema meteorológico foi simplificado e foram construídos templos.
Porém por volta de 2300 a.C os Acadinos, povos de origem semita, ocuparam a Mesopotâmia, dominando os sumérios que desaparecem quase por completo. Com as invasões estrangeiras na Mesopotâmia o Império Acadino se extingue. A Babilônia passa a ser a capital da Mesopotâmia dominada pelo rei Hamurabi.
Os babilônicos usavam um traço vertical para representar as unidades e outro desenho para as dezenas (SMITH, 1992):
No sistema decimal, os números de 1 a 99 eram representados por agrupamentos destes símbolos (SMITH, 1992):
O símbolo para 100 era composto por traços:
Números superiores a 100, representados novamente por agrupamento. Assim, por exemplo, temos (SMITH, 1992):
O símbolo ![]() indica 10 vezes 100, isto é, 1000. Os babilônios chegaram a empregar um símbolo, formado por duas cunhas inclinadas, para representar a ausência de um grupo. (SMITH, 1992).
indica 10 vezes 100, isto é, 1000. Os babilônios chegaram a empregar um símbolo, formado por duas cunhas inclinadas, para representar a ausência de um grupo. (SMITH, 1992).
Como este símbolo não era de uso frequente, e ainda, nunca foi usado no fim de uma expressão, o sistema babilônio apresentava ambiguidades. Por exemplo.
Este poderia representar o número: ![]() (SMITH, 1992). Muitas tábuas em escrita cuneiforme se encontram em museus e sua denominação depende da coleção a que pertence.
(SMITH, 1992). Muitas tábuas em escrita cuneiforme se encontram em museus e sua denominação depende da coleção a que pertence.
A tábua aqui apresentadas encontra-se no Louvre e é do antigo período da Babilônia (OB) que vai de 2004 a 1595 a.C.
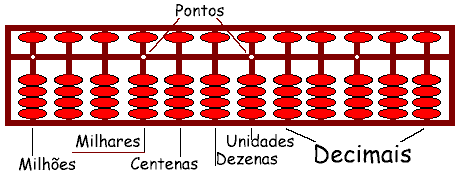
Um pouco mais a frente encontra-se o ábaco, este que foi um instrumento utilizado para facilitar os cálculos no período de 3500 a.C. Foi iniciado como uma tábua com sulcos e contadores, posteriormente evoluiu para uma estrutura com hastes metálicas com contas deslizantes.
Em sua forma geral, é uma moldura retangular com fileiras de arame, cada fileira representando uma classe decimal diferente, nas quais correm pequenas bolas. A figura ilustra o ábaco:
Figura 4 – Ábaco.
Com o passar do tempo o comércio egípcio passou a se desenvolver rapidamente e com isso era preciso efetuar cálculos com rapidez, onde a criação de símbolos foi um passo muito importante o desenvolvimento da matemática.
Por volta de 3600 a.C um faraó egípcio Aahmesu escreveu o Papiro Ahmes, um antigo manual de matemática com 80 problemas, todos resolvidos, sendo a maioria com assuntos do dia-a-dia com o preço de pão, armazenagem de grãos de trigo e alimentação de gado. (SMITH, 1992).
O sistema de numeração egípcio baseava-se em sete números-chave: 1 – 10 – 100 – 1000 – 10000 – 100000 – 1000000.
Todos os outros números eram escritos combinando os números-chave, da seguinte forma:
Figura 5– Combinação de números-chave

Com a civilização chinesa desenvolvida a partir do 3° milênio a.C surgem os primeiros numerais chineses inscritos sobre carapaças de tartaruga e ossos de animais utilizados para adivinhações.
Esses símbolos ainda são usados na China e no Japão, mas para cálculos são utilizados o sistema indo-arábico, conforme ilustra a figura a seguir:
Figura 7 – Símbolos utilizados na China.

A matemática utilizada pela civilização grega era de caráter dedutivo sem precisão de livros, e sim com utilização de demonstrações. Utilizavam ainda símbolos para representar os números.
No período da Idade Média (476 a 1453) a matemática grega se extingue na babilônia, fazendo com que os gregos criem o método axiomático-dedutivo que consiste em admitir como verdadeiras certas preposições (mais ou menos evidentes) e a partir delas, por meio de um encadeamento lógico, chegar a proposições mais gerais. (SHEN, et. al, 1999).
Posteriormente, tomando conhecimentos mais profundos, começando a ter descobertas que são utilizadas até os dias de hoje, segundo Oliveira (2004, p.02), (…) “um monge alemão, jordanus Nemorarius já começa a utilizar letras para significar um número qualquer, e ademais introduz os sinais de + (mais) e – (menos) sob a forma das letras p (plus = mais) e m (minus = menos).”
No ano 1202, o matemático italiano Leonardo de Pisa, cognominado de “Fibonacci cria uma obra intitulada “Leber abaci” na qual descreve a “arte de calcular” (Aritmética e Álgebra), apresentando soluções de equações do 1º, 2º e 3º graus.
Na Idade Moderna (1453 a 1789) a álgebra começa a ter seu aspecto formal e passa por franco desenvolvimento. No século XVII René Descartes descobre a Geometria Analítica que consiste em aplicações de métodos algébricos à geometria, enquanto Pierre Fermat desenvolve os números primos.
Por fim, na idade contemporânea (1789 até os tempos atuais) a geometria analítica e o cálculo impulsionam a matemática. A partir do século XIX a matemática começa a se ramificar em diversas disciplinas se tornando cada vez mais abstrata.
Hoje em dia a matemática é vista por muitos com muita dificuldade, muitas pessoas além de possuir dificuldades não procuram uma nova maneira de aprender.
2.2 MATEMÁTICA PARA DESENVOLVER OS CONCEITOS FORMAIS, PROCEDIMENTOS E SIMBOLISMOS DA MATEMÁTICA CONVENCIONAL – PROMOVENDO UMA ABORDAGEM METACOGNITIVA
O terceiro princípio do NRC está relacionado à importância do automonitoramento ou da autorregulação. Auto-regulação é apoiada pela capacidade das crianças de monitorar internamente e controlar estrategicamente as ações, tentar empreender uma tarefa ou resolver um problema. Segundo Vygotsky (1978), a auto-regulação é promovido através de interações com outros mais experientes que modelam e articulam suas estratégias bem-sucedidas. Por exemplo, ao aprender a completar um quebra-cabeças, a criança pode primeiro testemunhar (adultos ou colegas) usam estratégias como virar peças, experimentar peças, enfocando a forma, tamanho ou cor das peças.
O discurso que acompanha essas ações pode então ser internalizado pela criança fornecer estratégias de auto monitoramento ou autorregulação que mais tarde possam ser chamadas para resolver problemas. Uma importante capacidade de auto-regulação é a de gradualmente se tornar capaz de se falar através de tarefas semelhantes usando a fala externa, mas logo se movendo para a fala interna ou abstração (Berk & Winsler, 1995).
Uma das maneiras que eles fazem isso é estabelecer metas para si mesmos e verificando suas próprio progresso em direção a esses objetivos. O desenvolvimento da consciência metacognitiva, ou seja, a conscientização e controle da própria aprendizagem e pensar, ajuda as crianças a se tornarem aprendizes autorregulados. O reconhecimento de que crianças com idade 3–6 anos podem envolver-se em processos metacognitivos é relativamente recente (ver Coltman, 2006 para um revisão de literatura relevante).
Organizar o ambiente de sala de aula e as atividades de aprendizagem em formas particulares, com ênfase em estilos particulares de discurso e interações entre adultos e crianças e entre as próprias crianças é fundamental. Esses fatores podem fazer uma diferença significativa contribuição para ajudar as crianças a se tornarem aprendizes independentes e autorregulados (Whitebread, 2007). Pedir às crianças que expliquem seu pensamento contribui para o desenvolvimento da metacognição.
À medida que as crianças aprendem a se monitorar, elas desenvolvem e usam uma metalinguagem para descrever e expressar seu pensamento, ou seja, uma linguagem que inclui frases como “Eu sabia que eles iriam cair” ou “eu contei para ver quantos”. Em um estudo no Reino Unido (Coltman, 2006), as gravações em vídeo indiscutível evidência de que as crianças usaram uma ampla gama de meta-linguagem matemática como eles envolvida com atividades lúdicas planejadas destinadas a encorajar conversas matemáticas. Isso foi muitas vezes um surpresa para os educadores que trabalharam com eles. Exemplos incluídos ‘Vou preencher toda esta página com números ‘(conhecimento metacognitivo),’ Existem muitos hexágonos ‘(controle estratégico) e “Isso é divertido, não é isso” (motivação). As crianças também mostraram, através de suas falas, uma consciência de si e aos outros como aprendizes. Por exemplo, eles fizeram declarações sobre o que eram ou não foram capazes de fazer, ou demonstraram habilidades como contar para outras crianças envolvidas na peça.
A boa pedagogia, neste caso, planejou atividades lúdicas, facilita a aprendizagem matemática aprendizagem através de interações verbais que incentivam e apoiam o foco na consciência estratégica e pensamento metacognitivo.
Encorajar a autoavaliação é um aspecto importante do apoio à auto-regulação por crianças pequenas, uma vez que se concentra as crianças em pensar sobre processos cognitivos e ajuda-os, por exemplo, a identificar erros e monitorar o pensamento (ver Coltman, 2006 para uma revisão). Apoiando a autoavaliação das crianças pode ser feito usando perguntas apropriadas. Por exemplo, no contexto de construindo uma estrutura particular usando blocos, o questionamento pode incluir sondas como ‘O que fez você decidir fazer sua ponte usando esses blocos específicos? Existe algum outro caminho que você pode construí-lo? Em relação à seleção da estratégia mais eficiente para compartilhar uma bolsa de moedas para que todos tenham uma quantidade igual, as sondas podem incluir perguntas como: “Você tem certeza que todo mundo tem o mesmo valor? Como você sabe?
Reconhecendo erros decisões de autocorreção, verificação e justificação são alguns dos comportamentos que os educadores podem incentivar e desenvolver, a fim de apoiar as crianças a perceber suas capacidades em relação a Auto monitoramento. Esses comportamentos estão intimamente relacionados ao desenvolvimento do raciocínio adaptativo, um vertente de proficiência matemática.
Os exemplos acima indicam como o ambiente de aprendizagem pode ser estruturado para apoiar a auto regulação. Mas os educadores também podem fomentar uma abordagem metacognitiva apoiando o envolvimento das crianças com processos como a estimação e reconhecendo o papel que o senso numérico desempenha na aprendizagem das crianças para verificar a viabilidade de suas respostas a problemas baseados em números (Fuson et al., 2005).
2.3 PROCESSOS DIDÁTICOS E USO DE FERRAMENTAS MATEMÁTICAS
No que se refere ao ensino da matemática é preciso encontrar meios dinâmicos de integrar a pessoa jovem e adulta em uma sociedade tecnológica e científica. Sobre esta consideração, Almeida (1998, p. 21) disserta:
A função social da leitura e da escrita de nomes e números; os pontos de vista que eles têm sobre a escola e o que dela esperam; os mecanismos por eles utilizados para sobreviverem numa sociedade letrada (apanhar o ônibus, identificar preços dos produtos, dividir o salário no fim do mês, guardar o número de telefone, etc.); os conhecimentos e experiências que eles trazem.
Para a aprendizagem da pessoa jovem e adulta, o ensino da matemática deve envolver conteúdos direcionados para o processo de iniciação à formalização da disciplina. Ou seja, busca-se a construção de uma abordagem ampla que seja efetivada de forma gradativa.
Estima-se que desta forma o aluno ao final do processo seja capaz de resolver problemas envolvendo ideias das operações aritméticas, além de reconhecer figuras e formas geométricas presentes no seu cotidiano. (ALMEIDA, 1998).
Explica-se que existe uma preocupação acerca do uso do sistema monetário, leitura e produção de textos, pois há entre os alunos habilidades diversificadas em relação à escrita e à leitura.
Para resolver esta situação, costuma-se estimular trabalhos em pares de modo que alunos mais hábeis fiquem juntos com os que possuem alguma dificuldade.
Problemas matemáticos resolvidos de forma dinâmica pelos alunos em sala de aula promovem uma maior participação, onde os estudantes criam situações que representam a transação comercial apontada no problema resultam em discussões significativas sobre a matemática, ao utilizarem diferentes formas para expressarem o nível de conhecimento acerca do conteúdo. (LIMA; BARBOSA, 1999).
2.4 O ENSINO DA MATEMÁTICA ATRAVÉS DA RESOLUÇÃO DE PROBLEMAS
A resolução de problemas existe desde a antiguidade, mas somente há pouco tempo atrás, ela passou a ser prioriza, sendo inserida como uma ferramenta para o ensino da matemática, pois os conteúdos desta disciplina eram repassados de forma que os educandos apenas decoravam as fórmulas, sem que houvesse o entendimento. Porém, os Parâmetros Curriculares Nacionais para a Matemática exprimem claramente que os objetivos do ensino dessa disciplina são:
Resolver situações-problema, sabendo validar estratégias e resultados, desenvolvendo formas de raciocínio e processos, como dedução, indução, intuição, analogia, estimativa, e utilizando conceitos e procedimentos matemáticos, bem como instrumentos tecnológicos disponíveis (BRASIL, 1996, p. 51).
Deste modo, reitera-se que esta visa não apenas que os educandos decorem as fórmulas e técnicas existentes, mas que busquem através do raciocínio e da interpretação dos problemas, a resolução para os desafios que lhes são dispostos. Conforme Leite e Araújo (2010, p. 3):
Assim o conhecimento matemático ganha significado quando os alunos se defrontam com situações desafiadoras e trabalham para desenvolver estratégias de resolução. Daí a importância de tomar a resolução de problemas como ponto de partida da atividade matemática e não mais como uma série de exercícios para aferir se os alunos apreenderam determinado conteúdo ou não.
Sendo assim, a resolução de problemas é tida como uma metodologia de ensino, em que não se apresentam apenas cálculos, mas situações problemas que instigam o aluno a interpretá-los e explorar as possíveis formas para a sua resolução. De acordo com D’Ambrósio (1989, p. 3):
Essa proposta é mais atual e através dela o aluno pode construir os conceitos matemáticos através de situações que despertem sua curiosidade matemática, sendo que nesse processo o aluno envolve-se com o ‘fazer’ matemático no sentido de criar hipóteses e conjecturas e investigá-los a partir da situação problema proposta.
2.5 DIFICULDADES NA PRÁTICA DOCENTE DA MATEMÁTICA
É sabido que são várias as dificuldades encontradas no processo de ensino e aprendizagem de todos os componentes curriculares, em especial a matemática, por ser uma disciplina que o seu aproveitamento se dá de acordo com as práticas pedagógicas utilizadas pelos docentes.
Nos Parâmetros Curriculares Nacionais (1988) são encontradas sugestões para os educadores a cerca de como se trabalhar esta disciplina, os conteúdos a serem ministrados em cada nível da educação, além de outros itens que afetam e interferem neste processo.
Martins e Pereira (2002, p. 113) afirmam que:
O que tem ocorrido é uma política de desvalorização do professor, prevalecendo as concepções que o consideram como um mero técnico reprodutor de conhecimentos, um monitor de programas pré-elaborados, um profissional desqualificado , colocando-se à mostra a ameaça de extinção do professor na forma atual. A realidade retrata uma carreira quase inexistente, com condições de trabalho aviltadas, pouca retribuição financeira e discutível reconhecimento social.
Além destes, há a desvalorização dos docentes por parte dos educandos, o que faz com que muitas vezes estes sintam-se desestimulados a inovar suas práticas pedagógicas. Neste contexto Fontana (2005, p. 2) reitera que:
Tais dificuldades são: o retorno financeiro materializado pelo salário que muitas vezes é visto como representação concreta do desrespeito por parte do poder público e da sociedade para com o professor; o descrédito de sua capacidade profissional e a falta de incentivo para que ele dê continuidade a sua qualificação, juntamente com a intromissão do outro na sua prática pedagógica; e, mais especificamente no âmbito da sala de aula, o comportamento dos alunos que tanto pode incentivar como desestimular o interesse que o pedagogo tem em aprimorar suas técnicas de ensino.
Desta feita, a maior dificuldade em se trabalhar com a resolução de problemas se dá devido o fato de não haver um diálogo entre educador e educando de modo que, as situações expostas sejam interpretadas permitindo ao alunado a busca constante pelas respostas, permitindo assim o desenvolvimento do raciocínio lógico. Assim, percebe-se a necessidade da união entre as práticas pedagógicas utilizadas pelo educador, os conteúdos a serem trabalhados e o relacionamento entre educando e educador.
2.6 O PAPEL DO PROFESSOR
Os professores de matemática devem ver a matemática escolar como uma extensão das capacidades humanas pré-matemáticas, que se desenvolvem dentro do contexto social mais amplo. É somente a partir dessa perspectiva que a unidade do ensino da matemática, desde o primário até o nível secundário superior, pode ser estabelecida (FRAGOSO, 2001).
Também seria benéfico se os especialistas em matemática se considerassem parceiros no sistema matemático mais amplo descrito acima. Sem alguma mudança de consciência da parte deles, qualquer tentativa de mudar a imagem pública da matemática é muito difícil de ser bem-sucedida (CARVALHO, 2011).
Os professores devem participar do projeto das unidades de ensino, mas isso não pode ser desculpa para os educadores de matemática se retraírem dessa tarefa. Pelo contrário: O desenho de unidades de ensino substanciais, e particularmente de currículos substanciais, é uma tarefa muito difícil que deve ser realizada pelos especialistas na área (VYGOTSKY, 2006).
De maneira alguma pode ser deixado para os professores, embora os professores possam certamente fazer contribuições importantes dentro da estrutura de design fornecida por especialistas, particularmente quando eles são membros ou estão em contato direto com uma equipe de pesquisa. Além disso, a adaptação de unidades de ensino às condições de uma sala de aula especial requer um projeto de escala menor, que deve ser realizado pelos professores (DEMO, 2005).
No entanto, um professor pode ser comparado mais a um maestro do que a um compositor, ou talvez melhor a um diretor do que a um escritor de uma peça, com os segundos papéis dos dois paralelismos acima correspondentes ao pesquisador da educação matemática (MENDES, 2009).
Finalmente, é importante ressaltar a notável influência que as visões filosóficas existentes sobre a natureza da matemática têm no desenvolvimento da educação matemática, um fato que causa mudanças substanciais recentemente sucessivas no campo (MORAES; RENZ, 2005).
Isto significa que, independentemente das crenças e opções pessoais, os educadores matemáticos e os professores de matemática devem preparar as condições sob as quais a educação matemática receberá e assimilar com suavidade e criatividade as mudanças que avançam, obtendo o máximo lucro possível delas (OLIVEIRA, 2009).
2.7 USO DE MATERIAIS CONCRETOS NO PROCESSO DE ENSINO E APRENDIZAGEM DE TRIGONOMETRIA
Neste capítulo se tem a fundamentação teórica deste estudo, buscando o embasamento na literatura publicada sobre a exploração dos sentidos de alunos do ensino fundamental no processo de ensino e aprendizagem de Matemática. Inicialmente, discorre-se sobre o ensino de Trigonometria na atualidade, apresentando o que pesquisas atuais têm trazido sobre essa temática.
Em seguida, aborda-se o uso de materiais concretos no processo de Ensino e Aprendizagem de Geometria/Trigonometria e os resultados encontrados por diferentes autores em relação à facilitação desse processo.
2.2 O ENSINO DA MATEMÁTICA NA ATUALIDADE
O processo de ensino e aprendizagem de Matemática é comumente associada às dificuldades nos processo de ensino e aprendizagem, assim, buscar meios de facilitar esse processo, tornando a aprendizagem significativa é fundamental.
Chaves (2013) atribui as dificuldades no processo de ensino e aprendizagem em matemática a questões históricas, mais especificamente à reforma do ensino de Matemática ocorrido em 1950, apesar da busca ser de um maior rigor na apresentação dos conteúdos, os reformistas não conseguiram aplicar tal rigor em alguns fatos geométricos, o que fez com que fosse necessária a redução do conteúdo nas escolas, retirando a satisfatoriedade da Geometria.
Para o autor, as dificuldades persistem pelas aulas serem permeadas por conceitos e figuras abstratas, que precisam ser imaginadas pelos alunos, tornando o entendimento complexo.
Nesse mesmo sentido, Dionizio e Brandt (2011, p. 2) afirmam que a dificuldade no ensino e aprendizagem de Geometria: “pode ser devida a diversos fatores, dentre eles a dificuldade que os estudantes têm de conceituar os objetos matemáticos, que se apresentam de forma muito abstrata”.
Dessa forma, os autores concordam que as dificuldades do ensino de Geometria estão voltadas para a relação entre o conceito e as figuras geométricas, já que, na maioria das vezes, os alunos precisam contar com abstração.
É comum ouvir no cotidiano das aulas de Matemática que os conteúdos de Geometria, principalmente, Trigonometria, não fazem parte do dia a dia dos alunos, dificultando a contextualização e, consequentemente, a aprendizagem.
Todavia, autores como Porto e Novello (2010) afirmam que os conteúdos podem sim ser associados ás situações cotidianas, em suas palavras, o estudo da trigonometria é essencial para engenheiros, físicos, informáticos e para muitos cientistas, no entanto o desenvolvimento no ensino médio também é fundamental, pois ela está presente em situações cotidianas e de fácil entendimento, como no cálculo da altura de um prédio através de sua sombra e a distância a ser percorrida em uma pista circular de atletismo. A trigonometria permite, ainda, calcular medidas mais abrangentes, como: largura de rios e montanhas, medida do raio da Terra, distância entre a Terra e a Lua, entre outras (PORTO; NOVELLO, 2010, p. 04).
Desse modo, as dificuldades no processo de ensino e aprendizagem de Trigonometria precisam ser superadas, tendo em vista a sua importância no cotidiano dos alunos, sendo necesário buscar meios de reduzir essas dificuldades.
Com isso, se faz importante destacar o papel do professor como facilitador desse processo, de acordo com Oliveira e Velasco (2007), as aulas de Geometria requerem maior sensibilidade do professor, visto que ele precisa trabalhar a união das formas visuais com os conceitos e propriedades.
O ensino/aprendizagem no ensino médio, a partir da Lei de
Diretrizes e Bases da Educação, nº 9.394 de 1996, definiu uma nova forma de transmitir os conteúdos e educar os alunos nesse período do colegial, deixando de ser apenas um simples estágio introdutório.
Assim, percebe-se que a Lei de Diretrizes e Bases (LDB) não se limita apenas à transmissão de conteúdo para os alunos, mas sim, a formação do cidadão, o professor como um educador, que mais do que ensinar as teorias em sala de aula deve visar o aluno como um todo, como um cidadão de direitos em formação.
Destaca-se aqui o §1 citado da LDB, acredita-se ser fundamental que o professor se utilize de metodologias capazes de chamar o aluno para o aprendizado, levantar seu interesse para o conteúdo que esta sendo tratado, para a disciplina em questão.
Nesse contexto, verifica-se que o ensino de matemática na atualidade tem sido permeado por dificuldades, sendo buscados constantemente meios para facilitar esse processo, encontrando-se no uso de materiais concretos um importante caminho para tanto.
2.8 O ENSINO DA MATEMÁTICA E O USO DE MATERIAL CONCRETO
O uso de material concreto para o processo de ensino e aprendizagem tem sido apresentado como o caminho mais adequado para redução das dificuldades, podendo-se enquadrar esse uso na teoria da aprendizagem significativa de David Ausubel, que se dar em duas fases: descoberta e recepção.
Na descoberta o aluno deve descobrir algum princípio, relação, lei, como pode acontecer na solução de um problema, mas que acontece de forma isolada, sozinho.
Na recepção o aluno já recebe todas as informações e consiste basicamente na tarefa do aluno em trabalhar, ou seja, estudar o material fornecido, para que possa daí relacioná-lo a ideias importantes disponíveis em sua estrutura cognitiva. (AUSUBEL, 1976).
De acordo com Vasconcelos (2015), o processo de ensino e aprendizagem de Matemática é adquirido mais rapidamente quando o indvíduo tem contato com objetos tangíveis e acessíveis diretamente aos sentidos.
O autor elucida que as experiências concretas são mais eficazes no processo de ensino e aprendizagem, desde que esteja relacionada a alguma estrutura conceitual relevante.
Diferentes são os recursos didáticos que podem ser utilizados nas aulas de Matemática com o intuito de estimular o processo de ensino e aprendizagem, devendo-se considerar para a escolha o conteúdo matemático que se deseja ensinar para que se possa adequar à aula.
Dentre os recursos didáticos que podem ser utilizados cita-se o Teodolito, que, de acordo com Silva et al. (2013), se configura como um instrumento utilizado para medição de ângulos horizontais e verticais, utilizado em Engenharia Geológica.
Trata-se de um aparelho composto por um par de círculos graduados posicionados em ângulos retos entre si.
O uso do Teodolito nas aulas de Matemática é geralmente feito para ensino do conteúdo de Trigonometria.
Na pesquisa realizada por Silva et al. (2013) foi verificado que o uso de material contribui significativamente para o aprendizado dos alunos sobe relações trigonométricas, observando, também, maior interação entre os alunos.
Importante mencionar com base em Lorenzato (2006) que o uso de materiais concretos em sala de aula somente possibilitará uma aprendizagem significativa do aluno se estiver devidamente associado a um conteúdo, favorecendo a relação entre teoria e prática.
Em suas palavras, ele alerta: […] mais importante do que ter acesso aos materiais é saber utiliza-los corretamente […] Afinal, o material deve estar, sempre que necessário presente no estudo didático-metodológico de cada assunto do programa de metodologia ou didática do ensino de matemática, pois conteúdo e seu ensino devem ser planejados e ensinados de modo simultâneo e integrado (LORENZATO, 2006, p. 10).
Dessa forma, não bastaria chegar com o uso do Teodolito em sala de aula, por exemplo, é necessário que antes disso tenha passado o conteúdo para o aluno e, durante o uso do referido material, relembre aos alunos constantemente o conteúdo teórico.
Outro recurso didático que pode ser destacado é o Multiplano. De acordo com Machado (2004), trata-se de um recurso didático que auxilia no processo de ensino e aprendizagem de alunos videntes e com deficiência visual, promovendo a noção de função e construção de gráficos.
Trata-se, basicamente, de uma placa perfurada, onde são encaixados pinos, que apresentam identificação numérica tanto em braile quanto em algarismos indo-arábicos.
Os pontos são interligados para a onstrução dos gráficos.
Por fim, destaca-se o livro didático, que se configura como um dos recursos mais utilizados no processo de ensino e aprendizagem da Educação BásicaB no Brasil, sendo utilizado para estimular os sentidos do tato e da visão.
Considera-se os livros como materiais didáticos impressos, que de acordo com Fernandes (2009), possui como suporte de comunicação o papel, tendo como objetivo facilitar o processo de ensino-aprendizagem.
3. METODOLOGIA
Neste tópico apresentamos as informações da metodologia utilizada para a execução da pesquisa. Segundo Minayo (2011, p. 16), a compreensão da metodologia de uma pesquisa se baseia no “[…] caminho do pensamento e na prática exercida na abordagem da realidade”. Sendo assim, este capítulo aborda todo o processo de investigação para elaboração do trabalho.
3.1 CARACTERIZAÇÃO DA PESQUISA
Trata-se de uma pesquisa de natureza básica, com abordagem qualitativa. Gil (2010, p. 42) assevera que a pesquisa básica “procura desenvolver os conhecimentos científicos sem a preocupação direta com suas aplicações e consequências práticas”. E como tem a finalidade de adquirir conhecimentos ainda não vistos, contribui efetivamente para o avanço da ciência. Segundo Marconi e Lakatos (2010), a abordagem qualitativa se trata de uma pesquisa que tem como premissa, analisar e interpretar aspectos mais profundos, descrevendo a complexidade do comportamento humano e ainda fornecendo análises mais detalhadas sobre as investigações, atitudes e tendências de comportamento. Ao abordarmos a execução da pesquisa social, utilizando a metodologia qualitativa, compreendemos a extensão da discussão a respeito do objeto proposto para o estudo, levando em consideração que os estudos qualitativos possibilitam iluminar o dinamismo interno das situações, geralmente inacessível ao observador externo.
Quanto aos objetivos esta pesquisa, enquadrou-se como pesquisa descritiva e exploratória. Conforme Triviños (1987, p.110) a “[…] pesquisa descritiva exige do investigador uma série de informações sobre o que deseja pesquisar. Esse tipo de estudo pretende descrever os fatos e fenômenos de determinada realidade”. A exploratória, de acordo com Gil (2008), visa propiciar maior familiaridade com o problema (explicitá-lo). Pode envolver levantamento bibliográfico, entrevistas com pessoas experientes no problema pesquisado. Geralmente, assume a forma de pesquisa bibliográfica e estudo de caso.
Referente aos procedimentos técnicos, esta pesquisa fez uso da pesquisa bibliográfica. Na pesquisa bibliográfica os dados são coletados junto a materiais de autores que falaram sobre a temática. Fonseca distingue esses dois termos afirmando que: “a pesquisa bibliográfica utiliza fontes constituídas por material já elaborado, constituído basicamente por livros e artigos científicos localizados em bibliotecas”. (FONSECA, 2002, p. 32).
Para Gil (1994, p. 71), “[…] a principal vantagem da pesquisa bibliográfica reside no fato de permitir ao investigador a cobertura de uma gama de fenômenos muito mais ampla do que aquela que poderia pesquisar diretamente”. A pesquisa bibliográfica foi realizada durante todo o processo de investigação, porque, ao longo desse período, foi elaborado todo o referencial teórico que deu sustentação aos objetivos da pesquisa.
CONSIDERAÇÕES FINAIS
A capacidade de compreender matemática e julgamento matemático é crucial para o futuro dos alunos. Na sociedade hoje complexa, aprender e compreender matemática e ciências naturais tornou-se necessário para o pleno desenvolvimento de todos.
De acordo com os dados analisados neste estudo foi possível observar que o ensino de matemática destina-se a promover a aprendizagem da matemática. Mas, enquanto as teorias fornecem lentes para analisar a aprendizagem, a posição do ensino de matemática permanece teoricamente anômala e subdesenvolvida. Pode-se observar um dos problemas em mentir nas relações entre a aprendizagem, o ensino e a prática do ensino.
Os professores de matemática devem ver a matemática escolar como uma extensão das capacidades humanas pré-matemáticas, que se desenvolvem dentro do contexto social mais amplo. É somente a partir dessa perspectiva que a unidade do ensino da matemática, desde o primário até o nível secundário superior, pode ser estabelecida.
Com isso, é importante destacar que o formato das operações básicas é adequado para as crianças desenvolverem competência matemática, porque elas exigem uma maneira de calcular sem flexibilidade e sem controle das etapas intermediárias nos cálculos. Nesse caso, os alunos não têm toda a ideia do senso numérico.
Assim este artigo conclui que a matemática pode parecer algo complexo inicialmente, muitos alunos têm dificuldade no ensino e aprendizagem de matemática e é neste momento que o professor desempenha um papel importante. o professor deve estar sempre atualizado para buscar a melhor forma de ensinar matemática. Muitas vezes o conteúdo é maçante tornando a aprendizagem ainda mais dificultosa.
REFERÊNCIAS
ABREU, A. C. O uso de softwares na aprendizagem de Matemática. Especialização em Informática na Educação, Universidade Federal do Mato Grosso do Sul. Orientador: Prof. MSc. Ivailton M. Santos, 2011.
BRASIL. Lei de Diretrizes e Bases da Educação Nacional, nº 9394/96. Brasília: MEC, 1996.
BRASIL. Lei de Diretrizes e Bases da Educação Nacional. Lei número 9394, 20 de dezembro de 1996.
CAMACHO, Gabriela Silveira; CUSTÓDIO, Luciana Nascimento; DE OLIVEIRA, Renata Carmo. “Roda das Sensações”: uma atividade interativa com plantas no museu. Em Extensão, v. 12, n. 1, 2013.
CERVO, A. L. BERVIAN, P. A. Metodologia científica. 5.ed. São Paulo: Prentice Hall, 2002.
CHIZZOTTI, Antonio. Pesquisa qualitativa em ciências humanas e sociais. Petrópolis, RJ: Vozes, 2006.
CRUZ, Bruna Souza. Para aprender melhor é preciso usar todos os sentidos, dizem especialistas… Educação UOL, 2015. Disponível em: https://educacao.uol.com.br/noticias/2015/07/02/para-aprender-melhor-e-preciso-usar-todos-os-sentidos-dizem-especialistas.htm Acesso em: 10 out. 2018.
Curriculares Nacionais: Matemática – Brasília: MEC / SEF, 1998.
DIONIZIO, F.; BRANDT, C.F. Análise das dificuldades apresentadas pelos alunos do Ensino Médio em trigonometria. In: X Congresso Nacional De Educação Educere E I Seminário Internacional De Representações sociais, Subjetividade E Educação-Sirsse, 10. ; 2011, Curitiba. Anais… Curitiba: Champagnat, 2011.
EVES, H. Introdução à História da Matemática, 3ª Edição, Editora Unicamp, 2002.
FERNANDES, Domingos. Avaliar para aprender: fundamentos, práticas e políticas. São Paulo: Editora UNESP, 2009.
FOGAÇA, Jennifer. Pesquisa-ação. Brasil Escola, 2010. Disponível em: http://educador.brasilescola.uol.com.br/trabalho-docente/pesquisa-acao.htm Acesso em: 10 out. 2018.
FREITAS, H., CUNHA Jr. M.V.M. e MOSCAROLA, J. Aplicação de sistema de software para auxílio na análise de conteúdo. São Paulo: RAUSP, v. 32, nº 3, Jul/Set. 1997, pp. 97-109.
GELATTI, Leticia Degrandi. Contribuições da gestão escolar na qualidade da educação. Santa Maria: Universidade Federal de Santa Maria: 2013.
GRANJA, Carlos Eduardo, PASTORE, José Luiz. Atividades Experimentais de Matemática nos anos finais do Ensino Fundamental. São Paulo: Editora SM (somos mestres), 2012.
JELINEK, Karin Ritter. Jogos nas aulas de matemática: brincadeira ou aprendizagem? o que pensam os professores?. 2005. Dissertação de Mestrado. Pontifícia Uni versidade Católica do Rio Grande do Sul.
KAMII, C.; DECLARK, G. Reinventando a aritmética: implicações da teoria de Piaget. 6a ed. Campinas, SP: Papirus, 1992.
LORENZATO, S. Laboratório de ensino de matemática e materiais didáticos manipuláveis. In: LORENZATO, Sérgio. Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 3-38.
LUCCHESI, Eduardo Melloni; SEIDEL, Susana. Uso de software no ensino-
aprendizagem de Matemática. RENOTE. Revista Novas Tecnologias na Educação, v. 2, p. 1, 2004.
MACHADO, V.C. Aprendendo Matemática Através das Mãos: uma proposta para o uso do Multiplano no ensino dos educandos cegos. Criciúma, SC, 2004.
MOTTA, Ivany Aparecida Rodrigues da. Projeto Teia do Saber. Metodologias do Ensino de Matemática. SP. 2006.
MUELER, Liliane Carine. Uso de recursos computacionais nas aulas de Matemática. Dissertação (Mestrado). Centro Universitário UNIVATES. 2013.
OLIVEIRA, Liliane Lelis; VELASCO, Angela Dias. O ensino de geometria nas escolas de nível médio da rede pública da cidade de Guaratinguetá. Paraná: Gráphica, 2007.
OLIVEIRA, Maria Fatima; NEGREIROS, João Garrott Marques; NEVES, Ana Cristina. Condicionantes da aprendizagem da matemática: uma revisão sistêmica da literatura. Educação e Pesquisa, v. 41, n. 4, p. 1023-1037, 2015.
OLIVEIRA, Paulo Eduardo de. Filosofia e educação: aproximações e convergências. 1. ed. Curitiba: Círculo de Estudos Bandeirantes, 2012.
PACHECO, J.; BARROS, J. O uso de softwares educativos no ensino de matemática. Revista de Estudos Culturais e da Contemporaneidade, Garanhus, n. 8, p. 5-13, 2013.
PAIXÃO, Fátima et al. Aprender para além da escola… explorar os cinco sentidos num contexto de educação não formal com alunos do 1. º ciclo do ensino básico. Interacções, v. 11, p. 528-539, 2015.
PORTO, R. T.; NOVELLO, T. P. Estágio Supervisionado: Uma proposta metodológica para o ensino de Trigonometria. In: EREMATSUL, XVI EDIÇÃO. 2010.
Shen, Kangshen,; Crossley, John e Lun, Anthony. História da Matemática. The Nine Chapters on the Mathematical Art, Oxford University Press, 1999.
SILVA, G.A.O.; et.al. O uso do teodolito como uma ferramenta no ensino da trigonometria. VI Congresso Internacional de Ensino da Matemática. Ulbra- Canoas- Rio Grande do Sul 2013.
SILVA, Marcílio Farias; CORTEZ, Rita de Cássia; DE OLIVEIRA, Viviane Barbosa. Software Educativo como auxílio na aprendizagem da matemática: uma experiência utilizando as quatro operações com alunos do 4º Ano do Ensino Fundamental I. Educação, Cultura e Comunicação, v. 4, n. 7, 2013.
Smith, D. E.; C. History of Mathematics, vol II, Dover Publications, Inc. New York. Wells, David. The Penguin Book of Curious and Interesting Puzzles. Peguin Books, 1992.
SOUZA, J. Coleção novo olhar–matemática. São Paulo: Editora FTD, 2010.
SOUZA, Jonimar Souza et al.. A Utilização de Recursos Didáticos no Ensino da Matemática: Uma Experiência Vivenciada nas Séries Iniciais. Olhar Científico, v. 1, n. 2, p. 340-350, 2011.
VASCONCELOS, Cláudia Cristina. Ensino-Aprendizagem da Matemática: Velhos
problemas, Novos desafios. Disponível em: http://www.ipv.pt/millenium/20_ect6.htm. Acesso: out/ 2018.
[1] Pós-Graduado em Educação Matemática, Graduado em Ciências Matemática e Magistério.
Enviado: Julho, 2018
Aprovado: Janeiro, 2019