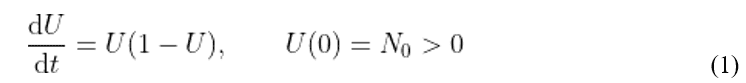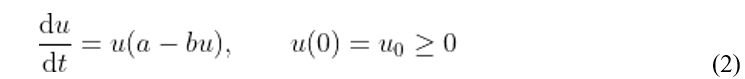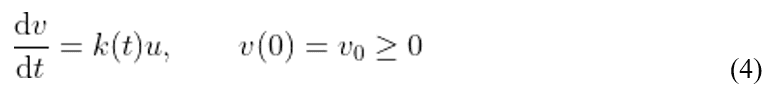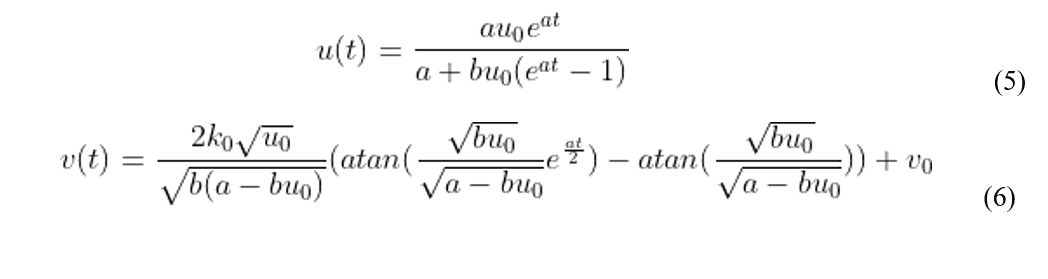ARTIGO ORIGINAL
COSTA, Esdras Jonathan Honorato [1]
COSTA, Esdras Jonathan Honorato. Modelo matemático para previsão da curva epidemiológica de COVID-19 no Brasil. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 05, Vol. 02, pp. 05-16. Maio de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/curva-epidemiologica, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/curva-epidemiologica
RESUMO
A COVID-19 surgiu no final de 2019 e em poucos meses já estava sem controle em vários países do mundo. Essa alta velocidade de contaminação pelo vírus levou o sistema de saúde de vários países ao colapso. Para possibilitar condições de tratamento a todos os infectados, a principal medida indicada pela OMS foi o isolamento social. O objetivo dessa medida era reduzir a curva epidemiológica. O conhecimento da curva epidemiológica baseada em condições do Brasil é importante para prever os momentos críticos e estudar como evitar tais momentos. Visando à importância dessa curva, o presente trabalho apresenta um modelo parametrizado para as condições nacionais, que prever uma curva epidemiológica da COVID-19 no Brasil. Através desta curva, pode-se determinar os períodos críticos, a quantidade de contaminados e o período de encerramento do surto.
Palavras-chave: Modelo matemático, COVID-19, infectados, curva epidemiológica.
INTRODUÇÃO
No final de 2019, na província de Wuhan (China), foi diagnosticado o primeiro caso de COVID-19, doença causada pelo vírus Sars-CoV-2. Devido à rapidez de contágio e à resistência do vírus, a COVID-19 rapidamente tomou proporções mundiais, sendo que, no início de 2020, a OMS declarou a doença como pandemia (Who, 2020).
A grande velocidade de infecção pela COVID-19 tem mudado os hábitos de convívio social em vários lugares no mundo. Sistemas de saúde estão entrando em colapso. A solução indicada pela OMS e realizada por vários países é o isolamento social. Para Hellewell et al. (2020), Watkins (2020) e Farias (2020), o isolamento social é uma das medidas mais eficazes contra o COVID-19.
O isolamento não impede o crescimento dos infectados, ele reduz que inúmeras pessoas sejam infectadas simultaneamente e, evita-se assim, o colapso no sistema de saúde. Segundo Aveni (2020), as fraquezas do nosso sistema de saúde foram expostas devido à COVID-19. Entretanto, a situação pode ter um agravamento se a curva epidemiológica não for reduzida.
Para a previsão dessa curva, modelos matemáticos foram desenvolvidos. Pode-se citar, para a previsão de COVID-19 no Brasil, o modelo dos autores Falavina et al. (2020) que usaram dados da COVID-19 na Itália e elaboraram três cenários: otimista, base e pessimista. Dias e Araújo (2020) desenvolveram um modelo matemático para previsão dos casos de COVID-19 no Brasil baseado numa metodologia denominada SIDR (Susceptible-Infected-DeceasedRemoved). Cherniha e Davydovych (2020) desenvolveram um modelo com base nos casos da China. Tal modelo apresentou boa concordância com os dados reais.
Nessa perspectiva, o presente trabalho propõe um modelo matemático para previsão da curva epidemiológica de COVID-19 no Brasil. Essa curva pode ser utilizada como base para prever ações efetivas para o enfrentamento do surto no Brasil.
MODELO MATEMÁTICO
O modelo matemático desenvolvido no presente trabalho é baseado em Cherniha e Davydovych (2020). Eles usaram um modelo clássico das ciências biológica para avaliar a evolução temporal de casos confirmados. Esse modelo diferencial foi desenvolvido por Verhulst (1838, apud Cherniha e Davydovych, 2020) sendo largamente conhecido como modelo logístico. Tal modelo, com variáveis adimensionais, possui a seguinte fórmula:
Para atender a equação (1), utilizou-se uma função suave u (t), que apresenta o número total de casos de COVID-19 identificados até dia t. Assumiu-se que t = 0 representa a data em que foi identificado o primeiro caso(u0). Obviamente, a função u(t) não é decrescente, visto que ela representa o número de casos acumulados até o dia t. Então, com essas considerações obtemos:
em que a e b são constantes positivas. A constante a representa o crescimento da infecção e o contato entre as pessoas infectadas com outras saudáveis. No modelo logístico essa constante deve ser menor que 1. A constante b indica os esforços governamentais para evitar contatos entre pessoas infectadas e saudáveis. De acordo com Cherniha e Davydovych (2020), o coeficiente b deve aumentar com o crescimento de u (t) a fim de reduzir o aumento de infectados. Ou seja, para poder ter o controle epidemiológico, faz-se necessário medidas mais fortes nos momentos mais crítico do surto, caso contrário, o controle sobre o processo epidêmico terá pouca eficácia.
As pessoas infectadas pela COVID-19 possuem apenas duas possibilidades: recuperação ou óbito. Considera-se as pessoas infectadas que se recuperam de w e os óbitos de v. Sendo assim, a soma dessas duas funções fornece a quantidade de infectados até o dia t:
De acordo Cherniha e Davydovych (2020), o modelo logístico possui uma equação típica para a evolução no tempo da função v:
É óbvio que há também uma equação semelhante para w, entretanto o modelo terá interesse pelos infectados e os óbitos. A constante v0 é o número de mortes em t = 0. Vale ressaltar que, de acordo com Cherniha e Davydovych (2020), o coeficiente k(t)> 0 e reflete a eficácia do sistema de saúde do país em questão e que, do ponto de vista matemático, este coeficiente deve ter o comportamento assintótico k(t) → 0, se t → ∞. Utiliza-se a forma útil que é k(t) = k0exp (-αt), α > 0.
A solução das derivadas apresentada por Cherniha e Davydovych (2020) é apresentada a seguir.
DETERMINAÇÃO DAS CONSTANTES
Neste tópico determina-se todos os parâmetros presentes nas equações (5) e (6) usando os dados para o surto de COVID-19 no Brasil. Tais dados foram obtidos no site oficial do Ministério da Saúde (Brasil, 2020).
O primeiro caso de COVID-19 no Brasil foi oficialmente registrado em 26 de fevereiro de 2020. Enquanto, o primeiro óbito ocorreu em 17 de março de 2020. Sendo assim, para que u0 e v0 sejam ambas maiores que zero e, por questões matemáticas, diferente de 1, definimos que a data que representaria o t = 0, no modelo matemático proposto, é 18 de março de 2020. Com isso, obtemos imediatamente u0 = 428 infectados e v0 = 4 óbitos.
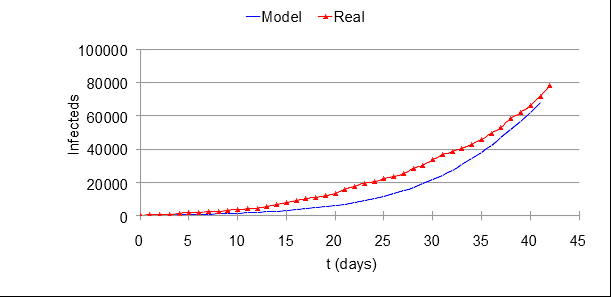
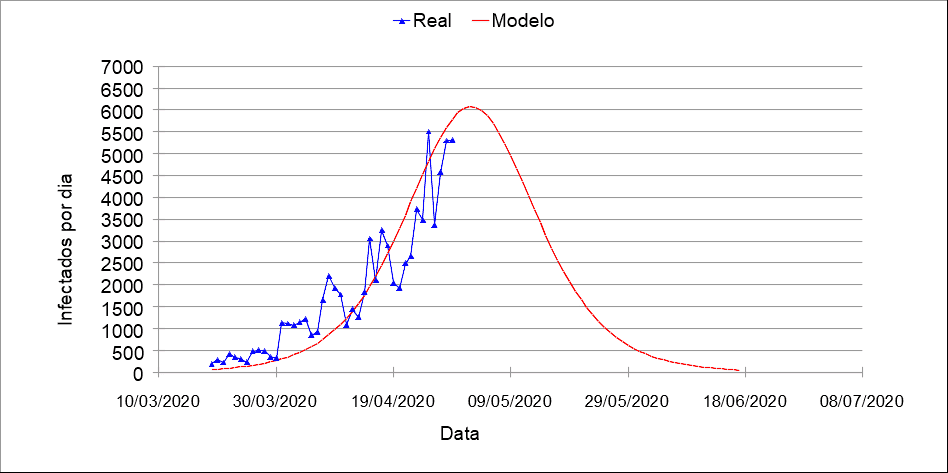
Para determinar as constantes a e b, se faz necessário um ajuste com os dados reais de casos confirmados no Brasil, desde t = 0 até o dia de projeção do presente modelo (29 de abril de 2020). A Figura 1 apresenta o melhor ajuste, que ocorreu quando a = 0,135 e b = 7,5E-7.
Figura 1 – Comparação entre os dados reais e do modelo ajustado com os parâmetros a = 0,135 e b = 7,5E-7.
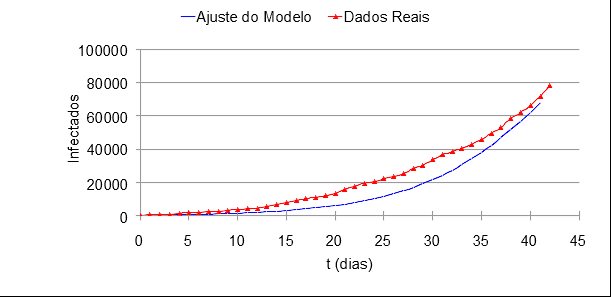
O modelo aparenta ter resposta inferior aos dados, porém ele possui a mesma tendência de crescimento dos casos que ocorreram nessa última semana. Então a e b então ajustadas para o modelo.
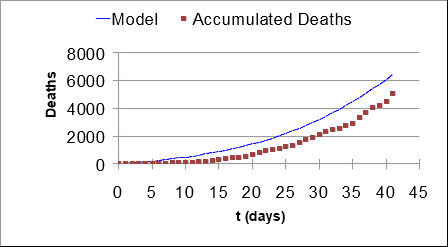
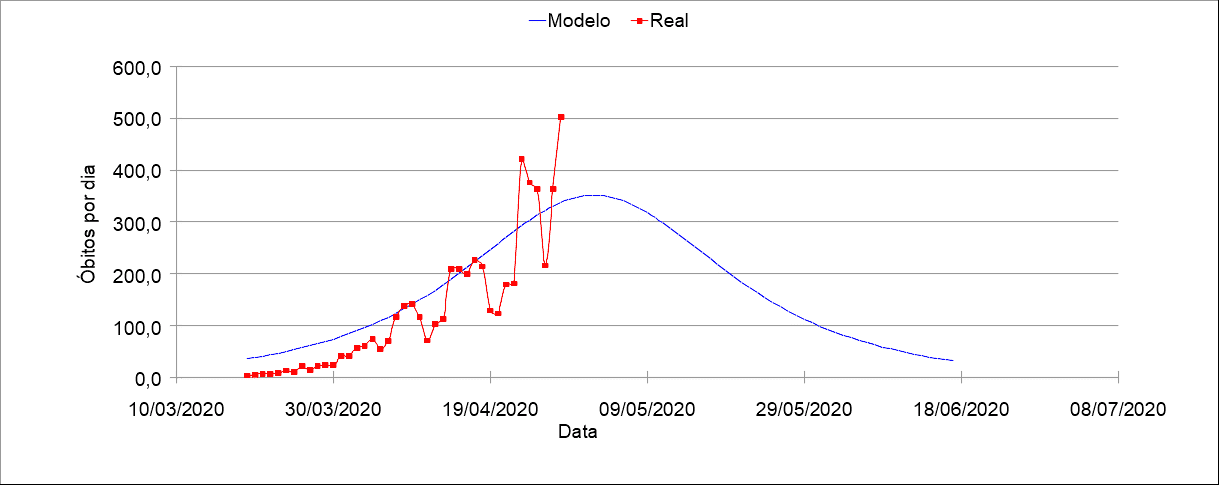
Na equação de previsão dos óbitos, existe o coeficiente k0. Para determinação desse coeficiente, faz-se necessário o ajuste da curva v(t) com os dados obtidos até o presente momento. A Figura 2 apresenta o melhor ajuste da curva que ocorre quando k0 = 0,07.
Figura 2 – Comparação entre os dados reais e do modelo ajustado com os parâmetros k0 = 0,07.
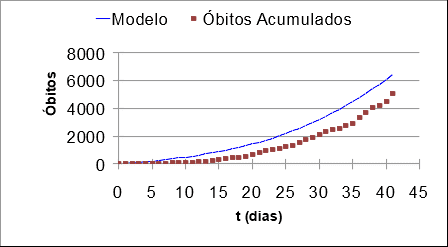
Diferente da curva de infectados, o modelo aparenta ter resposta superior aos dados de óbitos. Porém, como possui a mesma tendência de crescimento dos casos confirmados tem-se que k0 = 0,07 pode ser utilizado no modelo.
RESULTADOS E DISCUSSÃO
Neste artigo é apresentado um modelo matemático proposto para a descrição quantitativa do surto de COVID-19 no Brasil. O modelo é baseado no trabalho de Cherniha e Davydovych (2020). Embora ele seja relativamente simples, apresentou ótimos resultados para o caso da China. Isso justifica por que o utilizamos aqui para prever casos de COVID-19 no Brasil. Entretanto, as condições epidemiológicas no Brasil são diferentes daquelas que ocorreram na China. Então, para melhor ajuste, aplicou-se ao modelo as condições brasileiras e realizamos os ajustes das constantes através dos dados fornecidos pelo Ministério da Saúde.
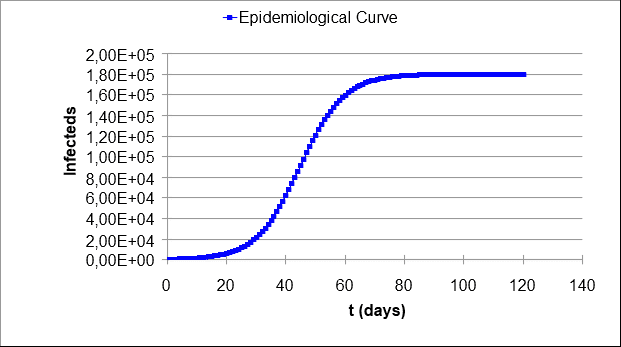
Usando-se as constantes determinadas no tópico anterior, pode-se determinar a curva epidemiológica do surto de COVID-19 no Brasil. O resultado é apresentado na Figura 3. Através dessa curva pode-se analisar a quantidade prevista de casos: 180 mil infectados pela COVID-19. A curva também apresenta que o fim do surto iniciará em junho de 2020. Luo (2020) em seu modelo prever 97% do surto no Brasil em 01 de junho de 2020.
Figura 3 – Previsão dos casos de COVID-19 no Brasil através do modelo logístico.
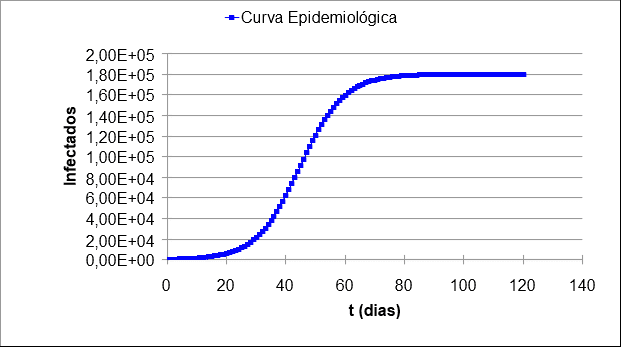
A maneira mais adequada para evitar que essa quantidade alarmante aconteça é reduzir a infecção (reduzindo assim o valor do parâmetro a da equação (5)) e aumentar o combate à doença (parâmetro b da equação (5)). De acordo com Hellewell et al. (2020), Watkins (2020) e Farias (2020), a melhor forma de reduzir a infecção é o isolamento. Esses autores explicam que se não houver um controle no surto os resultados serão catastróficos.
Outro ponto importante é a capacidade do sistema de saúde durante os picos do surto de COVID-19 no Brasil. Segundo Aveni (2020), as fraquezas do sistema nacional de saúde foram expostas devido à COVID-19. Entretanto, a situação pode se agravar durante o pico de casos. Garcia e Duarte (2020) citam a importância de reduzir contatos entre pessoas para reduzir o pico de casos de COVID-19.
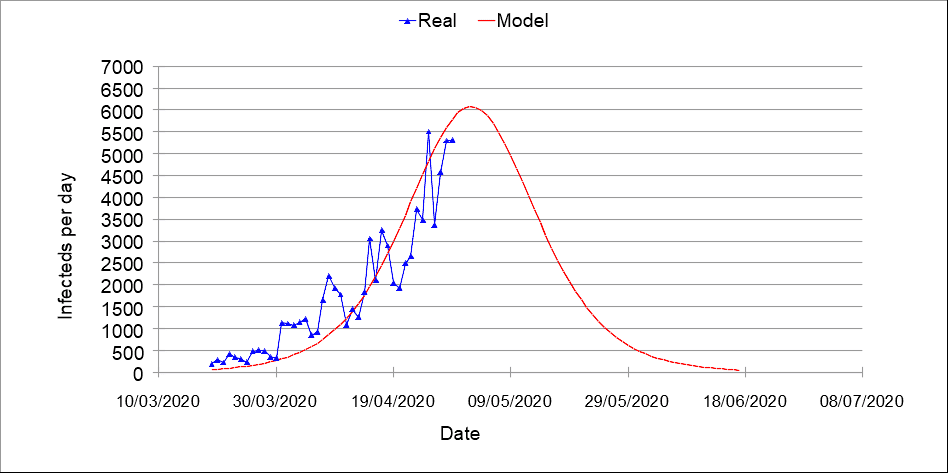
Aplicou-se o modelo proposto para prever o pico de casos de infectados no país. O resultado pode ser visualizado na Figura 4. De acordo com o modelo o momento crítico ocorrerá em meados de maio de 2020.
Figura 4 – Previsão de casos diários de COVID-19 no Brasil.
Vale ressaltar que o momento crítico de casos diários de COVID-19 no Brasil, não indicam que o surto esteja extirpado. Também é importante informar que, se houver variação nas condições de infecção e de contenção da doença a curva pode ser deslocada e, inclusive, com pico maiores.
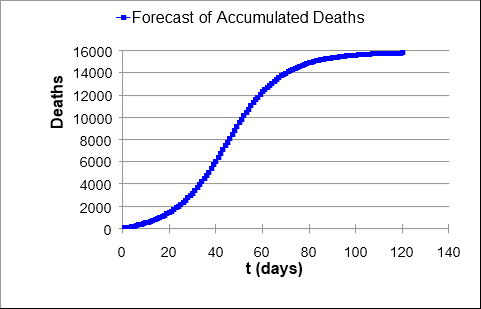
Todo o esforço para conter a pandemia, a nível mundial, é para evitar os óbitos. Por isso, adotou-se o modelo para prever a quantidade de óbitos no país. O resultado é apresentado na Figura 5. A previsão apresenta o resultado assustador de aproximadamente 16 mil óbitos.
Figura 5 – Previsão de óbitos no Brasil devido à COVID-19 de acordo com o modelo logístico.
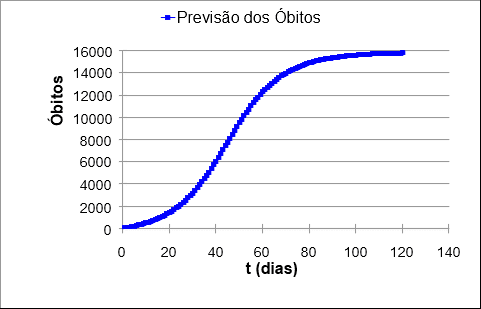
O número é preocupante e reforça a necessidade de medidas preventivas. Apesar de alguns países terem a mortalidade por COVID-19 baixa, o óbito pelo surto varia de acordo com as condições epidemiológicas do país, afirmam Roser et al. (2020).
Assim como o caso de grande aumento de infectados diários pode trazer colapso os sistema de saúde, o aumento brusco de óbitos trará colapso não só no sistema de saúde como também em outros setores. Pensando nesse momento de colapso, aplicamos o modelo para determinar o período crítico de óbitos. O resultado é apresentado na Figura 6. O período crítico de óbitos no Brasil está previsto para maio de 2020.
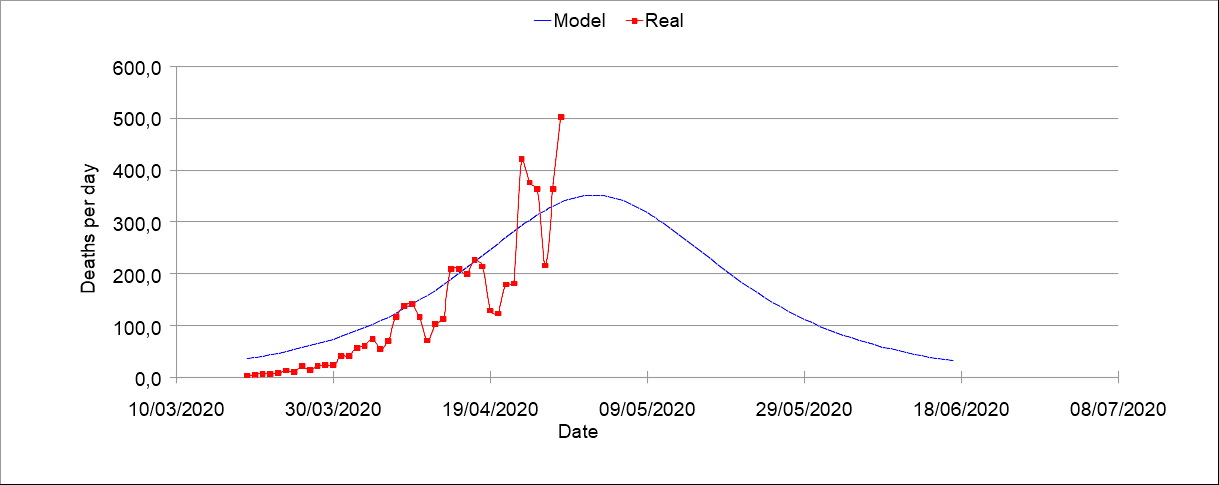
Figura 6 – Previsão de óbitos diários pela COVID-19 no Brasil.
Essa previsão indica que se próxima o pico de óbitos no Brasil e que a população deve manter os cuidados de prevenção. Ressalta-se que essa curva pode ser deslocada de acordo com a variação das condições dessa infecção no país.
CONCLUSÃO
O presente trabalho propôs um modelo matemático baseado no modelo logístico para prever a curva epidemiológica do surto de COVID-19 no Brasil. Para determinar o modelo realizou-se procedimentos de verificação com base nos dados disponíveis pelo Ministério da Saúde do Brasil. Através desse procedimentos, determinou-se com precisão os valores das constantes que representam as condições epidemiológicas brasileiras. O modelo proposto apresentou a perspectiva de casos de infectados e de óbitos no Brasil. E através dele foi possível gerar a curva epidemiológica que apresenta o ponto crítico do surto de COVID-19 em meados de maio e a queda drástica dos casos em meados de junho. O modelo matemático pode ser aprimorado se forem incluídos mais dados. No entanto, cabe ressaltar que suas simulações numéricas são importantes ferramentas que podem ser muito úteis para o planejamento da saúde pública.
AGRADECIMENTOS
Agradecemos a colaboração dos docentes do Instituto Federal de Alagoas Campus Coruripe: Alex Aguiar da Silva, Eugênio Bastos da Costa e Juliana de Araújo Melo. Também agradecemos ao apoio acadêmico do Instituto Federal de Alagoas, em especial, Campus Coruripe.
REFERÊNCIAS
AVENI, A. Sistemas de Saúde e Economia da Saúde – Impactos Causados pela COVID-19. Cadernos de Prospecção – Salvador, v. 13, n. 2, Edição Especial, p. 477-493, abril, 2020.
BRASIL. Ministério da Saúde. Coronavírus: Brasil. Brasilia, DF: 2020d. Disponível em: < https://covid.saude.go (v.br >. Acesso em: 28 Abril 2020.
CHERNIHA, R.; DAVYDOVYCH, V. A mathematical model for the coronavirus COVID-19 outbreak. arXiv:2004.01487 [physics.soc-ph], 09 April 2020.
DIAS, G. M. S.; ARAUJO, L. H. C. Modelagem Matemática para Epidemia de COVID-19 e Estimativa de Casos no Brasil no Curto Prazo. Revista da IME. URL http://covid19cientifico.ime.eb.br/artigo1.pdf
FALAVIANA, D. et al. Initial Modeling of Brazil Cases; Evolution in LatAm And Other Considerations. Latin America Equity Research 17 March 2020.
FARIAS, H. S. O avanço da Covid-19 e o isolamento social como estratégia para redução da vulnerabilidade. Revista Brasileira de Geografia Economica, volume 17, 2020.
GARCIA, L.P.; DUARTE, E. Intervenções não farmacológicas para o enfrentamento à epidemia da COVID-19 no Brasil. Epidemiol. Serv. Saúde 29 (2), 9 de abril de 2020.
HELLEWELL, J. et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts, The Lancet Global Health, Volume 8, Issue 4, April 2020, Pages e488-e496.
LUO, J. When Will COVID-19 End? Data-Driven Prediction. Singapore University of Technology and Design, April 29, 2020.
ROSER, W. et al. Coronavirus Pandemic (COVID-19). URL <https://ourworldindata.org/coronavirus> Visitado em 29 de abril de 2020.
VERHULST, P. F. Notice sur la loi que la population suit dans son accroissement, Corr. Math. Physics. 10 (1838) .
WATKIN, J. Preventing a covid-19 pandemic. BMJ 2020;368:m810
WHO – World Health Organization. Disponível em <WHO Director-General’s opening remarks at the media briefing on COVID-19 – 11 March 2020>. Acesso em 29 de Abr. de 2020.
ANEXO
Figuras em inglês
Figure 1.
Figure 2.
Figure 3.
Figure 4.
Figure 5.
Figure 6.
[1] Mestrado em Engenharia Civil. Especialização em Petróleo, Gás e Biocombustíveis. Graduação em Engenharia Civil.
Enviado: Abril, 2020.
Aprovado: Maio, 2020.