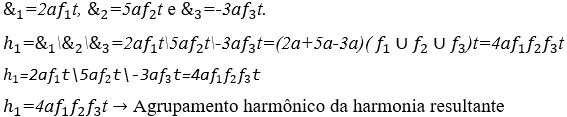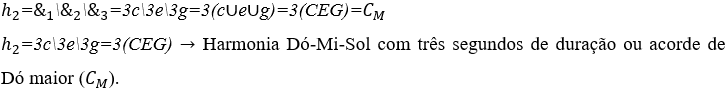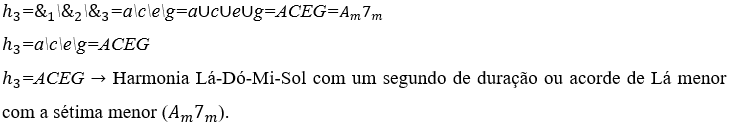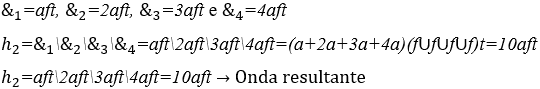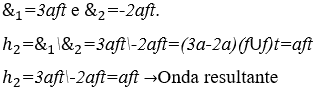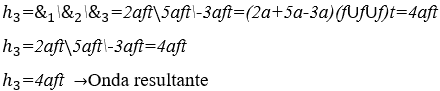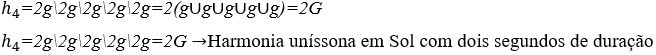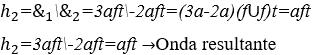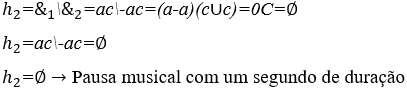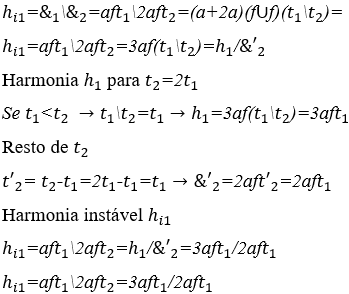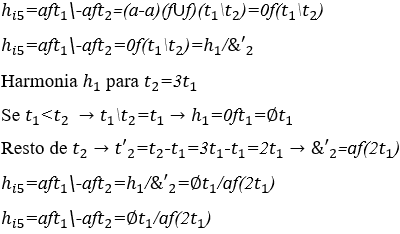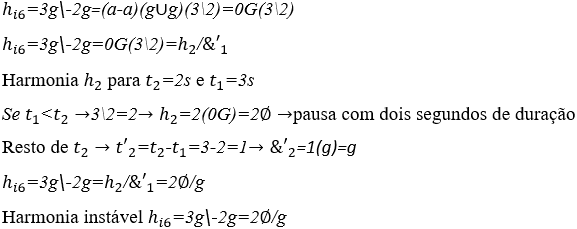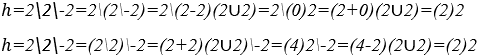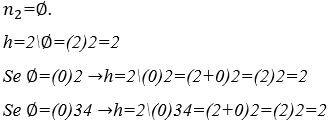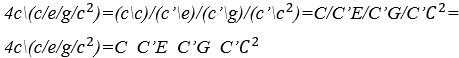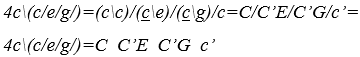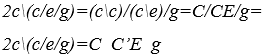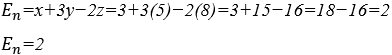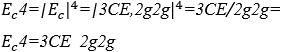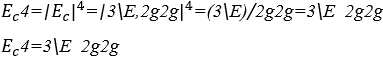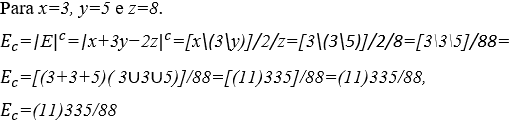A operação harmonização (H) e sua inversa operação melodiação (M)

ARTIGO ORIGINAL

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. A operação harmonização (H) e sua inversa operação melodiação (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 03, Vol. 03, pp. 144-171. Março de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/operacao-harmonizacao, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/operacao-melodiacao

RESUMO

A não existência de uma operação matemática para explicar as interações das ondas, principalmente entre as ondas sonoras de notas musicais, foi o problema que norteou a construção deste artigo. Neste contexto, o objetivo dessa pesquisa, visando a melhor visualização de uma onda sonora simples, foi demonstrar operações desenvolvidas pelo autor deste material, composta de três características mais importantes à Música: a amplitude , a frequência e o tempo de duração . Assim surgiu a forma  e, desse modo, se analisa as estruturas musicais de uma harmonia e de uma melodia formada pelos seus agrupamentos respectivamente harmônicos e melódicos, até se obter as propriedades operacionais dessas organizações em seus fenômenos físicos. No agrupamento onde essas notas musicais são emitidas simultaneamente, no espaço ou ao mesmo tempo, as ondas sonoras ficam fisicamente em Superposição, causando interferência entre elas, originando, dessa forma, um efeito sonoro chamado pelos músicos de Harmonia. Avaliando essa estrutura no espaço e no tempo, desenvolveu-se a operação matemática que causa esse fenômeno harmônico, adotando as operações fundamentais que surgiram, nessa interferência integrada, uma única operação especial, denominada de Operação Harmonização ou Operação H. Em consequência dessa operação, foi desenvolvida, também, a sua operação inversa, onde as ondas das notas musicais são emitidas continuamente no espaço ou uma após a outra no tempo, originando, dessa forma, um efeito sonoro chamado pelos músicos de melodia. Analisando essa estrutura no espaço e no tempo, foi também desenvolvida a operação matemática que origina esse fenômeno, denominada de Operação Melodiação ou Operação M, atendendo a finalidade dessa investigação, que visa prover à Ciência uma visão matemática das estruturas musicais das harmonias e das melodias musicais, proporcionando, de modo geral, novas operações matemáticas, que podem explicar fenômenos da Natureza, tornando mais simples a sua compreensão à Ciência.

Palavra-chave: Harmonização, Melodiação, Harmonia, Melodia.

1. INTRODUÇÃO

No começo do ano de 2006 foi desenvolvida, pelo autor deste material, a Operação Harmonização para os agrupamentos harmônicos de ondas sonoras das harmonias de notas musicais e, a Operação Melodiação, para os agrupamentos melódicos de ondas sonoras das suas melodias.

O problema que motivou a construção deste material o desenvolvimento destas operações foi a  não existência de uma operação matemática para explicar as interações das ondas, principalmente entre as ondas sonoras de notas musicais. Neste contexto, tem-se como objetivo demonstrar operações desenvolvidas pelo autor deste material, composta de três características mais importantes à Música: a amplitude , a frequência e o tempo de duração .

Para o desenvolvimento desta, inicialmente, considerou-se que somente para ondas sonoras e, depois, de um modo geral, para qualquer outro elemento com ou sem vibração, ocorre o fenômeno físico da “Superposição de ondas”, onde, no encontro entre duas ondas iguais, ocorre um aumento na amplitude resultante entre elas (SILVA, s.d.).

Utilizando a expressão , formulada neste estudo para representar uma onda sonora, com as características: amplitude , frequência e tempo de duração , pode-se analisar de forma simples a interferência entre duas ondas sonoras iguais .

Quando elas se encontram em um ponto comum , neste caso, as suas amplitudes se somam , permanecendo a mesma frequência, com o mesmo tempo de duração .

Avaliando o resultado desse fenômeno da interferência, observou-se que no ponto p de encontro da superposição entre essas duas ondas, além da soma algébrica existente entre as suas amplitudes , também existe a união entre as suas frequências  nesse tempo de duração, formando uma única onda sonora, com amplitude, frequência e tempo de duração.

Concluiu-se, também, nesta análise inicial, que essas duas operações, de Adição entre as amplitudes e de União entre as frequências, além de formarem o resultado desse fenômeno, também integram uma única operação matemática, caracterizada por essa Dualidade Operacional. Explicando, com isso, a emissão simultânea de ondas de notas musicais, cujo efeito sonoro é chamado de Harmonia. Por isso, admitiu-se o nome de Operação Harmonização ou operação H, adotando uma barra inclinada à esquerda (\) como seu símbolo matemático, denominado de operador H . Originando, com esse fenômeno, o Princípio da Harmonia, onde os elementos são harmônicos, se existir entre eles superposição em seus espaços-tempo.

Por consequência, foi desenvolvida a sua operação inversa, em que as ondas sonoras deixam à condição de superposição e passam à condição de ininterrupção, onde o tempo final de uma onda é igual ao tempo inicial da onda seguinte , e assim por diante , cujo efeito sonoro é chamado pelos músicos de Melodia. Por isso, adotou-se o nome de operação Melodiação ou M, com uma barra inclinada à direita (/) como seu símbolo matemático, denominado de operador M , originando o Princípio da Melodia, onde elementos são melódicos, se existir entre eles continuidade em seus espaços-tempos.

2. OPERAÇÃO HARMONIZAÇÃO (H)

De um modo geral, quando duas ou mais ondas periódicas rítmicas , com frequências e amplitudes distintas , ficam em operação Harmonização ou H elas formam um agrupamento harmônico, chamado de Harmonia, onde a frequência resultante é determinada pela operação de União entre as suas frequências e a amplitude resultante pela operação de Adição entre as suas amplitudes , que podem estar na mesma fase com sinais iguais, em interferência construtiva, ou em fases contrárias com sinais opostos, em interferência destrutiva.

Quanto mais ondas desses tipos existirem nessa operação, mais frequências serão unidas e mais amplitudes adicionadas no resultado dessa Harmonia , conforme demonstrado no exemplo abaixo.

Operação Harmonização e sua Harmonia entre três ondas periódicas distintas e rítmicas:

2.1 PROPRIEDADES DA OPERAÇÃO H (HARMONIZAÇÃO)

2.2 HARMONIA MUSICAL

Na operação Harmonização entre ondas sonoras, especificamente de notas musicais rítmicas, onde normalmente a harmonia de um acorde musical principal é formada por uma tríade ou três notas, com frequências distintas , o aumento na amplitude resultante é linear (MORAIS, 2020).

Considerando que estas ondas sejam iguais e o fato de que a intensidade sonora da audição humana é logarítmica com valor de  (SANTOS, s.d.), nesse caso, seu acréscimo é insignificante para ser percebido . Se essa fração fosse arredondada para uma unidade, matematicamente, é como se ela não existisse nessa harmonia .

Em função desse fenômeno e considerando esse arredondamento, a harmonia dessa operação foi formada somente pelo cálculo da operação de União entre as suas frequências . Portanto, para esse resultado simplificado, não é necessário saber qual a intensidade sonora a ser aplicada em uma harmonia com notas musicais em uma operação H, pois esta pode ser qualquer uma, sem que houvesse prejuízo à harmonia dessa operação.

São descritos abaixo algumas operações H com notas musicais identificadas pelas suas cifras, onde as cifras das notas Lá, Si, Dó, Ré, Mi, Fá e Sol, são respectivamente A, B, C, D, E, F, G, tomando como base a obra de Guest (2020, p. 33 a 41):

1) Calcular a harmonia entre as notas musicais: Fá e Si , ambas com dois segundos de duração e intensidades sonoras normais.

2) Calcular a harmonia entre as notas musicais: Dó , Mi e Sol , todas com três segundos de duração e intensidades sonoras normais.

3) Calcular a harmonia entre as notas musicais: Lá , Dó , Mi e Sol , todas com um segundo de duração e intensidades sonoras normais.

Observação: neste estudo, é definido que uma harmonia é denominada com as suas frequências em ordem crescente e acentuação tônica na última frequência. Por exemplo, é a harmonia Lá-Dó-Mi-Sol com um segundo de duração ou acorde de Lá menor com a sétima menor .

2.3 HARMONIA UNITÁRIA

Harmonia Unitária é o resultado da operação H entre duas ou mais ondas periódicas iguais , formando um agrupamento harmônico de uma única frequência , com a sua amplitude resultante e um tempo de duração

Este tipo de harmonia pode aparentar, neste espaço-tempo, que só existe uma onda periódica em sua estrutura, no entanto, nele coexistem duas ou mais ondas periódicas iguais ocupando o mesmo espaço-tempo, constituindo um Conjunto Unitário Harmônico capaz de gerar, de sua estrutura unitária, duas ou mais ondas periódicas iguais contínuas em um novo espaço-tempo . Diferente de um conjunto unitário simples formado por uma única onda, onde é gerado, somente uma única onda de sua estrutura .

Desse modo, duas ou mais harmonias unitárias só serão iguais, se todas as suas características e quantidades forem iguais e, quando essa harmonia for formada somente por ondas sonoras de notas musicais, ela passa a ser considerada como uma Harmonia Uníssona , por formar um único som, com a sua frequência, amplitude e tempo de duração , conforme demonstrado nos exemplos abaixo:

1) Harmonia uníssona entre quatro ondas rítmicas, com frequências iguais e amplitudes distintas.

Gráfico 1: Harmonia uníssonora

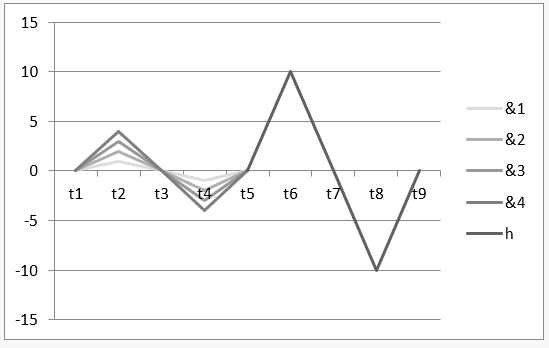
No gráfico 1, é demonstrado o intervalo de tempo t1 até t5, que caracteriza a operação H e, no intervalo de t5 até t9, se demonstra o resultado da operação ou da sua harmonia .

2) Harmonia com interferência destrutiva entre duas ondas periódicas rítmicas:

Gráfico 2: Harmonia com interferência destrutiva

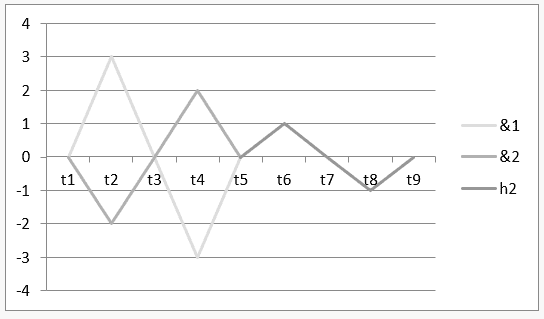
O intervalo de tempo t1 até t5, demonstrado no gráfico acima, representa o resultado da operação H  e, no intervalo de t5 até t9, se caracteriza o resultado dessa operação ou da sua harmonia .

3) Harmonia construtiva e destrutiva entre três ondas:

Gráfico 3: Harmonia com interferência construtiva e destrutiva

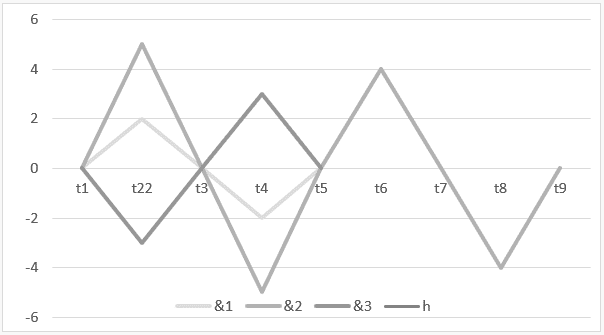
O intervalo de tempo t1 até t5, demonstra a operação H e, no intervalo de t5 até t9, representa-se o resultado dessa operação ou da sua harmonia .

4) Harmonia entre cinco ondas de notas musicais iguais a nota Sol, com dois segundos de duração.

2.4 HARMONIA VAZIA

Harmonia vazia é o resultado da operação H entre uma onda e sua onda oposta ou da operação entre várias ondas e suas ondas opostas , formando um agrupamento harmônico de uma única frequência , com a sua amplitude nula e um tempo de duração

Este tipo de harmonia , pode aparentar, neste espaço-tempo, a não existência de nenhuma onda periódica em sua estrutura. No entanto, nele coexiste uma frequência resultante, com amplitude nula , em estado de vibração infinitamente diminuta, na dimensão do tempo, denominada de Vibração Primordial Harmônica (VPH), sendo representada por um zero negado , constituindo, portanto, um Conjunto Vazio Harmônico, chamado pela Ciência de “Vácuo Quântico”, capaz de gerar em sua estrutura, mais de uma vibração em um espaço-tempo , diferente de um conjunto vazio simples, onde nada existe e nada pode ser gerado.

Desse modo, duas harmonias vazias, só serão iguais se suas características e quantidades forem iguais. Qualquer que seja a harmonia vazia , ela é considerada o Elemento Neutro da operação Harmonização , devido a ser somente um tempo de duração ativo, que oculta uma ou mais vibrações inativas ou impossibilitadas de interagir com qualquer elemento ativo.

Por isso, o resultado da harmonia entre um elemento neutro qualquer e um elemento ativo, é o próprio elemento ativo , não importando qual seja a origem desse elemento neutro, se for com frequências iguais ou com frequências iguais, independentemente dos seus tempos de duração , pois essas vibrações coexistem somente na Dimensão do Tempo.

Quando essa harmonia for formada por ondas sonoras de notas musicais opostas, a amplitude sonora é totalmente eliminada de sua frequência , originando em seu lugar um silêncio no tempo, formando uma Harmonia de Silêncio. Neste caso, o seu tempo de silêncio é percebido pelo ser humano, devido a sua duração ser igual ou maior que um décimo de segundo , sendo essa harmonia conhecida como Pausa Musical , que será demonstrada nos exemplos abaixo.

Quando essa harmonia for formada por vibrações luminosas, a luminosidade da amplitude de sua frequência é totalmente eliminada , originando, em seu lugar, uma escuridão no tempo, sendo denominada de Harmonia de Energia Escura  e, provavelmente, a escuridão que habita o Universo, seja originada por essa harmonia implícita no seu imenso Vazio Harmônico.

1) Harmonia entre duas ondas:  com o seu gráfico no sistema cartesiano.

Gráfico 4:  Harmonia Vazia de

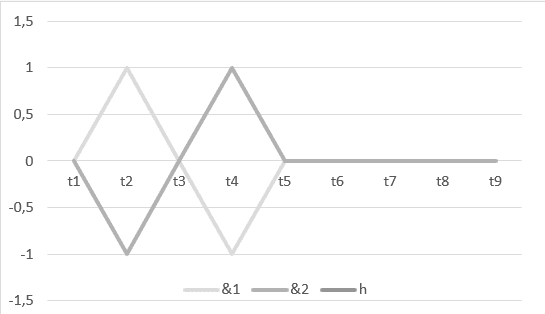
O intervalo de tempo t1 até t5, demonstrado no gráfico acima, representa a operação H e, o intervalo de t5 até t9, é o resultado dessa operação ou da sua harmonia .

2) Harmonia entre as notas musicais: Dó, com um segundo de duração, com suas amplitudes iguais e inversas

Observação: a Harmonia Vazia é um lugar no espaço tempo em que há o pensamento de que nada existe nele, entretanto ele pode estar repleto de vibrações não perceptíveis.

2.5 HARMONIA INSTÁVEL

A Harmonia Instável é o resultado da operação H entre duas ou mais ondas periódicas arrítmicas ou com durações diferentes , onde aquela de menor duração forma a harmonia dessa operação , devido à propriedade do ritmo igualar as durações dessa onda pela menor, restando uma parte da duração da maior , onde fica continua (/) a harmonia formada .

Quanto maior for o número dessas ondas arrítmicas nessa operação , maior será a instabilidade da harmonia formada , com degradações em harmonias secundárias , sobrando ou não um resto contínuo da onda de maior duração , conforme exemplos relacionados abaixo.

1) Harmonia Instável entre duas ondas arrítmicas:  com seu gráfico de linha nas coordenadas cartesianas.

Gráfico 5: Harmonia Instável de

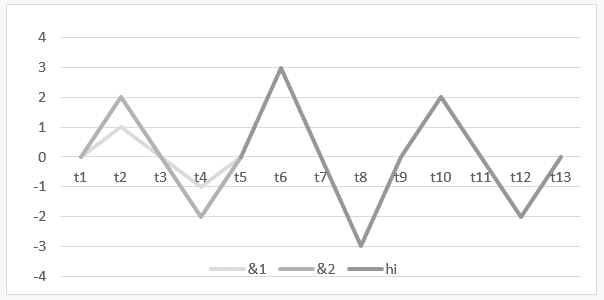
O intervalo de tempo t1 até t5, demonstra o gráfico da operação H e, no intervalo de t5 até t13, é representado o resultado dessa operação ou da sua harmonia .

2) Harmonia entre duas notas musicais arrítmicas: , respectivamente com as suas durações de três e dois segundos.

3) Harmonia Instável entre três notas musicais arrítmicas: , respectivamente com durações de quatro, três e dois segundos, com o seu gráfico no sistema dos eixos cartesianos.

Gráfico 6: Harmonia Instável de

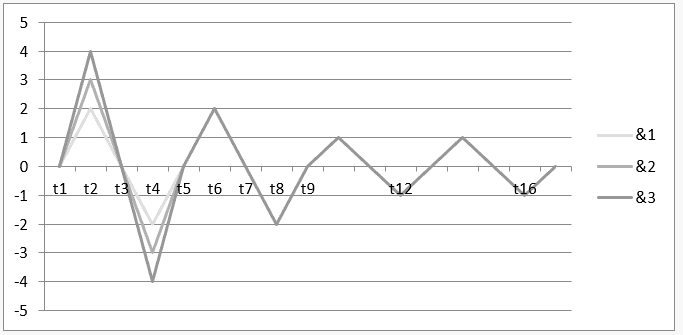
O intervalo de tempo t1 até t5, representa o gráfico da operação H e, no intervalo de t5 até t13, é demonstrado o resultado dessa operação ou da sua harmonia .

4) Harmonia instável entre três notas musicais arrítmicas com frequências iguais:

5) Harmonia Instável com harmonia vazia entre duas ondas:  sendo uma com o triplo da duração da outra

Gráfico 7: Harmonia Instável com harmonia vazia de

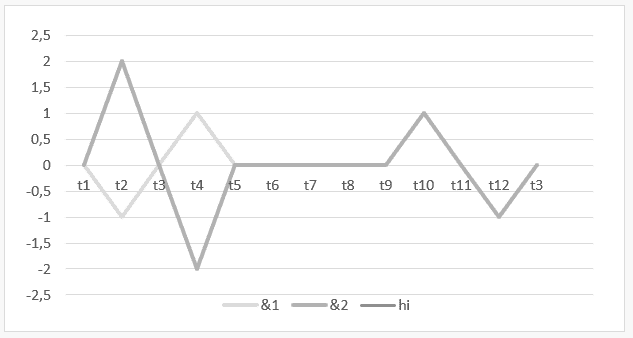
O intervalo de tempo t1 até t5, retrata a operação H e, no intervalo de t5 até t13, se demonstra o resultado dessa operação ou da sua harmonia

6) Harmonia entre duas notas musicais Sol com amplitudes iguais em fases opostas, sendo uma com duração de três segundos e a outra com duração de dois segundos

2.6 HARMONIA NUMÉRICA

Quando duas ou mais constantes numéricas  ficam em operação de Harmonização ou H, elas são consideradas vibrações rítmicas e, por apresentarem somente um parâmetro, que pode ser tanto a frequência, como a amplitude, elas são ao mesmo tempo unidas como frequências e adicionadas como amplitudes  formando a harmonia dessa operação

Qualquer agrupamento formado por uma combinação da Análise Combinatória é considerado resultado de uma operação H entre esses elementos  com o resultado da sua amplitude subentendida na união entre eles, conforme demonstrado nos exemplos abaixo.

1) Harmonia entre as constantes numéricas 1 e 1

Onde se lê: um H um é igual a harmonia de um, com amplitude dois.

2) Harmonia entre as constantes numéricas 1 e -1

 Onde se lê: um H menos um é igual a harmonia vazia.

3) Harmonias entre as constantes numéricas

Onde se lê: três H quatro é igual a harmonia três e quatro, com amplitude sete ou, ainda conforme a propriedade comutativa dessa operação,

4) Harmonias entre as constantes numéricas

Onde se lê: Três H quatro H menos oito é igual a harmonia três, quatro e oito, com amplitude menos um ou, ainda conforme a propriedade comutativa dessa operação, qualquer agrupamento da permutação entre esses três elementos, com amplitude menos um

5) Harmonias entre as constantes numéricas

Onde se lê: Dois H dois H menos dois é igual a harmonia de dois, com amplitude dois, aplicando a propriedade associativa dessa operação.

6) Harmonias entre uma constante numérica  e um elemento neutro qualquer

Observação: a harmonia da operação H entre uma constante numérica qualquer e um elemento neutro qualquer é a própria constante numérica com amplitude igual ao seu valor Nesta operação, sabemos que a amplitude do elemento neutro é zero porém a sua frequência é indeterminada e, mesmo que fosse conhecida ela estaria na dimensão do tempo, impossibilitada de interagir com qualquer elemento ativo de uma dimensão qualquer.

3. OPERAÇÃO MELODIAÇÃO OU OPERAÇÃO M

A operação Melodiação ou M, é a operação inversa da Harmonização, pois após o término do tempo de duração de uma harmonia, as vibrações periódicas que estavam em superposição, passam a condição de Ininterrupção, ou seja, elas formam uma continuidade entre os seus espaços-tempos, onde o tempo final de uma duração é igual ao tempo inicial da duração seguinte  sendo este fenômeno denominado de Princípio da Melodia.

Portanto, quando duas ou mais vibrações periódicas  ficam em operação M  o resultado é um agrupamento melódico, que se forem de ondas de notas musicais, o efeito sonoro resulta em uma Melodia  e, se esses elementos forem constantes numéricas em operação M, eles também formarão um agrupamento contínuo entre eles, formando a melodia numérica dessa operação  Desse modo, qualquer agrupamento formado por um Arranjo da matemática da Análise Combinatória é resultado de uma operação M, que não é de propriedade comutativa.

3.1 MELODIA COM FREQUÊNCIAS IGUAIS E AMPLITUDES OPOSTAS

Normalmente, as notas musicais em uma operação M possuem amplitudes em fases positivas, contudo, se houver uma nota com amplitude em fase negativa, ela pode ser modulada para fase positiva, pois a frequência permanece a mesma, produzindo o mesmo efeito sonoro na melodia formada

Entretanto, esse sinal negativo pode permanecer na cifra da nota musical e no resultado da melodia com um ponto sobre ela  Se esse elemento for uma constante numérica negativa nessa operação ele também pode ser modulado para positivo ou identificado um ponto sobre a constante na melodia resultante

3.2 A PAUSA MUSICAL (p)

A Pausa Musical é uma nota musical com a amplitude de sua frequência sonora nula, representada por um zero negado  Em outras palavras, é o elemento neutro da operação H, e a sua função principal em uma melodia é prover uma descontinuidade sonora entre as notas musicais melódicas ou deixar um espaço sem som entre elas Ela, ainda, pode ficar subentendida somente no início do primeiro compasso de um ritmo e no fim do último compasso desse ritmo, completando os seus períodos.

3.3 EXEMPLOS DA OPERAÇÃO M ENTRE ONDAS DE NOTAS MUSICAIS

3.4 APLICAÇÃO DA PROPRIEDADE DISTRIBUTIVA DA OPERAÇÃO H

Quando uma nota musical iniciar em um compasso e finalizar em outro sem perder a sua continuidade sonora, a sua cifra continuada recebe um apóstrofo no compasso seguinte, por exemplo:

1) Distributiva Rítmica:

2) Distributiva Arrítmica maior

3) Distributiva Arrítmica menor

3.5 EXEMPLOS DA OPERAÇÃO M COM CONSTANTES NUMÉRICAS

4. ÁLGEBRA DAS VIBRAÇÕES

A Álgebra das Vibrações, nada mais é que a Álgebra com pelo menos uma das operações Harmonização ou Melodiação em sua expressão.

Mesmo que não apresente nenhuma dessas operações, ela pode ser modulada para a Álgebra das Vibrações, através dos módulos ondulatórios disponíveis, como: o Módulo Melódico , que transforma uma expressão algébrica em uma melodia; o Módulo Harmônico , que transforma uma expressão algébrica em uma harmonia; o Módulo Composto , que transforma uma expressão algébrica em uma melodia com harmonia, cujos resultados normalmente arrítmicos são modulados em um ritmo qualquer.

Através dos módulos rítmicos padrões , que organizam as células musicais em agrupamentos sonoros rítmicos, somando as suas durações em períodos iguais, em compassos: Binário , Ternário  ou Quaternário . Neste caso, o primeiro e o último compasso de um ritmo qualquer pode ficar incompleto de notas musicais, conforme demonstrado no exemplo abaixo.

Dada à expressão: e as constantes numéricas  e sonoras  Calcula-se os valores, numérico , melódico , harmônico e composto

4.1 CÁLCULO DO VALOR NUMÉRICO DE E=x+3y−2z

Substituindo as variáveis na expressão

4.2 CÁLCULO DO VALOR SONORO MELÓDICO DE E=x+3y−2z

O módulo melódico  transforma uma expressão algébrica numérica em uma expressão algébrica melódica, substituindo todas as operações existentes por operações M (/).

O resultado normalmente arrítmico é modulado em um ritmo qualquer  para organizar as notas musicais em uma simples execução.

Observação: A operação M entre uma constante numérica e uma constante sonora é igual à melodia da constante sonora vezes

Módulo melódico da expressão

Substituindo em

melodia arrítmica

Módulo rítmico quaternário em

Melodia em ritmo quaternário

Comentário: a escolha de um ritmo é opcional e, se fosse escolhido o módulo rítmico ternário, a última nota seria dividida com uma parte no penúltimo compasso e outra contínua no último, identificada com um apóstrofo em sua cifra

4.3 VALOR MELÓDICO INTERATIVO DE E=x+3y−2z

Quando no módulo melódico ocorrer à substituição, tanto de constantes sonoras como numéricas, a expressão melódica resultante é chamada de interativa, pois inclui uma dinâmica física em função da constante numérica, conforme exemplo abaixo.

Dada à expressão e as constantes  Calcula-se o seu valor melódico.

melodia interativa arrítmica

Módulo ternário em

melodia em ritmo ternário

Observação: o valor numérico três (3) no primeiro compasso, representa uma ação física qualquer, por exemplo: contar de um até três em compasso ternário e, em seguida, executar a melodia indicada nos compassos seguintes  Essa contagem em ritmo binário ou quaternário, torna a execução dessa dinâmica complexa, difícil de ser cumprida, portanto, é importante a escolha de um ritmo adequado para uma expressão melódica interativa.

4.4 VALOR NUMÉRICO MELÓDICO DE E=x+3y−2z

agrupamento numérico melódico

4.5 VALOR SONORO HARMÔNICO DE E=x+3y−2z

O módulo sonoro harmônico transforma uma expressão algébrica numérica em uma expressão algébrica sonora harmônica, trocando todas as operações existentes por operações H (\). O resultado é, normalmente, arrítmico modulado para um ritmo qualquer para a sua fácil execução.

Observação: a operação H entre uma constante numérica e uma constante sonora é igual à harmonia uníssona da constante sonora

Módulo Harmônico  da expressão

Substituindo em

harmonia em ritmo ternário

4.6 VALOR HARMÔNICO INTERATIVO DE E=x+3y−2z

Quando no módulo harmônico ocorrer a substituição tanto de constantes sonoras como numéricas, a expressão harmônica resultante é chamada de interativa, pois inclui uma dinâmica física em função da constante numérica, conforme exemplo abaixo.

Calcula-se o valor sonoro harmônico da expressão , dada as constantes

harmonia em ritmo ternário devido a constante numérica

Observação: o valor numérico três (3) no único compasso representa uma ação física qualquer, por exemplo: contar de um até três em compasso ternário, executando ao mesmo tempo a harmonia indicada Essa contagem em outros ritmos torna a execução dessa dinâmica complexa e difícil de ser cumprida, portanto, é muito importante a escolha de um ritmo para uma expressão harmônica interativa.

4.7 VALOR NUMÉRICO HARMÔNICO DE E=x+3y−2z

Quando no módulo harmônico as constantes forem todas numéricas, o resultado é um agrupamento harmônico numérico, conforme exemplo abaixo.

4.8 VALOR SONORO COMPOSTO DE E=x+3y−2z

O módulo composto  transforma uma expressão algébrica numérica em expressões sonoras com melodias e harmonias, trocando todas as operações existentes por operações M e H. O resultado, normalmente, é arrítmico modulado para um ritmo qualquer  para a sua simples execução. Neste caso, haverá a opção de quais operações serão substituídas pelas sonoras, sendo que a cada escolha será formada uma expressão sonora composta diferente, conforme exemplo abaixo.

Calcula-se o valor sonoro composto da expressão substituindo as duas primeiras operações  por operações H e as duas últimas  por operações M, para as constantes sonoras

expressão composta sonora arrítmica

Módulo rítmico quaternário para

4.9 VALOR COMPOSTO INTERATIVO DE E=x+3y−2z

Quando no módulo composto ocorrer a substituição, tanto de constantes sonoras como numéricas, a expressão sonora composta resultante é interativa, pois inclui uma dinâmica física através da constante numérica, conforme exemplo abaixo.

Calcula-se o valor sonoro composto da expressão substituindo as duas primeiras operações  por operações H e as duas últimas  por operações M, para as constantes numérica  e sonoras

expressão composta sonora arrítmica

Módulo rítmico quaternário para

4.10 VALOR NUMÉRICO COMPOSTO DE E=x+3y−2z

Quando no módulo composto ocorrer a substituição de somente constantes numéricas, o resultado é um agrupamento composto numérico, conforme exemplo abaixo.

5. HIPÓTESES CIENTÍFICAS DO AUTOR

Com o desenvolvimento da operação Harmonização surgiram, neste estudo, algumas hipóteses científicas levantadas pelo autor deste material, para alguns fenômenos da natureza.

5.1 DUALIDADE ONDA-PARTÍCULA DA LUZ

O fenômeno da dualidade onda-partícula da luz, onde a luz tem característica ora de uma onda, ora de uma partícula, pode ser explicado pela propriedade da Dualidade Operacional da operação Harmonização.

Sabe-se que a luz é uma harmonia formada por várias tonalidades de vibrações luminosas em operação Harmonização ou H , onde a amplitude resultante tem como função a operação Adição entre as amplitudes dessas vibrações.

Quanto maior for o número de vibrações nessa operação, maior será a amplitude luminosa resultante , influenciando, com essa quantidade de energia luminosa, o seu lado de partícula, enquanto a sua forma de onda é mantida em função da operação União entre as frequências dessas vibrações luminosas , que formam o agrupamento harmônico da harmonia dessa operação , influenciando o seu lado de onda.

Devido ao comprimento dessas ondas, esse equilíbrio é mantido entre essas duas características onda e partícula, o que não ocorre com uma onda sonora, devido a seu grande comprimento de onda em relação a onda luminosa, com isto, prevalecendo de forma preponderante o seu lado de onda, em relação a insignificância do seu lado de partícula.

5.2 ORIGEM DA ENERGIA ESCURA

O fenômeno da Energia Escura existente no Universo pode ser consequência da Harmonia Vazia, resultado da operação Harmonização entre vibrações de partículas luminosas opostas , que eliminam as luminosidades dessas vibrações , originando em seu lugar a Escuridão que constitui a Energia Escura, onde a frequência resultante dessa harmonia coexiste em estado de Vibração Primordial Harmônica (VPH) em um Vazio Harmônico, também chamado de Vácuo Quântico.

5.3 A ESTRUTURA DO TEMPO E SUA FORÇA DE EXPANSÃO

Um intervalo de tempo é constituído por um período , formados por um tempo inicial  e um tempo final , cuja diferença entre eles mede a sua duração  Esses períodos estão interligados de forma ininterrupta, onde o tempo final de um período é igual ao tempo inicial do período seguinte e assim por diante, constituindo um intervalo de tempo fechado de um período passado, até um período presente, e aberto no início de um período futuro, formando o seu Espaço-Tempo , que pelo Princípio da Melodia é igual a operação M entre esses períodos passado , presente  e futuro

Sabe-se ainda que o tempo inicial  de cada período é caracterizado por um Batimento , causado por um impulso intrínseco, dado por uma força com uma duração instantânea  restando um tempo de silêncio  até o final desse período  dado pela diferença entre o tempo final desse período pelo tempo  de batimento desse impulso

Logo, um período pode ser definido pela operação M, entre o seu batimento e o seu tempo de silêncio  Substituindo os períodos pelos seus batimentos no Espaço-Tempo  forma-se a Cadência Rítmica do Espaço-Tempo  cuja velocidade de batimento, chamada de Andamento Rítmico  é inversamente proporcional ao seu período  dimensionado em pulsação por unidade de tempo.

Quanto menor for esse período  maior será o seu Andamento rítmico  Esse fenômeno ainda promove, com a sua influência no Espaço-Tempo, dois movimentos em corpos físicos situados no seu campo de ação, sendo um deles chamado de Regência Rítmica onde um corpo sem sair de sua posição de repouso, acompanha os batimentos do Andamento Rítmico  e outro chamado de Dança Rítmica  onde um corpo se desloca de sua posição de repouso para outras posições distintas, em função também do Andamento Rítmico  dessa cadência rítmica.

Considerando um período  onde o tempo de silêncio é nulo o tempo instantâneo de pulsação vai constituir a sua menor duração  verifica-se, portanto, uma força de repulsão implícita em sua estrutura, considerada fraca em sua cadência rítmica no Espaço-Tempo  porém capaz de afastar qualquer corpo celeste no Universo e promover com o seu Andamento Rítmico, os movimentos de Regência Rítmica e Dança Rítmica.

Sabe-se que o Universo está em expansão e que suas galáxias estão se afastando uma das outras, o que pode ser explicado através da Força de Expansão do Tempo de sua Cadência Rítmica  e, considerando que as órbitas das galáxias em torno do centro do Universo são aproximadamente elípticas, logo, a sua expansão acelerada ainda não é explicada devido a essa aproximação do seu centro de gravidade, onde provavelmente existe uma harmonia de buracos negros, com a sua força de atração.

Entretanto, essa aceleração deve deixar de existir após o afastamento das galáxias desse centro, havendo uma desaceleração e, aquelas que atingirem as maiores órbitas, vão formar a borda instável do Universo, como uma bolha líquida instável, pois estariam mudando de forma em função das infinidades de afcentros máximos dessas galáxias em todas as direções, em relação ao centro do Universo.

5.4 A SINGULARIDADE DO BIG BANG E A ESCURIDÃO DA TEORIA RELIGIOSA

Sabe-se que toda matéria é formada por átomos, que estão em constante vibração, que por sua vez são formados por partículas cada vez menores até chegarmos na menor de todas as partículas da matéria, chamada de Partícula Elementar ou Primordial (ANJOS, s.d.), representada, neste estudo, por uma vibração simples  com a sua frequência amplitude e tempo contínuo . Da mesma forma, existe a sua antipartícula primordial  de antimatéria, com a mesma frequência  a amplitude oposta  e  tempo oposto  ou harmônico, ou seja, em vez do tempo ir do presente ao futuro numa cadência melódica, ele vem do futuro ao presente, numa cadência harmônica.

Essas vibrações luminosas em Operação H  vão formar a Harmonia Unitária Primordial de Energia Escura, capaz de originar toda energia de matéria e de antimatéria, contida em sua estrutura em estado de Vibração Primordial Harmônica ou em um Vazio Harmônico, também chamado pela Ciência de Vácuo Quântico

Portanto, para qualquer que seja a Teoria da Origem do Universo, sempre se admite a existência de um ponto de origem de tudo, como a Singularidade do Big Bang, a Escuridão da Teoria Religiosa (Bíblia) ou outra qualquer, o que leva sempre a Harmonia Unitária Primordial de Energia Escura capaz de gerar toda a energia para a formação tanto do Universo de Matéria  na Cadência Rítmica do Tempo Continuo, com a sua Força de Expansão  bem como, toda energia na formação do Universo de Antimatéria ou Imaterial  na Cadência Rítmica  do Tempo Harmônico, denominado de “Tempo de Deus”, com a sua Força de atração infinita.

5.5 O TEMPO ZERO DA CRIAÇÃO DO UNIVERSO

Um período de tempo, por menor que seja a sua duração, sempre será formado por um tempo inicial com um batimento , formado por uma força e um tempo de duração de batimento maior que zero

Considerando esse tempo inicial, pode-se dizer que o Universo teve seu início em um batimento instantâneo  mas antes desse batimento acontecer, existia um tempo nulo ou zero  e, para que isso seja verdadeiro, deveria existir antes uma Harmonia Primordial Vazia , formada por infinitas ondas-partículas de matéria em harmonia com infinitas ondas-partículas de antimatéria

Neste caso, o tempo contínuo do Universo material  estava em harmonia, também, com o seu tempo oposto ou anti contínuo  do Universo de antimatéria, resultando em tempo nulo ou Tempo Zero  nessa harmonia, repleta de energia acumulada em uma única frequência em Vibração Primordial Harmônica.

Considerando o menor tempo possível para existir em uma harmonia, com o seu batimento, formado por uma força F com uma determinada intensidade  verifica-se que o tempo é uma onda-partícula, onde é a sua amplitude  e o inverso de seu tempo de batimento é a sua frequência  que em Harmonia com a sua onda-partícula oposta, também, com a sua amplitude oposta  e sua frequência  resulta em uma harmonia vazia de Tempo Zero  do Início do Universo.

5.6 HARMONIA UNITÁRIA ONIPOTENTE

Na formação do Universo Material, o tempo contínuo com a sua força de expansão, foi formando as inúmeras partículas distintas de matéria, através de suas combinações, com uma única partícula primordial

No caso da formação do Universo de Antimatéria, o tempo anti contínuo ou harmônico, com a sua força de atração, formou a Harmonia Unitária Primordial  atraindo todas as antivibrações primordiais em uma única harmonia, capaz de originar tudo de sua estrutura, formando o Universo Imaterial ou de Antimatéria  por isso denominada de Harmonia Unitária Onipotente (Deus).

6. CONSIDERAÇÕES FINAIS

Com o desenvolvimento da operação Harmonização e sua inversa operação Melodiação, possibilitou-se a origem de uma estrutura matemática para as avaliações das características musicais de uma melodia, bem como de uma harmonia, tornando a Música não só uma arte, mas também parte da Ciência.

Tornou-se possível, também, a Álgebra com expressões não só numéricas, mas também sonoras, formando a Álgebra das Vibrações, com interação entre valores numéricos e sonoros no resultado de uma expressão algébrica, permitindo que um ato físico seja acompanhado de uma melodia ou de uma harmonia, ou ainda de uma melodia acompanhada de uma harmonia

Propôs-se, ainda, uma nova forma de olhar o Universo, através de uma perspectiva macro e micro, através da concepção das estruturas das vibrações harmônicas e melódicas, pois tudo é vibração. Por isso, foram demonstradas algumas das hipóteses, levantadas pelo autor deste material, para algumas perguntas ainda sem respostas para a Ciência, como a da existência de Deus.

REFERÊNCIAS

ANJOS, Talita Alves dos. Partículas elementares. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/fisica/particulas-elementares.htm. Acesso em 21/03/2022.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

MORAIS, Gustavo. Teoria musical para iniciantes: você sabe o que são os acordes? Terra, julho de 2020. Disponível em: https://www.terra.com.br/diversao/musica/teoria-musical-pra-iniciantes-voce-sabe-o-que-sao-os-acordes,7c62b1fa5e0fe37c8e0180310bc04200tnys05tj.html Acesso em: 20/03/2022.

SILVA, Domiciano Correa Marques da. Interferência de ondas. Brasil Escola. s.d. Disponível em: https://brasilescola.uol.com.br/fisica/interferencia-ondas.htm. Acesso em 17/03/2022.

SANTOS. Marco Aurélio da Silva. A Sensibilidade Auditiva. Mundo da educação. Disponível em: https://mundoeducacao.uol.com.br/fisica/a-sensibilidade-auditiva.htm. Acesso em: 20/03/2022.

^[1] Graduado em Engenharia Elétrica, op. Eletrônica pela Universidade Federal do Pará-UFPA. ORCID: 0000-0001-7010-9114.

Enviado: Fevereiro, 2022.

Aprovado: Março, 2022.