ARTIGO ORIGINAL
COSTA, Cláudio Cesar Alves da [1]
COSTA, Cláudio Cesar Alves da. Todo número perfeito é par: A prova. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 02, Vol. 07, pp. 05-20. Fevereiro de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/numero-perfeito
RESUMO
Existe número perfeito ímpar? Um dos problemas mais antigos e famosos da Teoria dos Números é se existe algum número perfeito ímpar, bem como saber se são infinitos. Até o presente momento ninguém conseguiu encontrar um número ímpar que satisfaça a condição de ser perfeito, isto é, que a soma de seus divisores seja igual ao dobro do próprio número ou mesmo demonstrar a sua não existência. Em 1888 o matemático Sylvester publicou uma série de artigos que desencadeou na era moderna a criação de uma rede de pesquisa para encontrar ou refutar a existência de tais números – conhecida como Rede Sylvester. Atualmente, com a ajuda do grupo de matemáticos da GIMPS a lista consta com 51 números perfeitos, sendo todos pares, evidenciando a dificuldade prática de encontrá-los. Neste artigo vamos demonstrar que todo número perfeito é par utilizando do Teorema de Tales para elaborar uma prova direta. Representando um número natural arbitrário n e a soma de seus respectivos divisores por comprimentos de segmentos de retas concorrentes no ponto zero podemos aplicar o Teorema de Tales para calcular as parcelas proporcionais de n em relação aos seus divisores (partes de n), bem como o ângulo θ entre as retas. De posse desta configuração e sob a condição de existência de um número perfeito é possível também determinar o menor divisor primo p de n – o qual indica a paridade do número analisado, a saber: p=2 e θ=60°, confirmando que as simetrias que caracterizam um número como sendo perfeito só são possíveis de serem encontradas entre os números pares. Consequentemente, este fato nos permite afirmar que todo número perfeito tem paridade par e estabelecer que o Teorema de Euclides-Euler sobre números perfeitos é uma condição necessária e suficiente para defini-los, finalizando-se aqui a difícil e árdua procura por um número perfeito ímpar, pois este não existe.
Palavras-Chaves: Números perfeitos, Números perfeitos ímpares, Teorema de Tales, Teoria dos números, Primos de Mersenne.
1. INTRODUÇÃO HISTÓRICA
Rever a história de um número é um ato importante para pensar suas crises e construções e poder adentrar em suas “entranhas” para buscar conexões que nos permitam, de forma simples e bela, chegar a novos horizontes do saber. Conforme Devlin (2004) a história dos números se confunde com a história da humanidade e nasce com a nossa necessidade de se relacionar e compreender o meio em que vivemos. O pensar matemático necessita dos números (símbolos) para representar e quantizar suas criações – objetos matemáticos – para fins de reconhecimento de padrões dos fenômenos e das coisas que nos cercam.
A escola pitagórica, por volta de 540 A.C., acreditava que o número era o conceito fundamental do universo, mas imbuído de uma mística interna que lhes lembrava a presença do Ser Onipotente – Deus criou o mundo em 6 dias; A lua precisa de 28 dias para dar uma volta em torno da terra. Portanto, estes números deveriam ser perfeitamente criados por Deus. A ciência atual se afastou desta mística interna e se contenta com explicações puramente matemática da “criação”, seja do universo ou da própria vida. Ao estudar as propriedades destes números “perfeitamente criados” os matemáticos da época observaram que estes guardavam em comum a propriedade admirável de suas partes (divisores) somadas se igualar ao dobro do próprio número. E devido à importância que guardavam aos números perfeitos classificam os demais números com referência a estes. Assim um número natural: 1,2,3,… , podia ser considerado deficiente, perfeito ou abundante. Era classificado como deficiente se a soma dos seus divisores próprios (excetuando o próprio número) fosse menor que o próprio número e como abundante se a referida soma fosse superior ao próprio número.
Na busca para encontrar os números perfeitos os antigos gregos nos presentearam com os quatro primeiros que são: 6, 28, 496 e 8128 de uma lista que ainda não sabemos se é infinita. Foi com Euclides, no livro “Os elementos de Euclides” (300 a.C.) que surgiu o primeiro resultado registrado que se tem conhecimento (FERREIRA, 2014) de um belo e simples processo de como calcular um número perfeito, que em linguagem matemática moderna é expresso pela seguinte equação:
No entanto, para que os números gerados por essa equação (1) sejam perfeitos é necessário que haja duas “coincidências”, tanto o expoente k quanto o termo ![]() devem ser primos – número primo é todo número natural >1 que possui somente dois divisores: a unidade e o próprio número e forma um conjunto infinito: {2,3,5,7,11,13,17,19,…}. Esta restrição na proposição de Euclides tornam os números perfeitos mais raros que os números primos, já que nem todo k primo gera um número perfeito. Para se ter uma ideia da dificuldade envolvida na determinação destes números sem o uso dos modernos computadores o quinto elemento da lista, 33550336 (k=13), só foi descoberto no século XV e foi por volta de 1000 D.C que o matemático Ibn al-Haytham percebeu que se um número perfeito sendo par então deveria ser da forma apresentada em (1) sem, no entanto, conseguir demonstrar (COSTA, 2015). Somente no século XVIII que o grande matemático Leonhard Euler provou que todo número perfeito par é da forma 2k-1 p, em que p é um primo de Mersenne, ou seja, p=2k-1, com k primo. Este resultado é hoje conhecido como Teorema de Euclides-Euler (VIEIRA, 2015).
devem ser primos – número primo é todo número natural >1 que possui somente dois divisores: a unidade e o próprio número e forma um conjunto infinito: {2,3,5,7,11,13,17,19,…}. Esta restrição na proposição de Euclides tornam os números perfeitos mais raros que os números primos, já que nem todo k primo gera um número perfeito. Para se ter uma ideia da dificuldade envolvida na determinação destes números sem o uso dos modernos computadores o quinto elemento da lista, 33550336 (k=13), só foi descoberto no século XV e foi por volta de 1000 D.C que o matemático Ibn al-Haytham percebeu que se um número perfeito sendo par então deveria ser da forma apresentada em (1) sem, no entanto, conseguir demonstrar (COSTA, 2015). Somente no século XVIII que o grande matemático Leonhard Euler provou que todo número perfeito par é da forma 2k-1 p, em que p é um primo de Mersenne, ou seja, p=2k-1, com k primo. Este resultado é hoje conhecido como Teorema de Euclides-Euler (VIEIRA, 2015).
Após este fato da demonstração elaborada por Euler desencadeou uma procura por mais e mais números perfeitos que hoje, com o auxílio computacional – supercomputadores, forma uma lista de 51 números perfeitos pares, sendo o maior destes números 282.589.932 (282.589.933-1) com 49.724.095 algarismos, conforme consta em (GIMPS), consultado em 17 de setembro de 2020.
Conforme Parreira e Julca (2013) um dos problemas mais antigos e famosos da Teoria dos Números é se existe algum número perfeito ímpar, bem como saber se esta lista é infinita. No entanto, ninguém até o presente momento conseguiu encontrar um número perfeito ímpar que satisfaça a condição de ser perfeito, ou demonstrar a sua não existência. Em 1888 o matemático Sylvester publicou uma série de artigos que desencadeou na era moderna a criação de uma rede de pesquisa para encontrar ou refutar a existência de tais números – conhecida como Rede Sylvester – e muito esforço tem-se realizado nesta direção.
Este breve quadro histórico supracitado nutri e motiva o entusiasmo das mentes curiosas e sedentas do saber para enfrentar o desafio de frente. E é dentro deste espírito que este artigo tem por finalidade mostrar que todo número perfeito tem paridade par e, por conseguinte, afirmar que não existem números perfeitos ímpares.
2. PRELIMINARES
2,1 DA INTUIÇÃO E ESTRATÉGIA DA PROVA
“Às vezes, pode ser útil expressar conceitos familiares com uma nova linguagem”, afirma Vieira (2015), e ouço acrescentar que é preciso estar atento as bases do conhecimento para não deixar escapar do alcance das mãos o objeto desejado ou mesmo se perder nesta busca.
Para a escola pitagórica as partes de um número são seus divisores, então a definição clássica de número perfeito é geométrica, de maneira que um número pode ser formado por suas partes (soma de seus divisores), o que nos inspirou avaliar se a pista para determinar a paridade de um número perfeito poderia ser encontrada em sua própria natureza geométrica.
Então, com o pensamento grego em mente passamos a olhar para o número natural como representante de comprimento de segmento de reta e a buscar sua relação com suas partes (divisores), o que nos arremeteu ao Teorema de Tales da geometria plana que, como afirma Bongiovanni (2007), está no cerne do geométrico com o numérico, visto seu papel fundamental na solução de problemas práticos que envolvem teoria da semelhança e consequentemente funções trigonométricas.
A estratégia utilizada para alcançar a prova será direta e está descrita na Seção (3). Sairemos de uma representação geométrica geral com segmento de reta de comprimento arbitrário n ∈ N={1,2,3,…} e aplicando o Teorema de Tales, definido na Seção (2.2) a seguir, chegaremos à equação (10), que nos permitirá calcular as parcelas proporcionais ao comprimento deste segmento arbitrário em relação aos respectivos divisores (partes) de n. Então, aplicando a condição de existência de um número perfeito determinaremos o menor divisor primo p de n, o qual indica a paridade do número analisado (veja Seção (2.6)) e como demonstrado na Seção (3.1) tem-se p=2, e, consequentemente, concluir que para um número natural ser perfeito tem que ser par.
2.2 TEOREMA DE TALES (DEFINIÇÃO)
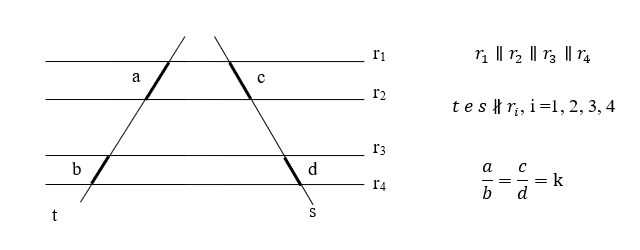
O enunciado clássico do Teorema de Tales diz que: “Se um feixe de retas paralelas é interceptado por duas retas transversais então os segmentos determinados pelas paralelas sobre as transversais são proporcionais”. A Figura (1) a seguir ilustra o enunciado de forma simples, mas suficiente para os fins deste trabalho.
Figura 1: Ilustração do Teorema de Tales com as retas paralelas r1, r2, r3, e r4 cortadas pelas transversais t e s
Por se tratar de um teorema básico da geometria plana e também pelo fato de que vamos utilizar de uma configuração particular na qual as retas formam um triângulo reto (ver item 3) julgamos necessário apenas trazer para o presente artigo uma definição clássica cuja demonstração pode ser encontrada em (BONGIOVANNI, 2007).
2.3 DIVISORES DE UM NÚMERO INTEIRO POSITIVO
Os divisores positivos de um número inteiro n pertencem aos naturais e formam o conjunto Dn = {d1, d2, …, di, …, dj-1, dj}j=1,2,3,…, onde j expressa a quantidade de divisores de n. Como todo número possui como divisores a unidade e o próprio número, os divisores d1 = 1 e dj = n em D são divisores triviais. Ademais, com base no Teorema Fundamental da Aritmética (VIEIRA, 2015) que afirma que todo número natural n>1 pode ser fatorado de maneira única como produto de primos, a menos da ordem dos fatores, se pode inferir que os divisores naturais di de n são seus fatores primos ou algum múltiplo destes fatores. Denotando por p o menor divisor primo de n, temos d2 = p ≥ 2 e dj-1 = n⁄p e Dn ={1, p, d3, …, n⁄p, n}j ∈ N.
2.3.1 PROPOSIÇÃO: O PRODUTO DOS DIVISORES DE UM NÚMERO n EQUIDISTANTES DOS EXTREMOS SÃO IGUAIS AO PRÓPRIO NÚMERO n
d1 dj = d2 dj-1 = ⋯ = di dj-i+1 = n com i, j ∈ N (2)
Exemplo: D147 = {1, 3, 7, 21, 49, 147}, então: 1×147=3×49=7×21=147
Demonstração (Proposição 2.3.1):
Sejam n, r e s números naturais, tais que 0 < r < s < n. Pelos critérios de divisibilidade se r divide n, denotado por r | n, existe um s tal que n=rs ⇒ s=n/r . Ou seja, nestas condições r e n/r são divisores de n, n=r n/r. Disto podemos escrever n como produto de dois de seus divisores equidistantes, a saber: 1.n = d2 . dj-1 = ⋯ = dj . dj-i+1, com di ∈ Dn, desde que di = n⁄dj-i+1, com i=j/2 se j par e i=(j+1)/2 se j ímpar, sendo j a quantidade de divisores de n e i=1,2,3,… ◻
2.4 SOMA DOS DIVISORES
A soma dos divisores de um número natural n > 1 é definida pela função aritmética σ (n): N → N, tal que:
σ(n) = (d1+ d2 + d3 + … + dj-1) +(dj) = (1 + p + d3 + ⋯ + n/p) + (n)
Ou na forma compactada
Note que separamos propositalmente com parênteses os divisores próprios (divisores menores que n) do maior divisor dj = n. A importante desta ação é inerente à definição de números perfeitos vista na Seção (2.5).
Exemplo: D27 = {1, 3, 9, 27}, σ(27) = (1 + 3 + 9) + (27) = (13) + (27) = 40
Onde 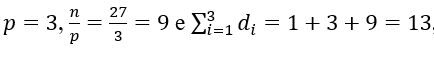 , que é a soma dos divisores próprios de 27.
, que é a soma dos divisores próprios de 27.
2.4.1 PROPOSIÇÃO: A SOMA DOS DIVISORES DE UM NÚMERO É SEMPRE MAIOR QUE O PRÓPRIO NÚMERO
σ(n) > n (4)
Demonstração: Todo número tem por divisores a unidade e o próprio número, assim σ(n) ≥ n + 1 para todo n ◻
2.5 NÚMERO PERFEITO
Um número natural n > 1 é definido com sendo número perfeito quando a soma de seus divisores for igual ao seu dobro.
σ(n) ≝ 2n = (n) + (n) (5)
Voltando a equação (3) e substituindo essa informação
Portanto, como consequência imediata da definição, temos que a soma dos divisores menores que n (divisores próprios) é igual ao próprio número, como mostra a equação (6). Certamente este interessante resultado excitava as mentes dos pitagóricos (e de qualquer estudioso da matemática) na busca de relações que possam ser desencadeadas deste fato.
Exemplo: Para o segundo número perfeito temos:
D28 = {1, 2, 4, 7, 14, 28}, σ(28) = (1 + 2 + 4 + 7 + 14) + (28) = (28) + (28) = 56
É conveniente explicitar da equação (6) o divisor n/p cuja importância será discutida no item 2.6 deste artigo.
Dado que os antigos gregos entendiam os números pela visão geométrica julgamos importante para melhor compreensão do próprio objetivo deste artigo observar as equações (5), (6) e (7) elaboradas acima, que expressam as simetrias básicas de um número perfeito, por essa ótica conforme Figura (2), onde o número perfeito n e a soma de seus divisores σ(n) representarem respectivamente o comprimento dos segmentos AM’ e AC sobre a reta s.
Figura 2: Ilustra o segmento AC de comprimento σ(n) e algumas de suas partes sobre a reta s para um número perfeito n.
Representamos as partes (divisores) AM’ = n e AN’ = n/p, onde M’ é o ponto médio de AC. Note que a posição do ponto N’ ∈ AM’ depende do menor divisor primo p de n, onde esclareceremos sua importância na Seção (2.6) a seguir.
2.6 PROPOSIÇÃO: O MENOR DIVISOR PRIMO p DE n DEFINE SUA PARIDADE
O divisor dj-1 = n/p, com p sendo o menor divisor primo de n, reparte o segmento AB, de comprimento n, em duas partes a e b inteiras que serão iguais se, e somente se, p = 2 e claramente define a paridade de n. Ou seja, se p = 2 o número n será par e se p > 2, n será ímpar, visto que todo primo p ≥ 2 é ímpar. A Figura (3) a seguir ilustra o raciocínio com o número n sobre a reta t,
Figura 3: Ilustra o segmento AB de comprimento n sobre a reta t.
Demonstração (Proposição 2.6):
Seja a, b ∈ N com a + b=n. Como por definição p é o menor divisor primo de n, então p | n ⇒ ∃a ∈ N tal que n = ap.
Sendo n = a + b ⇒ b= n – a e como n e a ∈ N ⇒ b ∈ N
Se p = 2 ⇒ n = ap = 2a ⇒ a = n/2. Como b = n – a = n – n/2 = n/2 ⇒ a = b
Por outro lado, se a = b ⇒ n/p = n – n/p ⇒ p = 2, portanto, se a = b ⟺ p = 2 ◻
Sendo assim, o menor divisor primo p define a paridade de n, como queríamos demonstrar.
3. DEMONSTRAÇÃO PRINCIPAL: TODO NÚMERO PERFEITO É PAR
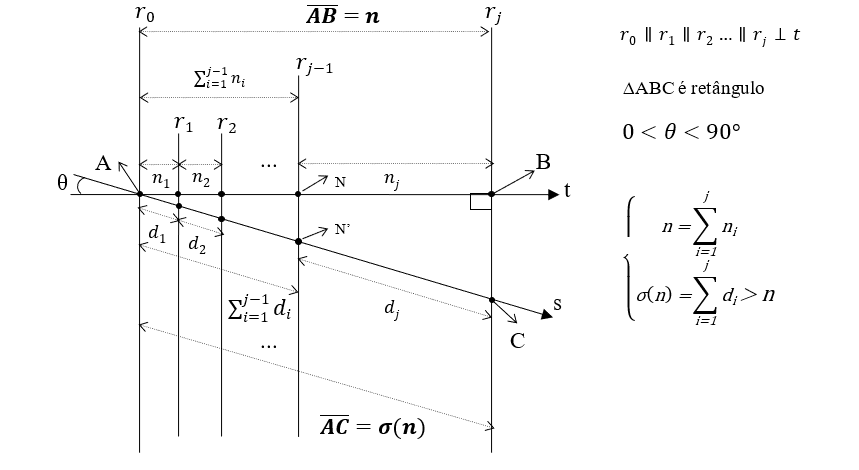
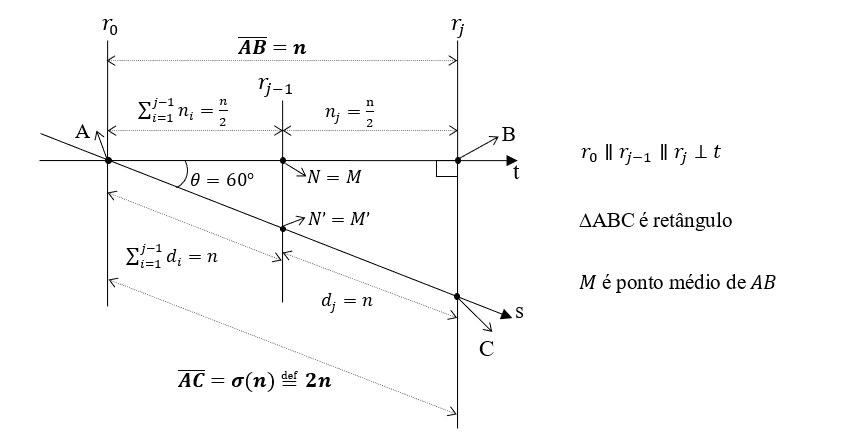
Agora vamos relacionar estas duas configurações que foram representadas respectivamente pelas Figuras (2) e (3) acima, através do teorema de Tales definido na Seção (2.2), que colocará as retas t e r em concorrência no ponto A, como ilustrado na Figura (4), de forma que poderemos segmentar o comprimento n do segmento AB em parcelas proporcionais aos respectivos divisores (partes) do comprimento do segmento AC, σ(n). Note que estamos passando de uma análise em linha para uma análise em duas dimensões com n e σ(n) em ângulo.
Figura 4: Ilustra as retas transversais t e s formando um ângulo θ e cortadas por feixe de retas paralelas ri e perpendicular à reta t.
Sabendo que σ(n) > n para todo n ∈ N (Seção (2.4.1)) poderemos lançar mão de uma configuração particular do teorema de Tales, definido na Seção (2.2), e construir a Figura (4) acima, que foi idealizada fazendo as retas t e s serem concorrentes no ponto A sobre um feixe de retas paralelas r0, r1, r2, …, rj-1, rj (com j sendo a quantidade de divisores de n) que são perpendiculares à reta t e cortam a reta s em segmentos de respectivos comprimentos d1, d2, …, dj+1, dj (que são os divisores de n), e consequentemente, cortarão a reta t em segmentos proporcionais de respectivos comprimentos n1, n2, …, nj+1, nj (que são as parcelas de n). Com esta configuração teremos uma família de triângulos semelhantes ao triângulo retângulo “A” B”C” com ângulos correspondentes iguais. Desta forma, fazendo 0° < θ < 90°, representar o ângulo entre as retas transversais t e s, ![]() seremos capazes de calcular o ângulo θ e as respectivas parcelas de n, denotadas por n1, n2, …, nj+1, nj (que são proporcionais aos respectivos divisores de n), cuja soma resulta, por construção, no próprio número n, como segue:
seremos capazes de calcular o ângulo θ e as respectivas parcelas de n, denotadas por n1, n2, …, nj+1, nj (que são proporcionais aos respectivos divisores de n), cuja soma resulta, por construção, no próprio número n, como segue:
n = (n1 + n2 + ⋯ + ni … + nj-1) + (nj), com ni ∈ ℝ e i=1,2,…,j
De forma compacta, teremos:
Os parentes indicam nossa intenção em separar as j-1 primeiras parcelas da j-ésima de n.
Do Teorema de Tales, Seção (2.2), podemos estabelecer a relação entre as respectivas partes do segmento AB com as do segmento AC:
O termo ![]() em (9) denota o coeficiente de proporcionalidade entre as parcelas e os seus respectivos divisores, de forma que a i-ésima parcela de n será:
em (9) denota o coeficiente de proporcionalidade entre as parcelas e os seus respectivos divisores, de forma que a i-ésima parcela de n será:
Aqui devemos observar que ni é um número racional, pois n, σ(n) ∈ N com σ(n) > n.
Visto que o triângulo ABC é reto se pode utilizar da função trigonométrica arco cosseno, denotada por cos-1, para o cálculo do ângulo θ.
3.1 DETERMINAÇÃO DO MENOR DIVISOR PRIMO p
Para o caso particular dos números perfeitos onde σ(n) ≝ 2n, as equações (9), (10) e (11) resultam respectivamente:
Surpreendentemente o coeficiente de proporcionalidade calculado em (12) entre as parcelas e os divisores de um número perfeito é igual a 1/2 , e consequentemente θ = 60º, que é o ângulo entre os segmentos ![]() . Cabe aqui exaltar o fato interessante que o ângulo θ resulta em um valor inteiro, θ = 60º, somente para quando n é um número perfeito. Uma maneira prática de verificar este fato é fazendo θ variar de 1º em 1º, 0º < θ < 90º, na equação 1/cos(θ).
. Cabe aqui exaltar o fato interessante que o ângulo θ resulta em um valor inteiro, θ = 60º, somente para quando n é um número perfeito. Uma maneira prática de verificar este fato é fazendo θ variar de 1º em 1º, 0º < θ < 90º, na equação 1/cos(θ).
Com base na equação (13) podemos calcular as parcelas de um número perfeito n e avaliar o valor do menor divisor primo p como segue.
Já sabemos que: d1 = 1; d2 = p; dj-1 = n/p e dj = n, então as respectivas parcelas de n assumirão os seguintes valores: ![]()
Com essas informações podemos reescrever a equação (8)
O que nos diz que a soma das primeiras (j-1) parcelas será igual a:
Portanto, um número perfeito n apresenta uma simetria peculiar onde a soma das (j-1) primeiras parcelas é igual à sua j-ésima, implicando que o segmento ![]() será dividido em duas partes de iguais comprimentos, ou seja,
será dividido em duas partes de iguais comprimentos, ou seja, ![]() . O que equivale a dizer que:
. O que equivale a dizer que:
Adaptando a Figura (4) com estas métricas do número perfeito teremos a Figura (5) abaixo.
Figura 5: Ilustra o caso particular do Teorema de Tales para quando n é um número perfeito.
O resultado obtido em (15) é fundamental para a determinação da paridade do número natural n, visto que claramente as somas das (j-1) primeiras parcelas de um número perfeito é a metade do seu valor, o que surpreendentemente divide o segmento AB de comprimento n em duas partes iguais seguindo o mesmo padrão de seus divisores. Este fato implica, como discutido anteriormente em (2.7) e ilustrado na figura (3), que se um segmento é dividido em duas partes iguais (sendo n = a + b e a = b ⟺ p = 2) a paridade do número n é par e, consequentemente, não existem números perfeitos ímpares. ∎
4. CONSIDERAÇÕES FINAIS
Dado que um número perfeito apresenta a simetria apresentada pela Equação (15), que diz que a soma de suas primeiras (j-1) parcelas é igual a metade o valor do próprio número, se pode concluir que todo número perfeito é par como demonstrado na Seção (3), de forma que podemos afirmar que a proposição de Euclides (1) é de caráter geral para um número perfeito qualquer.
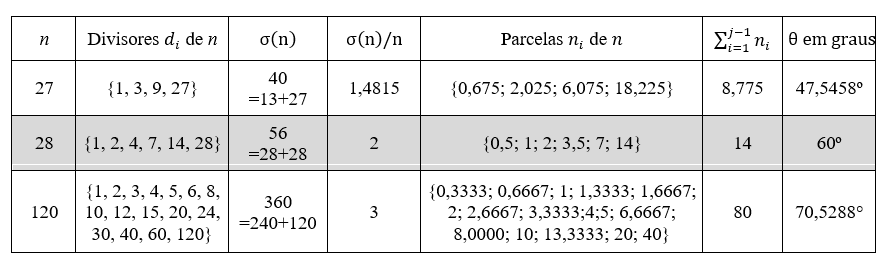
A título de poder apreciar a estética existente nas métricas do número perfeito elaboramos a Tabela (1) a seguir com um número ímpar, um número perfeito e um número k-perfeito, a saber: 27, 28 e 120. Um número natural n é denominado k-perfeito quando a soma de seus divisores for igual a kn, com k ≥ 3 (VIEIRA, 2015). Ademais, redesenhamos as Figuras (2) e (3), enquanto a Figura (6) mostra as partes (divisores), a Figura (7) mostra as parcelas proporcionais a estes divisores de n.
Tabela 1: Mostra as métricas de alguns números sendo o número 28 perfeito.
Figura 6: Ilustra o segmento AC de comprimento σ(n) e suas partes sobre a reta s para um número perfeito n.
Figura 7: Ilustra o segmento AB de comprimento n e suas partes sobre a reta t para um número perfeito.
Por fim, como visto na introdução que os antigos gregos classificavam os números em deficientes, perfeitos e abundantes podemos agora tomar das métricas que se pode calcular pela equação (13) para identificar um ponto M que divide um segmento AB, de comprimento n, em duas partes, a saber: ![]() de comprimento igual à soma das j-1 parcelas e
de comprimento igual à soma das j-1 parcelas e ![]() igual a j-ésima parcela. Como pode ser visto na Figura (8) a seguir, quando n for um número perfeito o ponto M coincidirá com o ponto médio de
igual a j-ésima parcela. Como pode ser visto na Figura (8) a seguir, quando n for um número perfeito o ponto M coincidirá com o ponto médio de ![]() e para os demais casos, quando o número for deficiente M ficará mais à esquerda
e para os demais casos, quando o número for deficiente M ficará mais à esquerda ![]() , e quando o número for abundante, mais para à direita
, e quando o número for abundante, mais para à direita ![]() .
.
Figura 8: Posições relativas do ponto M sobre o segmento ![]() (para igual a 27, 28 e 120).
(para igual a 27, 28 e 120).
CONCLUSÕES FINAIS
Utilizando-se das propriedades do Teorema de Tales foi possível demonstrar que todo número perfeito é par, confirmando que as simetrias que caracterizam um número como sendo perfeito só são possíveis de serem encontradas entre os números pares. Por conseguinte, estabelecer que o Teorema de Euclides-Euler sobre números perfeitos é uma condição necessária e suficiente para defini-los, dando fim a uma bela e fascinante corrida realizada por corajosos desbravadores da Teoria dos Números na busca por um tesouro perdido – a busca dos números perfeitos ímpares, pois estes não existem.
REFERÊNCIAS
BONGIOVANNI, V. O Teorema de Tales: uma ligação entre o geométrico e o numérico. REVEMAT: Revista Eletrônica de Educação Matemática, 2.5, 2007. 94-106.
COSTA, T. J. M. B. D. Os Números Perfeitos e os Primos de Mersenne. Lisboa: Universidade de Lisboa, 2015. Trabalho de Conclusão de Mestrado para Professores.
DEVLIN, K. O gene da matemática. Rio de Janeiro: Record, v. 1, 2004.
FERREIRA, A. J. L. Números perfeitos. [S.l.]: UEPB, 2014. Trabalho de fim de curso em matemática.
GIMPS, P. C. I. M. GIMPS. Creat Internet Mersenne Prime. Disponivel em: <http://www.mersenne.org>. Acesso em: 17 set. 2020.
PARREIRA, A. J.; JULCA, J. A. Existência de limitantes para os três primeiros fatores primos de um número perfeito ímpar. São João Del Rei: PROFMAT, 2013. Trabalho de Conclusão de Curso do Mestrado Profissional em Matemática – PROFMAT.
STEWART, I. O Fantástico Mundo dos Números – A matemática do zero ao infinito. [S.l.]: Zahar, 2015.
VIEIRA, V. L. Um curso em Teoria dos Números. Campina Grande: Editora da Universidade Estadual da Paraíba, 2015.
[1] Engenheiro Eletricista pela Universidade de Juiz de Fora UFJF-MG e Especialista em Engenharia Biomédica pela Universidade do Rio de Janeiro UFRJ-COPPE.
Enviado: Setembro, 2020.
Aprovado: Fevereiro, 2021.

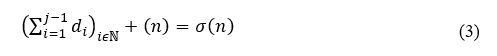
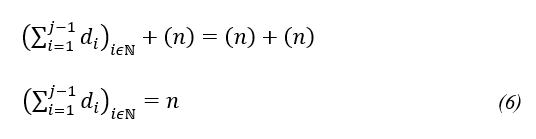




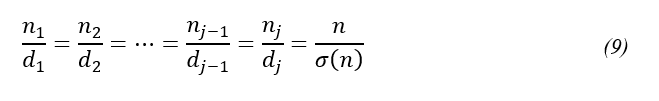

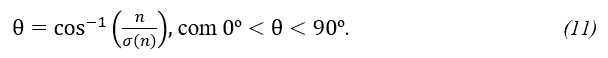

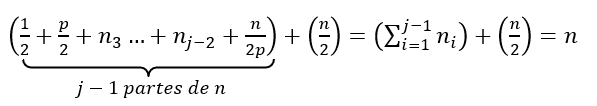




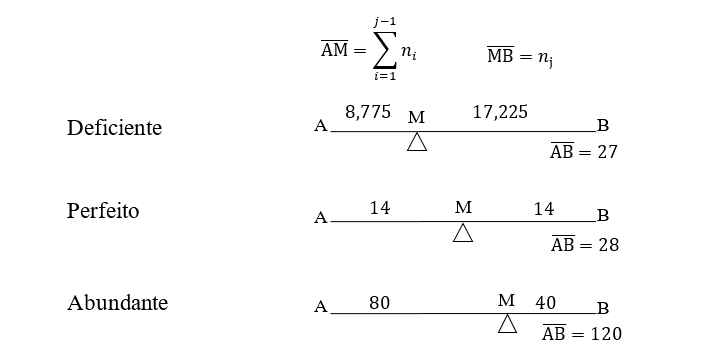

Uma resposta
ola Dr. Claudio!
Muito bonita esta explanação! Parabéns!
Por favor, gostaria de saber se esta prova aqui apresentada é de sua autoria ou de outra pessoa, e se for de outro o senhor saberia de quem?