ARTIGO ORIGINAL
SANTOS, Adecio da Silva [1]
SANTOS, Adecio da Silva. Demonstração Da Conjectura (Forte) De Goldbach. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 04, Vol. 06, pp. 05-10 Abril de 2019. ISSN: 2448-0959
RESUMO
A conjectura de Goldbach é um dos problemas abertos mais antigos da história da matemática, aproximadamente 300 anos sem solução. Ela foi proposta pelo matemático prussiano Christian Goldbach. Seu registo está em uma carta datada de 7 de junho de 1742 e destinada a Leonard Euler. Este, por sua vez, respondeu Goldbach em outra carta dizendo está absolutamente certo que esta conjectura era verdadeira, mas não era capaz de prova-la. Baseando nos nesta breve história e confiando na absoluta certeza de Euler, acreditamos que o método de demonstração por redução ao absurdo seja o mais viável para provar esse problema. Nosso artigo prova que esta famosa conjectura, de fato, é verdadeira. Além disto conjecturamos e provamos um resultado parecido com o de Goldbach, o chamemos de Conjectura de X. O mesmo está
exposto no APÊNDICE A. Por fim deixamos no APÊNDICE B, uma demonstração extra da Conjectura de Collatz como bônus.
Palavras-chave: Conjectura (forte), Demostração, Goldbach.
1. INTRODUÇÃO
Muitas vezes um problema simples de se entender pode ser difícil de se explicar. Este é o caso do conjectura (forte) de Goldbach. Pois ela afirma que qualquer número par maior que dois pode ser representado pela soma de dois primos. Intuitivamente somos levados a acreditar que tal afirmação é verdadeira. Mas este é o “x” da questão. Muitos matemáticos já tentaram, sem êxito, demonstra-la.
O portal do Geogebra (1) traz uma programação de verificação da Conjectura de Goldbach. O mesmo, também verifica para muitos números pares a veracidade da conjectura. Porém isto não é suficiente para provar que essa informação é de fato verdadeira e incontestável.
Baseando nos em nosso intuição, na crença da comunidade matemática e ainda nas várias verificações por computadores que a Conjectura de Goldbach é verdadeira. Entendemos que o
método de demonstração por redução ao absurdo é o mais viável para prova-la.
Nosso artigo expõe uma tentativa de resolver esse problema. Mostra, também, no APÊNDICE A, um resultado, chamado de Conjectura de X, semelhante ao de Goldbach e ainda fornece
um extra no APÊNDICE B da demonstração da Conjectura de Collatz.
Por fim, entendemos que é importante esclarecermos ao leitor que não é da área de matemática que não “estranhe” as citações neste artigo estarem mais nas seções da Introdução e do Referencial Teórico e nenhuma no corpo do texto, pois uma argumentação matemática de demonstração para um problema em aberto sempre é uma ideia original, além deste problema já ser conhecido por três gerações.
2. REFERENCIAL TEÓRICO
A conjectura de Goldbach é bem famosa, existem vários trabalhos sobre o tema. Mas nossas referências teóricas mais importante para chegarmos em nossos resultados foram as (2) e (3). Pois (2) nos forneceu a base de raciocínio lógico pelos princípios do terceiro excluído e 2 da não contradição, além de nos fornecer a estrutura da contra positiva para basearmos nossa prova na redução por absurdo. Já a referência (3) nos exercitou muito em seus exercícios para o amadurecimento de como ter uma ideia e como atacar a Conjectura (forte) de Goldbach.
Ao leitor interessa em conhecer mais sobre problemas matemáticos em aberto, problemas do milênio, ou conjecturas famosas, deixamos as referências (4), (5), (6) e (7) como indicações.
3. CONJECTURA (FORTE) DE GOLDBACH
Nesta seção apresentaremos o Conjectura (forte) de Goldbach e a prova da sua veracidade pelo método de demonstração por redução ao absurdo.
Conjectura (forte) de Goldbach: Todo número par maior que 2 pode ser escrito como a soma de dois primos.
Demonstração. Note que todo número par maior que 2 é a soma de dois primos ou é a soma de um primo com um ímpar composto ou é a soma de dois ímpares compostos.
Pelo fato da verificação em computadores que mostraram para vários números pares em sequência e muito grandes que os mesmos sempre são a soma de dois primos, iremos provar que
quaisquer somas de qualquer primo ímpar com qualquer ímpar composto ou a soma de quaisquer dois ímpares compostos, cuja as mesmas sejam maiores que 10, é a soma de dois primos.
Para tanto suponhamos, por absurdo, que algum número par maior que 10 fosse a soma de um número primo, p0, com um número ímpar composto, C0, ou seja p0+C0, e esta soma nunca fosse a soma de dois primos. Além disso, note que todo número par maior que 10 admite um número impar composto, digamos Cx, com Cx+2 sendo primo.
Agora, tomemos o maior número impar composto, digamos Cx, menor do que p0+C0 com Cx+2 sendo primo e o menor primo, digamos px, menor do que p0+C0 tais que Cx+ px < p0+
C0 . Veja que p0+C0=Cx+2+ px, contraria nossa suposição, pois px e Cx+2 são primos. Daí, pela minimalidade de px e pelo maximal de Cx, temos que Cx+px < p0+C0<Cx+2+px. Então, subtraindo o termo Cx+ px em todos os membros da expressão Cx+ px < p0+C0 <Cx+2+ px obtemos que 0 < p0 +C0 – (Cx + px) < 2. Ou seja, o número par p0+C0 -(Cx + px) = 1. ABSURDO!
Analogamente, suponhamos, por absurdo, que exista algum número par maior que 10 sendo a soma de dois números ímpares composto, digamos C0+C1, e esta soma nunca fosse a soma de dois primos. Além disto, podemos tomar um primo p0 <C0+C1 admitindo números ímpares compostos menores que ele.
Vamos, agora, tomar o maior número ímpar composto menor do que C0+C1, digamos Cx, e cujo seu sucesso impar seja primo e o menor primo ( que admita ímpares compostos menores que ele), digamos px, menor do que C0 +C1 , tais que Cx + px < C0 +C1. Isto implica, pela minimalidade de px e pelo maximal de Cx no seguinte resultado Cx+px <C0+C1 <Cx+2+px, pois, se C0 +C1 = Cx +2+ px, o fato de Cx+2 ser primo teríamos que a expressão C0 +C1 seria a soma de dois primos,o que contraria nossa suposição. Finalmente, subtraindo o termo Cx + px em todos os membros da expressão Cx + px < C0 +C1 < Cx +2+ px obtemos que 0 <C0+C1- (Cx+ px) < 2. Ou seja, o número par C0+C1-(Cx+ px) = 1. ABSURDO!
Portanto, todo número par maior do que 10 pode ser representado pela soma de dois números primos, pois a mesma, como provamos acima, representa sempre a soma de um número primo com um ímpar composto ou é a soma de dois ímpares compostos. Além disto, temos que 2+2 = 4, 3+3 = 6, 3+5 = 8 e 5+5 = 10 . Então podemos concluir que todo número par maior que 2 pode ser escrito como a soma de dois números primos.
4. CONSIDERAÇÕES FINAIS
Provar um resultado matemático vai muito além de um simples estudo contemporâneo ou uma invenção tecnológica, pois se tal afirmação matemática for provada ela se torna uma verdade universal e imortal.
A Conjectura (forte) de Goldbach é um exemplo disto. Nosso artigo expõe um resultado importante de aproximadamente 300 anos sem solução com uma solução não tão pesada. Não menos importante, a Demonstração da Conjectura de Collatz também é uma grata surpresa neste trabalho. Além da Conjectura de X que pode ser explorada ainda mais em futuros trabalhos.
Esperamos com este artigo incentivar os leitores a se tornarem estudiosos ou até mesmo pesquisadores na área da Teoria dos números, análise real ou afins em prol do desenvolvimento
dessa brilhando conquista da humanidade chamada de matemática.
REFERÊNCIAS
1. Portal do geogebra. Disponível em: https://www.geogebra.org/m/EmQ3jQdB. Acesso em 17 de abril de 2019.
2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel,
1975.
3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.
4. Portal do obaricentrodamente. Disponível em: https://www.obaricentrodamente.com/2014/01/ conjecturas-de-seba-sobre-distancia_25.html. /PROBLEMAS_MATEMATICOS_DO_SECULO_XXI.pdf. Acesso em 14 de abril de 2019.
5. Portal do wikipedia. Disponível em: https://pt.wikipedia.org/wiki/Problemas_em_aberto_da_ma tem%C3%A1tica. Acesso em 17 de abril de 2019.
6. Portal do cienciahoje. Disponível em: http://cienciahoje.org.br/artigo/primos-que-podemfazer- historia/. Acesso em 17 de abril de 2019.
7. Portal do hypescience. Disponível em: https://hypescience.com/problemas-matematica/. Acesso em 17 de abril de 2019.
APÊNDICE A
Conjectura de X: A soma de quaisquer dois números primos ímpares, cuja essa soma é maior que 10, pode ser representada pela soma de um primo ímpar com um ímpar composto ou por a
soma de dois ímpares compostos.
Demonstração. De fato, suponhamos por absurdo, que exista uma soma de dois primos ímpares
maior do que 10, digamos px+py, que nunca seja igual a soma de um primo ímpar com um ímpar composto, ou nunca seja a soma de dois ímpares compostos. Agora, tomemos o maior ímpar
composto, digamos C0, e o menor primo ímpar, digamos p0, tais que C0+ p0 < px+ py. Observe que se C0+(2+ p0) = px+ py então px+ py seria a soma de um número ímpar composto, Co,
com um número ímpar primo ou impar composto, pois 2+ p0 pode ser ou ímpar primo ou ímpar composto, mas isto está em contradição com nossa suposição. Logo como C0 é o maior composto ímpar e p0 é o menor primo tais que C0 + p0 < px + py então temos, obrigatoriamente, que C0+ p0 < px+ py < (C0+2)+ p0. Daí encontraríamos 0 < (px+ py)-(C0+ p0) < 2, porém
como (px+ py); (C0+ p0) são ambos números pares, então (px+ py)-(C0+ p0) = 1 seria um número par. ABSURDO!
Mas esta contradição ocorreu devido termos suposto a conjectura falsa, logo ela é verdadeira.
APÊNDICE B
Conjectura de Collatz: Para todo número natural não nulo vale a seguinte regra: “Caso o número for par divida-o por 2, se for ímpar multiplique o por 3 e adicione 1, e fazendo assim
sucessivamente, chega-se sempre ao número 1.”
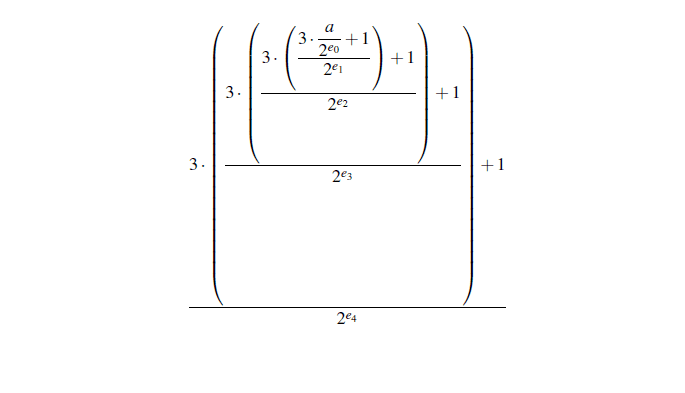
Demonstração. Suponhamos que exista pelo menos um número a natural não nulo que o procedimento dessa regra nunca chegue ao número 1. Ou seja, esse processo nunca tenha fim. Independente se esse número a seja par ou ímpar, teremos sempre uma expressão do tipo
Para simplificar a linguagem matemática escrevamos assim
Número natural não nulo a que seja exceção a esta regra. Portanto, a Conjectura de Collatz é verdadeira.
[1] Graduado e mestre em Matemática, professor de matemática no IFPI-SRN.
Enviado: Março, 2019
Aprovado: Abril, 2019

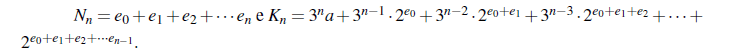


19 respostas
Muito bem. Perfeito
Parabéns Adecio , ótimo artigo !
Nao entendi oque o “e”.
Alguem pode me ajudar?
Boa tarde. Poderia me explicar a afirmação: “Além disso, note que todo número par maior que 10 admite um número impar composto, digamos Cx, com Cx+2 sendo primo.” Contida no terceiro parágrafo da demonstração?
O “e” sao as somas dos expoentes de base dois que se repetem infinitamente em cada etapa do processo. Obrigado por comentar!
Não entendi, você está afirmando que provou a conjectura de Goldbach que tem mais de 200 anos? Não tem um prêmio de milhões de reais pra quem fizer isso?
Na sequência natural dos números temos 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5 , 10 = 5 + 5, 12 = 5 + 7, 14 = 7 + 7, 16 = 5 + 11, 18 = 7 + 11, 20 = 7 + 13, 22 = 11 + 11, 24 = 11 + 13, 26 = 13 + 13, 28 = 11 + 17, 30 = 13 + 17, 32 = 13 + 19, 34 = 17 + 17, 36 = 17 + 19, 38 = 19 + 19, 40 = 23 + 17, 42 = 23 + 19, 44 = 27 + 17, 46 = 29 + 17, 48 = 31 + 17, 50 = 31 + 19 … e olhando para a lista dos números primos, verificamos que parece existir uma lógica na formação dos números pares a partir da lista dos números primos. Por exemplo, os números primos menores que 42 são o 2, 3, 5, 7, 11, 13, 17, 19, 23,29, 31, 37, 41 . Os números primos maiores que 42/2 e menores que 42 são o 23, 29, 31, 37, 41. Estes números desempenham um papel fundamental, pois sem eles não é possível obter dois números primos cuja soma seja 42. Assim podemos fazer 42 = 37 + 5, 42 = 29 + 13, 42 = 23 + 19. Caso os números 37, 29, 23 não fossem primos isso seria inviável. Mas faltando esses números primos isso teria outras consequências na existência doutros números, ou seja na decomposição dos mesmos em fatores primos. Por exemplo 185 = 5 x 37 não seria a decomposição única em fatores primos. A minha questão é esta: a conjetura de Goldbach não seria um axioma resultante de uma conjugação natural entre os números primos e a produção de números pares?
Teria sido melhor melhor se tivesse começado o artigo exemplificando com números todos os termos elencados, antes de usá-los genericamente, pois, salvo engano, se entendi os termos utilizados, o que foi dito não é consistente com alguns exemplos numéricos, por exemplo, com os pares 20 e 26.
Aguardo resposta.
Bom dia colegas José e Olavo, primeiramente, obrigado por separarem um tempo de vocês para ler o artigo. posso passar o pdf original para vocês e agente discutir…meu objetivo é começar a tentar fazer essas conjecturas matemática no meu meio de professores. Confesso que está difícil pois atualmente os professores estão focados mais na parte educacional do que na pesquisa. Porém, dei o 1° passo, estou aberto a contestações…até agora nenhum dos professores de matemática da minha instituição (IFPI ) e alguns amigos do IFMA nao mostraram se a prova esta certa, errada ou contribui de alguma forma para futuras abordagens. Irei ler novamente ela… pois estava ocupado em um tratamento de saúde. Sugiro aos amigos abordamos também o problema E.
Os profissionais aqui da revista Nucleo do conhecimento são muito comunicativos, basta falar no watts com eles que eles repassam o meu a vocês. Abraço espero o contato.
Tenho um grupo de zap,no qual a maioria dos membros trabalham em demonstrações para a conjectura de Collatz.Se tem interesse em debater o assunto,ou conhecer novos trabalhos,pode me mandar seu numero que adiciono.
O erro em Collatz é que Kn e Mn também tende para o infinito, então a raiz não tende para 1.
Eu consegui identificar um erro na conjuctura de x.
Você afirmou que não poderia levar em consideração que c0 + (p0 +2 ) = px + py pois ia de contra a sua hipótese.
Dessa forma, claro que c0 + (p0 +2 ) ≠ px + py.
Então há duas possibilidades a considerar:
• px + py < c0 + (p0 +2) e com isso c0 + p0 < Px + py < c0 + p0 +2
Ou
• c0 + (p0 +2) < Px + py e com isso c0 + p0 < c0 + (p0 +2) < Px + py
Você levou em consideração apenas a primeira. Realmente. Se fosse apenas ela, a conjuctura estaria correta. Mas tem a segunda hipótese e ela não se tira uma conclusão que nos ajude. Se a segunda hipótese chegasse também num absurdo, a conjectura x estaria provada.
O que ele quer dizer com a afirmação “note que todo número par maior que 10 admite um número impar composto, digamos Cx, com Cx+2 sendo primo.” é que eu sempre posso achar um número ímpar maior do que 10, Cx, para o qual Cx+2 é primo.
repare o seguinte Cristina Dias, com exceção so 1 e do 9 todos os números impares menores do que 10 são primos, a partir do dez, você pode começar a forma números pares da seguinte maneira, np + nc, ou seja, um número primo qualquer e um número composto.
Caro Adécio,
Não sei se você já encontrou algum erro na sua demonstração da conjectura forte, estou um pouco atrasado na discussão. Mas fica difícil de nós, leitores, encontrarmos erros, porque não sabemos o que você quis dizer com certas afirmações. Por exemplo esta já citada por outras pessoas:
“note que todo número par maior que 10 admite um número impar composto, digamos Cx, com Cx+2 sendo primo”
No mais, fiquei confuso na seguinte parte
“Agora, tomemos o maior número impar composto, digamos Cx, menor do que p0+C0 com Cx+2 sendo primo e o menor primo, digamos px, menor do que p0+C0 tais que Cx+ px < p0+
C0"
Veja que sendo Cx o maior ímpar composto menor que p0+C0 com Cx+2 primo pode ser o antecessor de p0+C0, isto é, nada impede que tenhamos Cx=p0+C0-1. Nesse caso, não existiria um tal primo px como a sequência da frase afirma.
Espero respostas, amigo. Até breve.
Boa tarde Adecio, trabalho no IFPI e gostei muito do teu artigo. Eu também desenvolver provas parciais de matemática. Gostaria de compartilhar e discutir estas ideias com você. Tem como eu entrar em contato com você?.
Caro mestre em Matemática ADECIO gostei muito do trabalho o que desejo e que entre em contato comigo é que descobrir onde estão os limites inicial e final, caso se interesse. Celular WhatsApp 83994169059
Só para refletir um primo tem que existir e estar entre meio décimo de raiz exata até a raiz exata e meia, para sucessor e raiz exata e meia até a raiz exata seguinte para antecessor:
1 ao quadrado até 1,5 ao quadro ( 2)
1,5 ao quadrado até 2 ao quadrado (3)
Um par é formado de uma Balança de primos para mais e para menos entre suas raízes…
Caro ADECIO, gostei de ver seu trabalho, tenho meu WhatsApp 83 994169059 e o e-mail abaixo para unir a sua demonstração com a minha resolução e prova desta conjetura, pois sei o limite inicial e final.
Para refletir um primo pelo menos existe e estar entre o quadrado de um número e este quadrado adicionado meio décimo. Este é o limite inicial de um primo e final da sua procura.
Exemplo: Para sucessor da raiz exata
sete ao quadrado = 49
sete e meio ao quadrado = 56,25
Existe pelo menos um primo entre eles = 53
Exemplo: Para antecessor da raiz exata e exata e meia
seis e meio ao quadrado = 42,25
sete ao quadrado=49
Existem 43 e o 47 (pelo menos um primo)
E no máximo 4
10,5*10,5=110,25
11*11=121
Existe pelo menos um primo=113
Em ambos procurar primos e primos formando um par (conjetura de Goldbach) Resolvo
Quanto a conjetura entre em contato pelo meu e-mail ou mande pelo WhatsApp