ARTIGO DE REVISÃO
MEDEIROS, Davison Machado [1], COSTA, Patrício Torres [2]
MEDEIROS, Davison Machado. COSTA, Patrício Torres. Sólidos de revolução e o Cálculo, uma extensão do estudo do volume e da área. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 03, Vol. 03, pp. 141-154. Março de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/solidos-de-revolucao
RESUMO
O presente trabalho se propõe a aplicar o Cálculo Diferencial e Integral aos sólidos de revolução sob uma perspectiva geométrica, significativa, para os alunos das diversas graduações que fazem uso do Cálculo. O Cálculo é um dos temas mais complexos da graduação, pois além de ser uma disciplina altamente técnica, exige de forma efetiva todo o conhecimento matemático adquirido na vida escolar do aluno: álgebra, geometria plana, geometria analítica, trigonometria, funções, entre outros. Daí surge a necessidade de uma aplicação aos sólidos de revolução com uma abordagem mais acessível a públicos que não são totalmente familiarizados com a linguagem matemática técnica e direta, como costumeiramente é nos livros de Cálculo. Para conseguir esses objetivos foram introduzidos os sólidos de revolução mais simples e comuns estudados desde a educação básica prosseguindo para sólidos mais elaborados e incomuns, como é o caso dos sólidos infinitos.
Palavras-chave: Sólidos de Revolução, volume e área dos sólidos de revolução, derivada, integral.
1. INTRODUÇÃO
Este artigo tem por objetivo precípuo empregar o Cálculo Diferencial e Integral para calcular a área da superfície e volume dos sólidos de revolução dados por uma função real de uma variável real, com uma abordagem matemática elucidativa.
O Cálculo Diferencial e Integral, que sem prejuízo será chamado apenas de Cálculo, é uma poderosa ferramenta da matemática moderna com aplicações imensuráveis, inclusive nas mais diversas áreas do conhecimento científico. A priori esse surgiu como resposta para se encontrar áreas de figuras curvilíneas e tangentes a curvas, respectivamente, mas suas aplicabilidades são muito maiores do que as antes imaginadas. Segundo Eves (2011, p. 417) “com essa invenção a matemática criativa passou a um plano superior e a história da matemática elementar essencialmente terminou”. Do mesmo modo os sólidos de revolução são objetos matemáticos fascinantes encontrados na arquitetura, engenharia, natureza e nos mais variados lugares com surpreendentes aplicações por meio de sua simetria e estética, mas nota-se que os conhecimentos matemáticos elementares de áreas e volumes são insuficientes para estudá-los, necessitando assim dessa extraordinária ferramenta matemática, o Cálculo.
2. SÓLIDOS DE REVOLUÇÃO
O estudo dos sólidos de revolução inicia-se de forma muito sutil no ensino médio com os chamados sólidos cilíndricos: cilindro, cone, tronco de cone e esfera. No entanto, aqui estenderemos o conceito de sólido de revolução de forma geral e formal.
Definição. Sólido de revolução. Um sólido de revolução ou corpo de revolução é uma região de ![]() que se obtém rotacionando uma região plana ao redor de um eixo de giro.
que se obtém rotacionando uma região plana ao redor de um eixo de giro.
A região plana é definida como o lugar geométrico compreendido entre o gráfico de uma função f (x) e as retas perpendiculares ao eixo das abscissas, x = a e x = b; o eixo de rotação será o eixo x das abscissas ou o eixo y das ordenadas. Graficamente tem-se um sólido de revolução como na figura a seguir.
Figura 1 – Sólido gerado pela rotação da região A ao redor do eixo x
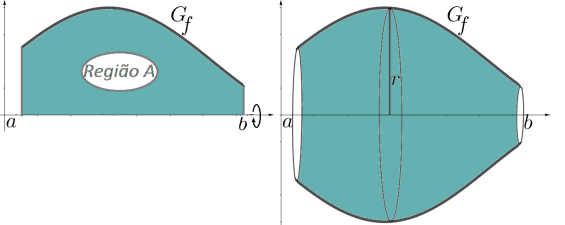
Percebe-se que o eixo de revolução passa pelo centro do sólido e que secções transversais geram círculos de raio r = f (x). Com isso os sólidos de revolução são objetos simétricos, com seu eixo de simetria sendo o eixo de revolução, por conta disso são chamados também de corpos cilíndricos.
Os fungos ascomicetos, um importante caso de sólido de revolução são encontrados abundantemente na natureza e possuí a forma de um parabolóide de revolução. O parabolóide, um sólido obtido pela rotação de uma parábola através de seu eixo, é amplamente utilizado por causa da propriedade da parábola de fazer convergir qualquer onda recebida para o seu ponto focal e com isso ampliando significativamente o sinal da onda, e o inverso também ocorre.
Esta superfície possui inúmeras aplicações interessantes, todas elas decorrentes de uma propriedade geométrica da parábola […]. A fama das superfícies parabólicas remonta à Antiguidade. Há uma lenda segundo a qual o extraordinário matemático grego Arquimedes, que viveu em Siracusa em torno do ano 250 A.C., destruiu a frota que sitiava aquela cidade incendiando os navios com os raios de sol refletidos em espelhos parabólicos. (LIMA, 2012, p. 154).
Das inúmeras aplicações do parabolóide as mais comuns são em faróis e em antenas parabólicas em geral. Na figura a seguir podemos ver na natureza os fungos ascomicetos que nos lembram antenas parabólicas.
Figura 2 – Fungos ascomicetos que se aproximam à forma de parabolóide

2.1 VOLUME DOS SÓLIDOS DE REVOLUÇÃO
Desde o ensino fundamental vê-se de forma resumida alguns sólidos de revolução e a fórmula para se calcular o volume e a área da superfície de casos particulares. No geral, os sólidos de revolução são objetos que possuem várias formas, inclusive algumas muito diferentes das que estamos acostumados. Com isso, percebe-se que o estudo destes através das fórmulas para volumes que conhecemos são ineficazes. Aplicando o Cálculo pode-se obter expressões para o volume e área da superfície de qualquer um desses sólidos.
2.1.1 VOLUME DE UM SÓLIDO OBTIDO PELA ROTAÇÃO DE UM CONJUNTO EM TORNO DO EIXO X (MÉTODO DOS DISCOS)
Seja f uma função contínua e positiva em [a, b] e 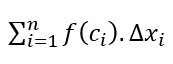 uma soma de Riemann. Essa é uma soma de áreas de retângulos. Ao girar esses retângulos ao redor do eixo x geramos cilindros retangulares retos (discos), cujo raio r da base é f (ci) e altura h = Δxi.
uma soma de Riemann. Essa é uma soma de áreas de retângulos. Ao girar esses retângulos ao redor do eixo x geramos cilindros retangulares retos (discos), cujo raio r da base é f (ci) e altura h = Δxi.
Figura 3 – Disco de raio f (ci) e altura Δxi em um corpo de revolução
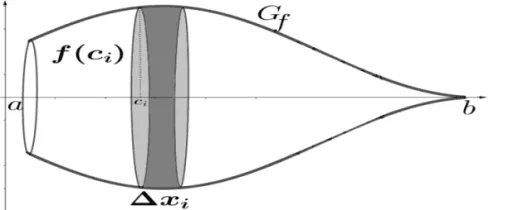
O volume de cada um desses discos são dados por ![]() . A soma do volume de todos esses discos é aproximada ao volume do sólido desejado. Então nada mais natural do que se definir o volume V do sólido como sendo:
. A soma do volume de todos esses discos é aproximada ao volume do sólido desejado. Então nada mais natural do que se definir o volume V do sólido como sendo:
Quando se faz máx Δxi → 0, então n → ∞; isto é, a quantidade de discos infinitesimais vai para infinitos discos, com isso exaurindo todo o volume do sólido.
2.1.2 VOLUME DE UM SÓLIDO OBTIDO PELA ROTAÇÃO DE UM CONJUNTO EM TORNO DO EIXO Y (MÉTODOS DOS CILINDROS)
Seja f uma função contínua definida em [a, b], positiva e A uma região limitada pelo gráfico de f, pelas retas verticais x = a, x = b. Girando esta região A ao redor do eixo das ordenadas y obtêm-se um sólido de revolução como na figura a seguir.
Figura 4 – Sólido obtido pela rotação da região A em torno do eixo y
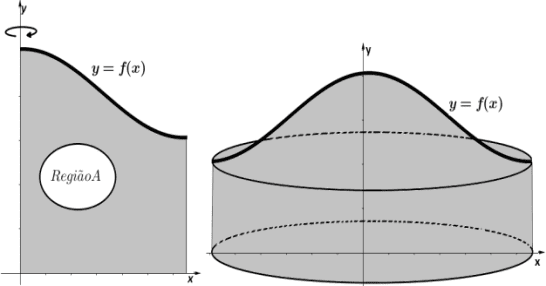
Seja 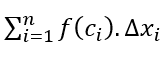 uma soma de Riemann. Esta é uma soma de áreas de retângulos. Ao girar esses retângulos ao redor do eixo y geramos cilindros retos, cujo raio menor r = xi-1 e o raio maior R = xi e altura R = f (ci), com
uma soma de Riemann. Esta é uma soma de áreas de retângulos. Ao girar esses retângulos ao redor do eixo y geramos cilindros retos, cujo raio menor r = xi-1 e o raio maior R = xi e altura R = f (ci), com 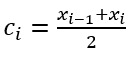 sendo o raio médio desses cilindros como podemos ver na figura a seguir.
sendo o raio médio desses cilindros como podemos ver na figura a seguir.
Figura 5 – Aproximação por cilindros do volume de sólido obtido pela rotação em y
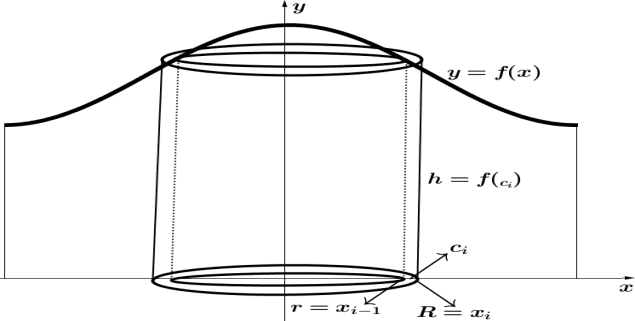
O volume Vi desse cilindro genérico é dado por:
Donde tem-se uma boa aproximação para o volume Vy do corpo inteiro somando todos os cilindros contidos no sólido de revolução:
Isto é, ao fazer as bases Δxi desses cilindros irem para zero a quantidade de cilindros vai para infinito, com isso exaurindo o volume do sólido, como queríamos.
Um dos conjuntos de sólidos de revolução mais simples é o que se encontra nos estudos do ensino médio. Os que são comumente estudados nessa etapa são: cilindro, cone, tronco de cone e esfera. Com o Cálculo, estudar esses sólidos torna-se algo extremamente simples, vejamos.
Exemplo 1. Calcular o volume e a área lateral de um cilindro. Observa-se que um cilindro é facilmente gerado por uma região retangular ao rotacionar-se esta através de um eixo, para tanto, tomamos a função y = r definida em [0,h]. Pela figura a seguir percebe-se que r é o raio do cilindro e [0,h], isto é, h é a altura.
Figura 6 – Cilindro gerado por uma região retangular
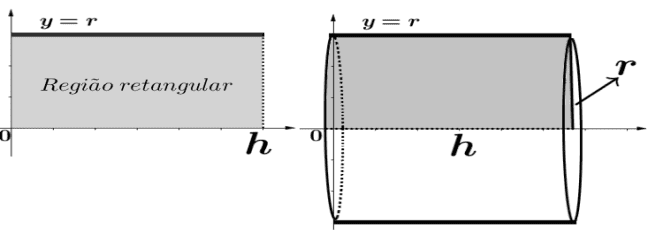
Aplicando os dados na relação Vx para volume pela rotação da região retangular em torno do eixo x tem-se:
Ou seja, o volume do cilindro é o produto da área da base circular, πr2, pela altura h.
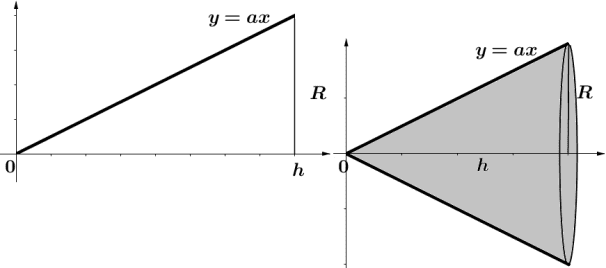
Exemplo 2. Calcular o volume de um cone. Observa-se que este é facilmente gerado pela rotação de um triângulo retângulo através de um eixo, para tanto, tomamos a função y = ax definida em [0,h]. Pela figura a seguir percebe-se que f(h) = ah = R é o raio da base do cone e h é a altura.
Figura 7 – Cone gerado pela rotação de um triângulo retângulo em x
Aplicando os dados na relação Vx para volume pela rotação da região triangular em torno do eixo x tem-se,
de f (h) = a.h = R percebe-se que a2h3 = (a.h)2 . h = R2 . h, de onde segue que o volume do cone Vx em função de seu raio R e altura h é dado por,
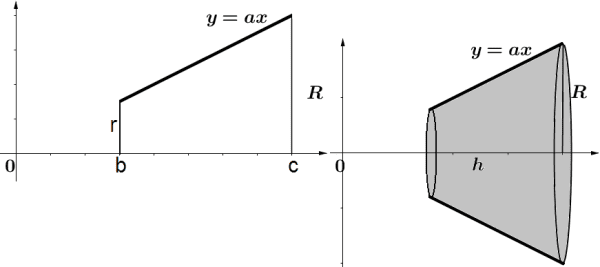
Exemplo 3. Calcular o volume de um tronco de cone. Observa-se que este é gerado pela rotação de um trapézio retângulo através de um eixo, para tanto, tomamos a função definida em y = ax. Pela figura a seguir percebe-se que f(b) = ab = r é o raio menor e f(c) = ac = R é o raio maior do tronco de cone e [b,c], isto é, [c – b] = h é a altura.
Figura 8 – Tronco de cone gerado pela rotação de um trapézio em x
Com isso podemos calcular facilmente o volume Vx e a área lateral Ax como segue,
Exemplo 4. Calcular o volume da superfície da esfera r.
Um problema muito simples de corpo de revolução é calcular o volume de uma esfera de raio .
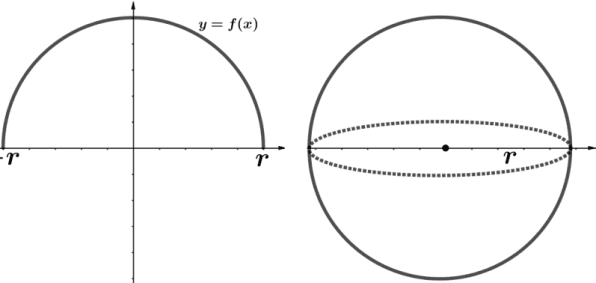
A função ![]() definida em [-r, r] gera o semicírculo de raio r que ao ser rotacionado através do eixo x produz a esfera de raio r, como podemos ver na figura a seguir.
definida em [-r, r] gera o semicírculo de raio r que ao ser rotacionado através do eixo x produz a esfera de raio r, como podemos ver na figura a seguir.
Figura 9 – Esfera de raio r
Utilizando a fórmula para volume de um sólido de revolução rotacionado pelo eixo x tem-se,
De onde tem-se,
Exemplo 5. A Geodésia é a ciência que se ocupa em estudar a forma, dimensão e características da Terra. É comum pensar que a Terra é esférica, isto não é correto, na verdade ela é achatada nos pólos e se aproxima à forma de um elipsóide de revolução.
O Elipsóide de Revolução […]. Constitui a forma definida matematicamente que mais se aproxima da forma verdadeira da Terra, portanto é, dentre todas, a forma que permite a maior precisão de representação da Terra. Os mapas e cartas topográficas, o sistema GPS e a grande maioria dos sistemas e processos envolvidos em cartografia e navegação, trabalham sobre o modelo elipsóidico terrestre. Esta é a forma padrão considerada pela Geodésia para trabalhos de precisão. (TIMBÓ, 2001, p. 10).
Com isso pode-se calcular com precisão o volume da Terra por um elipsóide de revolução. Defini-se elipsóide de revolução como sendo o sólido obtido pela rotação de uma elipse entorno de um eixo.
A elipse é dada por:
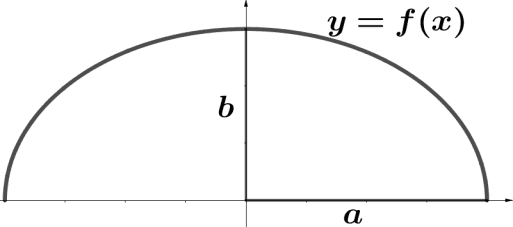
Geometricamente tem-se a parte positiva da elipse dada por y como na figura a seguir.
Figura 10 – Parte acima do eixo x da elipse 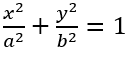
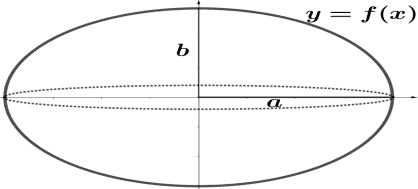
Ao rotacionar-se a região abaixo do gráfico de y = f (x) em torno do eixo x obtém-se o elipsóide como na figura a seguir.
Figura 11 – Elipsóide de revolução
Com isso seu volume é dado pela relação Vx:
De onde segue que o volume procurado é dado por,
Isto é, tendo-se os eixos da Terra, pode-se facilmente calcular o volume pela relação Vx.
Exemplo 6. Segundo Eves (2011, p. 358), Kepler um dos precursores do Cálculo interessou-se neste pela questão de se calcular o volume de barris de vinho da época e de um sólido chamado toro que apresenta o formato aproximado de uma câmara de pneu, pois não havia ferramentas matemáticas que fossem eficazes no cálculo desses volumes, e isto certamente influenciou o seu trabalho dos movimentos planetários. Surge então o problema de calcular o volume de um barril.
Pode-se aproximar este volume pela rotação de um segmento de parábola em torno do eixo x de [-b, b], isto é,
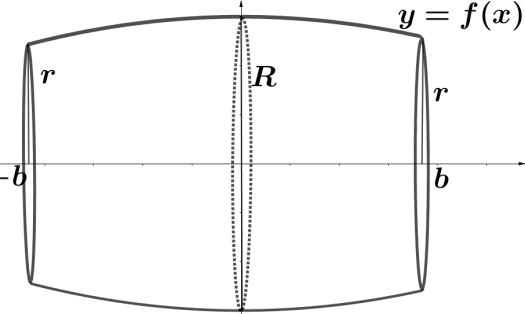
onde 2b = h é a altura, R é o raio maior e r é o raio menor do barril, geometricamente tem-se a figura a seguir.
Figura 12 – Barril aproximado por parábola
Deste modo o volume Vx é dado por,
De onde segue que o volume Vx é,
Exemplo 7. Calcular o volume de um Toro. O toro ou toróide é definido como o lugar geométrico formado pela rotação de uma superfície circular de raio r, em torno de um eixo, e se assemelha à forma de uma câmara de ar ou “rosquinha”. Com isso, r é o raio do tubo do toro e R é o raio do centro do tubo ao centro do toro.
As aplicações do toro são imensas, por exemplo, na topologia o toro é grandemente utilizado como um sólido elementar para transformação topológica (COURANT, 2000).
A figura a seguir nos mostra uma caixa d’água toroidal bastante excêntrica na Polônia.
Figura 13– Caixa de água toroidal na Polônia

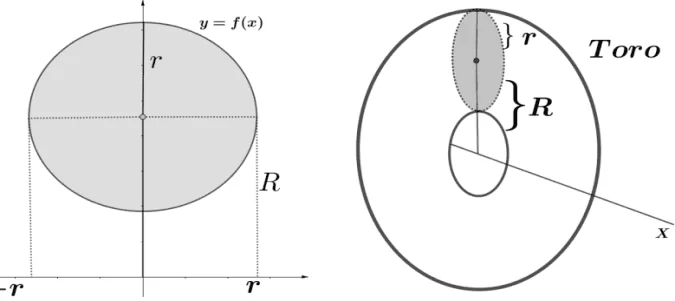
A figura a seguir nos mostra um toro gerado pela rotação, em torno do eixo das abscissas, da região circular definida por ![]() .
.
Figura 14 – Região circular e o toro
Com isso, podemos calcular o volume do toro pela rotação da região circular, 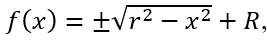 , definida em [-r, r]. Donde tem-se,
, definida em [-r, r]. Donde tem-se,
onde desenvolvendo 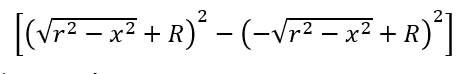 obtém-se facilmente
obtém-se facilmente ![]() , isto é, o volume Vx é:
, isto é, o volume Vx é:
fazendo x = r. cos u, e derivando ambos os membros dessa equação se tem,
dx = -r . sen u. du. E ainda, se x → –r, então u → π e se x → r, então u → 0. Desse modo tem-se:
mas,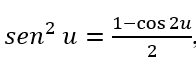 , conforme visto na seção 2.4. Então segue que,
, conforme visto na seção 2.4. Então segue que,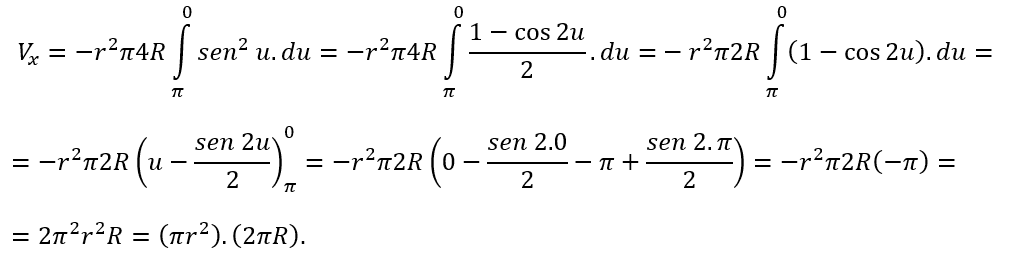
Isto é, o volume Vx é dado pelo produto da área de uma secção transversal do toro, (πr2), pelo comprimento da circunferência média, (2ΠR), deste.
CONSIDERAÇÕES FINAIS
Nos cursos de Cálculo o estudo dos sólidos de revolução é dado, muitas das vezes, de forma descontextualizada, ficando somente nas contas, fazendo o assunto não ter significação alguma para os discentes, causando um alto grau de dificuldade em diversos alunos. Como visto, alguns desses sólidos são estudados no ensino médio: cilindro, cone, tronco de cone e esfera. Contudo, nessa etapa da educação básica estes são vistos de forma resumida com fórmulas prontas. Neste trabalho procurou-se compreender esses e qualquer sólido de revolução de forma geral com a aplicação do Cálculo através de um entendimento geométrico, e ainda, como uma ampliação natural do conjunto de sólidos básicos estudados no ensino médio.
REFERÊNCIAS
BOYER, Carl Benjamin. História da matemática: tradução: Elza F. Gomide. São Paulo, Edgard Blucher, Ed. da Universidade de São Paulo, 1974.
COURANT, Richard. O que é matemática? Rio de Janeiro: Ciência Moderna, 2000.
EVES, Howard. Introdução à história da matemática/Howard Eves; tradução Hygino H. Domingues. 5ª Ed. – Campinas, SP: Editora da Unicamp, 2011.
FINNEY, Ross L. Cálculo de George B. Thomas Jr., Volume 1 / Ross L. Finney, Maurice D. Weir, Frank R. Giordano; tradução Paulo Boschcov; revisão técnica Leila Maria Vasconcellos Figueiredo. – São Paulo: Pearson Addison Wesley, 2002.
GUIDORIZZI, Hamilton Luiz. Um curso de Cálculo Vol. 1. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A, 2008.
LIMA, Elon Lages. A matemática do ensino médio – volume 2/ Elon Lages Lima, Paulo Cezar Pinto Carvalho, Eduardo Wagner, Augusto César Morgado. – 10 ed. – Rio de Janeiro: SBM 2012.
STEWART, James. Cálculo volume 1/ James Stewart; Tradução EZ2 Translate. — São Paulo: Cengage Learning, 2013.
TIMBÓ, Marcos A. Elementos de Cartografia. UFMG, 2001. Disponível em : <https://www.csr.ufmg.br/carto1/elementoscartografia_timbo>. Acesso em: 12 de maio de 2018.
[1] Pós-Graduação em Metodologia do ensino da Matemática e da Física pela Faculdade Única de Ipatinga-FUNIP, pós-Graduação em matemática financeira e estatística pela Faculdade Única de Ipatinga-FUNIP e Graduado em Licenciatura Plena em Matemática pelo Instituto Federal de Educação, Ciência e Tecnologia do Maranhão-IFMA.
[2] Mestrado profissional em mestrado profissional em matemática. Especialização em matemática – formação de professor. Graduação em Licenciatura plena em Matemática.
Enviado: Março, 2019.
Aprovado: Março, 2020.
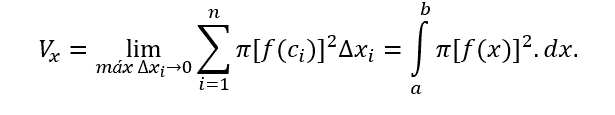
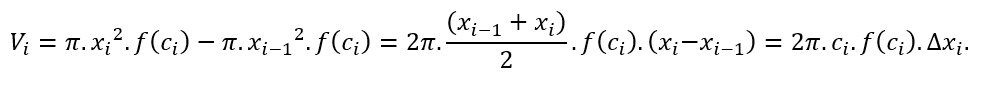
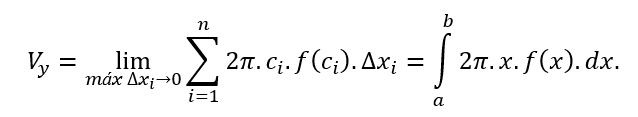
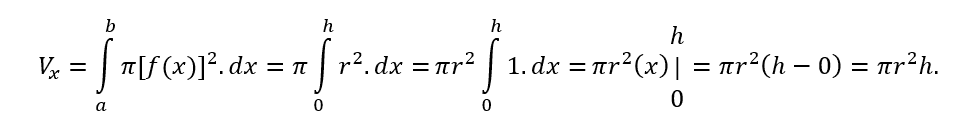

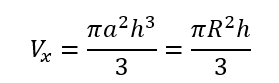
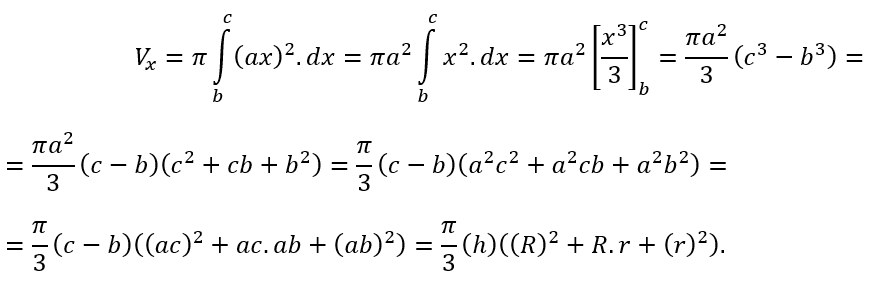
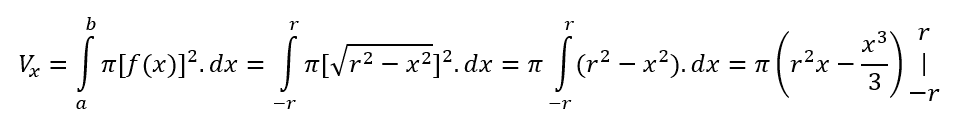
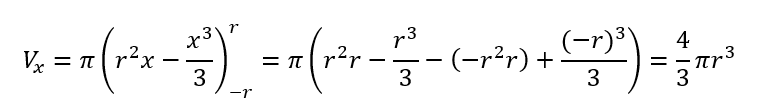
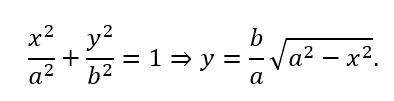
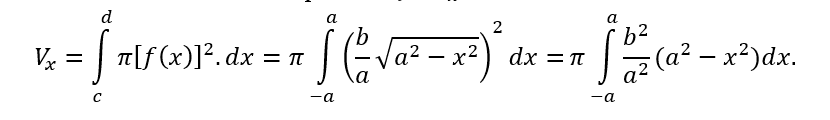
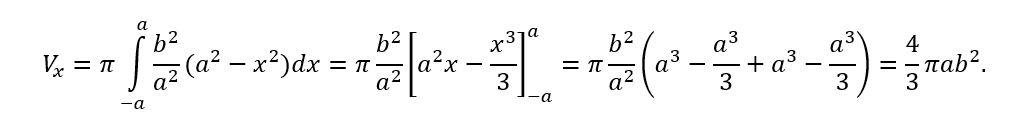
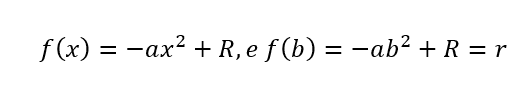
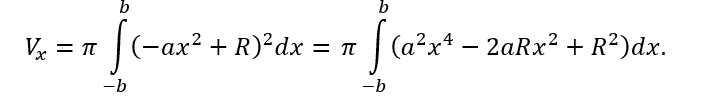
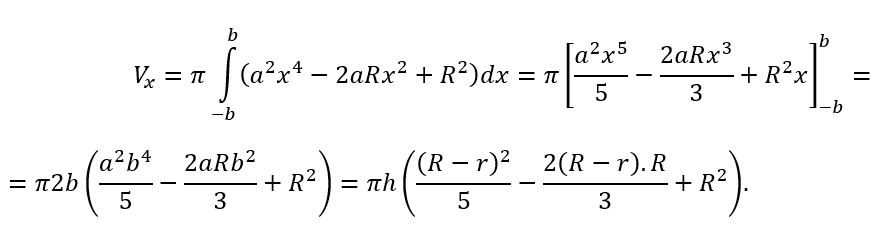


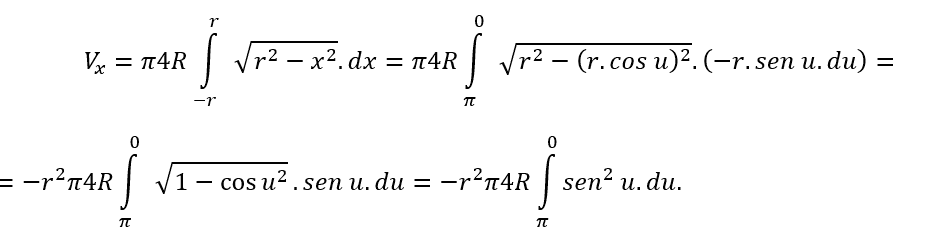

2 respostas
Artigo bem interessante
A matemática é linda