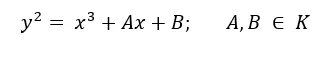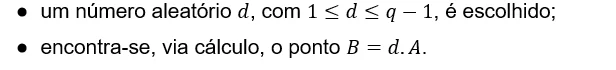ARTIGO ORIGINAL
SANTANA, Maycon de Castro [1], ALEANS, Deimer Jose Julio [2]
SANTANA, Maycon de Castro. ALEANS, Deimer Jose Julio. Fundamentos matemáticos da tecnologia blockchain aplicados ao bitcoin. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 08, Ed. 02, Vol. 03, pp. 14-24. Fevereiro de 2023. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/tecnologia-blockchain, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/tecnologia-blockchain
RESUMO
Visando estimular o desenvolvimento de pesquisas relacionadas com matemática e tecnologia, o presente artigo apresenta os resultados do estudo que tem como objetivo principal compreender a matemática que fundamenta a tecnologia blockchain, essencial no funcionamento do bitcoin. A fim de tornar a pesquisa viável, a primeira etapa consiste em uma revisão bibliográfica dos fundamentos criptográficos envolvidos no sistema blockchain-bitcoin, numa perspectiva tecnológica e histórica. Na etapa seguinte, são explorados conteúdos específicos da matemática que se relacionam com a blockchain: teoria de grupos e curvas elípticas. Por fim, buscou-se conhecer as aplicações desses elementos matemáticos na segurança computacional da rede bitcoin. Como principal resultado desta pesquisa, foi visto que os valores fornecidos pelo Algoritmo de Assinatura Digital de Curvas Elípticas (ECDSA) são impraticáveis por força bruta, o que explica o alto nível de segurança que o caracteriza.
Palavras-chave: Matemática, Criptografia, Bitcoin, Blockchain.
1. INTRODUÇÃO
Em termos gerais, a blockchain é uma plataforma tecnológica de armazenamento de dados, reunida em blocos encadeados, na qual periodicamente são adicionados novos registros correspondentes com as informações previamente armazenadas na base. Essa tecnologia teve origem com o surgimento do bitcoin, e, nos últimos anos, tem apresentado uma crescente relevância, não apenas por causa do surgimento de outras criptomoedas, mas também devido a outras possibilidades de aplicação (LEÃO, 2019).
O bitcoin, resultado de mais de duas décadas de pesquisa, trata-se da primeira criptomoeda mundial descentralizada, anunciada em 2008, cuja a real identidade de seu criador é desconhecida, sendo designado pelo pseudônimo de Satoshi Nakamoto. Nesse sistema, a blockchain é a tecnologia que fornece a estrutura necessária para que as operações aconteçam, armazenando informações em bancos de dados e possibilitando a realização de transações entre os usuários sem a necessidade de intermediários (NAKAMOTO, 2008).
De acordo com Pfleeger (1988), o interesse no estudo da criptografia que estabelece a blockchain tem crescido nas últimas décadas devido a diversas possibilidades de segurança oferecidas pela mesma. Nela, todas as transações realizadas são imutáveis e registradas permanentemente, de modo que não possam ser excluídas. Por tratar de uma criptomoeda, as informações de usuários precisam ser protegidas de alguma forma, e é neste ponto que a matemática está presente, já que possibilita o suporte necessário para assegurar o sigilo na comunicação.
Diante do exposto, o presente trabalho foi realizado por meio de uma pesquisa bibliográfica, que teve como objetivo compreender a tecnologia blockchain, que fundamenta o bitcoin, a partir de um ponto de vista matemático. Foram exploradas definições, propriedades e teoremas matemáticos necessários para o entendimento do seu funcionamento. Também se estudou as aplicações matemáticas nas características que conferem a segurança da plataforma, especialmente os processos de geração de chaves, codificação e decodificação por meio do algoritmo ECDSA.
2. CRIPTOGRAFIA
No campo da Tecnologia de Informação e Comunicação (TIC), Barbosa et al. (2003) apresenta a criptografia como o estudo de técnicas de proteção de dados a partir da transformação de registros originais em informações codificadas. Hoje, a grande vantagem trazida pela criptografia é a capacidade de possibilitar segurança digital das informações, já que seu propósito central é impedir que terceiros tenham acesso a determinadas informações. A necessidade de proteger mensagens compartilhadas ou registros armazenados virtualmente tem sido cada vez maior e, por causa disso, a segurança fornecida pelas diversas estratégias de criptografia precisa ser cada vez mais precisa (FIARRESGA, 2010).
Em um sistema criptográfico, chama-se encriptação o processo de representar uma mensagem através de códigos, de modo que seu significado não seja óbvio. O processo no qual uma mensagem criptografada é transformada de volta em sua forma original chama-se decriptação. Esses procedimentos são possíveis a partir de um elemento chamado chave, que é um mecanismo que deve ser compartilhado apenas entre as partes do sistema, funcionando como uma espécie de segredo que permite e controla a execução das operações (PIAZENTIN, 2011).
As variedades de criptografia existentes são classificadas de acordo com o uso de chaves. Se forem usados dois tipos de chaves, uma pública, usada no processo de encriptação, e a outra privada, usada para a decriptação, a criptografia será assimétrica. Antonopoulos (2014) diz que a criptografia do tipo assimétrica é um dos princípios básicos que fundamentam o sistema bitcoin, por permitir transações entre usuários sem a necessidade de se conhecer a chave privada, além de verificar a autenticidade das informações de transações a partir de uma assinatura digital.
Conforme expõe Portnoi (2005), Koblitz e Miller, em 1985, apresentaram um modelo de criptografia assimétrica denominado Criptografia de Curvas Elípticas (CCP), cuja estrutura lógica é baseada na utilização das propriedades matemáticas de curvas elípticas operadas em corpos finitos. No bitcoin, a CCP é usada especificamente a partir do Algoritmo de Assinatura Digital de Curvas Elípticas (ECDSA), que tem a função de assinar digitalmente a mensagem a partir do uso específico da curva elíptica secp256k1 (ARAUJO, 2006).
Os usuários de bitcoin possuem carteiras digitais com identificadores, podendo ser conhecidos por qualquer um que queira fazer envio de valores da moeda. A chave privada do receptor serve para validar e registrar uma transação, além de permitir que o destinatário tenha o total controle das operações sob sua carteira. Além disso, o ECDSA realiza a assinatura digital a partir do resultado de cálculos matemáticos feitos sobre a chave privada do recebedor por meio da chave pública do remetente.
3. A MATEMÁTICA QUE ESTABELECE O SISTEMA BLOCKCHAIN–BITCOIN
Ao analisar documentos e registros científicos sobre a história da criptografia, é incontestável a contribuição da matemática para o avanço dessa área do conhecimento. Visto que a plataforma blockchain faz uso de criptossistemas em suas operações, a matemática é essencial em todos os processos envolvidos nessa tecnologia. A seguir, serão apresentadas as propriedades de grupos cíclicos e curvas elípticas que as envolvem.
Definição 1 (grupo abeliano): um grupo, denotado por 
, é um conjunto não vazio, munido de uma operação binária
, definida sobre 
, em que os seguintes axiomas são verdadeiros:
Definição 1 (curvas elípticas): uma curva elíptica E sobre um corpo K é o conjunto dos pontos 
que satisfazem a equação:
Figura 1. 
Curvas elípticas desse tipo apresentam as seguintes propriedades:
- toda reta L não vertical que passa por dois pontos
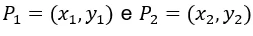e de E intercepta um terceiro ponto 
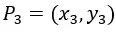dessa curva; - toda reta vertical L que passa pela curva E intercepta dois de seus pontos, podendo ser distintos ou coincidentes.
Definição 3.2 (ponto no infinito): seja L uma reta vertical que intercepta dois pontos de E, distintos ou não, define-se ponto no infinito, denotado por O, como sendo o terceiro ponto que essa reta vertical L intercepta em E.
A soma de dois pontos 
de uma curva elíptica E é definida como sendo o simétrico, em relação ao eixo horizontal, do terceiro ponto 
que essa reta intercepta na curva E. Essa propriedade possui as seguintes características:
Satisfeitas essas condições, uma curva elíptica E definida num corpo K, com a operação de soma, se constitui como um grupo abeliano.
Definição 3.3 (problema de logaritmo discreto em curvas elípticas): seja 
o grupo aditivo das curvas elípticas, onde 
é um gerador de E. Dado 
, o problema de logaritmo discreto (DPL) em curvas elípticas buscar encontrar um inteiro 
tal que 
. Nesse caso, 
indica o resultado de operações sucessivas de P consigo próprio, por uma quantidade 
de vezes.
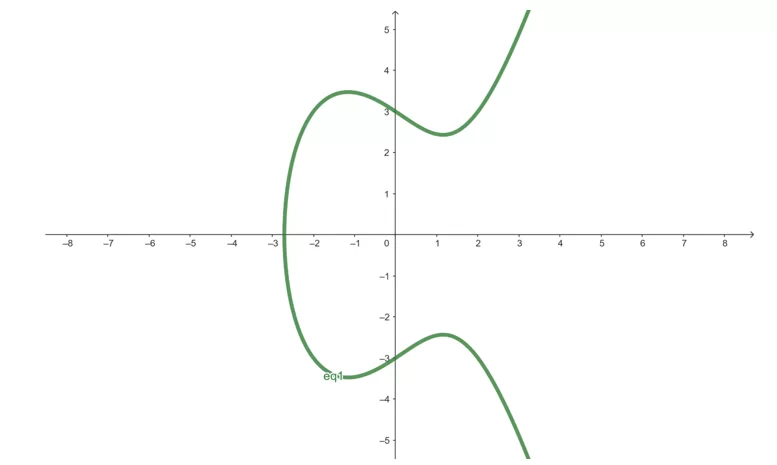
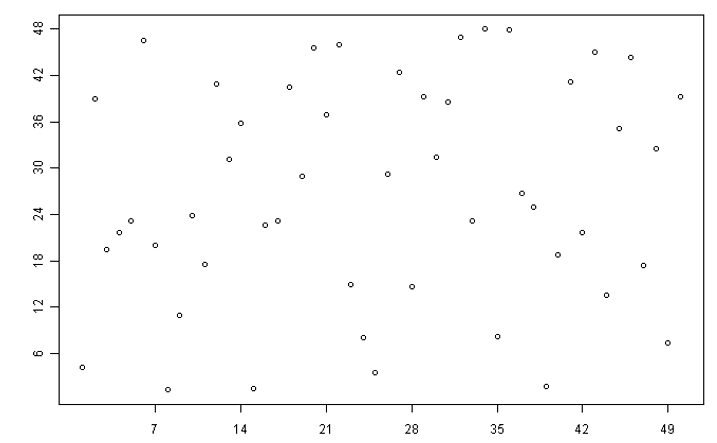
Na criptografia de curvas elípticas, as curvas elípticas são definidas no corpo finito 
. Assim, um DPL com essas configurações apresenta pouca semelhança com o logaritmo contínuo definido nos corpos dos reais R. Isso faz a exponenciação discreta apresentar uma variação irregular significativa, dificultando a detecção de padrões, como ocorre na exponenciação contínua.
Figura 2. Exemplo de curva elíptica definida num corpo finito
4. ALGORITMO DE ASSINATURA DIGITAL EM CURVAS ELÍPTICAS – ECDSA
A segurança de um sistema criptográfico de assinatura digital é baseada no princípio de que apenas o dono do par de chaves deve ter posse da chave privada, e de que o produto de suas operações não dê vestígio da mesma. Para alcançar essa dificuldade, os esquemas de assinatura digital se baseiam em problemas matemáticos de difícil resolução.
Com base no estudo desenvolvido por Meireles (2020), o ECDSA é um algoritmo baseado em aritmética de curvas elípticas, padronizado em 1998 pela American National Standards Institute – ANSI. Por se tratar de uma matemática muito recente, ainda não existem ataques robustos aos protocolos baseados em curvas elípticas. Logo, é obtido um nível satisfatório de segurança com números entre 160-256 bits, enquanto protocolos baseados em exponenciação de números inteiros necessitam de 1024-3072 bits.
4.1 GERAÇÃO DE CHAVES
Seja 
uma curva elíptica que forma um grupo sobre o corpo 
com p primo, sendo 
a ordem nesse grupo e A um gerador de E, o mecanismo de geração de chave segue as seguintes etapas:
Feito tal procedimento, o conjunto de valores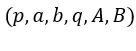 
constituem a chave pública e d forma a chave privada.
4.2 ASSINATURA DE MENSAGEM
O par de chaves gerado é utilizado para o processo de assinatura digital de uma mensagem , que consiste em:
Ao fim desse procedimento, assinatura e mensagens são enviadas na forma 
.
4.3 VERIFICAÇÃO DE ASSINATURA
O processo de verificação de uma mensagem assinada protocolo ECDSA segue os passos a seguir:
Para que determinada assinatura seja legítima, a coordenada do ponto deverá ser equivalente ao valor de 
. Caso contrário, a assinatura será inválida.
4.4 USO DO ECDSA NO SISTEMA BLOCKCHAIN–BITCOIN
O ECDSA é considerado um padrão seguro para a implantação de sistemas de assinatura digital. Atualmente, seu uso é bastante diversificado, sendo executado principalmente no fornecimento de segurança a sistemas operacionais e criptomoedas. O bitcoin recorre exclusivamente ao algoritmo ECDSA para obter o grau altíssimo de proteção que o particulariza. Essa alta segurança é possível graças à criptografia de curvas elípticas, que possibilitou mecanismos com custo muito menor, o que é consideravelmente vantajoso (OLIVEIRA, 2012).
As assinaturas efetuadas pelo ECDSA são dificilmente falsificadas, já que a potência computacional necessária para isso está fora dos limites atuais. No procedimento de assinatura, as chaves privadas utilizadas são munidas de um código hash, enquanto a lisura das informações faz uso apenas da chave em sua execução.
5. TRANSAÇÕES DE BITCOINS
Conforme reitera Martins (2018, p. 24), “No protocolo Bitcoin, transações são estruturas de dados que codificam a transferência de valores entre participantes do sistema”. Quando um usuário inicia uma transação, esta é transmitida para toda a rede e, em seguida, o computador de algum membro da rede, via mineração, captura essa transação e a revisa para se certificar de que ela seja válida. Ao ser reconhecida como verdadeira, essa transação é incluída em um bloco e adicionada na cadeia de modo permanente. Após isso, é executada uma função hash para cada uma das transações efetivadas.
Figura 3. Valores de hash para cada bloco
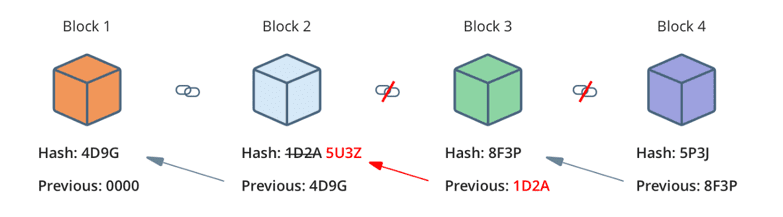
A função principal da blockchain é armazenar todos os dados das transações realizadas, preservando a ordem em que aconteceram, de modo a detectar qualquer tentativa de manipulação. A comunicação entre os nós dessa rede busca manter as conexões existentes ativas, estabelecer novas conexões e distribuir novas informações (ULRICH, 2014).
Os computadores que fazem parte da blockchain são equivalentes a testemunhas que podem afirmar se determinada transação está em concordância com seus registros. Por ser um sistema distribuído peer-to-peer, não há um computador central controlando as transações realizadas. Trata-se de um sistema aberto em que quem tiver interesse pode se conectar e submeter novos dados de transação ao sistema ou contribuir com recursos computacionais.
6. CONSIDERAÇÕES FINAIS
O estudo da criptografia mostra como a matemática possibilitou o desenvolvimento de métodos criptográficos cada vez mais seguros. Em específico, o estudo de criptossistemas baseados em curvas elípticas permitiu entender o motivo pelos quais os valores fornecidos pelo ECDSA são impraticáveis por força bruta, o que justifica sua eficiência e aplicação no sistema blockchain-bitcoin.
Teorias que envolvem o estudo de curvas elípticas formam o suporte necessário para o funcionamento do processo de assinatura digital das operações por meio do algoritmo ECDSA. Criptossistemas baseados em curvas elípticas oferecem uma segurança eficaz atualmente, pois sua construção apresenta uma variação muito mais irregular, sendo difícil observar a existência de um padrão quando se trabalha em corpos discretos. Trata-se de um objeto matemático que admite a estrutura algébrica de grupo abeliano.
REFERÊNCIAS
ANTONOPOULOS, Andreas M. Mastering bitcoin: unlocking digital cryptocurrencies. Sebastopol: O’Reilly Media, Inc., 2014.
ARAUJO, Afonso Comba de. Um algoritmo de criptografia de chave pública semanticamente seguro baseado em curvas elípticas. Dissertação (Mestrado em Ciência da Computação) – Universidade Federal do Rio Grande do Sul. Porto Alegre, RS, 2006. 95 f.
BARBOSA, Luis Alberto de Moraes et al. RSA: criptografia assimétrica e assinatura digital. Trabalho de curso (Especialização em Redes de Computadores) – Universidade Estadual de Campinas. Campinas, SP, 2003. 50 f.
DENDRO DABA. Asis. Dendro Daba, 2011. Disponível em: http://dendro.daba.lv/R/darbs_ar_R/grafiku_veidosana/asis/. Acesso em: 20 fev. 2023.
FIARRESGA, Victor Manuel Calhabrês. Criptografia e matemática. Dissertação (Mestrado em Matemática para Professores) – Universidade de Lisboa. Lisboa, Portugal, 2010. 161 f.
LEÃO, Luiz Carlos da Silva. Uma introdução ao estudo de bitcoins e blockchains. Dissertação (Mestrado Profissional em Matemática) – Universidade Federal do Estado do Rio de Janeiro. Rio de Janeiro, RJ, 2019. 118 f.
MARTINS, Thiago Fonseca. Prova de existência de arquivos digitais utilizando a tecnologia blockchain do protocolo bitcoin. Monografia (Bacharelado em Engenharia da Computação) – Universidade Federal do Rio Grande do Sul. Porto Alegre, RS, 2018. 65 f.
MEIRELES, Tiago Aprigio Bezerra. Curvas elípticas e criptografia. Trabalho de Conclusão de Curso (Bacharelado em Matemática) – Universidade Federal de Uberlândia. Uberlândia, MG, 2020. 73 f.
MIRO MEDIUM. Valores de hash para cada bloco. Miro Medium, s.d. Disponível em: https://miro.medium.com/v2/resize:fit:720/format:webp/0*TVKXnkVcsruHhCDB.png. Acesso em: 20 fev. 2023.
NAKAMOTO, Satoshi. Bitcoin: a peer-to-peer electronic cash system. Bitcoin, 2008. Disponível em: https://bitcoin.org/bitcoin.pdf. Acesso em: 20 fev. 2023.
OLIVEIRA, Ronielton Rezende. Criptografia simétrica e assimétrica-os principais algoritmos de cifragem. Segurança Digital, v. 31, p. 11-15, 2012. Disponível em: https://www.ronielton.eti.br/publicacoes/artigorevistasegurancadigital2012.pdf. Acesso em: 20 fev. 2023.
PFLEEGER, Charles P. Security in computing. Upper Saddle River: Prentice-Hall, 1988.
PIAZENTIN, Denis Renato de Moraes. Troca de chaves criptográficas utilizando criptografia neural. Trabalho de Curso (Bacharelado em Ciência da Computação) – Centro Universitário Eurípides de Marília. Marília, SP, 2011. 66 f.
PORTNOI, Marcos. Criptografia com curvas elípticas. Trabalho de Conclusão de Curso (Mestrado em Redes de Computadores) – Faculdade Salvador. Salvador, BA, 2005. 14 f.
ULRICH, Fernando. Bitcoin: a moeda na era digital. São Paulo: Instituto Ludwig Von Mises Brasil, 2014.
[1] Graduação. ORCID: 0000-0002-5846-4671. CURRÍCULO LATTES: http://lattes.cnpq.br/2676551205974166.
[2] Orientador. ORCID: 0000-0002-4780-7341.
Enviado: Fevereiro, 2023.
Aprovado: Fevereiro, 2023.
