Costruzione didattica della geometria e l’uso di materiali concreti come processo di apprendimento

ARTICOLO ORIGINALE

OLIVEIRA, José Luiz de Jesus Egues de ^[1], SILVA, Edevaldo Maximo da ^[2], SANTOS, Cleidison Da Silva ^[3], PONTES, Dalila Fonseca ^[4], SILVA, Jandaira Fernandes da ^[5], QUEIROZ, Jose Pereira de ^[6], SANTANA, Zenóbia Conceição Castro ^[7]

OLIVEIRA, José Luiz de Jesus Egues de. Et. al. Costruzione didattica della geometria e l’uso di materiali concreti come processo di apprendimento. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 10, Vol. 10, pp. 46-61. nell’ottobre 2020. ISSN: 2448-0959, collegamento di accesso: https://www.nucleodoconhecimento.com.br/formazione-it/costruzione-didattica, DOI: 10.32749/nucleodoconhecimento.com.br/formazione-it/costruzione-didattica

RIEPILOGO

La ricerca si è distinta per una riflessione didattica che risponde alla necessità di costruzioni sperimentali in classe, con materiali concreti per assistere nel processo di insegnamento e apprendimento della geometria nelle scuole elementari. In questo senso di attribuire un’analisi a questo problema, abbiamo come asse, educazione matematica, come un modo per stimolare gli studenti per lo sviluppo di laboratori in cui hanno mirato alla costruzione di materiali didattici come un processo di apprendimento della matematica. Il processo di costruzione del concetto di geometria che attribui le competenze e le competenze da sviluppare negli studenti in questa fase, ha permesso allo stesso di sviluppare un particolare tipo di pensiero per comprendere, descrivere e rappresentare, in modo organizzato, gli spazi geometrici, informando l’importanza che questo contenuto ha nella loro vita sociale di cittadino. Attraverso la costruzione di figure geometriche con materiali manipolati, studiamo tutti i concetti della figura, attraverso questo strumento, stimolando così l’interesse e la motivazione degli studenti, fornendo loro un ragionamento geometrico e matematico. Le definizioni della geometria possono essere costruite successivamente, prendendo come base la precedente conoscenza degli studenti o meno, in cui sottolineiamo che gli educatori dovrebbero creare attività in cui gli studenti fanno indagini su situazioni legate alle dimensioni geometriche, avendo così esperienze di significato e direzione di se stessi e di qualche figura inserita nello spazio. Tuttavia, per l’assorbimento di questo processo di insegnamento e apprendimento, oltre a presentare teorie agli studenti, è stato necessario mostrare le figure geometriche per le loro caratteristiche fisiche, vale a dire in modo tale che la natura ci fornisce e non solo dalle sue proprietà e concetti definiti. Infine, la ricerca ci ha permesso di analizzare la capacità intellettuale di ogni studente selezionato per questo scopo.

Parole chiave: Educazione matematica, costruzione educativa, geometria.

1. INTRODUZIONE

Come professionisti dell’Istruzione e di diverse aree, pensiamo a questa ricerca guidata dal desiderio di dialogare sull’insegnamento dell’apprendimento della matematica, più specificamente osservare l’importanza della geometria nel menu educativo dello studente e, in particolare, nella scuola elementare. Anche come ricercatori e intenditori di spazi geometrici, si evidenzia l’argomento di Malba Tahan (1967, p.31) nel suo testo che dice: “Ciò che rende difficile insegnare la matematica è l’abitudine latina inalterabile di iniziare sempre con l’astratto, senza passare attraverso il concreto”. Altri autori hanno anche un’importanza molto rilevante su questa parte della matematica. Ci affrontaremo anche il quasi abbandono della geometria nell’istruzione di base, riportato in alcuni studi che ci avviciniamo come base per questo lavoro. Sottolineiamo anche le specificità riguardanti l’insegnamento del contenuto geometrico nel contesto del mondo fisico per l’insegnamento, così come le competenze che questo settore della matematica deve fornire per gli studenti di essere inclusi in una società educativa de facto.

Tuttavia, il processo di insegnamento-apprendimento della Matematica è oggetto di molti studi e discussioni, perché nuove metodologie sorgono sempre per soddisfare una domanda che è in continua evoluzione in varie modalità di insegnamento.

Date le specificità del processo di apprendimento della matematica nelle elementari, e la prospettiva di sviluppare strumenti per stimolare la capacità intellettuale degli studenti e allo stesso tempo valorizza l’uso della matematica nella vita di tutti i giorni in cui innumerevoli problemi possono essere risolti, la discussione dell’importanza dell’insegnamento dei contenuti che coinvolgono la geometria viene alla pari, perché è un percorso molto interessante , è estremamente importante essere in grado di fornire allo studente una visione più organizzata del mondo in cui vive. Infatti, è molto importante studiare questo settore della matematica ed è difeso da diversi educatori, in cui sono discussi qui e discussi di seguito, in base all’importanza e alle specificità di questo settore.

Proviamo con questa ricerca per contribuire all’insegnamento dell’educazione matematica, basato sullo sviluppo di competenze e competenze negli studenti.

Lo sviluppo di laboratori finalizzati alla costruzione di materiali didattici manipolabili per l’insegnamento e il processo di apprendimento, esplorando i concetti geometrici che contemplano le competenze e le competenze che gli studenti devono sviluppare durante la fase chiamata “costruzione educativa”, permetterà allo studente di sviluppare un particolare tipo di pensiero per comprendere, descrivere e rappresentare, in modo organizzato, il mondo in cui vive , informando l’utente sull’importanza di questo contenuto. Pertanto, un giorno possono utilizzare questo prodotto educativo nella loro vita sociale, o nella vita quotidiana, oltre a consentire un aumento nella visione dell’uso della conoscenza di base geometrica.

2. TENDENZE DIDATTICHE PEDAGOGICHE NELL’INSEGNAMENTO DELLA GEOMETRIA

Crediamo che la costruzione educativa abbia fissato il processo di apprendimento memorizzando così il contenuto trasmesso, che sono stati effettuati con materiali di cemento manipolati.

Secondo Duval (1995), la geometria coinvolge tre forme di processo cognitivo: che riempiono specifiche funzioni epistemologiche;

Visualizzazione per l’esplorazione euristica di una situazione complessa; Costruzione di configurazioni, che possono essere lavorate come modello, in cui le azioni eseguite rappresentate e i risultati osservati sono collegati agli oggetti matematici rappresentati; Ragionamento, che è il processo che porta alla prova e alla spiegazione. (DUVAL, 1995).

Secondo l’autore, queste tre specie di processi cognitivi sono intrecciati nella loro sinergia e cognitivamente necessari per la competenza della geometria. D’altra parte, l’euristica dei problemi geometrici si riferisce a una registrazione spaziale che lascia il posto a forme di interpretazioni autonome.

Per Duval (1988), i problemi di geometria presentano una grande originalità in relazione a molti compiti matematici che possono essere proposti agli studenti. Inoltre, l’autore dice che favorire lo sviluppo di funzioni cognitive organizzando problemi di geometria matematicamente vicini che richiedono la stessa conoscenza, determina una categorizzazione cognitiva indispensabile per l’apprendimento.

Secondo Machado (2005), la maggior parte dei problemi di insegnamento e di apprendimento della geometria sono di origine didattica e linguistica. Per Duval (1995), il coordinamento dei diversi documenti di rappresentazione (scrittura algebrica, figure geometriche, discorso nel linguaggio naturale) legato al trattamento della conoscenza non funziona spontaneamente, anche nel corso di un insegnamento che mobilita questa diversità di documenti.

Tuttavia, lo studio proposto dovrebbe consentire allo studente di fare una diversa interpretazione della geometria intorno a loro, perché esercitando nella sua memoria attraverso il contatto, vale a dire “il concreto”, possono acquisire conoscenza in questo contesto educativo, e che servirà come strumento per essere incorporato nella loro vita quotidiana.

Secondo Fiorentini:

Diversi cambiamenti metodologici sono evidenziati come tendenze didattiche che cercano di privilegiare la partecipazione degli studenti, considerando la costruzione della conoscenza come una forma di apprendimento. La conoscenza matematica emerge dal mondo fisico e viene estratta dall’uomo attraverso i sensi. (FIORENTINI, 1995, p.9).

I Parametri Curriculari Nazionali (PCN, 1998) riconoscono anche la mancanza di rilievo che è stata data a questo settore della matematica e sottolinea anche che sviluppa un ruolo fondamentale nella formazione dello studente come cittadino.

Per (MACHADO, 2005), la maggior parte dei problemi di insegnamento e di apprendimento della geometria sono di origine didattica e linguistica.

Gli autori di cui sopra citano questi aspetti nei processi di apprendimento che si intrecciano nella loro sinergia e cognitivamente necessari per la competenza della geometria. D’altra parte, l’euristica dei problemi geometrici si riferisce a una registrazione spaziale che lascia il posto a forme di interpretazioni autonome.

Speriamo che la metodologia applicata sarà una tendenza pedagogica nella nostra vita quotidiana in questo settore ha funzionato, e che possiamo effettivamente usarlo nelle nostre classi, come strumento di apprendimento nelle classi di geometria.

3. L’USO DI MATERIALI CONCRETI NELL’INSEGNAMENTO DELLA GEOMETRIA

Gli ostacoli e le difficoltà incontrate dagli studenti al momento dell’apprendimento della matematica stessa sono innumerevoli. C’è chi non può capirlo e anche l’insegnante è disapprovato in una dichiarazione e chi, una volta approvato, non riesce ancora ad applicare la conoscenza acquisita. In altri termini, non capiscono la sua reale importanza.

Così, diversi studi dimostrano che l’uso di materiali manipolati produce prestazioni più elevate negli studenti rispetto al loro uso, a tutte le età e in tutti gli anni di scuola. Questo uso è un’indicazione metodologica che viene valutata dal momento dell’acquisizione al momento della costruzione di concetti che possono avvenire a tutti i livelli di istruzione. Così sorge la domanda: il materiale concreto come uso pedagogico può facilitare l’insegnamento e l’apprendimento della matematica? Secondo Carraher e Schilemann (1988), affermano nella loro ricerca che “non abbiamo bisogno di oggetti in classe, ma obiettivi. Abbiamo bisogno di situazioni in cui la soluzione di un problema implichi l’uso di principi logici matematici da insegnare” (p.179). Questo perché il materiale “nonostante sia formato da obiettivi, può essere considerato come un insieme di oggetti ‘astratti’ che si trovano solo a scuola ai fini dell’insegnamento, e non ha alcun legame con il mondo del bambino” (p.180). Per lui, il cemento per i bambini non è necessario, perché gli oggetti manipolatori possono essere astratti nelle mani in varie situazioni che il bambino dovrà affrontare socialmente. D’altra parte, Fiorentini e Miorim (1990), confermano le loro parole pronunciate sopra e spiegano che dietro ogni materiale utilizzato, si nasconde una visione dell’educazione matematica dell’uomo e del mondo. Ciò significa che esiste una proposta pedagogica che giustifica questo uso.

Da questa ricerca, abbiamo anche trovato domande per il pubblico di bambini con esigenze speciali. Come sarebbe successo questo uso? Come sarebbe il processo di insegnamento e apprendimento per questi bambini? Così, l’educatrice italiana e anche medico Maria Montessori, ci risponde portando risultati dopo la ricerca con bambini eccezionali, sviluppata all’inizio di questo secolo con vari materiali manipolativi incentrati sulla matematica stessa. Si credeva che non ci fosse apprendimento senza azione: “nulla dovrebbe essere dato al bambino, nel campo della matematica, senza prima presentargli una situazione concreta che lo porta ad agire per pensare, sperimentare, scoprire, e quindi immergersi nell’astrazione”. (AZEVEDO, 1979, p. 27)

Seguendo queste riflessioni percepiamo che questo materiale concreto menzionato qui e posto come oggetto di applicabilità per un apprendimento efficace ci fa capire che c’è bisogno di un esercizio delle facoltà sintetiche e analitiche del bambino come l’autore qui sotto afferma che:

Le facoltà sintetiche e analitiche del bambino devono essere esercitate. Sintetico per consentire allo studente di costruire un concetto dal calcestruzzo. Analitico perché in questo processo l’elemento figlio discerne nell’oggetto quegli elementi che costituiscono la globalizzazione. Per questo l’oggetto deve essere mobile, che può subire una trasformazione in modo che l’elemento figlio possa identificare l’operazione sottostante (CASTELUNUOVO, 1970, p.82-91)

I materiali manipolati possono essere fondamentali per imparare a verificarsi e non sempre il più appropriato è quello già costruito o più bello. Incoraggiando la costruzione educativa da parte dei bambini stiamo pensando di facilitare il processo di apprendimento ed è in questo momento che ci rendiamo conto che la partecipazione concreta di esso rende il tale processo in realtà hanno una convalida. Così siamo confrontati con il curriculum nazionale di istruzione di base che stabilisce: competenze essenziali (IDEB, 2001), per quanto riguarda l’uso delle risorse, afferma che:

Materiali manipolati di vario tipo è, in tutta la scuola, una risorsa privilegiata come punto di partenza o supporto di molti compiti scolastici, in particolare quelli volti a promuovere attività di ricerca e comunicazione matematica tra gli studenti… […] Tutti gli studenti dovrebbero imparare a utilizzare non solo la calcolatrice elementare, ma anche, come progrediscono nell’istruzione di base, gli studenti dovrebbero avere l’opportunità di lavorare con il foglio di calcolo e con vari programmi educativi, tra cui grafici a funzione e geometria dinamica (2001, p.17).

4. METODOLOGIA

La metodologia utilizzata è qualitativa, bibliografica e sperimentale. La ricerca è stata sviluppata durante laboratori pedagogici, organizzati da moduli che hanno permesso allo stesso tempo di sviluppare le attività legate alla “Costruzione di materiali didattici come processo didattico e di apprendimento”, che qui caratterizzamo come “costruzione educativa”.

Abbiamo fatto i workshop con incontri che sono stati divisi al fine di mettere lo studente in contatto con il tema. Applichiamo i concetti delle figure relative ai testi selezionati del libro di matematica della disciplina della geometria. Altre letture sono state selezionate in base allo sviluppo del lavoro. Abbiamo usato come concetti di pianificazione geometrica della figura nello spazio bidimensionale e assemblamo figure geometriche dello spazio tridimensionale. In questa fase, l’apprendimento della geometria è realizzato da attività legate all’azione, ci deve essere una predominanza di cemento sul simbolico, quindi lo studente manipola e costruisce oggetti di varie forme per poi analizzare le loro caratteristiche fisiche e geometriche. In questa prospettiva, dovrebbero essere svolte attività geometriche che consentano l’esplorazione di concetti legati allo spazio e alla forma, contribuendo al corso incentrato sulla formazione di uno studente inserito, perché devono comprendere il mondo geometrico in cui vivono.

4.1 DELLE OFFICINE APPLICATE

Due laboratori si sono svolti in una classe di 9^a elementare, composta da 27 studenti della mattinata del consigliere scolastico statale Bento Muniz del comune di Tangarà da Serra-MT. Così, è stata applicata una valutazione diagnostica, concepita anche come pre-test, e con l’obiettivo di avere informazioni sulle conoscenze precedenti degli studenti nel contesto della geometria euclidea, perché secondo la LDB-Legge di base nazionale e linee guida (1961)

Le linee guida e le proposte emanate dal MEC (Ministero della Pubblica Istruzione) evidenziano e rafforzano la necessità di riconoscere le conoscenze precedenti degli studenti, utilizzandole come strumento che facilita l’apprendimento e come fattore motivante, perché in questo modo, lo studente diventa soggetto attivo nel processo scolastico, non essendo più mero destinatario della conoscenza.

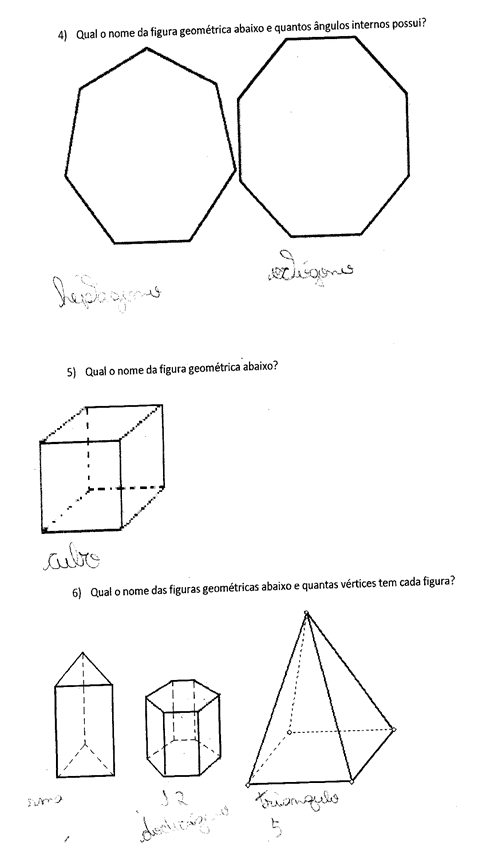
Le cifre presentano il questionario presentato, così come le risposte di alcuni studenti. Le prime tre domande miravano a verificare la comprensione degli studenti nella concezione delle definizioni di poligoni e polihedra, così come la denominazione di alcune figure geometriche elementari. Abbiamo osservato che la maggior parte degli studenti non aveva concepito le definizioni in discussione, il che va contro le dichiarazioni di Almouloud (2005) in cui l’autore afferma che diversi studi indicano questa disciplina come uno dei problemi di apprendimento. E questo diventa più evidente quando guardiamo le altre questioni contenute nel test.

Figura 01 – PROPOSTA APPLICATA.

Figura 2 – CONTINUITÀ DEL TEST

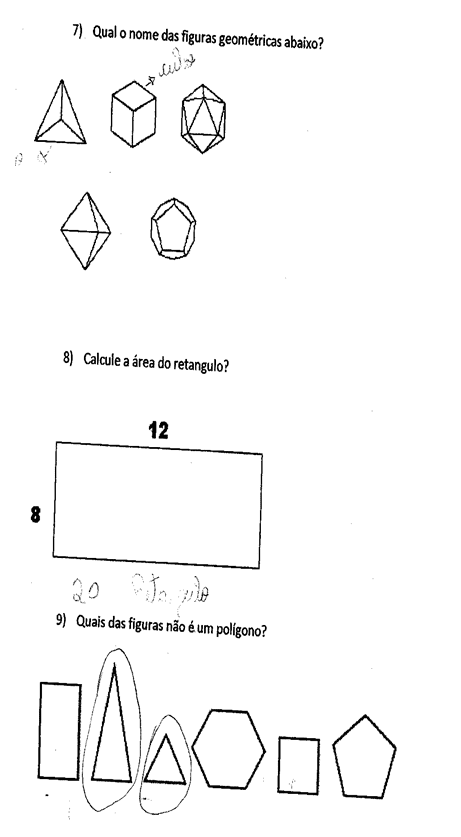
Figura – 3. Costruzioni

Figura – 4. Costruzioni

Figura – 5. Costruzioni

In questa indagine, si è scoperto che la stragrande maggioranza degli studenti non riconosce le forme poligonali e non poligonali e non sanno come correlarli al numero dei loro lati e vertici, e mostrano ancora di segmentare la geometria della loro vita quotidiana, anche se la vita quotidiana è il promotore dello studio della geometria come indicato dall’autore qui sotto:

La conoscenza matematica emerge dal mondo fisico e viene estratta dall’uomo attraverso i sensi” e Miguel e Miorim, (1986, p.66), che affermano, “la geometria è così importante per l’umanità che rende inconcepibile mettere in discussione la necessità di studiarla a scuola, perché il mondo in cui viviamo è quasi spontaneamente geometrico e il suo uso nella vita quotidiana è quasi una necessità umana. (FIORENTINI, 1995 p. 9.)

Forse questa situazione si aggraverà il modo in cui gli insegnanti presentano questo contenuto, che secondo i PCN è importante come in passato.

Le questioni relative alle forme e alle relazioni tra di loro, con le possibilità di occupazione spaziale, con la posizione e lo spostamento degli oggetti nello spazio, visti da diverse angolazioni sono necessari oggi come lo erano in passato. Le situazioni quotidiane e l’esercizio di varie professioni, come l’ingegneria, la biochimica, la coreografia, l’architettura, la meccanica, ecc., richiedono la capacità dell’individuo di pensare geometricamente (PCNs p. 122 – 1998).

In un secondo momento, sono state proposte le costruzioni delle figure piatte. Durante le costruzioni si è scoperto che gli studenti capiscono davvero le forme geometriche presentate attraverso le costruzioni con cartone, vale a parte il calcestruzzo. Quadrato, rettangolare, triangolare, circolare, pentagonale, esagonale, eptagonale, antitogonale, eneagonale, decagonale, dogogonale, tridecagonale, tetradecagonale, pentadecagonale, tutti progettati in cartoline da tagliare e infine costruiti sono stati assemblati. Abbiamo osservato che la costruzione da parte degli studenti ha contribuito alla creazione di significati degli studenti stessi, con un interesse a partecipare più che se queste figure sono state presentate alla lavagna dall’insegnante. Ciò che rafforza i detti di Azevedo (2006, p.27), che credeva che non ci fosse apprendimento senza azione: “nulla dovrebbe essere dato al bambino, nel campo della matematica, senza prima presentargli una situazione concreta che lo porta ad agire per pensare, sperimentare, scoprire, e quindi immergersi nell’astrazione”.

È stato aperto anche uno spazio in cui gli studenti hanno avuto l’opportunità di interrogarsi e discutere sulle attività svolte e sul rapporto delle forme nella nostra convivenza. Ma dopo che la discussione è stata aperta per un commento, alcuni studenti hanno contribuito solo se sono stati istigati e hanno chiesto di fare un commento. Il commento più frequente da parte degli studenti era che non avevano mai partecipato a un processo di insegnamento in questo modo e che trovavano interessante e piacevole costruire le figure invece di vedere solo l’insegnante presentarle. Così Machado (2005) afferma che la maggior parte dei problemi dell’insegnamento e della geometria di apprendimento sono di origine didattica e linguistica; e Pavanello (1993), spiega che alcuni fattori legati a tali difficoltà possono essere legati alla mancanza di interesse degli studenti generati dalla mancanza di risorse didattiche, alla mancanza di insegnanti interessati a utilizzare queste diverse risorse didattiche per sviluppare un insegnamento attraente e di qualità, che può utilizzare nuove concezioni didattiche come l’uso di materiali concreti o giochi pedagogici nello sviluppo delle loro pratiche didattiche.

Attraverso questa attività, è stato possibile verificare che il potenziale educativo fornito dalla costruzione di figure piatte sia molto rilevante per scopi didattici pedagogici e attraente per stabilire una correlazione tra il contenuto del tema da affrontare.

In questa fase, gli studenti sono stati anche invitati a costruire le figure piatte in gruppi, dove dovrebbero essere dipinte con i pastelli. Questo tipo di attività porta lo studente a fare una pianificazione preventiva della costruzione, in quanto richiede la conoscenza di forme geometriche o poligoni e richiede abilità motorie per gestire i materiali.

Il laboratorio per la costruzione di figure piatte, oltre alle dinamiche era ricreativo, motivante e pedagogicamente attraente, perché in vari momenti i gruppi discutevano su quale poligono avrebbe costruito, perché secondo. Fiorentini e Miorim (1990) “dice che dietro ogni materiale utilizzato, si nasconde una visione dell’educazione, della matematica, dell’uomo e del mondo; che c’è, alla base, una proposta pedagogica che la giustifica.”

È interessante notare che è stato possibile osservare che il workshop come processo didattico per le attività, attraverso risorse visive e sperimentazione, provoca un cambiamento nella postura degli studenti, con una maggiore motivazione e partecipazione della maggioranza, che rappresenta un maggiore coinvolgimento degli studenti in relazione al contenuto della geometria, perché secondo Castelunuovo:

Il calcestruzzo deve avere un duplice scopo: “esercitare le facoltà sintetiche e analitiche del bambino”; per consentire allo studente di costruire un concetto dal cemento; analitico perché, in questo processo l’elemento figlio riesce a discernere nell’oggetto quegli elementi che costituiscono la globalizzazione. Per questo l’oggetto deve essere mobile, che può subire una trasformazione in modo che l’elemento figlio possa identificare l’operazione sottostante. (CASTELUNUOVO, 1970, p.82-91).

Sono stati realizzati anche solidi geometrici, ma prima di presentare alcuni concetti di figure geometriche di tre dimensioni acriliche come piramidi, prismi, cubo, dodecaedro, icosaedro, tetraedro, octaedro, sfera, cilindro a loro, per fare una precedente pianificazione e solo allora assemblare i solidi, ma alcuni studenti avevano già acquisito i concetti delle forme piatte nel laboratorio precedente, perché per l’assemblaggio di solidi necessaria conoscenza degli spazi geometrici piatti richiede la capacità motoria , secondo alcuni studenti non aveva mai lavorato con questi solidi concretamente. Cartone, bastone barbecue, bastone da contatto, colla a contatto, forbici, ecc. sono stati utilizzati per assemblare i solidi geometrici.

In ogni figura costruita, è stata utilizzata la pianificazione dell’officina e il rapporto dei solidi geometrici con le figure piatte è stato applicato, gli assiemi sono stati fatti consecutivamente, e anche analizzato le forme acriliche di modello per la pianificazione. Questo potenziale pedagogico interagisce condizionalmente gli studenti nelle costruzioni delle figure, aprendo la discussione su come essere assemblati, è stato un esercizio di pazienza per la conclusione di questi calcestruzzo.

Possiamo anche usare l’interdisciplinarità in questo processo pedagogico, perché, secondo i parametri del curriculum nazionale (1998-MEC):

L’insegnante dovrebbe essere il mediatore che incoraggia lo sviluppo di procedure che contribuiscano a sviluppare nello studente l’interesse di cercare nuovi orizzonti e condividere le conoscenze acquisite in diverse situazioni. Tenendo conto di questo orientamento, c’è una grande necessità di promuovere l’interdisciplinarità e la contestualizzazione delle discipline e in particolare della matematica

Vale a dire, per facilitare ancora di più la visione ampia degli oggetti e delle loro relazioni. Tuttavia, sottolineiamo che, si può vedere che non tutti gli studenti hanno effettivamente una panoramica delle figure tridimensionali e abbiamo osservato che alcuni di loro avevano dubbi ancora di assemblare una delle forme di un solido. Abbiamo anche scoperto che questo tipo di azione prepara lo studente a cercare soluzioni e allo stesso tempo ottiene questo processo dinamico di apprendimento pedagogico per esplorare il ragionamento prima delle costruzioni di forme geometriche. Abbiamo verificato che questa attività è stata fatta con grande impegno e partecipazione degli studenti, tuttavia, ad un certo punto c’era la necessità di accompagnare alcuni studenti nel processo di assemblaggio dei solidi geometrici. Abbiamo registrato alcuni commenti fatti da loro, come:

• “Pensiamo che prendere una classe di geometria attraverso costruzioni geometriche di figura impari molto di più e oltre ad essere divertente.”
• “Oltre all’apprendimento in teoria possiamo imparare meglio nella pratica, l’insegnante non è solo passando sul tabellone ed è più interessante prendere lezioni pratiche.”

È evidente l’importanza di questa attività sviluppata nell’ambito educativo, perché questa trasposizione didattica mostra la realtà in classe e lavorando con questa attività collaborativa verifichiamo l’importanza di condividere insieme questa attività essenziale nella vita di studenti ed educatori di matematica.

Questo potenziale pedagogico presenta azioni che possono essere attuate nell’ambiente scolastico. L’esperimento e l’approssimazione della teoria geometrica nella loro vita contribuiscono alle attività educative, portando gli studenti ad essere più interessati all’apprendimento della geometria.

5. CONSIDERAZIONI FINALI

La ricerca mostra che l’incorporazione di attività che favoriscono l’interazione sociale, la cooperazione e la sperimentazione in classe può fare la differenza nell’ambiente scolastico, perché il contesto sociale in cui questi studenti sono inseriti non è isolato dalla scuola, e uno dei compiti dello stesso è quello di promuovere un’educazione che consenta la vita sociale degli studenti. Un’efficace partecipazione collaborativa è un altro punto che mettiamo in evidenza con i workshop, considerando che si è dimostrato un punto positivo, che è rafforzato da Lorenzato (2006) quando afferma che: l’insegnamento è diverso dall’insegnamento. L’insegnamento sta dando le condizioni per lo studente di costruire la propria conoscenza.

Sottolineiamo inoltre che l’uso di materiali concreti nell’insegnamento della geometria oltre a promuovere l’interazione degli studenti con l’oggetto dello studio e da questa interazione possono costruire le loro conoscenze, anche promuovere discussioni nel senso di identificare in questo modo nella vita quotidiana degli studenti, che accorcia la distanza dei concetti matematici e la loro applicabilità oltre ad essere più interessante e significativo , fungendo da alternativa per insegnare la geometria che sfugge al tradizionale.

Si nota che i laboratori sviluppati hanno raggiunto i loro obiettivi che sono partiti dallo sviluppo di competenze che permettono l’astrazione di contenuti geometrici, che possono essere utilizzati per comprendere, descrivere e rappresentare in modo organizzato il mondo in cui viviamo.

Si ritiene che la ricerca stessa sia fattibile come metodologia di lavoro quando preparata in precedenza e offre il potenziale per la semplicità presentata nel suo sviluppo, contribuendo così alla geometria di apprendimento del processo di insegnamento e alla matematica.

Pertanto, concludiamo che l’elaborata “costruzione educativa” ha avuto un risultato gratificante, con molta interazione abbiamo raggiunto i nostri obiettivi nel processo di insegnamento e apprendimento della matematica, speriamo con questo lavoro di essere incluso come una tendenza nel processo educativo di studenti ed educatori.

RIFERIMENTI

ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.

ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.

AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).

BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.

CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.

CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.

FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.

FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo

GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.

MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.

MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.

MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961

NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.

PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.

PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.

PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,

TAHAN, Malba. Didática da Matemática 1967, p.31.

^[1] Dottorando in Educazione presso l’UNR-Argentina, Professore di Matematica e Polizia Criminale di MT.

^[2] Dottorato in Istruzione; specialista in Gestione Scolastica e Gestione Persona; Laurea in inglese portoghese/inglese e letteratura, laurea di primo livello e laurea in Educazione Fisica.

^[3] Dottorato in Educazione presso l’Università Nazionale di Rosario – Unr, Argentina, ha conseguito una laurea in Lettere – English From Castelo Branco College (2006). Diritto e Filosofia. Specializzazione in lingua inglese.

^[4] Dottorando in Educazione presso l’Università Nazionale di Rosario – UNR Argentina. Laureato in Lettere Vernacolari presso l’UFBA – Università Federale di Bahia. Ha conseguito una laurea post-laurea e curriculum, didattica e valutazione presso l’Università Statale di Bahia – UNEB, Postgraduate in Metodologia dell’Insegnamento lingua portoghese e letteratura dalla Facoltà Regionale di Filosofia, Scienze e Lettere di Candeias- Bahia. Formazione in lingua spagnola certificata da DUCLE – ARGENTINA. insegnante di lingua spagnola e portoghese. Direttore dello State College Professor Maria Leal Lopes, Nova Ibia – Bahia.

^[5] Dottorato in Educazione presso l’Università Nazionale di Rosario – UNR Argentina, Laurea in Lettere. Università dello Stato di Bahia, UNEB e pedagogia dalla Facoltà Regionale di Filosofia, Scienze e Lettere di Candeias- Bahia. Laurea magistrale in teologia. Scuola Superiore di Educazione, EST, Brasile. Specializzazione in Studi Linguistici e Letterari. Università Federale di Bahia – UFBA. Specializzazione nella Pianificazione e Gestione di Sist. Educ. Distanza. Università Statale di Bahia, UNEB. Specializzazione nella metodologia dell’istruzione superiore. Facoltà integrate di anatre – FIP, specializzazione nella metodologia didattica per l’istruzione professionale, UNEB-BAHIA. Brasile. Formazione in lingua spagnola certificata da DUCLE – ARGENTINA.

^[6] Laureato in lettere portoghesi e inglesi presso l’UEG, si è laureato in insegnamento dell’istruzione superiore, da Ucan Rj; post-laurea in tecnologia in educazione da Puc Rio de Janeiro e post-laurea in metodologia di scuola elementare da UFG. Frequentare il dottorato in educazione all’UNR argentina.

^[7] Laureata in Geografia presso l’Università Cattolica di Salvador. Anno 1987. Si è laureata in Metodologia di Insegnamento Geografia. Partecipare al dottorato in Educazione presso l’Università Nazionale di Rosario -UNR Argentina.

Inviato: Luglio 2020.

Approvato: ottobre 2020.