ARTIGO ORIGINAL
OLIVEIRA, José Luiz de Jesus Egues de [1], SILVA, Edevaldo Maximo da [2], SANTOS, Cleidison Da Silva [3], PONTES, Dalila Fonseca [4], SILVA, Jandaira Fernandes da [5], QUEIROZ, Jose Pereira de [6], SANTANA, Zenóbia Conceição Castro [7]
OLIVEIRA, José Luiz de Jesus Egues de. Et al. Construção educativa de geometria e a utilização de materiais concretos como processo de aprendizagem. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 10, Vol. 10, pp. 46-61. Outubro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/construcao-educativa, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/construcao-educativa
RESUMO
A pesquisa destacou se para uma reflexão didática que atende a necessidade de que, haja construções experimentais na sala de aula, com materiais concretos para o auxílio no processo de ensino e aprendizagem de geometria no ensino fundamental. Neste sentido de atribuir uma análise para este problema, temos como eixo, a educação Matemática, como forma de estimular os alunos para o desenvolvimento de oficinas nas quais objetivaram a construção dos materiais didáticos como processo de aprendizagem de matemática. O processo da construção do conceito da geometria que atribuem as habilidades e as competências a serem desenvolvidas nos alunos nesta etapa, possibilitaram ao mesmo desenvolver um tipo de pensamento particular para compreender, descrever e representar, de forma organizada, os espaços geométricos, informando à importância que esse conteúdo tem na sua vida social como cidadão. Através das construções de figuras geométricas com materiais manipuláveis, estudamos todos os conceitos da figura, por meio dessa ferramenta, estimulando, assim, o interesse e a motivação dos alunos, proporcionando-lhes o raciocínio geométrico e matemático. As definições de geometria poderão ser construídas sucessivamente, pegando como base os conhecimentos prévios dos alunos ou não, na qual destacamos que os educadores devem criar atividades nas quais os educandos façam indagações de situações relacionados as dimensões geométricas, tendo assim experiências de sentido e direção de si próprio e de alguma figura inserida no espaço. Entretanto, para a absorção deste processo de ensino e aprendizagem, além de ser apresentada as teorias aos educandos, foram necessários mostrarmos as figuras geométricas pelas suas características físicas, ou seja, de forma como a natureza nos proporciona e não apenas por suas propriedades e conceitos definidos. Por fim, a pesquisa nos possibilitou analisar a capacidade intelectual de cada aluno selecionado para tal.
Palavras Chaves: Educação Matemática, construção educativa, geometria.
1. INTRODUÇÃO
Como profissionais da Educação e de áreas diversificadas, pensamos nesta pesquisa movidos pelo desejo de dialogarmos sobre o ensino de aprendizagem da matemática, mais especificamente observar a importância da Geometria na ementa educacional do aluno e, em específico, no ensino fundamental. Também como pesquisadores e apreciadores dos espaços geométricos, destacamos o argumento de Malba Tahan (1967, p.31) em seu texto que diz: “O que torna difícil o ensino da Matemática é o inalterável hábito latino de começar sempre pelo abstrato, sem passar pelo concreto”. Outros autores também apresentam importância muito relevante sobre esta parte da matemática. Também abordaremos o quase abandono da Geometria na Educação Básica, relatado em algumas pesquisas que abordamos como fundamentação para este trabalho. Ressaltamos também as especificidades quanto ao ensino de conteúdos de geometria no contexto do mundo físico para o ensino, bem como as habilidades que essa área da Matemática deve proporcionar para que os educandos sejam inclusos numa sociedade educativa de fato.
Entretanto, o processo de ensino-aprendizagem da Matemática é alvo de muito estudo e discussão, pois surgem sempre novas metodologias para atender uma demanda que se encontra em constante transformação em diversas modalidades de ensino.
Diante das especificidades do processo de aprendizagem da matemática no ensino fundamental, e da perspectiva de desenvolver ferramentas para estimular capacidade intelectual dos alunos e ao mesmo tempo em que valorize a utilização da Matemática na vida cotidiana na qual poderá ser resolvido inúmeros problemas, vem à tona a discussão da importância de se ensinar conteúdos que envolvam a geometria, pois além de ser um caminho muito interessante, é extremamente importante poder proporcionar ao educando uma visão mais organizada do mundo em que vive. De fato, é muito importante estudar esta área da matemática e, é defendida por diversos educadores, na qual são abordadas aqui e discutidas adiante, de acordo a importância e especificidades dessa área.
Tentamos com esta pesquisa contribuir com o ensino da educação matemática, pautado no desenvolvimento de habilidades e competências nos alunos.
O desenvolvimento de oficinas que objetivaram a construção dos materiais manipuláveis didáticos para processo de ensino e aprendizagem, explorando os conceitos geométricos que contemplam as habilidades e as competências a serem desenvolvidas pelos alunos durante a etapa chamada de “construção educativa”, possibilitará ao aluno desenvolver um tipo de pensamento particular para compreender, descrever e representar, de forma organizada, o mundo em que vive, informando à importância que esse conteúdo tem. Portanto, assim um dia poderão utilizar se desse produto educacional em seu convívio social, ou no dia a dia, além de possibilitar um aumento de visão da utilização dos conhecimentos básicos geométricos.
2. TENDÊNCIAS DIDÁTICAS PEDAGÓGICAS NO ENSINO DE GEOMETRIA
Acreditamos que a construção educativa fixou o processo de aprendizagem armazenando assim o conteúdo transmitido, que foram realizadas com materiais concretos manipuláveis.
Segundo Duval (1995), a geometria envolve três formas de processo cognitivo: que preenchem especificas funções epistemológicas;
Visualização para a exploração heurística de uma situação complexa; Construção de configurações, que pode ser trabalhada como um modelo, em que as ações realizadas representadas e os resultados observados são ligados aos objetos matemáticos representados; Raciocínio, que é o processo que conduz para a prova e a explicação. (DUVAL, 1995).
Segundo o autor, essas três espécies de processos cognitivos são entrelaçadas em sua sinergia e cognitivamente necessárias para a proficiência da geometria. Por outro lado, a heurística dos problemas de geometria refere se a um registro espacial que dá lugar a formas de interpretações autônomas.
Para Duval (1988), os problemas de geometria apresentam uma grande originalidade em relação a muitas tarefas matemáticas que podem ser propostas aos alunos. Ainda, o autor, diz que, favorecer o desenvolvimento das funções cognitivas, organizando problemas de geometria matematicamente próximos que solicitem os mesmos conhecimentos, determina uma categorização cognitiva indispensável ao aprendizado.
Segundo Machado (2005), a maior parte dos problemas de ensino e aprendizado da geometria é de origem didática e linguística. Para Duval (1995), a coordenação dos diferentes registros de representação (a escrita algébrica, as figuras geométricas, o discurso na língua natural) ligados ao tratamento dos conhecimentos não se opera espontaneamente, mesmo no curso de um ensino que mobilize essa diversidade de registros.
Entretanto, o estudo proposto, deverá possibilitar ao aluno uma diferente interpretação da geometria em sua volta, pois exercitando assim em sua memória através do contato, ou seja, “o concreto”, podem adquirirem conhecimentos neste contexto educacional, e que servirá como ferramenta a ser incorporada na sua vida do dia a dia.
Segundo Fiorentini:
Várias mudanças metodológicas são apontadas como tendências de ensino que buscam privilegiar a participação do aluno, considerando a construção do conhecimento como uma forma de aprendizagem. O conhecimento matemático emerge do mundo físico e é extraído pelo homem através dos sentidos. (FIORENTINI, 1995, p.9).
Os Parâmetros Curriculares Nacionais (PCN, 1998) também reconhecem a falta de destaque que se tem dado a essa área da Matemática e destaca ainda que ela desenvolva um papel fundamental na formação do aluno como cidadão.
Para (MACHADO, 2005), a maior parte dos problemas de ensino e aprendizado da geometria é de origem didática e linguística.
Os autores acima, citam esses aspectos nos processos de aprendizagem que são entrelaçadas em sua sinergia e cognitivamente necessárias para a proficiência da geometria. Por outro lado, a heurística dos problemas de geometria refere se a um registro espacial que dá lugar a formas de interpretações autônomas.
Esperamos que a metodologia aplicada seja uma tendência pedagógica no nosso dia a dia nesta área trabalhada, e que possamos utilizá-la de fato em nossas aulas, como uma ferramenta de aprendizagem nas aulas de geometria.
3. A UTILIZAÇÃO DE MATERIAIS CONCRETOS NO ENSINO DE GEOMETRIA
Os obstáculos e dificuldades encontradas pelos estudantes no momento do aprendizado da matemática propriamente dita são inumeráveis. Existem aqueles que não conseguem entendê-la e mesmo o professor ensinando é reprovado em nota e aqueles que quando aprovados, ainda assim, não conseguem aplicar o conhecimento adquirido. Ou seja, não compreendem a sua real importância.
Sendo assim, diversos estudos mostram que o uso de materiais manipuláveis produz maior rendimento nos alunos do que a sua utilização, em todas as idades e em todos os anos da escola. Essa utilização é uma indicação metodológica que é valorizada desde o momento de aquisição até o momento de construção de conceitos que passível de acontecer em todos os níveis de ensino. Desta forma surge o questionamento: o material concreto como utilização pedagógica poderá facilitar o ensino e aprendizagem da matemática? Segundo Carraher e Schilemann (1988), afirmam em suas pesquisas, que “não precisamos de objetos na sala de aula, mas de objetivos. Precisamos de situações em que a resolução de um problema implique na utilização dos princípios lógicos matemáticos a serem ensinados” (p.179). Isto porque o material “apesar de ser formado por objetivos, pode ser considerado como um conjunto de objetos ‘abstratos’ encontrados apenas na escola com a finalidade de ensino, e não tem qualquer conexão com mundo da criança” (p.180). Para ele o concreto para criança não é necessário, pois os objetos manipulativos podem ser abstratos nas mãos em diversas situações que a criança terá que enfrentar socialmente. Por outro lado, Fiorentini e Miorim (1990), confirmam suas palavras ditas acima e explicam que por traz de cada material utilizado, se esconde uma visão de educação matemática do homem e do mundo. Isto quer dizer que existe uma proposta pedagógica que justifica essa utilização.
A partir desta pesquisa, também encontramos questionamentos para o público de crianças com necessidades especiais. Como essa utilização aconteceria? Como seria o processo de ensino e de aprendizagem para essas crianças? Assim, a educadora Italiana e também médica Maria Montessori, nos responde trazendo resultados após pesquisa com crianças excepcionais, desenvolvidas no início deste século com vários materiais manipulativos com foco na matemática propriamente dita. Acreditava-se não haver aprendizado sem ação: “nada deve ser dada a criança, no campo da matemática, sem primeiro apresentar a ela uma situação concreta que a leva a agir a pensar, a experimentar, a descobrir, e daí, a mergulhar na abstração”. (AZEVEDO, 1979, p. 27)
Seguindo essas reflexões percebemos que esse material concreto aqui citado e posto como objeto de aplicabilidade para uma aprendizagem efetiva nos faz perceber que existe uma necessidade de que haja um exercício das faculdades sintéticas e analíticas da criança como dispõe o autor abaixo quando afirma que:
Deve-se exercitar as faculdades sintéticas e analíticas da criança. Sintéticas de permitir ao aluno construir um conceito a partir do concreto. Analítica porque neste processo a criança discerni no objeto aqueles elementos que constitui a globalização. Para isso o objeto tem que ser móvel, que possa sofrer uma transformação para que a criança possa identificar a operação que é subjacente (CASTELUNUOVO, 1970, p.82-91)
Os materiais manipuláveis podem ser fundamentais para que ocorra o aprendizado e nem sempre o mais adequado é aquele já construído ou mais bonito. Ao incentivarmos a construção educativa pelas crianças estamos pensando em facilitar o processo de aprendizagem e é nesse momento que percebemos que a participação concreta dele faz com que o dito processo de fato tenha uma validação. Assim nos deparamos com o currículo nacional do ensino básico que estabelece: Competências essenciais (IDEB, 2001), relativamente à utilização de recursos, afirma que:
Materiais manipuláveis de diversos tipos é, ao longo de toda a escolaridade, um recurso privilegiado como ponto partida ou suporte de muitas tarefas escolares, em particular dos que visam promover atividades de investigação e a comunicação matemática entre os alunos… […] Todos os alunos devem aprender a utilizar não só a calculadora elementar, mas também, à medida que progridem na educação básica, os alunos devem ter oportunidade de trabalhar com a folha de cálculo e com diversos programas educativos, nomeadamente de gráficos de funções e de geometria dinâmica (2001, p.17).
4. METODOLOGIA
A metodologia utilizada é qualitativa, bibliográfica e experimental. A pesquisa foi desenvolvida durante oficinas pedagógicas, organizada por módulos que permitiram ao mesmo tempo desenvolver as atividades ligadas a “Construções de Materiais Didáticos como Processo de Ensino e Aprendizagem”, que caracterizamos aqui como “construção educativa”.
Fizemos as oficinas com encontros que foram divididos de modo a colocar o estudante em contato com o tema. Aplicamos os conceitos das figuras relacionados aos textos selecionados do livro de matemática da disciplina de geometria. Outras leituras foram selecionadas de acordo com o desenvolvimento do trabalho. Utilizou se como conceitos de planificação de figuras geométricas no espaço bidimensional e montamos figuras geométricas do espaço tridimensional. Nesta fase, a aprendizagem da geometria se concretiza por atividades ligadas à ação, deve haver o predomínio do concreto sobre o simbólico, portanto o aluno manipula e constroem objetos das mais variadas formas para então analisar suas características físicas e geométricas. Nesta perspectiva deve-se realizar atividades geométricas que possibilitem a exploração dos conceitos relativos a espaço e forma, contribuindo para que a disciplina seja voltada para a formação de um educando inserido, pois devem compreender o mundo geométrico em que vive.
4.1 DAS OFICINAS APLICADAS
Foram realizadas duas oficinas em uma turma do 9º ano do ensino fundamental, composta por 27 alunos do período matutino da Escola Estadual Vereador Bento Muniz do município de Tangará da Serra-MT. Assim, foi aplicada uma avaliação de caráter diagnóstico, também concebido como pré-teste, e com o objetivo de termos informações dos conhecimentos prévios dos alunos no contexto da geometria euclidiana, pois segundo a LDB-Lei de Diretrizes e Base Nacional, (1961)
As diretrizes e propostas expedidas pelo MEC destacam e reforçam a necessidade de se reconhecer os conhecimentos prévios dos alunos, utilizando-os como uma ferramenta facilitadora do aprendizado e como um fator motivador, pois dessa forma, o educando se tornam sujeitos ativos no processo de escolarização, deixando de serem simples receptores do conhecimento.
As Figuras apresentam o questionário submetido, bem como as respostas de alguns alunos. As três primeiras perguntas objetivaram verificar o entendimento dos alunos na concepção das definições de polígonos e poliedros, bem como a denominação de algumas figuras geométricas elementares. Observamos que grande parte dos alunos não havia concebido as definições questionadas, o que vai de encontro com as afirmações de Almouloud (2005) em que o autor afirma que várias pesquisas apontam essa disciplina como um dos problemas de aprendizagem. E isso se torna mais evidente quando observamos as demais questões contidas no teste.
Figura 01 – PROPOSTA APLICADA.
Figura 2 – CONTINUIDADE DO TESTE
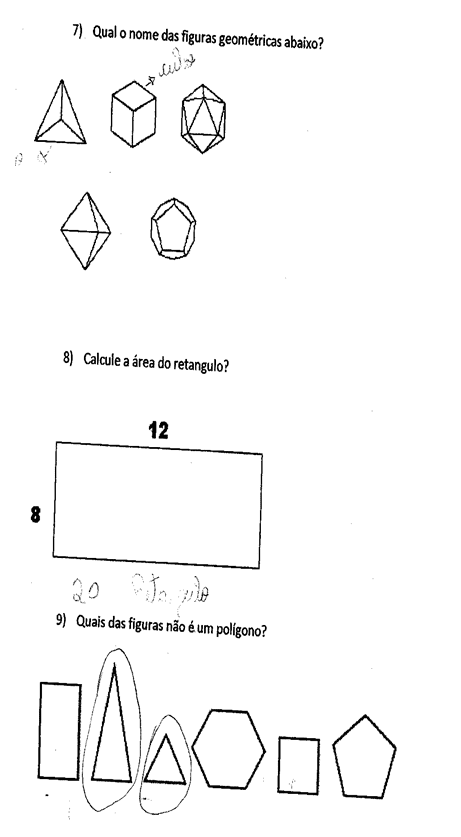
Figura – 3. Construções

Figura – 4. Construções

Figura – 5. Construções

Nesta investigação, constatou-se que grande maioria dos alunos não reconhece as formas poligonais e não poligonais e não sabem relacioná-las quanto ao número de seus lados e de vértices, e ainda se mostram a segmentarem a geometria dos seus cotidianos, apesar do cotidiano ser o fomentador do estudo da geometria como afirma o autor abaixo:
O conhecimento matemático emerge do mundo físico e é extraído pelo homem através dos sentidos” e Miguel e Miorim, (1986, p.66), que afirmam, “a geometria é tão importante para a humanidade que torna inconcebível questionar a necessidade de estudá-la na escola, pois o mundo em que vivemos é quase espontaneamente geométrico e seu uso no dia-a-dia é quase que uma necessidade humana. (FIORENTINI, 1995 p. 9.)
Talvez essa situação se torne agravada pela forma com que os professores apresentam esse conteúdo que segundo os PCN são tão importantes quanto no passado.
As questões relacionadas com as formas e relações entre elas, com as possibilidades de ocupação do espaço, com a localização e o deslocamento de objetos no espaço, vistos sob diferentes ângulos são tão necessárias hoje quanto o foram no passado. Situações quotidianas e o exercício de diversas profissões, como a engenharia, a bioquímica, a coreografia, a arquitetura, a mecânica etc., demandam do indivíduo a capacidade de pensar geometricamente (PCNs p. 122 – 1998).
Em um segundo momento, foi proposta construções das figuras planas. Durante as construções verificou-se que realmente os alunos compreendem as formas geométricas apresentadas através das construções com cartolina, ou seja, o concreto. Foram montadas as formas quadradas, retangulares, triangulares, circulares, pentagonais, hexagonais, heptagonais, octogonais, eneagonais, decagonais, dodecagonais, tridecagonais, tetradecagonais, pentadecagonais, todas desenhados em cartolinas para serem recortadas e por final construídas. Observamos que a construção pelos alunos contribuiu para a criação de significados dos próprios alunos, com um interesse em participar mais do que se tais figuras fossem apresentadas no quadro pelo professor. O que reforça os dizeres de Azevedo (2006, p.27), que acreditava não haver aprendizado sem ação: “nada deve ser dada a criança, no campo da matemática, sem primeiro apresentar se a ela uma situação concreta que a leva a agir a pensar, a experimentar, a descobrir, e daí, a mergulhar na abstração”.
Também foi aberto um espaço onde os alunos tiveram oportunidade de questionar e argumentar sobre as atividades realizadas e a relação das formas em nossa convivência. Porém após aberta a discussão para comentários, alguns alunos só contribuíram se fossem instigados e solicitados a fazer algum comentário. O comentário mais frequente pelos alunos discorreu no sentido de que nunca haviam participado de um processo de ensino dessa forma e que acharam interessantes e prazerosos construir as figuras ao em vez de ver apenas o professor apresentar as mesmas. Desta forma Machado (2005) afirma que a maior parte dos problemas de ensino e aprendizado da geometria é de origem didática e linguística; e Pavanello (1993), expõe que alguns fatores relacionados com tais dificuldades podem estar relacionados ao desinteresse dos alunos gerados pela falta de recursos didáticos, pela falta de professores interessados para utilizar esses diferentes recursos didáticos de forma a desenvolverem um ensino atrativo e de qualidade, que possa utilizar-se de novas concepções didáticas como a utilização de materiais concretos ou jogos pedagógicos no desenvolvimento de suas práticas didáticas.
Por meio dessa atividade, foi possível constatar que o potencial educativo proporcionado pelas construções de figuras planas é muito relevante para fins didático pedagógico e atrativa para estabelecer correlação entre o conteúdo do tema a ser abordado.
Nesta etapa ainda, foi solicitado aos alunos que, em grupos, construíssem as figuras planas, onde deveriam ser pintados com o lápis de cor. Este tipo de atividade conduz o aluno a fazer um planejamento prévio da construção, pois exige conhecimento das formas geométricas ou dos polígonos e requer habilidade motora para manusear os materiais.
A oficina para construções das figuras planas, além de dinâmica foi recreativa, motivadora e pedagogicamente atrativa, pois em vários momentos os grupos discutiram qual polígono iria construir, pois segundo. Fiorentini e Miorim (1990) “diz que por traz de cada material utilizado, se esconde uma visão de educação, matemática, do homem e do mundo; ou seja, existe, subjacente, uma proposta pedagógica que o justifica”.
Vale ressaltar que foi possível constatar que a oficina como processo didático para as atividades, por meio de recurso visual e experimentação, provoca mudança na postura dos alunos, ocorrendo uma maior motivação e participação da maioria, o que representa um envolvimento maior dos alunos em relação ao conteúdo da Geometria, pois segundo Castelunuovo:
O concreto deve ter uma dupla finalidade: “exercitar as faculdades sintéticas e analíticas da criança”; sintéticas de permitir ao aluno construir um conceito a partir do concreto; analítica porque, neste processo a criança consegue discernir no objeto aqueles elementos que constitui a globalização. Para isso o objeto tem que ser móvel, que possa sofrer uma transformação para que a criança possa identificar a operação que é subjacente. (CASTELUNUOVO, 1970, p.82-91).
Também foram feitas montagens dos sólidos geométricos, mas antes apresentamos alguns conceitos das figuras geométricas de três dimensões de acrílico como pirâmides, prismas, cubo, dodecaedro, icosaedro, tetraedro, octaedro, esfera, cilindro a eles, para fazermos um planejamento prévio e só depois montarem os sólidos, porém alguns alunos já tinham adquiram os conceitos das formas planas na oficina anterior, porque para montagem dos sólidos exigiam conhecimento dos espaços geométricos planos e requer habilidade motora para manusear os materiais, segundo alguns alunos nunca tinham trabalhado com estes sólidos concretamente. Para a montagem dos sólidos geométricos foram utilizadas cartolina, palito de churrasco, cola de contato, tesoura etc.
Em cada figura construída utilizou-se a planificação da oficina e aplicou-se a relação dos sólidos geométricos com as figuras planas, consecutivamente foram feitas as montagens, e também analisaram as formas de acrílico de modelo para a planificação. Esse potencial pedagógico interage condicionalmente os alunos nas construções das figuras, abrindo discussão quanto à forma a ser montada, foi um exercício de paciência para a conclusão desses concretos.
Podemos também utilizar a interdisciplinaridade neste processo pedagógico, pois, segundo os Parâmetros Curriculares Nacionais (1998-MEC):
O professor deve ser o mediador que incentive a desenvolver procedimentos que contribua para desenvolver no aluno o interesse de buscar novos horizontes e compartilhar conhecimentos adquiridos em diferentes situações. Levando em conta tal orientação, existe uma grande necessidade de se promover interdisciplinaridade e contextualização das disciplinas e principalmente da Matemática
Ou seja, para facilitar ainda mais a ampla visão dos objetos e suas relações. Porém ressaltamos que, se pode verificar que nem todos os alunos realmente têm uma visão geral das figuras de três dimensões e observamos que alguns deles tinham dúvidas ainda para montar uma das formas de um sólido. Constatamos também que este tipo de ação prepara o aluno a buscar soluções e ao mesmo tempo obtém este processo dinâmico de aprendizagem pedagógica para explorar o raciocínio diante das construções das formas geométricas. Verificamos que esta atividade foi feita com muito empenho e participação dos alunos, porém, em algum momento houve necessidade de acompanhar alguns alunos no processo de montagem dos sólidos geométricos. Registramos alguns comentários feitos por eles tais como:
- “A gente acha que fazendo aula de geometria através de construções de figuras geométricas aprende muito mais e além de ser divertido”.
- “Além de aprender na teoria podemos aprender melhor na prática, o professor não fica só passando no quadro e é mais interessante fazer aulas práticas”.
É evidente a importância dessa atividade desenvolvida no âmbito educacional, pois essa transposição didática mostra a realidade na sala de aula e trabalhando com essa atividade colaborativa verificamos a importância de compartilharmos em conjunto essa atividade essencial na vida dos educandos e educadores de matemática.
Esse potencial pedagógico apresenta ações possíveis de serem concretizadas no ambiente escolar. O experimento e a aproximação da teoria geométrica na vida deles, contribuem nas atividades educativas, levando os alunos a se interessar mais pelo aprendizado da Geometria.
5. CONSIDERAÇÕES FINAIS
A pesquisa evidencia que a incorporação de atividades que favoreçam a interação social, a cooperação e a experimentação em sala de aula, pode fazer a diferença no ambiente escolar, pois o contexto social em que esses alunos estão inseridos não está isolado da escola, sendo que uma das atribuições da mesma é promover uma educação que possibilite a vida social dos alunos. A participação colaborativa efetiva é outro ponto que evidenciamos com a realização das oficinas, tendo em vista que o mesmo se mostrou como um ponto positivo, o que se faz reforçado por Lorenzato (2006) quando afirma que: Dar aula é diferente de ensinar. Ensinar é dar condições para que o aluno construa seu próprio conhecimento.
Ressaltamos também que a utilização de materiais concretos no ensino de geometria além de promover a interação dos alunos com o objeto de estudo e a partir dessa interação os mesmos possam construir seus conhecimentos, também promovem discussões no sentido de identificação dessa forma no cotidiano dos alunos, o que encurta a distância dos conceitos matemáticos e sua aplicabilidade além de ser mais interessante e significativo, servindo como uma alternativa para o ensino de geometria que fuja do tradicional.
Salienta-se que as oficinas desenvolvidas atingiram seus objetivos que partiu do desenvolvimento de habilidades que possibilitem a abstração dos conteúdos geométricos, que possam ser usados para compreender, descrever e representar de forma organizada o mundo em que nós vivemos.
Acredita-se que a pesquisa em si é viável como metodologia de trabalho quando preparada previamente e oferece potencial pela simplicidade apresentada em seu desenvolvimento, contribuindo assim no processo de ensino aprendizagem da Geometria e da Matemática.
Portanto, concluímos que, a “construção educativa” elaborada teve um resultado gratificante, com muita interação atingimos nossos objetivos no processo de ensino e aprendizagem matemática, esperamos com esse trabalho seja incluído como tendência no processo educacional dos educandos e educadores.
REFERÊNCIAS
ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.
ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.
AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).
BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.
CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.
CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.
FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.
FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo
GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.
MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.
MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.
MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961
NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.
PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.
PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.
PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,
TAHAN, Malba. Didática da Matemática 1967, p.31.
[1] Doutorando em Educação na UNR-Argentina, Professor de Matemática, e Policial Penal de MT.
[2] Doutorando em Educação; especialista em Gestão Escolar e em Gestão de Pessoa; Graduação em Letras Português / Inglês e suas literatura, graduação em licenciatura e bacharel de Educação Física.
[3] Doutorando Em Educação Pela Universidade Nacional De Rosario – Unr, Argentina, Possui Graduação Em Letras – Inglês Pela Faculdade Castelo Branco (2006). Direito E Filosofia. Especialização Em Língua Inglesa.
[4] Doutoranda em Educação pela Universidade Nacional de Rosário – UNR Argentina. Graduada em Letras Vernáculas pela UFBA – Universidade Federal da Bahia. Possui pós-graduação e Currículo, didática e Avaliação pela Universidade Estadual da Bahia – UNEB, Pós-graduação em Metodologia do Ensino de língua Portuguesa e literatura pela Faculdade Regional de Filosofia, Ciências e letras de Candeias- Bahia. Formação em Língua Espanhola certificado pelo DUCLE – ARGENTINA. Professora de Língua Espanhola e Língua portuguesa. Gestora do Colégio Estadual Professora Maria Leal Lopes, Nova Ibia – Bahia.
[5] Doutoranda em Educação pela Universidade Nacional de Rosário – UNR Argentina, Graduação em licenciatura em Letras. Universidade do Estado da Bahia, UNEB e em Pedagogia pela Faculdade Regional de Filosofia, Ciências e letras de Candeias- Bahia. Mestrado profissional em Teologia. Escola Superior de Educação, EST, Brasil. Especialização em Estudos Linguísticos e Literários. Universidade Federal da Bahia – UFBA. Especialização em Planejamento e Gestão de Sist. Educ. Distância. Universidade do Estado da Bahia, UNEB. Especialização em Metodologia do Ensino Superior. Faculdades Integradas de Patos- FIP, Especialização em Metodologia de Ensino para Educação Profissional, UNEB-BAHIA. Brasil. Formação em Língua Espanhola certificado pelo DUCLE – ARGENTINA.
[6] Graduado em Letras Portuguesa e Inglês pela UEG, pós graduado em docência do ensino superior, pela Ucan Rj; pós-graduado em tecnologia na educação pela Puc Rio de Janeiro e Pós-graduado em metodologia do ensino fundamental pela UFG. Cursando Doutorado em Educação pela UNR da Argentina.
[7] Graduada em Licenciatura Plena em Geografia pela Universidade Católica do Salvador. Ano 1987. Pôs Graduada em Metodologia do Ensino da Geografia. Cursando Doutorado em Educação pela Universidade Nacional de Rosário -UNR Argentina.
Enviado: Julho, 2020.
Aprovado: Outubro, 2020.