Construction éducative de la géométrie et utilisation de matériaux concrets comme processus d’apprentissage

ARTICLE ORIGINAL

OLIVEIRA, José Luiz de Jesus Egues de ^[1], SILVA, Edevaldo Maximo da ^[2], SANTOS, Cleidison Da Silva ^[3], PONTES, Dalila Fonseca ^[4], SILVA, Jandaira Fernandes da ^[5], QUEIROZ, Jose Pereira de ^[6], SANTANA, Zenóbia Conceição Castro ^[7]

OLIVEIRA, José Luiz de Jesus Egues de. Et coll. Construction éducative de la géométrie et utilisation de matériaux concrets comme processus d’apprentissage. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 10, vol. 10, p. 46 à 61. octobre 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/education-fr/construction-educative, DOI: 10.32749/nucleodoconhecimento.com.br/education-fr/construction-educative

RÉSUMÉ

La recherche s’est distinguée par une réflexion didactique qui répond au besoin de constructions expérimentales en classe, avec des matériaux concrets pour aider au processus d’enseignement et d’apprentissage de la géométrie à l’école primaire. Dans ce sens d’attribuer une analyse à ce problème, nous avons comme axe, l’enseignement des mathématiques, comme un moyen de stimuler les étudiants pour le développement d’ateliers dans lesquels ils visaient à la construction de matériaux didactiques comme un processus d’apprentissage des mathématiques. Le processus de construction du concept de géométrie qui attribue les compétences et les compétences à développer chez les élèves à ce stade, a permis à la même de développer un type particulier de pensée pour comprendre, décrire et représenter, de manière organisée, les espaces géométriques, en informant l’importance que ce contenu a dans leur vie sociale en tant que citoyen. A travers la construction de figures géométriques à matériaux manipulés, nous étudions tous les concepts de la figure, à travers cet outil, stimulant ainsi l’intérêt et la motivation des étudiants, en leur fournissant un raisonnement géométrique et mathématique. Les définitions de la géométrie peuvent être construites successivement, en prenant comme base les connaissances antérieures des élèves ou non, dans lesquelles nous soulignons que les éducateurs devraient créer des activités dans lesquelles les élèves font des enquêtes sur des situations liées aux dimensions géométriques, ayant ainsi des expériences de sens et de direction d’eux-mêmes et d’une certaine figure insérée dans l’espace. Cependant, pour l’absorption de ce processus d’enseignement et d’apprentissage, en plus de présenter des théories aux élèves, il était nécessaire de montrer les figures géométriques par leurs caractéristiques physiques, c’est-à-dire de telle sorte que la nature nous fournit et pas seulement par ses propriétés et ses concepts définis. Enfin, la recherche nous a permis d’analyser la capacité intellectuelle de chaque étudiant sélectionné à cette fin.

Mots clés : Enseignement des mathématiques, construction éducative, géométrie.

1. INTRODUCTION

En tant que professionnels de l’éducation et des domaines variés, nous pensons à cette recherche motivée par le désir de dialoguer sur l’enseignement des mathématiques, plus précisément observer l’importance de la géométrie dans le menu éducatif de l’élève et, en particulier, à l’école primaire. En tant que chercheurs et connaisseurs des espaces géométriques, nous soulignons l’argument de Malba Tahan (1967, p.31) dans son texte qui dit : « Ce qui rend difficile l’enseignement des mathématiques, c’est l’inaltérable habitude latine de toujours commencer par l’abstrait, sans passer par le béton ». D’autres auteurs ont également une importance très pertinente sur cette partie des mathématiques. Nous aborderons également le quasi-abandon de la géométrie dans l’éducation de base, rapporté dans certaines études que nous abordons comme base pour ce travail. Nous soulignons également les spécificités concernant l’enseignement du contenu géométrique dans le contexte du monde physique pour l’enseignement, ainsi que les compétences que ce domaine des mathématiques doit fournir pour les étudiants d’être inclus dans une société éducative de facto.

Cependant, le processus d’enseignement-apprentissage des mathématiques fait l’objet de beaucoup d’études et de discussions, parce que de nouvelles méthodologies apparaissent toujours pour répondre à une demande qui est en constante évolution dans diverses modalités d’enseignement.

Compte tenu des spécificités du processus d’apprentissage des mathématiques à l’école primaire, et de la perspective de développer des outils pour stimuler la capacité intellectuelle des élèves et en même temps valoriser l’utilisation des mathématiques dans la vie quotidienne dans laquelle d’innombrables problèmes peuvent être résolus, la discussion sur l’importance de l’enseignement du contenu impliquant la géométrie vient à l’avant-plan, parce que c’est un chemin très intéressant , il est extrêmement important de pouvoir offrir à l’étudiant une vision plus organisée du monde dans lequel il vit. En fait, il est très important d’étudier ce domaine des mathématiques et est défendu par plusieurs éducateurs, dans lequel ils sont discutés ici et discutés ci-dessous, en fonction de l’importance et les spécificités de ce domaine.

Nous essayons avec cette recherche de contribuer à l’enseignement de l’enseignement des mathématiques, basé sur le développement des compétences et des compétences chez les étudiants.

Le développement d’ateliers visant à la construction de matériaux didactiques manipulables pour l’enseignement et le processus d’apprentissage, l’exploration des concepts géométriques qui envisagent les compétences et les compétences à développer par les étudiants au cours de la scène appelée « construction éducative », permettra à l’étudiant de développer un type particulier de pensée pour comprendre, décrire et représenter, de manière organisée, le monde dans lequel il vit , vous informant de l’importance de ce contenu. Par conséquent, un jour, ils peuvent utiliser ce produit éducatif dans leur vie sociale, ou dans la vie quotidienne, en plus de permettre une augmentation de la vue de l’utilisation des connaissances géométriques de base.

2. TENDANCES DIDACTIQUES PÉDAGOGIQUES DANS L’ENSEIGNEMENT DE LA GÉOMÉTRIE

Nous pensons que la construction éducative a fixé le processus d’apprentissage, stockant ainsi le contenu transmis, qui ont été réalisés avec des matériaux concrets manipulés.

Selon Duval (1995), la géométrie implique trois formes de processus cognitif : qui remplissent des fonctions épistémologiques spécifiques ;

Visualisation pour l’exploration heuristique d’une situation complexe; Construction de configurations, qui peuvent être travaillées comme un modèle, dans lequel les actions effectuées représentées et les résultats observés sont liés aux objets mathématiques représentés; Raisonnement, qui est le processus qui conduit à la preuve et l’explication. (DUVAL, 1995).

Selon l’auteur, ces trois espèces de processus cognitifs sont étroitement liées dans leur synergie et cognitivement nécessaires à la maîtrise de la géométrie. D’autre part, l’heuristique des problèmes de géométrie se réfère à un enregistrement spatial qui cède la place à des formes d’interprétations autonomes.

Pour Duval (1988), les problèmes de géométrie présentent une grande originalité par rapport à de nombreuses tâches mathématiques qui peuvent être proposées aux étudiants. En outre, l’auteur dit que favoriser le développement des fonctions cognitives en organisant mathématiquement des problèmes de géométrie étroite qui nécessitent les mêmes connaissances, détermine une catégorisation cognitive indispensable à l’apprentissage.

Selon Machado (2005), la plupart des problèmes d’enseignement et d’apprentissage de la géométrie sont d’origine didactique et linguistique. Pour Duval (1995), la coordination des différents registres de représentation (écriture algébrique, figures géométriques, discours dans le langage naturel) lié au traitement du savoir ne fonctionne pas spontanément, même au cours d’un enseignement qui mobilise cette diversité de documents.

Cependant, l’étude proposée devrait permettre à l’étudiant de faire une interprétation différente de la géométrie autour d’eux, parce que l’exercice dans sa mémoire par contact, c’est-à-dire « le concret », il peut acquérir des connaissances dans ce contexte éducatif, et cela servira d’outil pour être intégré dans sa vie quotidienne.

Selon la Fiorentini:

Plusieurs changements méthodologiques sont soulignés comme des tendances d’enseignement qui cherchent à privilégier la participation des étudiants, considérant la construction du savoir comme une forme d’apprentissage. La connaissance mathématique émerge du monde physique et est extraite par l’homme à travers les sens. (FIORENTINI, 1995, p.9).

Les Paramètres nationaux scolaires (PCN, 1998) reconnaissent également le manque d’importance qui a été donné à ce domaine des mathématiques et souligne également qu’il développe un rôle fondamental dans la formation de l’étudiant en tant que citoyen.

Pour (MACHADO, 2005), la plupart des problèmes d’enseignement et d’apprentissage de la géométrie sont d’origine didactique et linguistique.

Les auteurs ci-dessus citent ces aspects dans les processus d’apprentissage qui sont entrelacés dans leur synergie et cognitivement nécessaire pour la compétence de la géométrie. D’autre part, l’heuristique des problèmes de géométrie se réfère à un enregistrement spatial qui cède la place à des formes d’interprétations autonomes.

Nous espérons que la méthodologie appliquée sera une tendance pédagogique dans notre vie quotidienne dans ce domaine travaillé, et que nous pouvons effectivement l’utiliser dans nos classes, comme un outil d’apprentissage dans les classes de géométrie.

3. L’UTILISATION DE MATÉRIAUX CONCRETS DANS L’ENSEIGNEMENT DE LA GÉOMÉTRIE

Les obstacles et les difficultés rencontrés par les élèves au moment de l’apprentissage des mathématiques elles-mêmes sont innombrables. Il ya ceux qui ne peuvent pas le comprendre et même l’enseignant est désapprouvé dans une déclaration et ceux qui, une fois approuvé, ne parviennent toujours pas à appliquer les connaissances acquises. C’est-à-dire qu’ils ne comprennent pas son importance réelle.

Ainsi, plusieurs études montrent que l’utilisation de matériaux manipulés produit des performances plus élevées chez les élèves que leur utilisation, à tous les âges et à toutes les années d’école. Cette utilisation est une indication méthodologique qui est valorisée du moment de l’acquisition au moment de la construction de concepts qui peuvent se produire à tous les niveaux d’éducation. La question se pose ainsi : le matériel concret comme utilisation pédagogique peut-il faciliter l’enseignement et l’apprentissage des mathématiques ? Selon Carraher et Schilemann (1988), ils affirment dans leurs recherches que « nous n’avons pas besoin d’objets dans la salle de classe, mais d’objectifs. Nous avons besoin de situations dans lesquelles la résolution d’un problème implique l’utilisation de principes mathématiques logiques à enseigner » (p.179). C’est parce que le matériel « n dépit d’être formé par des objectifs, peut être considéré comme un ensemble d’objets « ntractif » trouvés uniquement à l’école dans le but d’enseigner, et n’a aucun lien avec le monde de l’enfan » (p.180). Pour lui, le béton pour les enfants n’est pas nécessaire, car les objets manipulateurs peuvent être abstraits dans les mains dans diverses situations auxquelles l’enfant devra faire face socialement. D’autre part, Fiorentini et Miorim (1990), confirment leurs paroles ci-dessus et expliquent que derrière chaque matériau utilisé, une vision de l’éducation mathématique de l’homme et du monde est cachée. Cela signifie qu’il y a une proposition pédagogique qui justifie cette utilisation.

À partir de cette recherche, nous avons également trouvé des questions pour le public des enfants ayant des besoins spéciaux. Comment cette utilisation se produirait-elle? À quoi ressemblerait le processus d’enseignement et d’apprentissage pour ces enfants? Ainsi, l’éducatrice italienne et aussi médecin Maria Montessori, répond à nous apporter des résultats après des recherches avec des enfants exceptionnels, développé au début de ce siècle avec divers matériaux de manipulation se concentrant sur les mathématiques elle-même. On croyait qu’il n’y avait pas d’apprentissage sans action : « rien ne devrait être donné à l’enfant, dans le domaine des mathématiques, sans lui présenter d’abord une situation concrète qui l’amène à agir pour penser, expérimenter, découvrir, et donc, s’immerger dans l’abstraction ». (AZEVEDO, 1979, p. 27)

Suite à ces réflexions, nous percevons que ce matériau concret mentionné ici et placé comme un objet d’applicabilité pour un apprentissage efficace nous fait réaliser qu’il ya un besoin d’un exercice des facultés synthétiques et analytiques de l’enfant que l’auteur ci-dessous déclare que:

Les facultés synthétiques et analytiques de l’enfant doivent être exercées. Synthétique pour permettre à l’élève de construire un concept à partir du béton. Analytique parce que dans ce processus l’enfant discerne dans l’objet les éléments qui constituent la mondialisation. Pour cela, l’objet doit être mobile, qui peut subir une transformation afin que l’enfant puisse identifier l’opération sous-jacente (CASTELUNUOVO, 1970, p.82-91)

Les matériaux manipulés peuvent être fondamentaux pour apprendre à se produire et pas toujours le plus approprié est celui déjà construit ou plus beau. En encourageant la construction éducative par les enfants, nous envisageons de faciliter le processus d’apprentissage et c’est en ce moment que nous nous rendons compte que la participation concrète de celui-ci rend ledit processus effectivement avoir une validation. Ainsi, nous sommes comparés au programme national d’éducation de base qui établit: Compétences essentielles (IDEB, 2001), en ce qui concerne l’utilisation des ressources, déclare que:

Les matériaux manipulés de différents types sont, tout au long de l’enseignement, une ressource privilégiée comme point de départ ou de soutien de nombreuses tâches scolaires, en particulier celles visant à promouvoir les activités de recherche et la communication mathématique entre les étudiants… […] Tous les élèves devraient apprendre à utiliser non seulement la calculatrice élémentaire, mais aussi, au fur et à mesure qu’ils progressent dans l’éducation de base, les élèves devraient avoir l’occasion de travailler avec la feuille de calcul et avec divers programmes éducatifs, y compris les tableaux de fonctions et la géométrie dynamique (2001, p.17).

4. MÉTHODOLOGIE

La méthodologie utilisée est qualitative, bibliographique et expérimentale. La recherche a été développée au cours d’ateliers pédagogiques, organisés par des modules qui ont permis en même temps de développer les activités liées à la construction des matériaux didactiques comme processus d’enseignement et d’apprentissage, que nous qualifions ici de « construction éducative ».

Nous avons fait les ateliers avec des réunions qui ont été divisées afin de mettre l’étudiant en contact avec le thème. Nous appliquons les concepts des figures liées aux textes sélectionnés du livre de mathématiques de la discipline de la géométrie. D’autres lectures ont été sélectionnées en fonction de l’évolution des travaux. Nous avons utilisé comme concepts de planification géométrique des figures dans l’espace bidimensionnel et nous assemblons des figures géométriques de l’espace tridimensionnel. Dans cette phase, l’apprentissage de la géométrie se réalise par des activités liées à l’action, il doit y avoir une prédominance de béton sur le symbolique, donc l’étudiant manipule et construit des objets de différentes formes pour ensuite analyser leurs caractéristiques physiques et géométriques. Dans cette perspective, des activités géométriques devraient être menées qui permettent l’exploration de concepts liés à l’espace et à la forme, contribuant à ce que le cours soit axé sur la formation d’un étudiant inséré, parce qu’ils doivent comprendre le monde géométrique dans lequel ils vivent.

4.1 DES ATELIERS APPLIQUÉS

Deux ateliers ont eu lieu dans une classe de 9^e année de l’école primaire, composée de 27 élèves de la matinée du conseiller de l’école d’État Bento Muniz de la municipalité de Tangará da Serra-MT. Ainsi, une évaluation diagnostique a été appliquée, également conçue comme un pré-test, et dans le but d’avoir des informations sur les connaissances antérieures des élèves dans le contexte de la géométrie euclidienne, parce que selon la loi LDB des lignes directrices et de la base nationale (1961)

Les lignes directrices et les propositions publiées par le MEC (Ministère de l’Éducation) soulignent et renforcent la nécessité de reconnaître les connaissances antérieures des élèves, en les utilisant comme un outil qui facilite l’apprentissage et comme facteur de motivation, parce que de cette façon, l’élève devient des sujets actifs dans le processus scolaire, n’étant plus de simples bénéficiaires de connaissances.

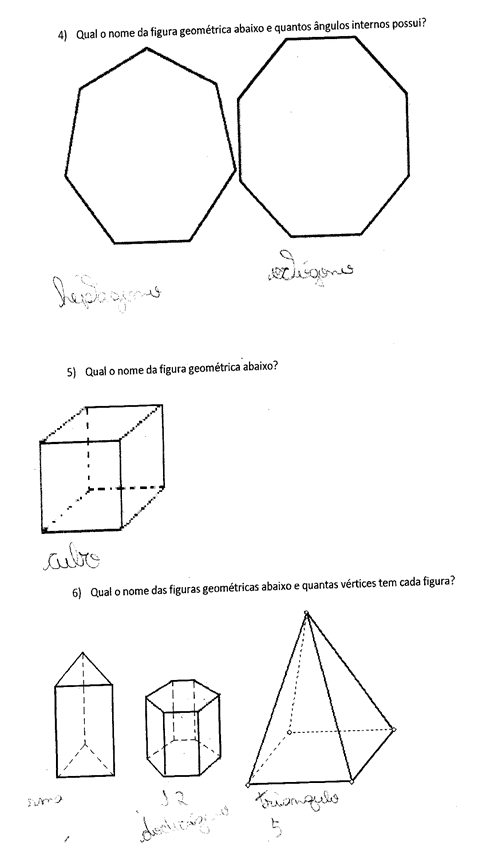
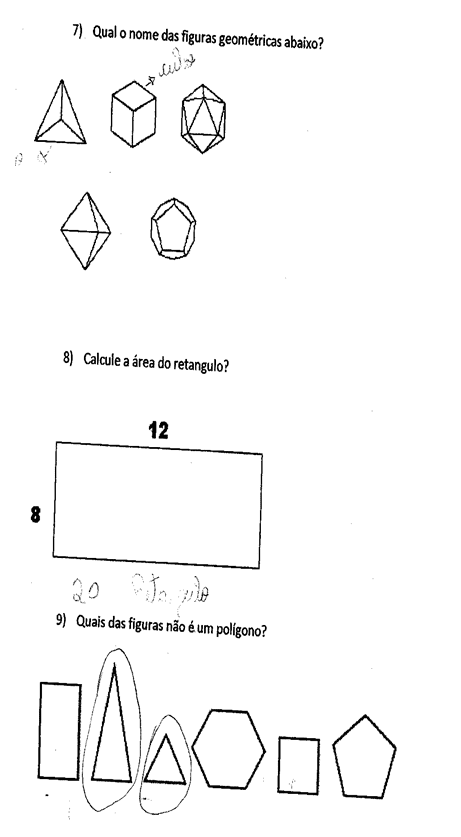
Les chiffres présentent le questionnaire soumis, ainsi que les réponses de certains étudiants. Les trois premières questions visaient à vérifier la compréhension des élèves dans la conception des définitions des polygones et du polyèdre, ainsi que la dénomination de certaines figures géométriques élémentaires. Nous avons observé que la plupart des étudiants n’avaient pas conçu les définitions remises en question, ce qui va à l’encontre des déclarations d’Almouloud (2005) dans lesquelles l’auteur affirme que plusieurs études indiquent que cette discipline est l’un des problèmes d’apprentissage. Et cela devient plus évident lorsque nous examinons les autres questions contenues dans le test.

Figure 01 – PROPOSITION APPLIQUÉE.

Figure 2 – CONTINUITÉ DES ESSAIS

Figure – 3. Constructions

Figure – 4. Constructions

Figure – 5. Constructions

Dans cette enquête, il a été constaté que la grande majorité des étudiants ne reconnaissent pas les formes polygonales et non polygonales et ne savent pas comment les relier au nombre de leurs côtés et des sommets, et montrent encore à segmenter la géométrie de leur vie quotidienne, bien que la vie quotidienne est le promoteur de l’étude de la géométrie comme indiqué par l’auteur ci-dessous:

La connaissance mathématique émerge du monde physique et est extraite par l’homme à travers les sen » et Miguel et Miorim, (1986, p.66), qui déclarent que « la géométrie est si importante pour l’humanité qu’il est inconcevable de remettre en question la nécessité de l’étudier à l’école, parce que le monde dans lequel nous vivons est presque spontanément géométrique et son utilisation dans la vie quotidienne est presque une nécessité humaine. (FIORENTINI, 1995 p. 9.)

Peut-être cette situation sera-t-elle aggravée par la façon dont les enseignants présentent ce contenu, qui selon le PCN est aussi important que par le passé.

Les questions liées aux formes et aux relations entre eux, avec les possibilités d’occupation de l’espace, avec l’emplacement et le déplacement des objets dans l’espace, vus sous différents angles sont aussi nécessaires aujourd’hui qu’ils l’étaient dans le passé. Les situations quotidiennes et l’exercice de diverses professions, telles que l’ingénierie, la biochimie, la chorégraphie, l’architecture, la mécanique, etc., exigent la capacité de l’individu à penser géométriquement (PCN p. 122 – 1998).

Dans un deuxième instant, des constructions des figures plates ont été proposées. Au cours des constructions, il a été constaté que les élèves comprennent vraiment les formes géométriques présentées à travers les constructions avec du carton, c’est-à-dire le béton. Carré, rectangulaire, triangulaire, circulaire, pentagonal, hexagonal, heptagonal, antitogonal, eneagonal, décagonal, dodécagonal, tridécagonal, tétradécagonal, pentadecagonal, tous conçus dans les cartolines à couper et enfin construits ont été assemblés. Nous avons observé que la construction par les élèves a contribué à la création de significations des élèves eux-mêmes, avec un intérêt à participer plus que si ces chiffres ont été présentés sur le conseil par l’enseignant. Ce qui renforce les paroles d’Azevedo (2006, p.27), qui croyait qu’il n’y avait pas d’apprentissage sans action : « rien ne devrait être donné à l’enfant, dans le domaine des mathématiques, sans lui présenter d’abord une situation concrète qui l’amène à agir pour penser, expérimenter, découvrir, et donc s’immerger dans l’abstraction ».

Un espace a également été ouvert où les élèves ont eu l’occasion de s’interroger et de discuter des activités menées et de la relation entre les formes de notre coexistence. Mais après l’ouverture de la discussion pour commentaires, certains étudiants n’ont contribué que s’ils étaient incités et ont demandé à faire un commentaire. Le commentaire le plus fréquent des élèves était qu’ils n’avaient jamais participé à un processus d’enseignement de cette façon et qu’ils trouvaient intéressant et agréable de construire les chiffres au lieu de simplement voir l’enseignant les présenter. Ainsi, Machado (2005) déclare que la plupart des problèmes d’enseignement et d’apprentissage de la géométrie sont d’origine didactique et linguistique; et Pavanello (1993), explique que certains facteurs liés à de telles difficultés peuvent être liés au manque d’intérêt des élèves générés par le manque de ressources didactiques, le manque d’enseignants intéressés à utiliser ces différentes ressources pédagogiques afin de développer un enseignement attrayant et de qualité, qui peut utiliser de nouvelles conceptions didactiques telles que l’utilisation de matériaux concrets ou de jeux pédagogiques dans le développement de leurs pratiques didactiques.

Grâce à cette activité, il a été possible de vérifier que le potentiel éducatif fourni par les constructions de figures plates est très pertinent à des fins didactiques pédagogiques et attrayant pour établir une corrélation entre le contenu du thème à traiter.

À ce stade, les élèves ont également été invités à construire les figures plates en groupes, où ils devraient être peints avec les crayons. Ce type d’activité conduit l’élève à faire une planification préalable de la construction, car il nécessite une connaissance des formes géométriques ou des polygones et nécessite des habiletés motrices pour manipuler les matériaux.

L’atelier de construction de figures plates, outre la dynamique, était récréatif, motivant et pédagogiquement attrayant, car à divers moments les groupes discutaient du polygone, parce que deuxièmement. Fiorentini et Miorim (1990) « dit que derrière chaque matériau utilisé, une vision de l’éducation, des mathématiques, de l’homme et du monde est cachée; c’est-à-dire qu’il y a, sous-jacent, une proposition pédagogique qui la justifie.

Il est à noter qu’il a été possible d’observer que l’atelier en tant que processus didactique pour les activités, par la ressource visuelle et l’expérimentation, provoque un changement dans la posture des élèves, avec une plus grande motivation et la participation de la majorité, ce qui représente une plus grande implication des étudiants par rapport au contenu de la géométrie, parce que selon Castelunuovo:

Le béton doit avoir un double objectif : « exercer les facultés synthétiques et analytiques de l’enfant » ; permettre à l’élève de construire un concept à partir du béton; analytique parce que, dans ce processus, l’enfant parvient à discerner dans l’objet les éléments qui constituent la mondialisation. Pour cela, l’objet doit être mobile, ce qui peut subir une transformation afin que l’enfant puisse identifier l’opération qui est sous-jacente. (CASTELUNUOVO, 1970, p.82-91).

Des solides géométriques ont également été fabriqués, mais avant de présenter quelques concepts de figures géométriques de trois dimensions acryliques telles que pyramides, prismes, cube, dodécaèdre, icosaèdre, tétraèdre, octaèdre, sphère, cylindre pour eux, pour faire une planification précédente et seulement alors assembler les solides, mais certains étudiants avaient déjà acquis les concepts des formes plates dans l’atelier précédent, en raison de l’assemblage de solides nécessaires connaissance des espaces géométriques plats et nécessite la capacité motrice de manipuler les matériaux , selon certains étudiants n’avaient jamais travaillé concrètement avec ces solides. Carton, bâton de barbecue, bâton de contact, colle de contact, ciseaux, etc. ont été utilisés pour assembler les solides géométriques.

Dans chaque figure construite, la planification de l’atelier a été utilisée et la relation des solides géométriques avec les figures plates a été appliquée, les assemblages ont été réalisés consécutivement, et a également analysé les formes acryliques de modèle pour la planification. Ce potentiel pédagogique interagit sous condition avec les élèves dans la construction des personnages, ouvrant la discussion sur la façon d’être assemblé, était un exercice de patience pour la conclusion de ces bétons.

Nous pouvons également utiliser l’interdisciplinarité dans ce processus pédagogique, car, selon les paramètres du curriculum national (1998-MEC):

L’enseignant doit être le médiateur qui encourage l’élaboration de procédures qui contribuent à développer chez l’élève l’intérêt de chercher de nouveaux horizons et de partager les connaissances acquises dans différentes situations. Compte tenu de cette orientation, il est grand besoin de promouvoir l’interdisciplinarité et la contextualisation des disciplines et surtout des mathématiques

C’est-à-dire pour faciliter encore plus la vision large des objets et de leurs relations. Cependant, nous soulignons que, on peut voir que tous les élèves n’ont pas réellement une vue d’ensemble des chiffres tridimensionnels et nous avons observé que certains d’entre eux avaient des doutes encore à assembler l’une des formes d’un solide. Nous avons également constaté que ce type d’action prépare l’étudiant à chercher des solutions et en même temps obtient ce processus dynamique d’apprentissage pédagogique pour explorer le raisonnement avant les constructions de formes géométriques. Nous avons vérifié que cette activité a été faite avec beaucoup d’engagement et de participation des étudiants, cependant, à un moment donné, il était nécessaire d’accompagner certains étudiants dans le processus d’assemblage des solides géométriques. Nous avons enregistré quelques commentaires qu’ils ont faits, tels que:

• « nous pensons que prendre un cours de géométrie à travers des constructions géométriques de figures apprend beaucoup plus et en plus d’être amusant. »
• « En plus d’apprendre en théorie, nous pouvons mieux apprendre dans la pratique, l’enseignant ne se contente pas de passer sur le tableau et il est plus intéressant de prendre des cours pratiques. »

Il est évident que l’importance de cette activité s’est développée dans le domaine de l’éducation, parce que cette transposition didactique montre la réalité en classe et en travaillant avec cette activité de collaboration, nous vérifions l’importance de partager ensemble cette activité essentielle dans la vie des étudiants en mathématiques et des éducateurs.

Ce potentiel pédagogique présente des actions qui peuvent être mises en œuvre dans le milieu scolaire. L’expérience et l’approximation de la théorie géométrique dans leur vie contribuent à des activités éducatives, ce qui conduit les élèves à s’intéresser davantage à l’apprentissage de la géométrie.

5. CONSIDÉRATIONS FINALES

La recherche montre que l’incorporation d’activités qui favorisent l’interaction sociale, la coopération et l’expérimentation en classe peut faire une différence dans l’environnement scolaire, parce que le contexte social dans lequel ces élèves sont insérés n’est pas isolé de l’école, et l’une des tâches de la même est de promouvoir une éducation qui permet la vie sociale des élèves. La participation collaborative efficace est un autre point que nous soulignons avec les ateliers, considérant qu’il s’est avéré être un point positif, qui est renforcé par Lorenzato (2006) quand il déclare que: L’enseignement est différent de l’enseignement. L’enseignement donne des conditions à l’élève pour qu’il construise ses propres connaissances.

Nous soulignons également que l’utilisation de matériaux concrets dans l’enseignement de la géométrie en plus de promouvoir l’interaction des étudiants avec l’objet de l’étude et de cette interaction, ils peuvent construire leurs connaissances, aussi promouvoir des discussions dans le sens de l’identification de cette façon dans la vie quotidienne des étudiants, ce qui raccourcit la distance des concepts mathématiques et leur applicabilité en plus d’être plus intéressant et significatif , servant d’alternative à l’enseignement de la géométrie qui s’échappe du traditionnel.

Il est à noter que les ateliers développés ont atteint leurs objectifs qui ont commencé à partir du développement de compétences qui permettent l’abstraction de contenus géométriques, qui peuvent être utilisés pour comprendre, décrire et représenter d’une manière organisée le monde dans lequel nous vivons.

On croit que la recherche elle-même est réalisable comme une méthodologie de travail lorsqu’elle est préparée précédemment et offre un potentiel pour la simplicité présentée dans son développement, contribuant ainsi au processus d’enseignement de l’apprentissage de la géométrie et des mathématiques.

Par conséquent, nous concluons que la « construction éducative » élaborée a eu un résultat gratifiant, avec beaucoup d’interaction que nous avons atteint nos objectifs dans le processus d’enseignement et d’apprentissage des mathématiques, nous espérons avec ce travail d’être inclus comme une tendance dans le processus éducatif des étudiants et des éducateurs.

RÉFÉRENCES

ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.

ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.

AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).

BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.

CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.

CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.

FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.

FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo

GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.

MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.

MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.

MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961

NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.

PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.

PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.

PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,

TAHAN, Malba. Didática da Matemática 1967, p.31.

^[1] Doctorant en éducation à l’UNR-Argentine, professeur de mathématiques et police criminelle de MT.

^[2] Doctorat en éducation; spécialiste en gestion scolaire et en gestion des personnes; Diplôme en anglais portugais/ anglais et sa littérature, baccalauréat et baccalauréat en éducation physique.

^[3] Doctorant en éducation à l’Université nationale de Rosario – Unr, Argentine, détient un diplôme en lettres – Anglais de Castelo Branco College (2006). Droit et philosophie. Spécialisation en anglais.

^[4] Doctorant en éducation à l’Université nationale de Rosario – UNR Argentine. Diplômé en lettres vernaculaires de l’UFBA – Université fédérale de Bahia. Il est titulaire d’un diplôme de troisième cycle et d’un programme d’études, de didactique et d’évaluation de l’Université d’État de Bahia – UNEB, post-universitaire en méthodologie de l’enseignement des langues portugaises et de la littérature de la Faculté régionale de philosophie, des sciences et des lettres de Candeias-Bahia. Formation en espagnol certifiée par DUCLE – ARGENTINA. Professeur d’espagnol et de langue portugaise. Directeur du State College Professeur Maria Leal Lopes, Nova Ibia – Bahia.

^[5] Doctorant en éducation à l’Université nationale de Rosario – UNR Argentine, Baccalauréat en Lettres. Université de l’État de Bahia, UNEB et pédagogie par la Faculté régionale de philosophie, des sciences et des lettres de Candeias-Bahia. Maîtrise professionnelle en théologie. École supérieure d’éducation, EST, Brésil. Spécialisation en études linguistiques et littéraires. Université fédérale de Bahia – UFBA. Spécialisation en planification et gestion de Sist. Educ. Distance. Université d’État de Bahia, UNEB. Spécialisation en méthodologie de l’enseignement supérieur. Facultés intégrées des canards – FIP, Spécialisation en méthodologie d’enseignement pour l’enseignement professionnel, UNEB-BAHIA. Brésil. Formation en espagnol certifiée par DUCLE – ARGENTINA.

^[6] Diplômé en lettres portugaises et anglaises de l’UEG, diplômé en enseignement supérieur, d’Ucan Rj; troisième cycle en technologie dans l’éducation de Puc Rio de Janeiro et post-diplômé en méthodologie de l’école primaire de l’UFG. Doctorat en éducation à l’UNR argentine.

^[7] Diplômé en plein diplôme en géographie de l’Université catholique de Salvador. Année 1987. Elle est diplômée en méthodologie d’enseignement de la géographie. Doctorat en éducation de l’Université nationale de Rosario -UNR Argentine.

Envoyé : juillet 2020.

Approuvé : octobre 2020.