ORIGINALER ARTIKEL
OLIVEIRA, José Luiz de Jesus Egues de [1], SILVA, Edevaldo Maximo da [2], SANTOS, Cleidison Da Silva [3], PONTES, Dalila Fonseca [4], SILVA, Jandaira Fernandes da [5], QUEIROZ, Jose Pereira de [6], SANTANA, Zenóbia Conceição Castro [7]
OLIVEIRA, José Luiz de Jesus Egues de. Et al. Pädagogische Konstruktion von Geometrie und die Verwendung von Betonmaterialien als Lernprozess. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 10, Vol. 10, S. 46-61. Oktober 2020. ISSN: 2448-0959, Zugriffsverbindung: https://www.nucleodoconhecimento.com.br/bildung-de/paedagogische-konstruktion, DOI: 10.32749nucleodoconhecimento.com.br/bildung-de/paedagogische-konstruktion
ZUSAMMENFASSUNG
Die Forschung zeichnete sich durch eine didaktische Reflexion aus, die dem Bedarf an experimentellen Konstruktionen im Klassenzimmer gerecht wird, mit Betonmaterialien, die den Prozess des Lehrens und Lernens von Geometrie in der Grundschule unterstützen. In diesem Sinne, eine Analyse diesem Problem zuzuschreiben, haben wir als Achse, Mathematik-Bildung, als eine Möglichkeit, Studenten für die Entwicklung von Workshops zu stimulieren, in denen sie auf den Aufbau von didaktischen Materialien als einen Prozess des Erlernens von Mathematik zielten. Der Prozess der Konstruktion des Konzepts der Geometrie, die die Fähigkeiten und Kompetenzen, die in diesem Stadium in den Schülern entwickelt werden, zuschreiben, ermöglichte es dem gleichen, eine bestimmte Art von Gedanken zu entwickeln, um die geometrischen Räume auf organisierte Weise zu verstehen, zu beschreiben und darzustellen, um die Bedeutung zu vermitteln, die dieser Inhalt in seinem gesellschaftlichen Leben als Bürger hat. Durch die Konstruktion geometrischer Figuren mit manipulierten Materialien untersuchen wir alle Konzepte der Figur, durch dieses Werkzeug, wodurch das Interesse und die Motivation der Studenten angeregt und ihnen geometrische und mathematische Argumentation vermittelt werden. Die Definitionen der Geometrie können sukzessive konstruiert werden, indem man sich auf das Vorwissen der Schüler bezieht oder nicht, in dem wir hervorheben, dass Pädagogen Aktivitäten schaffen sollten, in denen die Schüler Situationen im Zusammenhang mit geometrischen Dimensionen abfragen und so Erfahrungen von Bedeutung und Richtung ihrer selbst und einer Figur haben, die in den Raum eingefügt wird. Für die Aufnahme dieses Lehr- und Lernprozesses war es jedoch neben der Präsentation von Theorien für die Schüler notwendig, die geometrischen Figuren anhand ihrer physikalischen Eigenschaften zu zeigen, d.h. so, dass die Natur uns und nicht nur durch ihre Eigenschaften und definierten Konzepte versorgt. Schließlich erlaubte uns die Forschung, die intellektuelle Kapazität jedes Studenten zu analysieren, der zu diesem Zweck ausgewählt wurde.
Schlagworte: Mathematik-Erziehung, Pädagogischekonstruktion, Geometrie.
1. EINFÜHRUNG
Als Fachleute der Bildung und verschiedener Bereiche denken wir an diese Forschung, die durch den Wunsch nach Dialog über den Unterricht des Lernens Mathematik angetrieben wird, genauer gesagt beobachten die Bedeutung der Geometrie in der Bildungsmenü des Schülers und insbesondere in der Grundschule. Auch als Forscher und Kenner geometrischer Räume heben wir das Argument von Malba Tahan (1967, S.31) in seinem Text hervor, der sagt: “Was es schwierig macht, Mathematik zu lehren, ist die unveränderliche lateinische Gewohnheit, immer mit dem Abstrakten zu beginnen, ohne durch Beton zu gehen”. Auch andere Autoren haben für diesen Teil der Mathematik eine sehr relevante Bedeutung. Wir werden uns auch mit der fast Aufgabe der Geometrie in der Grundbildung befassen, die in einigen Studien berichtet wird, die wir als Grundlage für diese Arbeit angehen. Wir betonen auch die Besonderheiten in Bezug auf die Lehre von Geometrieinhalten im Kontext der physischen Welt für den Unterricht, sowie die Fähigkeiten, die dieser Bereich der Mathematik für die Aufnahme der Schüler in eine de facto Bildungsgesellschaft bieten muss.
Der Lehr-Lern-Prozess der Mathematik ist jedoch Gegenstand vieler Studien und Diskussionen, da immer neue Methoden entstehen, um einer Nachfrage gerecht zu werden, die sich in den verschiedenen Lehrmodalitäten ständig ändert.
Angesichts der Besonderheiten des Lernprozesses der Mathematik in der Grundschule und der Perspektive der Entwicklung von Werkzeugen, um die intellektuelle Leistungsfähigkeit der Schüler zu stimulieren und gleichzeitig den Einsatz von Mathematik im Alltag zu schätzen, in dem unzählige Probleme gelöst werden können, tritt die Diskussion über die Bedeutung von Lehrinhalten mit Geometrie in den Vordergrund, weil es ein sehr interessanter Weg ist. ist es äußerst wichtig, dem Schüler einen organisierteren Blick auf die Welt zu vermitteln, in der er lebt. In der Tat ist es sehr wichtig, diesen Bereich der Mathematik zu studieren und wird von mehreren Pädagogen verteidigt, in denen sie hier diskutiert und unten diskutiert werden, je nach der Bedeutung und Besonderheiten dieses Bereichs.
Wir versuchen mit dieser Forschung, zur Lehre der mathematikischen Ausbildung beizutragen, basierend auf der Entwicklung von Fähigkeiten und Kompetenzen in den Schülern.
Die Entwicklung von Workshops, die auf den Aufbau didaktischer manipulierbarer Materialien für den Lehr- und Lernprozess abzielten und die geometrischen Konzepte erforschen, die die Fähigkeiten und Kompetenzen berücksichtigen, die von den Schülern während der Phase des “Bildungsbaus” entwickelt werden sollen, wird es dem Schüler ermöglichen, eine bestimmte Art von Gedanken zu entwickeln, um die Welt, in der er lebt, auf organisierte Weise zu verstehen, zu beschreiben und darzustellen. , um Sie darüber zu informieren, wie wichtig dieser Inhalt ist. Daher können sie eines Tages dieses pädagogische Produkt in ihrem gesellschaftlichen Leben oder im täglichen Leben verwenden, abgesehen von einer Erhöhung der Sicht auf die Verwendung von geometrischen Grundkenntnissen.
2. PÄDAGOGISCH DIDAKTISCHE TRENDS IM GEOMETRIEUNTERRICHT
Wir glauben, dass die pädagogische Konstruktion den Lernprozess fixiert emittierte und somit die übertragenen Inhalte speicherte, die mit manipulierten Betonmaterialien durchgeführt wurden.
Laut Duval (1995) umfasst Geometrie drei Formen des kognitiven Prozesses: die spezifische erkenntnistheoretische Funktionen ausfüllen;
Visualisierung zur heuristischen Erforschung einer komplexen Situation; Konstruktion von Konfigurationen, die als Modell bearbeitet werden können, in denen die ausgeführten Aktionen dargestellt und die beobachteten Ergebnisse mit den dargestellten mathematischen Objekten verknüpft sind; Argumentation, das ist der Prozess, der zu Beweisen und Erklärungen führt. (DUVAL, 1995).
Nach Angaben des Autors sind diese drei Arten von kognitiven Prozessen in ihrer Synergie miteinander verflochten und kognitiv notwendig für die Befähigung der Geometrie. Andererseits bezieht sich die Heuristik von Geometrieproblemen auf eine räumliche Aufzeichnung, die Formen autonomer Interpretationen weicht.
Für Duval (1988) stellen Geometrieprobleme eine große Originalität in Bezug auf viele mathematische Aufgaben dar, die den Schülern vorgeschlagen werden können. Darüber hinaus sagt der Autor, dass die Förderung der Entwicklung von kognitiven Funktionen durch die Organisation mathematisch nahe Geometrie Probleme, die das gleiche Wissen erfordern, bestimmt eine kognitive Kategorisierung unverzichtbar für das Lernen.
Laut Machado (2005) sind die meisten Probleme des Lehrens und Lernens Geometrie didaktischer und sprachlicher Herkunft. Für Duval (1995) funktioniert die Koordination der verschiedenen Repräsentationsaufzeichnungen (algebraisches Schreiben, geometrische Figuren, Diskurs in der natürlichen Sprache), die mit der Behandlung von Wissen verbunden sind, nicht spontan, auch nicht im Laufe einer Lehre, die diese Vielfalt von Aufzeichnungen mobilisiert.
Die vorgeschlagene Studie sollte es dem Schüler jedoch ermöglichen, die Geometrie um ihn herum anders zu interpretieren, denn wenn er in seinem Gedächtnis durch Kontakt, d. h. “das Konkrete”, trainiert, kann er sich in diesem pädagogischen Kontext Wissen aneignen, und das wird als Werkzeug dienen, um in sein tägliches Leben integriert zu werden.
Nach Fiorentini:
Mehrere methodische Veränderungen werden als Lehrtrends herausgestellt, die die Teilnahme der Schüler zu privilegieren versuchen, indem sie den Aufbau von Wissen als eine Form des Lernens betrachten. Mathematisches Wissen entsteht aus der physischen Welt und wird vom Menschen durch die Sinne extrahiert. (FIORENTINI, 1995, S.9).
Die National Curricular Parameters (PCN, 1998) erkennen auch den Mangel an Bedeutung, die diesem Bereich der Mathematik gegeben wurde und hebt auch hervor, dass es eine grundlegende Rolle bei der Bildung des Studenten als Bürger entwickelt.
Für (MACHADO, 2005) sind die meisten Probleme des Lehrens und Lernens Geometrie didaktischen und sprachlichen Ursprungs.
Die oben genannten Autoren zitieren diese Aspekte in den Lernprozessen, die in ihrer Synergie verflochten und kognitiv notwendig für die Befähigung der Geometrie sind. Andererseits bezieht sich die Heuristik von Geometrieproblemen auf eine räumliche Aufzeichnung, die Formen autonomer Interpretationen weicht.
Wir hoffen, dass die angewandte Methodik ein pädagogischer Trend in unserem täglichen Leben in diesem Bereich sein wird, und dass wir sie tatsächlich in unseren Klassen als Lernwerkzeug in Geometrieklassen verwenden können.
3. DIE VERWENDUNG VON BETONMATERIALIEN IN DER LEHRE VON GEOMETRIE
Die Hindernisse und Schwierigkeiten, auf die die Schüler zum Zeitpunkt des Mathematiklernens selbst stoßen, sind unzählbar. Es gibt diejenigen, die es nicht verstehen können, und selbst der Lehrer wird in einer Erklärung abgelehnt, und diejenigen, die, wenn sie genehmigt werden, das erworbene Wissen immer noch nicht anwenden. Das heißt, sie verstehen ihre wirkliche Bedeutung nicht.
So zeigen mehrere Studien, dass die Verwendung von manipulierten Materialien bei schülern eine höhere Leistung bringt als ihre Verwendung, in jedem Alter und in allen Schuljahren. Diese Verwendung ist eine methodische Indikation, die vom Moment des Erwerbs bis zum Zeitpunkt der Konstruktion von Konzepten geschätzt wird, die auf allen Bildungsebenen passieren können. So stellt sich die Frage: Kann konkretes Material als pädagogische Nutzung das Lehren und Lernen von Mathematik erleichtern? Laut Carraher und Schilemann (1988) stellen sie in ihrer Forschung fest: “Wir brauchen keine Objekte im Klassenzimmer, sondern Ziele. Wir brauchen Situationen, in denen die Lösung eines Problems die Verwendung mathematischer logischer Prinzipien impliziert, um gelehrt zu werden” (S.179). Denn das Material “kann trotz der Ausweichung durch Ziele als eine Reihe von ‘abstrakten’ Objekten betrachtet werden, die nur in der Schule zum Zweck des Unterrichts gefunden werden, und hat keine Verbindung zur Welt des Kindes” (S.180). Für ihn ist Beton für Kinder nicht notwendig, denn manipulative Objekte können in verschiedenen Situationen abstrakt in den Händen sein, denen sich das Kind sozial stellen muss. Auf der anderen Seite bestätigen Fiorentini und Miorim (1990) ihre oben gesprochenen Worte und erklären, dass hinter jedem verwendeten Material eine Vision der mathematischen Erziehung des Menschen und der Welt verborgen ist. Das bedeutet, dass es einen pädagogischen Vorschlag gibt, der diese Verwendung rechtfertigt.
Aus dieser Forschung haben wir auch Fragen für die Öffentlichkeit von Kindern mit besonderen Bedürfnissen gefunden. Wie würde diese Verwendung geschehen? Wie würde der Lehr- und Lernprozess für diese Kinder aussehen? So, die italienische Pädagogin und auch Ärztin Maria Montessori, antwortet auf uns bringen Ergebnisse nach Forschung mit außergewöhnlichen Kindern, entwickelt zu Beginn dieses Jahrhunderts mit verschiedenen manipulativen Materialien, die sich auf die Mathematik selbst. Man glaubte, dass es kein Lernen ohne Handeln gebe: “Nichts sollte dem Kind gegeben werden, auf dem Gebiet der Mathematik, ohne ihm vorher eine konkrete Situation zu präsentieren, die ihn dazu bringt, zu handeln, zu denken, zu experimentieren, zu entdecken und damit in die Abstraktion einzutauchen”. (AZEVEDO, 1979, S. 27)
Nach diesen Überlegungen stellen wir fest, dass dieses konkrete Material, das hier erwähnt und als Objekt der Anwendbarkeit für effektives Lernen platziert wird, uns erkennen lässt, dass es notwendig ist, die synthetischen und analytischen Fähigkeiten des Kindes auszuüben, wie der Autor unten besagt:
Die synthetischen und analytischen Fähigkeiten des Kindes sollten ausgeübt werden. Synthetisch, damit der Schüler ein Konzept aus dem Beton erstellen kann. Analytisch, weil das Kind in diesem Prozess im Objekt jene Elemente erkennt, die die Globalisierung ausmacht. Dazu muss das Objekt mobil sein, das einer Transformation unterzogen werden kann, so dass das Kind die zugrunde liegende Operation identifizieren kann (CASTELUNUOVO, 1970, S.82-91)
Die manipulierten Materialien können grundlegend sein, um zu lernen, und nicht immer das am besten geeignete ist das, das bereits gebaut oder schöner ist. Indem wir den Bildungsaufbau von Kindern fördern, denken wir darüber nach, den Lernprozess zu erleichtern, und in diesem Moment erkennen wir, dass die konkrete Beteiligung dieses Prozesses tatsächlich eine Bestätigung hat. So werden wir mit dem nationalen Curriculum der Grundbildung verglichen, das feststellt: Wesentliche Kompetenzen (IDEB, 2001), in Bezug auf die Verwendung von Ressourcen, besagt, dass:
Manipulierte Materialien unterschiedlicher Art sind in der gesamten Schulbildung eine privilegierte Ressource als Ausgangspunkt oder Unterstützung vieler schulischer Aufgaben, insbesondere solche, die auf die Förderung von Forschungsaktivitäten und mathematischer Kommunikation zwischen Schülern abzielen… […] Alle Schüler sollten lernen, nicht nur den Elementarrechner zu verwenden, sondern auch, wie sie in der Grundbildung fortschritten, sollten die Schüler die Möglichkeit haben, mit der Tabelle und mit verschiedenen Bildungsprogrammen zu arbeiten, einschließlich Funktionsdiagramme und dynamische Geometrie (2001, S.17).
4. METHODIK
Die verwendete Methodik ist qualitativ, bibliographisch und experimentell. Die Forschung wurde in pädagogischen Workshops entwickelt, die von Modulen organisiert wurden, die es gleichzeitig ermöglichten, die Aktivitäten im Zusammenhang mit “Konstruktion didaktischer Materialien als Lehr- und Lernprozess” zu entwickeln, die wir hier als “Bildungsbau” bezeichnen.
Wir haben die Workshops mit Treffen durchgeführt, die geteilt wurden, um den Schüler mit dem Thema in Kontakt zu bringen. Wir wenden die Konzepte der Figuren im Zusammenhang mit den ausgewählten Texten des Mathematikbuches der Disziplin Geometrie an. Weitere Lesungen wurden entsprechend der Entwicklung des Werkes ausgewählt. Wir haben als Konzepte der geometrischen Figurenplanung im zweidimensionalen Raum verwendet und geometrische Figuren des dreidimensionalen Raumes zusammengefügt. In dieser Phase wird das Lernen der Geometrie durch Aktivitäten im Zusammenhang mit Aktion realisiert, es muss eine Dominanz des Betons über dem Symbolischen sein, daher manipuliert und konstruiert der Schüler Objekte verschiedener Formen, um dann ihre physikalischen und geometrischen Eigenschaften zu analysieren. In dieser Perspektive sollten geometrische Aktivitäten durchgeführt werden, die die Erforschung von Konzepten im Zusammenhang mit Raum und Form ermöglichen und dazu beitragen, dass sich der Kurs auf die Bildung eines eingefügten Studenten konzentriert, weil sie die geometrische Welt verstehen müssen, in der sie leben.
4.1 DER ANGEWANDTEN WERKSTÄTTEN
Zwei Workshops fanden in einer 9. Klasse der Grundschule statt, die sich aus 27 Schülern des staatlichen Schulrates Bento Muniz aus der Gemeinde Tangará da Serra-MT zusammensetzte. So wurde eine diagnostische Bewertung durchgeführt, die auch als Vortest konzipiert war und mit dem Ziel, Informationen über die Vorkenntnisse der Studierenden im Kontext der euklidischen Geometrie zu erhalten, da nach dem LDB-Richtliniengesetz und der nationalen Grundlage (1961)
Die Leitlinien und Vorschläge des MEC (Bildungsministerium) unterstreichen und unterstreichen die Notwendigkeit, die Vorkenntnisse der Schüler zu erkennen, indem sie als Lerninstrument und als motivierender Faktor verwendet werden, denn auf diese Weise wird der Schüler zu aktiven Fächern im Schulprozess und ist nicht mehr bloße Randbegabung von Wissen.
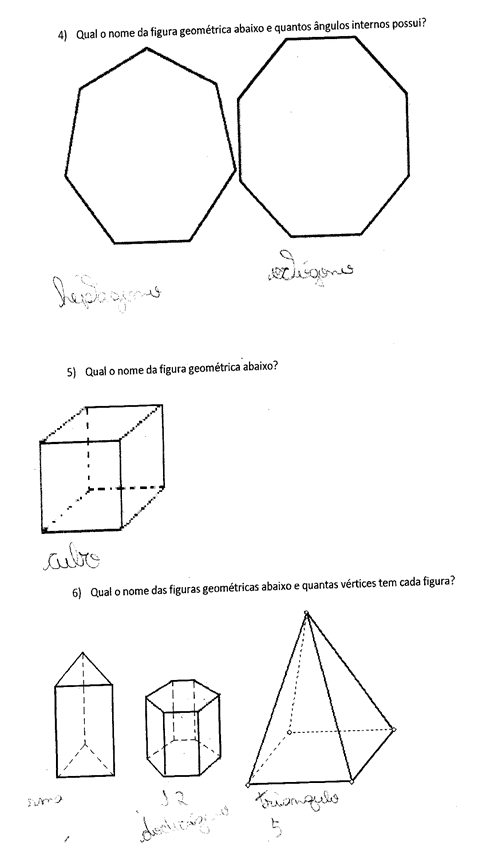
Die Zahlen enthalten den eingereichten Fragebogen sowie die Antworten einiger Studenten. Die ersten drei Fragen zielten darauf ab, das Verständnis der Schüler in der Konzeption der Definitionen von Polygonen und Polyedern sowie der Bezeichnung einiger elementarer geometrischer Figuren zu überprüfen. Wir stellten fest, dass die meisten Studenten die in Frage gestellten Definitionen nicht konzipiert hatten, was den Aussagen von Almouloud (2005) zuwiderläuft, in denen der Autor erklärt, dass mehrere Studien auf diese Disziplin als eines der Lernprobleme hinweisen. Und dies wird deutlicher, wenn wir uns die anderen Fragen ansehen, die im Test enthalten sind.
Abbildung 01 – APPLIED PROPOSAL.
Abbildung 2: TESTKONTINUITÄT
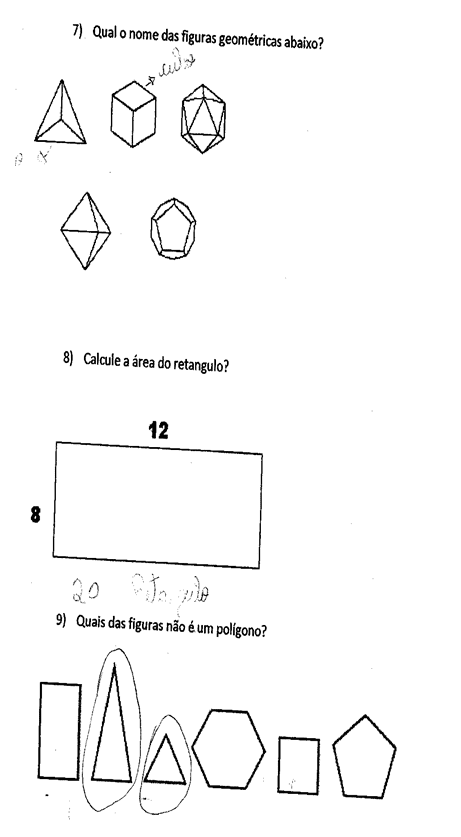
Abbildung – 3. Konstruktionen

Quelle: Eigene (2011)
Abbildung – 4. Konstruktionen

Quelle: Eigene (2011)
Abbildung – 5. Konstruktionen

In dieser Untersuchung wurde festgestellt, dass die überwiegende Mehrheit der Studenten die polygonalen und nicht-polygonalen Formen nicht erkennt und nicht weiß, wie sie mit der Anzahl ihrer Seiten und Scheitelpunkte in Beziehung gesetzt werden sollen, und dennoch zeigen, die Geometrie ihres täglichen Lebens zu segmentieren, obwohl das tägliche Leben der Förderer der Studie der Geometrie ist, wie der Autor unten erklärt:
Mathematisches Wissen entsteht aus der physischen Welt und wird vom Menschen durch die Sinne extrahiert” und Miguel und Miorim (1986, S.66), die sagen: “Geometrie ist für die Menschheit so wichtig, dass sie es unvorstellbar macht, die Notwendigkeit, sie in der Schule zu studieren, in Frage zu stellen, weil die Welt, in der wir leben, fast spontan geometrisch ist und ihre Verwendung im Alltag fast eine menschliche Notwendigkeit ist. (FIORENTINI, 1995 S. 9)
Vielleicht wird sich diese Situation durch die Art und Weise verschlimmern, wie Lehrer diesen Inhalt präsentieren, der laut PCN genauso wichtig ist wie in der Vergangenheit.
Die Fragen im Zusammenhang mit den Formen und Beziehungen zwischen ihnen, mit den Möglichkeiten der Raumbesetzung, mit der Lage und Verschiebung von Objekten im Raum, aus verschiedenen Blickwinkeln gesehen, sind heute genauso notwendig wie in der Vergangenheit. Alltagssituationen und die Ausübung verschiedener Berufe wie Ingenieurwesen, Biochemie, Choreographie, Architektur, Mechanik usw. erfordern die geometrisch denkende Fähigkeit des Einzelnen (PCNs S. 122 – 1998).
In einem zweiten Moment wurden Konstruktionen der flachen Zahlen vorgeschlagen. Während der Konstruktionen wurde festgestellt, dass die Schüler wirklich verstehen, die geometrische Formen durch die Konstruktionen mit Pappe präsentiert, das heißt, der Beton. Quadratisch, rechteckig, dreieckig, kreisförmig, fünfeckig, sechseckig, heptagonal, antitogonal, eneagonal, decagonal, dodecagonal, trideklagonal, tetradekaagonal, pentadeagonal, alle in Kartolines entworfen, um geschnitten und schließlich konstruiert zu werden, wurden montiert. Wir stellten fest, dass die Konstruktion durch die Schüler zur Schaffung von Bedeutungen der Schüler selbst beitrug, mit einem Interesse an einer mehr Beteiligung, als wenn diese Zahlen auf der Tafel vom Lehrer präsentiert wurden. Was die Sprüche von Azevedo (2006, S.27) verstärkt, der glaubte, dass es kein Lernen ohne Taten gibt: “Nichts sollte dem Kind auf dem Gebiet der Mathematik gegeben werden, ohne ihm vorher eine konkrete Situation zu präsentieren, die ihn dazu bringt, zu handeln, zu denken, zu experimentieren, zu entdecken und sich daher in die Abstraktion einzutauchen”.
Es wurde auch ein Raum eröffnet, in dem die Schüler die Möglichkeit hatten, die durchgeführten Aktivitäten und die Beziehung der Formen in unserem Zusammenleben zu hinterfragen und zu streiten. Aber nachdem die Diskussion für eine Stellungnahme eröffnet wurde, trugen einige Studenten nur bei, wenn sie angestiftet wurden und um einen Kommentar gebeten wurden. Die häufigste Bemerkung der Schüler war, dass sie nie an einem Unterricht auf diese Weise teilgenommen hatten und dass sie es interessant und angenehm fanden, die Figuren zu bauen, anstatt nur zu sehen, wie der Lehrer sie vorstellte. So stellt Machado (2005) fest, dass die meisten Probleme des Lehrens und Lernens Geometrie von didaktischer und sprachlicher Herkunft sind; und Pavanello (1993) erklärt, dass einige Faktoren im Zusammenhang mit solchen Schwierigkeiten mit dem mangelnden Interesse der Schüler zusammenhängen können, das durch den Mangel an didaktischen Ressourcen erzeugt wird, dem Mangel an interessierten Lehrern, diese unterschiedlichen Lehrmittel zu nutzen, um eine attraktive und qualitativ hochwertige Lehre zu entwickeln, die neue didaktische Konzepte wie den Einsatz von betonierten Materialien oder pädagogische Spiele bei der Entwicklung ihrer didaktischen Praktiken verwenden kann.
Durch diese Tätigkeit konnte überprüft werden, ob das pädagogische Potenzial, das die Konstruktionen von Flachziffern bieten, für pädagogische didaktische Zwecke sehr relevant und attraktiv ist, um eine Korrelation zwischen dem Inhalt des zu behandelnden Themas herzustellen.
In dieser Phase wurden die Schüler auch gebeten, die flachen Figuren in Gruppen zu bauen, wo sie mit den Buntstiften bemalt werden sollten. Diese Art von Aktivität führt den Schüler zu einer vorherigen Planung der Konstruktion, da es Kenntnisse der geometrischen Formen oder Polygone erfordert und motorische Fähigkeiten erfordert, um die Materialien zu handhaben.
Die Werkstatt für den Bau von flachen Figuren, neben Dynamik war Freizeit, motivierend und pädagogisch attraktiv, weil zu verschiedenen Zeiten diskutierten die Gruppen, welches Polygon bauen würde, weil zweitens. Fiorentini und Miorim (1990) “sagt, dass hinter jedem verwendeten Material eine Vision von Bildung, Mathematik, Mensch und Welt verborgen ist; das heißt, es liegt ein pädagogischer Vorschlag, der ihn rechtfertigt.”
Es ist bemerkenswert, dass es möglich war, zu beobachten, dass der Workshop als didaktischer Prozess für die Aktivitäten, durch visuelle Ressourcen und Experimente, eine Änderung der Haltung der Schüler bewirkt, mit einer größeren Motivation und Beteiligung der Mehrheit, die eine größere Beteiligung der Studenten in Bezug auf den Inhalt der Geometrie darstellt, weil nach Castelunuovo:
Beton muss einen doppelten Zweck haben: “die synthetischen und analytischen Fähigkeiten des Kindes auszuüben”; um es dem Schüler zu ermöglichen, ein Konzept aus Beton zu konstruieren; analytisch, weil es dem Kind in diesem Prozess gelingt, im Objekt jene Elemente zu erkennen, die die Globalisierung ausmacht. Dazu muss das Objekt mobil sein, das einer Transformation unterzogen werden kann, damit das Kind den zugrunde liegenden Vorgang identifizieren kann. (CASTELUNUOVO, 1970, S.82-91).
Geometrische Feststoffe wurden auch hergestellt, aber bevor wir einige Konzepte von geometrischen Figuren von drei Acryl-Dimensionen wie Pyramiden, Prismen, Würfel, Dodekaeder, Ikosaedron, Tetraeder, Oktaeder, Kugel, Zylinder zu ihnen präsentieren, um eine vorherige Planung zu machen und erst dann die Feststoffe zu montieren, aber einige Studenten hatten bereits die Konzepte der flachen Formen in der vorherigen Werkstatt erworben, weil für die Montage von Feststoffen erforderliche Kenntnisse der flachen geometrischen Räume und erfordert eisern. , nach einigen Studenten hatte nie mit diesen Feststoffen konkret gearbeitet. Pappe, Grillstab, Kontaktstab, Kontaktkleber, Schere usw. wurden verwendet, um die geometrischen Feststoffe zu montieren.
In jeder konstruierten Figur wurde die Planung der Werkstatt verwendet und das Verhältnis von geometrischen Festkörpern zu den flachen Figuren angewendet, die Baugruppen wurden nacheinander gefertigt und auch die Acryl-Modellformen für die Planung analysiert. Dieses pädagogische Potenzial interagiert die Schüler in den Konstruktionen der Figuren bedingt, die Diskussion über die Montage zu eröffnen, war eine Übung der Geduld für den Abschluss dieser Betone.
Wir können auch Interdisziplinarität in diesem pädagogischen Prozess verwenden, weil, nach den National Curriculum Parameters (1998-MEC):
Der Lehrer sollte der Vermittler sein, der die Entwicklung von Verfahren fördert, die dazu beitragen, in den Schülern das Interesse zu entwickeln, neue Horizonte zu suchen und wissen auszutauschen, das in verschiedenen Situationen erworben wurde. Unter Berücksichtigung dieser Ausrichtung besteht ein großer Bedarf an Derinterinterzierung und Kontextualisierung von Disziplinen und insbesondere mathematik
Das heißt, um den weiten Blick auf Objekte und ihre Beziehungen noch weiter zu erleichtern. Wir betonen jedoch, dass nicht alle Schüler tatsächlich einen Überblick über die dreidimensionalen Figuren haben, und wir haben festgestellt, dass einige von ihnen noch Zweifel hatten, eine der Formen eines Festkörpers zusammenzustellen. Wir fanden auch heraus, dass diese Art von Aktion den Schüler darauf vorbereitet, Lösungen zu suchen, und gleichzeitig diesen dynamischen Prozess des pädagogischen Lernens erhält, um die Argumentation vor den Konstruktionen geometrischer Formen zu erforschen. Wir überprüften, dass diese Aktivität mit großem Engagement und Beteiligung der Studenten durchgeführt wurde, aber irgendwann war es notwendig, einige Studenten beim Aufbau der geometrischen Festkörper zu begleiten. Wir haben einige Kommentare von ihnen aufgezeichnet, wie z. B.:
- “Wir denken, dass eine Geometrieklasse durch geometrische Figurenkonstruktionen viel mehr lernt und nicht nur Spaß macht.”
- “Neben dem theoretischen Lernen können wir in der Praxis besser lernen, der Lehrer gibt nicht nur das Brett weiter und es ist interessanter, praktische Kurse zu belegen.”
Es ist offensichtlich, wie wichtig diese Aktivität im pädagogischen Bereich entwickelt, weil diese didaktische Umsetzung zeigt die Realität im Klassenzimmer und die Arbeit mit dieser kollaborativen Aktivität überprüfen wir die Bedeutung der gemeinsamen Teilen dieser wesentlichen Aktivität im Leben der Mathematik-Studenten und Pädagogen.
Dieses pädagogische Potenzial stellt Maßnahmen dar, die im schulischen Umfeld umgesetzt werden können. Das Experiment und die Annäherung der geometrischen Theorie in ihrem Leben tragen zu pädagogischen Aktivitäten bei, was die Schüler dazu veranlasst, sich mehr für Lerngeometrie zu interessieren.
5. ABSCHLIEßENDE ÜBERLEGUNGEN
Die Forschung zeigt, dass die Einbeziehung von Aktivitäten, die soziale Interaktion, Zusammenarbeit und Experimente im Klassenzimmer begünstigen, einen Unterschied im schulischen Umfeld machen kann, weil der soziale Kontext, in den diese Schüler eingefügt werden, nicht von der Schule isoliert ist, und eine der Aufgaben derselben ist es, eine Ausbildung zu fördern, die das soziale Leben der Schüler ermöglicht. Eine effektive kollaborative Teilhabe ist ein weiterer Punkt, den wir mit den Workshops hervorheben, wenn man bedenkt, dass es sich als ein positiver Punkt erwiesen hat, was Lorenzato (2006) noch verstärkt, wenn er sagt: Lehren ist anders als Unterricht. Der Unterricht gibt den Schülern Bedingungen, ihr eigenes Wissen aufzubauen.
Wir betonen auch, dass die Verwendung von Betonmaterialien in der Lehre von Geometrie neben der Förderung der Interaktion der Studenten mit dem Ziel des Studiums und aus dieser Interaktion können sie ihr Wissen aufbauen, fördern auch Diskussionen in dem Sinne, dass auf diese Weise im täglichen Leben der Studenten zu identifizieren, die die Entfernung von mathematischen Konzepten und ihre Anwendbarkeit neben der Mehr-Interessantund bedeutungsvolle , die als Alternative für den Unterricht von Geometrie dient, die dem Traditionellen entweicht.
Es ist darauf hinzuweisen, dass die entwickelten Workshops ihre Ziele erreicht haben, die von der Entwicklung von Fähigkeiten ausgingen, die die Abstraktion geometrischer Inhalte ermöglichen, die verwendet werden können, um die Welt, in der wir leben, in organisierter Weise zu verstehen, zu beschreiben und darzustellen.
Es wird angenommen, dass die Forschung selbst als Arbeitsmethodik machbar ist, wenn sie zuvor vorbereitet wurde und Potenzial für die Einfachheit bietet, die in ihrer Entwicklung präsentiert wird, und so zum Lernprozess der Erlernte von Geometrie und Mathematik beiträgt.
Daher kommen wir zu dem Schluss, dass die aufwendige “Bildungskonstruktion” ein lohnendes Ergebnis hatte, mit viel Interaktion haben wir unsere Ziele im Prozess des Lehrens und Erlernens von Mathematik erreicht, wir hoffen, dass mit dieser Arbeit als Trend in den Bildungsprozess von Schülern und Pädagogen aufgenommen werden.
REFERENZEN
ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.
ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.
AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).
BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.
CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.
CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.
FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.
FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo
GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.
MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.
MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.
MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961
NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.
PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.
PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.
PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,
TAHAN, Malba. Didática da Matemática 1967, p.31.
[1] Doktorand in Bildung am UNR-Argentinien, Professor für Mathematik und Kriminalpolizei der MT.
[2] Doktortitel in Bildung; Facharzt für Schulmanagement und Personalmanagement; Abschluss in Englisch Portugiesisch/ Englisch und Literatur, Bachelor-Abschluss und Bachelor-Abschluss in Leibeserziehung.
[3] Doktorand in Bildung an der National University Of Rosario – Unr, Argentinien, hält einen Grad in Briefen – Englisch vom Castelo Branco College (2006). Recht und Philosophie. Spezialisierung in englischer Sprache.
[4] Doktorand in Bildung an der Nationalen Universität von Rosario – UNR Argentinien. Absolvent in Vernacular Letters von UFBA – Federal University of Bahia. Er hat einen postgradualen Abschluss und Lehrplan, Didaktik und Evaluation von der Staatlichen Universität Bahia – UNEB, Postgraduate in Methodologie der portugiesischen Sprachlehre und Literatur von der regionalen Fakultät für Philosophie, Wissenschaften und Briefe von Candeias- Bahia. Spanischsprachtraining zertifiziert durch DUCLE – ARGENTINA. Spanisch ersprach und portugiesischer Sprachlehrer. Direktorin des Staatlichen Kollegs Professor Maria Leal Lopes, Nova Ibia – Bahia.
[5] Doktorand in Bildung an der National University of Rosario – UNR Argentina, Bachelor es degree in Letters. Universität des Staates Bahia, UNEB und Pädagogik der Regionalen Fakultät für Philosophie, Wissenschaften und Briefe von Candeias- Bahia. Professioneller Master in Theologie. Hochschule für Bildung, EST, Brasilien. Spezialisierung in Linguistik und Literaturwissenschaft. Federal University of Bahia – UFBA. Spezialisierung in Planung und Management von Sist. Educ. Distanz. Bahia State University, UNEB. Spezialisierung in der Hochschulmethodik. Integrated Faculties of Ducks – FIP, Spezialisierung in Lehrmethodik für die berufliche Bildung, UNEB-BAHIA. Brazilien. Spanischsprachtraining zertifiziert durch DUCLE – ARGENTINA.
[6] Abschluss in Portugiesisch und Englisch Briefe von UEG, Postgraduierte in Hochschullehre, von Ucan Rj; Postgraduierter in Technologie in Bildung von Puc Rio de Janeiro und Postgraduierte in Grundschulmethodik von UFG. Teilnahme an der Promotion in Bildung an der UNR argentina.
[7] Abschluss in Geographie an der Katholischen Universität von Salvador. Jahr 1987. Sie absolvierte die Methodik des Geographieunterrichts. Teilnahme an der National University of Rosario -UNR Argentina.
Eingesandt: Juli 2020.
Genehmigt: Oktober 2020.