ARTICLE ORIGINAL
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Alternatives structurelles dans les fonds suspendus des réservoirs tubulaires en métal avec deux cellules pour la réserve d’eau. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 06, Vol. 12, pp. 111-135. juin 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/travaux-publics/alternatives-structurelles
RÉSUMÉ
Avec la demande croissante de réserves d’eau due à la mise en place de nouveaux allotissements et condominiums horizontaux, qui répondaient à la nécessité d’une pression dynamique minimale de 100 kPa, les réservoirs ont commencé à avoir des divisions physiques internes (cellules verticales) dont la cellule supérieure a le quota inférieur suspendu à une hauteur qui garantissait la pression manométrique nécessaire pour répondre à cette norme. En raison de l’absence de normes techniques brésiliennes spécifiques pour le stockage de l’eau dans un réservoir métallique, il a été utilisé comme paramètre de dimensionnement pour les réservoirs métalliques avec plusieurs cellules verticales de stockage de l’eau, l’AWWA D100 dans son intégralité ou seulement partiellement, principalement en raison d’efforts axiales dans les côtes (virolas) pour déterminer les contraintes admissibles au flambage (FL). Cet article aborde le problème du choix du type le plus approprié de fond métallique vertical suspendu et compatit les résultats de cinq différents types de fonds, classés selon AWWA D100-05. Dans la typologie des 5 fonds analysés, le fonds le plus économique était le fonds sphérique segmenté.
Mots-clés: Réservoir métallique, norme AWWA D100, fonds suspendus.
1. INTRODUCTION
Cet article aborde le problème du choix du type le plus approprié de fond métallique vertical suspendu et compatit les résultats de cinq différents types de fonds, classés selon AWWA D100-05.
Avec la mise en œuvre de nouveaux lotissements et copropriétés horizontales en raison des incitations de la politique gouvernementale du logement, principalement en raison du programme de logement du ministère des Villes, Programme Minha Casa Minha Vida (Pereira, 2017), qui a provoqué une forte augmentation de la demande de réservoirs de stockage. eau potable, principalement aérienne (above ground), cylindrique et de diamètre et de hauteur variables, appelée château d’eau.
En raison de la nécessité d’une pression dynamique minimale dans le réseau public d’approvisionnement, qui, selon NBR 12.218/1994, doit être de 100 kPa (10,20 m.c.a.), les réservoirs ont maintenant des divisions physiques internes (cellules verticales) dont la cellule supérieure a la dimension inférieure suspendue à une hauteur qui garantissait la pression manométrique nécessaire pour répondre à cette norme, puisque normalement les quotas terrestres n’offrent pas pour le réservoir d’être pris en charge.
Selon Trees (1911), les fonds des réservoirs métalliques suspendus peuvent être de différents types, tels que plat, conique, sphérique ou sphérique segmenté.
Visal (2017) affirme que les réservoirs de stockage fonctionnent sans pression (ou très peu), appelés réservoirs atmosphériques, les différeciant des navires sous pression. Ils sont généralement de forme cylindrique, perpendiculaires au sol avec un fond plat et un plafond fixe ou flottant.
La conception et la construction de réservoirs cylindriques atmosphériques nécessitent la connaissance de normes techniques, de matériaux et de main-d’œuvre spécifiques adaptés à chaque type d’application et impliquent un certain nombre d’autres soins spéciaux parce que les anomalies et les irrégularités dans ces équipements peuvent causer de grandes pertes financières, voire des pertes de vie (Nunes, 2013).
Selon Gomes (2017), les normes couramment utilisées au Brésil pour les projets et les constructions de réservoirs métalliques sont NBR 7821, API 650 et AWWA D100.
NBR 7821/1983 – Welded Steel Tanks for Oil and Derivatives Storage, de l’Association brésilienne des normes techniques (ABNT) et de la norme réglementaire américaine API 650 – 2013 – Welded Steel Tanks for Oil Storage – de l’American Petroleum Institute (API), sont spécifiques à la réserve de pétrole et de dérivés.
La norme AWWA D100-05 – Welded Carbon Steel Tanks for Water Storage de l’American Water Works Associations vise à fournir des exigences minimales pour la conception, la construction, l’inspection et l’essai de nouveaux réservoirs d’acier au carbone soudés pour le stockage de l’eau sous pression atmosphérique.
Dans le cadre des exigences de dimensionnement, l’AWWA D100 présente trois méthodes pour déterminer le stress de flambage admissible (FL) pour les sections cylindriques, ce qui permet de vérifier le stress de compression maximal dû à la charge axiales et à la charge axiales en raison de la charge éolienne appliquée sur les côtes.
En raison de l’absence de normes techniques brésiliennes spécifiques pour le stockage de l’eau dans un réservoir métallique, il a été utilisé comme paramètre de dimensionnement pour les réservoirs métalliques avec plusieurs cellules verticales de stockage de l’eau, l’AWWA D100 dans son intégralité ou seulement partiellement, principalement en raison d’efforts axiales dans les côtes (virolas) pour déterminer les contraintes admissibles au flambage (FL).
2. OBJECTIFS
Objectif général
L’objectif général de cet article est la dimension de plusieurs types de fonds suspendus de la cellule supérieure verticale de réservoir métallique composée de deux cellules, dans les recommandations d’AWWA D100-05, en utilisant le logiciel Autodesk Simulation Mechanical 2018.
Objectifs spécifiques
Les objectifs spécifiques sont les suivants :
- Déterminer les contraintes axiales sur les côtés de la cellule inférieure du réservoir métallique, résultant de charges axiale et latérales et les comparer au stress permis au flambage selon ce qui prescrit 3,4 – Formules de stabilité colonne, jambe et coquille d’AWWA D100 – 05.
- Déterminer les déplacements verticaux des arrière-plans suspendus.
- Déterminer le poids total des fonds suspendus proposés en quantifiant la superficie et l’épaisseur des plaques de taille et des structures de soutien.
3. MATÉRIEL ET MÉTHODE
Le réservoir présenté dans cet article est un réservoir métallique, pour réserve d’eau, composé de deux cellules, d’une capacité de 150,00 m³ chacune (total de 300,00 m³), avec couvercle de cône métallique (figure 1), avec cinq types de fonds suspendus (figures 2A; 2B; 2C; 2D et 2E).
Figure 1 : Réservoir métallique de deux cellules d’une capacité de 300,00 m³.

Typologie des 5 fonds suspendus proposés :
Fig.: 2A – Poutres radiales à fond plat et mât
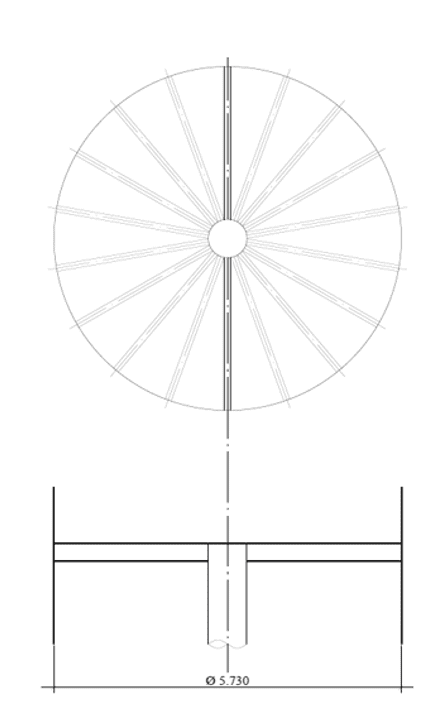
Fig.: 2B – Poutres radiales à fond plat sans mât
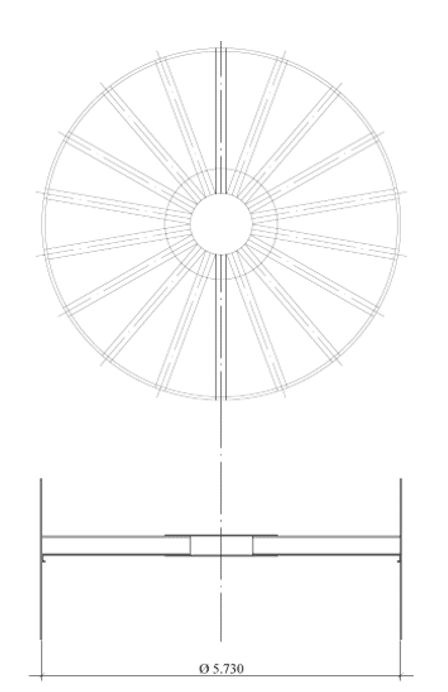
Fig.: 2C – Poutres orthogonales à fond plat
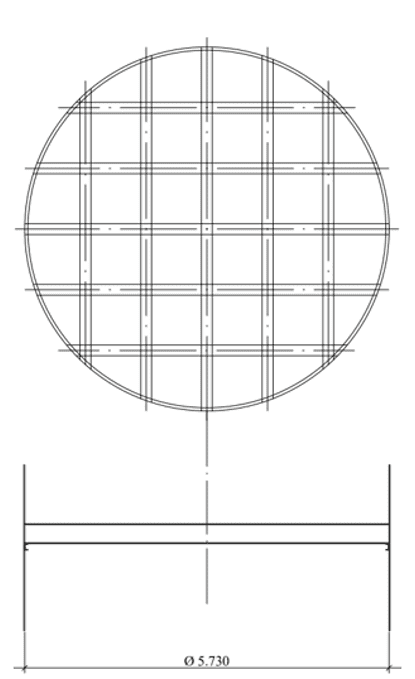
Source: L’auteur lui-même
Fig.: 2D – Fond conique
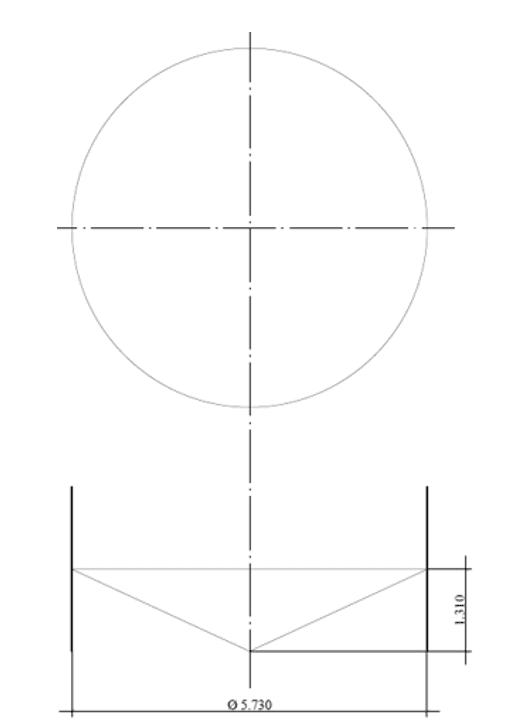
Fig.: 2E – Fond sphérique segmenté
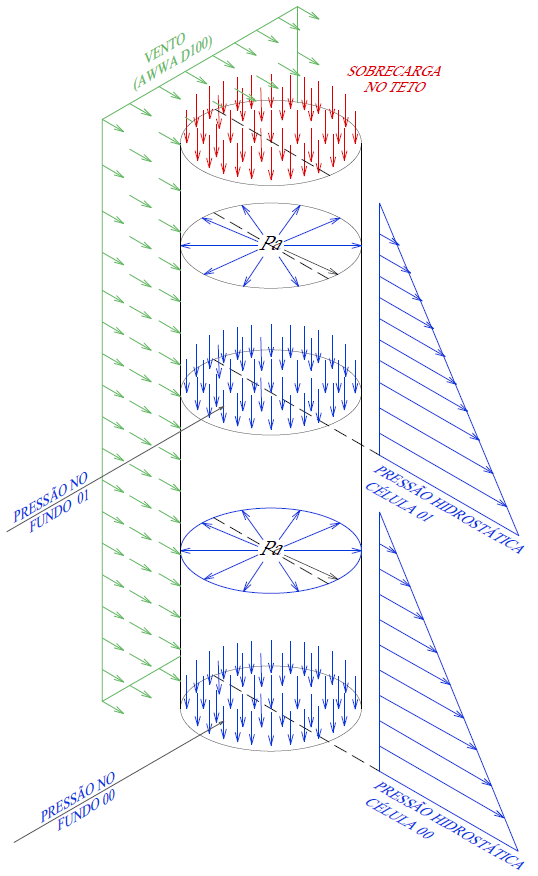
Les actions envisagées sont celles du vent, de l’eau stockée (action hydrostatique), de la surcharge de plafond et du poids propre de la structure (figure 3A), publiée dans le logiciel Autodesk Simulation Mechanical.
Figure 3A – Téléchargements
Source: L’auteur lui-même
Figure 3B – Lancement des téléchargements dans le logiciel
Source: L’auteur lui-même
Selon Andrade junior (1998), l’action du vent est calculée selon NBR 6123 – Forces dues au veto dans les bâtiments (1987) et, en règle générale, on suppose que le vent peut agir dans n’importe quelle direction horizontale. Comme la structure du réservoir est asymétrique par rapport à l’axe Z, perpendiculaire à la direction du vent, il est considéré que le vent peut se concentrer perpendiculairement à n’importe quel geratriz du réservoir.
La composante statique de la pression du vent, qui agit perpendiculairement sur un élément de zone, est donnée par : Les coefficients de pression externes Cpe sont exprimés pour le type de corps de la structure, en supposant pour l’application de l’AWWA D100-05 que Cpe = Cf (tableau 1).
Les coefficients de pression externes Cpe sont exprimés pour le type de corps de la structure, en supposant pour l’application de l’AWWA D100-05 que Cpe = Cf (tableau 1).
Lorsque q est la pression du vent à un point où la stagnation de l’air se produit, obtenue à partir de  l’expression 2:
l’expression 2:
Le V0 Speed est appelé vitesse de base, correspond à une rafale de 3 secondes, exercée en moyenne une fois en 50 ans, mesurée à 10 m au-dessus du sol, dans un endroit plat et ouvert. NBR 6123 (1987) présente les isopletas de base, en m/s. Pour nos exemples, V0 = 40 m/s a été adopté.
Le facteur topographique S1 est utilisé pour évaluer le relief du terrain autour du bâtiment et adopté égal à 1,0 pour nos exemples.
Le facteur S2 tient compte de l’effet combiné de la rugosité du terrain, de la variation de la vitesse du vent avec la hauteur au-dessus du relief et des dimensions du bâtiment. Le facteur S2est obtenu par l’expression 4 : Où: Z = hauteur au-dessus du sol, Fr = Facteur rafale de vent, b = paramètre météorologique, p = fonction de rugosité du terrain et intervalle de temps. Pour la hauteur du réservoir de 16,0 m, rugosité II, classe A, on a S2 = 1,05.
Où: Z = hauteur au-dessus du sol, Fr = Facteur rafale de vent, b = paramètre météorologique, p = fonction de rugosité du terrain et intervalle de temps. Pour la hauteur du réservoir de 16,0 m, rugosité II, classe A, on a S2 = 1,05.
Le facteur S3 est un facteur statistique qui tient compte du degré de sécurité requis et de la durée de vie utile de la structure, compte tenu de l’installation de réservoirs ayant un faible facteur d’occupation humaine (Andadre Junior, 1998), la valeur de 0,95 a été utilisée.
Selon Haffez et al (2011), on suppose que les réservoirs sont soumis à une pression de vent uniforme (q), agissant le long de l’axe Z, comme le montrent les figures 3e et 3B. AWWA D100-05 recommande l’utilisation du coefficient de traînée (Cf), selon la forme de la structure, selon le tableau 1. Pour les réservoirs tubulaires de forme cylindrique, le Cf adopté est de 0,6.
Tableau 1 – Coefficient de traînée Cf

Source: AWWA D100-05
Ont:
Vk = 40 . 10 . 1,05 . 0,95 = 39,90 m/s
q = 0,613 . 39,902 = 975,90 N/m² ou 99,51 kgf/m²
Δp = 0,6 . 975,90 = 585,54 N/m² ou 58,71 kgf/m².
L’action hydrostatique génère des effets qui agissent dans les directions radiales et verticales et entraînent une pression latérale sur le côté et une pression au fond du réservoir.
Les frais généraux de conception appliqués au plafond, selon l’article 3.1.3.2 de l’AWWA D100-05, devraient être de 750 N/m² (15 lb/pi²).
Le propre poids de la structure est automatiquement libéré par le logiciel Autodesk Simulation Mechanical 2018, considéré comme le poids spécifique des aciers utilisés dans le dimensionnement des réservoirs.
L’épaisseur des ferolas de pression feroline due à la pression hydraulique du réservoir doit être calculée selon l’équation sec 3-40. 3.7 AWWA D100-05 – Cylindrical Shell Plates (équation 7) : Où:
Où:
t = épaisseur de conception de coque (ferrule), en mm
hp = hauteur liquide, en m
D = diamètre du réservoir, en m
S = Tension en acier admissible, à Mpa
E = Efficacité du soudage
G = Poids liquide spécifique (pour l’eau = 1)
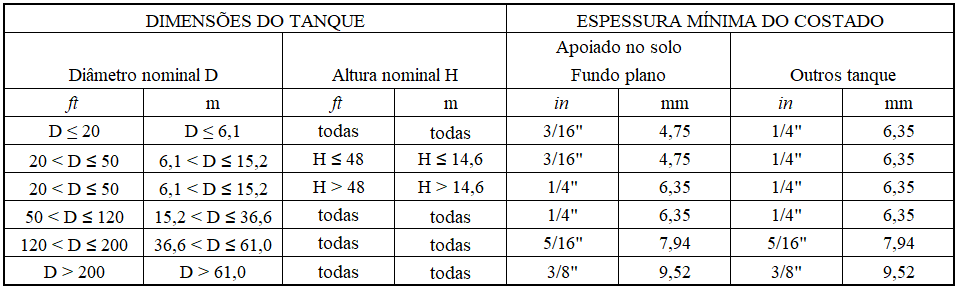
L’épaisseur minimale du brin cylindrique en contact avec l’eau devrait être conforme au tableau 2 selon la Sec. 3.2 d’AWWA D100-05. Pour le réservoir de 5,73 m de diamètre nominal, l’épaisseur minimale prescrite est de 4,76 mm.
Tableau 2 – Coefficient de traînée Cf
Source: AWWA D100-05
AWWA D100-05 classe les matériaux structurels à utiliser dans les réservoirs en 3 classes, selon la limite de débit (Fy). Le tableau 3 montre cette classification.
Tableau 3 – Classe matérielle en fonction de Fy
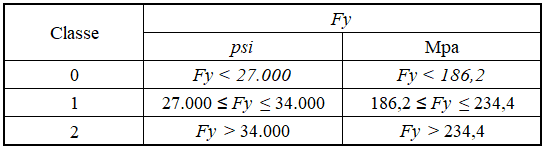
Source: AWWA D100-05
Le matériau utilisé sur les côtes, les fonds et le plafond est l’ASTM A36, caractérisé par un module d’élasticité (E) égal à 205.000 Mpa, coefficient de Poisson (μ) égal à 0,30, densité (γ) de 77.000 N/mm³, fy de tension de débit = 250.00 Mpa et dernière tension fu = 400.00 Mpa. Le matériau utilisé dans les structures de soutien des fonds suspendus (poutres W et C) est l’ASTM A572 (grade 50) avec fy de tension de débit = 345,00 Mpa et dernière tension fu = 450,00 Mpa. Ils sont classés comme matériel de classe 2.
Le tableau 4 montre les principales contraintes admissibles prescrites par l’AWWA D100-05, selon la classe de matériaux et d’applications dans les réservoirs.
Tableau 4 – Tensions admissibles dans les applications
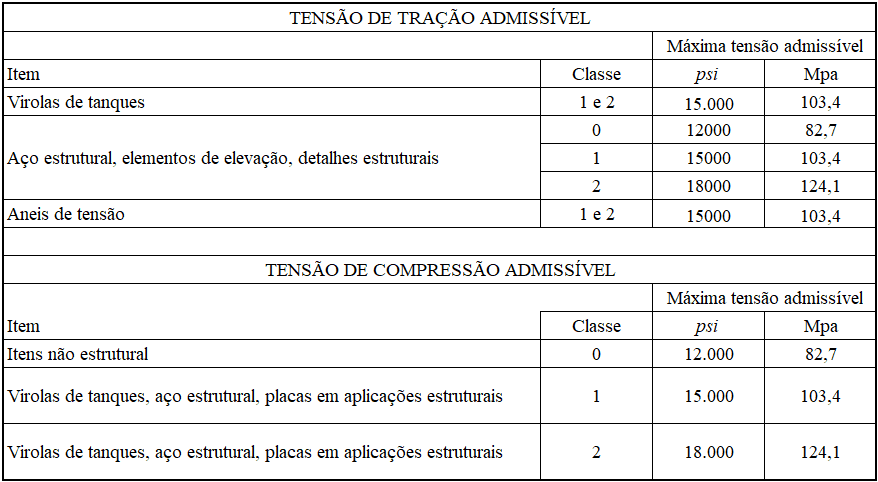
Source: AWWA D100-05 – modifié par l’auteur.
Pour la vérification de la stabilité due au flambage de la côte du réservoir, l’AWWA D100-05 prescrit 3 méthodes d’analyse. Pour ce travail, la méthode 1 a été utilisée, qui est une procédure simplifiée basée sur des techniques d’analyse membranaire. Pour les matériaux de classe 2, le rapport épaisseur/rayon du réservoir auquel le flambage change d’élastique à inélastique (t/R)c est de 0,0025372. Le stress permis pour le flambage pour le matériel de classe 2 est donné par les formules suivantes :
Lorsque 0 ≤ t/R ≤ (t/R)c signifie que le flambage se produit dans le régime élastique et que le stress permis pour le flambage est donné par l’équation 8 :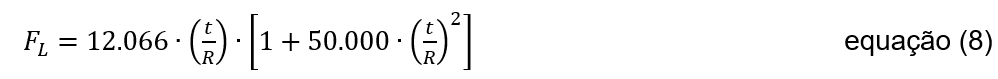 Lorsque (t/R)c ≤ t/R ≤ 0,0125 signifie que le flambage se produit dans le régime inélastique et que le stress admissible pour le flambage est donné par l’équation 9 :
Lorsque (t/R)c ≤ t/R ≤ 0,0125 signifie que le flambage se produit dans le régime inélastique et que le stress admissible pour le flambage est donné par l’équation 9 : Lorsque t/R > 0,0125, cela signifie que le flambage se produit dans le plastique et que le stress permis pour le flambage est constant et vaut la peine :
Lorsque t/R > 0,0125, cela signifie que le flambage se produit dans le plastique et que le stress permis pour le flambage est constant et vaut la peine :![]()
Le tableau 5 – Les valeurs d’efficacité de soudage sont présentées partiellement à partir de Table 15 Weld design value– tank plate joints, où seules les valeurs de soudage continu ont été présentées. Pour les travaux sur toile, une double soudure de chanfrein avant avec remplissage complet a été envisagée.
Tableau 5 – Valeurs d’efficacité du soudage en %

Source: AWWA D100-05 – modifié par l’auteur.
4. RÉSULTATS
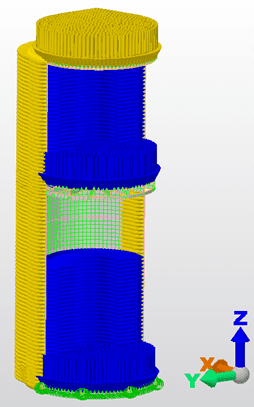
La modélisation et l’analyse numériques ont été effectuées à l’aide d’un logiciel commercial d’analyse et de conception structurelle Autocad Simulation Mechanical 2018. Chaque ferrule du réservoir a été modélisé comme un élément de coquille avec des épaisseurs de conception constantes, avec des propriétés isotropiques et avec un plan moyen positionné centralement. En haut du réservoir, il y a un anneau vertical circulaire modélisé avec le profil L rigidement attaché aux elemnetos. Les dimensions des éléments finis sont de 0,20 x 0,20 m (discrétion). Pour chaque type de réservoir, selon la typologie de chaque fond suspendu, un modèle d’élément fini 3D a été créé (figure 4).
Figure 4 : Réservoir métallique discret

Source: L’auteur lui-même
À partir de l’épaisseur minimale selon le tableau 2, pour le dimensionnement du brin a également vérifié l’épaisseur due à la pression circonférentielle, en utilisant l’équation (7) et l’épaisseur due au flambage, avec la détermination du stress permis (FL), en utilisant les équations (8) et (9) et les contraintes axiales des brins déterminés par le logiciel de Simulation Mechanical et par rapport aux contraintes admissibles calculées (FL). L’épaisseur requise de chaque ferrule est la plus grande épaisseur dans les 3 critères.
Le tableau 6 montre en détail la Van Misse, la tension circonférentielle et la tension axiale dans chaque ferrule des 5 réservoirs étudiés avec différents types de fonds suspendus.
Tableau 6 – Dimensionnement des côtes selon AWWA D100 – 05
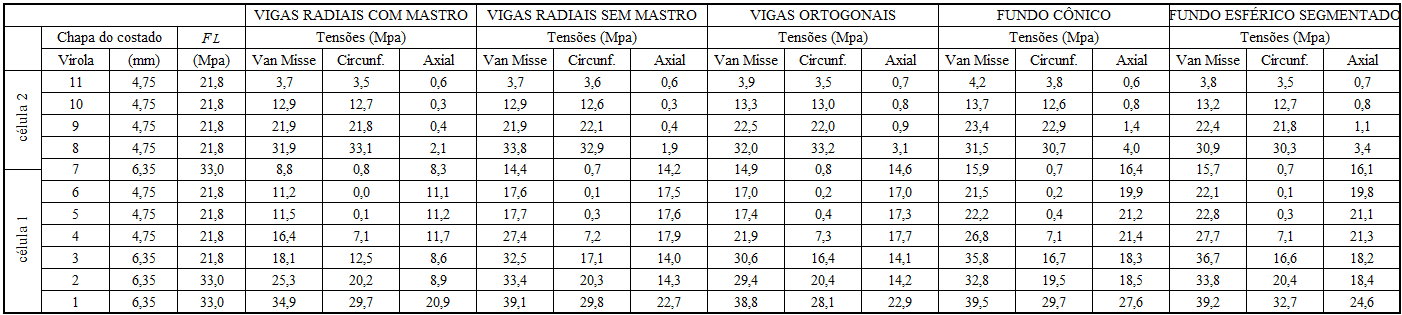
La figure 5 montre le réservoir avec les épaisseurs requises pour chaque ferrule du côté.
Figure 5 : Réservoir avec les épaisseurs finales du brin
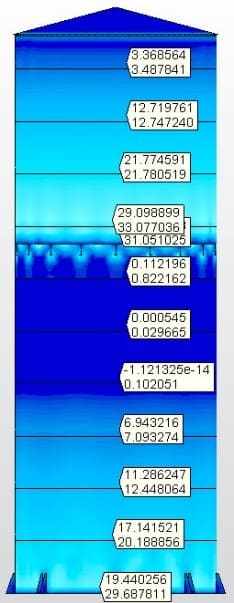
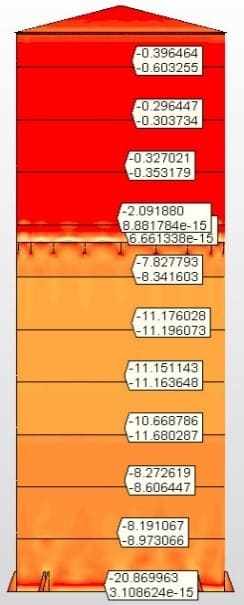
Les figures 6A, 6B, 6C et 6D montrent les résultats des analyses avec les contraintes Van Misse, les contraintes circonférentielles et les contraintes axiale dans chaque ferrule pour le réservoir avec le fond de la cellule 2, avec des faisceaux W radiaux et un mât central. Les valeurs obtenues ont alimenté le tableau 6. Une analyse égale a été faite sur les 4 autres réservoirs qui complètent ce travail.
Fig. 6A: Van Misse Tensions en coupe 3D
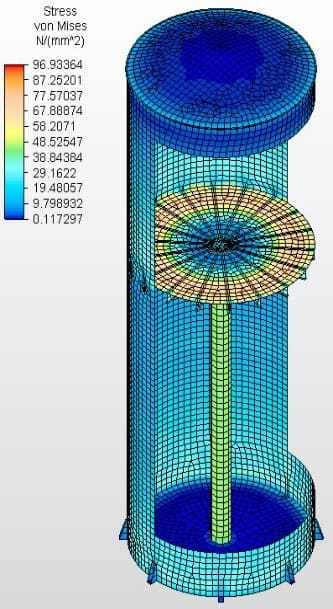
Fig. 6B: Van Misse Tensions

Fig. 6C: Tensions circonférentielles
Source: L’auteur lui-même
Fig. 6D: Souches axials
Les fonds suspendus analysés dans le cadre de ces travaux, à l’exception du fond à l’appui des poutres radiales et du mât central (figure 2A), ont été conçus comme autonomes et soutenus uniquement sur le côté des réservoirs. Les résultats des analyses sont présentés ci-dessous.
Le fond suspendu avec poutres radiales de type W et mât central, dont la géométrie est indiquée à la figure 7, où il a le même diamètre nominal du réservoir, D = 5 730,00 mm, nombre de poutres de soutien = 18 pièces, profil du faisceau W = 310 x 28,3, matériau de faisceau W = ASTM A572 – grade 50, diamètre du mât central = 640,00 mm, épaisseur du mât central = 6,35 mm, matériau de plaque centrale = ASTM A36, épaisseur de la plaque inférieure = 7,95 mm (5/16 »), matériau de plaque inférieure = ASTM A36.
Chargement du fond = pression hydrostatique h = 5,80 m.c.a.
Figure 7 : Disposition de fond avec poutres radiales et mât central
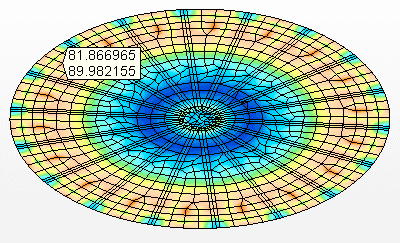
Les contraintes sur la plaque inférieure et les poutres de soutien sont indiquées dans les figures 8A et 8B.
Figure 8A : Contraintes sur le fond suspendu Tension maximale = 90,0 Mpa
Source: L’auteur lui-même
Figure 8B : Contraintes sur les faisceaux de soutien Tension maximale= 64,9 MPa

Source: L’auteur lui-même
Figure 8C : Décalages verticaux (mm)
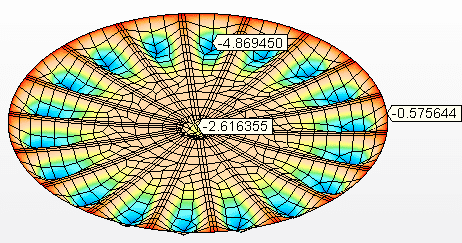
Source: L’auteur lui-même
Figure 8D : Contraintes axiaales sur le mât Tension maximale = 37,6 Mpa

Source: L’auteur lui-même
Le fond suspendu avec poutres radiales de type W et sans central, dont la géométrie est indiquée dans la figure 9, où il a le même diamètre nominal du réservoir, D = 5 730,00 mm, nombre de poutres de soutien = 18 pièces, profil de faisceau W = 310 x 44,5, matériau de faisceau W = ASTM A572 – grade 50, faisceau de soutien circonférentiel U 6 » première âme, matériau de faisceau U = ASTM A572 – grade 50, épaisseur de la plaque inférieure = 7,95 mm (5/16 »), matériau de plaque inférieure = ASTM A36.
Chargement du fond = pression hydrostatique h = 5,80 m.c.a.
Figure 9: – Disposition de fond avec poutres radiales et sans mât
Figure 9A – Contraintes sur le fond suspendu Tension maximale = 87,4 Mpa
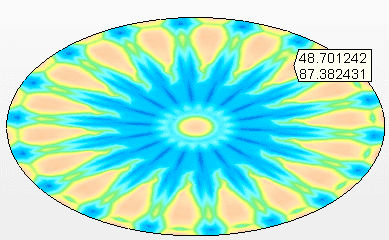
Source: L’auteur lui-même
Figure 9B – Contraintes sur les faisceaux de soutien Tension maximale= 89,2 MPa
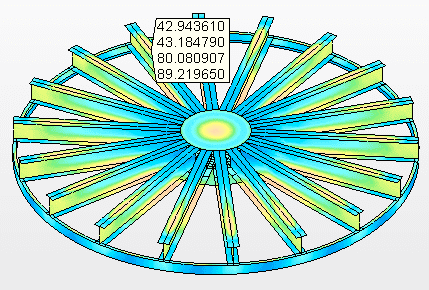
Source: L’auteur lui-même
Figure 9C – Offsets verticaux (mm)
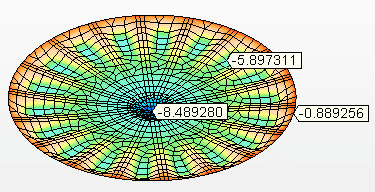
Source: L’auteur lui-même
Le fond suspendu avec poutres orthogonales (grille) de type W et sans central, dont la géométrie est indiquée dans la figure 10, où il a le même diamètre nominal du réservoir, D = 5 730,00 mm, nombre de poutres de soutien = 10 pièces, profil de faisceau W = 360 x 72, matériau de faisceau W = ASTM A572 – grade 50, faisceau de soutien circonférentiel U 6 » première âme, matériau de faisceau U = ASTM A572 – grade 50, épaisseur de plaque inférieure = 9,53 mm (3/8 »), matériau de plaque inférieure = ASTM A36.
Chargement du fond = pression hydrostatique h = 5,80 m.c.a.
Figure 10 : – Disposition de fond avec poutres orthogonales (calandre) et sans mât
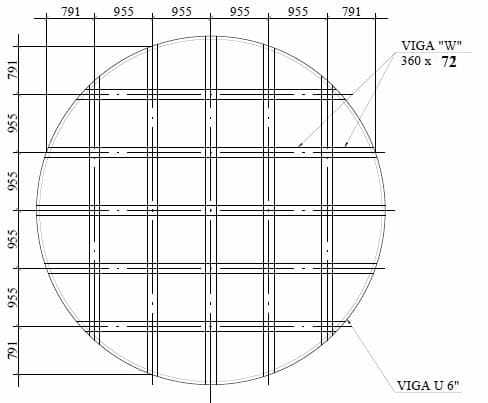
Source: L’auteur lui-même
Figure 10A – Contraintes sur le fond suspendu Tension maximale = 79,9 Mpa
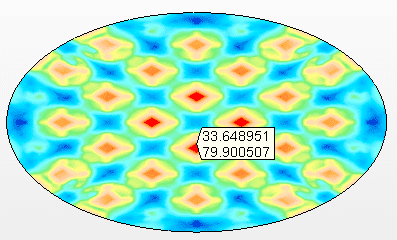
Source: L’auteur lui-même
Figure 10B – Contraintes sur les faisceaux de soutien Tension maximale = 85,7 MPa
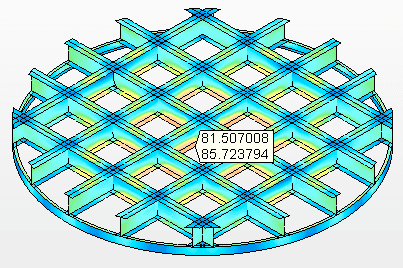
Source:L’auteur lui-même
Figure 10C – Offsets verticaux (mm)
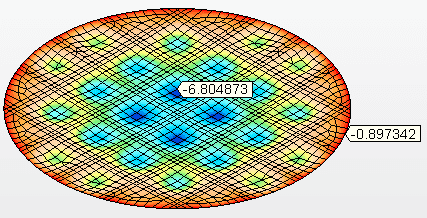
Source: L’auteur lui-même
Le fond suspendu en forme de cône, dont la géométrie est indiquée dans la figure 11 (coupe), où il a le même diamètre nominal du réservoir, D = 5 730,00 mm, épaisseur de la plaque inférieure = 9,53 mm (3/8 »), matériau de plaque inférieure = ASTM A36. Chargement du fond = pression hydrostatique h = 5,80 m.c.a.
Figure 11: – Schéma de fond effilée en coupe
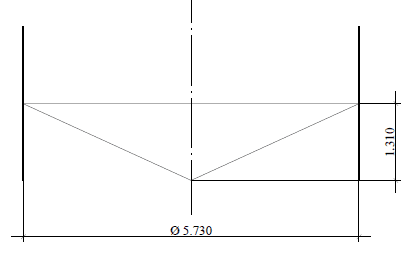
Figure 11A – Contraintes sur le fond suspendu Tension maximale = 90,8 Mpa
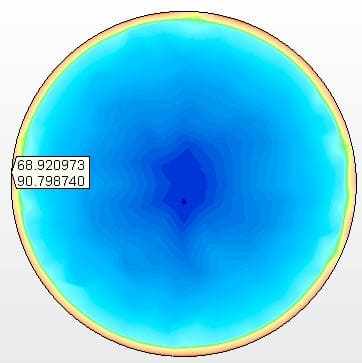
Source: L’auteur lui-même
Figure 11B – Déplacements verticaux (mm) Tension maximale = 7,359 mm
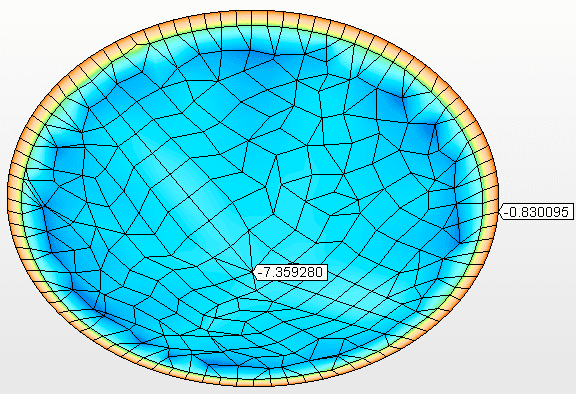
Source: L’auteur lui-même
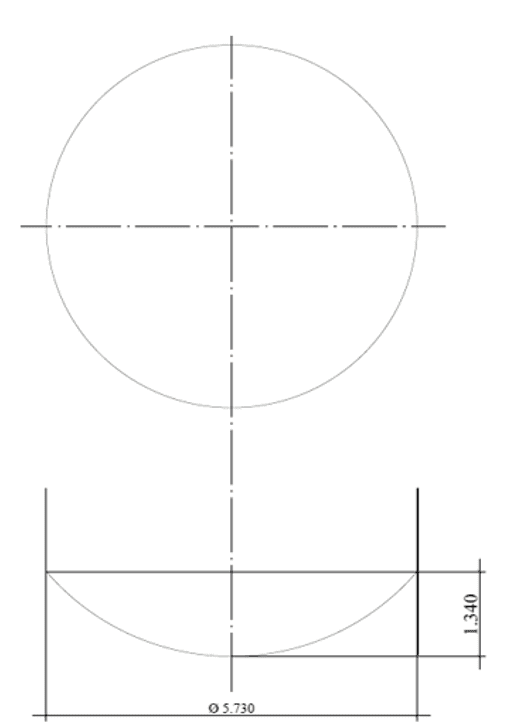
Le fond suspendu en demi-sphère ou format de fond sphérique segmenté dont la géométrie est indiquée dans la figure 12 (coupe), où il a le même diamètre nominal du réservoir, D = 5 730,00 mm, épaisseur de la plaque inférieure = 4,75 mm (3/16 »), matériau de plaque inférieure = ASTM A36. Chargement du fond = pression hydrostatique h = 5,80 m.c.a.
Figure 12 : – Schéma du fond sphérique segmenté coupé.
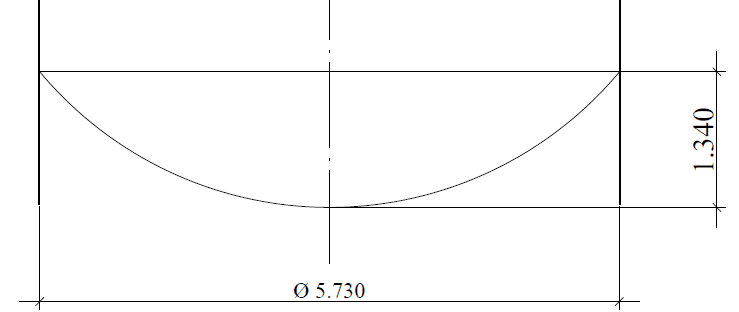
Figure 12A – Contraintes sur le fond suspendu Tension maximale = 88,32 Mpa

Source: L’auteur lui-même
Figure 12B – Déplacements verticaux (mm) Tension maximale = 7,359mm
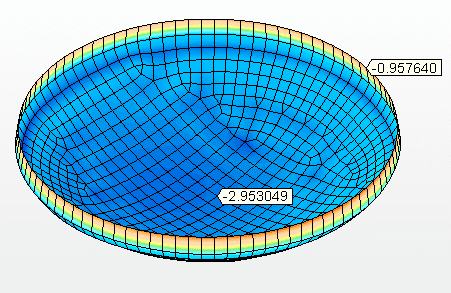
Source: L’auteur lui-même
Les poids des fonds suspendus ont été calculés sans déterminer les coupures ou l’utilisation des volets et des restes, ne calculant que les surfaces des plaques multipliées par poids/m². Le tableau 7 montre le résumé général du poids des 5 types de fonds suspendus et ces différences peuvent être observées dans le tableau de type poids total x fonds de la figure 13.
Tableau 7 – Poids des fonds suspendus

Figure 13 – Comparaisons des pondérations des fonds
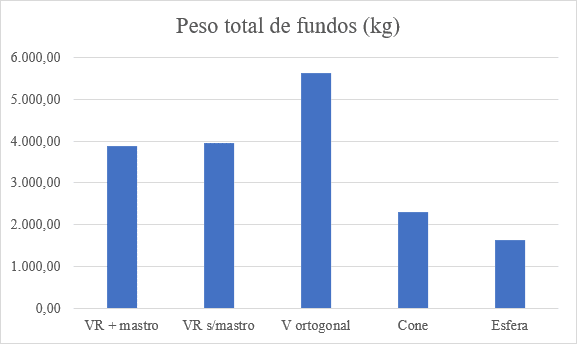
Source: L’auteur lui-même
Les décalages maximaux verticaux des fonds suspendus sont indiqués comparativement à la figure 14.
Figure 14 – Comparaisons des déplacements maximaux verticaux
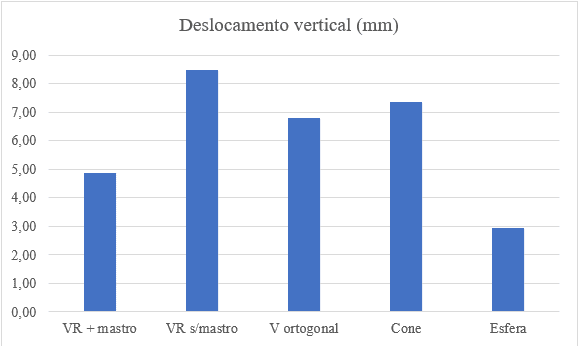
5. CONCLUSIONS
D’après les résultats obtenus, il est conclu que le fonds segmenté de suspension sphérique est le plus viable économiquement et aussi le plus techniquement recommandé, car il présente le plus petit déplacement vertical, sous chargement complet.
Le fond suspendu de type cône est également économiquement viable, mais a un déplacement vertical sous une charge quelque peu excessive, et il doit être vérifié s’il interfère avec les tuyaux. Le déplacement vertical pourrait être diminué avec l’utilisation de plaques de renforcement triangulaires, soutenant le fond sur les côtés latéraux.
Le fond suspendu soutenu par des faisceaux orthogonaux est totalement non rentable.
RÉFÉRENCES
ABNT – Associação Brasileira de Normas Técnicas, NBR 7.821, Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro, RJ. Abril de 1983.
ABNT – Associação Brasileira de Normas Técnicas, NBR 6.123, Forças devido ao vento em edificações. Rio de Janeiro, RJ. Junho de 1988.
ABNT – Associação Brasileira de Normas Técnicas, NBR 12.218, Projeto de rede de distribuição de água para abastecimento público. Rio de Janeiro, RJ. Julho de 1994.
ANDRADE JUNIOR, L. J. Análise estrutural das chapas metálicas de silos e reservatórios cilíndricos. Dissertação de mestrado. Escola de Engenharia de São Carlos. Universidade de São Paulo, 1998.
API – American Petroleum Institute, API 650, Welded Steel Tanks for Oil Storage, decima terceira edição, Washington D. C., Março de 2013.
AWWA – American Water Works Association, AWWA D100-05, Welded Steel Tanks for Water Storage. Edição atualizada. Denver, Colorado. Maio 2005.
GOMES, E. F. Soldagem em reservatórios metálicos para armazenamento de água. Trabalho de conclusão de curso. Curso de especialização em Engenharia de soldagem. Universidade Federal de Minas Gerais, 2017.
HAFEEZ, G., EL ANSARY, A. M. & EL DAMATTY, A. A. Effects of winds load son the stability of conical tanks. Can. J. Civ. Eng. 38, Published by NCR Research Press, 2011.
PEREIRA, P. M. F. Análise dos conjuntos habitacionais do programa Minha Casa, Minha Vida na cidade de Monte Alegre de Minas- MG. Dissertação de mestrado. Faculdade de Geografia. Universidade Federal de Uberlândia, 2017.
TREES, M. J. Design of elevated steel tanks. Thesis. University of Illinois, Urbana-Champaign, 1911.
VISAL, B. & SIBIN, B. Design and analysis of storage tanks. International Journal of Innovative Research in Science, Engineering and Technology. Vol. 6, Issue 5. maio 2017.
[1] Maîtrise en structures et construction civile; Spécialisation dans les constructions industrielles; Spécialisation en génie environnemental; Spécialisation en ingénierie de la sécurité; Ingénieur civil et ingénieur d’opération mécanique.
[2] Spécialisation en génie structurel et génie civil.
[3] Ingénieur civil.
Envoyé : Mars, 2020.
Approuvé : juin 2020.



