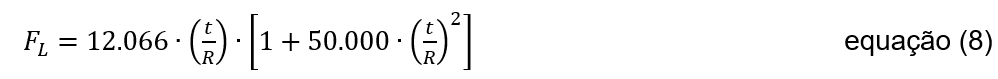ARTIGO ORIGINAL
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Alternativas estruturais em fundos suspensos de tanques metálicos tubulares com duas células para reservação de água. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 06, Vol. 12, pp. 111-135. Junho de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/alternativas-estruturais, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-civil/alternativas-estruturais
RESUMO
Com a crescente demanda por reservação de água devido a implantação de novos loteamentos e condomínios horizontais, que atendesse a necessidade da pressão dinâmica mínima de 100 kPa, os tanques passaram a ter divisões físicas internas (células verticais) cujo célula superior tenha a cota do fundo suspenso em uma altura que garantisse pressão manométrica necessária para atender a referida norma. Devido à falta de normas técnicas brasileiras especificas para armazenamento de água em reservatório metálico, tem se utilizado como parâmetro de dimensionamento para reservatórios metálicos com várias células verticais de armazenamento de água, a AWWA D100 na sua integralidade ou apenas parcialmente, principalmente em função dos esforços axiais nos costados (virolas) para determinação de tensões admissíveis à flambagem (FL). Este artigo aborda o problema da escolha do tipo mais adequado de fundo suspenso de tanques metálicos vertical e compara os resultados de cinco tipos diferentes de fundos, dimensionados de acordo com a norma AWWA D100-05. Dentro da tipologia dos 5 fundos analisados, o fundo mais econômico foi o esférico segmentado.
Palavras chave: Tanque metálico, norma AWWA D100, fundos suspensos.
1. INTRODUÇÃO
Este artigo aborda o problema da escolha do tipo mais adequado de fundo suspenso de tanques metálicos vertical e compara os resultados de cinco tipos diferentes de fundos, dimensionados de acordo com a norma AWWA D100-05.
Com a implantação de novos loteamentos e condomínios horizontais em razão dos incentivos da política habitacional governamental, principalmente pelo programa habitacional do Ministério das Cidades, Programa Minha Casa Minha Vida (Pereira, 2017), que provocou um grande aumento de demanda de tanques de armazenamento de água potável, na sua grande maioria aéreos (above ground), cilíndricos e com diâmetro e alturas variáveis, denominado de castelo d’água.
Devido a necessidade de pressão dinâmica mínima em rede de abastecimento público, que de acordo com a NBR 12.218/1994, deve ser de 100 kPa (10,20 m.c.a.), os tanques passaram a ter divisões físicas internas (células verticais) cujo célula superior tenha a cota do fundo suspenso em uma altura que garantisse pressão manométrica necessária para atender a referida norma, uma vez que normalmente as cotas dos terrenos não oferecem condições para que o tanque seja apoiado.
De acordo com Trees (1911), os fundos dos tanques metálicos suspensos podem ser de vários tipos, como plano, cônico e esférico ou esférico segmentado.
Visal (2017) afirma que os tanques de armazenamento operam sem pressão (ou muito pouca), denominados tanques atmosféricos, diferenciando-os dos vasos de pressão. São geralmente de forma cilíndrica, perpendicular ao solo com fundo plano e um teto fixo ou flutuante.
O projeto e a construção de tanques cilíndricos atmosféricos exigem o conhecimento de normas técnicas específicas, materiais e mão de obra adequados para cada tipo de aplicação e envolvem uma série de outros cuidados especiais pois anomalias e irregularidades nesses equipamentos podem ocasionar grandes prejuízos financeiros ou, até mesmo, perdas de vidas (Nunes, 2013).
Segundo Gomes (2017), as normas comumente utilizadas no Brasil para projetos e construções de tanques metálicos são a NBR 7821, a API 650 e a AWWA D100.
A NBR 7821/1983 – Tanques Soldados para Armazenamento de Petróleo e Derivados, da Associação Brasileira de Normas Técnicas (ABNT) e a norma regulamentadora americana API 650 – 2013 – Welded Steel Tanks for Oil Storage – da American Petroleum Institute (API), são especificas à reservação de petróleo e derivados.
Já a norma AWWA D100-05 – Welded Carbon Steel Tanks for Water Storage, da American Water Works Associations, tem como objetivo fornecer requisitos mínimos para o projeto, construção, inspeção e teste de novos tanques de aço carbono soldados para o armazenamento de água à pressão atmosférica.
Dentro dos requisitos de dimensionamentos, a AWWA D100 apresenta três métodos para determinação da tensão admissível de flambagem (FL) para seções cilíndricas, que permite a verificação da tensão máxima de compressão devido à carga axial e carga axial devido ao carregamento do vento aplicados nos costados.
Em razão de falta de normas técnicas brasileiras especificas para armazenamento de água em reservatório metálico, tem se utilizado como parâmetro de dimensionamento para reservatórios metálicos com várias células verticais de armazenamento de água, a AWWA D100 na sua integralidade ou apenas parcialmente, principalmente em função dos esforços axiais nos costados (virolas) para determinação de tensões admissíveis à flambagem (FL).
2. OBJETIVOS
Objetivo Geral
O objetivo geral deste artigo é o dimensionamento de diversas tipologias de fundos suspensos da célula superior de tanque metálico vertical composto de duas células, dentro das recomendações da AWWA D100-05, utilizando o software Autodesk Simulation Mechanical 2018.
Objetivos Específicos
Os objetivos específicos são:
- Determinar as tensões axiais nos costados da célula inferior do tanque metálico, resultante dos carregamentos axiais e laterais e compara-las à tensão admissível à flambagem de acordo com o que prescreve a 3.4 – Column, Strut, and Shell Stability Formulas da AWWA D100 – 05.
- Determinar os deslocamentos verticais dos fundos suspensos.
- Determinar do peso total dos fundos suspensos propostos, através da quantificação da área e espessuras das chapas dimensionadas e das estruturas de suporte.
3. MATERIAL E MÉTODO
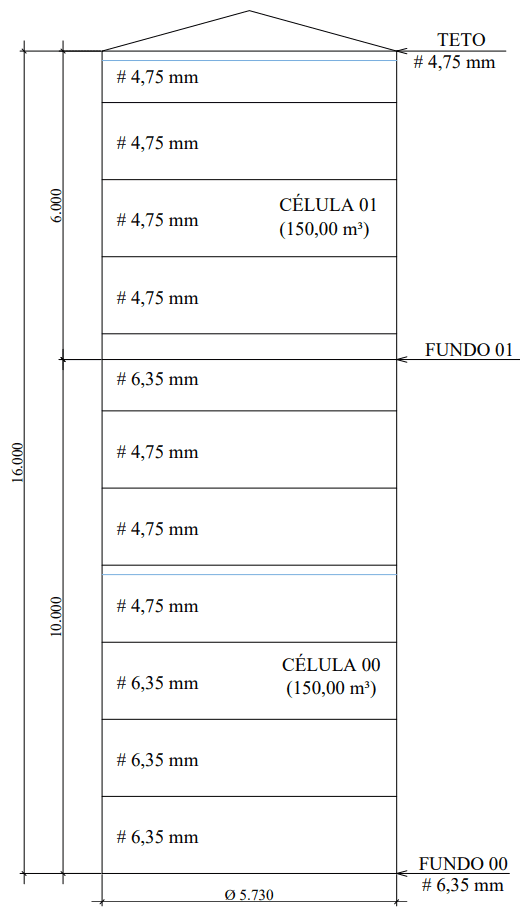
O tanque apresentado neste artigo é um reservatório metálico, para reservação de água, composto de duas células, com capacidade de 150,00 m³ cada (total de 300,00 m³), com cobertura metálica tipo cone (Figura 1), com cinco tipologias de fundos suspensos (Figuras 2A; 2B; 2C; 2D e 2E).
Figura 1: Tanque metálico de duas células com capacidade de 300,00 m³.

Tipologia dos 5 fundos suspensos propostos:
Fig.: 2A – Fundo plano vigas radiais e mastro
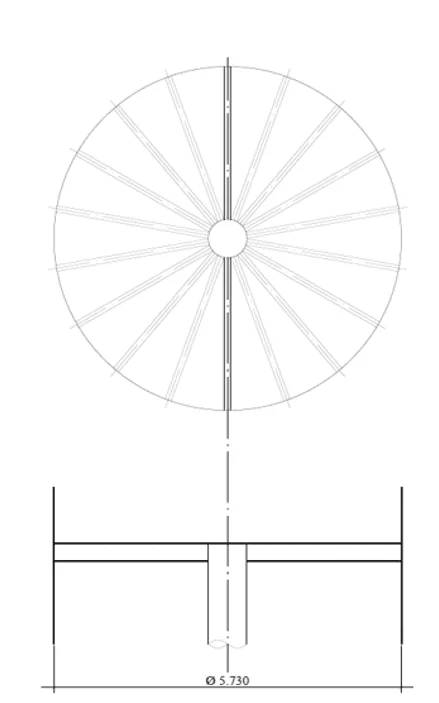
Fig.: 2B – Fundo plano vigas radiais sem mastro
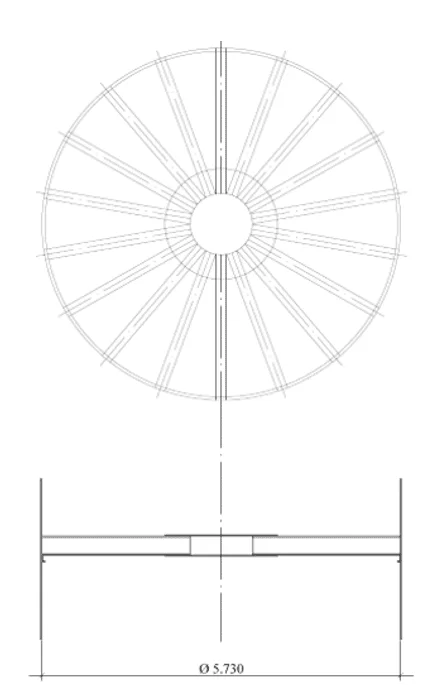
Fig.: 2C – Fundo plano vigas ortogonais
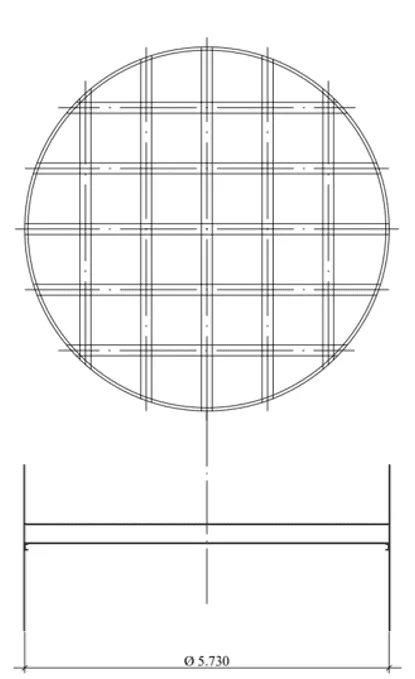
Fig.: 2D – Fundo cônico
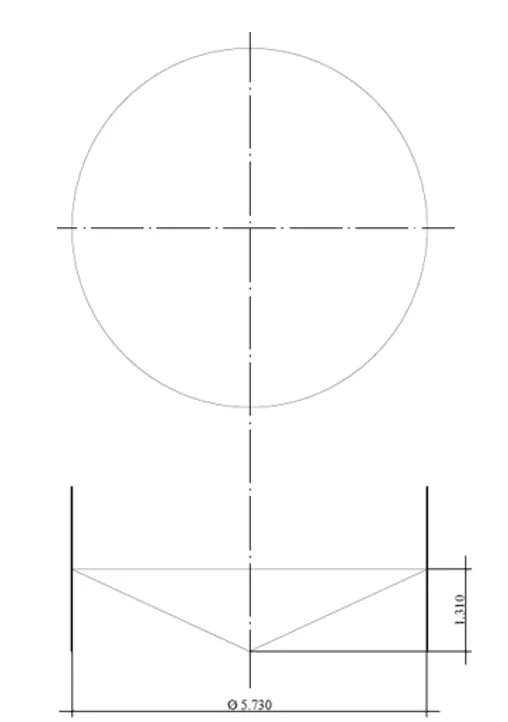
Fig.: 2E – Fundo esférico segmentado
As ações consideradas são as do vento, da água armazenada (ação hidrostática), da sobrecarga no teto e do peso próprio da estrutura (Figura 3A), lançadas no software Autodesk Simulation Mechanical.
Figura 3A – Carregamentos
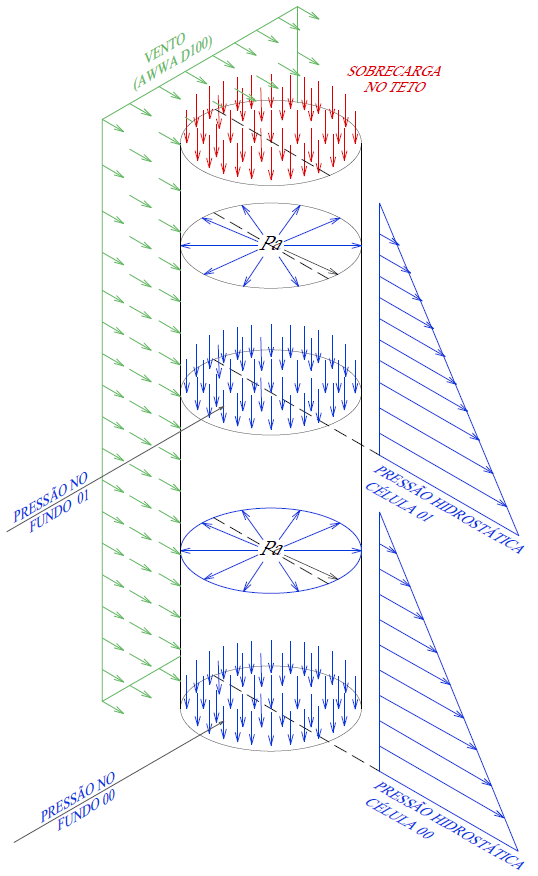
Figura 3B – Lançamento dos carregamentos no software
Segundo Andrade junior (1998), a ação do vento está calculada de acordo com a NBR 6123 – Forças devido ao Veto em Edificações (1987) e, como regra geral, assume-se que o vento pode atuar em qualquer direção horizontal. Como a estrutura do tanque é assimétrica em relação ao eixo Z, perpendicular à direção do vento, considera-se que o vento pode incidir perpendicularmente a qualquer geratriz do tanque.
A componente estática de pressão do vento, , que atua perpendicularmente sobre um elemento de área, é dado por:
Os coeficientes de pressão externa Cpe são expressos para o tipo de corpo da estrutura, assumindo para a aplicação da AWWA D100-05 que Cpe = Cf (Tabela 1).
Onde q é a pressão do vento em um ponto onde ocorre a estagnação do ar, obtida da expressão 2:
A Velocidade V0 é chamada de velocidade básica, corresponde a uma rajada de 3 segundos, exercida em média uma vez em 50 anos, medida a 10 m acima do terreno, em local plano e aberto. A NBR 6123 (1987) apresenta as isopletas básicas, em m/s. Para os nossos exemplos, adotou-se V0 = 40 m/s.
O fator topográfico S1 é utilizado para avaliação do relevo do terreno no entorno da edificação e adotado igual a 1,0 para os nossos exemplos.
O fator S2 considera o efeito combinado da rugosidade do terreno, da variação da velocidade do vento com a altura acima do terreno e das dimensões da edificação. O fator S2 é obtida por intermédio da expressão 4:
Em que: Z = altura acima do terreno, Fr = Fator de rajada do vento, b = parâmetro meteorológico, p = função da rugosidade do terreno e do intervalo de tempo. Para a altura do tanque de 16,0 m, rugosidade II, classe A, tem-se S2 = 1,05.
O fator S3 é um fator estatístico que considera o grau de segurança requerido e a vida útil da estrutura, consideradas as instalações de reservatórios com baixo fator de ocupação humana (Andadre Junior, 1998), foi utilizado o valor de 0,95.
De acordo com Haffez et al (2011), assume-se que os tanques estão submetidos à pressão uniforme do vento (q), atuando ao longo do eixo Z, como mostrado nas figuras 3ª e 3B. A AWWA D100-05 recomenda a utilização de coeficiente de arrasto (Cf), de acordo com a forma da estrutura, conforme Tabela 1. Para tanque tubular com o formato cilíndrico, o Cf adotado é de 0,6.
Tabela 1 – Coeficiente de arrasto Cf

Temos:
Vk = 40 . 10 . 1,05 . 0,95 = 39,90 m/s
q = 0,613 . 39,902 = 975,90 N/m² ou 99,51 kgf/m²
Δp = 0,6 . 975,90 = 585,54 N/m² ou 58,71 kgf/m².
A ação hidrostática gera efeitos que atuam nas direções radial e vertical e resultam em pressão lateral no costado e pressão no fundo do reservatório.
A sobrecarga de projeto aplicada no teto, de acordo com o item 3.1.3.2 da AWWA D100-05, deverá ser 750 N/m² (15 lb/ft²).
O peso próprio da estrutura é lançado automaticamente pelo software Autodesk Simulation Mechanical 2018, considerado o peso específico dos aços utilizados no dimensionamento do tanque.
A espessuras das virolas sob pressão circunferencial devido a pressão hidráulico do tanque deve ser calculado de acordo com a equação 3-40 da Sec. 3.7 da AWWA D100-05 – Cylindrical Shell Plates (equação 7):
Onde:
t = espessura de projeto do casco (virola), em mm
hp = altura de liquido, em m
D = diâmetro do tanque, em m
S = Tensão admissível do aço, em Mpa
E = Eficiência de soldagem
G = Peso especifico do liquido (para água = 1)
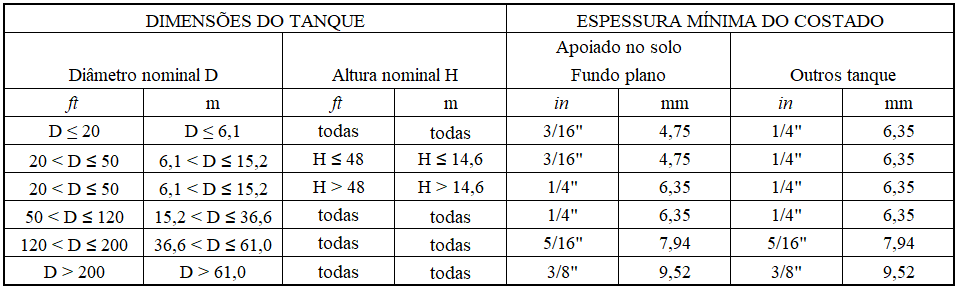
A espessura mínima do costado cilíndrico em contato com a água deverá estar em consonante com a Tabela 2 de acordo com a Sec. 3.2 da AWWA D100-05. Para o tanque de diâmetro nominal de 5,73 m, a espessura mínima prescrita é 4,76 mm.
Tabela 2 – Coeficiente de arrasto Cf
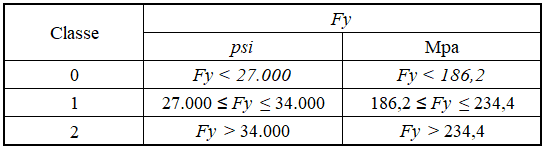
A AWWA D100-05 classifica os matérias estruturais a serem utilizados nos tanques em 3 classes, em função do limite de escoamento (Fy). A Tabela 3 mostra essa classificação.
Tabela 3 – Classe de material em função do Fy
O material empregado nos costados, fundos e teto é o ASTM A36, caracterizado por um módulo de elasticidade (E) igual a 205.000 Mpa, coeficiente de Poisson (µ) igual a 0,30, densidade (γ) de 77.000 N/mm³, tensão de escoamento fy = 250,00 Mpa e tensão última fu = 400,00 Mpa. O material empregado nas estruturas de sustentação dos fundos suspensos (vigas W e C) é o ASTM A572 (grau 50) com tensão de escoamento fy = 345,00 Mpa e tensão última fu = 450,00 Mpa. São classificados como material Classe 2.
A Tabela 4 mostra as principais tensões admissíveis prescrita pela AWWA D100-05, em função da classe dos materiais e aplicações nos reservatórios.
Tabela 4 – Tensões admissíveis em aplicações
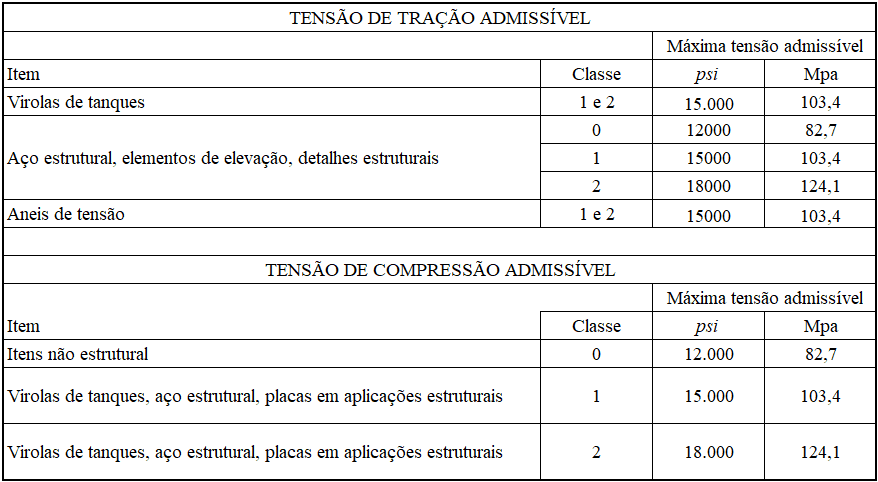
Para a verificação da estabilidade em função da flambagem do costado do tanque, a AWWA D100-05 prescreve 3 métodos de análise. Para este trabalho, utilizou-se o Método 1, que é um procedimento simplificado baseado nas técnicas de análise de membranas. Para materiais da Classe 2, a relação espessura / raio do reservatório a qual a flambagem muda do regime elástico para inelástico (t/R)c é 0,0025372. A tensão admissível para flambagem para material Classe 2 é dada pelas fórmulas seguintes:
Quando 0 ≤ t/R ≤ (t/R)c significa que a flambagem ocorre no regime elástico e a tensão admissível para flambagem é dado pela equação 8:
Quando (t/R)c ≤ t/R ≤ 0,0125 significa que a flambagem ocorre no regime inelástico e a tensão admissível para flambagem é dado pela equação 9:
Quando t/R > 0,0125, significa que a flambagem ocorre em regime plástico e a tensão admissível para flambagem é constante e vale:
A Tabela 5 – Valores de eficiência de soldagem é apresentada parcialmente da Table 15 Weld design values – tank plate joints, onde foram apresentados apenas os valores de soldagem continua. Para o trabalho em tela, foram considerado solda de duplo chanfro frontal com completo preenchimento.
Tabela 5 – Valores de eficiência de soldagem em %

4. RESULTADOS
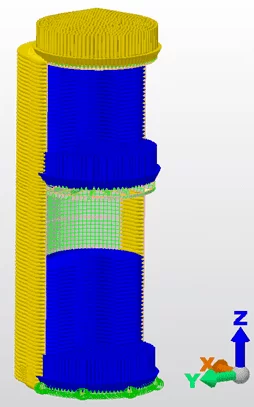
A modelagem e análise numérica foram feitas usando um software comercial de análise e projeto estrutural Autocad Simulation Mechanical 2018. Cada virola do tanque foi modelado como elemento shell com as espessuras de projeto constante, com propriedades isotrópicas e com um plano médio posicionado centralmente. Na parte superior do tanque, há um anel vertical circular modelado com perfil L rigidamente ligados aos elemnetos. As dimensões dos elementos finitos são de 0,20 x 0,20 m (discretização). Para cada tipo de tanque, de acordo com a tipologia de cada fundo suspenso, foi criado um modelo de elemento finito em 3D (Figura 4).
Figura 4: Tanque metálico discretizado

Partindo da espessura mínima de acordo com a Tabela 2, para o dimensionamento do costado foi verificado também a espessura devido à pressão circunferencial, com utilização da equação (7) e a espessura devido à flambagem, com a determinação da tensão admissível (FL), utilizando as equações (8) e (9) e as tensões axiais dos costados determinadas pelo software Simulation Mechanical e comparadas com as tensões admissíveis calculadas (FL). ´A espessura requerida de cada virola é a maior espessura dentro dos 3 critérios.
A Tabela 6 mostra detalhadamente as tensões Van Misse, Tensão circunferencial e tensão axial em cada virola dos 5 tanques estudados com diferentes tipologias de fundos suspensos.
Tabela 6 – Dimensionamento dos costados de acordo com a AWWA D100 – 05
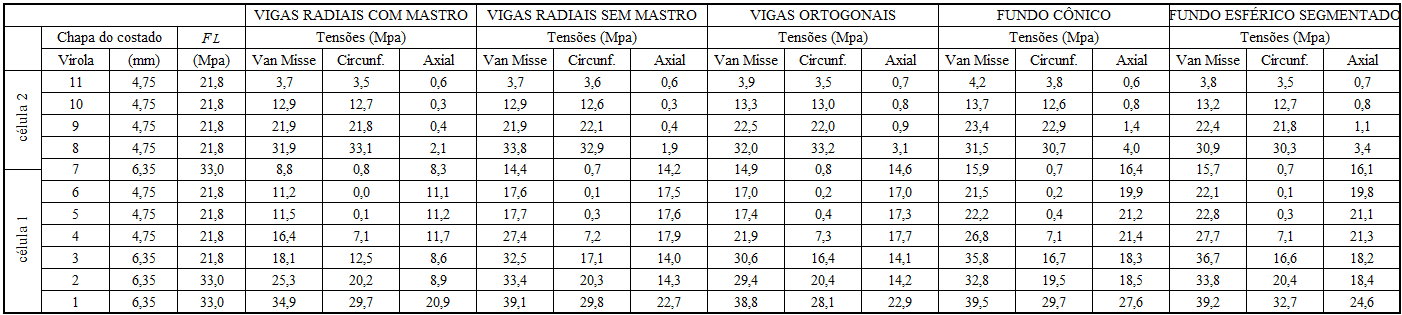
A Figura 5 mostra o tanque com as espessuras requeridas para cada virola do costado.
Figura 5: Tanque com as espessuras finais de costado
As figuras 6A, 6B, 6C e 6D mostram os resultados das análises com as tensões Van Misse, tensões circunferenciais e tensões axiais em cada virola para o tanque com fundo da célula 2, com vigas W radiais e mastro central. Os valores obtidos alimentaram a tabela 6. Análise igual foram feitas nos outros 4 tanques que completam este trabalho.
Fig. 6A: Tensões Van Misse em corte 3D
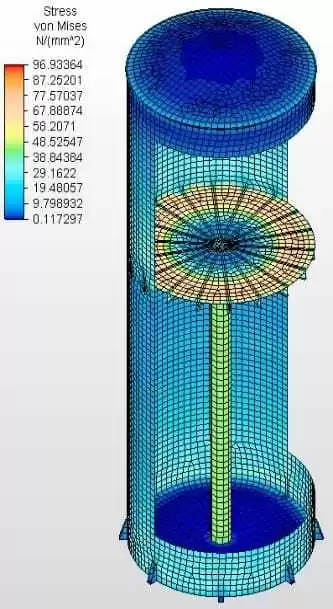
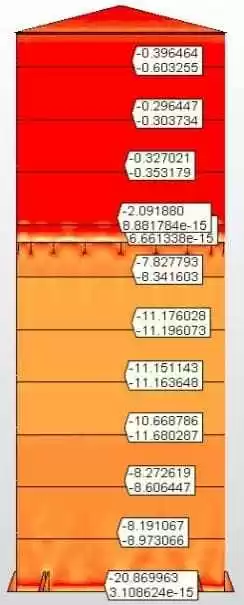
Fig. 6B: Tensões Van Misse

Fig. 6C: Tensões circunferenciais

Fig. 6D: Tensões axiais
Os fundos suspensos analisados neste trabalho, com exceção do fundo com vigas radiais e mastro central (Figura 2A), foram projetados como auto suportado e apoiados apenas nos costados dos tanques. Os resultados das análises são apresentados a seguir.
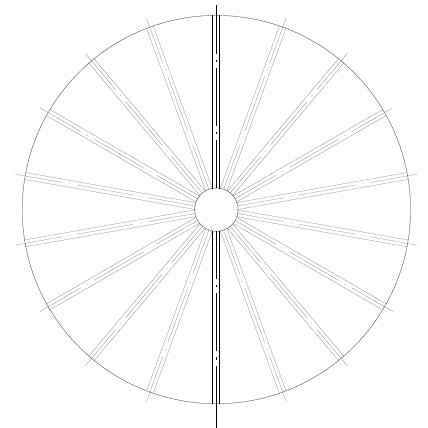
O fundo suspenso com vigas radiais tipo W e mastro central, cuja geometria é mostrada na Figura 7, onde possui diâmetro nominal o mesmo do tanque, D = 5.730,00 mm, número de vigas de suporte = 18 peças, perfil da viga W = 310 x 28,3, material da viga W = ASTM A572 – grau 50, diâmetro do mastro central = 640,00 mm, espessura do mastro central = 6,35 mm, material da chapa do mastro central = ASTM A36, espessura da chapa do fundo = 7,95 mm (5/16”), material da chapa do fundo = ASTM A36.
Carregamento do fundo = pressão hidrostática h = 5,80 m.c.a.
Figura 7: Esquema do fundo com vigas radiais e mastro central
As tensões na chapa do fundo e das vigas de apoio são mostradas nas Figuras 8A e 8B.
Figura 8A: Tensões no fundo suspenso Tensão máxima = 90,0 Mpa
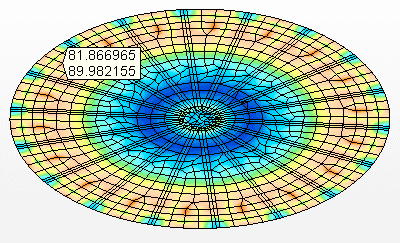
Figura 8B: Tensões nas vigas de apoio Tensão máxima = 64,9 MPa

Figura 8C: Deslocamentos verticais (mm)
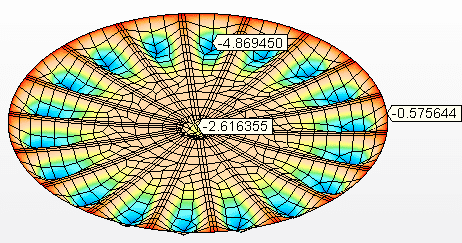
Figura 8D: Tensões axiais no mastro Tensão máxima = 37,6 Mpa

O fundo suspenso com vigas radiais tipo W e sem central, cuja geometria é mostrada na Figura 9, onde possui diâmetro nominal o mesmo do tanque, D = 5.730,00 mm, número de vigas de suporte = 18 peças, perfil da viga W = 310 x 44,5, material da viga W = ASTM A572 – grau 50, viga de apoio circunferencial U 6” primeira alma, material da viga U = ASTM A572 – grau 50, espessura da chapa do fundo = 7,95 mm (5/16”), material da chapa do fundo = ASTM A36.
Carregamento do fundo = pressão hidrostática h = 5,80 m.c.a.
Figura 9: – Esquema do fundo com vigas radiais e sem mastro
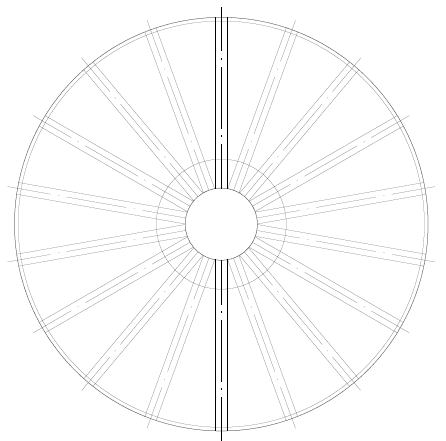
Figura 9A – Tensões no fundo suspenso Tensão máxima = 87,4 Mpa
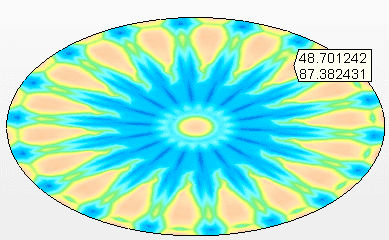
Figura 9B – Tensões nas vigas de apoio Tensão máxima = 89,2 MPa
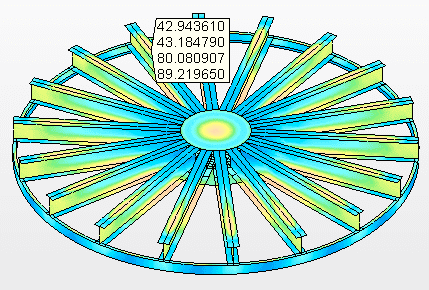
Figura 9C – Deslocamentos verticais (mm)
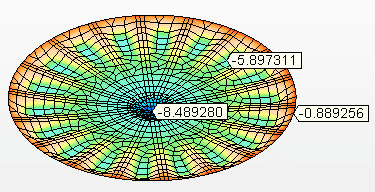
O fundo suspenso com vigas ortogonais (grelha) tipo W e sem central, cuja geometria é mostrada na Figura 10, onde possui diâmetro nominal o mesmo do tanque, D = 5.730,00 mm, número de vigas de suporte = 10 peças, perfil da viga W = 360 x 72, material da viga W = ASTM A572 – grau 50, viga de apoio circunferencial U 6” primeira alma, material da viga U = ASTM A572 – grau 50, espessura da chapa do fundo = 9,53 mm (3/8”), material da chapa do fundo = ASTM A36.
Carregamento do fundo = pressão hidrostática h = 5,80 m.c.a.
Figura 10: – Esquema do fundo com vigas ortogonais (grelha) e sem mastro
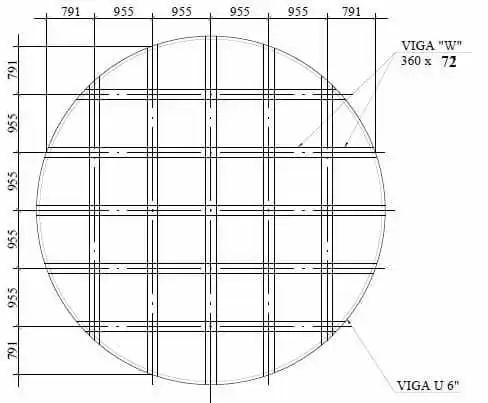
Figura 10A – Tensões no fundo suspenso Tensão máxima = 79,9 Mpa
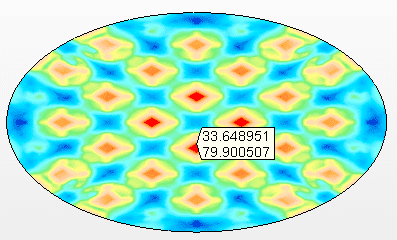
Figura 10B – Tensões nas vigas de apoio Tensão máxima = 85,7 MPa
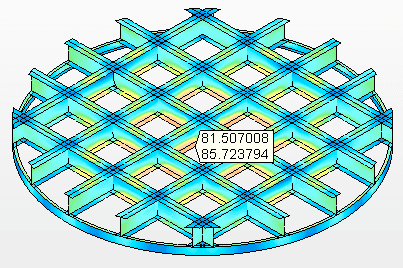
Figura 10C – Deslocamentos verticais (mm)
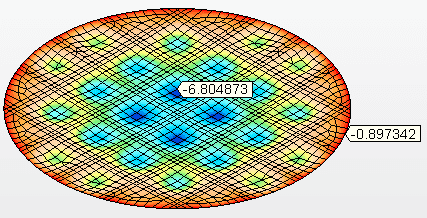
O fundo suspenso em formato de cone, cuja geometria é mostrada na Figura 11 (corte), onde possui diâmetro nominal o mesmo do tanque, D = 5.730,00 mm, espessura da chapa do fundo = 9,53 mm (3/8”), material da chapa do fundo = ASTM A36. Carregamento do fundo = pressão hidrostática h = 5,80 m.c.a.
Figura 11: – Esquema do fundo cônico em corte
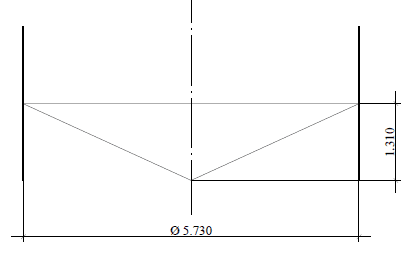
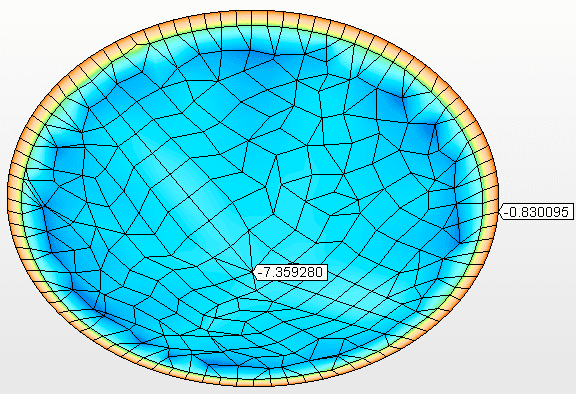
Figura 11A – Tensões no fundo suspenso Tensão máxima = 90,8 Mpa
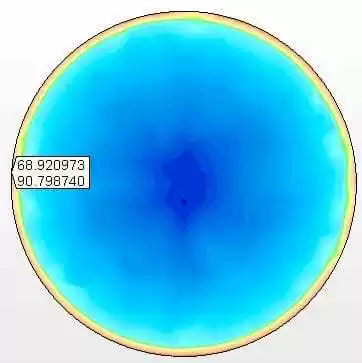
Figura 11B – Deslocamentos verticais (mm) Tensão máxima = 7,359 mm
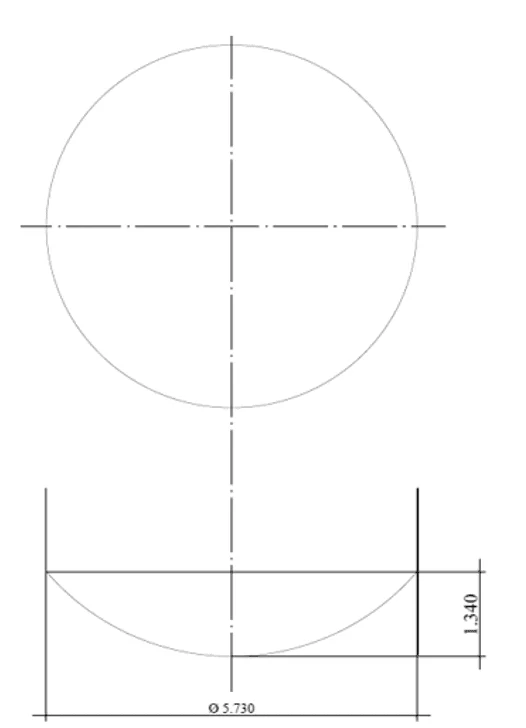
O fundo suspenso em formato de semi esfera ou fundo esférico segmentado cuja geometria é mostrada na Figura 12 (corte), onde possui diâmetro nominal o mesmo do tanque, D = 5.730,00 mm, espessura da chapa do fundo = 4,75 mm (3/16”), material da chapa do fundo = ASTM A36. Carregamento do fundo = pressão hidrostática h = 5,80 m.c.a.
Figura 12: – Esquema do fundo esférico segmentado em corte.
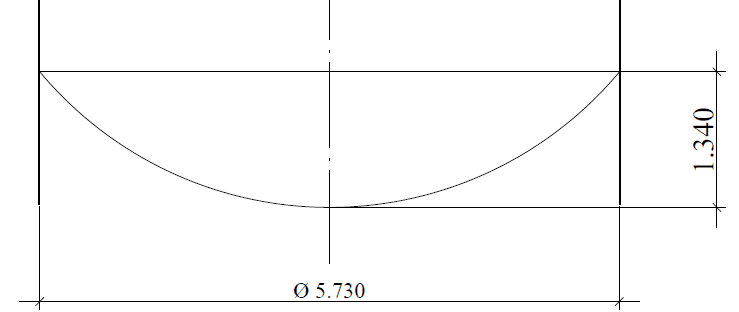
Figura 12A – Tensões no fundo suspenso Tensão máxima = 88,32 Mpa

Figura 12B – Deslocamentos verticais (mm) Tensão máxima = 7,359 mm
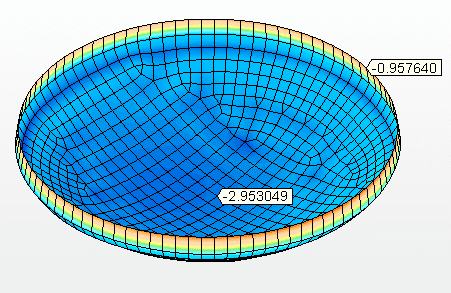
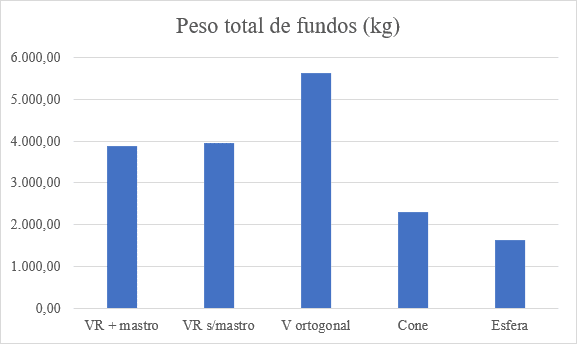
Os pesos dos fundos suspensos foram calculados sem apurar recortes ou aproveitamento de retalhos e sobras, apurando apenas as superfícies de chapas multiplicado pelo peso / m². A Tabela 7 mostra o resumo geral dos pesos dos 5 tipos de fundos suspensos e essas diferenças podem ser vista no gráfico peso total x tipo de fundos, na Figura 13.
Tabela 7 – Pesos dos fundos suspensos

Figura 13 – Comparativos dos pesos dos fundos
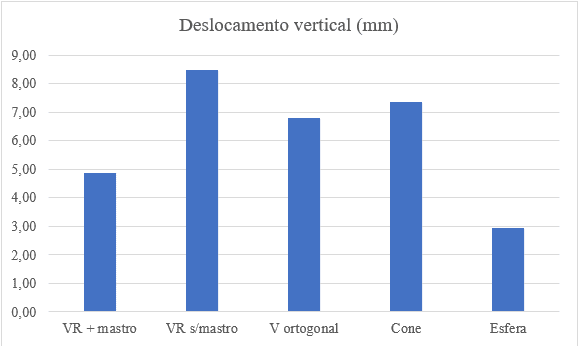
Os deslocamentos máximos verticais dos fundos suspensos são mostrados comparativamente na Figura 14.
Figura 14 – Comparativos dos deslocamentos máximos verticais
5. CONCLUSÕES
Pelos resultados obtidos, conclui-se que o fundo suspenso do tipo esférico segmentado é o mais economicamente viável e também o mais tecnicamente recomendável, pois apresenta o menor deslocamento vertical, sob carregamento completo.
O fundo suspenso tipo cone é também economicamente viável mas apresenta deslocamento vertical sob carregamento um pouco excessivo, devendo ser verificado se interfere com as tubulações. O deslocamento vertical poderia ser diminuído com a utilização de chapas de reforços triangulares, apoiando o fundo nos costados laterais.
O fundo suspenso apoiado em vigas ortogonais é totalmente anti econômico.
REFERÊNCIAS
ABNT – Associação Brasileira de Normas Técnicas, NBR 7.821, Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro, RJ. Abril de 1983.
ABNT – Associação Brasileira de Normas Técnicas, NBR 6.123, Forças devido ao vento em edificações. Rio de Janeiro, RJ. Junho de 1988.
ABNT – Associação Brasileira de Normas Técnicas, NBR 12.218, Projeto de rede de distribuição de água para abastecimento público. Rio de Janeiro, RJ. Julho de 1994.
ANDRADE JUNIOR, L. J. Análise estrutural das chapas metálicas de silos e reservatórios cilíndricos. Dissertação de mestrado. Escola de Engenharia de São Carlos. Universidade de São Paulo, 1998.
API – American Petroleum Institute, API 650, Welded Steel Tanks for Oil Storage, decima terceira edição, Washington D. C., Março de 2013.
AWWA – American Water Works Association, AWWA D100-05, Welded Steel Tanks for Water Storage. Edição atualizada. Denver, Colorado. Maio 2005.
GOMES, E. F. Soldagem em reservatórios metálicos para armazenamento de água. Trabalho de conclusão de curso. Curso de especialização em Engenharia de soldagem. Universidade Federal de Minas Gerais, 2017.
HAFEEZ, G., EL ANSARY, A. M. & EL DAMATTY, A. A. Effects of winds load son the stability of conical tanks. Can. J. Civ. Eng. 38, Published by NCR Research Press, 2011.
PEREIRA, P. M. F. Análise dos conjuntos habitacionais do programa Minha Casa, Minha Vida na cidade de Monte Alegre de Minas- MG. Dissertação de mestrado. Faculdade de Geografia. Universidade Federal de Uberlândia, 2017.
TREES, M. J. Design of elevated steel tanks. Thesis. University of Illinois, Urbana-Champaign, 1911.
VISAL, B. & SIBIN, B. Design and analysis of storage tanks. International Journal of Innovative Research in Science, Engineering and Technology. Vol. 6, Issue 5. maio 2017.
[1] Mestrado em Estruturas e Construção Civil; Especialização em Construções Industriais; Especialização em Engenharia Ambiental; Especialização em Engenharia de Segurança; Engenheiro Civil, e Engenheiro de Operação Mecânico.
[2] Especialização em Engenharia de estruturas e Engenharia Civil.
[3] Engenheiro Civil.
Enviado: Março, 2020.
Aprovado: Junho, 2020.