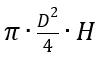ARTICLE ORIGINAL
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Réservoir métallique pour réservoir d’eau au Brésil: une étude de l’application partielle de l’API 650. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 05, Vol. 01, pp. 33-62. mai 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/travaux-publics/reservoir-metallique
RÉSUMÉ
Compte fait de la demande croissante de réserves d’eau et de l’absence de normes techniques pour les réservoirs métalliques au Brésil, plusieurs fabricants de réservoirs ont partiellement utilisé l’API 650 pour dimensionner et vérifier ces réservoirs. Dans le cadre de ces travaux, des études ont été réalisées pour vérifier l’application partielle et intégrale de l’API 650, méthode 1 pied, par la dimension de 7 réservoirs métalliques ayant le même volume en fonction de différents ratios hauteur/diamètre (H/D). Il analyse les contraintes circonférentielles dans les deux cas et le dimensionnement prévu dans l’API 650 et détermine les ratios de hauteur/diamètre les plus économiques pour le stockage de l’eau.
Mots-clés: Réservoir métallique, norme API 650, dimensionnement, optimisation.
1. INTRODUCTION
Les réservoirs cylindriques sont des structures couramment utilisées pour le stockage de l’eau, des déchets industriels, des déchets pétrochimiques, des huiles, des céréales, etc. (HECKE, 2010).
Selon Barros (2010), il s’agit d’équipements de chaudière lourde, soumis à une pression atmosphérique approximative, généralement de l’âge de 0 à 0,5 psi et destinés principalement au stockage du pétrole et de ses dérivés.
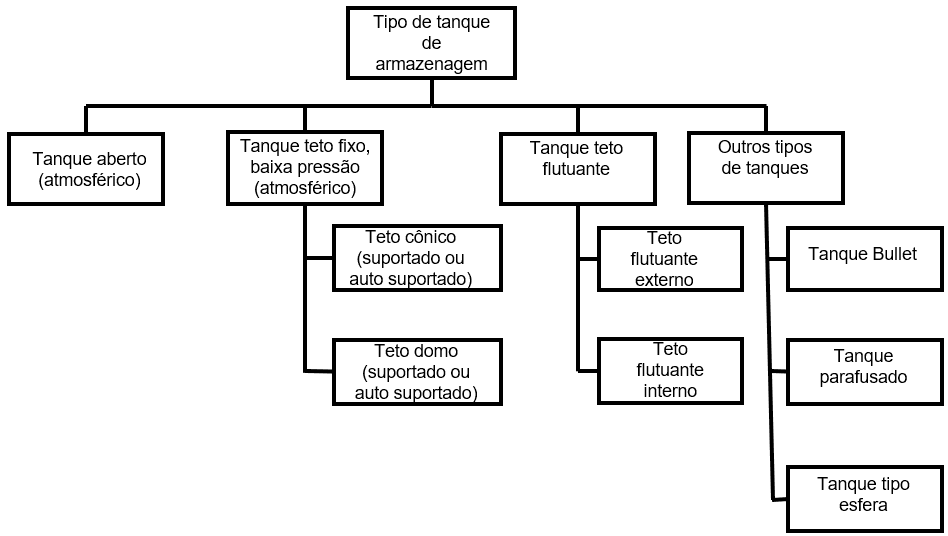
Roncetti (2011) indique qu’il y a eu une augmentation de la demande de stockage de vrac liquide dans diverses activités économiques ainsi que l’augmentation de la demande d’activités intermédiaires telles que l’assainissement, le traitement des déchets, la réfrigération et d’autres procédés de fabrication, où il est nécessaire de stocker des graneis liquides. La figure 1 illustre les divers types de réservoirs de stockage couramment utilisés par les industries (KUAN, 2009).
Figure 1 – Types de réservoir de stockage.
La conception et la construction de réservoirs cylindriques atmosphériques nécessitent une série de soins spéciaux et nécessitent la connaissance de normes techniques et matérielles adaptées à chaque type d’application, car les défaillances de ces équipements peuvent entraîner de grandes pertes financières, voire des pertes de vie (NUNES, 2013).
Au Brésil, il existe une norme pour la construction de ces équipements. La norme NBR 7821 – Réservoirs soudés pour le stockage du pétrole et des dérivés – publiée par l’Association brésilienne des normes techniques (ABNT). Toutefois, la norme la plus utilisée dans les industries en général est l’API 650 de l’American Regulatory Standard – Welded Steel Tanks for Oil Storage – de l’American Petroleum Institute (API), tous deux destinés à la réserve de pétrole et de produits dérivés (SATO, 2015).
Selon Barros (2010), l’API 650 couvre les spécifications sur les matériaux, la conception, la fabrication, l’assemblage et l’essai de réservoirs de stockage verticaux, cylindriques et non enterrés, avec le dessus fermé ou ouvert, la construction soudée, avec différentes dimensions et capacités, pour un service non réfrigéré, avec une température de conception maximale de 260 ºC et une pression interne approximativement atmosphérique (ne dépassant pas 2,5 psig).
Selon Azzumi et Guzey (2015), conformément à l’API 650, les trois méthodes de détermination de l’épaisseur du réservoir des réservoirs cylindriques de stockage en acier conçus conformément à l’API 650 sont les suivante :
La méthode d’un pied (1FM – one foot method), la méthode de point de conception variable (VDM), et l’analyse linéaire. Nous avons comparé les conceptions de coquille basées sur ces trois méthodes pour différentes propriétés de réservoir : diamètre, hauteur et tension permises.
La méthode d’un pied (1FM), qui est basée sur la théorie de la membrane « ». L’épaisseur requise de la plaque de pelure pour chaque coup de peau est calculée à l’aide du stress circonférentiel à un point de 0,3 m (1 pied) au-dessus de la couture horizontale de la soudure inférieure de la furule de casserole en raison de la pression hydrostatique du liquide stocké. Le 1FM est utilisé avec succès pour la plupart des réservoirs. Toutefois, les projets basés sur 1FM peuvent devenir conservateurs et coûter prohibitifs pour les réservoirs de plus grand diamètre. Par conséquent, l’API 650 limite l’applicabilité de cette méthode aux réservoirs jusqu’à 61 m (200 pi) de diamètre.
La deuxième méthode de calcul de l’épaisseur requise de la plaque de coquille est la méthode du point de conception variable (VDM) qui est également basée sur la « théorie de la membrane ». Le VDM a été proposé par Zick et McGrath en 1968 et adopté plus tard par l’API 650 comme méthode raffinée pour calculer l’épaisseur requise de la plaque de coque, en particulier pour les réservoirs de plus de 61 m (200 pi) de diamètre. Le VDM tient compte de la restriction prévue par les plaques inférieures du réservoir pour la première course de la ferrule et de la restriction fournie par chaque ferrule inférieur pour le chemin de ferrule supérieur. Le VDM utilise une distance variable au lieu d’une distance fixe de 0,3 m (1 pied), comme utilisé dans 1FM, au-dessus de la soudure circonférentielle (couture) pour chaque runof run, pour calculer le stress circonférentiel maximal dû à la pression hydrostatique.
La troisième méthode fournie dans l’API 650 est le calcul de l’épaisseur de la coquille à l’aide d’une analyse linéaire. Dans cette approche, les conditions limites de l’analyse devraient être un moment plastique lié au rendement de la plaque sous la coque et au mouvement radial totalement limité au fond de la coquille. L’API 650 ne décrit pas de méthode d’analyse linéaire spécifique. Dans cette étude, nous avons développé une nouvelle méthode utilisant la théorie de l’écorce fine pour effectuer une analyse linéaire de l’épaisseur de l’écorce de calcul. Dans cette méthode, nous utilisons la rigidité exacte – les relations de flexibilité et les fonctions exactes de la forme provenant de la solution dite « coquille courte » des équations qui régissent à partir de la théorie de la peau élastique fine.
Il y avait peu d’informations littéraires pour le calcul d’un réservoir métallique pour la réserve d’eau et l’absence de normes techniques spécifiques pour les réservoirs soudés pour le stockage de l’eau au Brésil.
En raison de l’absence d’une norme technique spécifique, il a été utilisé comme paramètre de calcul pour les réservoirs métalliques destinés aux réserves d’eau, l’API 650 dans son intégralité ou seulement partiellement, en particulier en ce qui concerne la détermination de l’épaisseur des côtes de l’eau et les contraintes admissibles, puisque les critères de sécurité pour les incendies et les explosions du matériel stocké ne s’appliqueraient pas à l’eau.
2. MATÉRIEL ET MÉTHODE
L’objectif principal de ces travaux est de vérifier la conception de réservoirs métalliques ouverts, sans abri, avec le même volume et différents H/D, selon l’API 650, par la méthode d’un pied (1FM), en deux étapes, la première ne tenant compte que des épaisseurs calculées par l’équation décrite dans l’élément 5.6.3.2 de cette norme;
td = épaisseur de conception, en mm;
D = diamètre nominal du réservoir, en m;
H = niveau de conception liquide, en m;
G = poids liquide spécifique dans le cas de l’eau: 1;
AC = surcolyse de corrosion, spécifiée par l’acheteur, en mm;
Sd = tension admissible (tableau 5-2 API 650), en Mpa.
Et dans la deuxième étape, en plus de la vérification de l’épaisseur calculée par l’équation 1, les épaisseurs minimales sont également adoptées, telles que décrites dans l’article 5.6.1.1 et indiquées dans le tableau 1.
Tableau 1 – Épaisseurs minimales des brins

Comme objectif complémentaire, déterminer la plage de rapport H/D qui est la plus économiquement viable, avec le poids le plus bas de la construction du réservoir soudé.
Le critère pour déterminer la relation entre la hauteur (H) et le diamètre (D) des modèles est le volume du réservoir, maintenu constant, avec 660,00 m³ et un diamètre maximum inférieur à 15,00 m selon l’article 5.6.1.1 – API 650, indiqué dans le tableau 1. En conséquence, pour le volume constant (V0) et considéré les rapports hauteur / diamètre (H / D) entre 0,25 et 4,0.
Défini: H = hauteur du cylindre; D = diamètre et V= volume =
Les dimensions des diamètres, des hauteurs et des proportions entre eux sont décrites dans le tableau 2 et la figure 2.
Tableau 2 – Ratios hauteur/diamètre à volume constant de 660,00 m³

Figure 2 – Modèles géométriques de réservoirs cylindriques étudiés

L’acier utilisé est ASTM A36, caractérisé par un module d’élasticité (E) égal à 205 000 Mpa, coefficient de Poisson (µ) égal à 0,30, densité (γ) de 77 000 N / mm³, limite élastique fy = 250 .00 Mpa et dernière tension fu = 400.00 Mpa. Selon le tableau 5-2 Permissible Plate Materials and Allowable Stresses de l’API 650, la contrainte admissible pour l’acier ASTM A36 est de 160,00 Mpa (tableau 3).
Tableau 3 – Matériaux plats autorisés et contraintes admissibles
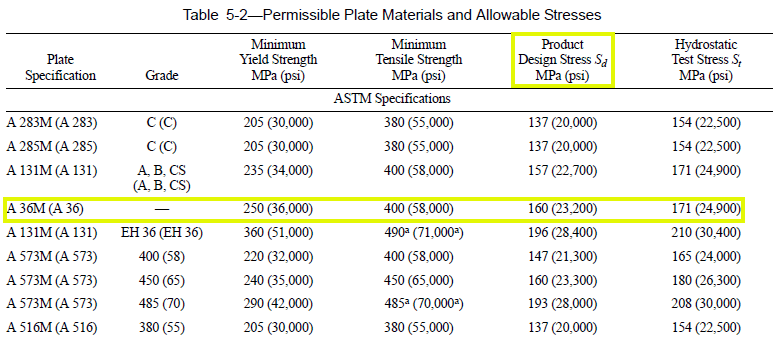
Source: API 650 (2007) – modifié par l’auteur.
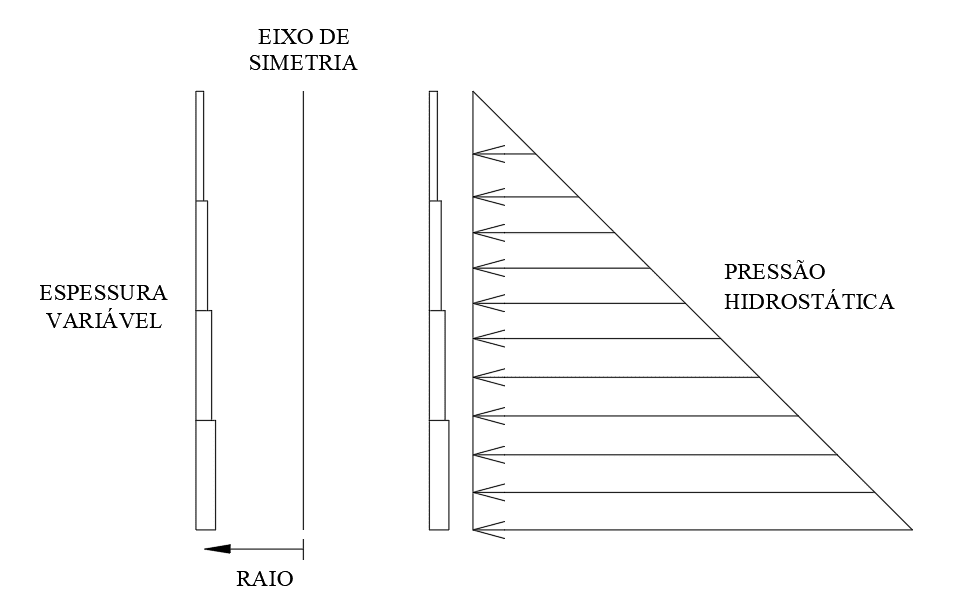
L’épaisseur des plaques du corps du réservoir est considérée comme variable le long de la hauteur du réservoir (figure 3).
Figure 3 – Variation de la plaque le long de la hauteur du réservoir
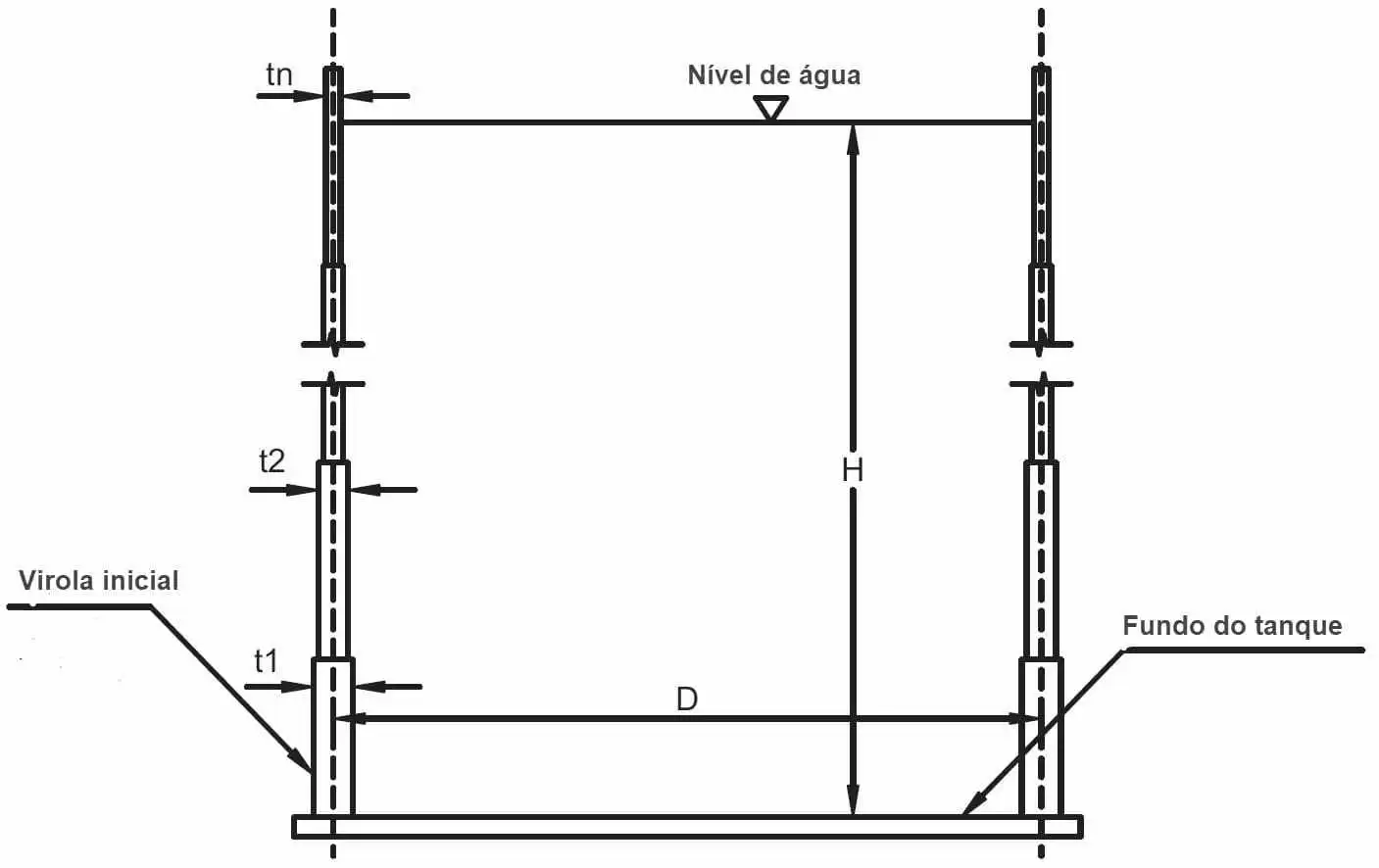
Source: Adapté de Azzumi et Guzey (2015)
Compte tenu de l’absence de frottement due au matériau stocké (eau), l’état du réservoir est complètement plein, la non-application du vent et les conditions de l’épaisseur es des plaques des corps des réservoirs (virolas), ne résulte que 1(un) cas d’analyse (figure 4) :
Figure 4 – Réservoir avec épaisseur de mur liquide et variable au-dessus de la hauteurr
Source: L’auteu
Le flux decalcul des épaisseurs des mains de guerre des réservoirs soudés détermine le diagramme indiqué à la figure 5.
Figure 5 – Diagramme d’écoulement du calcul de l’épaisseur des cannes d’eau des réservoirs
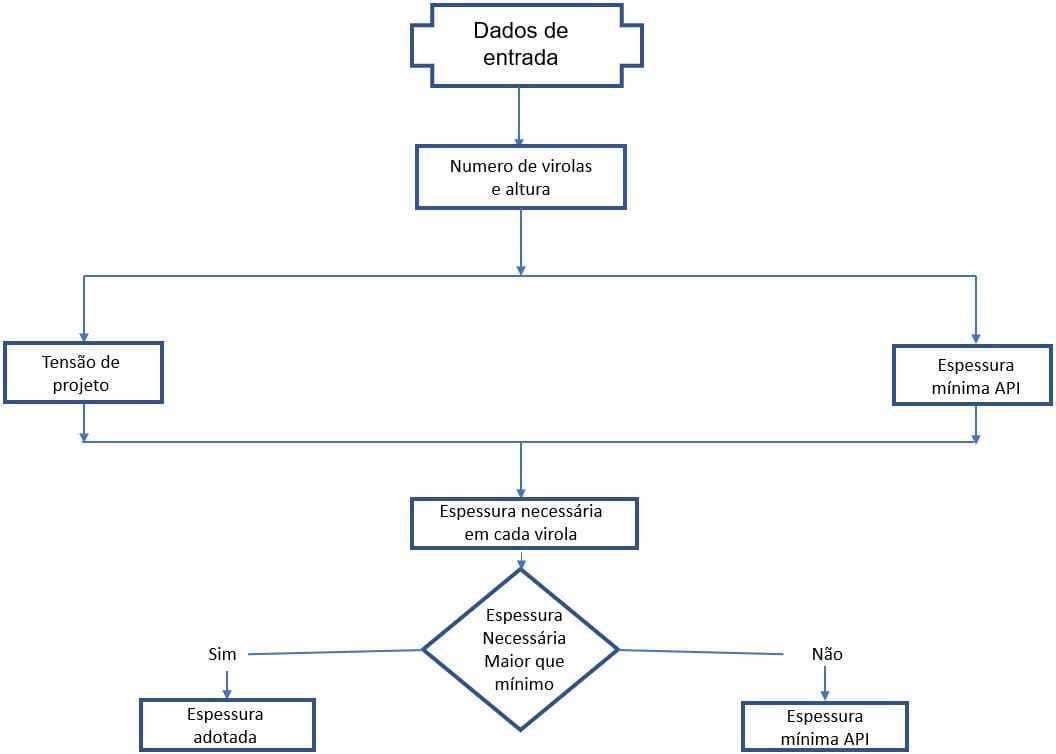
Source: L’auteur lui-même
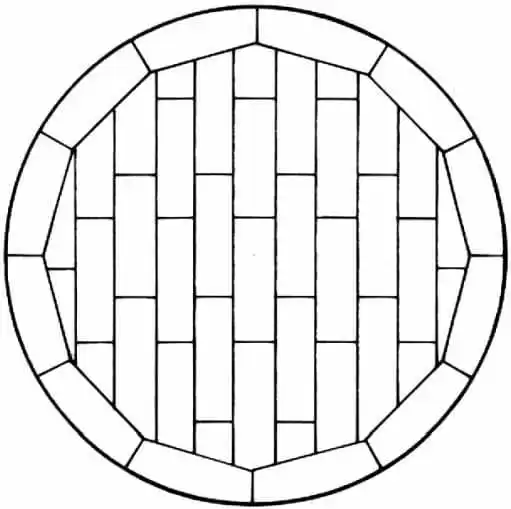
Le poids des 7 réservoirs proposés dans ce travail a été calculé en deux étapes. La première étape a calculé le poids des fonds du réservoir, compte tenu des fonds avec des plaques annulaires (figure 6), selon l’article 5.4.1 de l’API 650 (Botton Plates), qui prescrit l’épaisseur minimale de 6,00 mm (1/4). Le chevauchement des plaques d’environ 2,26 % a été pris en compte dans le poids des fonds du réservoir.
Figure 6 – Disposition typique des plaques inférieures avec plaques annulaires.
Les poids des profils d’angle de renforcement du bord supérieur ont également été pris en considération, comme indiqué dans le tableau 4 prescrit dans l’article 5.1.5.9 de l’API 650 – Roof and Top-Angle Joints », superposés sur le dernier anneau (ferrule) du côté, avec volet horizontal faisant face au côté externe du réservoir.
Tableau 4 -Renforcement du bord supérieur du côté.

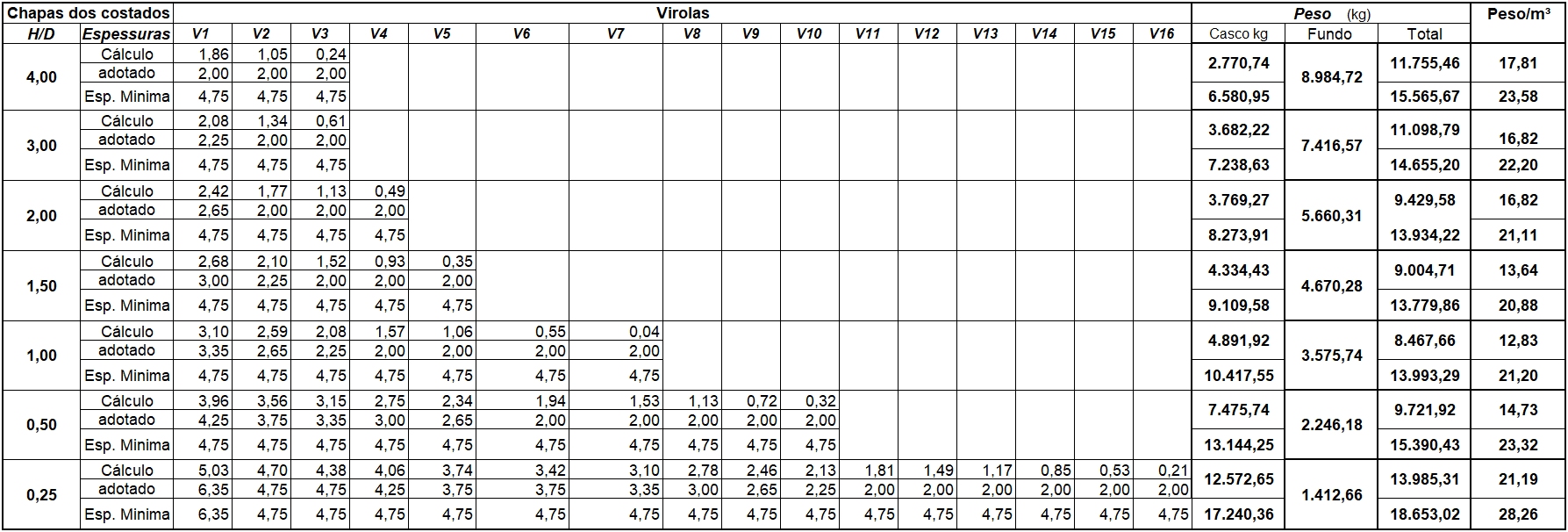
Le poids des brins a été déterminé après avoir déterminé l’épaisseur de chaque plaque qui compose les cannes d’eau des réservoirs pour chaque rapport H/D, compte tenu des épaisseurs calculées uniquement avec l’équation 1 et des épaisseurs compte tenu des épaisseurs minimales prescrites par l’API 650 (tableau 5). La méthode d’un pied (1FM) a été utilisée, avec une efficacité de soudure de 1,00 (100 %) et sans tenir compte de la surcolyse de corrosion et des forces résultant de l’action des vents n’ont pas été appliquées. Les épaisseurs utilisées pour la dimensionnement des virolas étaient (en millimètres): 2,00; 2,25; 2,65; 3,00; 3,35; 3,75; 4,25; 4,75 et 6,35 mm, tous d’une largeur de 1 500,00 mm.
Tableau 5 – Épaisseur de la plaque des brins et des poids des réservoirs étudiés.
3. ANALYSE DE MÉTHODE D’ÉLÉMENT FINI
Pour l’analyse par la méthode des éléments finis (MEF) des 7 réservoirs d’une capacité de 660,00 m³ et de dimensions décrites dans le tableau 2, le logiciel AUTODESK SIMULATION MECHANICAL 2018 a été utilisé, avec discrétisation du maillage à 150 x 150 mm (Figures 7 et 8 ).
Figure 7 – Discrétion du réservoir H/D 1,00 – diamètre et hauteur 9,43 m.
Figure 8 – Application du réservoir de chargement de l’eau H/D 1,00

4. RÉSULTATS
Suivez les résultats de l’analyse selon la méthode des éléments finis – MEF, des 7 réservoirs proposés, à l’aide du logiciel AUTODESK SIMULATION MECHANICAL 2018
4.1 RÉSERVOIR H/D = 4.00 – DIAMÈTRE14.98 M ET HAUTEUR 3.75 M
Les figures 9 et 10 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et supposées comme 2,00 mm. La tension maximale de l’ambiance 1 était de 147,81 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 9 – Contraintes circonférentielles H/D 4.00 en 3D – épaisseurs calculées
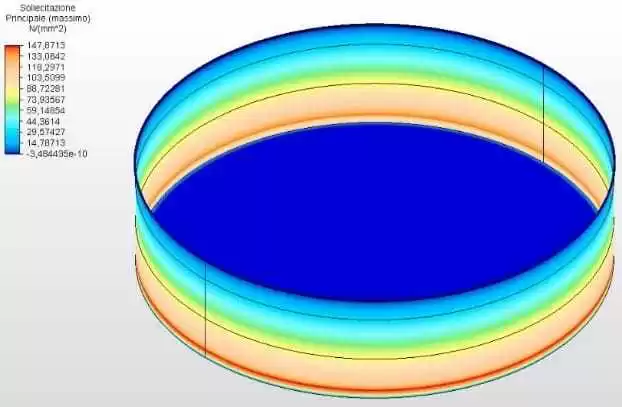
Figure 10 – Contraintes circonférentielles H/D 4.00 en 2D – épaisseurs calculées
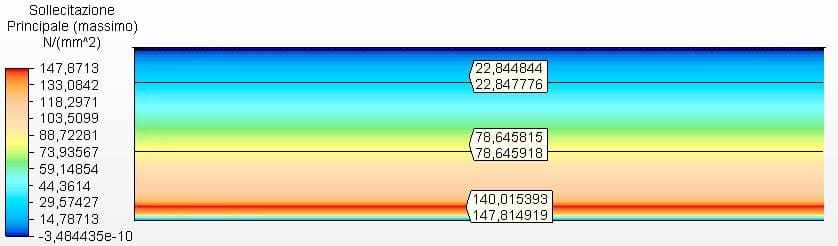
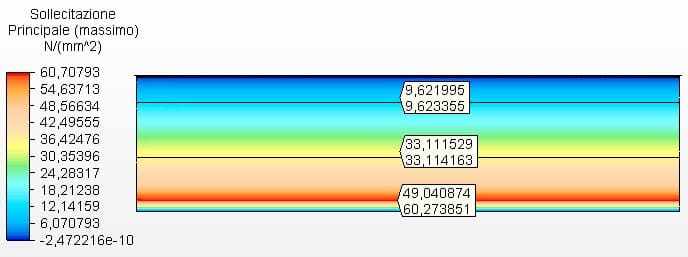
La figure 11 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, au cas où 4,75 mm. La tension maximale était de 60,27 MPa.
Figure 11 – Contraintes circonférentielles H/D 4.00 en épaisseurs 2D-minimas
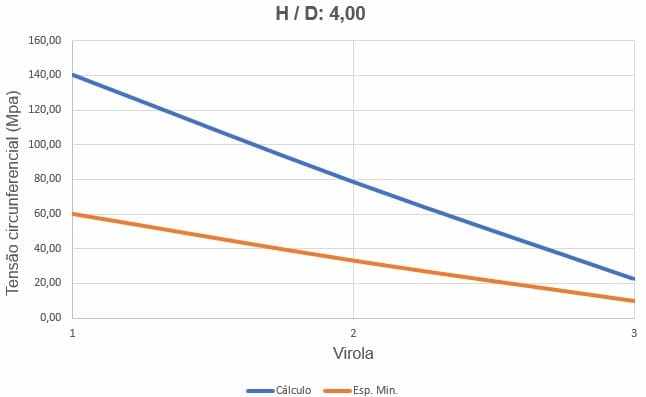
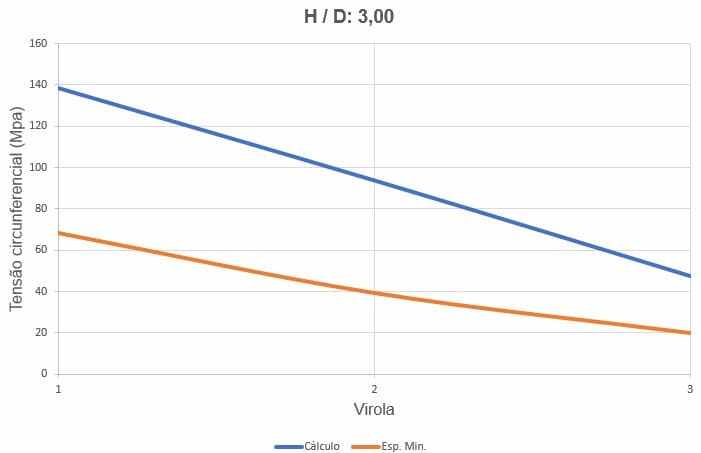
La figure 12 montre les courbes des contraintes circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 12 – Courbes des circonférences du réservoir H/D 4.00
4.2 RÉSERVOIR H/D = 3.00 – DIAMÈTRE 13.61 M ET HAUTEUR 4.54 M
Les figures 13 et 14 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et supposées comme ferrule 1 avec 2,25 mm et l’autre avec 2,00 mm. La tension maximale de virule 1 était de 146,67 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 13 – Tensions circonférentielles H/D 3.00 en 3D – épaisseurs calculées
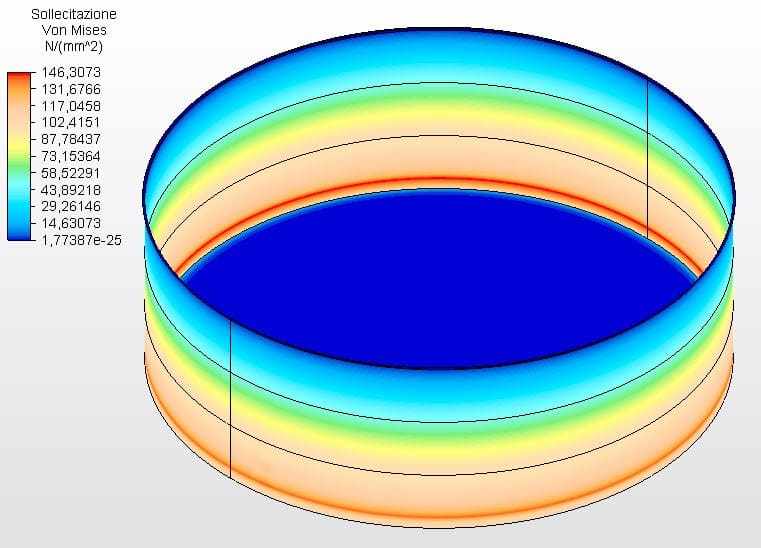
Figure 14 – Contraintes circonférentielles H/D 3.00 en 2D – épaisseurs calculées
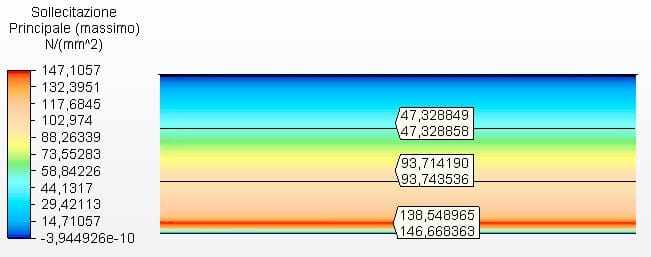
La figure 15 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, dans ce cas 4,75 mm. La tension maximale était de 68,17 MPa.
Figure 15 – Contraintes circonférentielles H/D 3.00 en épaisseurs 2D-minimas
La figure 16 montre les courbes des contraintes circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 16 – Courbes des contraintes circonférentielles du réservoir H/D 3,00
Source: L’auteur lui-même
4.3 RÉSERVOIR H/D = 2.00 – DIAMÈTRE 11.89 M ET HAUTEUR 5.94 M
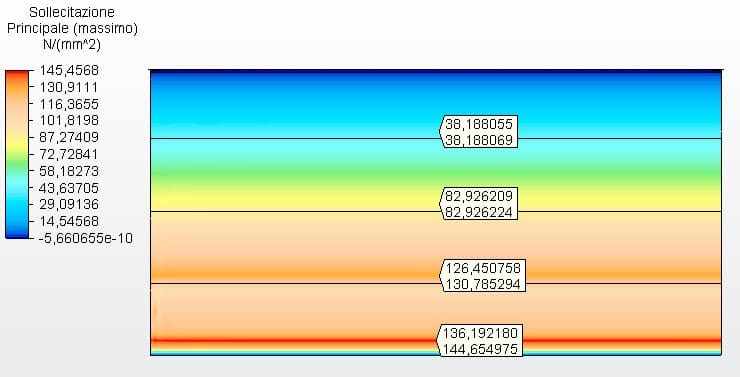
Les figures 17 et 18 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et supposées comme ferrule 1 avec 2,65 mm et l’autre avec 2,00 mm. La tension maximale de l’ambiance 1 était de 144,65 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 17 – Contraintes circonférentielles H/D 2.00 en 3D – épaisseurs calculées
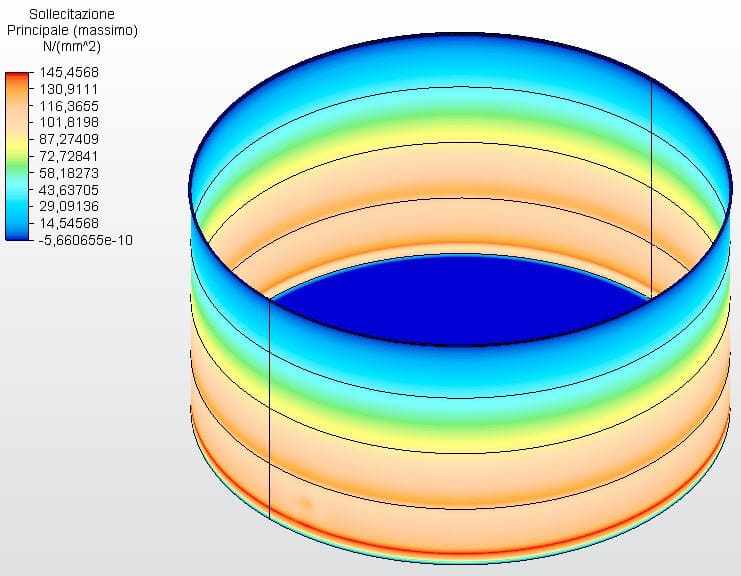
Figure 18 – Contraintes circonférentielles H/D 2.00 en 2D – épaisseurs calculées
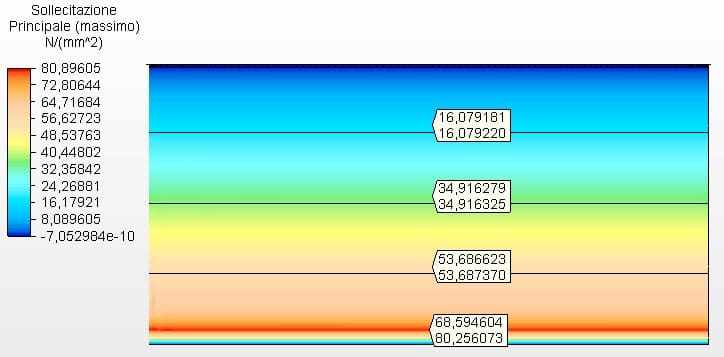
La figure 19 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, au cas où 4,75 mm. La tension maximale était de 80,26 MPa.
Figure 19 – Contraintes circonférentielles H/D 2.00 en épaisseurs 2D-minimas
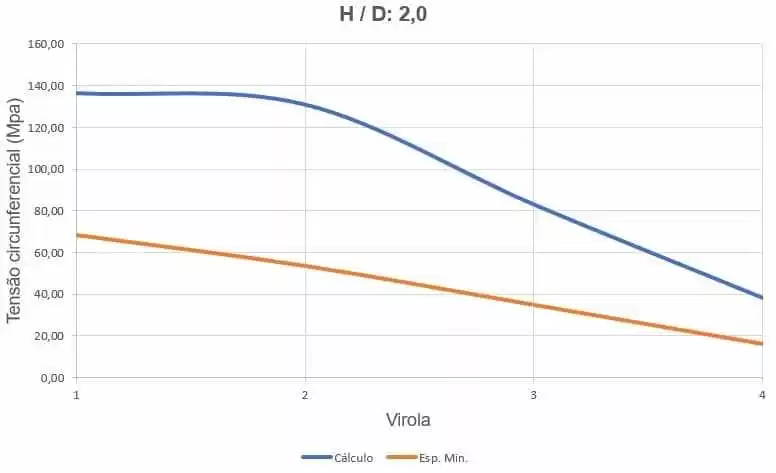
La figure 20 montre les courbes des contraintes circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 20 – Courbes des contraintes circonférentielles du réservoir H/D 2,00
Source: L’auteur lui-même
4.4 RÉSERVOIR H/D = 1.00 – DIAMÈTRE 9.43 M ET HAUTEUR 9.43 M
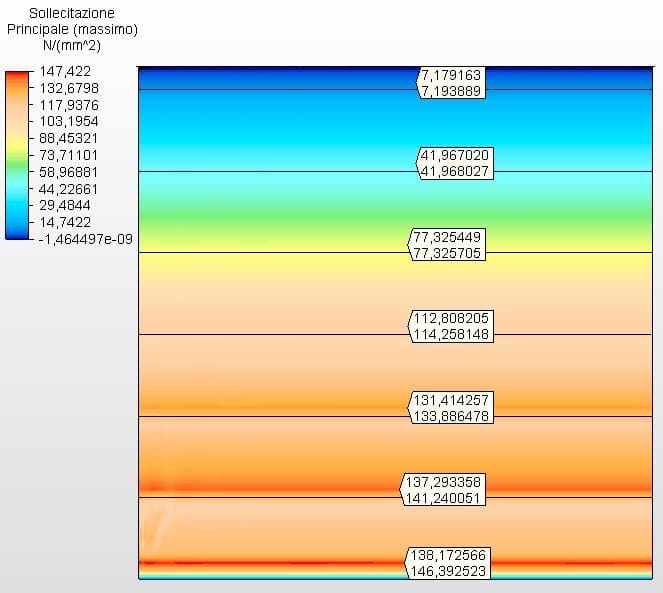
Les figures 21 et 22 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et supposées comme ferrule 1 avec 3,35 mm, ferrule 2 avec 2,65 mm, ferrule 3 avec 2,25 mm et l’autre avec 2,00 mm. La tension maximale de l’ambiance 1 était de 146,39 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 21 – Contraintes circonférentielles H/D 1.00 en 3D – épaisseurs calculées
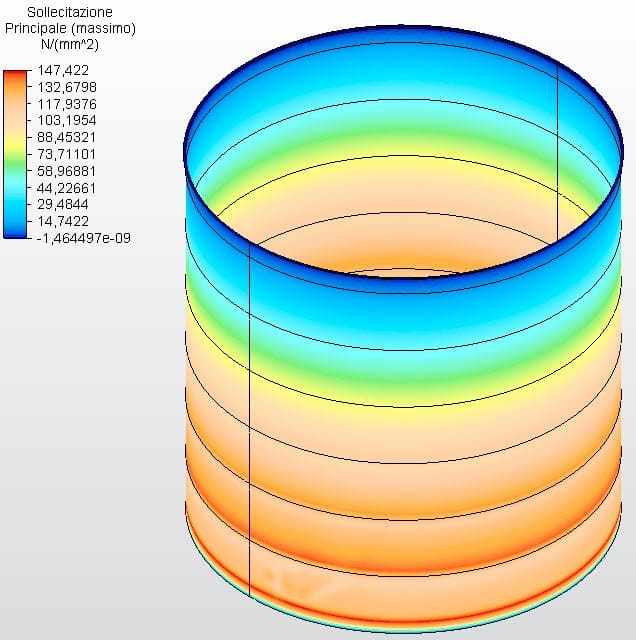
Figure 22 – Contraintes circonférentielles H/D 1.00 en 2D – épaisseurs calculées
La figure 23 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, dans ce cas 4,75 mm. La tension maximale était de 104,02 MPa.
Figure 23 – Contraintes circonférentielles H/D 1.00 en épaisseurs 2D-minimas
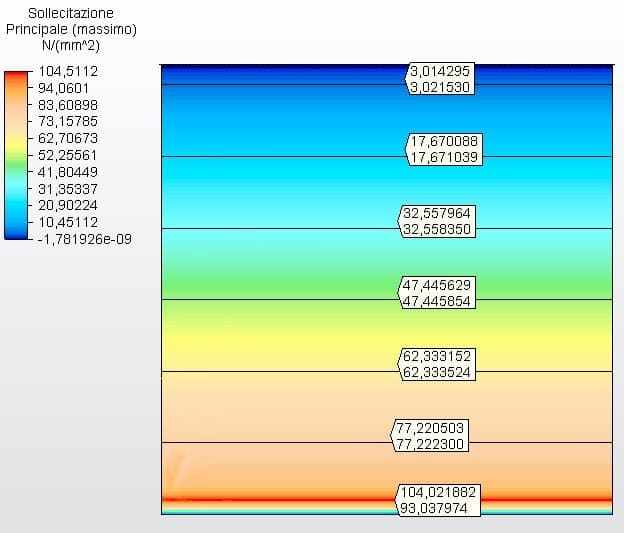
Source: L’auteur lui-même
La figure 24 montre les courbes de stress circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 24 – Courbes de contraintes circonférentielles du réservoir H/D 1,00
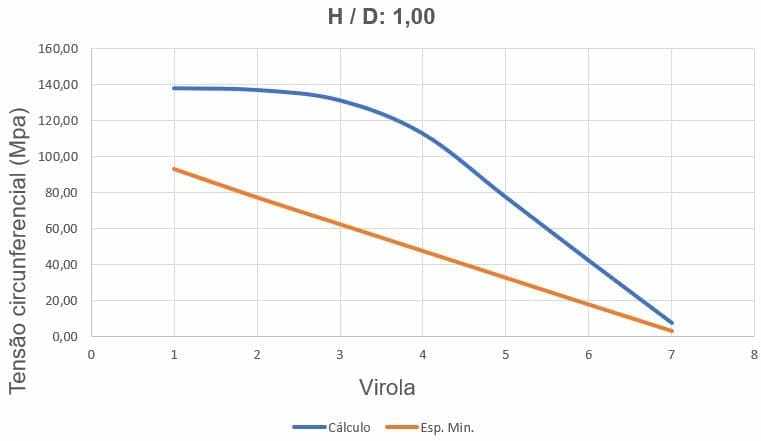
Source: L’auteur lui-même
4.5 RÉSERVOIR H/D = 0.50 – DIAMÈTRE 7.49 M ET HAUTEUR 14.98 M
Les figures 25 et 26 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et assumées comme ferrule 1 avec 4,25 mm, ferrule 2 avec 3,75 mm, ferrule 3 avec 3,35 mm, ferrule 4 avec 3,00, ferrule 5 avec 2,65 mm et l’autre avec 2,00 mm. La tension maximale de l’ambiance 1 était de 146,86 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 25 – Tensions circonférentielles H/D 0,50 en 3D – épaisseurs calculées
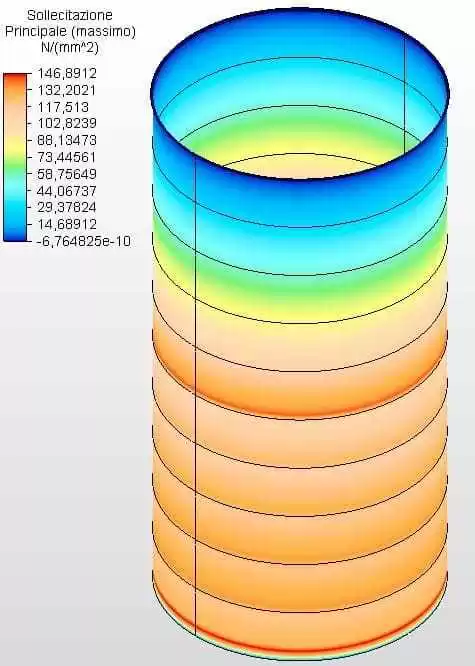
Figure 26 – Contraintes circonférentielles H/D 0,50 en 2D – épaisseurs calculées

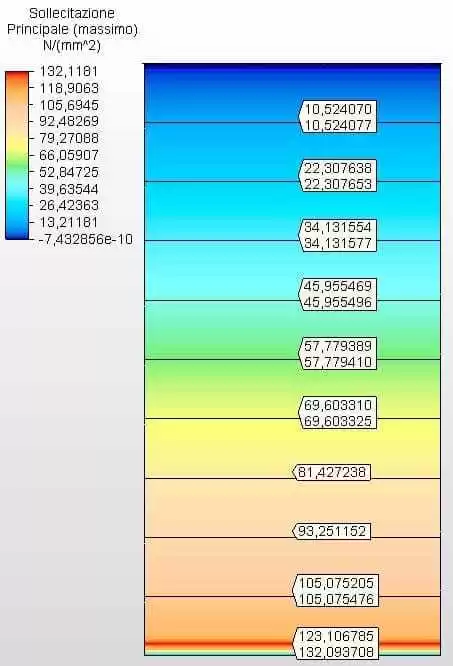
La figure 27 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, au cas où 4,75 mm. La tension maximale était de 132,09 MPa.
Figure 27 – Tensions circonférentielles H/D 0,50 en épaisseurs 2D-minimas
La figure 28 montre les courbes des contraintes circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 28 – Courbes des contraintes circonférentielles du réservoir H/D 0,50
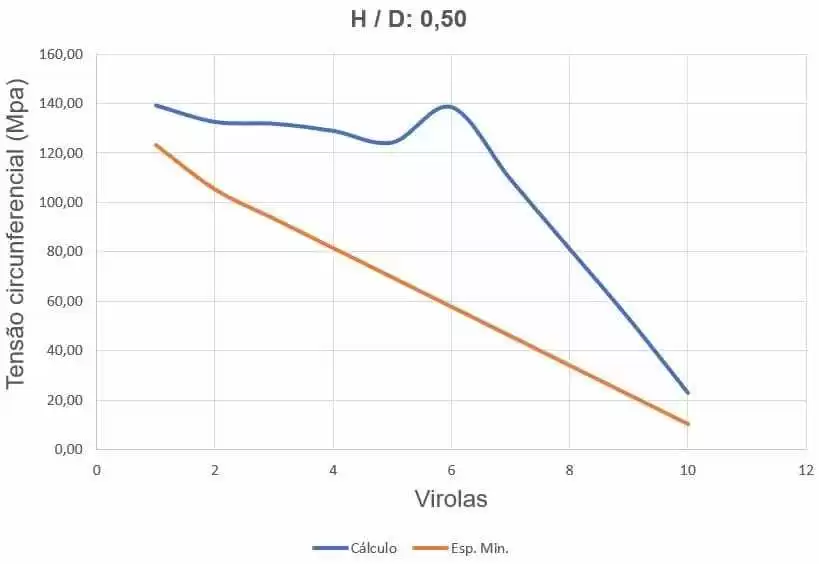
Source: L’auteur lui-même
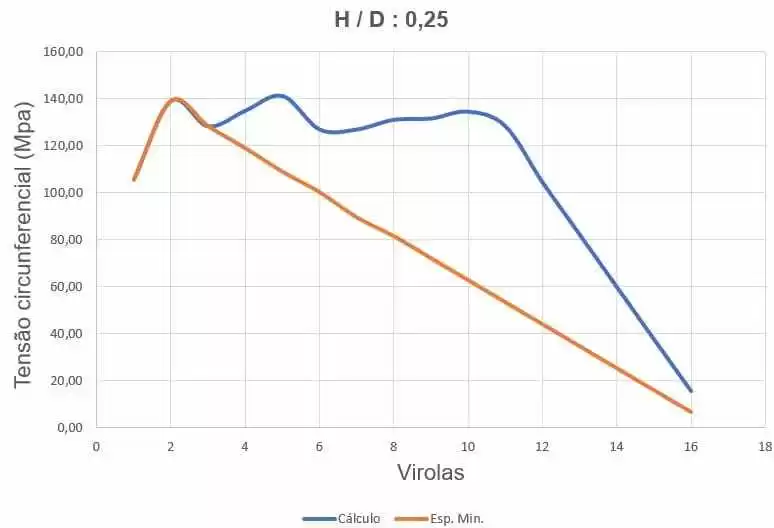
4.6 RÉSERVOIR H/D = 0.25 – DIAMÈTRE 5.94 M ET HAUTEUR 23.77 M
Les figures 29 et 30 montrent les contraintes circonférentielles avec les épaisseurs du réservoir calculées selon l’équation 1 et supposées comme ferrule 1 avec 6,35 mm, ferrule 2 avec 4,75 mm, ferrule 3 avec 4,25 mm, ferrule 4 avec 4,25, ferrule 5 avec 3,75 mm, ferrule 6 avec 3,75 mm, ferrule 7 avec 3,35 mm, ferrule 8 avec 3,00 mm , ferrule 9 avec 2,65 mm, ferrule 10 avec 2,25 mm et l’autre avec 2,00 mm. La tension maximale de l’ambiance 1 était de 129,72 Mpa, inférieure au stress autorisé de l’acier ASTM A36 de 160,00 Mpa, selon le tableau 5-2 de l’API 650.
Figure 29 – Contraintes circonférentielles H/D 0,25 en 3D – épaisseurs calculées
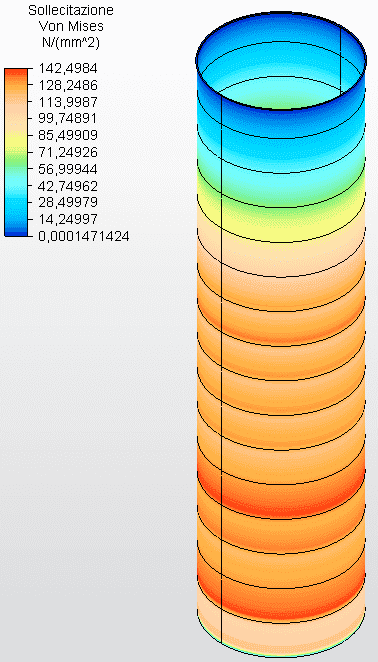
Figure 30 – Contraintes circonférentielles H/D 0,25 en 2D – épaisseurs calculées
La figure 31 montre les contraintes circonférentielles avec les épaisseurs du réservoir calculées en fonction des épaisseurs minimales de l’API 650, dans ce cas 6,35 mm. La tension maximale était de 129,72 MPa.
Figure 31 – Contraintes circonférentielles H/D 0,25 en épaisseurs 2D-minimas

Source: L’auteur lui-même
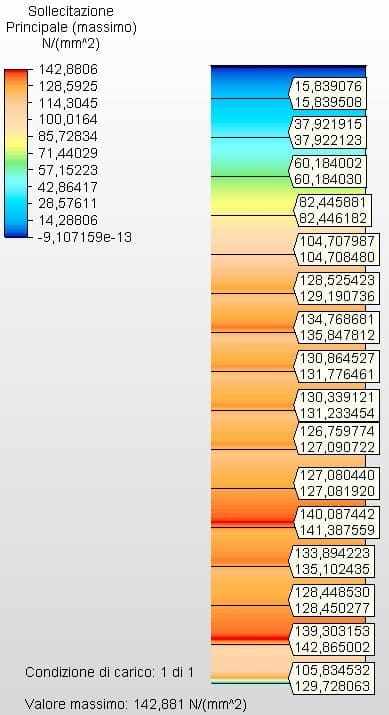
La figure 32 montre les courbes des contraintes circonférentielles, selon l’épaisseur des ferrules et la hauteur de chargement de l’eau.
Figure 32 – Courbes des circonférences du réservoir H/D 0,25
4.7 COURBE OPTIMALE DE BANDE DE PLEIN POIDS X H/D
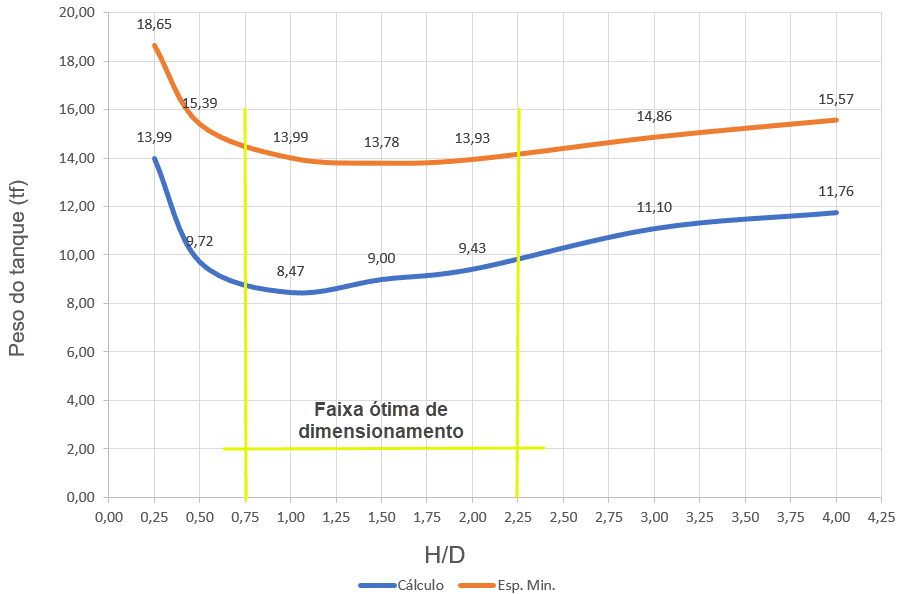
La figure 33 montre les courbes de poids typiques en fonction du H/D, pour les réservoirs sans abri, d’épaisseurs variables, dimensionnées selon la prescription de l’API 650, avec application de l’équation 1 (courbe rouge) et des épaisseurs minimales (courbe bleue).
La plage optimale, pour les deux critères de dimensionnement, se situe entre H/D = 0,75 à H/D = 2,25.
Figure 33 – Courbes de poids typiques des réservoirs pour sans-abri en fonction du rapport H/D.
Source: L’auteur lui-même
5. CONCLUSION
D’après les résultats présentés, il est conclu qu’il est possible, pour la réserve d’eau, d’établir des ratios H/D optimaux qui indiquent un poids minimum du réservoir, même compte tenu des 2 critères de dimensionnement, c’est-à-dire des épaisseurs avec seulement l’application de l’équation 1 et des épaisseurs tenant compte des épaisseurs minimales prescrites par l’API 650.
Pour la dimensionnement des réservoirs métalliques pour la réserve d’eau, lorsque les critères de sécurité pour les incendies et les explosions ne s’appliquent pas, l’utilisation de dimensionnement avec seulement les épaisseurs déterminées par l’équation 1 peut être acceptable, parce que les contraintes de circonférence déterminées par la MEF (Méthode des éléments finis) étaient toujours inférieures au stress admissible établi dans le tableau 5-2 de l’API 650.
RÉFÉRENCES
AMERICAN PETROLEUM INSTITUTE. API Standard 650: Welded steel tanks for oil storage. 12 th ed. Washington DC, 20013.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7821 – Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro. 1983.
AZZUMI, E., GUZEY, S. Comparison of the shell design methods for cylindrical liquid storage tanks. Engineering Structures 101. 2015.
BARROS, S. M. Tanques de armazenamento. Universidade Petrobras. Rio de Janeiro. 2010.
HECKE, M. B. Elementos finitos aplicados à engenharia de estruturas. Reservatórios cilíndricos e silos metálicos. Universidade Federal do Paraná. Curitiba. 2010.
KUAN, S. Y. Design, Construction and Operation of the Floating Roof Tank. University of Soutthern Queensland. Queensland. 2009.
NUNES, C. P. Uma metodologia de projetos de tanques atmosféricos verticais para armazenamento de petróleo e seus derivados. Monografia. Escola de Engenharia da Universidade Federal do Rio Grande do Sul. Porto Alegre. 2013.
RONCETTI, L. Otimização estrutural e econômica de tanques de armazenamento construídos em aço. Anais do 66º Congresso Anual da Associação Brasileira de Metalurgia e Materiais – ABM. São Paulo. 2011.
SATO, A. K. Projeto de um tanque de armazenamento atmosférico com teto flutuante para estocagem de gasolina. Trabalho de graduação. Faculdade de Engenharia do Campus de Guaratinguetá, UNESP. Guaratinguetá, 2015.
ZICK L.P., MCGRATH R.V. Design of large diameter cylindrical shells. Proc. Division Refining, AMERICAM PETROLEUM INSTITUTE. New York. 1968.
[1] Maîtrise en structures et construction civile; Spécialisation dans les constructions industrielles; Spécialisation en génie environnemental; Spécialisation en ingénierie de la sécurité; Ingénieur civil et ingénieur d’opération mécanique.
[2] Spécialisation en génie structurel et génie civil.
[3] Ingénieur civil.
Envoyé : Avril, 2020.
Approuvé : mai 2020.