ARTICOLO ORIGINALE
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Alternative strutturali in fondi sospesi di serbatoi metallici tubolari con due celle per l’accumulo dell’acqua. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 06, Vol. 12, pp. 111-135. giugno 2020. ISSN: 2448-0959, Collegamento di accesso: https://www.nucleodoconhecimento.com.br/ingegneria-civile/alternative-strutturali
RIEPILOGO
Con la crescente domanda di riserva idrica dovuta alla realizzazione di nuovi lotti e condomini orizzontali, che soddisfacevano la necessità della pressione dinamica minima di 100 kPa, i serbatoi iniziarono ad avere divisioni fisiche interne (celle verticali) la cui cella superiore ha la quota inferiore sospesa ad un’altezza che garantiva la pressione manometrica necessaria per soddisfare questo standard. A causa della mancanza di standard tecnici brasiliani specifici per lo stoccaggio dell’acqua in un serbatoio metallico, è stato utilizzato come parametro di dimensionamento per serbatoi metallici con diverse celle verticali di stoccaggio dell’acqua, l’AWWA D100 nella sua interezza o solo parzialmente, principalmente a causa degli sforzi assiali nelle coste (virolas) per determinare le sollecitazioni ammissibili all’instabilità (FL). Questo articolo affronta il problema della scelta del tipo più appropriato di fondo metallico verticale sospeso e commissiona i risultati di cinque diversi tipi di fondi, dimensionati secondo AWWA D100-05. All’interno della tipologia dei 5 fondi analizzati, il fondo più economico è stato il fondo sferico segmentato.
Parole chiave: serbatoio metallico, standard AWWA D100, fondi sospesi.
1. INTRODUZIONE
Questo articolo affronta il problema della scelta del tipo più appropriato di fondo metallico verticale sospeso e commissiona i risultati di cinque diversi tipi di fondi, dimensionati secondo AWWA D100-05.
Con l’implementazione di nuove suddivisioni e condomini orizzontali grazie agli incentivi della politica abitativa del governo, principalmente grazie al programma abitativo del Ministero delle Città, Minha Casa Minha Vida Program (Pereira, 2017), che ha causato un forte aumento della domanda di serbatoi di stoccaggio. acqua potabile, prevalentemente aerea (above ground), cilindrica e di diametro e altezza variabile, denominata castello d’acqua.
A causa della necessità di una pressione dinamica minima nella rete pubblica di approvvigionamento, che secondo NBR 12.218/1994, deve essere di 100 kPa (10,20 m.c,a.), i serbatoi hanno ora divisioni fisiche interne (celle verticali) la cui cella superiore ha la dimensione inferiore sospesa ad un’altezza che garantiva la pressione manometrica necessaria per soddisfare questo standard, poiché normalmente le quote terrestri non offrono il supporto del serbatoio.
Secondo Trees (1911), i fondi dei serbatoi metallici sospesi possono essere di vari tipi, come piatti, conici e sferici o sferici segmentati.
Visal (2017) afferma che i serbatoi di stoccaggio operano senza pressione (o molto poco), chiamati serbatoi atmosferici, differenziandoli dai recipienti a pressione. Di solito sono di forma cilindrica, perpendicolari al terreno con un fondo piatto e un soffitto fisso o galleggiante.
La progettazione e la costruzione di serbatoi cilindrici atmosferici richiedono la conoscenza di specifici standard tecnici, materiali e manodopera appropriati per ogni tipo di applicazione e comportano una serie di altre cure speciali perché anomalie e irregolarità in queste apparecchiature possono causare grandi perdite finanziarie o addirittura perdite di vite umane (Nunes, 2013).
Secondo Gomes (2017), gli standard comunemente utilizzati in Brasile per progetti e costruzioni di serbatoi metallici sono NBR 7821, API 650 e AWWA D100.
NBR 7821/1983 – I serbatoi di acciaio saldati per lo stoccaggio di petrolio e derivati, dell’Associazione brasiliana degli standard tecnici (ABNT) e dello standard normativo americano API 650 – 2013 – Welded Steel Tanks for Oil Storage – dell’American Petroleum Institute (API), sono specifici della riserva di petrolio e derivati.
Lo standard AWWA D100-05 – Welded Carbon Steel Tanks for Water Storage delle American Water Works Associations mira a fornire requisiti minimi per la progettazione, la costruzione, l’ispezione e il collaudo di nuovi serbatoi saldati in acciaio al carbonio per lo stoccaggio dell’acqua a pressione atmosferica.
Nell’ambito dei requisiti di dimensionamento, l’AWWA D100 presenta tre metodi per determinare la sollecitazione di deformazione ammissibile (FL) per le sezioni cilindriche, che consente la verifica della massima sollecitazione di compressione dovuta al carico assiale e al carico assiale dovuto al carico del vento applicato alle coste.
A causa della mancanza di standard tecnici brasiliani specifici per lo stoccaggio dell’acqua in un serbatoio metallico, è stato utilizzato come parametro di dimensionamento per serbatoi metallici con diverse celle verticali di stoccaggio dell’acqua, l’AWWA D100 nella sua interezza o solo parzialmente, principalmente a causa degli sforzi assiali nelle coste (virolas) per determinare le sollecitazioni ammissibili all’instabilità (FL).
2. OBIETTIVI
Obiettivo generale
L’obiettivo generale di questo articolo è il dimensionamento di diversi tipi di fondi sospesi della cella verticale superiore del serbatoio metallico composta da due celle, all’interno delle raccomandazioni di AWWA D100-05, utilizzando il software Autodesk Simulation Mechanical 2018.
Obiettivi specifici
Gli obiettivi specifici sono:
- Determinare le sollecitazioni assiali nei lati della cella inferiore del serbatoio metallico, risultanti dai carichi assiali e laterali e confrontarle con la tensione di instabilità ammissibile secondo le disposizioni di AWWA D100 – 05 3.4 – Column, Strut, and Shell Stability Formulas.
- Determinare gli spostamenti verticali degli sfondi sospesi.
- Determinare il peso totale dei fondi sospesi proposti quantificando l’area e gli spessori delle piastre di dimensioni e delle strutture di supporto.
3. MATERIALE E METODO
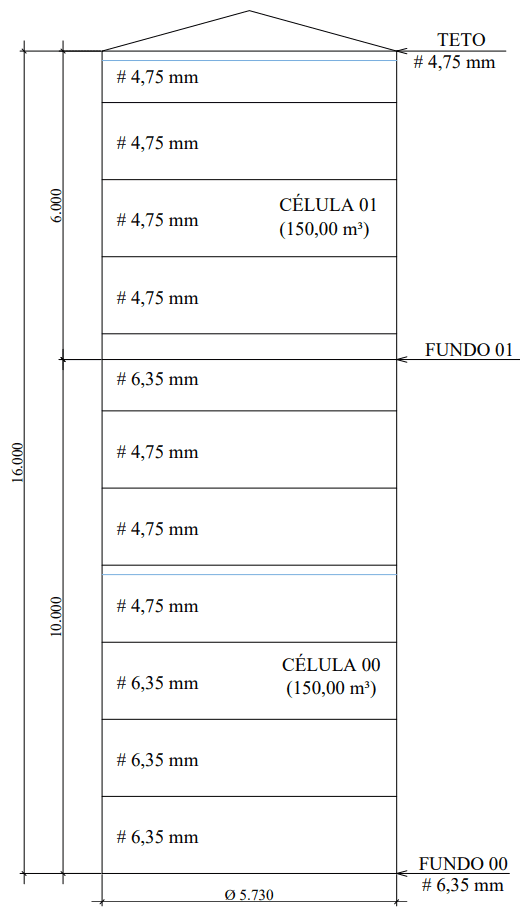
Il serbatoio presentato in questo articolo è un serbatoio metallico, per riserva d’acqua, composto da due celle, con una capacità di 150,00 m³ ciascuna (totale di 300,00 m³), con coperchio del cono metallico (Figura 1), con cinque tipi di fondi sospesi (Figure 2A; 2B; 2C; 2D e 2E).
Figura 1: Serbatoio metallico di due celle con una capacità di 300,00 m³.

Tipologia dei 5 fondi sospesi proposti:
Figura.: 2A – Travi radiali a fondo piatto e albero
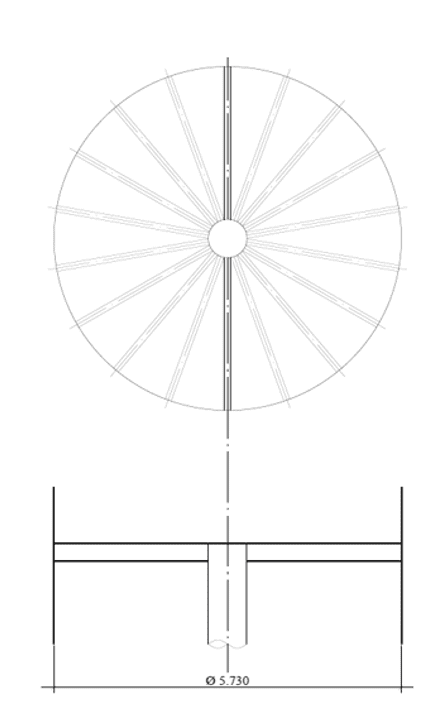
Fonte: L’autore stesso
Figura.: 2B – Travi radiali a fondo piatto senza albero
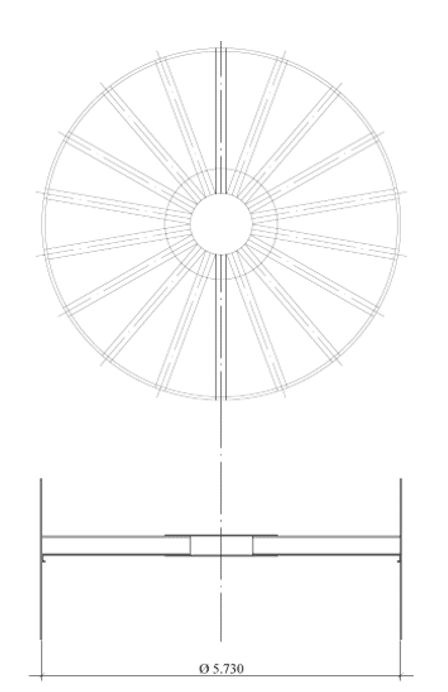
Fonte: L’autore stesso
Figura.: 2C – Travi ortogonali a fondo piatto
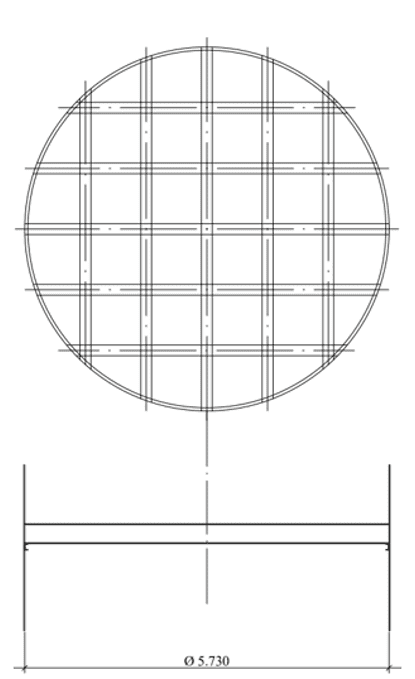
Fonte: L’autore stesso
Figura.: 2D – Sfondo conico
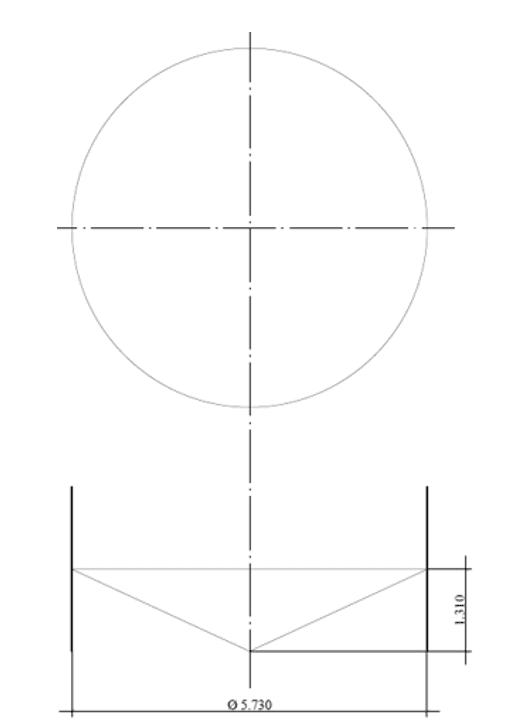
Figura.: 2E – Sfondo sferico segmentato
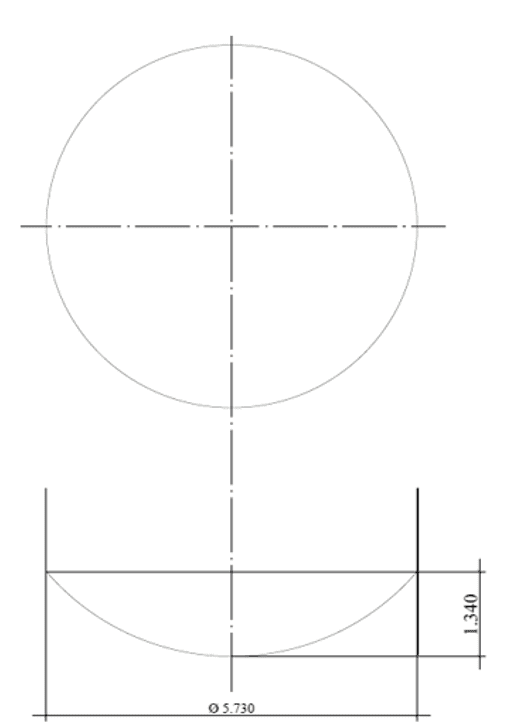
Le azioni considerate sono quelle del vento, dell’acqua immagazzinata (azione idrostatica), del sovraccarico del soffitto e del peso della struttura stessa (Figura 3A), rilasciata nel software Autodesk Simulation Mechanical.
Figura 3A – Caricamenti
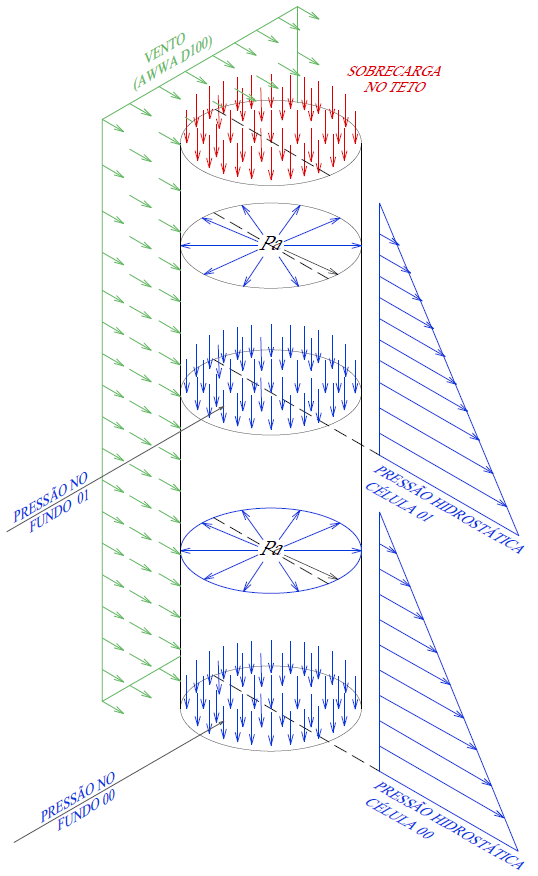
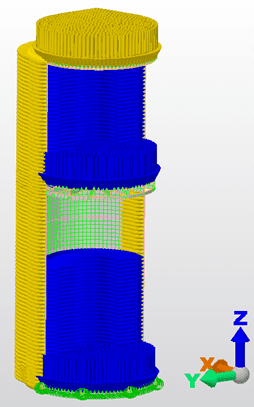
Figura 3B – Avvio dei caricamenti nel software
Secondo Andrade junior (1998), l’azione del vento è calcolata secondo NBR 6123 – Forze dovute al Veto negli edifici (1987) e, come regola generale, si presume che il vento possa agire in qualsiasi direzione orizzontale. Poiché la struttura del serbatoio è asimmetrica rispetto all’asse Z, perpendicolare alla direzione del vento, si ritiene che il vento possa concentrarsi perpendicolarmente su qualsiasi geratriz del serbatoio.
La componente statica della pressione del vento, che agisce perpendicolarmente su un elemento di area, è data da:
 I coefficienti di pressione esterni Cpe sono espressi per il tipo di corpo della struttura, assumendo per l’applicazione di AWWA D100-05 che Cpe = Cf (Tabella 1).
I coefficienti di pressione esterni Cpe sono espressi per il tipo di corpo della struttura, assumendo per l’applicazione di AWWA D100-05 che Cpe = Cf (Tabella 1).
Dove q è la pressione del vento in un punto in cui si verifica il ristagno d’aria, ottenuta dall’espressione 2: La velocità V0 è chiamata velocità di base, corrisponde a una raffica di 3 secondi, esercitata in media una volta in 50 anni, misurata 10 m dal suolo, in un luogo piatto e aperto. NBR 6123 (1987) presenta gli isopletas di base, in m/s. Per i nostri esempi, È stato adottato V0 = 40 m/s.
La velocità V0 è chiamata velocità di base, corrisponde a una raffica di 3 secondi, esercitata in media una volta in 50 anni, misurata 10 m dal suolo, in un luogo piatto e aperto. NBR 6123 (1987) presenta gli isopletas di base, in m/s. Per i nostri esempi, È stato adottato V0 = 40 m/s.
Il fattore topografico S1 viene utilizzato per valutare il rilievo del terreno intorno all’edificio e adottato pari a 1,0 per i nostri esempi.
Il fattore S2 considera l’effetto combinato della rugosità del terreno, della variazione della velocità del vento con l’altezza sopra il terreno e delle dimensioni dell’edificio. Il fattore S2 si ottiene attraverso l’espressione 4:
Dove: Z = altezza fuori terra, Fr = fattore di raffica di vento, b = parametro meteorologico, p = funzione di rugosità del terreno e intervallo di tempo. Per l’altezza del serbatoio di 16,0 m, rugosità II, classe A, si ha S2 = 1,05.
Il fattore S3 è un fattore statistico che considera il grado di sicurezza richiesto e la vita utile della struttura, considerando gli impianti di serbatoi a basso fattore di occupazione umana (Andadre Junior, 1998), è stato utilizzato il valore di 0,95.
Secondo Haffez et al (2011), si presume che i serbatoi siano sottoposti a pressione del vento uniforme (q), agendo lungo l’asse Z, come mostrato nelle figure 3rd e 3B. AWWA D100-05 raccomanda l’uso del coefficiente di resistenza aerodinamica (Cf), a seconda della forma della struttura, secondo la tabella 1. Per i serbatoi tubolari di forma cilindrica, il Cf adottato è 0,6.
Tabella 1 – Coefficiente di resistenza aerodinamica amica Cf

Fonte: AWWA D100-05
Avere:
Vk = 40 . 10 . 1,05 . 0,95 = 39,90 m/s
q = 0,613 . 39,902 = 975,90 N/m² ou 99,51 kgf/m²
Δp = 0,6 . 975,90 = 585,54 N/m² ou 58,71 kgf/m².
L’azione idrostatica genera effetti che agiscono nelle direzioni radiale e verticale e si traducono in pressione laterale sul lato e pressione sul fondo del serbatoio.
Il sovraccarico di progettazione applicato al soffitto, secondo l’articolo 3.1.3.2 di AWWA D100-05, dovrebbe essere di 750 N/m² (15 lb/ft²).
Il proprio peso della struttura viene rilasciato automaticamente dal software Autodesk Simulation Mechanical 2018, considerato il peso specifico degli acciai utilizzati nel dimensionamento del serbatoio.
Lo spessore delle ferole di pressione ferolina dovute alla pressione idraulica del serbatoio deve essere calcolato secondo l’equazione sec 3-40. 3.7 AWWA D100-05 – Cylindrical Shell Plates (equazione 7): Dove:
Dove:
t = spessore del design dello scafo (ferrule), in mm
hp = altezza del liquido, in m
D = diametro serbatoio, in m
S = Tensione in acciaio ammissibile, in Mpa
E = Efficienza di saldatura
G = Peso liquido specifico (per acqua = 1)
Lo spessore minimo del trefolo cilindrico a contatto con l’acqua deve essere in linea con la tabella 2 secondo la sec. 3.2 di AWWA D100-05. Per il serbatoio di diametro nominale di 5,73 m, lo spessore minimo prescritto è di 4,76 mm.
Tabella 2 – Coefficiente di resistenza aerodinamica Cf
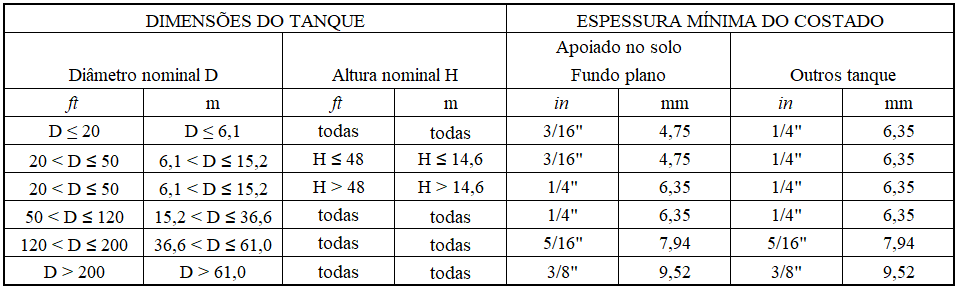
Fonte: AWWA D100-05
AWWA D100-05 classifica i materiali strutturali da utilizzare nei serbatoi in 3 classi, a seconda del limite di portata (Fy). La tabella 3 illustra questa classificazione.
Tabella 3 – Classe di materiali in funzione di Fy
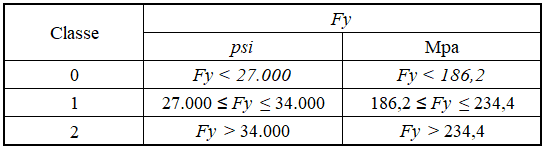
Fonte: AWWA D100-05
Il materiale utilizzato nelle coste, inferiore e soffitto è ASTM A36, caratterizzato da un modulo di elasticità (E) pari a 205.000 Mpa, coefficiente di Poisson (μ) uguale a 0,30, densità (γ) di 77.000 N/mm³, tensione di flusso fy = 250,00 Mpa e ultima tensione di fu = 400,00 Mpa. Il materiale utilizzato nelle strutture di supporto dei fondi sospesi (travi W e C) è l’ASTM A572 (grado 50) con tensione di flusso fy = 345,00 Mpa e ultima tensione fu = 450,00 Mpa. Sono classificati come materiale di classe 2.
La tabella 4 mostra le principali sollecitazioni ammissibili prescritte dall’AWWA D100-05, a seconda della classe di materiali e applicazioni nei serbatoi.
Tabella 4 – Tensioni ammissibili nelle applicazioni
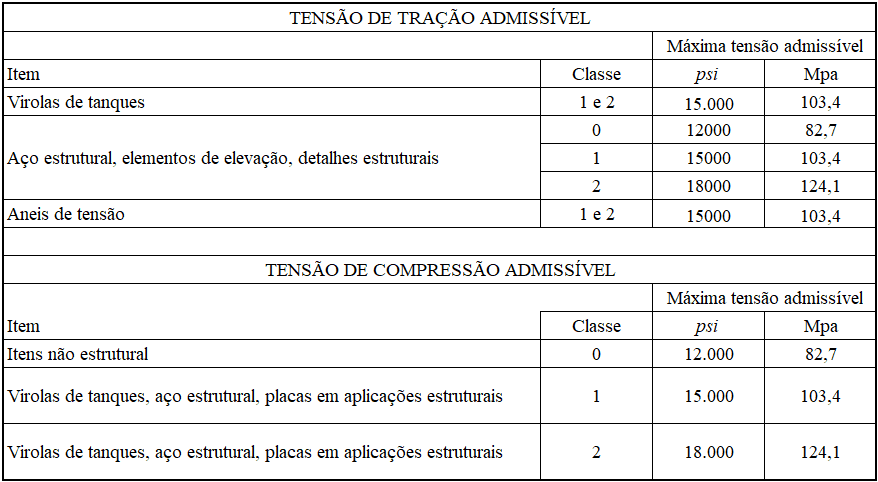
Fonte: AWWA D100-05 – modificata dall’autore.
Per la verifica della stabilità dovuta all’instabilità della costa del serbatoio, l’AWWA D100-05 prescrive 3 metodi di analisi. Per questo lavoro è stato utilizzato il metodo 1, che è una procedura semplificata basata su tecniche di analisi a membrana. Per i materiali di classe 2, il rapporto spessore/raggio del serbatoio al quale l’instabilità passa da elastico a anelastico (t/R)c è 0,0025372. La sollecitazione ammissibile per l’instabilità per il materiale di classe 2 è data dalle seguenti formule:
Quando 0 ≤ t/R ≤ (t/R)c significa che l’instabilità si verifica nel regime elastico e lo stress ammissibile per l’instabilità è dato dall’equazione 8: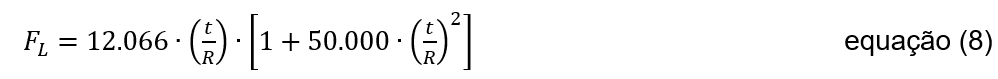
Quando (t/R)c ≤ t/R ≤ 0,0125 significa che l’instabilità si verifica nel regime anelastico e lo stress ammissibile per l’instabilità è dato dall’equazione 9:
Quando t/R > 0,0125, significa che l’instabilità si verifica in plastica e lo stress consentito per l’instabilità è costante e vale:![]() Tabella 5 – I valori di efficienza di saldatura sono presentati parzialmente da Table 15 Weld design values– tank plate joints, dove sono stati presentati solo i valori di saldatura continua. Per il lavoro su tela è stata considerata la saldatura a doppio smusso frontale con riempimento completo.
Tabella 5 – I valori di efficienza di saldatura sono presentati parzialmente da Table 15 Weld design values– tank plate joints, dove sono stati presentati solo i valori di saldatura continua. Per il lavoro su tela è stata considerata la saldatura a doppio smusso frontale con riempimento completo.
Tabella 5 – Valori di efficienza della saldatura in %

Fonte: AWWA D100-05 – modificata dall’autore.
4. RISULTATI
La modellazione e l’analisi numeriche sono state fatte utilizzando un software commerciale di analisi e progettazione strutturale Autocad Simulation Mechanical 2018. Ogni ferrule del serbatoio è stato modellato come un elemento guscio con spessori di design costanti, con proprietà isotropiche e con un piano medio posizionato centralmente. Nella parte superiore del serbatoio, c’è un anello verticale circolare modellato con profilo L rigidamente attaccato agli elemnetos. Le dimensioni degli elementi finiti sono 0,20 x 0,20 m (discretizzazione). Per ogni tipo di serbatoio, in base alla tipologia di ogni fondo sospeso, è stato creato un modello di elemento finito 3D (Figura 4).
Figura 4: Serbatoio metallico discretizzato

Fonte: L’autore stesso
Partendo dallo spessore minimo secondo la tabella 2, per il dimensionamento del trefolo è stato verificato anche lo spessore dovuto alla pressione circonferenziale, utilizzando l’equazione (7) e lo spessore dovuto all’instabilità, con la determinazione della sollecitazione ammissibile (FL), utilizzando le equazioni (8) e (9) e le sollecitazioni assiali dei trefoli determinate dal software di sSimulation Mechanical e confrontate con le sollecitazioni ammissibili calcolate (FL). ́ Lo spessore richiesto di ogni ferrule è lo spessore più grande all’interno dei 3 criteri.
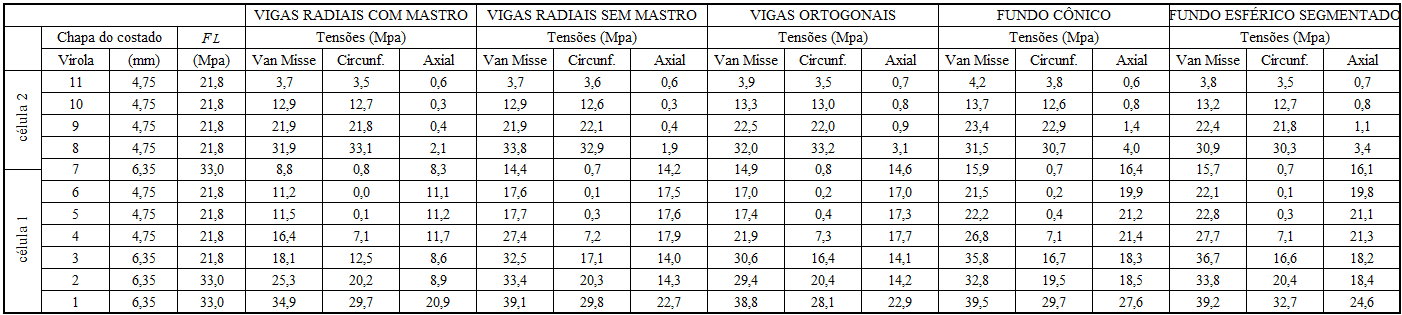
La tabella 6 mostra in dettaglio la Van Misse, la tensione circonferenziale e la tensione assiale in ogni ferrule dei 5 serbatoi studiati con diversi tipi di fondi sospesi.
Tabella 6 – Dimensionamento delle coste secondo AWWA D100 – 05
La figura 5 mostra il serbatoio con gli spessori richiesti per ogni ferrule del lato.
Figura 5: Serbatoio con gli spessori finali del trefolo
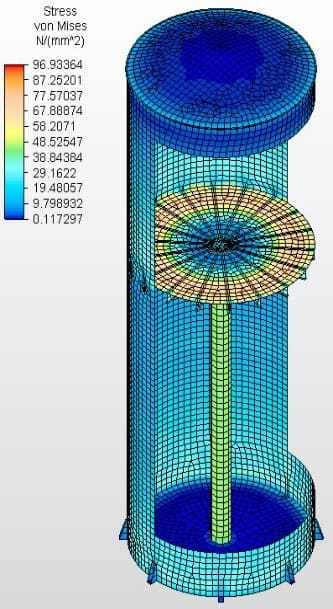
Le figure 6A, 6B, 6C e 6D mostrano i risultati delle analisi con sollecitazioni Van Misse, sollecitazioni circonferenziali e sollecitazioni assiali in ogni ferrule per il serbatoio con fondo della cella 2, con travi W radiali e albero centrale. I valori ottenuti sono stati alimentati nella tabella 6. Un’analisi uguale è stata fatta sugli altri 4 serbatoi che completano questo lavoro.
Figura. 6A: Tensioni van Misse nel taglio 3D
Fonte: L’autore stesso
Figura. 6B: Tensioni van Misse

Figura. 6C: Tensioni circonferenziali
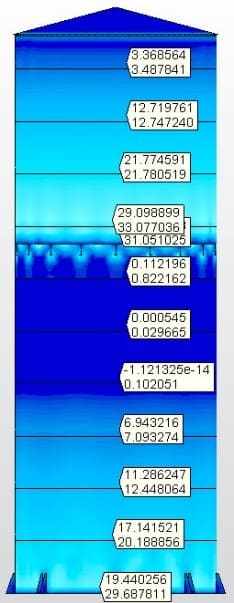
Figura. 6D: Ceppi assiali
I fondi sospesi analizzati in questo lavoro, ad eccezione del fondo con travi radiali e albero centrale (Figura 2A), sono stati progettati come autosostinte e supportati solo sul lato dei serbatoi. I risultati delle analisi sono presentati qui di seguito.
Il fondo sospeso con travi radiali tipo W e albero centrale, la cui geometria è mostrata nella figura 7, dove ha lo stesso diametro nominale del serbatoio, D = 5.730,00 mm, numero di travi di supporto = 18 pezzi, profilo del fascio W = 310 x 28,3, materiale del fascio W = ASTM A572 – grado 50, diametro dell’albero centrale = 640,00 mm, spessore dell’albero centrale = 6,35 mm, materiale centrale della piastra dell’albero = ASTM A36, spessore della piastra inferiore = 7,95 mm (5/16″), materiale della piastra inferiore = ASTM A36.
Carico inferiore = pressione idrostatica h = 5,80 m.c.a.
Figura 7: Layout di sfondo con travi radiali e albero centrale
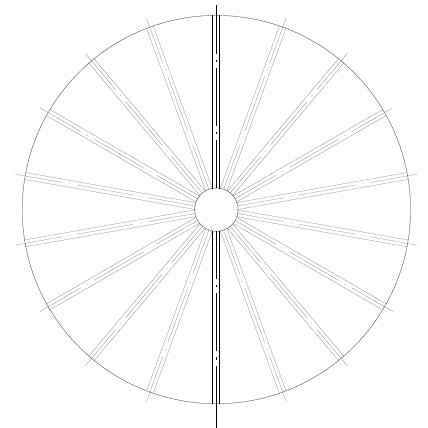
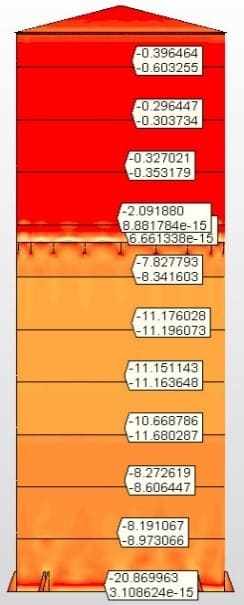
Le sollecitazioni sulla piastra inferiore e sulle travi di supporto sono riportate nelle figure 8A e 8B.
Figura 8A: Sollecitazioni sul fondo sospeso Tensione massima = 90,0 Mpa
Fonte: L’autore stesso
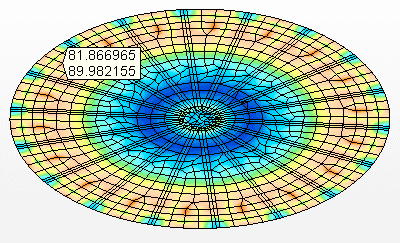
Figura 8B: Sollecitazioni sui fasci di supporto Tensione massima = 64,9 MPa

Fonte: L’autore stesso
Figura 8C: Offset verticali (mm)
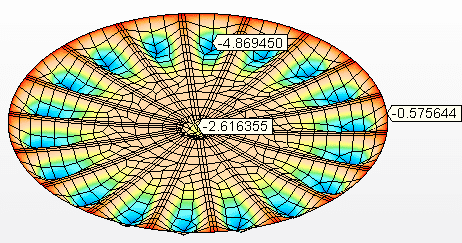
Figura 8D: Sollecitazioni assiali sull’albero Tensione massima = 37,6 Mpa

Il fondo sospeso con travi radiali di tipo W e senza centrale, la cui geometria è mostrata nella figura 9, dove ha lo stesso diametro nominale del serbatoio, D = 5.730,00 mm, numero di travi di supporto = 18 pezzi, profilo del fascio W = 310 x 44,5, materiale del fascio W = ASTM A572 – grado 50, fascio di supporto circonferenziale U 6″ prima anima, materiale del fascio U = ASTM A572 – grado 50, spessore della piastra inferiore = 7,95 mm (5/16″), materiale della piastra inferiore = ASTM A36.
Carico inferiore = pressione idrostatica h = 5,80 m.c.a.
Figura 9: – Layout di sfondo con travi radiali e senza albero
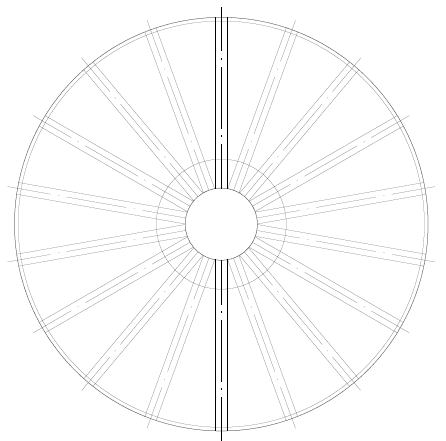
Figura 9A – Sollecitazioni sul fondo sospeso Tensione massima = 87,4 Mpa
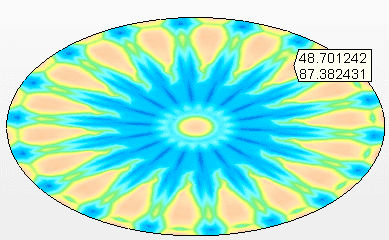
Fonte: L’autore stesso
Figura 9B – Sollecitazioni sui fasci di supporto Tensione massima = 89,2 MPa
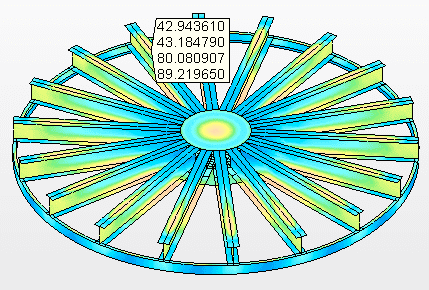
Fonte: L’autore stesso
Figura 9C – Offset verticali (mm)
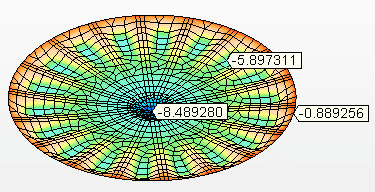
Fonte:o sospeso con travi ortogonali (griglia) tipo W e senza centrale, la cui geometria è mostrata nella figura 10, dove ha lo stesso diametro nominale del serbatoio, D = 5.730,00 mm, numero di travi di supporto = 10 pezzi, profilo del fascio W = 360 x 72, materiale del fascio W = ASTM A572 – grado 50, fascio di supporto circonferenziale U 6″ prima anima, materiale del fascio U = ASTM A572 – grado 50, spessore della piastra inferiore = 9,53 mm (3/8″), materiale della piastra inferiore = ASTM A36.
Carico inferiore = pressione idrostatica h = 5,80 m.c.a.
Figura 10: – Layout di sfondo con travi ortogonali (griglia) e senza albero
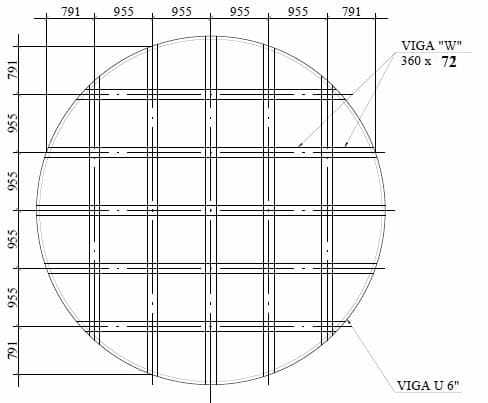
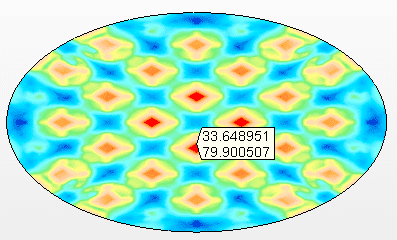
Figura 10A – Sollecitazioni sul fondo sospeso Tensione massima = 79,9 Mpa
Fonte: L’autore stesso
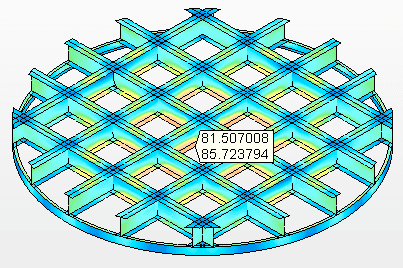
Figura 10B – Sollecitazioni sui fasci di supporto Tensione massima = 85,7 MPa
Fonte: L’autore stesso
Figura 10C – Offset verticali (mm)
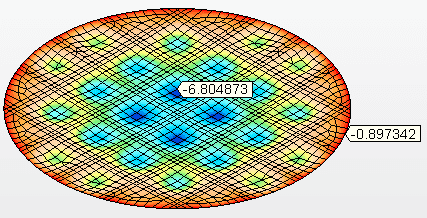
Il fondo sospeso a forma di cono, la cui geometria è mostrata nella figura 11 (taglio), dove ha lo stesso diametro nominale del serbatoio, D = 5.730,00 mm, spessore della piastra inferiore = 9,53 mm (3/8″), materiale della piastra inferiore = ASTM A36. Carico inferiore = pressione idrostatica h = 5,80 m.c.a.
Figura 11: – Schema inferiore affusolato in taglio
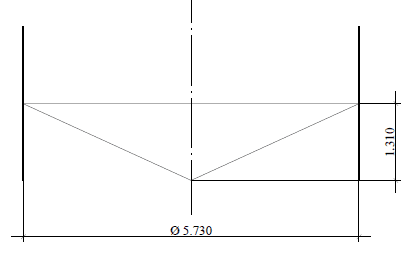
Fonte: L’autore stesso
Figura 11A – Sollecitazioni sul fondo sospeso Tensione massima = 90,8 Mpa
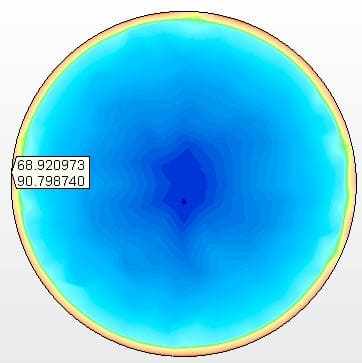
Fonte: L’autore stesso
Figura 11B – Spostamenti verticali (mm) Tensione massima = 7,359 mm
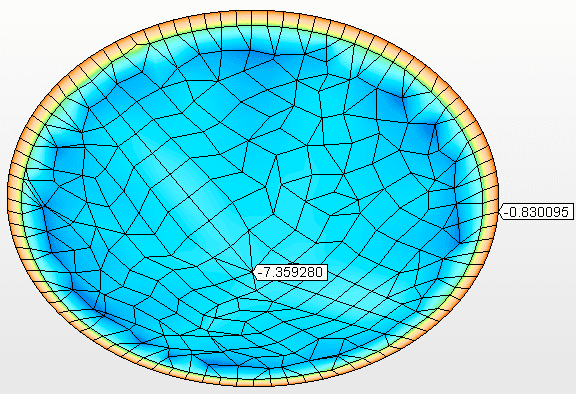
Il fondo sospeso in semisfere o in formato inferiore sferico segmentato la cui geometria è mostrata nella figura 12 (taglio), dove ha lo stesso diametro nominale del serbatoio, D = 5.730,00 mm, spessore della piastra inferiore = 4,75 mm (3/16″), materiale della piastra inferiore = ASTM A36. Carico inferiore = pressione idrostatica h = 5,80 m.c.a.
Figura 12: – Schema dello sfondo sferico segmentato.
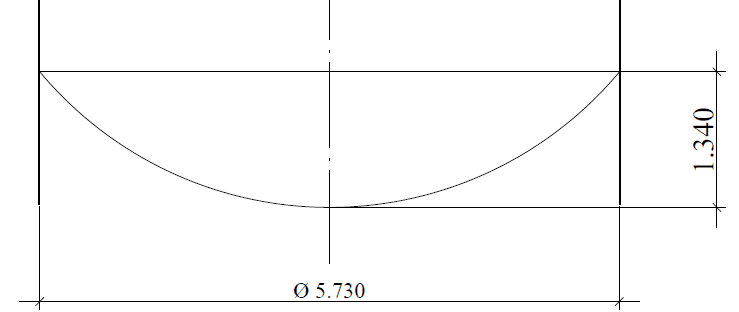
Figura 12A – Sollecitazioni sul fondo sospeso Tensione massima = 88,32 Mpa

Fonte: L’auto8,32 Mpa
Figura 12B – Spostamenti verticali (mm) Tensione massima =7,359 mm
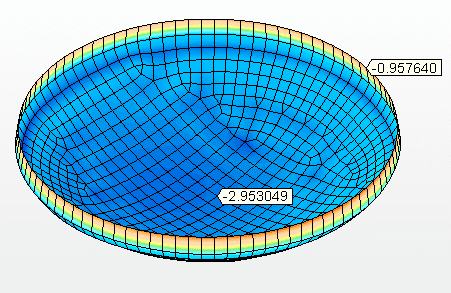
Fonte: L’autore stesso
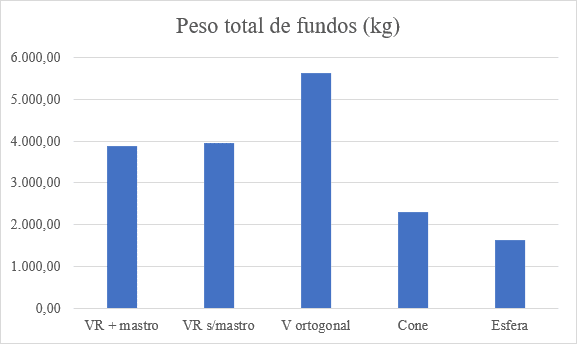
I pesi dei fondi sospesi sono stati calcolati senza determinare ritagli o l’uso di lembi e avanzi, calcolando solo le superfici delle lastre moltiplicate per peso / m². La tabella 7 mostra il riepilogo generale dei pesi dei 5 tipi di fondi sospesi e queste differenze si possono vedere nel grafico del peso totale x tipo di fondo nella figura 13.
Tabella 7 – Pesi dei fondi sospesi

Figura 13 – Raffronti dei pesi dei fondi
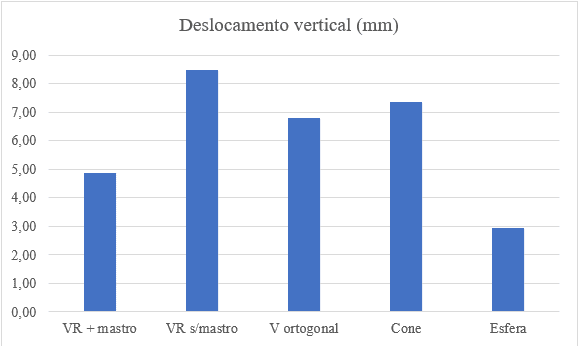
Gli offset massimi verticali dei fondi sospesi sono mostrati comparativamente nella figura 14.
Figura 14 – Raffronti degli spostamenti massimi verticali
5. CONCLUSIONI
Dai risultati ottenuti, si conclude che il fondo di sospensione sferica segmentata è il più economicamente sostenibile e anche il più tecnicamente raccomandato, perché presenta il più piccolo spostamento verticale, in pieno carico.
Anche il fondo sospeso di tipo cono è economicamente redditizio ma ha uno spostamento verticale sotto carico un po ‘eccessivo e dovrebbe essere controllato se interferisce con i tubi. Lo spostamento verticale potrebbe essere ridotto con l’uso di piastre di rinforzo triangolari, sostenendo il fondo sui lati laterali.
Il fondo sospeso sorretti da travi ortogonali è totalmente antieconomico.
RIFERIMENTI
ABNT – Associação Brasileira de Normas Técnicas, NBR 7.821, Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro, RJ. Abril de 1983.
ABNT – Associação Brasileira de Normas Técnicas, NBR 6.123, Forças devido ao vento em edificações. Rio de Janeiro, RJ. Junho de 1988.
ABNT – Associação Brasileira de Normas Técnicas, NBR 12.218, Projeto de rede de distribuição de água para abastecimento público. Rio de Janeiro, RJ. Julho de 1994.
ANDRADE JUNIOR, L. J. Análise estrutural das chapas metálicas de silos e reservatórios cilíndricos. Dissertação de mestrado. Escola de Engenharia de São Carlos. Universidade de São Paulo, 1998.
API – American Petroleum Institute, API 650, Welded Steel Tanks for Oil Storage, decima terceira edição, Washington D. C., Março de 2013.
AWWA – American Water Works Association, AWWA D100-05, Welded Steel Tanks for Water Storage. Edição atualizada. Denver, Colorado. Maio 2005.
GOMES, E. F. Soldagem em reservatórios metálicos para armazenamento de água. Trabalho de conclusão de curso. Curso de especialização em Engenharia de soldagem. Universidade Federal de Minas Gerais, 2017.
HAFEEZ, G., EL ANSARY, A. M. & EL DAMATTY, A. A. Effects of winds load son the stability of conical tanks. Can. J. Civ. Eng. 38, Published by NCR Research Press, 2011.
PEREIRA, P. M. F. Análise dos conjuntos habitacionais do programa Minha Casa, Minha Vida na cidade de Monte Alegre de Minas- MG. Dissertação de mestrado. Faculdade de Geografia. Universidade Federal de Uberlândia, 2017.
TREES, M. J. Design of elevated steel tanks. Thesis. University of Illinois, Urbana-Champaign, 1911.
VISAL, B. & SIBIN, B. Design and analysis of storage tanks. International Journal of Innovative Research in Science, Engineering and Technology. Vol. 6, Issue 5. maio 2017.
[1] Laurea magistrale in Strutture e Edilizia Civile; Specializzazione in Costruzioni Industriali; Specializzazione in Ingegneria Ambientale; Specializzazione in Ingegneria della Sicurezza; Ingegnere civile e ingegnere operativo meccanico.
[2] Specializzazione in Ingegneria Strutturale e Ingegneria Civile.
[3] Ingegnere civile.
Inviato: marzo 2020.
Approvato: giugno 2020.