ORIGINALER ARTIKEL
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Strukturelle Alternativen in hängenden Böden von rohrförmigen Metalltanks mit zwei Zellen zur Wasserspeicherung. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 06, Vol. 12, S. 111-135. Juni 2020. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/bauingenieurwesen/strukturelle-alternativen
ZUSAMMENFASSUNG
Mit der steigenden Nachfrage nach Wasserreserven aufgrund der Einführung neuer Zuteilungen und horizontaler Eigentumswohnungen, die den Bedarf an einem minimalen dynamischen Druck von 100 kPa erfüllten, begannen die Tanks interne physikalische Teilungn (vertikale Zellen) zu haben, deren obere Zelle die untere Quote in einer Höhe ausgesetzt hat, die den manometrischen Druck garantierte, der notwendig war, um diesen Standard zu erfüllen. Aufgrund des Fehlens spezifischer brasilianischer technischer Standards für die Wasserspeicherung in einem Metallreservoir wurde es als Größenparameter für Metallreservoirs mit mehreren vertikalen Wasserspeicherzellen, der AWWA D100 in ihrer Gesamtheit oder nur teilweise, hauptsächlich aufgrund axialer Anstrengungen an den Küsten (Virolas) zur Bestimmung zulässiger Knickspannungen (FL) verwendet. Dieser Artikel befasst sich mit dem Problem der Auswahl der am besten geeigneten Art von vertikalen Metallboden aufgehängt und kommishes die Ergebnisse von fünf verschiedenen Arten von Böden, Größe nach AWWA D100-05. Innerhalb der Typologie der 5 analysierten Fonds war der wirtschaftlichste Fonds der segmentierte sphärische Fonds.
Stichworte: Metalltank, AWWA D100 Standard, suspendierte Fonds.
1. EINFÜHRUNG
Dieser Artikel befasst sich mit dem Problem der Auswahl der am besten geeigneten Art von vertikalen Metallboden aufgehängt und kommishes die Ergebnisse von fünf verschiedenen Arten von Böden, Größe nach AWWA D100-05.
Mit der Einführung neuer Unterteilungen und horizontaler Eigentumswohnungen aufgrund der Anreize der staatlichen Wohnungspolitik, hauptsächlich aufgrund des Wohnungsprogramms des Ministeriums für Städte, des Minha Casa Minha Vida-Programms (Pereira, 2017), das zu einem starken Anstieg der Nachfrage nach Lagertanks führte. Trinkwasser, meistens aus der Luft (above ground), zylindrisch und mit unterschiedlichem Durchmesser und unterschiedlicher Höhe, Wasserburg genannt.
Aufgrund der Notwendigkeit eines minimalen dynamischen Drucks im öffentlichen Versorgungsnetz, der nach NBR 12.218/1994 100 kPa (10,20 m.c.a.) betragen muss, haben die Tanks nun interne physikalische Teilungen (vertikale Zellen), deren obere Zelle die untere Dimension in einer Höhe aufgehängt hat, die einen manometrischen Druck garantiert, der für die Erfüllung dieser Norm erforderlich ist, da die Bodenkontingente normalerweise keine Unterstützung des Tanks bieten.
Nach Trees (1911) können die Böden von aufgehängten Metalltanks verschiedener Arten sein, z. B. flach, konisch und kugelförmig oder kugelförmig segmentiert.
Visal (2017) erklärt, dass Lagertanks ohne Druck (oder sehr wenig), so genannte atmosphärische Tanks, arbeiten, die sie von Druckbehältern unterscheiden. Sie sind in der Regel zylindrisch in Form, senkrecht zum Boden mit einem flachen Boden und einer festen oder schwimmenden Decke.
Die Konstruktion und Konstruktion von atmosphärischen zylindrischen Tanks erfordert die Kenntnis spezifischer technischer Standards, Materialien und Arbeit, die für jede Art von Anwendung geeignet sind, und beinhaltet eine Reihe anderer besonderer Vorsichtsmaßnahmen, da Anomalien und Unregelmäßigkeiten in diesen Geräten große finanzielle Verluste oder sogar Verluste an Menschenleben verursachen können (Nunes, 2013).
Laut Gomes (2017) sind die in Brasilien gebräuchlichen Standards für Metalltankprojekte und -konstruktionen NBR 7821, API 650 und AWWA D100.
NBR 7821/1983 – Geschweißte Stahltanks für die Lagerung von Öl und Derivaten, der Brasilianischen Vereinigung technischer Standards (ABNT) und der amerikanischen Regulierungsnorm API 650 – 2013 – Welded Steel Tanks for Oil Storage – des American Petroleum Institute (API) sind spezifisch für die Reserve von Öl und Derivaten.
Der AWWA D100-05 – Welded Carbon Steel Tanks for Water Storage Standard der American Water Works Associations zielt darauf ab, Mindestanforderungen für die Konstruktion, Konstruktion, Inspektion und Prüfung neuer geschweißter Kohlenstoffstahltanks für die atmosphärische Druckwasserspeicherung zu erfüllen.
Innerhalb der Größenanforderungen stellt der AWWA D100 drei Methoden zur Bestimmung der zulässigen Knickspannung (FL) für zylindrische Abschnitte vor, die die Überprüfung der maximalen Kompressionsspannung aufgrund von Axiallast und Axialbelastung aufgrund der an den Küsten aufgebrachten Windbelastung ermöglicht.
Aufgrund des Fehlens spezifischer brasilianischer technischer Standards für die Wasserspeicherung in einem Metallreservoir wurde es als Größenparameter für Metallreservoirs mit mehreren vertikalen Wasserspeicherzellen, der AWWA D100 in ihrer Gesamtheit oder nur teilweise, hauptsächlich aufgrund axialer Anstrengungen an den Küsten (Virolas) zur Bestimmung zulässiger Knickspannungen (FL) verwendet.
2. ZIELE
Allgemeines Ziel
Das allgemeine Ziel dieses Artikels ist die Bemaßung mehrerer Arten von aufgehängten Böden der oberen vertikalen Metalltankzelle, die aus zwei Zellen besteht, innerhalb der Empfehlungen von AWWA D100-05, mit der Autodesk Simulation Mechanical 2018 Software.
Spezifische Ziele
Die spezifischen Ziele sind:
- Bestimmen Sie die axialen Spannungen an den Seiten der Metalltankunterzelle, die durch axiale und seitliche Belastungen entstehen, und verglichen sie mit der zulässigen Belastung zum Knicken gemäß den Vorgaben 3.4 – Column, Strut, and Shell Stability Formulas– und Schalenstabilitätsformeln von AWWA D100 – 05.
- Bestimmen Sie die vertikalen Verschiebungen der schwebenden Hintergründe.
- Bestimmen Sie das Gesamtgewicht der vorgeschlagenen ausgesetzten Mittel, indem Sie die Fläche und die Dicke der großen Platten und Stützstrukturen quantifizieren.
3. MATERIAL UND METHODE
Der in diesem Artikel vorgestellte Tank ist ein metallisches Reservoir für Wasserreserven, bestehend aus zwei Zellen, mit einer Kapazität von je 150,00 m3 (insgesamt 300,00 m3), mit Metallkegelabdeckung (Abbildung 1), mit fünf Arten von aufgehängten Böden (Abbildungen 2A; 2B; 2C; 2D und 2E).
Abbildung 1: Metalltank aus zwei Zellen mit einer Kapazität von 300,00 m3.

Typologie der 5 vorgeschlagenen ausgesetzten Fonds:
Feige.: 2A – Flache Boden Radialbalken und Mast
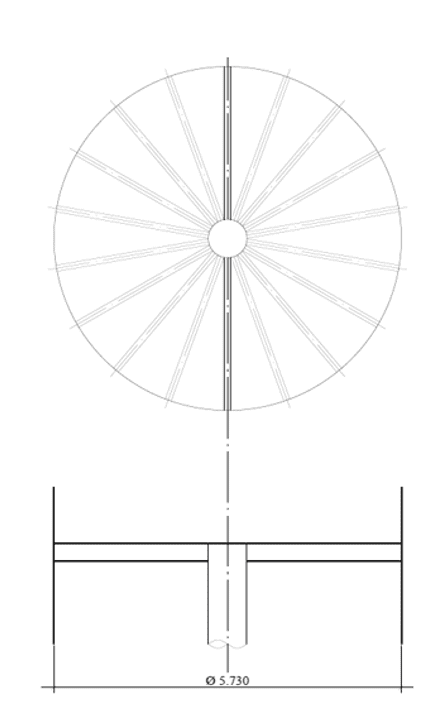
Feige.: 2B – Flache Boden radiale Balken ohne Mast
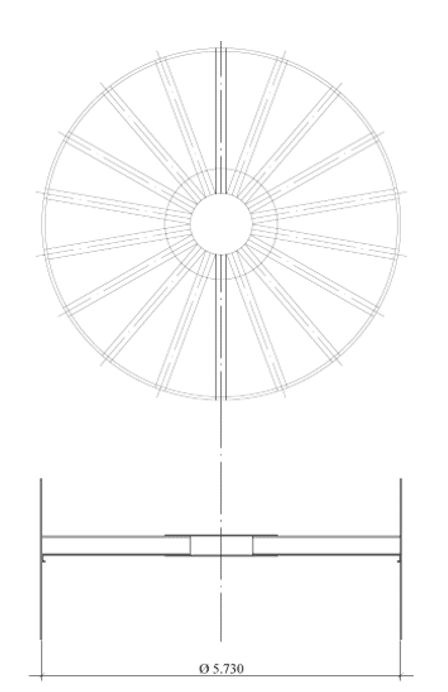
Feige.: 2C – Flache Boden orthogonale Balken
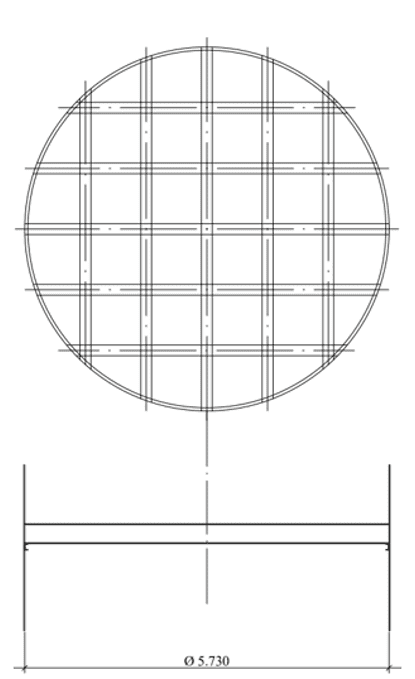
Feige.: 2D – Konischer Hintergrund
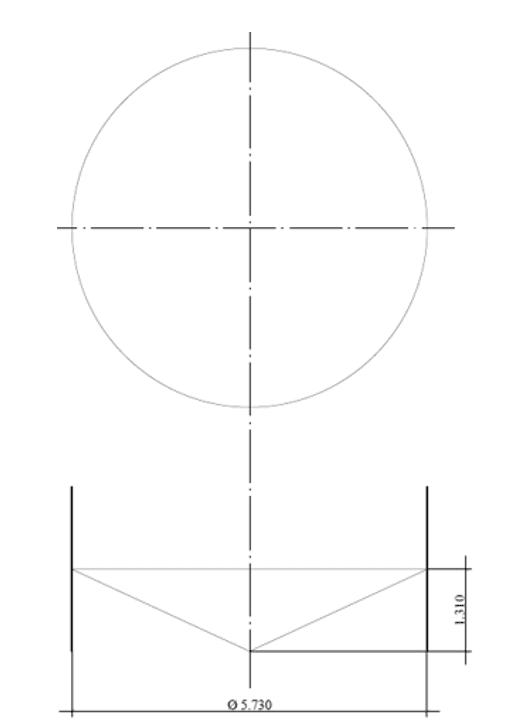
Quelle: Der Autor selbst
Feige.: 2E – Segmentierter sphärischer Hintergrund
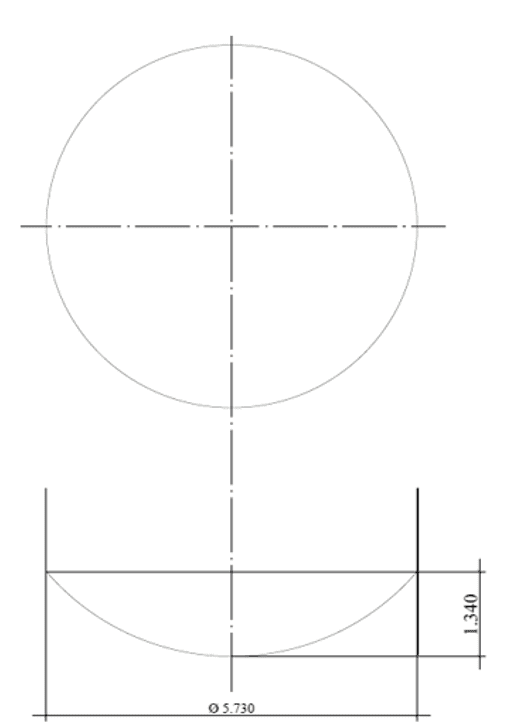
Quelle: Der Autor selbst
Die in Betracht gezogenen Aktionen sind Wind, gespeichertes Wasser (hydrostatische Wirkung), Deckenüberlastung und das Eigengewicht der Struktur (Abbildung 3A), das in der Autodesk Simulation Mechanical-Software veröffentlicht wird.
Abbildung 3A – Uploads
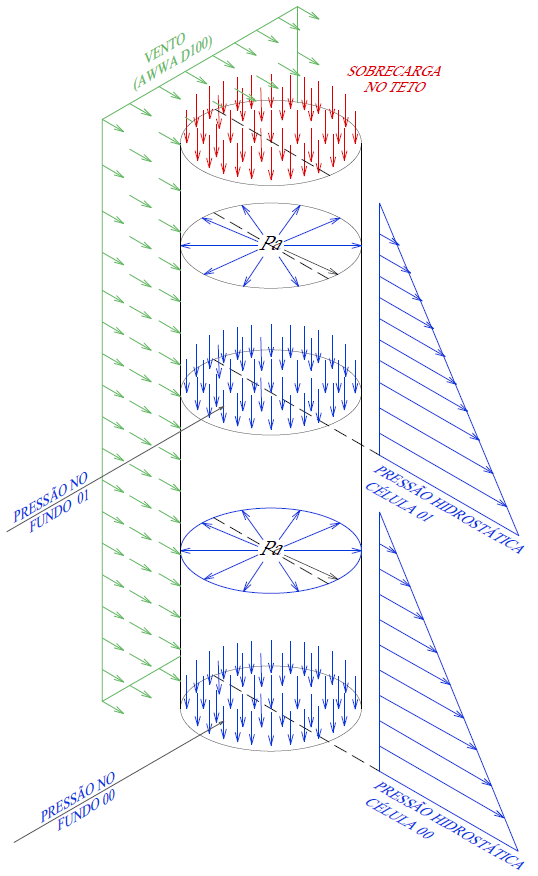
Abbildung 3B – Starten von Uploads in der Software
Laut Andrade junior (1998) wird die Windaktion nach NBR 6123 – Kräfte aufgrund des Vetos in Gebäuden (1987) berechnet und in der Regel wird davon ausgegangen, dass der Wind in jede horizontale Richtung wirken kann. Da die Struktur des Tanks in Bezug auf die Z-Achse senkrecht zur Windrichtung asymmetrisch ist, wird davon ausgegangen, dass sich der Wind senkrecht auf jede Geratriz des Tanks konzentrieren kann.
Die statische Komponente des Winddrucks, die senkrecht auf ein Flächenelement wirkt, wird gegeben durch: Die externen Druckkoeffizienten Cpe werden für den Körpertyp der Struktur ausgedrückt, vorausgesetzt, für die Anwendung von AWWA D100-05 ist Cpe = Cf (Tabelle 1).
Die externen Druckkoeffizienten Cpe werden für den Körpertyp der Struktur ausgedrückt, vorausgesetzt, für die Anwendung von AWWA D100-05 ist Cpe = Cf (Tabelle 1).
Wobei q der Winddruck an einem Punkt ist, an dem Luftstagnation auftritt, erhalten aus Ausdruck 2: Die V0 Geschwindigkeit wird Als Grundgeschwindigkeit bezeichnet, entspricht einer Böe von 3 Sekunden, die durchschnittlich einmal in 50 Jahren, gemessen 10 m über dem Boden, an einem flachen und offenen Ort ausgeübt wird. NBR 6123 (1987) stellt die grundlegenden Isopletas in m/s vor. Für unsere Beispiele wurde V0= 40 m/s angenommen.
Die V0 Geschwindigkeit wird Als Grundgeschwindigkeit bezeichnet, entspricht einer Böe von 3 Sekunden, die durchschnittlich einmal in 50 Jahren, gemessen 10 m über dem Boden, an einem flachen und offenen Ort ausgeübt wird. NBR 6123 (1987) stellt die grundlegenden Isopletas in m/s vor. Für unsere Beispiele wurde V0= 40 m/s angenommen.
Der topografische Faktor S1 wird verwendet, um die Entlastung des Grundstücks um das Gebäude herum zu bewerten und für unsere Beispiele gleich 1,0 angenommen.
Faktor S2 berücksichtigt den kombinierten Effekt von Geländerauheit, Windgeschwindigkeitsschwankungen mit Höhe über Gelände und Gebäudeabmessungen. Faktor S2 wird durch Ausdruck 4 erreicht:

Wo: Z = Höhe über dem Boden, Fr = Windböenfaktor, b = meteorologischer Parameter, p = Geländerauheitsfunktion und Zeitintervall. Für die Tankhöhe von 16,0 m, Rauheit II, Klasse A, hat man S2 = 1,05.
Faktor S3 ist ein statistischer Faktor, der den erforderlichen Sicherheitsgrad und die Nutzungsdauer der Struktur berücksichtigt, wenn man die Anlagen von Reservoirs mit niedrigem faktor für menschliche Belegung berücksichtigt (Andadre Junior, 1998), der Wert von 0,95 wurde verwendet.
Nach Haffez et al (2011) wird davon ausgegangen, dass die Tanks einem gleichmäßigen Winddruck (q) ausgesetzt sind, der entlang der Z-Achse wirkt, wie in den Abbildungen 3rd und 3B dargestellt. AWWA D100-05 empfiehlt die Verwendung eines Luftwiderstandskoeffizienten (Cf) entsprechend der Form der Struktur gemäß Tabelle 1. Für Rohrtanks mit zylindrischer Form beträgt der angenommene Cf 0,6.
Tabelle 1 – Ziehkoeffizient Cf

Haben:
Vk = 40 . 10 . 1,05 . 0,95 = 39,90 m/s
q = 0,613 . 39,902 = 975,90 N/m² ou 99,51 kgf/m²
Δp = 0,6 . 975,90 = 585,54 N/m² ou 58,71 kgf/m².
Die hydrostatische Wirkung erzeugt Effekte, die in radialer und vertikaler Richtung wirken und zu seitlichem Druck auf der Seite und Druck am Boden des Reservoirs führen.
Der design-Overhead, der auf die Decke aufgebracht wird, sollte gemäß AWWA D100-05 Artikel 3.1.3.2 750 N/m2 (15 lb/ft2) betragen.
Das eigengewicht der Struktur wird automatisch von der Autodesk Simulation Mechanical 2018 Software freigegeben, unter Dem spezifischen Gewicht der Stähle, die bei der Tankgröße verwendet werden.
Die Dicke der Ferolindruckferolas aufgrund des hydraulischen Drucks des Tanks muss nach Der gleichung 3-40 berechnet werden. 3.7 AWWA D100-05 – Cylindrical Shell Plates (Gleichung7): 
Wo:
t = Rumpfkonstruktionsdicke (Ferrule), in mm
hp = Flüssigkeitshöhe, in m
D = Tankdurchmesser, in m
S = Zulässige Stahlspannung, in Mpa
E = Schweißeffizienz
G = Spezifisches Flüssigkeitsgewicht (für Wasser = 1)
Die Mindestdicke des zylindrischen Strangs, der mit Wasser in Berührung kommt, sollte gemäß Tabelle 2 gemäß der Abs. 3.2 von AWWA D100-05. Für den Tank mit einem Nenndurchmesser von 5,73 m beträgt die vorgeschriebene Mindestdicke 4,76 mm.
Tabelle 2 – Ziehkoeffizient Cf
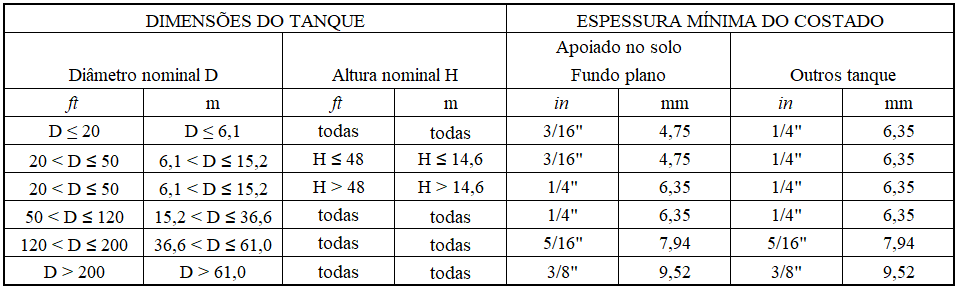
AWWA D100-05 klassifiziert die in Tanks zu verwendenden Strukturmaterialien in 3 Klassen, abhängig von der Strömungsgrenze (Fy). Tabelle 3 zeigt diese Klassifizierung.
Tabelle 3 – Materialklasse als Funktion von Fy
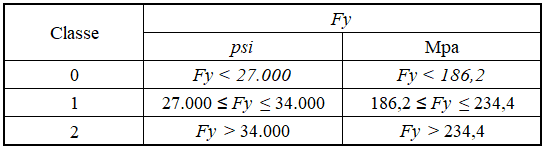
Das Material, das in den Küsten, Böden und Decken verwendet wird, ist ASTM A36, gekennzeichnet durch einen Elastizitätsmodul (E) gleich 205.000 Mpa, Poisson-Koeffizient (μ) gleich 0,30, Dichte (γ) von 77.000 N/mm3, Durchflussspannung fy = 250,00 Mpa und letzte fu-Spannung = 400,00 Mpa. Das Material, das in den Tragstrukturen der Schwebemittel (Strahlen W und C) verwendet wird, ist der ASTM A572 (Grad 50) mit Durchflussspannung fy = 345.00 Mpa und letzter fu-Spannung = 450.00 Mpa. Sie werden als Material der Klasse 2 klassifiziert.
Tabelle 4 zeigt die von AWWA D100-05 vorgeschriebenen Hauptspannungen, abhängig von der Materialklasse und den Anwendungen in den Reservoirs.
Tabelle 4 – Zulässige Spannungen in Anwendungen
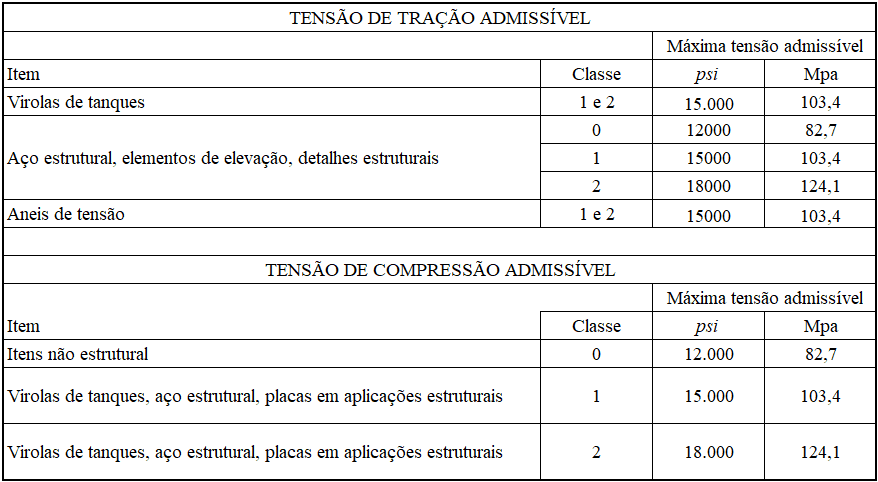
Quelle: AWWA D100-05 – modifiziert vom Autor.
Für die Überprüfung der Stabilität durch das Knicken der Tankküste, die AWWA D100-05 vorgeschrieben 3 Methoden der Analyse. Für diese Arbeit wurde Methode 1 verwendet, ein vereinfachtes Verfahren, das auf Membrananalysetechniken basiert. Bei Materialien der Klasse 2 beträgt das Dicken-Radius-Verhältnis des Reservoirs, zu dem sich das Knicken von elastisch zu unelastisch (t/R)c ändert, 0,0025372. Die zulässige Beanspruchung für das Knicken von Material der Klasse 2 ist durch folgende Formeln gegeben:
Wenn 0 ≤ t/R ≤ (t/R)c bedeutet, dass Knicken im elastischen Regime auftritt und die zulässige Spannung für knicken durch Gleichung 8 angegeben ist: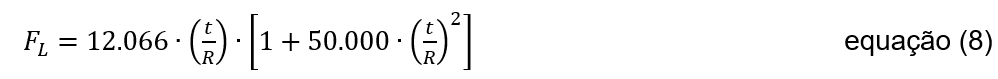
Wenn (t/R)c ≤ t/R ≤ 0,0125 bedeutet, dass Knicken im unelastischen Regime auftritt und die zulässige Belastung für Knicken durch Gleichung 9 angegeben ist:
Wenn t/R > 0,0125, bedeutet dies, dass Knicken in Kunststoff auftritt und die zulässige Belastung für knicken konstant![]() ist und wert ist:
ist und wert ist:
Tabelle 5 – Schweißeffizienzwerte werden teilweise aus Table 15 Weld design values – tank plate joints, bei denen nur die Schweißwerte dargestellt werden. Für die Arbeit auf Leinwand wurde das doppelfrontale Fasenschweißen mit voller Polsterung berücksichtigt.
Tabelle 5 – Schweißeffizienzwerte in %

4. ERGEBNISSE
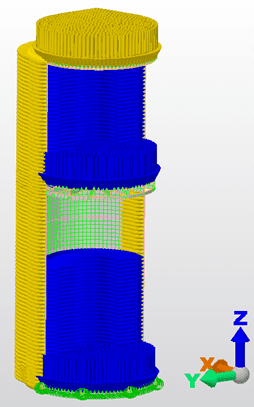
Numerische Modellierung und Analyse wurden mit einer kommerziellen Software der Analyse und Konstruktion Autocad Simulation Mechanical 2018 durchgeführt. Jede Ferrule des Tanks wurde als Schalenelement mit konstanten Konstruktionsstärken, mit isotropen Eigenschaften und mit einer mittelgroßen Ebene zentral positioniert modelliert. An der Oberseite des Tanks befindet sich ein kreisförmiger vertikaler Ring, der mit L-Profil modelliert ist, der fest an den Elemnetos befestigt ist. Die Finite-Elemente-Dimensionen sind 0,20 x 0,20 m (Diskretisierung). Für jeden Tanktyp wurde gemäß der Typologie jedes aufgehängten Bodens ein 3D-Finite-Elemente-Modell erstellt (Abbildung 4).
Abbildung 4: Diskretisierter Metalltank

Ausgehend von der Mindestdicke nach Tabelle 2 wurde für die Dimensionierung des Strangs auch die Dicke aufgrund des Umfangsdrucks unter Verwendung der Gleichung (7) und der Dicke durch Knicken, mit der Bestimmung der zulässigen Spannung (FL), unter Verwendung der Gleichungen (8) und (9) und der axialen Spannungen der Stränge, die von der Software Simulation Mechanical bestimmt und mit den berechneten zulässigen Spannungen (FL) verglichen werden, überprüft. Die erforderliche Dicke jeder Ferrule ist die größte Dicke innerhalb der 3 Kriterien.
Tabelle 6 zeigt im Einzelnen die Van Misse, Die Umfangsspannung und die axiale Spannung in jeder Ferrule der 5 untersuchten Tanks mit verschiedenen Arten von suspendierten Mitteln.
Tabelle 6 – Dimensionierung der Küsten nach AWWA D100 – 05
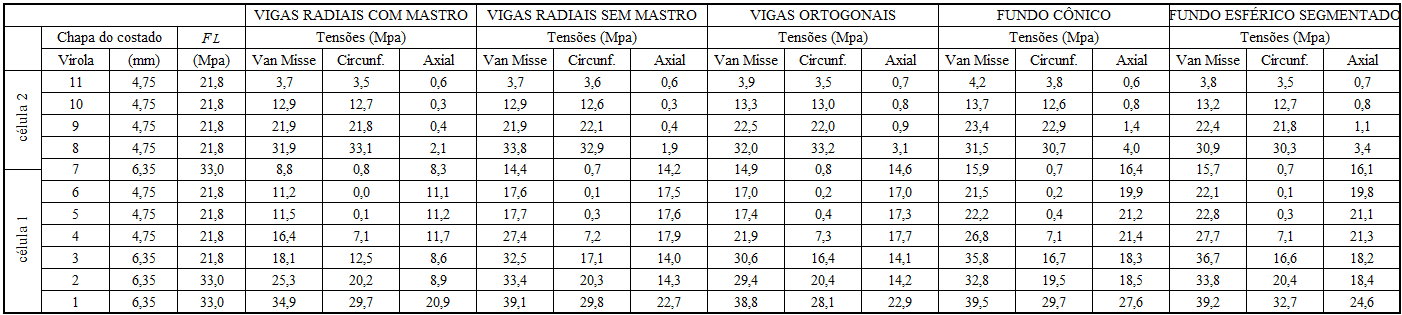
Abbildung 5zeigt den Tank mit den dicken Dicken, die für jede Ferrule der Seite erforderlich sind.
Abbildung 5: Tank mit den endletzten Dicken des Strangs
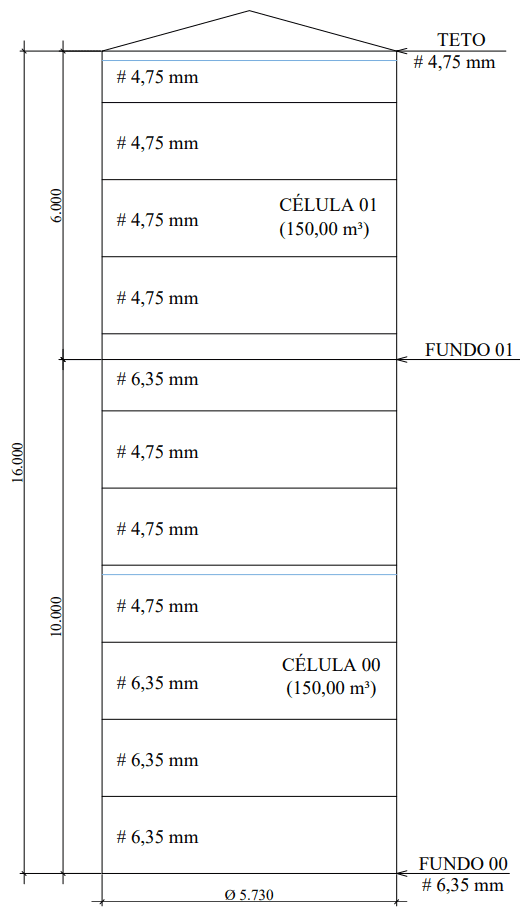
Quelle: Der Autor selbst
Die Abbildungen 6A, 6B, 6C und 6D zeigen die Ergebnisse der Analysen mit Van Misse-Spannungen, Umfangsspannungen und Axialspannungen in jeder Ferrule für den Tank mit Dem Boden der Zelle 2, mit radialen W-Strahlen und Zentralmast. Die erhaltenen Werte werden in Tabelle 6 eingespeist. Die gleiche Analyse wurde an den anderen 4 Tanks durchgeführt, die diese Arbeit abschließen.
Feige. 6A: Van Misse Spannungen in 3D-Schnitt
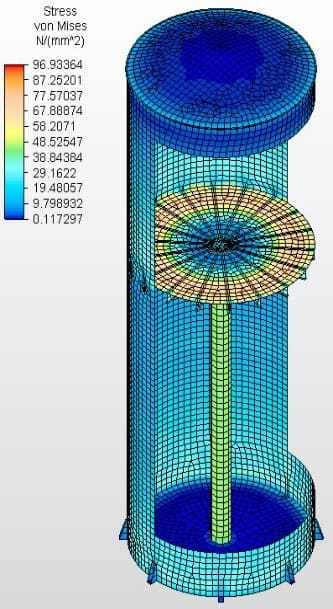
Quelle: Der Autor selbst
Feige. 6B: Van Misse Spannungen

Quelle: Der Autor selbst
Feige. 6C: Umfangsspannungen
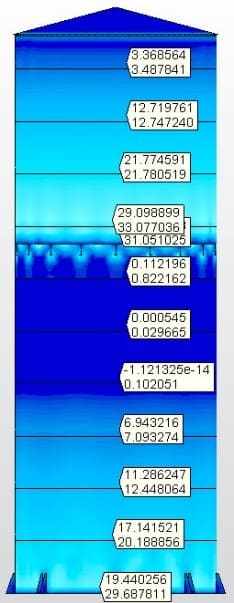
Feige. 6D: Axialstämme
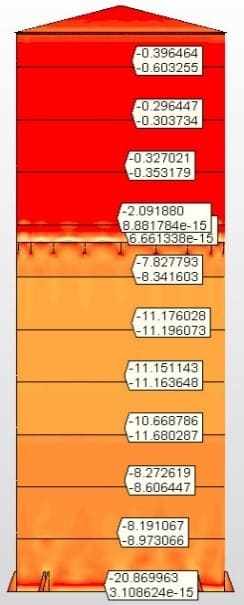
Die bei dieser Arbeit analysierten suspendierten Mittel, mit Ausnahme des Bodens mit Radialbalken und Zentralmast (Abbildung 2A), wurden als selbstunterstützt und nur auf der Seite der Tanks unterstützt. Die Ergebnisse der Analysen werden im Folgenden vorgestellt.
Der abgehängte Boden mit Radialträgern Typ W und Zentralmast, dessen Geometrie in Abbildung 7 dargestellt ist, wo er den gleichen Nenndurchmesser des Tanks hat, D = 5.730,00 mm, Anzahl der Stützträger = 18 Stück, Trägerprofil W = 310 x 28,3, Trägermaterial W = ASTM A572 – Grad 50, Durchmesser des Zentralmastes = 640,00 mm, Zentralmaststärke = 6,35 mm, Zentralmastplattenmaterial = ASTM A36, Bodenplattendicke = 7,95 mm (5/16″), Bodenplattenmaterial = ASTM A36.
Bodenbelastung = hydrostatischer Druck h = 5,80 m.c.a.
Abbildung 7: Hintergrundlayout mit Radialbalken und Zentralmast
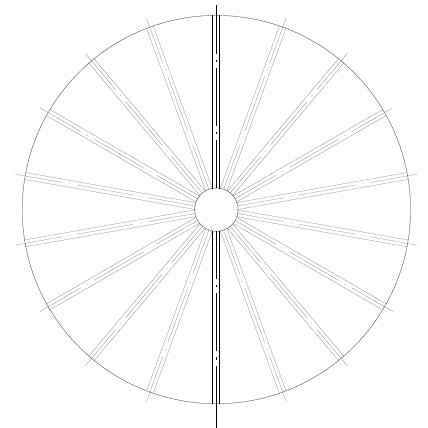
Die Spannungen auf der Bodenplatte und den Stützträgern sind in den Abbildungen 8A und 8B dargestellt.
Abbildung 8A: Spannungen auf dem abgehängten Boden Maximale Spannung = 90,0 Mpa
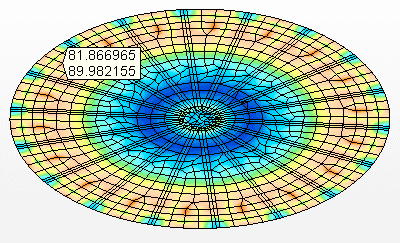
Quelle: Der Autor selbst
Abbildung 8B: Spannungen an den Stützstrahlen Maximale Spannung = 64,9 MPa

Abbildung 8C: Vertikale Verschiebungen (mm)
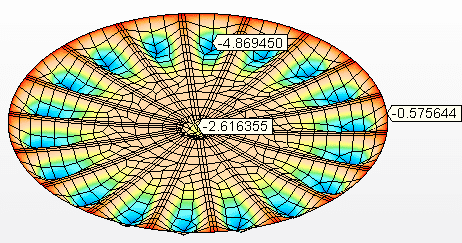
Abbildung 8D: Axiale Spannungen am Mast Maximale Spannung = 37,6 MPa

Der aufgehängte Boden mit Radialträgern Typ W und ohne Zentral, dessen Geometrie in Abbildung 9 dargestellt ist, wo er den gleichen Nenndurchmesser des Tanks hat, D = 5.730,00 mm, Anzahl der Stützträger = 18 Stück, Trägerprofil W = 310 x 44,5, Trägermaterial W = ASTM A572 – Grad 50, Umfangsträger U 6″ erste Seele, Trägermaterial U = ASTM A572 – Grad 50, Bodenplattendicke = 7,95 mm (5/16), Bodenplattenmaterial = ASTM A36.
Bodenbelastung = hydrostatischer Druck h = 5,80 m.c.a.
Abbildung 9: – Hintergrundlayout mit Radialbalken und ohne Mast
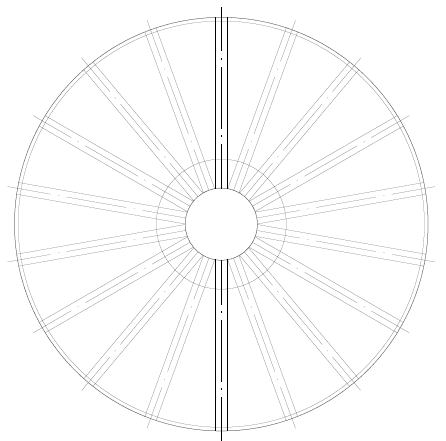
Quelle: Der Autor selbst
Abbildung 9A – Spannungen auf dem abgehängten Boden Maximale Spannung = 87,4 Mpa
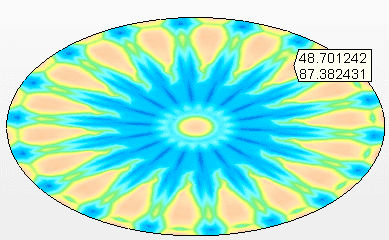
Quelle: Der Autor selbst
Abbildung 9B – Spannungen an den Stützbalken Maximale Spannung = 89,2 MPa
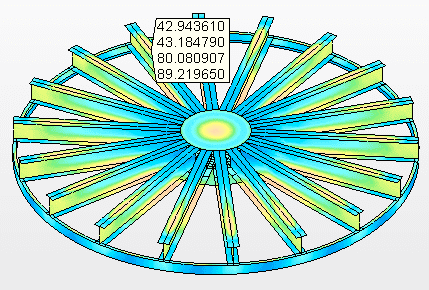
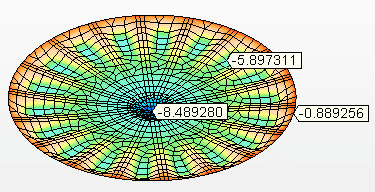
Abbildung 9C – Vertikale Versätze (mm)
Der abgehängte Boden mit orthogonalen Trägern (Gitter) Typ W und ohne Zentral, dessen Geometrie in Abbildung 10 dargestellt ist, wo er den gleichen Nenndurchmesser des Tanks hat, D = 5.730,00 mm, Anzahl der Stützträger = 10 Stück, Trägerprofil W = 360 x 72, Trägermaterial W = ASTM A572 – Grad 50, Umfangsträger U 6″ erste Seele, Trägermaterial U = ASTM A572 – Grad 50, Bodenplattendicke = 9,53 mm (3/8″), Bodenplattenmaterial = ASTM A36.
Bodenbelastung = hydrostatischer Druck h = 5,80 m.c.a.
Abbildung 10: – Hintergrundlayout mit orthogonalen Balken (Grill) und ohne Mast
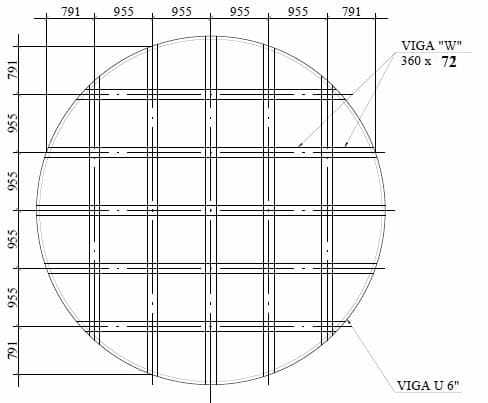
Quelle: Der Autor selbst
Abbildung 10A – Spannungen auf dem abgehängten Boden Maximale Spannung = 79,9 Mpa
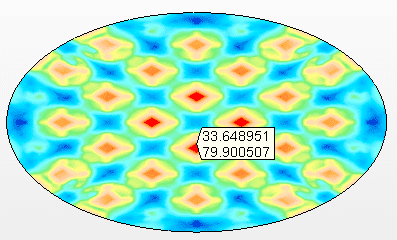
Quelle: Der Autor selbst
Abbildung 10B – Spannungen an den Stützbalken Maximale Spannung = 85,7 MPa
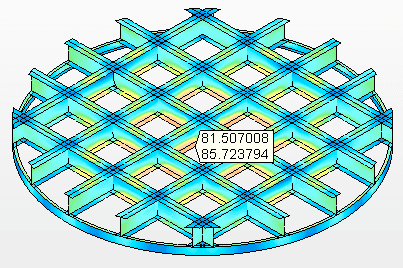
Abbildung 10C – Vertikale Versätze (mm)
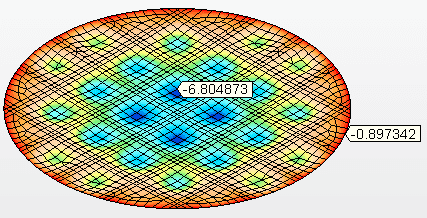
Quelle: Der Autor selbst
Der kegelförmige Hängeboden, dessen Geometrie in Abbildung 11 (Schnitt) dargestellt ist, wo er den gleichen Nenndurchmesser des Tanks hat, D = 5.730,00 mm, Dicke der Bodenplatte = 9,53 mm (3/8″), Bodenplattenmaterial = ASTM A36. Bodenbelastung = hydrostatischer Druck h = 5,80 m.c.a.
Abbildung 11: – Verjüngtes Bodenschema im Schnitt
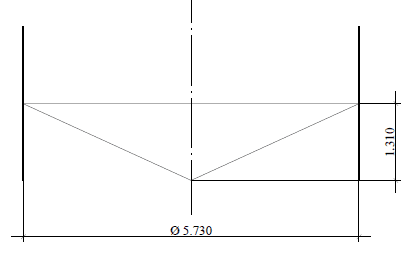
Abbildung 11A – Spannungen auf dem abgehängten Boden Maximale Spannung= 90,8 Mpa
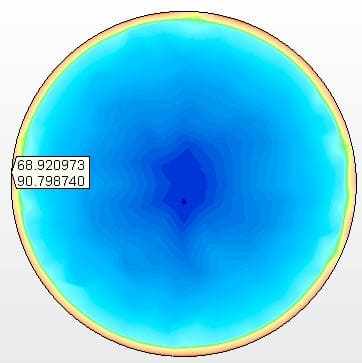
Quelle: Der Autor selbst
Abbildung 11B – Vertikale Verschiebungen (mm) Maximale Spannung= 7.359 mm
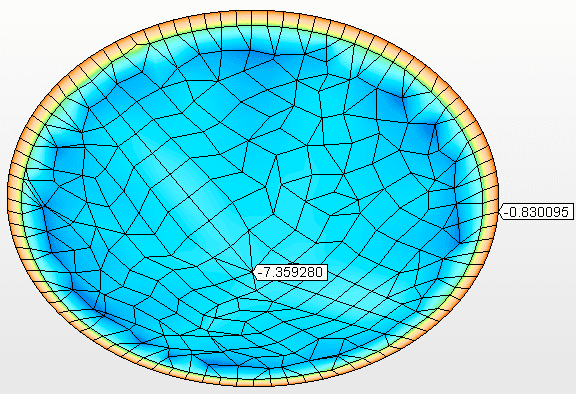
Quelle: DerAutor selbst
Der aufgehängte Boden im Halbkugel- oder segmentierten kugelförmigen Bodenformat, dessen Geometrie in Abbildung 12 (Schnitt) dargestellt ist, wo er den gleichen Nenndurchmesser des Tanks hat, D = 5.730,00 mm, Dicke der Bodenplatte = 4,75 mm (3/16″), Bodenplattenmaterial = ASTM A36. Bodenbelastung = hydrostatischer Druck h = 5,80 m.c.a.
Abbildung 12: Schematic des geschnittenen sphärischen Hintergrunds.
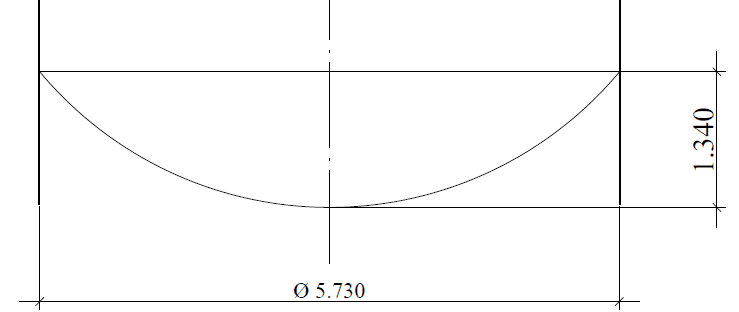
Abbildung 12A – Spannungen auf dem abgehängten Boden Maximale Spannung = 88,32 Mpa

Quelle: Der Autor selbst
Abbildung 12B – Vertikale Verschiebungen (mm) Maximale Spannung = 7.359 mm
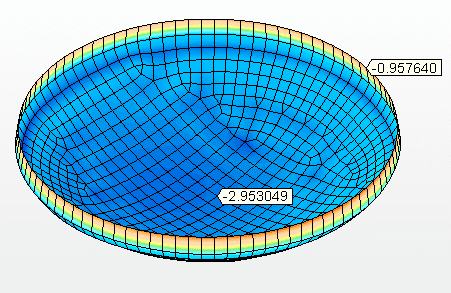
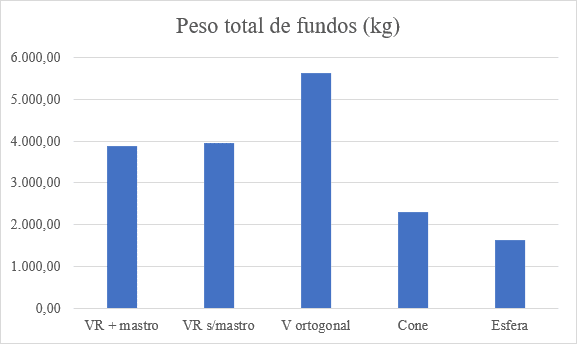
Die Gewichte der suspendierten Mittel wurden ohne Bestimmung von Clippings oder Verwendung von Klappen und Resten berechnet, wodurch nur die Flächen der Platten multipliziert mit Dem Gewicht/m2 berechnet wurden. Tabelle 7 zeigt die allgemeine Zusammenfassung der Gewichte der 5 Arten von suspendierten Fonds, und diese Unterschiede sind im Gesamtgewicht x Fondstypdiagramm in Abbildung 13 zu sehen.
Tabelle 7 – Suspendierte Fondsgewichte

Quelle: Der Autor selbst
Abbildung 13 – Vergleiche der Fondsgewichte
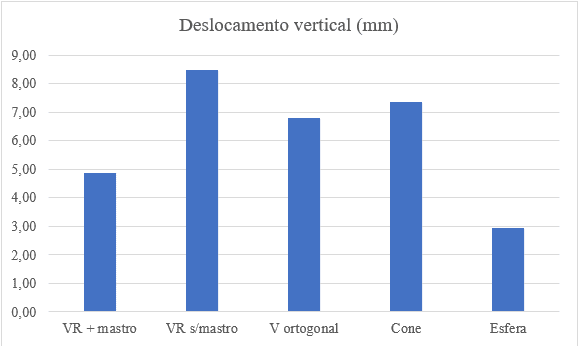
Die vertikalen maximalen Versätze der abgehängten Böden sind in Abbildung 14 vergleichsweise dargestellt.
Abbildung 14 – Vergleiche vertikaler maximaler Verschiebungen
5. SCHLUSSFOLGERUNGEN
Aus den erzielten Ergebnissen wird der Schluss gezogen, dass der segmentierte kugelförmige Suspensionsfonds der wirtschaftlichste und technisch am besten empfohlene ist, da er unter vollständiger Belastung die kleinste vertikale Verschiebung darstellt.
Der Kegel-Schwebboden ist ebenfalls wirtschaftlich lebensfähig, hat aber eine vertikale Verdrängung bei etwas überhöhter Belastung, und er sollte überprüft werden, ob er die Rohre stört. Die vertikale Verschiebung konnte durch die Verwendung von dreieckigen Verstärkungsplatten verringert werden, die den Boden an den Seitenseiten stützen.
Der abgehängte Boden, der von orthogonalen Strahlen gestützt wird, ist völlig unwirtschaftlich.
REFERENZEN
ABNT – Associação Brasileira de Normas Técnicas, NBR 7.821, Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro, RJ. Abril de 1983.
ABNT – Associação Brasileira de Normas Técnicas, NBR 6.123, Forças devido ao vento em edificações. Rio de Janeiro, RJ. Junho de 1988.
ABNT – Associação Brasileira de Normas Técnicas, NBR 12.218, Projeto de rede de distribuição de água para abastecimento público. Rio de Janeiro, RJ. Julho de 1994.
ANDRADE JUNIOR, L. J. Análise estrutural das chapas metálicas de silos e reservatórios cilíndricos. Dissertação de mestrado. Escola de Engenharia de São Carlos. Universidade de São Paulo, 1998.
API – American Petroleum Institute, API 650, Welded Steel Tanks for Oil Storage, decima terceira edição, Washington D. C., Março de 2013.
AWWA – American Water Works Association, AWWA D100-05, Welded Steel Tanks for Water Storage. Edição atualizada. Denver, Colorado. Maio 2005.
GOMES, E. F. Soldagem em reservatórios metálicos para armazenamento de água. Trabalho de conclusão de curso. Curso de especialização em Engenharia de soldagem. Universidade Federal de Minas Gerais, 2017.
HAFEEZ, G., EL ANSARY, A. M. & EL DAMATTY, A. A. Effects of winds load son the stability of conical tanks. Can. J. Civ. Eng. 38, Published by NCR Research Press, 2011.
PEREIRA, P. M. F. Análise dos conjuntos habitacionais do programa Minha Casa, Minha Vida na cidade de Monte Alegre de Minas- MG. Dissertação de mestrado. Faculdade de Geografia. Universidade Federal de Uberlândia, 2017.
TREES, M. J. Design of elevated steel tanks. Thesis. University of Illinois, Urbana-Champaign, 1911.
VISAL, B. & SIBIN, B. Design and analysis of storage tanks. International Journal of Innovative Research in Science, Engineering and Technology. Vol. 6, Issue 5. maio 2017.
[1] Master in Strukturen und Bauwesen; Spezialisierung im Industriellenbau; Spezialisierung in Umwelttechnik; Spezialisierung in Sicherheitstechnik; Bauingenieur und Maschinenbauingenieur.
[2] Spezialisierung im Hoch- und Tiefbau.
[3] Bauingenieur.
Eingesandt: März 2020.
Genehmigt: Juni 2020.



