ARTICLE ORIGINAL
SILVA, Sarley De Araújo [1] MAGNO, Rui Nelson Otoni [2]
SILVA, Sarley De Araújo. Probabilité, carte de contrôle appliquée aux logiciels de sciences de l’éducation. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 06, Ed. 06, Vol. 11, p. 43 à 73. Juin 2021. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/sciences-de-leducation
RÉSUMÉ
La présente étude mentionne la réduction de la variabilité et des pertes dues à des causes spéciales dans les applications des sciences de l’éducation, visant à détecter et à corriger les écarts de variabilité grâce à des cartes de contrôle logiciel dans les problèmes statistiques appliqués. Ainsi, nous avons cherché à étudier les concepts sur les cartes de contrôle par variables et attributs dans le contrôle des anomalies. Dans la réalisation de ce thème, la méthodologie quantitative et la carte de contrôle du logiciel Minitab ont été utilisées. Les résultats obtenus ont permis de réduire les pertes et d’améliorer le processus de qualité grâce à des ajustements d’échantillons entre les limites de contrôle minitab, permettant de comprendre et d’analyser les causes des anomalies. Par conséquent, il est conclu que l’outil issé des mesures correctives est capable de stabiliser les écarts-types et d’améliorer la qualité des probabilités et des applications statistiques.
Mots-clés : Probabilité, Logiciel Minitab, Carte de contrôle.
1. INTRODUCTION
La statistique est une branche des mathématiques qui utilise l’outil des probabilités pour expliquer les regroupements de données, à la fois dans les études observationnelles et dans les expériences pour modéliser, estimer et prédire les phénomènes futurs. Son but est d’obtenir, d’organiser, d’analyser des données, de calculer des cartes de contrôle, des corrélations et des régressions, permettant de contrôler la variabilité, les applications statistiques et les établissements d’enseignement. Les méthodes statistiques se réfèrent aux données obtenues à partir d’observations sous forme de mesures ou de comptage. À partir de l’information, il est possible d’étudier des problèmes statistiques liés au contrôle de la variabilité appliquée dans les sciences de l’ingénierie, de la chimie, de la physique, des mathématiques, de la géographie, etc. L’utilisation de logiciels statistiques est un outil important pour les études et l’applicabilité dans le contrôle des variations de probabilité et des problèmes statistiques.
Les institutions sont soucieux de maintenir des indices de performance élevés en ce qui concerne la qualité et la productivité en raison des exigences de la prestation de services. L’information et les nouvelles technologies ont établi un environnement mondialisé de forte concurrence, dans lequel le prix et le délai doivent être respectés (VILAÇA et OLIVEIRA, 2011). Dans « Tout processus de production, aussi bien conçu ou entretenu soit-il, sera toujours soumis à une variabilité naturelle ou inhérente, qui est le résultat de l’effet cumulatif de nombreuses causes petites et inévitables, appelées causes communes » (MONTGOMERY, 2004, p.154). Par conséquent, la réduction de l’anomalie dans les familles de variables est d’une importance capitale dans le processus statistique.
Selon Souza et Rigão (2005), le CEP agit de manière préventive sur le processus en utilisant les statistiques comme élément de base pour évaluer ses changements. Ces caractéristiques permettent au CEP d’aider à la surveillance du processus et permettent de prendre des mesures de manière à résoudre les problèmes, à aider à la stabilisation du processus et à éviter la production d’articles non conformes (HORA et COSTA, 2009; MAYER, 2004).
L’objectif de ce travail est d’utiliser des techniques statistiques dans les logiciels pour identifier, corriger et éliminer les anomalies présentes dans les problèmes des sciences de l’éducation. L’importance des cartes de contrôle des logiciels statistiques dans le contrôle des anomalies.
L’objectif principal du contrôle statistique des processus est de détecter rapidement l’apparition de causes attribuables dans les changements de processus, de sorte que l’enquête sur le processus et les mesures correctives puissent être effectuées avant la fabrication de nombreuses unités non conformes (MONTGOMERY, 2013, p. 280).
Par conséquent, les logiciels statistiques sont pertinents dans le processus d’identification et d’élimination de la variabilité.
La fonction du contrôle statistique des processus dans les diagrammes logiciels est de mettre en évidence les modulations qui se sont produites pendant le traitement et de développer des graphiques statistiques qui peuvent fournir un paramètre plus précis, en aidant dans les pratiques qui peuvent améliorer les points prédominants de la fabrication, en plus de reconnaître, corriger, éliminer ou adapter les processus avec anomalie, donnant un paramètre plus précis, afin que des améliorations puissent être appliquées dans la ligne de production (OLIVEIRA, 2015, p.22).
Les cartes de contrôle du logiciel statistique permettent de trouver la variabilité démontrée à travers les graphiques, permettant une meilleure visualisation du processus, afin de démontrer d’éventuels défauts, pour l’application de corrections plus efficaces, dans la recherche d’amélioration continue.
Même avec l’avancement du processus grâce au contrôle de la qualité, il existe toujours des causes de variabilité dans le processus, c’est-à-dire que lorsqu’il y a une oscillation autour de la moyenne ou du point idéal de la spécification, une surveillance constante du comportement de production est nécessaire. « Grâce à l’analyse des données collectées et à la caractérisation de la cause de l’instabilité ou de la variabilité du système, utilisées dans les cartes de contrôle, des outils de contrôle statistique des processus en conséquence pour obtenir une amélioration continue des processus » (JURAN et GRYNA, 1992).
Tous les processus présentent une variabilité, c’est-à-dire que plus la variabilité est grande, plus le contrôle des résultats produits et des résultats souhaités est grand. (MONTGOMERY, 1997).
Pour améliorer la qualité d’un produit, il est nécessaire d’utiliser un logiciel statistique:
Dans un environnement concurrentiel, l’amélioration continue des processus permet de surveiller, de contrôler et d’améliorer les processus de production chaque fois qu’une anomalie est détectée. S’il y a un caractère préventif, ces actions contribuent à minimiser les pertes et à augmenter la productivité (BORTOLOTTI, 2009, p.02).
Ces techniques statistiques utilisant le logiciel minitab contribuent à l’analyse de divers produits, à la détection et à la réduction d’éventuelles anomalies, garantissant des stocks dans les paramètres de qualité. « L’un des principaux résultats de l’étude sur la qualité industrielle a été l’utilisation généralisée de méthodes statistiques de contrôle des processus pour éliminer les causes spéciales dans les processus et réduire les causes courantes de variation » (MONTGOMERY, 1997). Dans ce contexte, le contrôle statistique des processus est un outil extrêmement important pour l’application de techniques statistiques dans la réduction de la variation. Le contrôle statistique des processus peut être défini comme un ensemble de sept outils de dépannage pour atteindre la stabilité du processus, en plus d’améliorer sa capacité. (FERREIRA et. al., 2008).
Les cartes de contrôle du logiciel statistique aident à identifier et à stabilité les causes de la variabilité des processus, servant de base aux décisions et aux mesures correctives de contrôle, réduisant la variabilité et évitant les données d’échantillon hors de contrôle.
Le contrôle statistique des processus est une puissante collection d’outils pour la collecte, l’analyse et l’interprétation des données, dans le but d’améliorer la qualité en éliminant les causes particulières de variation, et peut être utilisé pour la plupart des processus. (MONTGOMERY, 2004, p. 279-281).
L’étude sur les cartes de contrôle dans les logiciels statistiques contribue à l’analyse des applications en sciences de l’éducation dans la réduction de la variabilité dans les échantillons analysés, générant de meilleurs résultats dans le contrôle de la qualité.
2. MATÉRIAUX ET MÉTHODES
2.1 MATÉRIAUX
Les matériaux utilisés pour contrôler la variabilité dans les applications des sciences de l’éducation étaient les cartes de contrôle du logiciel Minitab.
2.2 MÉTHODES
Pour mener à bien l’étude, la méthode quantitative et la carte de contrôle du logiciel minitab ont été utilisées pour réduire la variabilité dans les applications des sciences de l’éducation. La méthodologie vise la validation des données par l’utilisation de données statistiques. L’étude avait la distribution suivante: choix de l’application à analyser, détermination des limites inférieure et supérieure des paramètres moyens et de l’amplitude, distribution des échantillons et vérification de leurs points, analyse des problèmes par cartes de contrôle et correction des causes spéciales à partir des analyses d’échantillons hors de contrôle.
« La méthode quantitative cherche la validation des données par l’utilisation de données statistiques, avec l’analyse d’un grand nombre de cas représentatifs. Il cherche à quantifier les données et à appliquer une certaine forme d’analyse statistique » (OLIVEIRA, 2011). L’approche quantitative est fréquemment utilisée dans les études descriptives, qui cherchent à classer la relation entre les variables et la relation causale entre les phénomènes.
Richardson (1999, p. 70) conceptualise :
l’approche quantitative, comme son nom l’indique, se caractérise par l’utilisation de la quantification à la fois dans les modalités de collecte de l’information et dans le traitement de celles-ci par des techniques statistiques, du plus simple en pourcentage, en moyenne, en écart-type, au plus complexe, en tant que coefficient de corrélation, analyse de régression, etc. Elle représente, en principe, l’intention d’assurer l’exactitude des résultats et d’éviter les distorsions d’analyse et d’interprétation, permettant ainsi une marge de sécurité par rapport aux inférences.
Selon Michel (2005, p. 31), l’approche quantitative est une méthodologie de recherche sociale qui utilise la quantification dans les modalités de collecte de l’information et son traitement par des techniques statistiques, telles que le pourcentage moyen, l’écart-type, le coefficient de corrélation, l’analyse de régression, entre autres. Les cartes de contrôle sont un outil bénéfique qui apporte des améliorations et une assurance qualité des déchets augmentant les coûts, la disparition de la ferraille et la résolution de divers problèmes de production liés à des méthodes spécifiques, etc. (ROSA, 2009).
Les cartes de contrôle ont été utilisées par les variables et les attributs comme techniques dans la construction de graphiques dans des applications probabilistes et statistiques, où une amélioration de la stabilité a été observée par rapport à la variabilité des défauts de l’échantillon. Pour trouver une cause possible de variabilité et vérifier si le processus est sous contrôle, les graphiques ont été utilisés pour contrôler les anomalies aux points d’échantillonnage. Grâce aux graphiques, il a été possible d’identifier et de comparer la variabilité des questions de sciences statistiques.
Il a utilisé le logiciel minitab comme outil d’analyse de données. À partir des résultats entre les limites de contrôle, il a été possible de résoudre les défauts et d’améliorer la qualité. Les graphiques de contrôle de la moyenne, de l’amplitude et de l’écart-type ont été choisis pour contrôler les variations de la moyenne en statistique.
L’instrument visant à identifier, analyser, comparer, corriger et réduire la variabilité dans les applications des sciences de l’éducation a fait appel à Minitab qui est un programme informatique propriétaire destiné à des fins statistiques (MINITAB, 2016). « C’est un outil qui nous permet d’effectuer des calculs statistiques complexes et de visualiser les résultats, rendant l’analyse des données accessible à l’utilisateur occasionnel et pratique pour l’utilisateur plus expérimenté » (PEREIRA et PATRÍCIO, 2016).
Pour améliorer la qualité, la technologie des logiciels statistiques est utilisée:
Les outils statistiques en plus de hiérarchiser les applications proposées en fonction du degré d’importance, ils font l’identification et aident à l’action sur les problèmes pour l’élimination des causes possibles. Permettre à l’institution d’avoir un degré plus élevé de stabilité dans les applications analysées (WERKEMA, 2006, p.32).
Stratification : « La stratification consiste à diviser les secteurs en sous-secteurs en fonction des facteurs souhaités, appelés facteurs de stratification, c’est-à-dire pour le processus de division de l’ensemble hétérogène en sous-groupes homogènes » (VIEIRA, 1999).
Checksheet: Pour Werkema (2006), la fiche de vérification est un formulaire qui a dans son champ d’application des critères à analyser, afin de faciliter la collecte et le remplissage des données. Il s’agit d’un outil utilisé pour faciliter la collecte de données et qui doit être adéquat pour que la collecte soit efficace. Par conséquent, la feuille de contrôle doit préciser clairement le type de données à recueillir, l’opération à effectuer, la date de collecte, l’analyste et toute autre information utile pour identifier la cause d’une mauvaise performance fonctionnelle (CARPINETTI, 2010; MONTGOMERY, 2009). Selon Vieira (1999), le type de feuille de contrôle dépendra de ses objectifs, à savoir: comment augmenter la proportion d’articles non conformes; inspecter l’attribut; indiquer où se trouve le défaut dans le produit final; augmenter les causes des défauts; analyser la distribution d’une variable; et surveiller un processus de fabrication.
Graphique de Pareto: C’est l’outil qui fait la distribution de la fréquence des données, en soulignant le défaut qui se produit le plus fréquemment, et peut être ceux de pourcentage ou d’ordre réel. Se rappeler qu’un défaut plus souvent peut ne pas être le problème principal ou le plus critique du processus (CARPINETTI, 2010; MONTGOMERY, 2009). Vieira (1999) dit que le diagramme de Pareto est utilisé pour identifier les causes de problèmes tels que les produits manufacturés qui nécessitent des retouches, les dépenses inutiles, les accidents de travail, les pannes d’équipement, les erreurs et les retards de livraison, entre autres.
Diagramme de cause à effet: Également connu sous le nom de diagramme d’Ishikawa, il a pour fonction d’identifier et d’analyser les causes qui favorisent un effet indésirable. C’est un diagramme efficace pour identifier la racine du problème (CARPINETTI, 2010; MONTGOMERY, 2009). Werkema (2006) indique que le diagramme de cause à effet est un outil utilisé pour présenter la relation entre l’effet ou le problème et la cause qui pourrait modifier le résultat. Le diagramme de cause à effet organise l’information de manière à ce qu’elle soit plus claire pour faciliter l’analyse et l’identification des causes du problème, ce qui permet de prendre des mesures correctives pour éliminer la cause du problème (TRIVELLATO, 2010).
Histogramme : Selon Werkema (1995), un histogramme peut être défini comme un graphique à barres dans lequel l’axe horizontal, subdivisé en plusieurs petits intervalles, présente les valeurs assumées par une variable d’intérêt.
Diagramme de dispersion: Le diagramme de dispersion est chargé d’aider à identifier les relations entre un défaut et une cause, c’est-à-dire qu’il vise à identifier la relation entre deux variables ou même la relation d’une troisième cause. Les relations entre les variables peuvent être : positives, négatives ou inexistantes (CARPINETTI, 2010; MONTGOMERY, 2009).
Carte de contrôle: Selon Werkema (2006), toute immobilisation corporelle ou incorporelle, lorsqu’elle est élaborée et/ou fabriquée, présente une variation découlant du processus. On sait que ces variations doivent être strictement réduites. Pour Werkema (2006), les cartes de contrôle sont utilisées pour surveiller la variabilité, distinguer les types de variation et évaluer la stabilité du processus, qu’il soit sous contrôle ou non. Cependant, le processus peut varier de causes communes ou de causes spéciales
Les cartes de contrôle ont été créées par Shewhart et sont composées de limite centrale ou moyenne (LC), limite inférieure (LI) et limite supérieure (LS). Sa fonction principale est d’indiquer si le processus est sous contrôle ou non, c’est-à-dire si le processus fabrique des produits selon les spécifications ou non. L’analyse du processus est effectuée à partir de la vérification de la carte de contrôle, en observant si les points qui y sont tracés se situent entre les limites supérieure et inférieure de spécification (CARPINETTI, 2010; MONTGOMERY, 2009).
Cartes de contrôle: Sert à analyser les variations de processus des causes courantes et à détecter les causes spéciales, est un outil appelé Graphiques ou Cartes de contrôle. L’analyse de la capacité d’un processus est un élément essentiel d’un programme mondial de qualité. Parmi les principales utilisations des données d’une analyse de la capacité des procédés, on peut se démarquer (MONTGOMERY, 2004) :
2.2.1 RÈGLES STATISTIQUES POUR IDENTIFIER LES CAUSES SPÉCIALES
Suggère un ensemble de règles de décision pour distinguer les modèles non aléatoires dans les cartes de contrôle. Plus précisément, il suggère de conclure que le processus est hors de contrôle si (MONTGOMERY, 2004) :
1er cas : identifiez six, huit points ou plus au-dessus ou au-dessous de la ligne médiane. Causes possibles: changement dans le processus de réglage de la machine, la méthode ou un matériau différent, panne d’un composant dans la machine, bris de la machine et grande variation dans le matériau reçu.
2ème cas : trouvez six, sept points ou plus vers le haut ou vers le bas. Causes possibles : usure progressive de l’outil, usure de l’équipement ou usure liée à l’instrument de mesure.
3ème cas : vérifier le déplacement de la moyenne. Causes possibles: nouvelle méthode, nouvelle machine en amélioration de la qualité et un nouveau lot de matériau.
4ème cas : points en dehors des limites de contrôle. Causes possibles: erreur de mesure ou de frappe, bris d’outil ou instrument de mesure non réglementé, qui ne permet pas l’identification de la mesure.
5ème cas : périodicité des points. Causes possibles : non-uniformité de la matière première reçue, rotation des opérateurs, des gabarits et des instruments, et différence entre les quarts de travail.
2.2.2 CARTES DE CONTRÔLE DES VARIABLES ET DES ATTRIBUTS
Les cartes de contrôle par variables sont destinées à informer sur l’amélioration de la qualité, la capacité du processus, la prise de décision concernant les spécifications du produit, le processus de production et les décisions sur les pièces nouvellement produites. Ils sont appliqués là où les caractéristiques de qualité peuvent être mesurées quantitativement. Ils peuvent être, par exemple, les dimensions des pièces, le volume, le poids, entre autres. Ainsi, son large champ d’application est perçu, puisque plusieurs types de procédés ont ces types de caractéristiques (MAGALHÃES, 2011).
« Les cartes de contrôle pour les variables sont plus utilisées que les cartes de contrôle pour les attributs, car elles ont des informations plus concrètes, travaillant avec de petits échantillons, permettant d’identifier plus rapidement les causes qui affectent la stabilité du processus » (REBELATO, 2006). « Les cartes de contrôle des variables sont des cartes pour les moyennes, utilisées pour contrôler la valeur moyenne de la performance du procédé, une carte d’amplitude ou une carte d’écart-type, étant le graphique d’amplitude le plus utilisé, car, dans la plupart des cas, l’écart-type du processus n’est pas connu » (CASTRO, 2012).
Les cartes de contrôle peuvent être classées en deux groupes: les cartes de contrôle pour les variables: elles enregistrent les caractéristiques de qualité mesurées à l’échelle quantitative. Et les cartes de contrôle par attributs : il enregistre les caractéristiques de qualité, étant mesuré sur une échelle qualitative, par exemple, il est considéré comme conforme et non conforme (SIQUEIRA, 1997). Ainsi, selon Spiegel et Stephens (2007), les termes « variables » et « attributs » sont associés au type de données collectées à partir du processus.
2.2.3 GRAPHIQUE DE CONTRÔLE POUR LE MILIEU (X-BAR) ET L’AMPLITUDE (R)
Le graphique moyen ![]() est utilisé pour contrôler la moyenne du processus (centralité) et le graphique d’amplitude
est utilisé pour contrôler la moyenne du processus (centralité) et le graphique d’amplitude ![]() contrôler la variabilité du processus considéré (IPEK et al., 1999).
contrôler la variabilité du processus considéré (IPEK et al., 1999).
Expressions pour calculer les limites de contrôle de ![]() et R.
et R.
Graphique de contrôle ![]() . La ligne centrale et les limites de contrôle supérieure et inférieure pour la carte de contrôle
. La ligne centrale et les limites de contrôle supérieure et inférieure pour la carte de contrôle ![]() elles sont:
elles sont: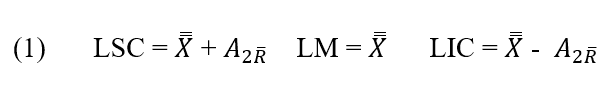
Carte de contrôle R. La ligne centrale et les limites de contrôle supérieure et inférieure de la carte de contrôle R sont les suivantes :
![]()
2.2.4 GRAPHIQUE MOYEN (X-BAR) ET ÉCART TYPE (S)
La carte de contrôle de la moyenne (graphique à barres X) est utilisée pour contrôler la moyenne du processus, tandis que la carte de contrôle (carte d’écart type S) est utilisée pour contrôler la variabilité du processus. Lorsque la taille de l’échantillon (sous-groupe) est inférieure ou égale à dix, les graphiques R et S se ressemblent. Cependant, lorsque la taille de l’échantillon augmente, le graphique S devient plus précis que le graphique R et devrait être utilisé (SIQUEIRA, 1997).
Graphique de contrôle ![]() . La ligne centrale et les limites de contrôle supérieure et inférieure pour la carte de contrôle
. La ligne centrale et les limites de contrôle supérieure et inférieure pour la carte de contrôle ![]() elles sont:
elles sont:
![]()
Carte de contrôle S: 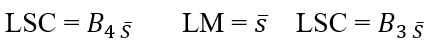
2.2.4.1 CARTES DE CONTRÔLE PAR ATTRIBUTS
Les diagrammes d’attributs sont utilisés pour contrôler l’analyse des défauts. Ces graphiques sont particulièrement utiles dans le contrôle des matières premières et des produits finis, et sont également utilisés dans l’analyse des évaluations de la qualité dans les lettres des consommateurs. Un attribut est une caractéristique d’un produit, d’un processus ou de toute autre population qui peut être comptée, mais ne peut pas être décrite, de sorte que ses valeurs sont incrémentées (RODRIGUES, 1998). Ce sont des graphiques qui nous permettent d’identifier comment les ensembles d’échantillons se comportent autour des limites, des tendances et des échanges de niveaux. Dans les variables, il est rapidement perçu lorsque les données ne suivent pas une distribution aléatoire. Dans les cartes de contrôle des attributs, les unités sont classées comme parfaites ou défectueuses selon les critères établis. Par conséquent, la probabilité qu’une unité défectueuse soit produite est constante et, par conséquent, la distribution de l’échantillon correspondante est binomiale (CHAVES et TEIXEIRA, 1997). Les diagrammes d’attributs sont utilisés pour contrôler l’analyse des défauts. Ces graphiques sont particulièrement utiles dans le contrôle des matières premières et des produits finis, et sont également utilisés dans l’analyse des commentaires sur la qualité et les caractéristiques exprimées qualitativement, c’est-à-dire lorsque ces caractéristiques analysées ne sont pas représentées numériquement et peuvent être classées selon ou non conformes (SOUZA, 2005). Ce sont les mesures représentatives qui résultent du décompte du nombre d’articles du produit sur une échelle discrète qui présentent une caractéristique particulière d’intérêt. Les mesures sont effectuées par inspection visuelle et les caractéristiques non mesurables sont enregistrées. On peut dire diagramme de contrôle par variable aléatoire discrète avec fonction de densité de probabilité de Poisson (LAGO, 1999).
Les mathématiques des cartes attributaires ne nécessitent pas de tables. Elles peuvent être appliquées à des systèmes dans lesquels les mesures consistent à approuver ou à désapprouver ou à des processus dans lesquels il est très difficile, voire impossible, d’obtenir des mesures de variables (RODRIGUES, 1998).
Les informations statistiques des mesures par attributs dans les solutions aux problèmes des sciences de l’éducation, sont classées dans les produits présentant des anomalies ou des défauts. L’un des principaux objectifs de l’analyse de mesure d’attributs est d’identifier, de détecter et de corriger les défauts, la qualité peut être définie comme l’ensemble des attributs qui rendent un bien ou un service entièrement adapté à l’utilisation pour laquelle il a été conçu (MONTGOMERY, 1985). Les quatre cartes de contrôle des attributs dans les anomalies et les défauts, utilisées selon Montgomery (2004), sont les suivantes : Cartes de contrôle par attributs qui sont : Lettre p (proportions non conformes), Graphique Np (unités non conformes), Lettre C (nombre de non-conformité par unité) et Lettre u (taux de non-conformité par unité).
2.2.5 GRAPHIQUE P (PROPORTIONS NON CONFORMES)
Pour Werkema (2006), le graphique p est utilisé lorsque la caractéristique de la qualité de l’intérêt est représentée par la proportion d’articles défectueux produits par le processus analysé.
Carte de contrôle P:
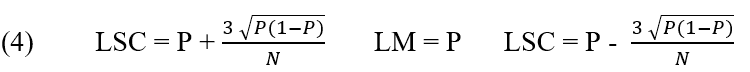
2.2.6 GRAPHIQUE NP (UNITÉS NON CONFORMES)
La lettre n’indique pas le nombre de défauts par échantillon et est utilisée pour contrôler le nombre de produits défectueux dans chaque lot et s’assurer que le processus est sous contrôle (RODRIGUES, 1998).
L’extrémité médiane et les limites de contrôle supérieure et inférieure du graphique np sont les suivantes :
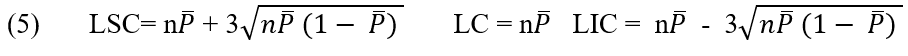
2.2.7 GRAPHIQUE C NOMBRE DE (NON CONFORME PAR UNITÉ)
Le graphique c est utilisé pour déterminer si le numéro de défaut sur un seul article se situe dans les limites de contrôle définies. Elle peut être considérée comme une inspection finale (RODRIGUES, 1998). Le graphique c est le plus approprié lorsque les défauts sont dispersés dans un milieu continu, tels que: nombre de défauts par zone de tissu, nombre d’imperfections par longueur de plancher; et lorsqu’un produit peut avoir plus d’un type de défaut (RIBEIRO et CATEN, 2012).
Par conséquent, les limites de contrôle du graphique C seront calculées à l’aide des équations suivantes :
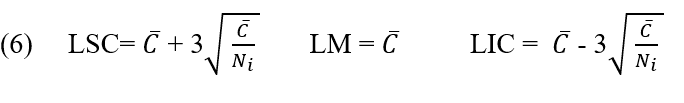
2.2.8 TAUX DE NON-CONFORMITÉ GRAPHIQUE U PAR UNITÉ
Le graphique u est utilisé pour surveiller les défauts d’une unité de production (MONTGOMERY, 1997). Le tableau u est recommandé lorsque le produit est composé de diverses pièces et de nombreuses caractéristiques de qualité qui doivent être inspectées et aussi lorsque la taille de l’unité de produit est variable (CORTIVO, 2005).
L’angle central et les limites de contrôle supérieure et inférieure du graphique en U sont les suivants :
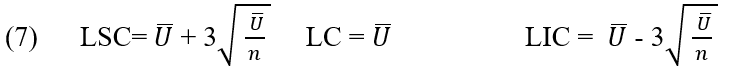
2.2.9 RÉGRESSION LINÉAIRE MULTIPLE
L’analyse de régression multiple est une technique utilisée pour étudier la relation entre une variable dépendante et un ensemble de variables indépendantes (MONTGOMERY et RUNGER, 2009). La technique permet l’estimation de valeurs futures pour la variable dépendante, étant donné un ensemble de données d’entrée pour les variables indépendantes (PEDRINI et CATEN, 2009 ; DOWNING et CLARK, 2002)
Le modèle de base de la régression linéaire multiple où ![]() pour j=0,1,2…..k sont des coefficients de régression, Y est la variable dépendante des régresseurs
pour j=0,1,2…..k sont des coefficients de régression, Y est la variable dépendante des régresseurs ![]() et la valeur e est l’erreur aléatoire de l’équation. (MONTGOMERY, 2015).
et la valeur e est l’erreur aléatoire de l’équation. (MONTGOMERY, 2015).
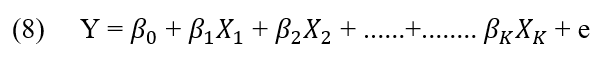
Le processus est étudié pour comprendre les besoins d’analyse des applications des sciences de l’éducation et de leurs étapes de processus. Les sources d’analyse sont soulevées, les applications qui y sont analysées, sont la variabilité les principaux facteurs qui l’influencent. Identifier le type de carte de contrôle le plus approprié pour analyser les données par le logiciel minitab. Avec la méthode, le contrôle stochastique du processus a cherché la structuration de la recherche afin de contribuer au progrès de la même chose.
3. RÉSULTATS ET DISCUSSION
3.1 L’UTILISATION DES CARTES DE CONTRÔLE MINITAB POUR RÉDUIRE LA VARIABILITÉ
Après avoir collecté et tracé les données dans les applications d’ingénierie, certains graphiques ont été construits pour les variables et des graphiques pour les attributs dans les cartes de contrôle du logiciel Minitab afin de surveiller les pertes dues aux variations de production. Pour l’analyse des résultats, la plage de tolérance composée des composants a été déterminée par les composants suivants : Limite supérieure de contrôle LSC, LC Ligne médiane et Limite inférieure de contrôle LIC.
Il a été observé qu’après avoir identifié, éliminé et réduit les causes de variabilité apportait la possibilité d’améliorer la qualité des produits. Grâce à l’analyse des résultats obtenus dans les applications statistiques sera présenté le contrôle de la stabilité dans les causes des défauts dans les points d’échantillonnage dans les graphiques, et le contrôle du processus dans l’échantillon a été effectué afin de contrôler la variabilité. Les cartes de contrôle présentaient les résultats suivants parmi les paramètres statistiques: Calcul de la moyenne du processus, Calcul de l’écart type, Calcul des limites de contrôle LSC, LIC et amplitude dans les applications ci-dessous:
3.2 PROBABILITÉS ET APPLICATIONS STATISTIQUES EN INGÉNIERIE PAR CARTE DE CONTRÔLE DANS LE LOGICIEL MINITAB DANS LA RÉDUCTION DE LA VARIABILITÉ
Constructions graphiques dans les applications de statistiques descriptives exécutées par la carte de contrôle dans Minitab Software.
01) Les données se réfèrent à un processus d’usinage à broches, dans lequel les diamètres sont mesurés en échantillonnant 5 pièces sur 25 lots. Passez en revue le processus avec Minitab Software.
Tableau 1 : Mesures du diamètre des broches
| Lot | Mensurations | ||||||
| 1 | 2,08495 | 2,09203 | 1,01425 | 0,47627 | 1,75308 | ||
| 2 | 2,44288 | 1,84913 | 1,02012 | 1,5103 | 0,5167 | ||
| 3 | 2,08819 | 0,34567 | 0,67246 | 2,14641 | 0,51528 | ||
| 4 | 1,42411 | 1,04348 | 1,15683 | 0,9108 | 1,23562 | ||
| 5 | 1,43307 | 0,22926 | 1,51612 | 0,82627 | 1,29935 | ||
| 6 | 1,2113 | 0,63715 | 0,97815 | 2,30782 | 1,0003 | ||
| 7 | 2,14731 | 1,95837 | 0,95294 | 1,35384 | 0,73037 | ||
| 8 | 2,02444 | 1,60384 | 1,64667 | 1,66449 | 0,92746 | ||
| 9 | 1,4743 | 1,93916 | 1,06107 | 1,55396 | 0,8049 | ||
| 10 | 1,09096 | 2,09033 | 0,62161 | 1,45256 | 1,77208 | ||
| 11 | 1,90879 | 1,274 | 1,46827 | 1,36343 | 1,06161 | ||
| 12 | 0,81791 | 1,89952 | 1,24044 | 0,72729 | 1,44959 | ||
| 13 | 0,58784 | 1,57195 | 0,73316 | 1,05367 | 3,29273 | ||
| 14 | 2,12184 | 0,90374 | 0,59773 | 1,63101 | 0,82706 | ||
| 15 | 1,2819 | 0,89479 | 1,05394 | 1,25779 | 0,99451 | ||
| 16 | 0,82836 | 0,16347 | 2,12864 | 1,69732 | 0,90752 | ||
| 17 | 0,14026 | 1,0432 | 0,76948 | 1,72083 | 3,95445 | ||
| 18 | 2,19158 | 0,87777 | 0,955 | 1,50304 | 1,1604 | ||
| 19 | 0,93195 | 1,82231 | 1,2179 | 1,72608 | 1,45375 | ||
| 20 | 0,84523 | 2,79753 | 2,30041 | 0,47693 | 0,58081 | ||
| 21 | 1,84098 | 2,37729 | 1,89976 | 1,2079 | 3,2343 | ||
| 22 | 1,15648 | 2,5689 | 0,90064 | 3,7548 | 1,24616 | ||
| 23 | 2,21913 | 0,91997 | 2,15777 | 1,48548 | 0,25288 | ||
| 24 | 1,41393 | 0,71069 | 0,63707 | 1,71835 | 1,52855 | ||
| 25 | 1,5938 | 1,19839 | 0,88228 | 1,23019 | 0,41643 | ||
Source : Action (2019)
Figure 01 : Carte de contrôle des broches défectueuse hors de contrôle
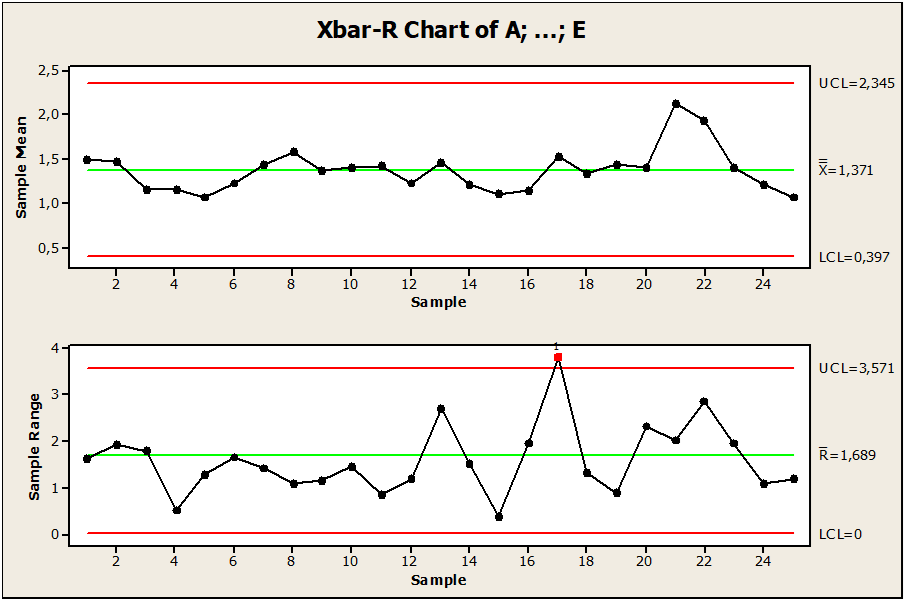
Les données de l’échantillon présentent un processus d’usinage des broches observé dans 25 lots de broches. Comme le montre la figure 01. Nous avons observé qu’il existe une variation entre le point 17 au-dessus de la limite supérieure de contrôle LSC, où le point est en dehors de la limite de contrôle. Sa limite centrale est égale à 1,68, sa limite de contrôle supérieure avec la valeur 3,57 et sa limite inférieure égale à 0,0, ce qui implique que le point 17 de la broche de valeur 3,95445 est influencé par la variabilité. Donc, pour garder le processus sous contrôle, il a été recommandé de supprimer, de modifier les valeurs ou de créer un nouveau graphique.
Figure 02 : Carte de contrôle avec les limites ajustées
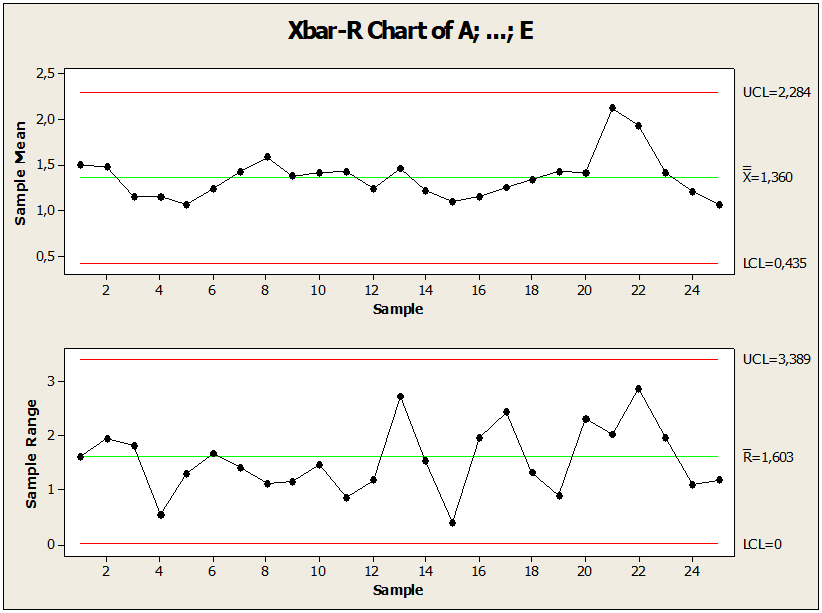
Après avoir vérifié l’anomalie, Figure 02. Le graphique montre le point sous contrôle par rapport à la moyenne, où il y a eu des modifications afin de garder le processus sous contrôle. Dans l’échantillon du point 17 de la valeur de non-conformité 3,95445, elle est passée à 2,55445. Ce changement effectué par la carte de contrôle suivie de règles statistiques a réduit la variabilité et le point en dehors de la limite de contrôle a été ajusté. Nous concluons que toutes ces mesures statistiques ont maintenu la stabilité du processus. Après avoir identifié, analysé, corrigé, réduit et contrôlé le processus des échantillons de non-conformité, il a été possible de comparer les résultats obtenus avec les résultats précédents entre le procédé: processus hors de contrôle, LC égale à 1,68, écart type égal à 0,69 et amplitude de la valeur limite 3,81 un point au-dessus de la limite. LSC. Procédé sous contrôle LC égal à 1,60, écart type égal à et 0,66 Amplitude de la valeur limite 3,61. Après comparaison avec les valeurs calculées dans les 1er et 2ème tests, il y a eu une amélioration des paramètres statistiques.
Figure 03 : montre les diamètres des broches
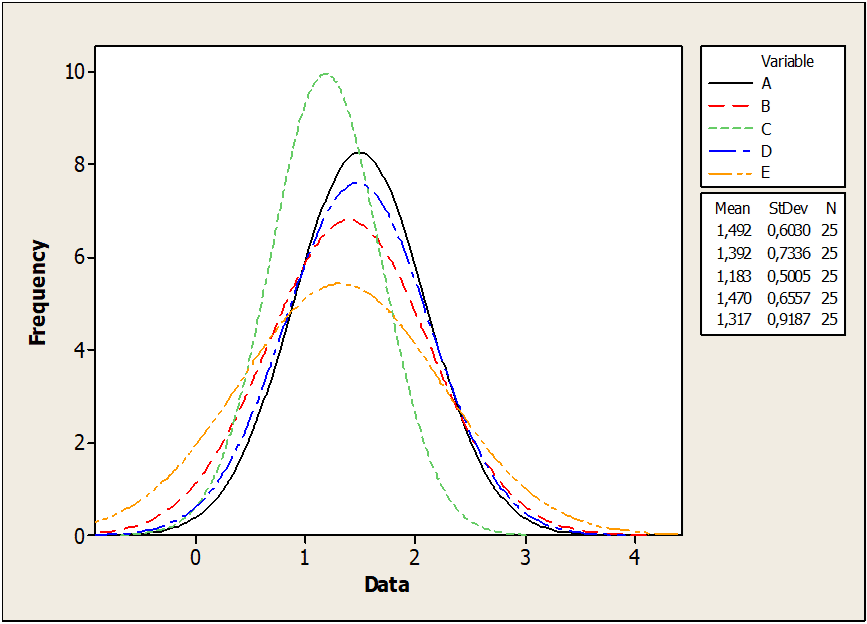
La figure 03 montre une courbe de dispersion des diamètres de broches dans les sous-groupes E avec une plus grande précision que la courbe de dispersion des sous-groupes D. L’écart-type pour les échantillons du sous-groupe E (0,91) est beaucoup plus grand que les échantillons du sous-groupe D. (0,50). Par conséquent, la distribution ajustée pour le sous-groupe E est aplatie et plus précise.
02) Une étude a été réalisée pour déterminer l’augmentation des défauts dans les portes en acier inoxydable des équipements de cuisine produits dans une entreprise de métallurgie. Au cours de l’étude, les défauts ci-dessous sont apparus avec leurs occurrences et les coûts associés. Construisez les diagrammes de Pareto respectifs.
Tableau 2 : pièces défectueuses
| Type de défauts | Nº. de pièces défectueuses | Coût unitaire de réparation/rebut | |
| Soudage mal exécuté | 55 | 50 | |
| Mauvais forage | 9 | 50 | |
| Défauts de flexion | 274 | 5 | |
| Emballage | 15 | 50 | |
| Mauvaise qualité de la plaque | 16 | 50 | |
| Coupes | 126 | 30 | |
| autre | 12 | 50 |
Source : Core Formation -Nufec (2006)
Figure 04 : Numéros de pièces défectueux
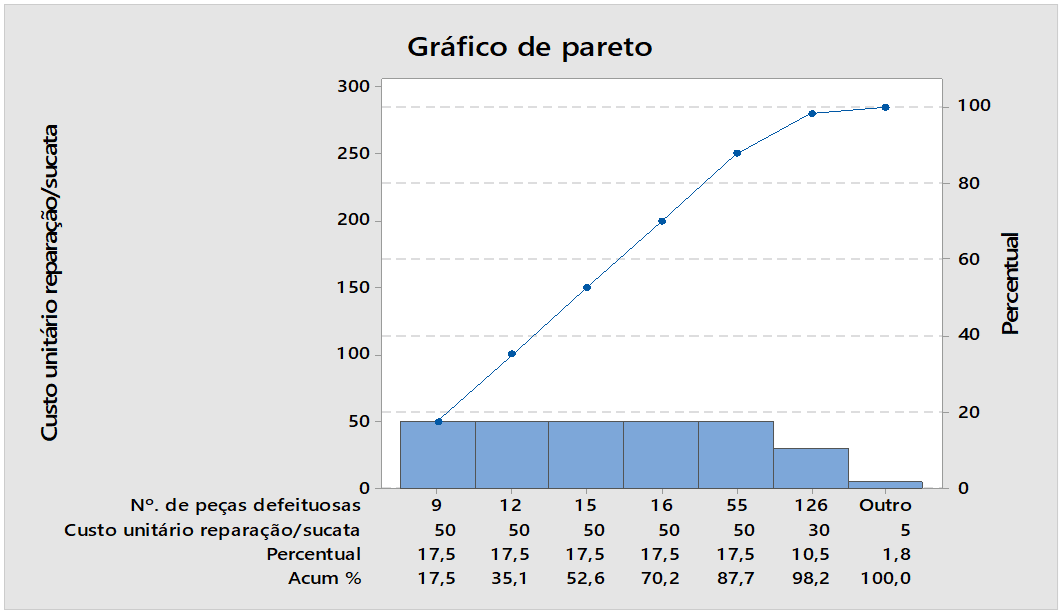
La figure 04 montre les résultats des numéros de pièces défectueuses, pourcentage, la plus grande source 9 pièces défectueuses qui correspond à un pourcentage de 17,5 %. Lors de l’analyse de la figure, on perçoit la présence d’une concentration de causes de variabilité particulière nécessitant une correction par la carte de contrôle du logiciel Minitab.
Figure 05 : Processus de numéros de pièces défectueux hors de contrôle
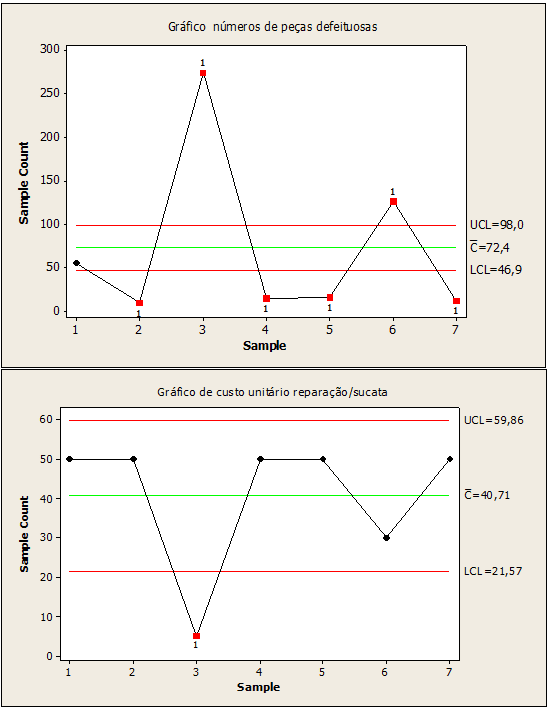
Il a été vérifié que la figure 05, se référant aux pièces défectueuses, montrait une variabilité aux points 2,3,4,5,6,7 avec des valeurs (9,274,15,16,126,12). D’autre part, coût unitaire dans la réparation de la ferraille ponctuelle avec variabilité 3 avec une valeur égale à 5. On conclut qu’il y a des causes particulières dans ces points et qu’il est nécessaire de les corriger.
Figure 06 : Processus de numéros de pièces défectueux sous contrôle
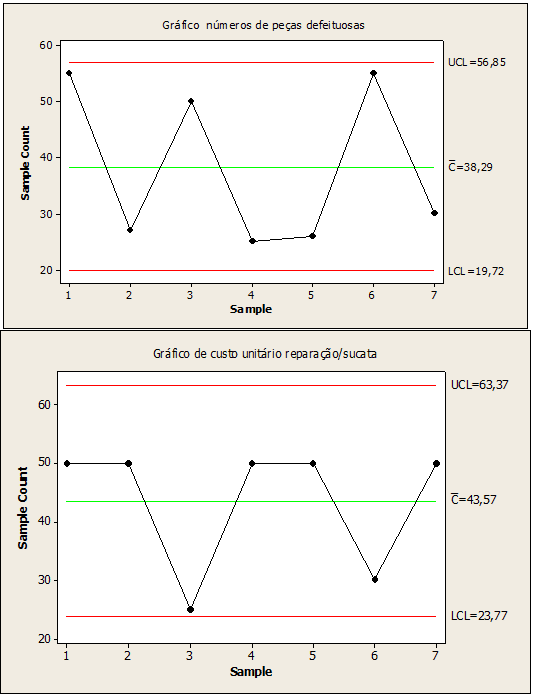
Dans la figure 06, les valeurs utilisées à la place des valeurs des points hors de contrôle 2,3,4,5,6,7, suivies sont 27,50,25,26,55,30 pour les pièces défectueuses et 25 pour la réparation de rebuts à coût unitaire au point 3. Ces données de remplacement générées par la carte de contrôle ont amélioré le processus stochastique en gardant sous contrôle, réduisant la variabilité dans la fabrication des portails en acier inoxydable, maintenant la qualité du produit stable.
03) Un moule d’extrusion est utilisé pour produire des tiges d’aluminium. Le diamètre des canes est une caractéristique essentielle de la qualité. Le tableau suivant indique les valeurs x et r pour 20 échantillons de cinq cannes chacun. Les spécifications sur les canes sont de 0,5035 +/- 0,0010 pouce. Les valeurs de données sont les trois derniers chiffres de la mesure, c’est-à-dire que 34,2 est lu comme 0,50342.
a) À l’aide de toutes les données, recherchez les limites de contrôle pour les graphiques X et R, construisez le graphique et tracez les données.
b) Utiliser les limites des tentatives de contrôle d’élément (a) pour identifier les points hors de contrôle. Si nécessaire, passez en revue vos limites de contrôle, en considérant que tout échantillon en dehors des limites de contrôle peut être éliminé.
Tableau 3 : Échantillons d’ongles
| Échantillon | R | Échantillon | R | ||
| 1 | 34,2 | 3 | 11 | 35,4 | 8 |
| 2 | 31,6 | 4 | 12 | 34,0 | 6 |
| 3 | 31,8 | 4 | 13 | 36,0 | 4 |
| 4 | 33,4 | 5 | 14 | 37,2 | 7 |
| 5 | 35,0 | 4 | 15 | 35,2 | 3 |
| 6 | 32,1 | 2 | 16 | 33,4 | 10 |
| 7 | 32,6 | 7 | 17 | 35,0 | 4 |
| 8 | 33,8 | 9 | 18 | 34,4 | 7 |
| 9 | 34,8 | 10 | 19 | 33,9 | 8 |
| 10 | 38,6 | 4 | 20 | 34,0 | 4 |
Source : Montgomery (2013)
Figure 07 : Échantillons de tiges hors de contrôle
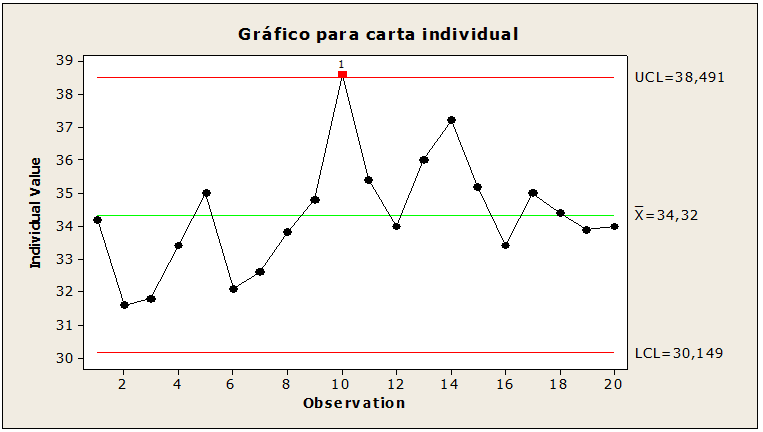
Contrôle statistique pour 20 échantillons de cinq bâtonnets chacun. Lors de l’interprétation de la figure 07, les valeurs de la limite supérieure étaient de 38,49, la moyenne de 34,32, l’écart-type de 1,72, la limite inférieure de 30,14 avec le point 10 de la valeur 38, 6 au-dessus de la limite supérieure donnant des indications de causes spéciales qui peuvent être correctes. Une correction à ce stade est suggérée afin que les limites soient ajustées.
Figure 08 : Échantillons d’ongles sous contrôle
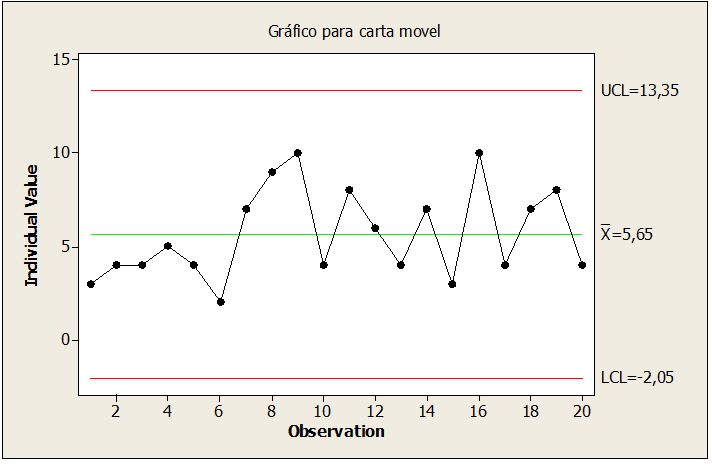
En corrigeant le point de la figure 08, le point 10 a été ajusté, réduisant la valeur de l’échantillon à 36,6, maintenant le processus stable et sous contrôle dans la fabrication du diamètre des tiges d’aluminium.
Figure 09 : Échantillons de tiges de capacité de procédé
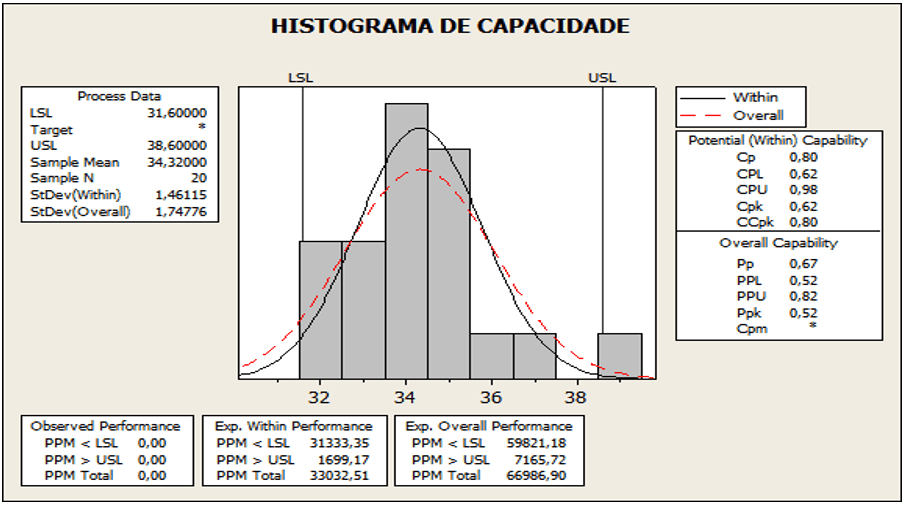
Selon l’analyse de la figure 09, il présente la valeur pour Cpk égale à 0,49, moyenne 5,65, écart type 2,434 et valeur p 0,025. Résultat CPk hors limites, si Ppk < CPk. La moyenne obtenue était de 5,65, avec déplacement vers le LSE. Le CPk 0,49 inférieur aux valeurs établies qui implique 1,33 est en dehors de la limite stable.
Figure 10 : Pourcentage de défauts
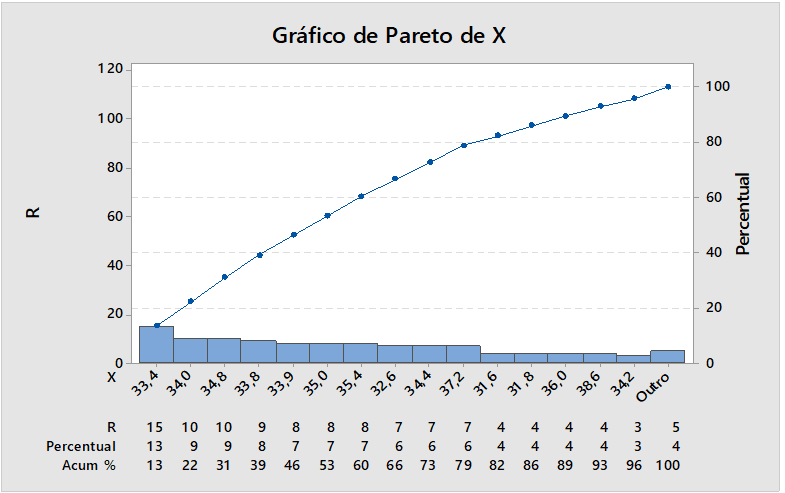
Graphique 10. Le graphique de Pareto fournit le pourcentage des échantillons analysés de défectueux produits dans ce processus, pourcentage, la plus grande source 15 pièces défectueuses qui correspond à un pourcentage 13%. Il est nécessaire d’éliminer les variations.
En observant les chiffres, il a été vérifié que sur la figure 07, le point 10 est en dehors de la limite de contrôle, présentant une anomalie dans le diamètre des tiges qui peut être correcte. Déjà dans la figure 09, le cpk est hors limites. Cependant, la figure 10 présente un défaut dans les tiges. Figure suivante 08. Après interprétation, analyse et élimination des causes spéciales au point du diamètre sont restées stables.
La figure 11 montre les cartes de contrôle des moyennes, de l’écart-type et du nombre de non-conformités mesurées par échantillonnage de 5 pièces sur 25 lots. À travers les graphiques présentés, nous pouvons observer qu’il y a un point en dehors de la limite de contrôle et est distribué autour de la moyenne, ainsi que cela nous a permis d’observer l’ordre de grandeur des écarts de processus et a finalement permis de trouver les points de causes spéciales, où il présente un point en dehors de la limite. Grâce à ces analyses, nous avons constaté qu’il existe une variabilité de cause spéciale au point 17 LSC, où le point est en dehors de la limite de contrôle, nécessitant des corrections et une réduction de la variabilité. Cette anomalie a été détectée par la carte de contrôle du logiciel Minitab lors du 1er test où le processus était nécessaire pour se stabiliser. Donc, pour garder le processus sous contrôle, le 2ème test a été appliqué pour compléter le 1er test afin de créer une nouvelle carte de contrôle qui a le processus sous contrôle.
Trois situations ont été recommandées lors de la construction du graphique limite sous contrôle : la suppression de l’observation de la valeur 3,95445, la modification des valeurs de non-conformité ou la construction d’un nouveau graphique. Le 2e test de la figure 12. Montrer la correction, la comparaison et la réduction des variations dans la construction d’un nouveau graphique avec le point sous contrôle par rapport à la moyenne, avec modification du point de prélèvement afin de garder le processus sous contrôle. La valeur de l’échantillon 3,95445 a changé la valeur 2,55445. Après avoir contrôlé le processus, il a été possible de comparer les résultats obtenus avec les résultats précédents entre les processus. Par rapport aux valeurs du calcul de l’échantillon dans le procédé sous contrôle, la moyenne présentait une valeur égale à 1,60, un écart-type de 0,66 et une amplitude de la valeur limite de 3,66. Alors que le processus hors de contrôle signifie égal à 1,68, écart type 0,69 et amplitude limite avec la valeur 3,81.
Figure 11 : Lettre hors de contrôle
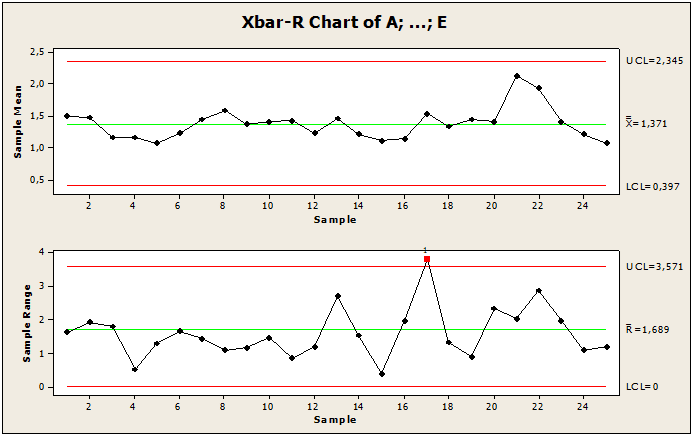
Figure 12 : Lettre sous contrôle
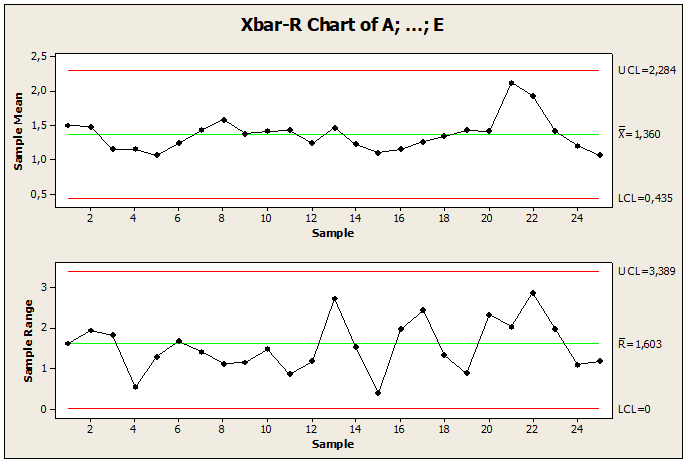
Les résultats obtenus dans cette étude montrent que les cartes de contrôle sont un outil efficace pour réduire la variabilité dans les applications des sciences de l’éducation en trouvant la stabilité du processus et en améliorant la qualité.
4. CONCLUSION
Grâce aux cartes de contrôle du logiciel Minitab, il a été possible de tracer et d’analyser les changements dans la distribution de l’échantillon dans le processus statistique en informant les points critiques avec la variabilité dans les applications des sciences de l’éducation. Grâce à l’analyse des cartes de contrôle, nous pouvons percevoir que les applications statistiques présentaient une variabilité.
Le graphique est un outil utilisé pour contrôler l’anomalie par des tests statistiques et la variabilité a été trouvée dans certains points d’échantillonnage d’applications statistiques. Par conséquent, il était nécessaire de faire des inférences dans le contrôle des variables avec des points hors de contrôle. Il a été vérifié par le 1er test que les sous-groupes qui sont inhabituels par rapport à d’autres sous-groupes présentaient des anomalies, et il était nécessaire d’appliquer le 2ème test pour corriger et garder le processus sous contrôle.
Les graphiques ont permis de vérifier les variations et de stabiliser les variables entre les paramètres moyens, les écarts-types et l’amplitude. Les graphiques ont permis d’approximer les points de prélèvement en dehors des limites et d’ajuster les défauts entre les limites, aidant à l’amélioration continue du processus, permettant de percevoir les défauts et de contrôler les causes de variation anormale entre les paramètres limités du graphique en comparaison des échantillons dans les tests de vérification.
En analysant les graphiques afin de fixer des limites pour les inspections futures, il serait nécessaire d’éliminer la variabilité spatiale et, après avoir modifié les échantillons, il deviendrait possible de créer de nouveaux graphiques dans minitab pour éliminer ces points de calcul des limites révisées.
Les objectifs énoncés dans cette recherche ont été atteints avec succès en permettant l’utilisation de techniques statistiques pour identifier et éliminer les anomalies qui ne sont pas conformes aux problèmes statistiques. De telles techniques permettaient l’inférence dans des applications d’ingénierie à travers des échantillons. Les actions ont réduit l’occurrence de la variabilité dans minitab Software et ont ainsi maintenu le processus stochastique stable et sous contrôle. Ce thème a révélé qu’il est possible de collecter, d’analyser et d’interpréter des données à l’aide de cartes de contrôle, car grâce à cet outil, il est possible de vérifier l’anomalie dans les problèmes statistiques.
On trouve que le logiciel statistique est capable de répondre aux spécifications en matière de contrôle des processus. Il a été vérifié la nécessité d’utiliser Minitab pour prévenir les causes possibles de variabilité. Enfin, avec la présente étude de la variabilité, il a été possible de percevoir et de comprendre la contribution des ressources des cartes de contrôle en appliquant le logiciel à la réduction de l’anomalie dans les applications de la science statistique.
RÉFÉRENCES
BORTOLOTTI, S. L. V. et al. Análise da qualidade do produto final no processo de envase de azeitonas verdes. Tecnol. & Hum., Curitiba, ano 23, n. 36, jan/jun. 2009. Disponível em: https://revistas.utfpr.edu.br/rth/article/viewFile/6238/3889
CARPINETTI, L. C. R. Gestão da Qualidade, Conceitos e Técnicas. São Paulo: Atlas S.A., 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CASTRO, D. R. C. et al. A aplicabilidade dos gráficos de controle nas empresas como modelo de inspeção para a avaliação da qualidade. In: XXXII Encontro Nacional de Engenharia de Produção. Bento Gonçalves, RS, 2012. Disponível em: http://www.abepro.org.br/biblioteca/enegep2012_tn_stp_158_921_20804.pdf
CHAVES, J. B. P. Controle de Qualidade na Indústria de Alimentos. Viçosa,
MG, (s.n.), 1997.
CHAVES, J. B. P.; TEIXEIRA, M. A. Controle Estatístico de Qualidade:
inspeção por amostragem/ mapas de controle. DTA/UFV. Viçosa, MG: (s.n.), p. 162,
1997.
CORTIVO, Z. D. Aplicação do Controle Estatístico de Processo em sequências curtas de produção e análise estatística de processo através do planejamento econômico. Curitiba: Universidade Federal do Paraná, 2005.
FERREIRA, J. M.; OLIVEIRA, M. S. de. Controle estatístico da qualidade. Lavras: UFLA/FAEPE, p.87, 2008.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
HORA, H. R. M., COSTA, H. G. Tomada de decisão no MASP: uma contribuição para decisões utilizando a matriz AHP. XXIX Encontro Nacional de Engenharia de Produção. Salvador. ENEGEP, 2009.
IPEK, H. et al. The application of statistical process control. Minerals Engineering, Vol. 12, Issue 7, p. 827-835, 1999. ISSN 0892-6875. Disponível em: https://doi.org/10.1016/S0892-6875(99)00067-9.
JURAN, J. M.; GRYNA, F. M. Controle da Qualidade: Métodos Estatísticos Clássicos Aplicados à Qualidade. São Paulo, Ed. Makron, 1992.
LAGO NETO, J. C. do. O efeito da autocorrelação em gráficos de controle para variável contínua: Um estudo de caso. Florianópolis, 1999.
MAGALHÃES, M. S. de; MOURA NETO, F. D. Economic-statistical design of variable parameters non-central chi-square control chart. Production, v. 21, n. 2, p. 259–270, 2011.
MICHEL, M. H. Metodologia e Pesquisa Científica em Ciências Sociais: Um Guia Prático para Acompanhamento da Disciplina e Elaboração de Trabalhos Monográficos. São Paulo: Atlas, 2005.
MINITAB. Conheça o Minitab para Windows. 1º. ed. São Paulo: Editora Minitab
Inc., 2010.
MONTGOMERY, D. C. Estatística Aplicada e Probabilidade para Engenheiros. Tradução e revisão técnica Verônica Calado. Rio de Janeiro, LTC, 2015.
MONTGOMERY, D. C. Introdução Ao Controle Estatístico Da Qualidade. 4. ed. Rio de Janeiro: LTC, 2009.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 1997.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 4. ed. Rio de Janeiro: LTC, 2004.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 2013.
MONTGOMERY, D. C. Introdução ao controle estatístico de qualidade. Rio de Janeiro: LTC, 2016.
OLIVEIRA, T. S.; LIMA, R. H. P. Aplicação do controle estatístico de processo na mensuração da variabilidade em uma usina de etanol. Anais. INGEPRO Inovação, Gestão e Produção, v. 3, n. 6, p. 022-033, 2015.
OLIVEIRA, V. F. de. Mobilidade e acessibilidade urbana: uma análise socioespacial a partir dos bairros Jardim Morada do Sol e Conjunto Habitacional Ana Jacinta, em Presidente Prudente. Faculdade de Ciências e Tecnologia – FCT, Unesp, 2011.
PALLADINI, E. P. et al. Gestão da Qualidade: Teoria e Casos. 2. Ed. São Paulo: Atlas, 2010.
PEDRINI, D. C. Proposta de um método para aplicação de gráficos de controle de regressão no monitoramento de processos. Universidade Federal do Rio Grande do Sul: UFRGS, 2009.
PEREIRA, A.; PATRÍCIO, T. Guia prático de utilização: análise de dados para Ciências Sociais e Psicologia. 8.ª ed. Lisboa : Sílabo, 2013.
REBELATO, M. G. et al. Estudo sobre a aplicação de gráficos de controle em processos de saturação de papel. XIII SIMPEP. Bauru, SP: 2006.
RIBEIRO, J. L.; CATEN, C. T. Controle estatístico de processos: Apostila de Curso. Porto Alegre: UFRGS, 2012.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. 3 ed. São Paulo: Atlas, 1999.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
RODRIGUES, G. P. Controle Estatístico de Qualidade e de Processo na Indústria de Alimentos. Universidade Federal de Viçosa, MG, p. 152,1998.
ROSA, L. C. Introdução ao Controle Estatístico de Processos. Santa Maria, Ed. Da UFSM, 2009.
SIQUEIRA, L. G. P. Controle Estatístico de Processos – Equipe Grifo – Série Qualidade Brasil. São Paulo: Pioneira, 1997.
SOUZA, A. M., RIGÃO, M. H. Identificação de variáveis fora de controle em processos produtivos multivariados. Revista Produção, São Paulo, V.15 no.1, p.74-86, abr. 2005.
SOUZA, R. Case Research in Operations Management. EDEN Doctoral Seminar on Research Methodology in Operations Management, Brussels, Belgium, 2005.
SPIEGEL, M. R.; STEPHENS, L. J. Schaum’s esboço de teoria e problemas de estatística: Aprenda a si mesmo. 4ª ed., Rio de Janeiro: LTC, 2007.
TRIVELLATO, A. A. Aplicação das sete ferramentas básicas da qualidade no ciclo PDCA para melhoria contínua: estudo de caso numa empresa de autopeças. Trabalho de conclusão de curso, Universidade de São Paulo, 2010.
VIEIRA, S. Estatística para a qualidade: como avaliar com precisão a qualidade em produtos e serviços. Rio de Janeiro: Elsevier, 1999.
VILAÇA, A. C.; OLIVEIRA, R. C. B. Utilização do Controle Estatístico de Processo para Avaliação de Peso de Massas para Pastel. FAZU em Revista, Uberaba, n. 8, p. 137-146. 2011.
WERKEMA, M. C. C. Avaliação de sistemas de medição. 2.ed. Belo Horizonte: Werkema. 2012.
WERKEMA, M. C. C. Ferramentas estatísticas básicas para o gerenciamento de processos. Belo Horizonte: Werkema, 2006.
YIN, R. K. Estudo de caso: planejamento e métodos. 2. Ed. Porto Alegre: Bookman, 2001.
[1] Master en Génie des Procédés – PPGEP/ITEC-UFPA.
[2] Docteur en ingénierie des ressources naturelles de l’Université fédérale du Pará.
Soumis : Avril 2021.
Approuvé : Juin 2021.