ARTIGO ORIGINAL
SILVA, Sarley De Araújo [1] MAGNO, Rui Nelson Otoni [2]
SILVA, Sarley De Araújo. MAGNO, Rui Nelson Otoni. Probabilidade, carta de controle aplicada a software em ciência da educação. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 06, Vol. 11, pp. 43-73. Junho de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/ciencia-da-educacao, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/ciencia-da-educacao
RESUMO
O presente estudo menciona sobre a redução de variabilidade e as perdas por causas especiais em aplicações das ciências da educação, tendo como objetivo detectar e corrigir desvios de variabilidade por meio das cartas de controle do software em problemas de estatística aplicada. Desta forma, buscou-se estudar conceitos sobre as cartas de controle por variáveis e atributos no controle de anormalidades. Na realização desta temática foi utilizada a metodologia quantitativa e a carta de controle do Software Minitab. Os resultados obtidos permitiram reduzir as perdas e melhorar o processo da qualidade através dos ajustes amostrais entre os limites de controle do Minitab, propiciando compreender e analisar as causas de anomalias. Portanto, conclui-se que a ferramenta a partir das ações corretivas é capaz de estabilizar os desvios padrão e melhorar a qualidade das aplicações de probabilidade e estatística.
Palavras-chaves: Probabilidade, Software Minitab, Carta de Controle.
1. INTRODUÇÃO
A estatística é um ramo da matemática que utiliza-se da ferramenta probabilidade para explicar agrupamentos de dados, tanto em estudos observacionais quanto em experimentos para modelar, estimar e fazer previsão de fenômenos futuros. Tem por finalidade obter, organizar, analisar dados, calcular as cartas de controle, correlações e regressões, possibilitando fazer controle em variabilidade, aplicações estatísticas e instituições educacionais. Os métodos estatísticos referem-se a dados obtidos de observações na forma de medidas ou contagem. A partir de informações é possível estudar problemas de estatística referente ao controle de variabilidade aplicada nas ciências em engenharia, química, física, matemática, geografia e etc. A utilização do Software estatístico é uma importante ferramenta para estudos e aplicabilidades no controle de variações em problemas de probabilidade e estatística.
As instituições têm preocupação em manter elevados índices de desempenho no que diz respeito à qualidade e à produtividade devido às exigências nas prestações de serviços. As informações e as novas tecnologias estabeleceram um ambiente globalizado de alta concorrência, em que preço e prazo devem ser atendidos (VILAÇA e OLIVEIRA, 2011). Em “Qualquer processo de produção, independente de quão bem projetado ou mantido ele seja, sempre estará sujeito a uma variabilidade natural ou inerente, que é resultado do efeito cumulativo de muitas causas pequenas e inevitáveis, chamadas de causas comuns” (MONTGOMERY, 2004, p.154). Sendo assim, a redução de anormalidade em famílias de variáveis é de suma importância no processo estatístico.
De acordo com Souza e Rigão (2005), o CEP atua de maneira preventiva sobre o processo utilizando a estatística como elemento base para avaliar suas alterações. Estas características possibilitam que o CEP auxilie no monitoramento do processo e permite que as ações sejam tomadas de maneira direcionada a resolução dos problemas, auxiliando na estabilização do processo e evitando a produção de itens não conformes (HORA e COSTA, 2009; MAYER, 2004).
O objetivo deste trabalho é utilizar técnicas estatísticas em software para identificar, corrigir e eliminar anormalidades presentes em problemas de ciências da educação. A importância das cartas de controle do software estatístico no controle das anormalidades.
O objetivo maior do controle estatístico de processo é detectar rapidamente a ocorrência de causas atribuíveis nas mudanças de processo, de modo que a investigação do processo e a ação corretiva possam ser realizadas antes que muitas unidades não conformes sejam fabricadas (MONTGOMERY, 2013, p.280).
Sendo assim, o software estatístico é relevante no processo de identificação e eliminação de variabilidade.
A função do controle estatístico de processo nas cartas do Software é evidenciar as modulações ocorridas durante o processamento e desenvolver gráficos estatísticos que possam fornecer um parâmetro mais preciso, auxiliando nas práticas que possam melhorar os pontos predominantes da manufatura, além de, reconhecer, corrigir, eliminar, ou adequar os processos com anormalidade, dando um parâmetro mais preciso, de forma que possam ser aplicadas melhorias na linha de produção (OLIVEIRA, 2015, p.22).
As cartas de controle do Software estatístico possibilitam encontrar as variabilidades demonstradas através dos gráficos, possibilitando melhor visualização do processo, com intuito de demonstrar possíveis defeitos, para aplicação de correções mais eficientes, na busca da melhoria contínua.
Mesmo com o avanço no processo por meio do controle de qualidade, ainda assim existem causas da variabilidade no processo, ou seja, quando há uma oscilação em torno da média ou do ponto ideal da especificação, precisa-se de um monitoramento constante do comportamento da produção. “Por meio de análise dos dados coletados e caracterização da causa da instabilidade ou variabilidade do sistema, utilizado nas cartas de controle, ferramentas do controle estatístico do processo como resultado para obter melhoria contínua do processo” (JURAN e GRYNA, 1992).
Todos os processos exibem variabilidade, ou seja, quanto maior for à variabilidade, maior será o descontrole em relação aos resultados produzidos e os resultados desejados. (MONTGOMERY, 1997).
Na melhoria da qualidade de um produto é necessário fazer uso de software estatístico:
Em um ambiente competitivo, a melhoria contínua do processo possibilita monitorar, controlar e melhorar os processos produtivos, sempre que for detectado alguma anormalidade. Se houver um caráter preventivo, estas ações contribuem para minimizar as perdas e aumentar a produtividade (BORTOLOTTI, 2009, p.02).
Tais técnicas estatísticas com uso do software Minitab contribui na análise de vários produtos, detectando e reduzindo possíveis anormalidades, garantindo estoques dentro dos parâmetros de qualidade. “Um dos resultados principais do estudo de qualidade industrial foi o uso difundido de métodos de controle estatísticos de processo para eliminar causas especiais em processos e reduzir as causas comuns de variação” (MONTGOMERY, 1997). Nesse contexto, o controle estatístico de processos apresenta-se como uma ferramenta extremamente importante para aplicações das técnicas estatísticas na redução de variação. O controle estatístico de processo pode ser definido como um conjunto de sete ferramentas de resolução de problemas para obter estabilidade de processos, além da melhoria de sua capacidade. (FERREIRA et. al., 2008).
As cartas de controle do software estatístico auxilia na identificação e estabilidade das causas de variabilidade dos processos, servindo de base para decisões e ações corretivas de controle, reduzindo as variabilidades e evitando dados amostrais fora de controle.
O controle estatístico de processo é uma poderosa coleção de ferramentas para a coleta, análise e interpretação de dados, com o objetivo de melhorar a qualidade através da eliminação de causas especiais de variação, podendo ser utilizado para a maioria dos processos. (MONTGOMERY, 2004, p.279-281).
O estudo sobre as cartas de controle em software estatístico contribui com as análises das aplicações em ciências da educação na redução de variabilidades nas amostras analisadas, gerando melhores resultados no controle de qualidade.
2. MATERIAIS E MÉTODOS
2.1 MATERIAIS
Os materiais utilizados para o controle de variabilidade em aplicações das ciências da educação foram as cartas de controle em Software Minitab.
2.2 MÉTODOS
Para realização do estudo foi utilizado o método quantitativo e a carta de controle do Software Minitab na redução de variabilidade em aplicações de ciência da educação. A metodologia busca a validação dos dados mediante a utilização de dados estatísticos. O estudo teve a seguinte distribuição: Escolha da aplicação a ser analisada, determinação dos limites inferiores e superiores em parâmetros média e a amplitude, distribuição de amostras e verificação de seus pontos, análise dos problemas pelas cartas de controle e correção de causas especiais a partir das análises amostrais fora de controle.
“O método quantitativo busca a validação dos dados mediante a utilização de dados estatísticos, com análise de um grande número de casos representativos. Procura-se quantificar os dados e aplicar alguma forma da análise estatística” (OLIVEIRA, 2011). A abordagem quantitativa é utilizada com frequência nas pesquisas descritivas, que buscam classificar a relação entre as variáveis e a relação de causalidade entre fenômenos.
Richardson (1999, p.70) conceitua:
a abordagem quantitativa, como o próprio nome indica, caracteriza-se pelo emprego da quantificação tanto nas modalidades de coleta de informações, quanto no tratamento delas por meio de técnicas estatísticas, desde as mais simples como percentual, média, desvio-padrão, às mais complexas, como coeficiente de correlação, análise de regressão, etc. Representa, em princípio, a intenção de garantir a precisão dos resultados e evitar distorções de análise e interpretação, possibilitando, consequentemente, uma margem de segurança quanto às inferências.
De acordo com Michel (2005, p. 31), a abordagem quantitativa é uma metodologia de pesquisa social que utiliza a quantificação nas modalidades de coleta de informações e no seu tratamento mediante técnicas estatísticas, tais como percentual média, desvio-padrão, coeficiente de correlação, análise de regressão, entre outros. As cartas de controle são uma ferramenta benéfica que traz melhorias e garantia da qualidade de resíduos de custos crescente, desaparecimento de refugo e resolução de diversos problemas da produção relacionados com específicos métodos etc (ROSA, 2009).
Utilizou-se das cartas de controle por variáveis e atributos como técnicas na construção de gráficos em aplicações de probabilidade e estatística, onde foi constatada melhoria de estabilidade em relação à variabilidade dos defeitos amostrais. Para encontrar uma possível causa de variabilidade e verificar se o processo está sob controle, utilizou-se dos gráficos no controle de anormalidades em pontos amostrais. Por meio dos gráficos possibilitou-se identificar e comparar variabilidade em questões de ciências estatística.
Fez uso do Software Minitab como ferramenta de análise de dados. A partir dos resultados entres os limites de controle foi possível solucionar defeitos e melhorar a qualidade. Os gráficos de controle da média, amplitude e desvio-padrão foram escolhidos para o controle das variações da média em estatística.
O instrumento teve como finalidade identificar, analisar, comparar, corrigir e reduzir variabilidade em aplicações da ciência da educação fez o uso do Minitab que é um programa de computador proprietário voltado para fins estatísticos (MINITAB, 2016). “É uma ferramenta que nos permite realizar cálculos estatísticos complexos e visualizar os resultados, tornando as análises de dados acessíveis para o utilizador casual e conveniente para o utilizador mais experiente” (PEREIRA e PATRÍCIO, 2016).
Na melhoria da qualidade utiliza-se a tecnologia de software de estatística:
As ferramentas estatísticas além de priorizarem as aplicações proposta conforme o grau de importância, as mesmas tornam a identificação e auxiliam na ação sobre os problemas para a eliminação das possíveis causas. Possibilitando que a instituição possua um maior grau de estabilidade nas aplicações analisadas (WERKEMA, 2006, p.32).
Estratificação: “A estratificação consiste em dividir setores em subsetores conforme fatores desejados, os quais são denominados fatores de estratificação, ou seja, para o processo de dividir o todo heterogêneo em subgrupos homogêneos” (VIEIRA, 1999).
Folha de verificação: Para Werkema (2006), folha de verificação é um formulário que possui em seu escopo critérios a serem analisados, isso com o intuito de facilitar a coleta e o preenchimento dos dados. É uma ferramenta utilizada para auxiliar na coleta de dados e deve estar adequada para que a coleta seja eficaz. Sendo que para isso a folha de verificação deve especificar claramente o tipo de dados a coletar, a operação a ser executada, a data da coleta, o analista e qualquer outra informação que seja útil para a identificação da causa de um mau desempenho funcional (CARPINETTI, 2010; MONTGOMERY, 2009). De acordo com Vieira (1999), o tipo de folha de verificação dependerá de quais serão os seus objetivos, sendo estes: como levantar a proporção de itens não-conformes; inspecionar atributo; indicar onde se localiza o defeito no produto final; levantar as causas dos defeitos; analisar a distribuição de uma variável; e monitorar um processo de fabricação.
Gráfico de Pareto: É a ferramenta que faz a distribuição de frequência de dados, apontando o defeito que ocorre com maior frequência, podendo ser estes de ordem percentual ou de ordem real. Lembrando que um defeito com maior frequência pode não ser o principal ou mais crítico problema do processo (CARPINETTI, 2010; MONTGOMERY, 2009). Vieira (1999) diz que o gráfico de Pareto é utilizado para identificar as causas dos problemas como produtos confeccionados que necessitam de retrabalho, gastos desnecessários, acidente de trabalho, quebra de equipamento, erros e atrasos de entrega, entre outros.
Diagrama de causa e efeito: Conhecido também como Diagrama de Ishikawa tem a função de identificar e analisar as causas que promovem um efeito indesejado. É um diagrama eficaz para a identificação da raiz do problema (CARPINETTI, 2010; MONTGOMERY, 2009). Werkema (2006) afirma que o Diagrama de causa e efeito é uma ferramenta utilizada para apresentar a relação entre o efeito ou problema e a causa que possa alterar o resultado. O Diagrama de causa e efeito organiza as informações de modo que as tornem mais claras para facilitar a análise e identificação das causas do problema, permitindo que sejam tomadas ações corretivas para a eliminação da causa do problema (TRIVELLATO, 2010).
Histograma: De acordo com Werkema (1995), um histograma pode ser definido como um gráfico de barras no qual o eixo horizontal, subdividido em vários pequenos intervalos, apresenta os valores assumidos por uma variável de interesse.
Diagrama de dispersão: O diagrama de dispersão é responsável pelo auxílio à identificação de relações entre um defeito e uma causa, ou seja, objetiva identificar a relação entre duas variáveis ou até mesmo a relação de uma terceira causa. Sendo que as relações entre as variáveis podem ser: positivas, negativas ou inexistentes (CARPINETTI, 2010; MONTGOMERY, 2009).
Gráfico de controle: De acordo com Werkema (2006), todo bem tangível ou intangível, ao ser elaborado e/ou confeccionado, possui uma variação decorrentes do processo. Sabe-se que essas variações devem ser estritamente reduzidas. Para Werkema (2006), os gráficos de controle são utilizados para monitorar a variabilidade, distinguindo os tipos de variação, e avaliar a estabilidade do processo, estando este sob controle ou não. Porém o processo pode sofrer variações de causas comuns ou causas especiais
Os gráficos de controle foram criados por Shewhart, e são compostos por limite central ou médio (LC), limite inferior (LI) e limite superior (LS). Sendo que sua principal função é indicar se o processo se encontra sob controle ou não, ou seja, se o processo está confeccionando produtos conforme ou não conforme às especificações. A análise do processo é feita a partir da verificação do gráfico de controle, observando se os pontos plotados no mesmo estão entre os limites superior e inferior de especificação (CARPINETTI, 2010; MONTGOMERY, 2009).
Gráficos de Controle: Serve para analisar as variações do processo de causas comuns, e detectar as causas especiais, é uma ferramenta denominada de Cartas ou Gráficos de Controle. A análise da capacidade de um processo é uma parte vital de um programa global de qualidade. Entre as principais utilizações de dados de uma análise de capacidade de um processo destacam-se (MONTGOMERY, 2004):
2.2.1 REGRAS ESTATÍSTICAS PARA IDENTIFICAR CAUSAS ESPECIAIS
Sugere um conjunto de regras de decisão para a distinção de padrões não aleatórios em gráficos de controle. Especificamente, sugere que se conclua que o processo está fora de controle se (MONTGOMERY, 2004):
1º caso: identificar seis, oito ou mais pontos acima ou abaixo da linha central. Possíveis causas: mudança no ajuste de máquina processo, método ou material diferente, avaria de um componente na máquina, quebra de máquina e grande variação no material recebido.
2º caso: encontrar seis, sete ou mais pontos subindo ou descendo. Possíveis causas: desgaste de ferramenta gradual, desgaste do equipamento ou desgaste relacionado ao instrumento de medição.
3º caso: verificar o deslocamento da média. Possíveis causas: novo método, nova máquina na melhoria de qualidade e um novo lote de material.
4º caso: pontos fora dos limites de controle. Possíveis causas: erro na medição ou digitação, quebra de ferramenta ou instrumento de medição desregulado, o que não permite a identificação da medida.
5º caso: periodicidade dos pontos. Possíveis causas: não-uniformidade na matéria prima recebida, rodízio de operadores, gabaritos e instrumentos, e diferença entre os turnos.
2.2.2 CARTAS DE CONTROLE POR VARIÁVEIS E ATRIBUTOS
As cartas de controle por variáveis tem a finalidade de informar a respeito da melhoria da qualidade, capacidade do processo, tomadas de decisões relativas à especificação do produto, processo de produção e decisões sobre peças recém produzidas. São aplicadas onde as características de qualidade possam ser medidas quantitativamente. Podem ser, por exemplo, dimensões de peças, volume, peso, dentre outros. Assim, percebe-se o seu amplo espaço de aplicação, já que diversos tipos de processos possuem esses tipos de características (MAGALHÃES, 2011).
“As cartas de controle para variáveis são mais utilizados que os gráficos de controle para atributos, pois possuem informações mais concretas, trabalhando com amostras pequenas, permitindo identificar de forma mais rápida as causas que afetam a estabilidade do processo” (REBELATO, 2006). “As cartas de controle para variáveis são cartas para médias, utilizadas para o controle do valor médio do desempenho do processo, gráfico da amplitude ou gráfico de desvio padrão, sendo o gráfico da amplitude mais utilizado, pelo fato de que, na maioria das vezes, o desvio padrão do processo não é conhecido” (CASTRO, 2012).
As cartas de controle podem ser classificadas em dois grupos: cartas de controle para variáveis: registra as características de qualidade que são mensuradas em uma escala quantitativa. E as cartas de controle por atributos: registra as características de qualidade, sendo mensuradas em uma escala qualitativa, por exemplo, julga-se conforme e não conforme (SIQUEIRA, 1997). Sendo assim, segundo Spiegel e Stephens (2007), os termos ‘variáveis’ e ‘atributos’ estão associados com o tipo de dados coletados do processo.
2.2.3 GRÁFICO DE CONTROLE PARA MÉDIA (X-BARRA) E AMPLITUDE (R)
O gráfico da média ![]() é utilizado para controlar a média do processo (centralidade) e, o gráfico da amplitude
é utilizado para controlar a média do processo (centralidade) e, o gráfico da amplitude ![]() para controlar a variabilidade do processo considerado (IPEK et al., 1999).
para controlar a variabilidade do processo considerado (IPEK et al., 1999).
Expressões para o cálculo do limites de controle dos ![]() e R.
e R.
Gráfico de controle ![]() . A linha central e os limites superior e inferior de controle para o gráfico de controle
. A linha central e os limites superior e inferior de controle para o gráfico de controle ![]() são:
são:
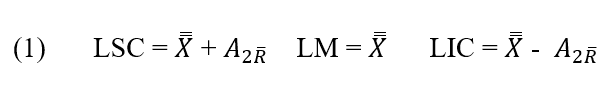
Gráfico de controle R. A linha central e os limites superior e inferior de controle para o gráfico de controle R são:
![]()
2.2.4 GRÁFICO DA MÉDIA (X-BARRA) E DESVIO PADRÃO (S)
O gráfico de controle para média (gráfico X-barra) é usado para controlar a média do processo, já o gráfico de controle de (gráfico desvio padrão S) é empregado para o controle da variabilidade do processo. Quando o tamanho da amostra (subgrupo) é menor ou igual a dez, os gráficos R e S terão o mesmo aspecto. No entanto, quando o tamanho da amostra cresce, o gráfico S se torna mais preciso do que o gráfico R, e deve ser usado (SIQUEIRA, 1997).
Gráfico de controle ![]() . A linha central e os limites superior e inferior de controle para o gráfico de controle
. A linha central e os limites superior e inferior de controle para o gráfico de controle ![]() são:
são:
![]()
Gráfico de controle S: 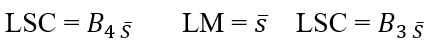
2.2.4.1 CARTAS DE CONTROLES POR ATRIBUTOS
As cartas de atributo são usadas para o controle da análise de defeitos. Esses gráficos são especialmente úteis no controle de matérias-primas e de produtos acabados, sendo também usados na análise de comentários sobre a qualidade em cartas de consumidores. Um atributo é uma característica de um produto, de um processo ou de qualquer outra população que puder ser contada, mas não puder ser descrita, de modo que seus valores sejam incrementados (RODRIGUES, 1998). São gráficos que nos possibilitam identificar como os conjuntos de amostras se comportam em torno dos limites, tendências e troca de níveis. Nas variáveis, percebe-se rapidamente quando os dados não seguem uma distribuição aleatória. Nos gráficos de controle por atributos, as unidades são classificadas em perfeitas ou defeituosas de acordo com o critério estabelecido. Portanto, a probabilidade de ser produzida uma unidade defeituosa é constante, e, consequentemente, a distribuição amostral correspondente é binomial (CHAVES e TEIXEIRA, 1997). As cartas de atributo são usadas para o controle da análise de defeitos. Esses gráficos são especialmente úteis no controle de matérias-primas e de produtos acabados, sendo também usados na análise de comentários sobre a qualidade e as características expressas qualitativamente, ou seja, quando essas características analisadas não são representadas numericamente, podendo ser classificadas em conforme ou não conforme (SOUZA, 2005). São as medidas representativas que resultam de contagens do número de itens do produto em escala discreta que apresentam uma característica particular de interesse. As medições são feitas por inspeção visual, sendo registradas as características não mensuráveis. Pode ser dito gráfico de controle por variável aleatória discreta com função de densidade de probabilidade de Poisson (LAGO, 1999).
A matemática das cartas de atributo não requer tabelas. Elas podem ser aplicadas a sistemas nos quais as medidas consistem em aprovar ou reprovar ou a processos em que é muito difícil ou impossível obter medidas de variáveis (RODRIGUES, 1998).
As informações estatísticas de medições por atributos em soluções de problemas de ciências da educação, classificam-se em produtos com anormalidades ou defeitos. Um dos principais objetivos da análise de medição por atributo está em identificar, detectar e corrigir defeitos, a qualidade pode ser definida como o conjunto de atributos que tornam um bem ou serviço plenamente adequado ao uso para o qual foi concebido (MONTGOMERY, 1985). As quatro cartas de controle por atributos em anormalidades e defeitos, usadas segundo Montgomery (2004), são as seguintes: Cartas de controles por atributos as quais são: Carta p (proporções não conforme), Carta np (unidades não conforme), Carta C (número de não conformidade por unidade) e Carta u (taxa de não conformidade por unidade).
2.2.5 GRÁFICO P (PROPORÇÕES NÃO CONFORME)
Para Werkema (2006), o gráfico de p é utilizado quando a característica da qualidade de interesse é representada pela proporção de itens defeituosos produzidos pelo processo analisado.
Gráfico de controle P:
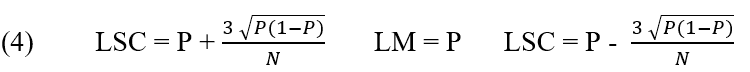
2.2.6 GRÁFICO NP (UNIDADES NÃO CONFORME)
A carta não indica o número de defeitos por amostra e é usada para controlar o número de produtos defeituosos em cada lote e assegurar que o processo esteja sob controle (RODRIGUES, 1998).
A linha central e os limites superior e inferior de controle para o gráfico np são:
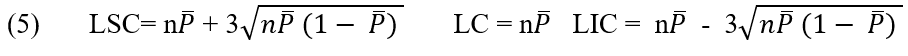
2.2.7 GRÁFICO C NÚMERO DE (NÃO CONFORMIDADE POR UNIDADE)
A carta c é usada para determinar se o número de defeito em um único item está dentro dos limites de controle determinados. Pode ser considerada como inspeção final (RODRIGUES, 1998). A carta c é mais apropriada quando os defeitos estão dispersos em um meio contínuo, como por exemplo: número de falhas por área de tecido, número de imperfeições por comprimento de pavimento; e quando um produto pode apresentar mais de um tipo de defeito (RIBEIRO e CATEN, 2012).
Portanto, os limites de controle do gráfico C serão calculados por meio das equações:
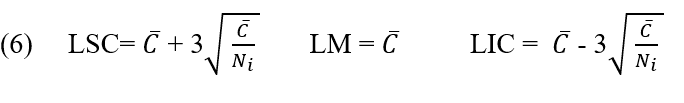
2.2.8 GRÁFICO U TAXA DE NÃO CONFORMIDADE POR UNIDADE
O gráfico u é utilizado para monitorar defeitos em uma unidade de produção (MONTGOMERY, 1997). A carta u é recomendada quando o produto é composto de várias partes e muitas características da qualidade que devem ser inspecionadas e também quando o tamanho da unidade do produto é variável (CORTIVO, 2005).
A linha central e os limites superior e inferior de controle para o gráfico U são:
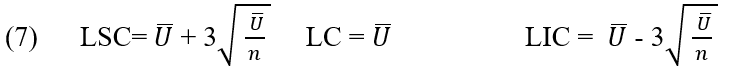
2.2.9 REGRESSÃO LINEAR MÚLTIPLA
A análise de regressão múltipla é uma técnica utilizada para investigar a relação entre uma variável dependente e um conjunto de variáveis independentes (MONTGOMERY e RUNGER, 2009). A técnica permite a estimação de valores futuros para a variável dependente, dado um conjunto de dados de entrada para as variáveis independentes (PEDRINI e CATEN, 2009; DOWNING e CLARK, 2002).
O modelo base de regressão linear múltipla onde ![]() para j=0,1,2…..k são coeficientes de regressão, Y é a variável dependente dos regressores
para j=0,1,2…..k são coeficientes de regressão, Y é a variável dependente dos regressores ![]() e o valor e é o erro aleatório da equação. ( MONTGOMERY, 2015).
e o valor e é o erro aleatório da equação. ( MONTGOMERY, 2015).
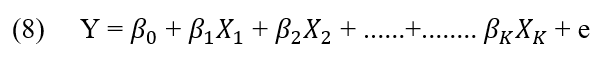
O processo é estudado para entender as necessidades de analisar as aplicações de ciências da educação e suas etapas do processo. São levantadas fontes de análises, as aplicações que nela são analisadas, são as variabilidades os principais fatores que o influenciam. Identificando o tipo de carta de controle mais adequado para analisar os dados pelo software Minitab. Com o método controle estocástico de processo buscou-se a estruturação da pesquisa de maneira a auxiliar o andamento do mesmo.
3. RESULTADOS E DISCUSSÃO
3.1 A UTILIZAÇÃO DAS CARTAS DE CONTROLE DO MINITAB NA REDUÇÃO DE VARIABILIDADE
Após coletados e plotados os dados em aplicações de engenharia, foram construídos alguns gráficos para variáveis e gráficos para atributos nas cartas de controle do software Minitab para monitorar as perdas por variações em produção. Para análise dos resultados, posteriores determinou-se a faixa de tolerância composta pelos componentes: Limite Superior de Controle LSC, Linha Média LC e Limite Inferior de Controle LIC.
Observou-se que após identificar, eliminar e reduzir causas de variabilidade trouxe possibilidade de melhoria na qualidade dos produtos. Por meio das análises dos resultados obtidos nas aplicações estatísticas será apresentado o controle da estabilidade nas causas dos defeitos em pontos amostrais nos gráficos, sendo que o controle de processo em amostra foi realizado com o intuito de controlar a variabilidade. As cartas de controle apresentaram os seguintes resultados entre os parâmetros estatísticos: Cálculo da média do processo, Cálculo do desvio-padrão, Cálculo dos limites de controle LSC, LIC e amplitude nas aplicações abaixo:
3.2 APLICAÇÕES DE PROBABILIDADE E ESTATÍSTICA NA ENGENHARIA POR CARTA DE CONTROLE EM SOFTWARE MINITAB NA REDUÇÃO DE VARIABILIDADE
Construções de gráficos em aplicações de estatística descritiva executada pela carta de controle em Software Minitab.
01) Os dados referem-se a um processo de usinagem de pinos, em que os diâmetros são medidos por amostragem de 5 peças em 25 lotes. Analise o processo com o Software Minitab.
Tabela 1: Medições do diâmetro de pinos
| Lote | Medições | ||||||
| 1 | 2,08495 | 2,09203 | 1,01425 | 0,47627 | 1,75308 | ||
| 2 | 2,44288 | 1,84913 | 1,02012 | 1,5103 | 0,5167 | ||
| 3 | 2,08819 | 0,34567 | 0,67246 | 2,14641 | 0,51528 | ||
| 4 | 1,42411 | 1,04348 | 1,15683 | 0,9108 | 1,23562 | ||
| 5 | 1,43307 | 0,22926 | 1,51612 | 0,82627 | 1,29935 | ||
| 6 | 1,2113 | 0,63715 | 0,97815 | 2,30782 | 1,0003 | ||
| 7 | 2,14731 | 1,95837 | 0,95294 | 1,35384 | 0,73037 | ||
| 8 | 2,02444 | 1,60384 | 1,64667 | 1,66449 | 0,92746 | ||
| 9 | 1,4743 | 1,93916 | 1,06107 | 1,55396 | 0,8049 | ||
| 10 | 1,09096 | 2,09033 | 0,62161 | 1,45256 | 1,77208 | ||
| 11 | 1,90879 | 1,274 | 1,46827 | 1,36343 | 1,06161 | ||
| 12 | 0,81791 | 1,89952 | 1,24044 | 0,72729 | 1,44959 | ||
| 13 | 0,58784 | 1,57195 | 0,73316 | 1,05367 | 3,29273 | ||
| 14 | 2,12184 | 0,90374 | 0,59773 | 1,63101 | 0,82706 | ||
| 15 | 1,2819 | 0,89479 | 1,05394 | 1,25779 | 0,99451 | ||
| 16 | 0,82836 | 0,16347 | 2,12864 | 1,69732 | 0,90752 | ||
| 17 | 0,14026 | 1,0432 | 0,76948 | 1,72083 | 3,95445 | ||
| 18 | 2,19158 | 0,87777 | 0,955 | 1,50304 | 1,1604 | ||
| 19 | 0,93195 | 1,82231 | 1,2179 | 1,72608 | 1,45375 | ||
| 20 | 0,84523 | 2,79753 | 2,30041 | 0,47693 | 0,58081 | ||
| 21 | 1,84098 | 2,37729 | 1,89976 | 1,2079 | 3,2343 | ||
| 22 | 1,15648 | 2,5689 | 0,90064 | 3,7548 | 1,24616 | ||
| 23 | 2,21913 | 0,91997 | 2,15777 | 1,48548 | 0,25288 | ||
| 24 | 1,41393 | 0,71069 | 0,63707 | 1,71835 | 1,52855 | ||
| 25 | 1,5938 | 1,19839 | 0,88228 | 1,23019 | 0,41643 | ||
Fonte: Action (2019)
Figura 01: Carta de controle pino defeituoso fora de controle
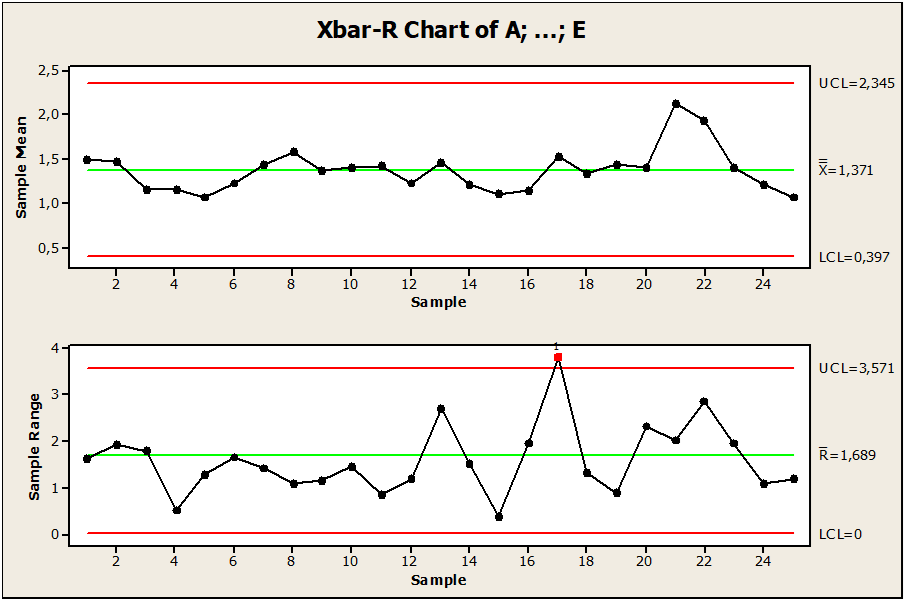
Os dados amostrais apresentam um processo de usinagem de pinos observado em 25 lotes de pinos. Como mostra a Figura 01. Observamos que há variação entre o ponto 17 acima do limite superior de controle LSC, onde o ponto encontra-se fora do limite de controle. Seu limite central é igual 1,68, limite superior de controle com o valor 3,57 e limite inferior igual a 0,0, isso implica que o ponto 17 no pino de valor 3,95445 sofre influência de variabilidade. Então para manter o processo sob controle recomendou-se remover, alterar valores ou construir um novo gráfico.
Figura 02: Carta de controle com os limites ajustados
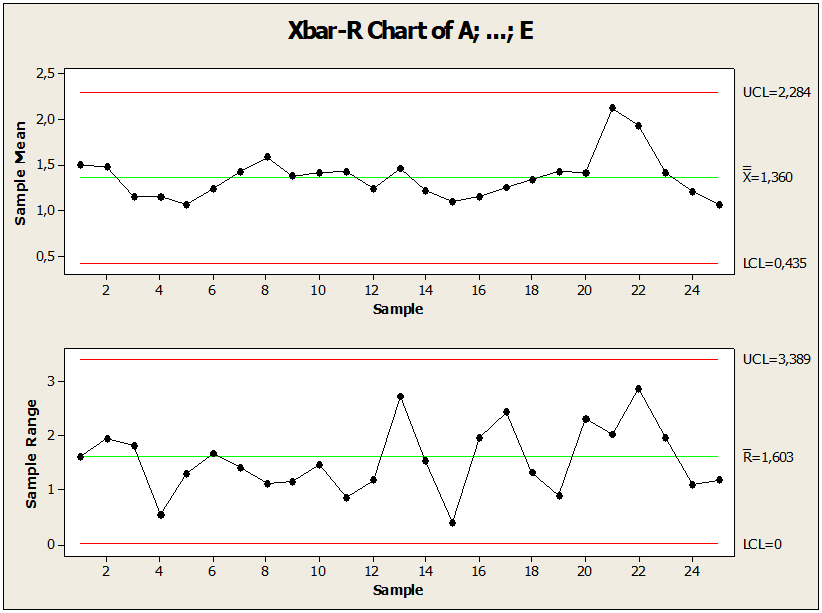
Após verificação da anormalidade, a Figura 02. O gráfico mostra o ponto sob controle em relação à média, onde houve modificação com a finalidade de manter o processo sob controle. Na amostra do ponto 17 de valor 3,95445 de não-conformidade alterou-se para 2,55445. Essa mudança executada pela carta de controle seguida de regras estatísticas reduziu as variabilidades e o ponto fora do limite de controle foi ajustado. Concluímos que todas essas medidas estatísticas manteve o processo estável. Depois de identificado, analisado, corrigido, reduzido e controlado o processo das amostras de não conformidade foi possível comparar os resultado obtido com os resultado anterior entre o processo: Processo fora de controle, LC igual a 1,68, desvio padrão igual a 0,69 e amplitude do limite valor 3,81 um ponto acima fora do limite. LSC. Processo sob controle LC igual a 1,60, desvio padrão igual e 0,66 Amplitude do limite valor 3,61. Após comparação com os valores calculados no 1º e 2º teste verificou-se melhoria nos parâmetros estatísticos.
Figura 03: Mostra diâmetros de pinos
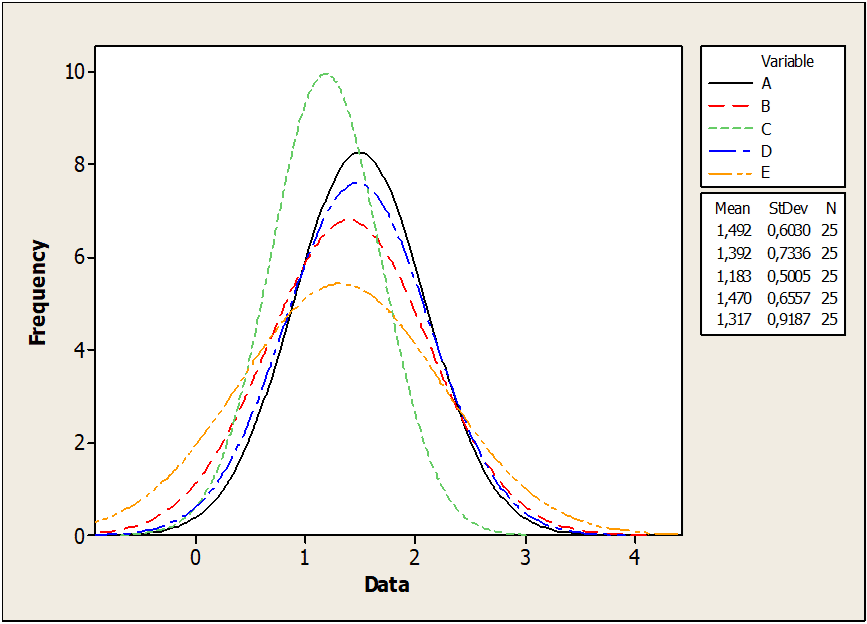
A figura 03 apresenta curva de dispersão dos diâmetros de pinos nos subgrupos de E com maior precisão do que a curva de dispersão dos subgrupos de D. O desvio padrão para amostras do subgrupo E (0,91) é muito maior do que as amostras do subgrupo D. (0,50). Logo, a distribuição ajustada para o subgrupo E é mais achatada e mais precisa.
02) Foi realizado um estudo para determinar o aumento de defeitos, em portas inox de equipamentos para cozinha, produzidas numa empresa metalomecânica. Durante o estudo apareceram os defeitos abaixo indicados com as respectivas ocorrências e custos associados. Construir os respectivos diagramas de Pareto.
Tabela 2: peças com defeitos
| Tipo de defeitos | Nº. de peças defeituosas | Custo unitário reparação/sucata | |
| Soldadura mal executada | 55 | 50 | |
| Furação deficiente | 9 | 50 | |
| Defeitos de dobragem | 274 | 5 | |
| Acondicionamento | 15 | 50 | |
| Má qualidade da chapa | 16 | 50 | |
| Cortes | 126 | 30 | |
| Outros | 12 | 50 |
Fonte: Núcleo de Formação -Nufec (2006)
Figura 04: Números de peças defeituosas
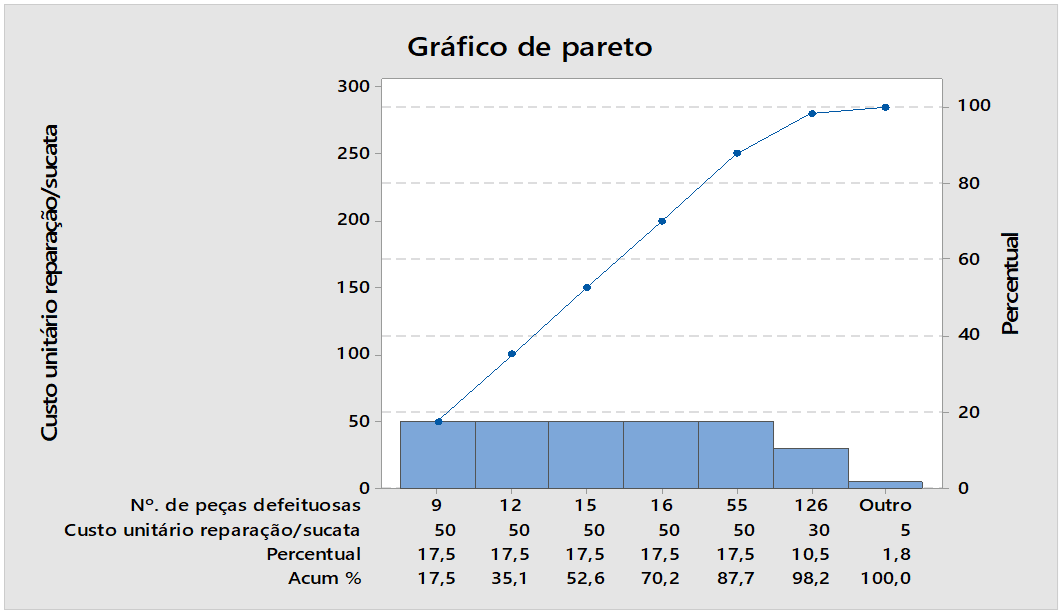
A Figura 04 mostra os resultados dos números de peças defeituosas, percentual, a maior fonte 9 peças defeituosas que corresponde um percentual 17,5 %. Ao analisar a figura percebe-se a presença de concentração de causas de variabilidade especiais necessitando correção pela carta de controle do software Minitab.
Figura 05: Números de peças defeituosas processo fora de controle
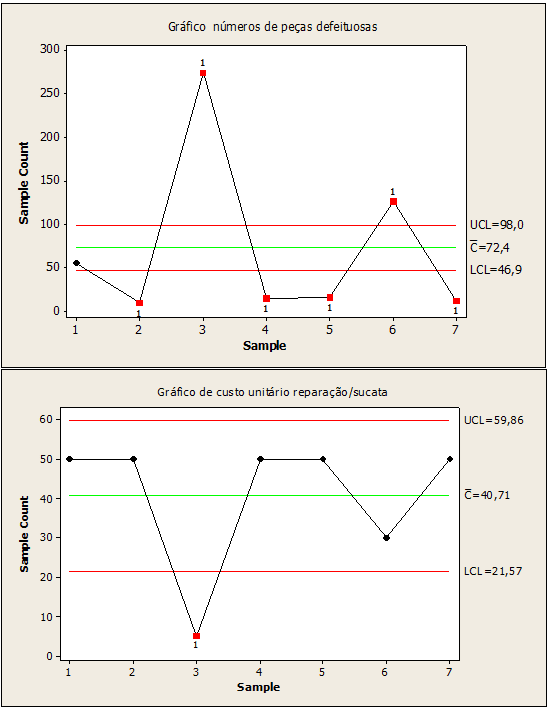
Verificou-se que a figura 05, referente as peças defeituosas apresentaram as variabilidades nos pontos 2,3,4,5,6,7 com valores ( 9,274,15,16,126,12). Já a de custo unitário na reparação da sucata ponto com variabilidades 3 com valor igual a 5. Conclui-se que há causas especiais nesses pontos, havendo necessidade de correção.
Figura 06: Números de peças defeituosas processo sob controle
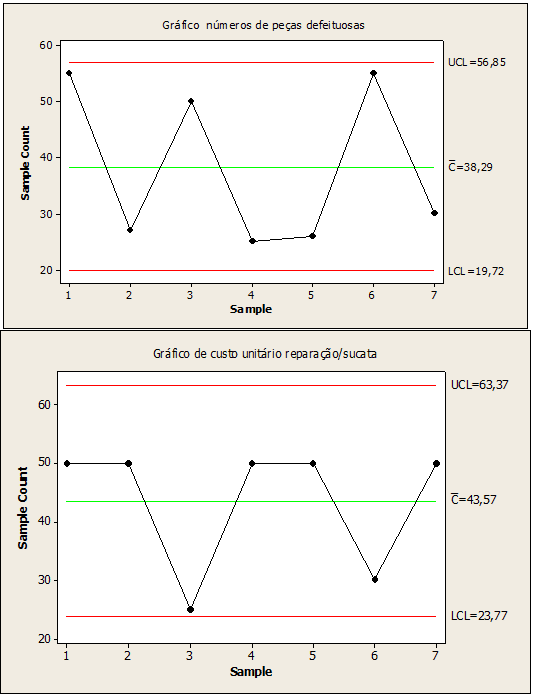
Na figura 06, os valores utilizados em substituição aos valores dos pontos fora de controle 2,3,4,5,6,7, segue-se 27,50,25,26,55,30 para peças defeituosas e 25 para custo unitário reparação sucata no ponto 3. Esses dados em substituição gerado pela carta de controle melhorou o processo estocástico mantendo sob controle havendo redução de variabilidade na fabricação das porta de inox mantendo estável a qualidade na fabricação do produto.
03) Um molde para extrusão é usado para produzir bastões de alumínio. O diâmetro dos bastões é uma característica crítica da qualidade. A seguinte tabela mostra os valores de x e r para 20 amostras de cinco bastões cada. Especificações sobre os bastões são 0,5035 +/- 0,0010 polegada. Os valores dados são os três últimos dígitos da medida, ou seja, 34,2 é lido como 0,50342.
a) Usando todos os dados, encontre os limites de controle para os gráficos X e R, construa o gráfico e plote os dados.
b) Use os limites das tentativas de controle do item (a) para identificar pontos fora de controle. Se necessário, reveja seus limites de controle, considerando que qualquer amostra fora dos limites de controle poderá ser eliminada.
Tabela 3: Amostras de hastes
| Amostra | R | Amostra | R | ||
| 1 | 34,2 | 3 | 11 | 35,4 | 8 |
| 2 | 31,6 | 4 | 12 | 34,0 | 6 |
| 3 | 31,8 | 4 | 13 | 36,0 | 4 |
| 4 | 33,4 | 5 | 14 | 37,2 | 7 |
| 5 | 35,0 | 4 | 15 | 35,2 | 3 |
| 6 | 32,1 | 2 | 16 | 33,4 | 10 |
| 7 | 32,6 | 7 | 17 | 35,0 | 4 |
| 8 | 33,8 | 9 | 18 | 34,4 | 7 |
| 9 | 34,8 | 10 | 19 | 33,9 | 8 |
| 10 | 38,6 | 4 | 20 | 34,0 | 4 |
Fonte: Montgomery (2013)
Figura 07: Amostras de hastes fora de controle
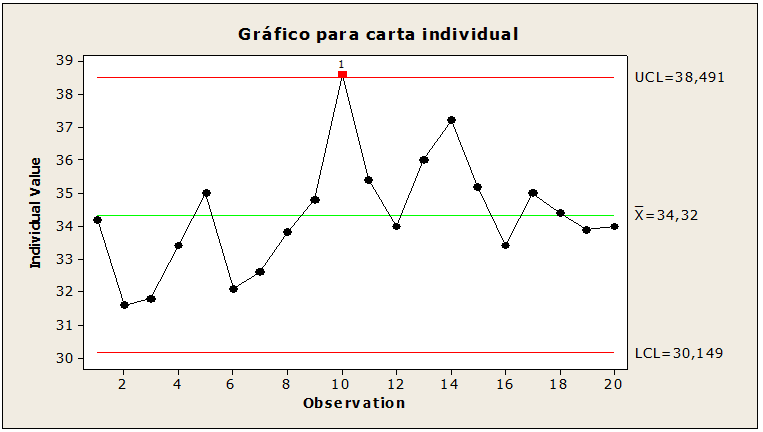
Controle estatístico para 20 amostra de cinco hastes cada. Ao interpretar a figura 07, os valores do limite superior foi de 38,49, a média 34,32, o desvio padrão 1,72, o limite inferior 30,14 com o ponto 10 de valor 38, 6 acima do limite superior dando indícios de causas especiais passíveis de correção. Sugere-se correção nesse ponto para que os limites fiquem ajustados.
Figura 08: Amostras de hastes sob controle
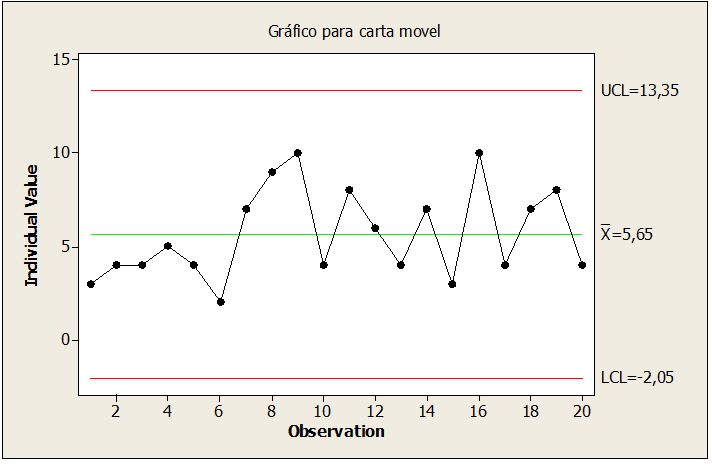
Pela correção do ponto na figura 08, ajustou-se o ponto 10 reduzindo o valor amostral para 36, 6, mantendo o processo estável e sob controle na fabricação do diâmetro das hastes de alumínio.
Figura 09: Capacidade de processo amostras de hastes
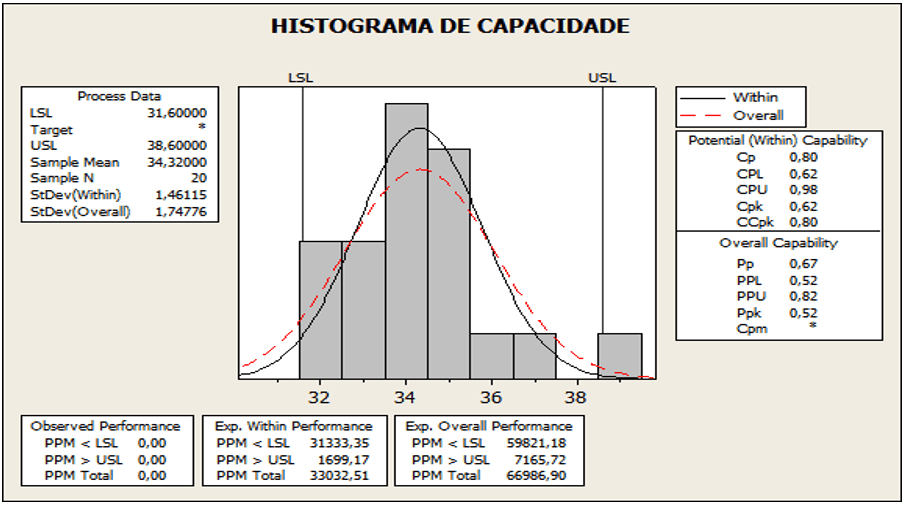
Segundo a análise da figura 09, apresenta o valor para Cpk igual a 0,49, média 5,65, desvio padrão 2,434 e valor-p 0,025. Resultado de CPk fora do limite, se Ppk < CPk. A média obtida foi de 5.65, com deslocamento para o LSE. O CPk 0,49 menor que os valores estabelecido que é 1,33 implicando está fora do limite estável.
Figura 10: Percentual de defeito
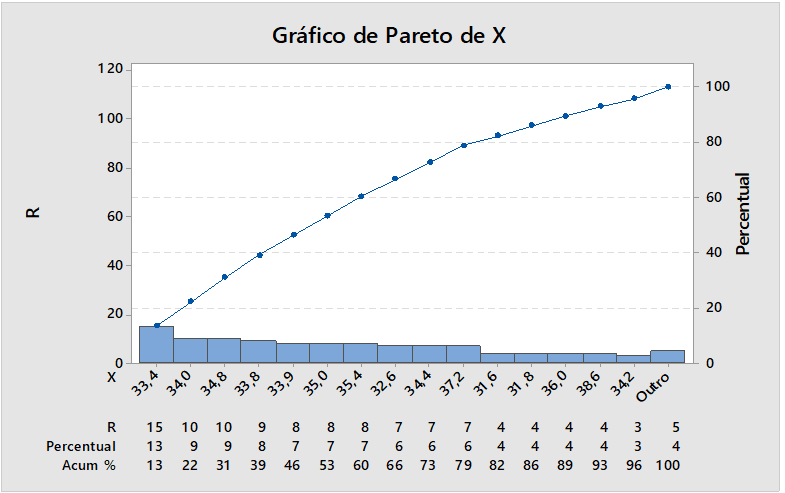
A Figura 10. O gráfico de pareto fornece o percentual das amostras analisadas de defeituosos produzidas nesse processo, percentual, a maior fonte 15 peças defeituosa que corresponde um percentual 13%. Há necessidade na eliminação de variação.
Observando as figuras, verificou-se que na figura 07, o ponto 10 encontra-se fora do limite de controle apresentando anormalidade no diâmetro das hastes passíveis de correção. Já na figura 09, o cpk está fora do limite. Entretanto a figura 10, possui defeito nas hastes. Por seguinte a figura 08. Após interpretada, analisada e eliminada as causas especiais no ponto do diâmetro manteve-se estável.
Na Figura 11 mostra-se as cartas de controle para as médias, desvio padrão e o número de não-conformidades medidos por amostragem de 5 peças em 25 lotes. Através dos gráficos apresentados podemos observar que há ponto fora do limite de controle e está distribuído ao redor da média, como também nos possibilitou observar a ordem da grandeza dos desvios de processo e por fim tornou possível encontrar os pontos de causas especiais, onde apresenta um ponto fora do limite. Por meio dessas análises constatamos que há variabilidade de causa especiais no ponto 17 LSC, onde o ponto encontra-se fora do limite de controle, necessitando de correções e redução de variabilidade. Essa anormalidade foi detectada pela carta de controle do Software Minitab no 1° teste onde, houve a necessidade de estabilização do processo. Então para manter o processo sob controle aplicou-se o 2° teste para suplementar o 1° teste a fim de criar uma nova carta de controle que tenha o processo sob controle.
Recomendou-se três situações na construção do gráfico do limite sob controle: remover a observação de valor 3,95445, alterar valores de não-conformidade ou construir um novo gráfico. O 2° teste na figura 12. Mostrar a correção, comparação e redução de variações na construção de um novo gráfico com o ponto sob controle em relação à média, havendo modificação no ponto amostral com a finalidade de manter o processo sob controle. A amostra de valor 3,95445, alterou-se valor 2,55445. Após controlar o processo foi possível comparar os resultados obtidos com os resultados anteriores entre os processos. Em comparação com os valores do cálculo amostral no processo sob controle a média apresentou o valor igual a 1,60, desvio padrão 0,66 e Amplitude do limite valor 3,66. Enquanto o processo fora de controle a média é igual a 1,68, desvio padrão 0,69 e amplitude do limite com valor 3,81.
Figura 11: Carta fora de controle
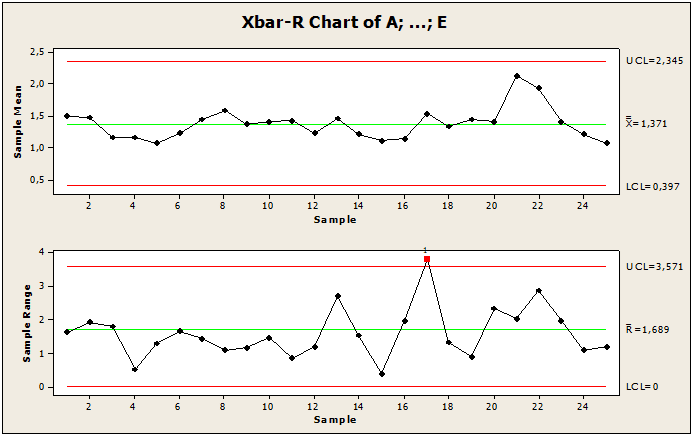
Figura 12: Carta sob controle
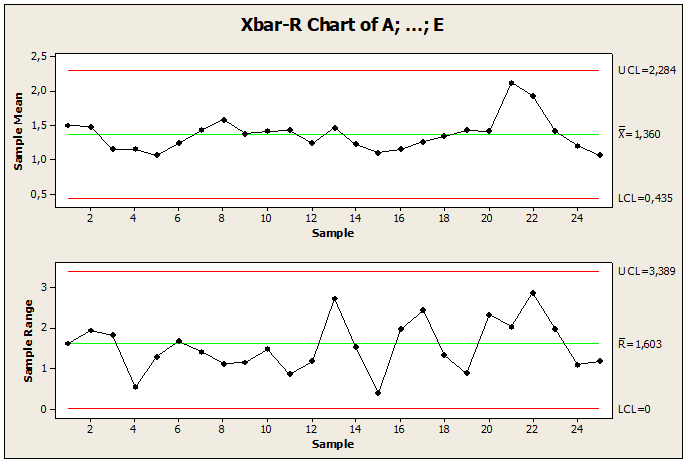
Os resultados obtidos neste estudo mostram as cartas de controle como ferramenta eficaz na redução de variabilidade nas aplicações das ciências da educação ao encontrar a estabilidade do processo e melhorar a qualidade.
4. CONCLUSÃO
Por meio das cartas de controle do software Minitab, foi possível plotar e analisar alterações na distribuição amostral no processo estatístico informando pontos críticos com variabilidade em aplicações das ciências da educação. Através da análise das cartas de controle podemos perceber que as aplicações estatísticas apresentaram variabilidade.
A carta é uma ferramenta utilizada no controle de anormalidade pelos testes estatísticos e constatou-se variabilidades em alguns pontos amostrais das aplicações de estatística. Diante disso, houve a necessidade de fazer inferência no controle das variáveis com pontos fora de controle. Verificou-se pelo 1º teste que os subgrupos que são incomuns em comparação com outros subgrupos apresentaram anormalidades, havendo a necessidade de aplicar o 2° teste para corrigir e manter o processo sob controle.
As cartas possibilitaram verificar variações e estabilizar variáveis entre os parâmetros médios, desvios padrão e amplitude. Os gráficos permitiram aproximar os pontos amostrais fora dos limites e ajustar defeitos entre limites, auxiliando na melhoria contínua do processo, permitindo perceber defeitos e controlar causas de variação anormais entre os parâmetros limitados da carta sob comparação das amostras nos testes de verificação.
Analisando-se as cartas a fim de estabelecer limites para inspeções futuras seria necessário eliminar as variabilidades espaciais e após alterar amostras construir um novo gráficos no minitab torna-se viável na eliminação destes pontos para cálculo dos limites revisados
Os objetivos expostos nessa pesquisa foram alcançados com êxito ao possibilitar utilizar técnicas estatísticas para identificar e eliminar anormalidades não conforme em problemas de estatística. Tais técnicas permitiram que por meio das amostras fosse feita a inferência em aplicações de engenharia. Ações reduziram a ocorrência de variabilidades em Software Minitab e com isso mantiveram o processo estocástico estável e sob controle. Essa temática expôs que é possível coletar, analisar e interpretar dados através das cartas de controle, pois através dessa ferramenta é possível verificar anormalidade em problemas de estatística.
Constata-se que o software estatístico é capaz de atender às especificações no controle de processos. Verificou-se a necessidade de utilizar o Minitab na prevenção das possíveis causas de variabilidade. Por fim, com o presente estudo das variabilidades foi possível perceber e compreender a contribuição dos recursos das cartas de controle aplicando o software na redução de anormalidade em aplicações de ciências estatísticas.
REFERÊNCIAS
BORTOLOTTI, S. L. V. et al. Análise da qualidade do produto final no processo de envase de azeitonas verdes. Tecnol. & Hum., Curitiba, ano 23, n. 36, jan/jun. 2009. Disponível em: https://revistas.utfpr.edu.br/rth/article/viewFile/6238/3889
CARPINETTI, L. C. R. Gestão da Qualidade, Conceitos e Técnicas. São Paulo: Atlas S.A., 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CASTRO, D. R. C. et al. A aplicabilidade dos gráficos de controle nas empresas como modelo de inspeção para a avaliação da qualidade. In: XXXII Encontro Nacional de Engenharia de Produção. Bento Gonçalves, RS, 2012. Disponível em: http://www.abepro.org.br/biblioteca/enegep2012_tn_stp_158_921_20804.pdf
CHAVES, J. B. P. Controle de Qualidade na Indústria de Alimentos. Viçosa,
MG, (s.n.), 1997.
CHAVES, J. B. P.; TEIXEIRA, M. A. Controle Estatístico de Qualidade:
inspeção por amostragem/ mapas de controle. DTA/UFV. Viçosa, MG: (s.n.), p. 162,
1997.
CORTIVO, Z. D. Aplicação do Controle Estatístico de Processo em sequências curtas de produção e análise estatística de processo através do planejamento econômico. Curitiba: Universidade Federal do Paraná, 2005.
FERREIRA, J. M.; OLIVEIRA, M. S. de. Controle estatístico da qualidade. Lavras: UFLA/FAEPE, p.87, 2008.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
HORA, H. R. M., COSTA, H. G. Tomada de decisão no MASP: uma contribuição para decisões utilizando a matriz AHP. XXIX Encontro Nacional de Engenharia de Produção. Salvador. ENEGEP, 2009.
IPEK, H. et al. The application of statistical process control. Minerals Engineering, Vol. 12, Issue 7, p. 827-835, 1999. ISSN 0892-6875. Disponível em: https://doi.org/10.1016/S0892-6875(99)00067-9.
JURAN, J. M.; GRYNA, F. M. Controle da Qualidade: Métodos Estatísticos Clássicos Aplicados à Qualidade. São Paulo, Ed. Makron, 1992.
LAGO NETO, J. C. do. O efeito da autocorrelação em gráficos de controle para variável contínua: Um estudo de caso. Florianópolis, 1999.
MAGALHÃES, M. S. de; MOURA NETO, F. D. Economic-statistical design of variable parameters non-central chi-square control chart. Production, v. 21, n. 2, p. 259–270, 2011.
MICHEL, M. H. Metodologia e Pesquisa Científica em Ciências Sociais: Um Guia Prático para Acompanhamento da Disciplina e Elaboração de Trabalhos Monográficos. São Paulo: Atlas, 2005.
MINITAB. Conheça o Minitab para Windows. 1º. ed. São Paulo: Editora Minitab
Inc., 2010.
MONTGOMERY, D. C. Estatística Aplicada e Probabilidade para Engenheiros. Tradução e revisão técnica Verônica Calado. Rio de Janeiro, LTC, 2015.
MONTGOMERY, D. C. Introdução Ao Controle Estatístico Da Qualidade. 4. ed. Rio de Janeiro: LTC, 2009.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 1997.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 4. ed. Rio de Janeiro: LTC, 2004.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 2013.
MONTGOMERY, D. C. Introdução ao controle estatístico de qualidade. Rio de Janeiro: LTC, 2016.
OLIVEIRA, T. S.; LIMA, R. H. P. Aplicação do controle estatístico de processo na mensuração da variabilidade em uma usina de etanol. Anais. INGEPRO Inovação, Gestão e Produção, v. 3, n. 6, p. 022-033, 2015.
OLIVEIRA, V. F. de. Mobilidade e acessibilidade urbana: uma análise socioespacial a partir dos bairros Jardim Morada do Sol e Conjunto Habitacional Ana Jacinta, em Presidente Prudente. Faculdade de Ciências e Tecnologia – FCT, Unesp, 2011.
PALLADINI, E. P. et al. Gestão da Qualidade: Teoria e Casos. 2. Ed. São Paulo: Atlas, 2010.
PEDRINI, D. C. Proposta de um método para aplicação de gráficos de controle de regressão no monitoramento de processos. Universidade Federal do Rio Grande do Sul: UFRGS, 2009.
PEREIRA, A.; PATRÍCIO, T. Guia prático de utilização: análise de dados para Ciências Sociais e Psicologia. 8.ª ed. Lisboa : Sílabo, 2013.
REBELATO, M. G. et al. Estudo sobre a aplicação de gráficos de controle em processos de saturação de papel. XIII SIMPEP. Bauru, SP: 2006.
RIBEIRO, J. L.; CATEN, C. T. Controle estatístico de processos: Apostila de Curso. Porto Alegre: UFRGS, 2012.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. 3 ed. São Paulo: Atlas, 1999.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
RODRIGUES, G. P. Controle Estatístico de Qualidade e de Processo na Indústria de Alimentos. Universidade Federal de Viçosa, MG, p. 152,1998.
ROSA, L. C. Introdução ao Controle Estatístico de Processos. Santa Maria, Ed. Da UFSM, 2009.
SIQUEIRA, L. G. P. Controle Estatístico de Processos – Equipe Grifo – Série Qualidade Brasil. São Paulo: Pioneira, 1997.
SOUZA, A. M., RIGÃO, M. H. Identificação de variáveis fora de controle em processos produtivos multivariados. Revista Produção, São Paulo, V.15 no.1, p.74-86, abr. 2005.
SOUZA, R. Case Research in Operations Management. EDEN Doctoral Seminar on Research Methodology in Operations Management, Brussels, Belgium, 2005.
SPIEGEL, M. R.; STEPHENS, L. J. Schaum’s esboço de teoria e problemas de estatística: Aprenda a si mesmo. 4ª ed., Rio de Janeiro: LTC, 2007.
TRIVELLATO, A. A. Aplicação das sete ferramentas básicas da qualidade no ciclo PDCA para melhoria contínua: estudo de caso numa empresa de autopeças. Trabalho de conclusão de curso, Universidade de São Paulo, 2010.
VIEIRA, S. Estatística para a qualidade: como avaliar com precisão a qualidade em produtos e serviços. Rio de Janeiro: Elsevier, 1999.
VILAÇA, A. C.; OLIVEIRA, R. C. B. Utilização do Controle Estatístico de Processo para Avaliação de Peso de Massas para Pastel. FAZU em Revista, Uberaba, n. 8, p. 137-146. 2011.
WERKEMA, M. C. C. Avaliação de sistemas de medição. 2.ed. Belo Horizonte: Werkema. 2012.
WERKEMA, M. C. C. Ferramentas estatísticas básicas para o gerenciamento de processos. Belo Horizonte: Werkema, 2006.
YIN, R. K. Estudo de caso: planejamento e métodos. 2. Ed. Porto Alegre: Bookman, 2001.
[1] Mestrando em Engenharia de Processos – PPGEP/ITEC-UFPA.
[2] Doutor em Engenharia de Recursos Naturais pela Universidade Federal do Pará.
Enviado: Abril, 2021.
Aprovado: Junho, 2021.