ORIGINALER ARTIKEL
SILVA, Sarley De Araújo [1] MAGNO, Rui Nelson Otoni [2]
SILVA, Sarley De Araújo. MAGNO, Rui Nelson Otoni. Wahrscheinlichkeit, Kontrollkarte angewendet auf bildungswissenschaftliche Software. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 06, Ed. 06, Vol. 11, S. 43-73. Juni 2021. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/bildungswissenschaftliche
ZUSAMMENFASSUNG
Die vorliegende Studie erwähnt die Verringerung von Variabilität und Verlusten aufgrund spezieller Ursachen in Anwendungen der Erziehungswissenschaften, mit dem Ziel, Variabilitätsabweichungen durch Software-Regelkarten in angewandten statistischen Problemen zu erkennen und zu korrigieren. Daher versuchten wir, Konzepte über Regelkarten nach Variablen und Attributen bei der Kontrolle von Anomalien zu untersuchen. Bei der Umsetzung dieses Themas wurden die quantitative Methodik und das Regeldiagramm der Minitab-Software verwendet. Die erzielten Ergebnisse ermöglichten es, Verluste zu reduzieren und den Qualitätsprozess durch Probenanpassungen zwischen Minitab-Kontrollgrenzen zu verbessern, um die Ursachen von Anomalien zu verstehen und zu analysieren. Daher wird der Schluss gezogen, dass das Werkzeug aus Korrekturmaßnahmen in der Lage ist, die Standardabweichungen zu stabilisieren und die Qualität von Wahrscheinlichkeits- und statistischen Anwendungen zu verbessern.
Schlüsselwörter: Wahrscheinlichkeit, Minitab-Software, Regelkarte.
1. EINLEITUNG
Statistik ist ein Zweig der Mathematik, der das Wahrscheinlichkeitswerkzeug verwendet, um Datengruppierungen zu erklären, sowohl in Beobachtungsstudien als auch in Experimenten, um zukünftige Phänomene zu modellieren, zu schätzen und vorherzusagen. Sein Zweck ist es, Daten zu erhalten, zu organisieren, zu analysieren, Regelkarten, Korrelationen und Regressionen zu berechnen und die Kontrolle in Variabilität, statistischen Anwendungen und Bildungseinrichtungen zu ermöglichen. Statistische Methoden beziehen sich auf Daten, die aus Beobachtungen in Form von Messungen oder Zählungen gewonnen werden. Aus Informationen ist es möglich, statistische Probleme im Zusammenhang mit der Kontrolle der Variabilität in den Wissenschaften in den Ingenieurwissenschaften, Chemie, Physik, Mathematik, Geographie usw. zu untersuchen. Die Verwendung statistischer Software ist ein wichtiges Werkzeug für Studien und Anwendbarkeit bei der Kontrolle von Variationen in wahrscheinlichen und statistischen Problemen.
Institutionen sind damit beschäftigt, aufgrund der Anforderungen bei der Erbringung von Dienstleistungen leistungsfähige Indizes in Bezug auf Qualität und Produktivität aufrechtzuerhalten. Informationen und neue Technologien haben ein globalisiertes Umfeld mit hohem Wettbewerb geschaffen, in dem Preis und Termin eingehalten werden sollten (VILAÇA und OLIVEIRA, 2011). In “Jeder Produktionsprozess, unabhängig davon, wie gut er entworfen oder gewartet wird, wird immer einer natürlichen oder inhärenten Variabilität unterliegen, die das Ergebnis der kumulativen Wirkung vieler kleiner und unvermeidlicher Ursachen ist, die als gemeinsame Ursachen bezeichnet werden” (MONTGOMERY, 2004, S.154). Daher ist die Verringerung von Anomalien in Variablenfamilien von größter Bedeutung im statistischen Prozess.
Laut Souza und Rigão (2005) handelt die CEP präventiv auf den Prozess, indem sie Statistiken als Basiselement verwendet, um ihre Veränderungen zu bewerten. Diese Eigenschaften ermöglichen es dem CEP, bei der Überwachung des Prozesses zu helfen und Maßnahmen zu ergreifen, die auf die Lösung von Problemen ausgerichtet sind, die Stabilisierung des Prozesses unterstützen und die Produktion von nicht konformen Artikeln vermeiden (HORA und COSTA, 2009; MAYER, 2004).
Ziel dieser Arbeit ist es, statistische Techniken in Software zu verwenden, um Anomalien in bildungswissenschaftlichen Problemen zu identifizieren, zu korrigieren und zu beseitigen. Die Bedeutung der Kontrollkarten statistischer Software bei der Kontrolle von Anomalien.
Das Hauptziel der statistischen Prozesskontrolle ist es, das Auftreten von zurechenbaren Ursachen bei Prozessänderungen schnell zu erkennen, so dass Prozessuntersuchungen und Korrekturmaßnahmen durchgeführt werden können, bevor viele nicht konforme Einheiten hergestellt werden (MONTGOMERY, 2013, S.280).
Daher ist statistische Software relevant für den Prozess der Identifizierung und Beseitigung von Variabilität.
Die Funktion der statistischen Prozesskontrolle in den Softwarediagrammen besteht darin, die Während der Verarbeitung aufgetretenen Modulationen zu belegen und statistische Diagramme zu entwickeln, die einen präziseren Parameter liefern können, der bei Praktiken hilft, die die vorherrschenden Fertigungspunkte verbessern können, neben dem Erkennen, Korrigieren, Beseitigen oder Anpassen von Prozessen mit Anomalien, wodurch ein präziserer Parameter gegeben wird, so dass Verbesserungen in der Produktionslinie angewendet werden können (OLIVEIRA, 2015, S.22).
Die Regelkarten der Statistiksoftware ermöglichen es, die durch die Diagramme demonstrierte Variabilität zu finden, was eine bessere Visualisierung des Prozesses ermöglicht, um mögliche Fehler für die Anwendung effizienterer Korrekturen auf der Suche nach kontinuierlicher Verbesserung aufzuzeigen.
Auch mit dem Fortschritt im Prozess durch Qualitätskontrolle gibt es immer noch Ursachen für Variabilität im Prozess, das heißt, wenn es eine Oszillation um den Mittelwert oder den idealen Punkt der Spezifikation gibt, ist eine ständige Überwachung des Produktionsverhaltens erforderlich. “Durch die Analyse der gesammelten Daten und die Charakterisierung der Ursache der Systeminstabilität oder -variabilität, die in Regelkarten verwendet werden, Werkzeuge der statistischen Prozesskontrolle als Ergebnis, um eine kontinuierliche Prozessverbesserung zu erreichen” (JURAN und GRYNA, 1992).
Alle Prozesse weisen Variabilität auf, das heißt, je größer die Variabilität, desto größer die Kontrolle über die erzielten Ergebnisse und die gewünschten Ergebnisse. (MONTGOMERY, 1997).
Um die Qualität eines Produkts zu verbessern, ist es notwendig, statistische Software zu verwenden:
In einem wettbewerbsintensiven Umfeld ermöglicht die kontinuierliche Prozessverbesserung die Überwachung, Steuerung und Verbesserung von Produktionsprozessen, wenn Anomalien festgestellt werden. Wenn es einen präventiven Charakter gibt, tragen diese Maßnahmen dazu bei, Verluste zu minimieren und die Produktivität zu steigern (BORTOLOTTI, 2009, S.02).
Solche statistischen Techniken mit Minitab-Software tragen zur Analyse verschiedener Produkte bei, erkennen und reduzieren mögliche Anomalien und stellen Bestände innerhalb der Qualitätsparameter sicher. “Eines der Hauptergebnisse der industriellen Qualitätsstudie war der weit verbreitete Einsatz statistischer Prozesskontrollmethoden, um spezielle Ursachen in Prozessen zu beseitigen und die gemeinsamen Ursachen von Variationen zu reduzieren” (MONTGOMERY, 1997). In diesem Zusammenhang ist die statistische Prozesskontrolle ein äußerst wichtiges Instrument für die Anwendung statistischer Techniken bei der Verringerung von Variationen. Statistische Prozesskontrolle kann als ein Satz von sieben Tools zur Fehlerbehebung definiert werden, um die Prozessstabilität zu erreichen und ihre Kapazität zu verbessern. (FERREIRA et. al., 2008).
Die Regelkarten der statistikischen Software helfen bei der Identifizierung und Stabilität der Ursachen der Variabilität der Prozesse, dienen als Grundlage für Entscheidungen und Korrekturmaßnahmen der Kontrolle, reduzieren die Variabilität und vermeiden außer Kontrolle geratene Stichprobendaten.
Statistische Prozesskontrolle ist eine leistungsstarke Sammlung von Werkzeugen zur Datenerfassung, -analyse und -interpretation mit dem Ziel, die Qualität durch Beseitigung spezieller Variationsursachen zu verbessern, und kann für die meisten Prozesse verwendet werden. (MONTGOMERY, 2004, S.279-281).
Die Studie zu Regelkarten in statistischer Software trägt zur Analyse von Anwendungen in den Erziehungswissenschaften bei der Verringerung der Variabilität in den analysierten Proben bei und generiert bessere Ergebnisse in der Qualitätskontrolle.
2. MATERIALIEN UND METHODEN
2.1 MATERIALIEN
Die Materialien, die zur Steuerung der Variabilität in bildungswissenschaftlichen Anwendungen verwendet wurden, waren die Regelkarten in Minitab Software.
2.2 METHODEN
Zur Durchführung der Studie wurden die quantitative Methode und die Kontrollkarte der minitab-Software verwendet, um die Variabilität in bildungswissenschaftlichen Anwendungen zu reduzieren. Die Methodik zielt auf die Datenvalidierung durch die Verwendung statistischer Daten ab. Die Studie hatte folgende Verteilung: Wahl der zu analysierenden Anwendung, Bestimmung der Unter- und Obergrenzen in Mittelwertparametern und Amplitude, Verteilung der Proben und Überprüfung ihrer Punkte, Analyse von Problemen durch Regelkarten und Korrektur spezieller Ursachen aus den außer Kontrolle geratenen Probenanalysen.
“Die quantitative Methode strebt eine Datenvalidierung durch die Verwendung statistischer Daten mit Analyse einer großen Anzahl repräsentativer Fälle an. Es versucht, die Daten zu quantifizieren und eine Form der statistischen Analyse anzuwenden” (OLIVEIRA, 2011). Der quantitative Ansatz wird häufig in deskriptiven Studien verwendet, die versuchen, die Beziehung zwischen Variablen und die kausale Beziehung zwischen Phänomenen zu klassifizieren.
Richardson (1999, S.70) konzeptualisiert:
Der quantitative Ansatz ist, wie der Name schon sagt, durch die Verwendung von Quantifizierung sowohl in den Modalitäten der Informationserhebung als auch in der Behandlung durch statistische Techniken gekennzeichnet, von den einfachsten wie Prozentsatz, Mittelwert, Standardabweichung bis hin zu den komplexesten, als Korrelationskoeffizient, Regressionsanalyse usw. Sie stellt grundsätzlich die Absicht dar, die Genauigkeit der Ergebnisse zu gewährleisten und Verzerrungen der Analyse und Interpretation zu vermeiden, wodurch eine Sicherheitsmarge in Bezug auf Schlussfolgerungen ermöglicht wird.
Laut Michel (2005, S. 31) ist der quantitative Ansatz eine Sozialforschungsmethodik, die Quantifizierung in den Modalitäten der Informationserhebung und ihrer Behandlung durch statistische Techniken wie Mittlerer Prozentsatz, Standardabweichung, Korrelationskoeffizient, Regressionsanalyse und andere verwendet. Die Kontrollkarten sind ein nützliches Werkzeug, das Verbesserungen und Qualitätssicherung von Abfallkosten, Verschwinden von Schrott und Lösung verschiedener Produktionsprobleme im Zusammenhang mit bestimmten Methoden usw. bringt (ROSA, 2009).
Die Regelkarten wurden von Variablen und Attributen als Techniken bei der Konstruktion von Graphen in Wahrscheinlichkeits- und statistischen Anwendungen verwendet, wobei eine Stabilitätsverbesserung in Bezug auf die Variabilität von Probendefekten beobachtet wurde. Um eine mögliche Ursache für die Variabilität zu finden und zu überprüfen, ob der Prozess unter Kontrolle ist, wurden die Diagramme verwendet, um Anomalien an Probenahmestellen zu kontrollieren. Durch die Graphen war es möglich, Variabilitäten in Fragen der statistischen Wissenschaften zu identifizieren und zu vergleichen.
Er verwendete minitab-Software als Datenanalyse-Tool. Aus den Ergebnissen zwischen den Kontrollgrenzen war es möglich, Defekte zu beheben und die Qualität zu verbessern. Die Kontrollgraphen des Mittelwerts, der Amplitude und der Standardabweichung wurden ausgewählt, um die Variationen des Mittelwerts in der Statistik zu steuern.
Das Instrument zur Identifizierung, Analyse, Zum Vergleich, Korrektur und Reduzierung der Variabilität in bildungswissenschaftlichen Anwendungen verwendete Minitab, ein proprietäres Computerprogramm für statistische Zwecke (MINITAB, 2016). “Es ist ein Werkzeug, das es uns ermöglicht, komplexe statistische Berechnungen durchzuführen und die Ergebnisse zu visualisieren, wodurch die Datenanalyse für den gelegentlichen Benutzer zugänglich und für den erfahreneren Benutzer bequem ist” (PEREIRA und PATRÍCIO, 2016).
Zur Verbesserung der Qualität wird statistische Softwaretechnologie verwendet:
Die statistischen Werkzeuge priorisieren nicht nur die vorgeschlagenen Anwendungen nach dem Grad der Wichtigkeit, sondern helfen bei der Identifizierung und Hilfe bei der Aktion auf die Probleme zur Beseitigung möglicher Ursachen. Die Institution kann ein höheres Maß an Stabilität in den analysierten Anwendungen haben (WERKEMA, 2006, S.32).
Schichtung: “Die Schichtung besteht darin, Sektoren nach gewünschten Faktoren in Teilsektoren einzuteilen, die als Schichtungsfaktoren bezeichnet werden, d. m. für den Prozess der Aufteilung des heterogenen Ganzen in homogene Untergruppen” (VIEIRA, 1999).
Checksheet: Für Werkema (2006) ist das Verifizierungsblatt ein Formular, das in seinem Umfang Kriterien hat, die analysiert werden müssen, um die Sammlung und das Ausfüllen von Daten zu erleichtern. Es ist ein Instrument zur Unterstützung der Datenerhebung und muss für die Wirksamkeit der Datenerhebung ausreichend sein. Daher muss das Prüfblatt die Art der zu erhebenden Daten, den durchzuführenden Vorgang, das Datum der Erfassung, den Analytiker und alle anderen Informationen, die zur Identifizierung der Ursache für eine schlechte Funktionsleistung nützlich sind, eindeutig angeben (CARPINETTI, 2010; MONTGOMERY, 2009). Laut Vieira (1999) hängt die Art des Kontrollbogens davon ab, welche Ziele es haben wird, nämlich: wie der Anteil der nicht konformen Artikel erhöht werden kann; Attribut überprüfen; angabe, wo sich der Mangel im Endprodukt befindet; die Ursachen von Defekten erhöhen; die Verteilung einer Variablen zu analysieren; und überwachen Sie einen Herstellungsprozess.
Pareto-Diagramm: Es ist das Werkzeug, das die Verteilung der Häufigkeit von Daten vorningt und auf den Fehler hinweist, der am häufigsten auftritt, und zwar in prozentualer oder tatsächlicher Reihenfolge. Sich daran zu erinnern, dass ein Defekt häufiger nicht das Haupt- oder kritischste Problem des Prozesses ist (CARPINETTI, 2010; MONTGOMERY, 2009). Vieira (1999) sagt, dass das Pareto-Diagramm verwendet wird, um die Ursachen von Problemen wie hergestellte Produkte, die Nacharbeit erfordern, unnötige Ausgaben, Arbeitsunfälle, Geräteausfälle, Fehler und Lieferverzögerungen zu identifizieren.
Ursache-Wirkungs-Diagramm: Auch bekannt als Ishikawa-Diagramm hat die Funktion, die Ursachen zu identifizieren und zu analysieren, die einen unerwünschten Effekt fördern. Es ist ein effektives Diagramm zur Identifizierung der Wurzel des Problems (CARPINETTI, 2010; MONTGOMERY, 2009). Werkema (2006) stellt fest, dass das Ursache-Wirkungs-Diagramm ein Werkzeug ist, das verwendet wird, um die Beziehung zwischen dem Effekt oder Problem und der Ursache darzustellen, die das Ergebnis verändern könnte. Das Ursache-Wirkungs-Diagramm organisiert die Informationen so, dass es klarer wird, die Analyse und Identifizierung der Ursachen des Problems zu erleichtern, so dass Korrekturmaßnahmen ergriffen werden können, um die Ursache des Problems zu beseitigen (TRIVELLATO, 2010).
Histogramm: Nach Werkema (1995) kann ein Histogramm als Balkendiagramm definiert werden, bei dem die horizontale Achse, unterteilt in mehrere kleine Intervalle, die von einer interessierenden Variablen angenommenen Werte darstellt.
Ausbreitungsdiagramm: Das Ausbreitungsdiagramm ist dafür verantwortlich, Beziehungen zwischen einem Defekt und einer Ursache zu identifizieren, dh es zielt darauf ab, die Beziehung zwischen zwei Variablen oder sogar die Beziehung einer dritten Ursache zu identifizieren. Die Beziehungen zwischen den Variablen können sein: positiv, negativ oder nicht existent (CARPINETTI, 2010; MONTGOMERY, 2009).
Regelkarte: Laut Werkema (2006) hat jeder materielle oder immaterielle Vermögenswert, wenn er ausgearbeitet und/oder hergestellt wird, eine Variation, die sich aus dem Prozess ergibt. Es ist bekannt, dass diese Variationen strikt reduziert werden sollten. Für Werkema (2006) werden Regelkarten verwendet, um die Variabilität zu überwachen, die Arten von Variationen zu unterscheiden und die Stabilität des Prozesses zu bewerten, unabhängig davon, ob er unter Kontrolle ist oder nicht. Der Prozess kann jedoch von häufigen Ursachen oder besonderen Ursachen abweichen
Die Regelkarten wurden von Shewhart erstellt und bestehen aus Mittel- oder Mittelgrenze (LC), Untergrenze (LI) und Obergrenze (LS). Seine Hauptfunktion besteht darin, anzuzeigen, ob der Prozess unter Kontrolle ist oder nicht, dh ob der Prozess Produkte gemäß den Spezifikationen herstellt oder nicht. Die Prozessanalyse erfolgt aus der Überprüfung der Regelkarte, wobei beobachtet wird, ob die darin dargestellten Punkte zwischen den oberen und unteren Grenzen der Spezifikation liegen (CARPINETTI, 2010; MONTGOMERY, 2009).
Regelkarten: Dient zur Analyse von Prozessvariationen häufiger Ursachen und zur Erkennung spezieller Ursachen, ist ein Werkzeug namens Diagramme oder Regelkarten. Die Analyse der Leistungsfähigkeit eines Prozesses ist ein wesentlicher Bestandteil eines globalen Qualitätsprogramms. Zu den wichtigsten Datenanwendungen einer Prozesskapazitätsanalyse gehören (MONTGOMERY, 2004):
2.2.1 STATISTISCHE REGELN ZUR IDENTIFIZIERUNG BESONDERER URSACHEN
Es schlägt eine Reihe von Entscheidungsregeln vor, um nicht-zufällige Muster in Regelkarten zu unterscheiden. Insbesondere schlägt es vor, den Schluss zu ziehen, dass der Prozess außer Kontrolle ist, wenn (MONTGOMERY, 2004):
1. Fall: Identifizieren Sie sechs, acht oder mehr Punkte oberhalb oder unterhalb der Mittellinie. Mögliche Ursachen: Änderung des Maschineneinstellprozesses, der Methode oder des anderen Materials, Ausfall eines Bauteils in der Maschine, Maschinenbruch und große Variation des erhaltenen Materials.
2. Fall: Finden Sie sechs, sieben oder mehr Punkte nach oben oder unten. Mögliche Ursachen: allmählicher Werkzeugverschleiß, Geräteverschleiß oder Verschleiß im Zusammenhang mit dem Messgerät.
3. Fall: Überprüfen Sie die Verschiebung des Mittelwerts. Mögliche Ursachen: neue Methode, neue Maschine in der Qualitätsverbesserung und eine neue Materialcharge.
4. Fall: Punkte außerhalb der Kontrollgrenzen. Mögliche Ursachen: Mess- oder Tippfehler, Werkzeugbruch oder ungeregeltes Messgerät, das die Identifizierung der Messung nicht zulässt.
5. Fall: Periodizität der Punkte. Mögliche Ursachen: Ungleichmäßigkeit des aufgenommenen Rohmaterials, Rotation von Bedienern, Vorrichtungen und Instrumenten sowie Unterschied zwischen den Schichten.
2.2.2 REGELKARTEN FÜR VARIABLEN UND ATTRIBUTE
Die Regelkarten nach Variablen sollen über die Verbesserung der Qualität, der Prozesskapazität, der Entscheidungsfindung in Bezug auf Produktspezifikationen, Produktionsprozesse und Entscheidungen über neu produzierte Teile informieren. Sie werden dort eingesetzt, wo Qualitätsmerkmale quantitativ gemessen werden können. Sie können zum Beispiel Abmessungen von Teilen, Volumen, Gewicht, unter anderem sein. So wird sein breiter Anwendungsbereich wahrgenommen, da mehrere Arten von Prozessen diese Art von Eigenschaften aufweisen (MAGALHÃES, 2011).
“Regelkarten für Variablen werden häufiger verwendet als Regelkarten für Attribute, weil sie konkretere Informationen enthalten, mit kleinen Stichproben arbeiten und es ermöglichen, die Ursachen, die die Stabilität des Prozesses beeinflussen, schneller zu identifizieren” (REBELATO, 2006). “Die Regelkarten für Variablen sind Diagramme für Mittelwerte, die zur Kontrolle des Durchschnittswerts der Prozessleistung, des Amplitudendiagramms oder des Standardabweichungsdiagramms verwendet werden, da in den meisten Fällen die Standardabweichung des Prozesses nicht bekannt ist” (CASTRO, 2012).
Regelkarten können in zwei Gruppen eingeteilt werden: Regelkarten für Variablen: Sie erfasst die Qualitätsmerkmale, die auf einer quantitativen Skala gemessen werden. Und die Regelkarten nach Attributen: Es zeichnet die Qualitätsmerkmale auf, gemessen auf einer qualitativen Skala, zum Beispiel gilt es als konform und nicht konform (SIQUEIRA, 1997). So sind laut Spiegel und Stephens (2007) die Begriffe “Variablen” und “Attribute” mit der Art der aus dem Prozess gesammelten Daten verbunden.
2.2.3 REGELKARTE FÜR MEDIUM (X-BAR) UND AMPLITUDE (R)
Die durchschnittliche Grafik ![]() wird verwendet, um den Durchschnitt des Prozesses (Zentralität) und den Amplitudengraphen zu steuern
wird verwendet, um den Durchschnitt des Prozesses (Zentralität) und den Amplitudengraphen zu steuern ![]() um die Variabilität des betrachteten Prozesses zu kontrollieren (IPEK et al., 1999).
um die Variabilität des betrachteten Prozesses zu kontrollieren (IPEK et al., 1999).
Ausdrücke zur Berechnung der Kontrollgrenzen von ![]() und R.
und R.
Kontrollkarte ![]() . Die Mittellinie sowie obere und untere Kontrollgrenzen für die Kontrollkarte
. Die Mittellinie sowie obere und untere Kontrollgrenzen für die Kontrollkarte ![]() sie sind:
sie sind: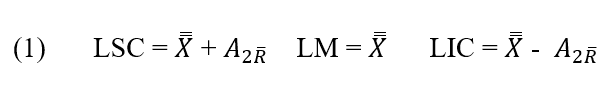
Regelkarte R. Die Mittellinie und die oberen und unteren Steuergrenzen für das Regeldiagramm R sind:
![]()
2.2.4 MITTELDIAGRAMM (X-BAR) UND STANDARDABWEICHUNG (S)
Das Regeldiagramm für den Mittelwert (X-Balkendiagramm) dient zur Steuerung des Prozessmittelwerts, während das Regeldiagramm (Standardabweichungsdiagramm S) zur Steuerung der Prozessvariabilität verwendet wird. Wenn die Stichprobengröße (Untergruppe) kleiner oder gleich zehn ist, sehen die R- und S-Diagramme gleich aus. Wenn jedoch die Stichprobengröße zunimmt, wird das S-Diagramm genauer als das R-Diagramm und sollte verwendet werden (SIQUEIRA, 1997).
Kontrollkarte ![]() . Die Mittellinie sowie obere und untere Kontrollgrenzen für die Kontrollkarte
. Die Mittellinie sowie obere und untere Kontrollgrenzen für die Kontrollkarte ![]() sie sind:
sie sind:
![]()
Kontrollkarte S:
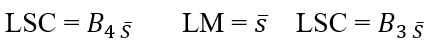
2.2.4.1 REGELKARTEN NACH ATTRIBUTEN
Attributdiagramme werden verwendet, um die Fehleranalyse zu steuern. Diese Diagramme sind besonders nützlich bei der Kontrolle von Rohstoffen und Fertigprodukten und werden auch bei der Analyse von Qualitätsbewertungen in Verbraucherbriefen verwendet. Ein Attribut ist ein Merkmal eines Produkts, eines Prozesses oder einer anderen Grundgesamtheit, das gezählt, aber nicht beschrieben werden kann, so dass seine Werte erhöht werden (RODRIGUES, 1998). Es handelt sich um Diagramme, mit denen wir identifizieren können, wie sich Sample-Sets um Limits, Trends und Level-Austausch verhalten. Bei Variablen wird es schnell wahrgenommen, wenn die Daten keiner zufälligen Verteilung folgen. In Attributregelkarten werden Einheiten nach den festgelegten Kriterien als perfekt oder fehlerhaft eingestuft. Daher ist die Wahrscheinlichkeit, dass eine defekte Einheit erzeugt wird, konstant, und folglich ist die entsprechende Probenverteilung binomial (CHAVES und TEIXEIRA, 1997). Attributdiagramme werden verwendet, um die Fehleranalyse zu steuern. Diese Diagramme sind besonders nützlich bei der Kontrolle von Rohstoffen und Fertigprodukten und werden auch bei der Analyse von Kommentaren zu Qualität und qualitativ ausgedrückten Merkmalen verwendet, d.b. wenn diese analysierten Merkmale nicht numerisch dargestellt werden und nach oder nicht konform klassifiziert werden können (SOUZA, 2005). Es sind die repräsentativen Maße, die sich aus der Zählung der Anzahl der Artikel des Produkts auf einer diskreten Skala ergeben, die ein bestimmtes Merkmal von Interesse darstellen. Messungen werden durch visuelle Inspektion durchgeführt und nicht messbare Merkmale werden aufgezeichnet. Es kann gesagt werden, dass Kontrolldiagramm durch diskrete Zufallsvariable mit Poisson-Wahrscheinlichkeitsdichtefunktion (LAGO, 1999) dargestellt wird.
Die Mathematik der Attributkarten erfordert keine Tabellen. Sie können auf Systeme angewendet werden, in denen die Maßnahmen in der Genehmigung oder Ablehnung bestehen, oder auf Prozesse, bei denen es sehr schwierig oder unmöglich ist, Variablenmaße zu erhalten (RODRIGUES, 1998).
Statistische Informationen über Messungen nach Attributen in Lösungen für Probleme der Erziehungswissenschaften werden in Produkte mit Anomalien oder Defekten klassifiziert. Eines der Hauptziele der Attributmessanalyse ist die Identifizierung, Erkennung und Korrektur von Fehlern, Qualität kann als die Reihe von Attributen definiert werden, die eine Gute oder Dienstleistung vollständig für die Verwendung geeignet machen, für die sie entworfen wurde (MONTGOMERY, 1985). Die vier Kontrollkarten für Attribute in Anomalien und Defekten, die nach Montgomery (2004) verwendet werden, lauten wie folgt: Regelkarten nach Attributen, die sind: Buchstabe p (nicht konforme Proportionen), Np-Diagramm (nicht konforme Einheiten), Buchstabe C (Anzahl der Nichtkonformität pro Einheit) und Buchstabe u (Nichtkonformitätsrate pro Einheit).
2.2.5 SCHAUBILD P (NICHT KONFORME PROPORTIONEN)
Für Werkema (2006) wird das p-Diagramm verwendet, wenn das Merkmal der Qualität von Interesse durch den Anteil der fehlerhaften Artikel dargestellt wird, die durch den analysierten Prozess erzeugt werden.
Regelkarte P:
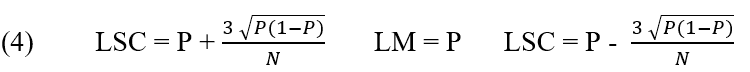
2.2.6 NP-DIAGRAMM (NICHT KONFORME EINHEITEN)
Der Brief gibt nicht die Anzahl der Mängel pro Probe an und wird verwendet, um die Anzahl der fehlerhaften Produkte in jeder Charge zu kontrollieren und sicherzustellen, dass der Prozess unter Kontrolle ist (RODRIGUES, 1998).
Die Mittellinie und die oberen und unteren Kontrollgrenzen für das np-Diagramm sind:
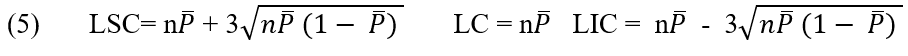
2.2.7 SCHAUBILD C ANZAHL VON (NICHT KONFORM PRO EINHEIT)
Diagramm c wird verwendet, um zu bestimmen, ob die Fehlernummer eines einzelnen Artikels innerhalb der definierten Kontrollgrenzen liegt. Es kann als Endkontrolle betrachtet werden (RODRIGUES, 1998). Diagramm c ist am besten geeignet, wenn Defekte in einem kontinuierlichen Medium verteilt sind, z. B.: Anzahl der Fehler pro Gewebefläche, Anzahl der Unvollkommenheiten pro Bodenlänge; und wenn ein Produkt mehr als eine Art von Defekt aufweisen kann (RIBEIRO und CATEN, 2012).
Daher werden die Kontrollgrenzen von Graph C mit den folgenden Gleichungen berechnet:
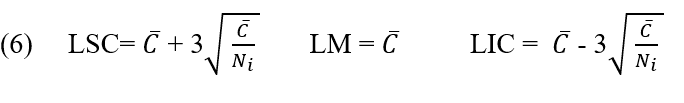
2.2.8 GRAFIK U NICHTEINHALTUNGSRATE PRO EINHEIT
Das u-Diagramm wird verwendet, um Defekte in einer Produktionseinheit zu überwachen (MONTGOMERY, 1997). Das u-Diagramm wird empfohlen, wenn das Produkt aus verschiedenen Teilen und vielen Qualitätsmerkmalen besteht, die überprüft werden müssen, und auch, wenn die Größe der Produkteinheit variabel ist (CORTIVO, 2005).
Die Mittellinie und die oberen und unteren Kontrollgrenzen für das U-Diagramm sind:
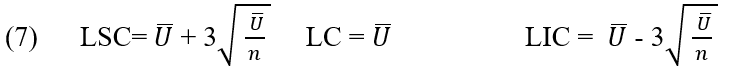
2.2.9 MULTIPLE LINEARE REGRESSION
Die multiple Regressionsanalyse ist eine Technik, die verwendet wird, um die Beziehung zwischen einer abhängigen Variablen und einem Satz unabhängiger Variablen zu untersuchen (MONTGOMERY und RUNGER, 2009). Die Technik ermöglicht die Schätzung zukünftiger Werte für die abhängige Variable, wenn ein Satz von Eingabedaten für die unabhängigen Variablen gegeben ist (PEDRINI und CATEN, 2009; DOWNING und CLARK, 2002)
Das Basismodell der multiplen linearen Regression wobei ![]() für j=0,1,2…..k sind Regressionskoeffizienten, Y ist die abhängige Variable der Regressoren
für j=0,1,2…..k sind Regressionskoeffizienten, Y ist die abhängige Variable der Regressoren ![]() und der Wert e ist der zufällige Fehler der Gleichung. (MONTGOMERY, 2015).
und der Wert e ist der zufällige Fehler der Gleichung. (MONTGOMERY, 2015).
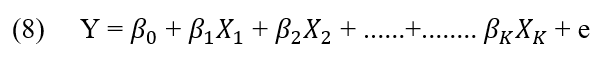
Der Prozess wird untersucht, um die Bedürfnisse der Analyse der Anwendungen der Erziehungswissenschaften und ihrer Prozessschritte zu verstehen. Quellen der Analyse werden angesprochen, die Anwendungen, die darin analysiert werden, sind die Variabilität die Hauptfaktoren, die es beeinflussen. Identifizieren des am besten geeigneten Regelkartentyps zur Analyse der Daten mit minitab-Software. Mit der Methode stochastische Prozesskontrolle wurde die Strukturierung der Forschung angestrebt, um den Fortschritt derselben zu unterstützen.
3. ERGEBNISSE UND DISKUSSION
3.1 DIE VERWENDUNG VON MINITAB-REGELKARTEN ZUR VERRINGERUNG DER VARIABILITÄT
Nach dem Sammeln und Plotten der Daten in technischen Anwendungen wurden einige Diagramme für Variablen und Diagramme für Attribute in den Minitab-Software-Regelkarten erstellt, um Verluste aufgrund von Produktionsschwankungen zu überwachen. Zur weiteren Analyse der Ergebnisse wurde der aus den Komponenten: Obere Kontrollgrenze LSC, Mittellinie LC und untere Kontrollgrenze LIC.
Es wurde beobachtet, dass nach der Identifizierung, Beseitigung und Reduzierung der Ursachen der Variabilität die Möglichkeit zur Verbesserung der Qualität der Produkte geschaffen wurde. Durch die Analyse der in den statistischen Anwendungen erhaltenen Ergebnisse wird die Stabilitätskontrolle der Fehlerursachen an Stichprobenpunkten in den Diagrammen dargestellt und die Stichprobenprozesskontrolle wurde durchgeführt, um die Variabilität zu kontrollieren. Die Regelkarten zeigten unter den statistischen Parametern folgende Ergebnisse: Berechnung des Prozessmittelwerts, Berechnung der Standardabweichung, Berechnung der Kontrollgrenzen LSC, LIC und Amplitude in den folgenden Anwendungen:
3.2 WAHRSCHEINLICHKEIT UND STATISTISCHE ANWENDUNGEN IM ENGINEERING DURCH KONTROLLBUCHSTABE IN MINITAB SOFTWARE BEI DER REDUZIERUNG DER VARIABILITÄT
Diagrammkonstruktionen in deskriptiven Statistikanwendungen, die von der Kontrollkarte in Minitab Software ausgeführt werden.
01) Die Daten beziehen sich auf einen Stiftbearbeitungsprozess, bei dem die Durchmesser durch Bemusterung von 5 Stück in 25 Chargen gemessen werden. Analysieren Sie den Prozess mit der Minitab-Software.
Tabelle 1: Messungen des Stiftdurchmessers
| Charge | Messungen | ||||||
| 1 | 2,08495 | 2,09203 | 1,01425 | 0,47627 | 1,75308 | ||
| 2 | 2,44288 | 1,84913 | 1,02012 | 1,5103 | 0,5167 | ||
| 3 | 2,08819 | 0,34567 | 0,67246 | 2,14641 | 0,51528 | ||
| 4 | 1,42411 | 1,04348 | 1,15683 | 0,9108 | 1,23562 | ||
| 5 | 1,43307 | 0,22926 | 1,51612 | 0,82627 | 1,29935 | ||
| 6 | 1,2113 | 0,63715 | 0,97815 | 2,30782 | 1,0003 | ||
| 7 | 2,14731 | 1,95837 | 0,95294 | 1,35384 | 0,73037 | ||
| 8 | 2,02444 | 1,60384 | 1,64667 | 1,66449 | 0,92746 | ||
| 9 | 1,4743 | 1,93916 | 1,06107 | 1,55396 | 0,8049 | ||
| 10 | 1,09096 | 2,09033 | 0,62161 | 1,45256 | 1,77208 | ||
| 11 | 1,90879 | 1,274 | 1,46827 | 1,36343 | 1,06161 | ||
| 12 | 0,81791 | 1,89952 | 1,24044 | 0,72729 | 1,44959 | ||
| 13 | 0,58784 | 1,57195 | 0,73316 | 1,05367 | 3,29273 | ||
| 14 | 2,12184 | 0,90374 | 0,59773 | 1,63101 | 0,82706 | ||
| 15 | 1,2819 | 0,89479 | 1,05394 | 1,25779 | 0,99451 | ||
| 16 | 0,82836 | 0,16347 | 2,12864 | 1,69732 | 0,90752 | ||
| 17 | 0,14026 | 1,0432 | 0,76948 | 1,72083 | 3,95445 | ||
| 18 | 2,19158 | 0,87777 | 0,955 | 1,50304 | 1,1604 | ||
| 19 | 0,93195 | 1,82231 | 1,2179 | 1,72608 | 1,45375 | ||
| 20 | 0,84523 | 2,79753 | 2,30041 | 0,47693 | 0,58081 | ||
| 21 | 1,84098 | 2,37729 | 1,89976 | 1,2079 | 3,2343 | ||
| 22 | 1,15648 | 2,5689 | 0,90064 | 3,7548 | 1,24616 | ||
| 23 | 2,21913 | 0,91997 | 2,15777 | 1,48548 | 0,25288 | ||
| 24 | 1,41393 | 0,71069 | 0,63707 | 1,71835 | 1,52855 | ||
| 25 | 1,5938 | 1,19839 | 0,88228 | 1,23019 | 0,41643 | ||
Quelle: Aktion (2019)
Abbildung 01: Steuerkarte defekter Pin außer Kontrolle
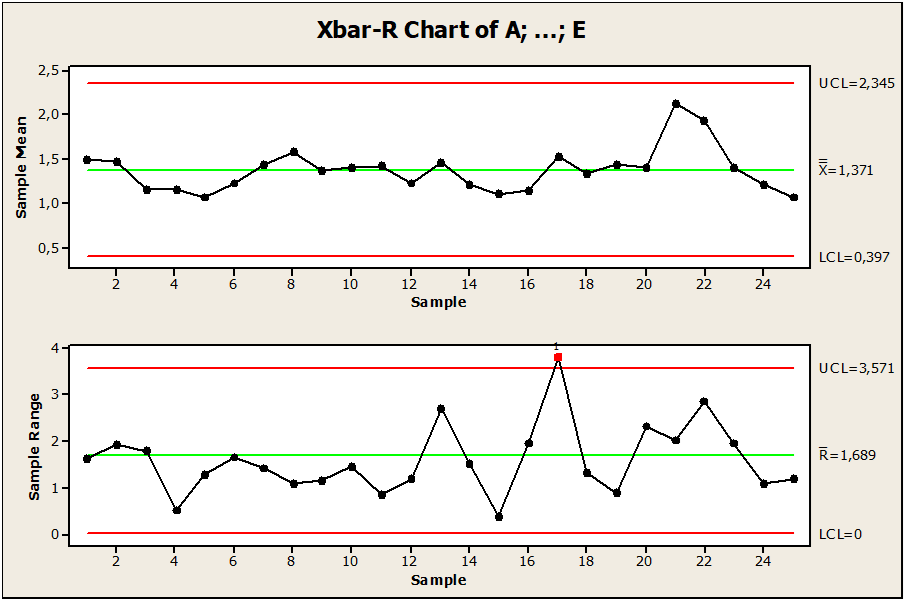
Die Beispieldaten zeigen einen Stiftbearbeitungsprozess, der in 25 Pins beobachtet wurde. Wie in Bild 01 gezeigt. Wir beobachteten, dass es eine Variation zwischen Punkt 17 oberhalb der oberen Grenze der LSC-Kontrolle gibt, wobei der Punkt außerhalb der Kontrollgrenze liegt. Seine zentrale Grenze ist gleich 1,68, die obere Kontrollgrenze mit dem Wert 3,57 und die untere Grenze gleich 0,0, was bedeutet, dass Punkt 17 im Wertpin 3,95445 durch Variabilität beeinflusst wird. Um den Prozess unter Kontrolle zu halten, wurde empfohlen, Werte zu entfernen, zu ändern oder ein neues Diagramm zu erstellen.
Bild 02: Regelkarte mit angepassten Grenzwerten
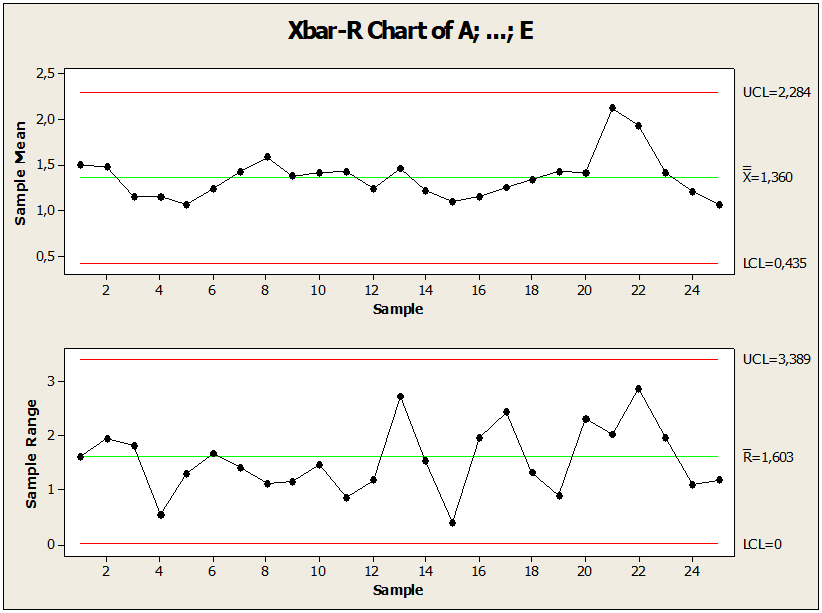
Nach Überprüfung der Anomalie, Abbildung 02. Die Grafik zeigt den Punkt unter Kontrolle in Bezug auf den Mittelwert, an dem es Änderungen gab, um den Prozess unter Kontrolle zu halten. In der Stichprobe von Nummer 17 des Nichtkonformitätswerts 3,95445 wurde sie in 2,55445 geändert. Diese Änderung, die von der Regelkarte gefolgt von statistischen Regeln durchgeführt wurde, reduzierte die Variabilität und der Punkt außerhalb der Kontrollgrenze wurde angepasst. Wir kommen zu dem Schluss, dass all diese statistischen Maßnahmen den Prozess stabil gehalten haben. Nach der Identifizierung, Analyse, Korrektur, Reduzierung und Kontrolle des Prozesses von nicht konformen Proben war es möglich, die Ergebnisse mit den vorherigen Ergebnissen zwischen dem Prozess zu vergleichen: Außer Kontrolle geratener Prozess, LC gleich 1,68, Standardabweichung gleich 0,69 und Amplitude des Grenzwerts 3,81 einen Punkt über dem Grenzwert LSC. Prozess unter Kontrolle LC gleich 1,60, Standardabweichung gleich und 0,66 Amplitude des Grenzwertes 3,61. Nach dem Vergleich mit den im 1. und 2. Test berechneten Werten kam es zu einer Verbesserung der statistischen Parameter.
Bild 03: Zeigt Stiftdurchmesser
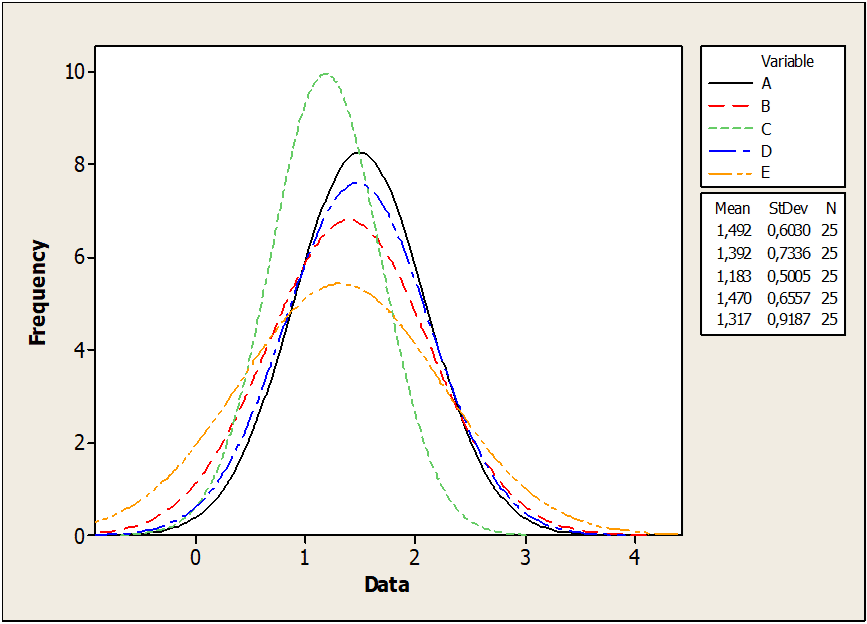
Bild 03 zeigt eine Dispersionskurve der Stiftdurchmesser in Untergruppen von E mit größerer Genauigkeit als die Dispersionskurve der Untergruppen D. Die Standardabweichung für Proben der Untergruppe E (0,91) ist viel größer als die Proben der Untergruppe D. (0,50). Daher ist die angepasste Verteilung für Untergruppe E abgeflacht und genauer.
02) Eine Studie wurde durchgeführt, um die Zunahme von Mängeln an Edelstahltüren von Küchengeräten zu bestimmen, die in einem metallverarbeitenden Unternehmen hergestellt werden. Während der Studie traten die folgenden Mängel mit ihrem Auftreten und den damit verbundenen Kosten auf. Erstellen Sie die entsprechenden Pareto-Diagramme.
Tabelle 2: Defekte Teile
| Art der Mängel | Nº. von defekten Teilen | StückkostenReparatur/Ausschuss | |
| Schlecht ausgeführtes Schweißen | 55 | 50 | |
| Schlechtes Bohren | 9 | 50 | |
| Biegefehler | 274 | 5 | |
| Verpackung | 15 | 50 | |
| Schlechte Plattenqualität | 16 | 50 | |
| Schneidet | 126 | 30 | |
| Andere | 12 | 50 |
Quelle: Core Formation -Nufec (2006)
Bild 04: Defekte Teilenummern
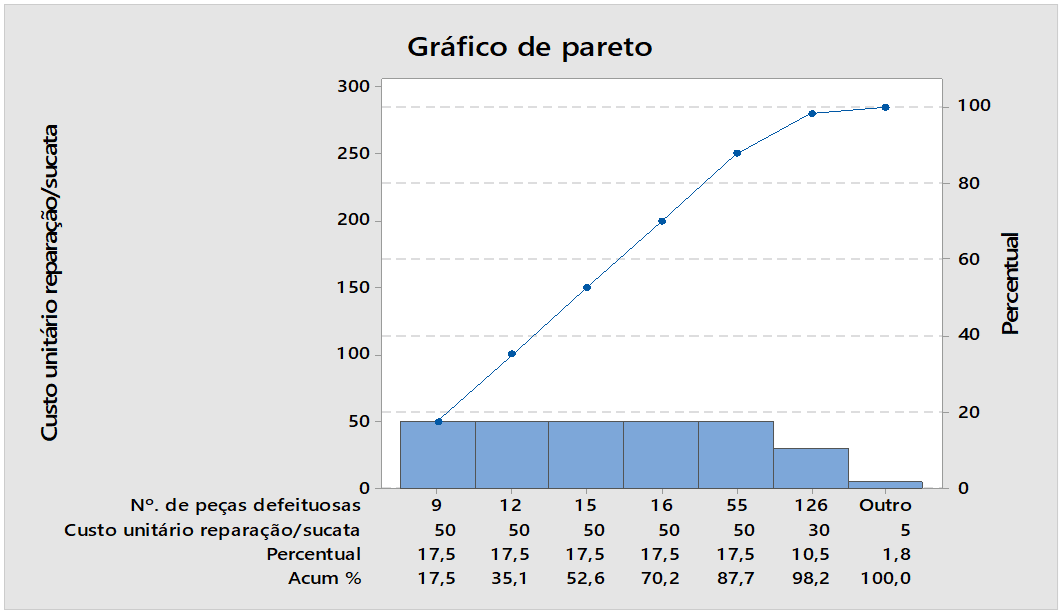
Bild 04 zeigt die Ergebnisse der fehlerhaften Teilenummern, Prozentsatz, die größte Quelle 9 fehlerhafte Teile, die einem Prozentsatz von 17,5 % entspricht. Bei der Analyse der Abbildung wird das Vorhandensein von Konzentrationen von Ursachen besonderer Variabilität wahrgenommen, die durch die Regelkarte der Minitab-Software korrigiert werden müssen.
Bild 05: Defekte Teilenummern geraten außer Kontrolle
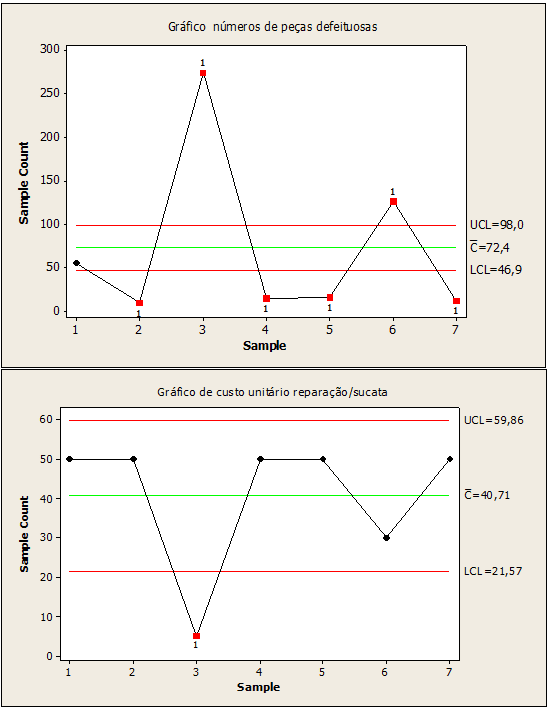
Es wurde überprüft, dass Abbildung 05, die sich auf fehlerhafte Teile bezieht, Variabilität in den Punkten 2,3,4,5,6,7 mit Werten (9.274,15,16,126,12) aufwies. Auf der anderen Seite, Stückkosten bei der Reparatur des Punktschrotts mit Variabilität 3 mit einem Wert gleich 5. Es wird der Schluss gezogen, dass es in diesen Punkten besondere Ursachen gibt und dass korrekturbedürftig ist.
Bild 06: Fehlerhafte Teilenummern im Griff
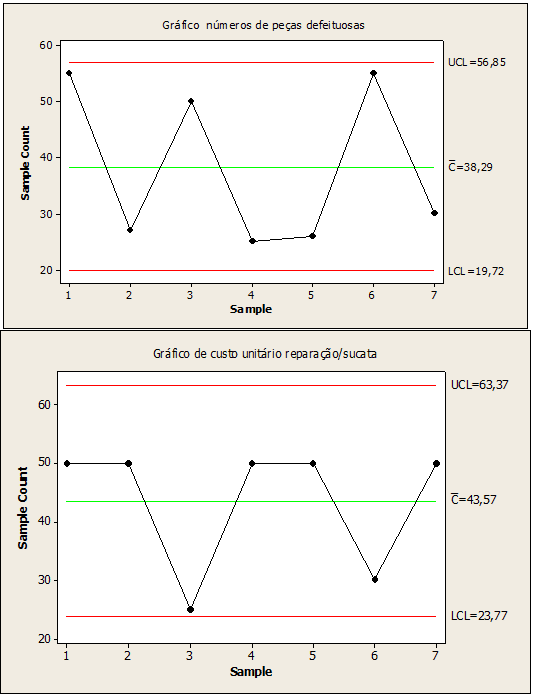
In Abbildung 06 werden anstelle der Werte der außer Kontrolle geratenen Punkte 2,3,4,5,6,7 werteten in Nummer 3 27,50,25,26,55,30 für defekte Teile und 25 für die Reparatur von Stückkostenschrott verwendet. Diese durch die Regelkarte generierten Ersatzdaten verbesserten den stochastischen Prozess, der unter Kontrolle blieb, reduzierten die Variabilität bei der Herstellung von Edelstahlportalen und hielten die Qualität des Produkts stabil.
03) Eine Extrusionsform wird verwendet, um Aluminiumstäbe herzustellen. Der Durchmesser der Stangen ist ein kritisches Qualitätsmerkmal. Die folgende Tabelle zeigt die x- und r-Werte für 20 Proben von jeweils fünf Rohren. Spezifikationen auf den Rohren sind 0,5035 +/- 0,0010 Zoll. Die Datenwerte sind die letzten drei Ziffern der Kennzahl, dh 34,2 wird als 0,50342 gelesen.
a) Ermitteln Sie anhand aller Daten die Kontrollgrenzen für die X- und R-Diagramme, erstellen Sie das Diagramm und zeichnen Sie die Daten.
b) Verwenden Sie die Grenzen von Elementsteuerungsversuchen (a), um außer Kontrolle geratene Punkte zu identifizieren. Überprüfen Sie bei Bedarf Ihre Kontrollgrenzwerte, wobei zu berücksichtigen ist, dass jede Probe außerhalb der Kontrollgrenzen eliminiert werden kann.
Tabelle 3: Nagelproben
| Beispiel | R | Beispiel | R | ||
| 1 | 34,2 | 3 | 11 | 35,4 | 8 |
| 2 | 31,6 | 4 | 12 | 34,0 | 6 |
| 3 | 31,8 | 4 | 13 | 36,0 | 4 |
| 4 | 33,4 | 5 | 14 | 37,2 | 7 |
| 5 | 35,0 | 4 | 15 | 35,2 | 3 |
| 6 | 32,1 | 2 | 16 | 33,4 | 10 |
| 7 | 32,6 | 7 | 17 | 35,0 | 4 |
| 8 | 33,8 | 9 | 18 | 34,4 | 7 |
| 9 | 34,8 | 10 | 19 | 33,9 | 8 |
| 10 | 38,6 | 4 | 20 | 34,0 | 4 |
Quelle: Montgomery (2013)
Bild 07: Außer Kontrolle geratene Stabproben
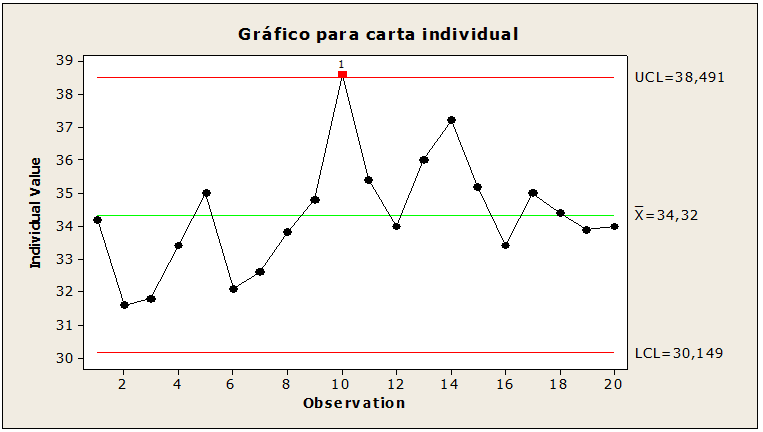
Statistische Kontrolle für 20 Proben von jeweils fünf Stäbchen. Bei der Interpretation von Abbildung 07 lagen die Werte der Obergrenze bei 38,49, der Mittelwert bei 34,32, bei der Standardabweichung bei 1,72, bei der Untergrenze bei 30,14 mit Punkt 10 des Wertes 38, 6 über der Obergrenze, die Hinweise auf besondere Ursachen gibt, die richtig sein können. An dieser Stelle wird eine Korrektur vorgeschlagen, damit die Grenzwerte angepasst werden.
Bild 08: Nagelproben unter Kontrolle
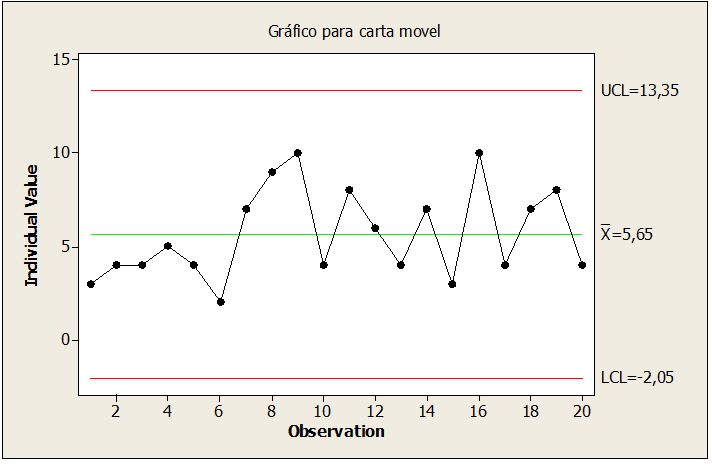
Durch die Korrektur des Punktes in Abbildung 08 wurde Punkt 10 angepasst, wodurch der Probenwert auf 36,6 reduziert wurde, wodurch der Prozess bei der Herstellung des Durchmessers von Aluminiumstäben stabil und unter Kontrolle gehalten wurde.
Bild 09: Stammproben mit Prozesskapazität
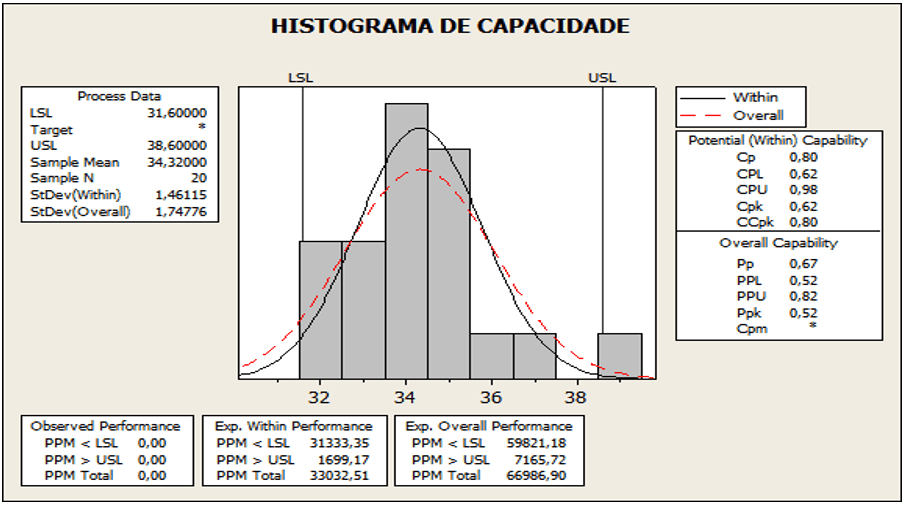
Nach der Analyse von Bild 09 stellt es den Wert für Cpk gleich 0,49, Mittelwert 5,65, Standardabweichung 2,434 und p-Wert 0,025 dar. CPk-Ergebnis außerhalb der Grenzen, wenn Ppk < CPk. Der erhaltene Mittelwert betrug 5,65, mit Verschiebung zur LSE. Der CPk 0,49 unter den festgelegten Werten, die 1,33 implizieren, liegt außerhalb des stabilen Grenzwerts.
Abbildung 10: Fehlerprozentsatz
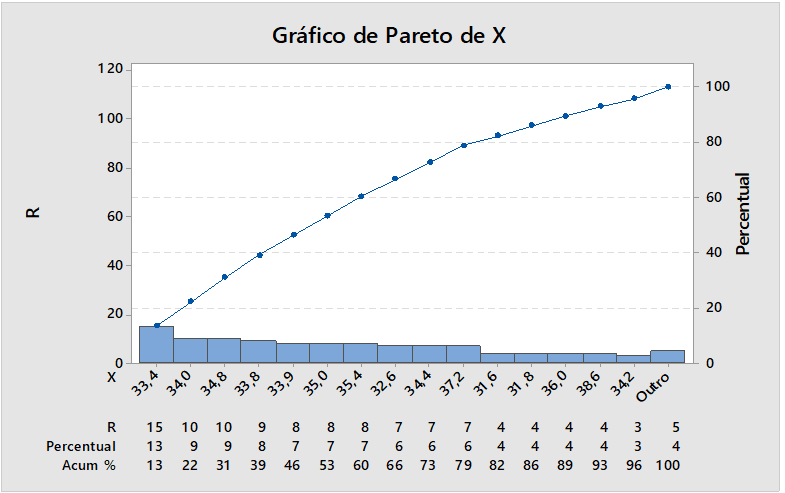
Abbildung 10. Das Pareto-Diagramm zeigt den Prozentsatz der analysierten Proben von Defekten, die in diesem Prozess produziert wurden, Prozentsatz, die größte Quelle 15 defekte Teile, die einem Prozentsatz von 13% entspricht. Es besteht die Notwendigkeit, Variationen zu eliminieren.
Bei der Beobachtung der Zahlen wurde bestätigt, dass in Abbildung 07 Punkt 10 außerhalb der Kontrollgrenze liegt und eine Anomalie im Durchmesser der Stäbe auftut, die korrekt sein kann. Bereits in Bild 09 ist der cpk out of bounds. Abbildung 10 weist jedoch einen Defekt in den Stäben auf. Nächstes Bild 08. Nach der Interpretation, Analyse und Beseitigung blieben die speziellen Ursachen an der Stelle des Durchmessers stabil.
Abbildung 11 zeigt die Regelkarten für die Mittelwerte, die Standardabweichung und die Anzahl der Nichtkonformitäten, die durch Probenahme von 5 Stück in 25 Losen gemessen wurden. Durch die vorgestellten Diagramme können wir beobachten, dass es einen Punkt außerhalb der Kontrollgrenze gibt und um den Mittelwert verteilt ist, sowie es uns ermöglichte, die Größenordnung der Prozessabweichungen zu beobachten und es schließlich zu ermöglichen, die Punkte spezieller Ursachen zu finden, wo es einen Punkt außerhalb des Grenzwerts darstellt. Durch diese Analysen fanden wir heraus, dass es eine Variabilität der besonderen Ursache in Punkt 17 LSC gibt, wo der Punkt außerhalb der Kontrollgrenze liegt, was Korrekturen und eine Verringerung der Variabilität erfordert. Diese Anomalie wurde von der Minitab-Software-Regelkarte im 1. Test erkannt, bei dem der Prozess zur Stabilisierung erforderlich war. Um den Prozess unter Kontrolle zu halten, wurde der 2. Test als Ergänzung zum 1. Test angewendet, um eine neue Regelkarte zu erstellen, die den Prozess unter Kontrolle hat.
Beim Erstellen des Grenzwertdiagramms unter Kontrolle wurden drei Situationen empfohlen: Entfernen der 3,95445-Wertbeobachtung, Ändern von Nichtkonformitätswerten oder Erstellen eines neuen Diagramms. Der 2. Test in Abbildung 12. Zeigen Sie die Korrektur, den Vergleich und die Verringerung von Variationen bei der Konstruktion eines neuen Diagramms mit dem kontrollierten Punkt in Bezug auf den Mittelwert, mit Änderung in der Probenahmestelle, um den Prozess unter Kontrolle zu halten. Der Stichprobenwert 3,95445 änderte den Wert 2,55445. Nach der Steuerung des Prozesses war es möglich, die erzielten Ergebnisse mit den vorherigen Ergebnissen zwischen den Prozessen zu vergleichen. Im Vergleich zu den Werten der Stichprobenberechnung im kontrollierten Prozess stellte der Mittelwert den Wert gleich 1,60, die Standardabweichung 0,66 und die Amplitude des Grenzwertes 3,66 dar. Während der außer Kontrolle geratene Prozess gleich 1,68 bedeutet, ist die Standardabweichung 0,69 und die Grenzamplitude mit dem Wert 3,81.
Abbildung 11: Außer Kontrolle geratener Buchstabe
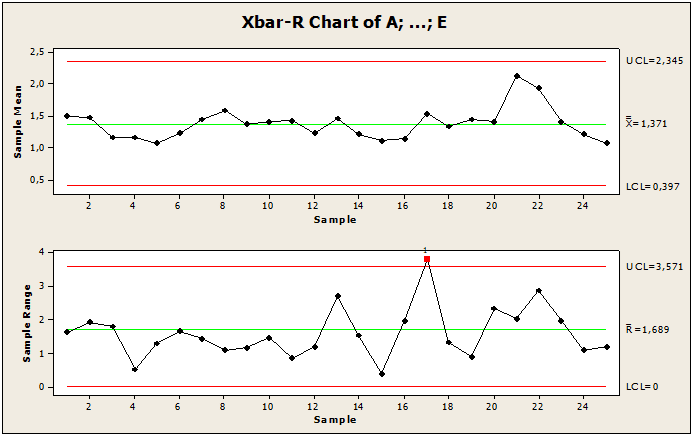
Abbildung 12: Brief unter Kontrolle
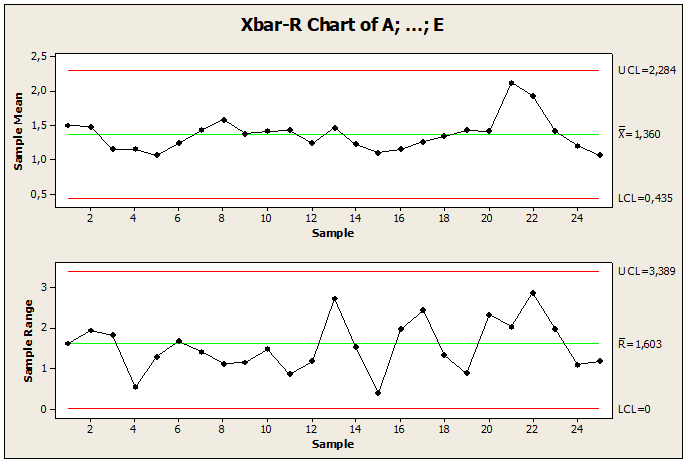
Die in dieser Studie erzielten Ergebnisse zeigen, dass die Kontrollkarten ein wirksames Instrument sind, um die Variabilität in den Anwendungen der Erziehungswissenschaften zu reduzieren, indem sie die Stabilität des Prozesses finden und die Qualität verbessern.
4. FAZIT
Durch die Regelkarten der Minitab-Software war es möglich, Änderungen in der Probenverteilung im statistischen Prozess zu zeichnen und zu analysieren, um kritische Punkte mit Variabilität in Anwendungen der Erziehungswissenschaften zu informieren. Durch die Analyse der Regelkarten können wir erkennen, dass die statistischen Anwendungen Variabilität aufweisten.
Das Diagramm ist ein Werkzeug, das verwendet wird, um Anomalien durch statistische Tests zu kontrollieren, und Variabilität wurde in einigen Stichprobenpunkten statistischer Anwendungen gefunden. Daher bestand die Notwendigkeit, Rückschlüsse bei der Kontrolle von Variablen mit außer Kontrolle geratenen Punkten zu ziehen. Es wurde durch den 1. Test bestätigt, dass die Untergruppen, die im Vergleich zu anderen Untergruppen ungewöhnlich sind, Anomalien aufwiesen, und es bestand die Notwendigkeit, den 2. Test anzuwenden, um den Prozess zu korrigieren und unter Kontrolle zu halten.
Die Diagramme ermöglichten es, Variationen zu überprüfen und Variablen zwischen Mittelwertparametern, Standardabweichungen und Amplituden zu stabilisieren. Die Diagramme ermöglichten es, die Probenahmestellen außerhalb der Grenzwerte anzunähern und Fehler zwischen den Grenzwerten anzupassen, was zur kontinuierlichen Verbesserung des Prozesses beistand, es ermöglichte, Defekte wahrzunehmen und Ursachen für abnormale Abweichungen zwischen den begrenzten Parametern des Diagramms unter Vergleich der Proben in den Verifizierungstests zu kontrollieren.
Bei der Analyse der Diagramme, um Grenzwerte für zukünftige Inspektionen festzulegen, wäre es notwendig, die räumliche Variabilität zu eliminieren, und nach dem Ändern der Stichproben wird ein neues Diagramm in Minitab erstellt, um diese Punkte für die Berechnung der überarbeiteten Grenzwerte zu eliminieren
Die in dieser Forschung dargelegten Ziele wurden erfolgreich erreicht, indem der Einsatz statistischer Techniken zur Identifizierung und Beseitigung von Anomalien ermöglicht wurde, die nicht mit statistischen Problemen übereinstimmen. Solche Techniken ermöglichten Inferenz in technischen Anwendungen durch Proben. Aktionen reduzierten das Auftreten von Variabilität in Der Minitab-Software und hielten dadurch den stochastischen Prozess stabil und unter Kontrolle. Dieses Thema zeigte, dass es möglich ist, Daten durch Kontrollkarten zu sammeln, zu analysieren und zu interpretieren, da es mit diesem Tool möglich ist, Anomalien bei statistischen Problemen zu überprüfen.
Es stellt sich heraus, dass die Statistiksoftware in der Lage ist, die Spezifikationen in der Prozesssteuerung zu erfüllen. Es wurde überprüft, ob Minitab verwendet werden muss, um mögliche Ursachen für Variabilität zu vermeiden. Schließlich war es mit der vorliegenden Studie der Variabilität möglich, den Beitrag der Ressourcen der Kontrollkarten durch die Anwendung der Software bei der Verringerung von Anomalien in statistischen Wissenschaftsanwendungen wahrzunehmen und zu verstehen.
VERWEISE
BORTOLOTTI, S. L. V. et al. Análise da qualidade do produto final no processo de envase de azeitonas verdes. Tecnol. & Hum., Curitiba, ano 23, n. 36, jan/jun. 2009. Disponível em: https://revistas.utfpr.edu.br/rth/article/viewFile/6238/3889
CARPINETTI, L. C. R. Gestão da Qualidade, Conceitos e Técnicas. São Paulo: Atlas S.A., 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CASTRO, D. R. C. et al. A aplicabilidade dos gráficos de controle nas empresas como modelo de inspeção para a avaliação da qualidade. In: XXXII Encontro Nacional de Engenharia de Produção. Bento Gonçalves, RS, 2012. Disponível em: http://www.abepro.org.br/biblioteca/enegep2012_tn_stp_158_921_20804.pdf
CHAVES, J. B. P. Controle de Qualidade na Indústria de Alimentos. Viçosa,
MG, (s.n.), 1997.
CHAVES, J. B. P.; TEIXEIRA, M. A. Controle Estatístico de Qualidade:
inspeção por amostragem/ mapas de controle. DTA/UFV. Viçosa, MG: (s.n.), p. 162,
1997.
CORTIVO, Z. D. Aplicação do Controle Estatístico de Processo em sequências curtas de produção e análise estatística de processo através do planejamento econômico. Curitiba: Universidade Federal do Paraná, 2005.
FERREIRA, J. M.; OLIVEIRA, M. S. de. Controle estatístico da qualidade. Lavras: UFLA/FAEPE, p.87, 2008.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
HORA, H. R. M., COSTA, H. G. Tomada de decisão no MASP: uma contribuição para decisões utilizando a matriz AHP. XXIX Encontro Nacional de Engenharia de Produção. Salvador. ENEGEP, 2009.
IPEK, H. et al. The application of statistical process control. Minerals Engineering, Vol. 12, Issue 7, p. 827-835, 1999. ISSN 0892-6875. Disponível em: https://doi.org/10.1016/S0892-6875(99)00067-9.
JURAN, J. M.; GRYNA, F. M. Controle da Qualidade: Métodos Estatísticos Clássicos Aplicados à Qualidade. São Paulo, Ed. Makron, 1992.
LAGO NETO, J. C. do. O efeito da autocorrelação em gráficos de controle para variável contínua: Um estudo de caso. Florianópolis, 1999.
MAGALHÃES, M. S. de; MOURA NETO, F. D. Economic-statistical design of variable parameters non-central chi-square control chart. Production, v. 21, n. 2, p. 259–270, 2011.
MICHEL, M. H. Metodologia e Pesquisa Científica em Ciências Sociais: Um Guia Prático para Acompanhamento da Disciplina e Elaboração de Trabalhos Monográficos. São Paulo: Atlas, 2005.
MINITAB. Conheça o Minitab para Windows. 1º. ed. São Paulo: Editora Minitab
Inc., 2010.
MONTGOMERY, D. C. Estatística Aplicada e Probabilidade para Engenheiros. Tradução e revisão técnica Verônica Calado. Rio de Janeiro, LTC, 2015.
MONTGOMERY, D. C. Introdução Ao Controle Estatístico Da Qualidade. 4. ed. Rio de Janeiro: LTC, 2009.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 1997.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 4. ed. Rio de Janeiro: LTC, 2004.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 2013.
MONTGOMERY, D. C. Introdução ao controle estatístico de qualidade. Rio de Janeiro: LTC, 2016.
OLIVEIRA, T. S.; LIMA, R. H. P. Aplicação do controle estatístico de processo na mensuração da variabilidade em uma usina de etanol. Anais. INGEPRO Inovação, Gestão e Produção, v. 3, n. 6, p. 022-033, 2015.
OLIVEIRA, V. F. de. Mobilidade e acessibilidade urbana: uma análise socioespacial a partir dos bairros Jardim Morada do Sol e Conjunto Habitacional Ana Jacinta, em Presidente Prudente. Faculdade de Ciências e Tecnologia – FCT, Unesp, 2011.
PALLADINI, E. P. et al. Gestão da Qualidade: Teoria e Casos. 2. Ed. São Paulo: Atlas, 2010.
PEDRINI, D. C. Proposta de um método para aplicação de gráficos de controle de regressão no monitoramento de processos. Universidade Federal do Rio Grande do Sul: UFRGS, 2009.
PEREIRA, A.; PATRÍCIO, T. Guia prático de utilização: análise de dados para Ciências Sociais e Psicologia. 8.ª ed. Lisboa : Sílabo, 2013.
REBELATO, M. G. et al. Estudo sobre a aplicação de gráficos de controle em processos de saturação de papel. XIII SIMPEP. Bauru, SP: 2006.
RIBEIRO, J. L.; CATEN, C. T. Controle estatístico de processos: Apostila de Curso. Porto Alegre: UFRGS, 2012.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. 3 ed. São Paulo: Atlas, 1999.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
RODRIGUES, G. P. Controle Estatístico de Qualidade e de Processo na Indústria de Alimentos. Universidade Federal de Viçosa, MG, p. 152,1998.
ROSA, L. C. Introdução ao Controle Estatístico de Processos. Santa Maria, Ed. Da UFSM, 2009.
SIQUEIRA, L. G. P. Controle Estatístico de Processos – Equipe Grifo – Série Qualidade Brasil. São Paulo: Pioneira, 1997.
SOUZA, A. M., RIGÃO, M. H. Identificação de variáveis fora de controle em processos produtivos multivariados. Revista Produção, São Paulo, V.15 no.1, p.74-86, abr. 2005.
SOUZA, R. Case Research in Operations Management. EDEN Doctoral Seminar on Research Methodology in Operations Management, Brussels, Belgium, 2005.
SPIEGEL, M. R.; STEPHENS, L. J. Schaum’s esboço de teoria e problemas de estatística: Aprenda a si mesmo. 4ª ed., Rio de Janeiro: LTC, 2007.
TRIVELLATO, A. A. Aplicação das sete ferramentas básicas da qualidade no ciclo PDCA para melhoria contínua: estudo de caso numa empresa de autopeças. Trabalho de conclusão de curso, Universidade de São Paulo, 2010.
VIEIRA, S. Estatística para a qualidade: como avaliar com precisão a qualidade em produtos e serviços. Rio de Janeiro: Elsevier, 1999.
VILAÇA, A. C.; OLIVEIRA, R. C. B. Utilização do Controle Estatístico de Processo para Avaliação de Peso de Massas para Pastel. FAZU em Revista, Uberaba, n. 8, p. 137-146. 2011.
WERKEMA, M. C. C. Avaliação de sistemas de medição. 2.ed. Belo Horizonte: Werkema. 2012.
WERKEMA, M. C. C. Ferramentas estatísticas básicas para o gerenciamento de processos. Belo Horizonte: Werkema, 2006.
YIN, R. K. Estudo de caso: planejamento e métodos. 2. Ed. Porto Alegre: Bookman, 2001.
[1] Master in Verfahrenstechnik – PPGEP/ITEC-UFPA.
[2] Doktor in Natural Resources Engineering an der Föderalen Universität von Pará.
Eingereicht: April 2021.
Genehmigt: Juni 2021.