ARTICOLO ORIGINALE
SILVA, Sarley De Araújo [1] MAGNO, Rui Nelson Otoni [2]
SILVA, Sarley De Araújo. Probabilità, carta di controllo applicata al software di scienze dell’educazione. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 06, Ed. 06, Vol. 11, pp. 43-73. giugno 2021. ISSN: 2448-0959, Link di accesso: https://www.nucleodoconhecimento.com.br/olimpiadi-di-matematica/scienze-delleducazione
RIEPILOGO
Il presente studio menziona la riduzione della variabilità e delle perdite dovute a cause speciali nelle applicazioni delle scienze dell’educazione, con l’obiettivo di rilevare e correggere le deviazioni della variabilità attraverso le carte di controllo del software nei problemi di statistica applicata. Pertanto, abbiamo cercato di studiare i concetti sulle carte di controllo per variabili e attributi nel controllo delle anomalie. Nello svolgimento di questo tema sono state utilizzate la metodologia quantitativa e la carta di controllo del Software Minitab. I risultati ottenuti hanno permesso di ridurre le perdite e migliorare il processo di qualità attraverso aggiustamenti di campionamento tra i limiti di controllo di Minitab, consentendo di comprendere e analizzare le cause delle anomalie. Pertanto, si conclude che lo strumento basato sulle azioni correttive è in grado di stabilizzare le deviazioni standard e migliorare la qualità delle applicazioni probabilistiche e statistiche.
Parole chiave: Probabilità, Minitab Software, Grafico di controllo.
1. INTRODUZIONE
La statistica è una branca della matematica che utilizza lo strumento della probabilità per spiegare i raggruppamenti di dati, sia negli studi osservazionali che negli esperimenti per modellare, stimare e prevedere fenomeni futuri. Il suo scopo è quello di ottenere, organizzare, analizzare i dati, calcolare grafici di controllo, correlazioni e regressioni, consentendo il controllo della variabilità, delle applicazioni statistiche e delle istituzioni educative. I metodi statistici si riferiscono ai dati ottenuti dalle osservazioni sotto forma di misurazioni o conteggio. Dalle informazioni è possibile studiare problemi statistici relativi al controllo della variabilità applicati nelle scienze in ingegneria, chimica, fisica, matematica, geografia e così via. L’uso di software statistici è uno strumento importante per gli studi e l’applicabilità nel controllo delle variazioni di probabilità e problemi statistici.
Gli enti si preoccupano di mantenere indici di performance elevati per quanto riguarda la qualità e la produttività a causa dei requisiti nella fornitura di servizi. L’informazione e le nuove tecnologie hanno creato un ambiente globalizzato di alta concorrenza, in cui il prezzo e la scadenza dovrebbero essere rispettati (VILAÇA e OLIVEIRA, 2011). In “Qualsiasi processo di produzione, indipendentemente da quanto sia ben progettato o mantenuto, sarà sempre soggetto a una variabilità naturale o intrinseca, che è il risultato dell’effetto cumulativo di molte piccole e inevitabili cause, chiamate cause comuni” (MONTGOMERY, 2004, p.154). Pertanto, la riduzione dell’anomalia nelle famiglie di variabili è di fondamentale importanza nel processo statistico.
Secondo Souza e Rigão (2005), il CEP agisce preventivamente sul processo utilizzando le statistiche come elemento di base per valutare i suoi cambiamenti. Queste caratteristiche consentono al CEP di assistere nel monitoraggio del processo e consentono di intraprendere azioni in modo diretto a risolvere i problemi, assistendo nella stabilizzazione del processo ed evitando la produzione di articoli non conformi (HORA e COSTA, 2009; MAYER, 2004).
L’obiettivo di questo lavoro è quello di utilizzare tecniche statistiche nei software per identificare, correggere ed eliminare le anomalie presenti nei problemi della scienza dell’educazione. L’importanza delle carte di controllo del software statistico nel controllo delle anomalie.
L’obiettivo principale del controllo statistico di processo è quello di rilevare rapidamente il verificarsi di cause attribuibili nei cambiamenti di processo, in modo che l’indagine di processo e l’azione correttiva possano essere eseguite prima che vengano prodotte molte unità non conformi (MONTGOMERY, 2013, p.280).
Pertanto, il software statistico è rilevante nel processo di identificazione ed eliminazione della variabilità.
La funzione del controllo statistico del processo nei grafici software è quella di dimostrare le modulazioni che si sono verificate durante l’elaborazione e sviluppare grafici statistici in grado di fornire un parametro più preciso, assistendo in pratiche che possono migliorare i punti predominanti della produzione, oltre a riconoscere, correggere, eliminare o adattare i processi con anomalie, dando un parametro più preciso, in modo che i miglioramenti possano essere applicati nella linea di produzione (OLIVEIRA, 2015, p.22).
Le tabelle di controllo del software statistico consentono di trovare la variabilità dimostrata attraverso i grafici, consentendo una migliore visualizzazione del processo, al fine di dimostrare eventuali difetti, per l’applicazione di correzioni più efficienti, nella ricerca del miglioramento continuo.
Anche con l’avanzamento del processo attraverso il controllo di qualità, ci sono ancora cause di variabilità nel processo, cioè quando c’è un’oscillazione intorno alla media o al punto ideale della specifica, è richiesto un monitoraggio costante del comportamento di produzione. “Attraverso l’analisi dei dati raccolti e la caratterizzazione della causa dell’instabilità o variabilità del sistema, utilizzati nelle carte di controllo, strumenti di controllo statistico del processo come risultato per ottenere un miglioramento continuo dei processi” (JURAN e GRYNA, 1992).
Tutti i processi presentano variabilità, cioè maggiore è la variabilità, maggiore è l’controllo sui risultati prodotti e sui risultati desiderati. (MONTGOMERY, 1997).
Per migliorare la qualità di un prodotto è necessario fare uso di software statistici:
In un ambiente competitivo, il miglioramento continuo dei processi consente di monitorare, controllare e migliorare i processi di produzione ogni volta che viene rilevata un’anomalia. Se c’è una natura preventiva, queste azioni contribuiscono a minimizzare le perdite e aumentare la produttività (BORTOLOTTI, 2009, p.02).
Tali tecniche statistiche che utilizzano software minitab contribuiscono all’analisi di vari prodotti, rilevando e riducendo possibili anomalie, garantendo scorte entro parametri di qualità. “Uno dei principali risultati dello studio sulla qualità industriale è stato l’uso diffuso di metodi statistici di controllo dei processi per eliminare cause speciali nei processi e ridurre le cause comuni di variazione” (MONTGOMERY, 1997). In questo contesto, il controllo statistico dei processi è uno strumento estremamente importante per l’applicazione di tecniche statistiche nella riduzione della variazione. Il controllo statistico del processo può essere definito come un insieme di sette strumenti di risoluzione dei problemi per raggiungere la stabilità del processo, oltre a migliorarne la capacità. (FERREIRA et. al., 2008).
Le carte di controllo del software statistico aiutano nell’identificazione e nella stabilità delle cause di variabilità dei processi, fungendo da base per decisioni e azioni correttive di controllo, riducendo la variabilità ed evitando dati campione fuori controllo.
Il controllo statistico dei processi è una potente raccolta di strumenti per la raccolta, l’analisi e l’interpretazione dei dati, con l’obiettivo di migliorare la qualità eliminando cause speciali di variazione e può essere utilizzato per la maggior parte dei processi. (MONTGOMERY, 2004, p.279-281).
Lo studio sui grafici di controllo nei software statistici contribuisce all’analisi delle applicazioni nelle scienze dell’educazione nella riduzione della variabilità nei campioni analizzati, generando risultati migliori nel controllo di qualità.
2. MATERIALI E METODI
2.1 MATERIALI
I materiali utilizzati per controllare la variabilità nelle applicazioni di scienze educative erano le carte di controllo in Minitab Software.
2.2 METODI
Per realizzare lo studio, il metodo quantitativo e la tabella di controllo del software minitab sono stati utilizzati per ridurre la variabilità nelle applicazioni della scienza dell’istruzione. La metodologia cerca la convalida dei dati attraverso l’uso di dati statistici. Lo studio ha avuto la seguente distribuzione: scelta dell’applicazione da analizzare, determinazione dei limiti inferiore e superiore nei parametri e nell’ampiezza media, distribuzione dei campioni e verifica dei loro punti, analisi dei problemi mediante carte di controllo e correzione di cause speciali dalle analisi dei campioni fuori controllo.
“Il metodo quantitativo cerca la convalida dei dati attraverso l’uso di dati statistici, con l’analisi di un gran numero di casi rappresentativi. Cerca di quantificare i dati e applicare una qualche forma di analisi statistica” (OLIVEIRA, 2011). L’approccio quantitativo è spesso utilizzato negli studi descrittivi, che cercano di classificare la relazione tra variabili e la relazione causale tra i fenomeni.
Richardson (1999, p.70) concettualizza:
l’approccio quantitativo, come suggerisce il nome, è caratterizzato dall’uso della quantificazione sia nelle modalità di raccolta delle informazioni che nel trattamento delle esse attraverso tecniche statistiche, dalle più semplici come percentuale, media, deviazione standard, alle più complesse, come coefficiente di correlazione, analisi di regressione, ecc. Essa rappresenta, in linea di principio, l’intenzione di garantire l’esattezza dei risultati ed evitare distorsioni dell’analisi e dell’interpretazione, consentendo così un margine di sicurezza rispetto alle inferenze.
Secondo Michel (2005, p. 31), l’approccio quantitativo è una metodologia di ricerca sociale che utilizza la quantificazione nelle modalità di raccolta delle informazioni e il suo trattamento attraverso tecniche statistiche, come percentuale media, deviazione standard, coefficiente di correlazione, analisi di regressione, tra gli altri. Le tabelle di controllo sono uno strumento utile che porta miglioramenti e garanzia di qualità dei rifiuti aumentando i costi, la scomparsa dei rottami e la risoluzione di vari problemi di produzione relativi a metodi specifici ecc. (ROSA, 2009).
Le carte di controllo sono state utilizzate da variabili e attributi come tecniche nella costruzione di grafici in probabilità e applicazioni statistiche, in cui è stato osservato un miglioramento della stabilità in relazione alla variabilità dei difetti del campione. Per trovare una possibile causa di variabilità e verificare se il processo è sotto controllo, i grafici sono stati utilizzati per controllare le anomalie nei punti di campionamento. Attraverso i grafici è stato possibile identificare e confrontare la variabilità nelle questioni di scienze statistiche.
Ha fatto uso del software minitab come strumento di analisi dei dati. Dai risultati tra i limiti di controllo è stato possibile risolvere i difetti e migliorare la qualità. I grafici di controllo della media, dell’ampiezza e della deviazione standard sono stati scelti per controllare le variazioni della media nelle statistiche.
Lo strumento volto a identificare, analizzare, confrontare, correggere e ridurre la variabilità nelle applicazioni di scienze dell’educazione ha fatto uso di Minitab che è un programma informatico proprietario finalizzato a scopi statistici (MINITAB, 2016). “È uno strumento che ci consente di eseguire calcoli statistici complessi e visualizzare i risultati, rendendo l’analisi dei dati accessibile all’utente occasionale e conveniente per l’utente più esperto” (PEREIRA e PATRÍCIO, 2016).
Per migliorare la qualità, viene utilizzata la tecnologia software statistica:
Gli strumenti statistici oltre a dare priorità alle applicazioni proposte in base al grado di importanza, fanno l’identificazione e l’aiuto nell’azione sui problemi per l’eliminazione di possibili cause. Consentire all’istituzione di avere un più alto grado di stabilità nelle applicazioni analizzate (WERKEMA, 2006, p.32).
Stratificazione : “La stratificazione consiste nel dividere i settori in sottosettori in base ai fattori desiderati, che sono chiamati fattori di stratificazione, cioè per il processo di divisione del tutto eterogeneo in sottogruppi omogenei” (VIEIRA, 1999).
Checksheet: Per Werkema (2006), il foglio di verifica è un modulo che ha nel suo ambito criteri da analizzare, al fine di facilitare la raccolta e la compilazione dei dati. È uno strumento utilizzato per assistere nella raccolta dei dati e deve essere adeguato affinché la raccolta sia efficace. Pertanto, il foglio di controllo deve specificare chiaramente il tipo di dati da raccogliere, l’operazione da eseguire, la data di raccolta, l’analista e ogni altra informazione utile per individuare la causa delle scarse prestazioni funzionali (CARPINETTI, 2010; MONTGOMERY, 2009). Secondo Vieira (1999), il tipo di foglio di controllo dipenderà da quali saranno i suoi obiettivi, vale a dire: come aumentare la percentuale di articoli non conformi; ispezionare l’attributo; indicare dove si trova il difetto nel prodotto finale; aumentare le cause dei difetti; analizzare la distribuzione di una variabile; e monitorare un processo di produzione.
Grafico di Pareto: è lo strumento che effettua la distribuzione della frequenza dei dati, sottolineando il difetto che si verifica più frequentemente, e possono essere quelli di ordine percentuale o reale. Ricordando che un difetto più spesso potrebbe non essere il problema principale o più critico del processo (CARPINETTI, 2010; MONTGOMERY, 2009). Vieira (1999) afferma che il grafico di Pareto viene utilizzato per identificare le cause di problemi come i prodotti fabbricati che richiedono rilavorazioni, spese inutili, incidenti sul lavoro, guasti alle apparecchiature, errori e ritardi di consegna, tra gli altri.
Diagramma di causa ed effetto : Conosciutoanche come diagramma di Ishikawa ha la funzione di identificare e analizzare le cause che promuovono un effetto indesiderato. È un diagramma efficace per identificare la radice del problema (CARPINETTI, 2010; MONTGOMERY, 2009). Werkema (2006) afferma che il diagramma di causa ed effetto è uno strumento utilizzato per presentare la relazione tra l’effetto o il problema e la causa che potrebbe alterare il risultato. Il Diagramma di Causa ed Effetto organizza le informazioni in modo che rendano più chiare per facilitare l’analisi e l’identificazione delle cause del problema, consentendo di intraprendere azioni correttive per eliminare la causa del problema (TRIVELLATO, 2010).
Istogramma: Secondo Werkema (1995), un istogramma può essere definito come un grafico a barre in cui l’asse orizzontale, suddiviso in diversi piccoli intervals, visualizza i valori assunti da una variabile di interesse.
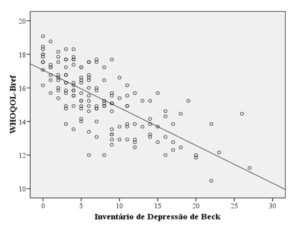
Diagramma di dispersione: Il diagramma di dispersione è responsabile di aiutare a identificare le relazioni tra un difetto e una causa, cioè mira a identificare la relazione tra due variabili o anche la relazione di una terza causa. Le relazioni tra le variabili possono essere: positive, negative o inesistenti (CARPINETTI, 2010; MONTGOMERY, 2009).
Tabella di controllo: Secondo Werkema (2006), qualsiasi bene materiale o immateriale, quando elaborato e / o realizzato, ha una variazione derivante dal processo. È noto che queste variazioni dovrebbero essere rigorosamente ridotte. Per Werkema (2006), le carte di controllo vengono utilizzate per monitorare la variabilità, distinguendo i tipi di variazione e valutare la stabilità del processo, indipendentemente dal fatto che sia sotto controllo o meno. Tuttavia, il processo può variare da cause comuni o cause speciali
I grafici di controllo sono stati creati da Shewhart e sono composti da limite centrale o medio (LC), limite inferiore (LI) e limite superiore (LS). La sua funzione principale è quella di indicare se il processo è sotto controllo o meno, cioè se il processo sta realizzando prodotti secondo le specifiche o meno. L’analisi di processo viene effettuata dalla verifica della tabella di controllo, osservando se i punti tracciati in essa sono compresi tra i limiti superiore e inferiore della specifica (CARPINETTI, 2010; MONTGOMERY, 2009).
Grafici di controllo: serve per analizzare le variazioni di processo di cause comuni e rilevare cause speciali, è uno strumento chiamato Grafici o Grafici di controllo. Analizzare la capacità di un processo è una parte vitale di un programma di qualità globale. Tra i principali utilizzi dei dati di un’analisi della capacità di processo spiccano (MONTGOMERY, 2004):
2.2.1 REGOLE STATISTICHE PER L’IDENTIFICAZIONE DI CAUSE SPECIALI
Suggerisce un insieme di regole decisionali per distinguere i modelli non casuali nei grafici di controllo. In particolare, suggerisce di concludere che il processo è fuori controllo se (MONTGOMERY, 2004):
1° caso: identificare sei, otto o più punti sopra o sotto la linea centrale. Possibili cause: cambiamento nel processo di regolazione della macchina, metodo o materiale diverso, rottura di un componente nella macchina, rottura della macchina e ampia variazione del materiale ricevuto.
2 ° caso: trova sei, sette o più punti su o giù. Possibili cause: usura graduale dell’utensile, usura dell’attrezzatura o usura correlata allo strumento di misura.
3° caso: controllare lo spostamento della media. Possibili cause: nuovo metodo, nuova macchina nel miglioramento della qualità e un nuovo lotto di materiale.
4° caso: punti al di fuori dei limiti di controllo. Possibili cause: errore di misurazione o di battitura, rottura dell’utensile o strumento di misura non regolamentato, che non consente l’identificazione della misurazione.
5° caso: periodicità dei punti. Possibili cause: non uniformità nella materia prima ricevuta, rotazione degli operatori, maschere e strumenti, e differenza tra i turni.
2.2.2 GRAFICI DI CONTROLLO PER VARIABILI E ATTRIBUTI
Le tabelle di controllo per variabili hanno lo scopo di informare sul miglioramento della qualità, della capacità di processo, del processo decisionale in merito alle specifiche del prodotto, al processo di produzione e alle decisioni sulle parti di nuova produzione. Sono applicati dove le caratteristiche di qualità possono essere misurate quantitativamente. Possono essere, ad esempio, dimensioni di parti, volume, peso, tra gli altri. Pertanto, viene percepito il suo ampio ambito di applicazione, poiché diversi tipi di processi hanno questi tipi di caratteristiche (MAGALHÃES, 2011).
“I grafici di controllo per le variabili sono più utilizzati dei grafici di controllo per gli attributi, perché hanno informazioni più concrete, lavorando con piccoli campioni, consentendo di identificare più rapidamente le cause che influenzano la stabilità del processo” (REBELATO, 2006). “I grafici di controllo per le variabili sono grafici per mezzi, utilizzati per controllare il valore medio delle prestazioni del processo, il grafico di ampiezza o il grafico di deviazione standard, essendo il grafico di ampiezza più utilizzato, perché, nella maggior parte dei casi, la deviazione standard del processo non è nota” (CASTRO, 2012).
I grafici di controllo possono essere classificati in due gruppi: grafici di controllo per le variabili: registra le caratteristiche di qualità che vengono misurate su scala quantitativa. E le carte di controllo per attributi: registra le caratteristiche di qualità, misurando su una scala qualitativa, ad esempio, è considerato conforme e non conforme (SIQUEIRA, 1997). Pertanto, secondo Spiegel e Stephens (2007), i termini “variabili” e “attributi” sono associati al tipo di dati raccolti dal processo.
2.2.3 TABELLA DI CONTROLLO PER MEDIE (X-BAR) E AMPIEZZA (R)
Il grafico medio ![]() viene utilizzato per controllare la media del processo (centralità) e il grafico dell’ampiezza
viene utilizzato per controllare la media del processo (centralità) e il grafico dell’ampiezza ![]() controllare la variabilità del processo considerato (IPEK et al., 1999).
controllare la variabilità del processo considerato (IPEK et al., 1999).
Espressioni per il calcolo dei limiti di controllo di ![]() e R.
e R.
Grafico di controllo ![]() . La linea centrale e i limiti di controllo superiore e inferiore per la carta di controllo
. La linea centrale e i limiti di controllo superiore e inferiore per la carta di controllo ![]() loro sono:
loro sono:
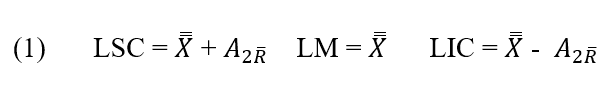
Grafico di controllo R. La linea centrale e i limiti di controllo superiore e inferiore per il diagramma di controllo R sono:
![]()
2.2.4 GRAFICO MEDIO (X-BAR) E DEVIAZIONE STANDARD (S)
Il grafico di controllo per la media (grafico a barre X) viene utilizzato per controllare la media del processo, mentre il grafico di controllo (grafico di deviazione standard S) viene utilizzato per controllare la variabilità del processo. Quando la dimensione del campione (sottogruppo) è inferiore o uguale a dieci, i grafici R e S avranno lo stesso aspetto. Tuttavia, quando la dimensione del campione cresce, il grafico S diventa più accurato del grafico R e dovrebbe essere usato (SIQUEIRA, 1997).
Grafico di controllo ![]() . La linea centrale e i limiti di controllo superiore e inferiore per la carta di controllo
. La linea centrale e i limiti di controllo superiore e inferiore per la carta di controllo ![]() loro sono:
loro sono:
![]()
Tabella di controllo S: 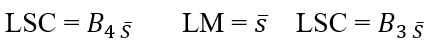
2.2.4.1 GRAFICI DI CONTROLLO PER ATTRIBUTI
I grafici degli attributi vengono utilizzati per controllare l’analisi dei difetti. Questi grafici sono particolarmente utili nel controllo delle materie prime e dei prodotti finiti e vengono utilizzati anche nell’analisi delle recensioni di qualità nelle lettere dei consumatori. Un attributo è una caratteristica di un prodotto, di un processo o di qualsiasi altra popolazione che può essere contata, ma non può essere descritta, in modo che i suoi valori vengano incrementati (RODRIGUES, 1998). Sono grafici che ci permettono di identificare come i set di campioni si comportano intorno a limiti, tendenze e scambio di livelli. Nelle variabili, viene rapidamente percepito quando i dati non seguono una distribuzione casuale. Nei grafici di controllo degli attributi, le unità sono classificate come perfette o difettose in base ai criteri stabiliti. Pertanto, la probabilità che un’unità difettosa venga prodotta è costante e, di conseguenza, la corrispondente distribuzione del campione è binomiale (CHAVES e TEIXEIRA, 1997). I grafici degli attributi vengono utilizzati per controllare l’analisi dei difetti. Questi grafici sono particolarmente utili nel controllo delle materie prime e dei prodotti finiti e vengono utilizzati anche nell’analisi dei commenti sulla qualità e sulle caratteristiche espresse qualitativamente, cioè quando queste caratteristiche analizzate non sono rappresentate numericamente e possono essere classificate in base o non conformi (SOUZA, 2005). Sono le misure rappresentative che risultano dai conteggi del numero di articoli del prodotto su una scala discreta che presentano una particolare caratteristica di interesse. Le misurazioni vengono effettuate mediante ispezione visiva e vengono registrate caratteristiche non misurabili. Si può dire grafico di controllo per variabile casuale discreta con funzione di densità di probabilità di Poisson (LAGO, 1999).
La matematica delle schede attributi non richiede tabelle. Possono essere applicati a sistemi in cui le misure consistono nell’approvazione o nella disapprovazione o a processi in cui è molto difficile o impossibile ottenere misure di variabili (RODRIGUES, 1998).
Le informazioni statistiche delle misurazioni per attributi nelle soluzioni ai problemi delle scienze dell’educazione, sono classificate in prodotti con anomalie o difetti. Uno degli obiettivi principali dell’analisi della misurazione degli attributi è quello di identificare, rilevare e correggere i difetti, la qualità può essere definita come l’insieme di attributi che rendono un bene o un servizio pienamente adatto all’uso per il quale è stato progettato (MONTGOMERY, 1985). I quattro grafici di controllo per gli attributi in anomalie e difetti, utilizzati secondo Montgomery (2004), sono i seguenti: Grafici di controllo per attributi che sono: Lettera p (proporzioni non conformi), Grafico Np (unità non conformi), Lettera C (numero di non conformità per unità) e Lettera u (tasso di non conformità per unità).
2.2.5 GRAFICO P (PROPORZIONI NON CONFORMI)
Per Werkema (2006), il grafico p viene utilizzato quando la caratteristica della qualità di interesse è rappresentata dalla proporzione di articoli difettosi prodotti dal processo analizzato.
Grafico di controllo P:
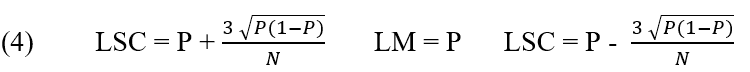
2.2.6 GRAFICO NP (UNITÀ NON CONFORMI)
La lettera non indica il numero di difetti per campione e viene utilizzata per controllare il numero di prodotti difettosi in ciascun lotto e garantire che il processo sia sotto controllo (RODRIGUES, 1998).
L’asse di mezzeria e i limiti di controllo superiore e inferiore per il grafico np sono:
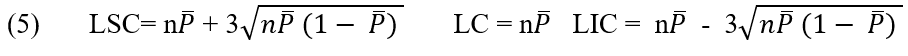
2.2.7 GRAFICO C NUMERO DI (NON CONFORME PER UNITÀ)
Il grafico c viene utilizzato per determinare se il numero di difetto su un singolo elemento rientra nei limiti di controllo definiti. Può essere considerata come un’ispezione finale (RODRIGUES, 1998). Il grafico c è più appropriato quando i difetti sono dispersi in un mezzo continuo, come ad esempio: numero di difetti per area del tessuto, numero di imperfezioni per lunghezza del pavimento; e quando un prodotto può avere più di un tipo di difetto (RIBEIRO e CATEN, 2012).
Pertanto, i limiti di controllo del grafico C saranno calcolati utilizzando le equazioni:
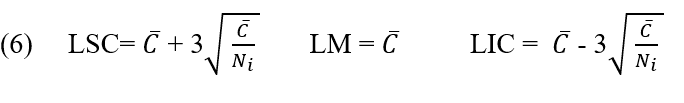
2.2.8 GRAFICO U TASSO DI NON CONFORMITÀ PER UNITÀ
Il grafico a u viene utilizzato per monitorare i difetti in un’unità di produzione (MONTGOMERY, 1997). La tabella u è consigliata quando il prodotto è composto da varie parti e molte caratteristiche di qualità che devono essere ispezionate e anche quando la dimensione dell’unità di prodotto è variabile (CORTIVO, 2005).
L’asse di mezzeria e i limiti di controllo superiore e inferiore per il grafico U sono:
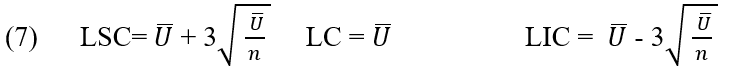
2.2.9 REGRESSIONE LINEARE MULTIPLA
L’analisi di regressione multipla è una tecnica utilizzata per indagare la relazione tra una variabile dipendente e un insieme di variabili indipendenti (MONTGOMERY e RUNGER, 2009). La tecnica consente la stima di valori futuri per la variabile dipendente, dato un insieme di dati di input per le variabili indipendenti (PEDRINI e CATEN, 2009; DOWNING e CLARK, 2002)
Il modello base di regressione lineare multipla dove ![]() per j=0,1,2…..k sono coefficienti di regressione, Y è la variabile dipendente dei regressori
per j=0,1,2…..k sono coefficienti di regressione, Y è la variabile dipendente dei regressori ![]() e il valore ed è l’errore casuale dell’equazione. (MONTGOMERY, 2015).
e il valore ed è l’errore casuale dell’equazione. (MONTGOMERY, 2015).
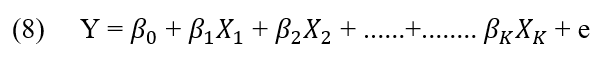
Il processo è studiato per comprendere le esigenze di analisi delle applicazioni delle scienze dell’educazione e le loro fasi di processo. Le fonti di analisi sono sollevate, le applicazioni che vengono analizzate in esso, sono la variabilità i principali fattori che lo influenzano. Identificare il tipo più appropriato di grafico di controllo per analizzare i dati tramite software minitab. Con il metodo del controllo stocastico del processo ha cercato la strutturazione della ricerca al fine di aiutare il progresso della stessa.
3. RISULTATI E DISCUSSIONE
3.1 L’USO DELLE TABELLE DI CONTROLLO MINITAB PER RIDURRE LA VARIABILITÀ
Dopo aver raccolto e tracciato i dati nelle applicazioni di ingegneria, sono stati costruiti alcuni grafici per le variabili e i grafici per gli attributi nelle tabelle di controllo del software Minitab per monitorare le perdite dovute alle variazioni della produzione. Per l’analisi dei risultati, l’intervallo di tolleranza composto dai componenti è stato determinato dai seguenti componenti: Limite di controllo superiore LSC, LC della linea mediana e LIC limite di controllo inferiore.
È stato osservato che dopo aver identificato, eliminato e ridotto le cause di variabilità ha portato la possibilità di miglioramento della qualità dei prodotti. Attraverso l’analisi dei risultati ottenuti nelle applicazioni statistiche verrà presentato il controllo della stabilità nelle cause dei difetti nei punti campione nei grafici, e il controllo del processo nel campione è stato eseguito al fine di controllare la variabilità. Le tabelle di controllo presentavano i seguenti risultati tra i parametri statistici: Calcolo della media di processo, Calcolo della deviazione standard, Calcolo dei limiti di controllo LSC, LIC e ampiezza nelle applicazioni seguenti:
3.2 PROBABILITÀ E APPLICAZIONI STATISTICHE IN INGEGNERIA PER GRAFICO DI CONTROLLO NEL SOFTWARE MINITAB NELLA RIDUZIONE DELLA VARIABILITÀ
Costruzioni grafiche in applicazioni di statistica descrittiva eseguite dalla tabella di controllo in Minitab Software.
01) I dati si riferiscono ad un processo di lavorazione a perno, in cui i diametri vengono misurati campionando 5 pezzi in 25 lotti. Rivedi il processo con Minitab Software.
Tabella 1: Misure del diametro del perno
| Tanto | Misure | ||||||
| 1 | 2,08495 | 2,09203 | 1,01425 | 0,47627 | 1,75308 | ||
| 2 | 2,44288 | 1,84913 | 1,02012 | 1,5103 | 0,5167 | ||
| 3 | 2,08819 | 0,34567 | 0,67246 | 2,14641 | 0,51528 | ||
| 4 | 1,42411 | 1,04348 | 1,15683 | 0,9108 | 1,23562 | ||
| 5 | 1,43307 | 0,22926 | 1,51612 | 0,82627 | 1,29935 | ||
| 6 | 1,2113 | 0,63715 | 0,97815 | 2,30782 | 1,0003 | ||
| 7 | 2,14731 | 1,95837 | 0,95294 | 1,35384 | 0,73037 | ||
| 8 | 2,02444 | 1,60384 | 1,64667 | 1,66449 | 0,92746 | ||
| 9 | 1,4743 | 1,93916 | 1,06107 | 1,55396 | 0,8049 | ||
| 10 | 1,09096 | 2,09033 | 0,62161 | 1,45256 | 1,77208 | ||
| 11 | 1,90879 | 1,274 | 1,46827 | 1,36343 | 1,06161 | ||
| 12 | 0,81791 | 1,89952 | 1,24044 | 0,72729 | 1,44959 | ||
| 13 | 0,58784 | 1,57195 | 0,73316 | 1,05367 | 3,29273 | ||
| 14 | 2,12184 | 0,90374 | 0,59773 | 1,63101 | 0,82706 | ||
| 15 | 1,2819 | 0,89479 | 1,05394 | 1,25779 | 0,99451 | ||
| 16 | 0,82836 | 0,16347 | 2,12864 | 1,69732 | 0,90752 | ||
| 17 | 0,14026 | 1,0432 | 0,76948 | 1,72083 | 3,95445 | ||
| 18 | 2,19158 | 0,87777 | 0,955 | 1,50304 | 1,1604 | ||
| 19 | 0,93195 | 1,82231 | 1,2179 | 1,72608 | 1,45375 | ||
| 20 | 0,84523 | 2,79753 | 2,30041 | 0,47693 | 0,58081 | ||
| 21 | 1,84098 | 2,37729 | 1,89976 | 1,2079 | 3,2343 | ||
| 22 | 1,15648 | 2,5689 | 0,90064 | 3,7548 | 1,24616 | ||
| 23 | 2,21913 | 0,91997 | 2,15777 | 1,48548 | 0,25288 | ||
| 24 | 1,41393 | 0,71069 | 0,63707 | 1,71835 | 1,52855 | ||
| 25 | 1,5938 | 1,19839 | 0,88228 | 1,23019 | 0,41643 | ||
Fonte: Azione (2019)
Figura 01: Grafico di controllo pin difettoso fuori controllo
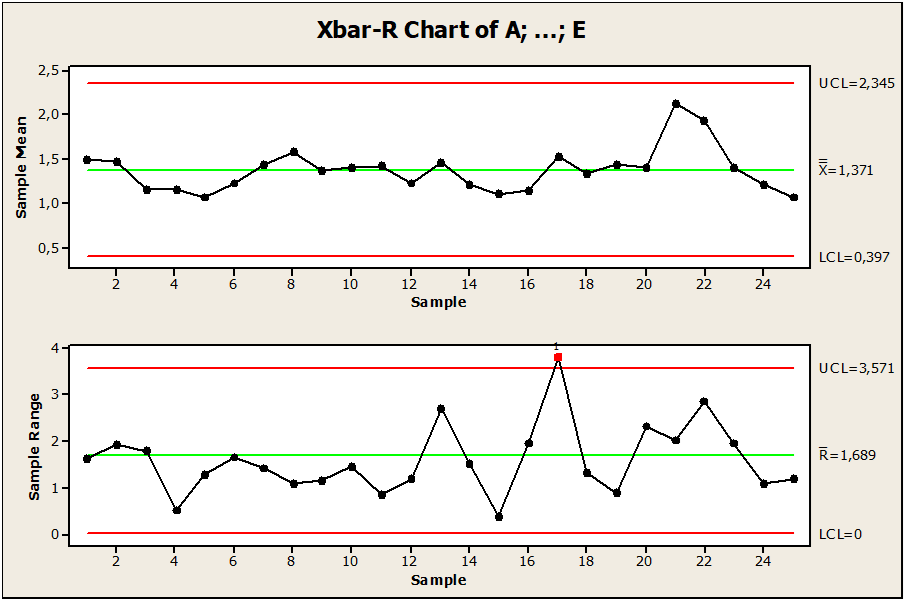
I dati del campione presentano un processo di lavorazione dei perni osservato in 25 lotti di perni. Come mostrato nella Figura 01. Abbiamo osservato che c’è una variazione tra il punto 17 sopra il limite superiore del controllo LSC, dove il punto è al di fuori del limite di controllo. Il suo limite centrale è pari a 1,68, limite di controllo superiore con il valore 3,57 e limite inferiore pari a 0,0, questo implica che il punto 17 nel pin del valore 3,95445 è influenzato dalla variabilità. Quindi per tenere sotto controllo il processo si consigliava di rimuovere, modificare i valori o costruire un nuovo grafico.
Figura 02: Tabella di controllo con i limiti regolati
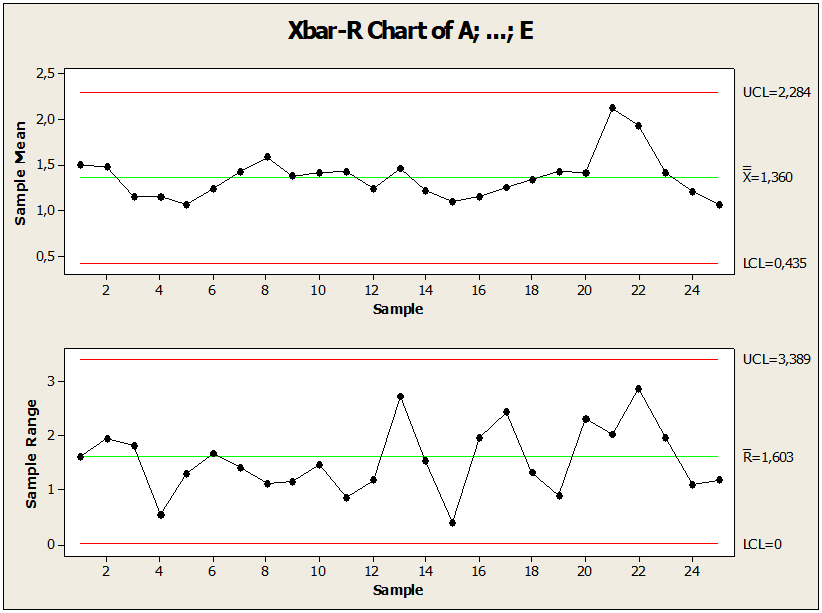
Dopo aver verificato l’anomalia, Figura 02. Il grafico mostra il punto sotto controllo in relazione alla media, dove c’è stata una modifica al fine di tenere sotto controllo il processo. Nel campione del punto 17 del valore di non conformità 3,95445, è passato a 2,55445. Questa modifica eseguita dalla tabella di controllo seguita da regole statistiche ha ridotto la variabilità e il punto al di fuori del limite di controllo è stato regolato. Concludiamo che tutte queste misure statistiche hanno mantenuto stabile il processo. Dopo aver identificato, analizzato, corretto, ridotto e controllato il processo dei campioni di non conformità, è stato possibile confrontare i risultati ottenuti con i risultati precedenti tra il processo: Processo fuori controllo, LC pari a 1,68, deviazione standard pari a 0,69 e ampiezza del valore limite 3,81 un punto sopra il limite. LSC. Processo sotto controllo LC pari a 1,60, deviazione standard pari a e 0,66 Ampiezza del valore limite 3,61. Dopo il confronto con i valori calcolati nel 1 ° e 2 ° test, c’è stato un miglioramento dei parametri statistici.
Figura 03: Mostra i diametri dei pin
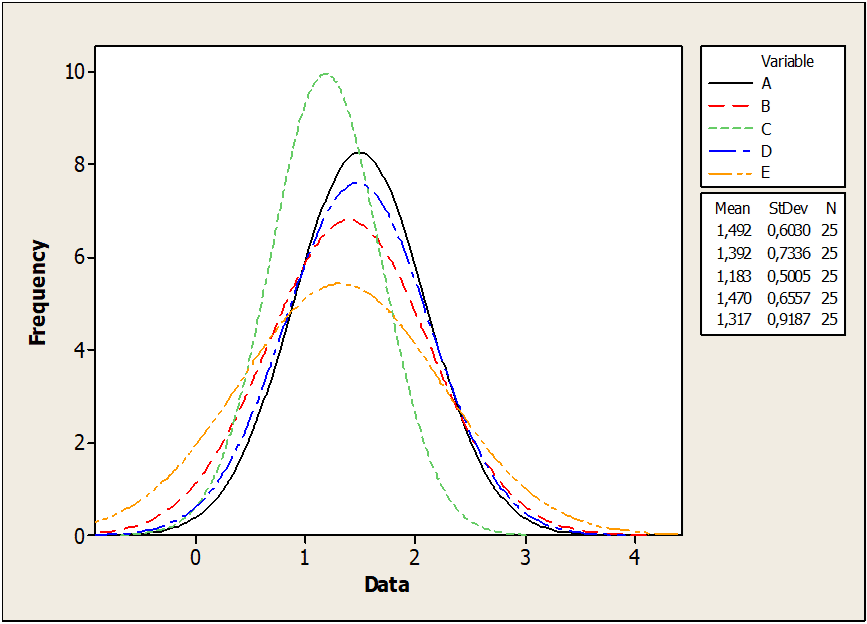
La figura 03 mostra una curva di dispersione dei diametri dei perni nei sottogruppi di E con maggiore precisione rispetto alla curva di dispersione dei sottogruppi D. La deviazione standard per i campioni del sottogruppo E (0,91) è molto più grande dei campioni del sottogruppo D. (0,50). Pertanto, la distribuzione corretta per il sottogruppo E è appiattita e più accurata.
02) È stato condotto uno studio per determinare l’aumento dei difetti nelle porte in acciaio inossidabile delle attrezzature da cucina prodotte in un’azienda metalmeccanica. Durante lo studio, i difetti di seguito sono apparsi con i loro eventi e costi associati. Costruisci i rispettivi diagrammi di Pareto.
Tabella 2: parti difettose
| Tipo di difetti | Nº. di parti difettose | Riparazione/scarto del costo unitario | |
| Saldatura mal eseguita | 55 | 50 | |
| Scarsa perforazione | 9 | 50 | |
| Difetti di flessione | 274 | 5 | |
| Imballaggio | 15 | 50 | |
| Scarsa qualità del piatto | 16 | 50 | |
| Tagli | 126 | 30 | |
| Altro | 12 | 50 |
Fonte: Core Formation -Nufec (2006)
Figura 04: Numeri di parti difettose
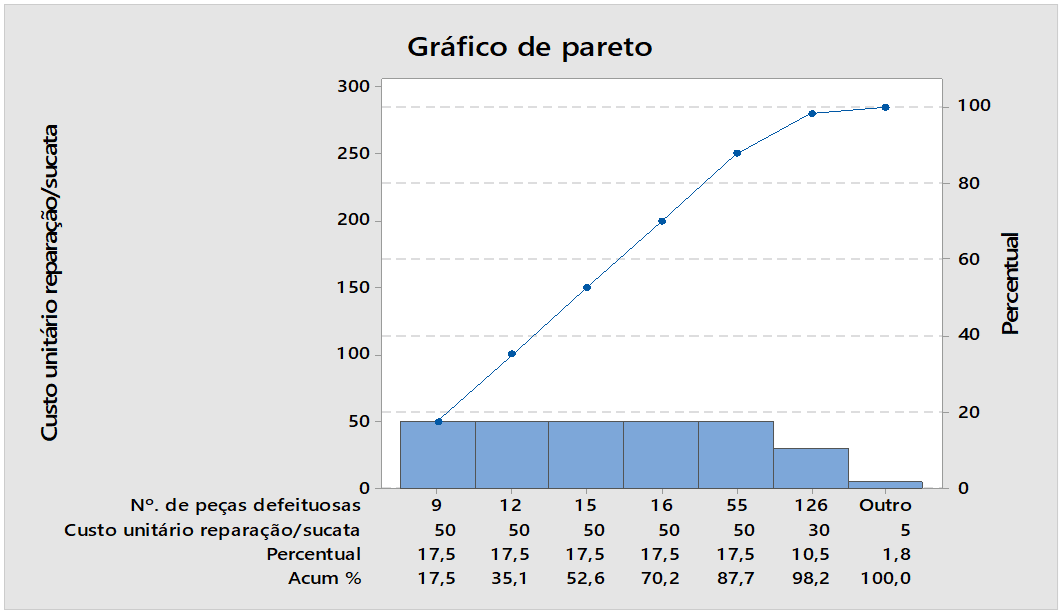
La figura 04 mostra i risultati dei numeri di parti difettose, percentuale, la fonte più grande 9 parti difettose che corrisponde a una percentuale del 17,5 %. Quando si analizza la figura, si percepisce la presenza di concentrazione di cause di particolare variabilità che richiedono la correzione da parte della tabella di controllo del software Minitab.
Figura 05: Processo fuori controllo dei numeri di parti difettose
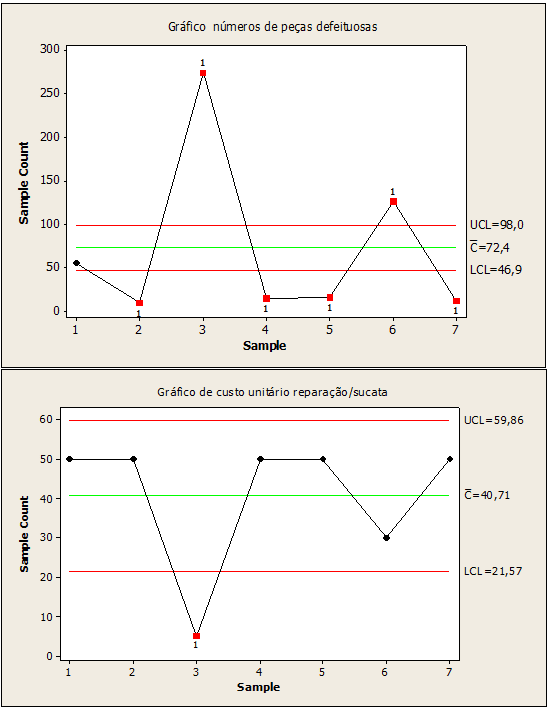
È stato verificato che la figura 05, riferita alle parti difettose, mostrava variabilità nei punti 2,3,4,5,6,7 con valori (9,274,15,16,126,12). Dall’altro, costo unitario nella riparazione del punto rottame con variabilità 3 con valore pari a 5. Si conclude che ci sono cause speciali in questi punti e c’è bisogno di correzione.
Figura 06: Processo di controllo dei numeri di parti difettosi
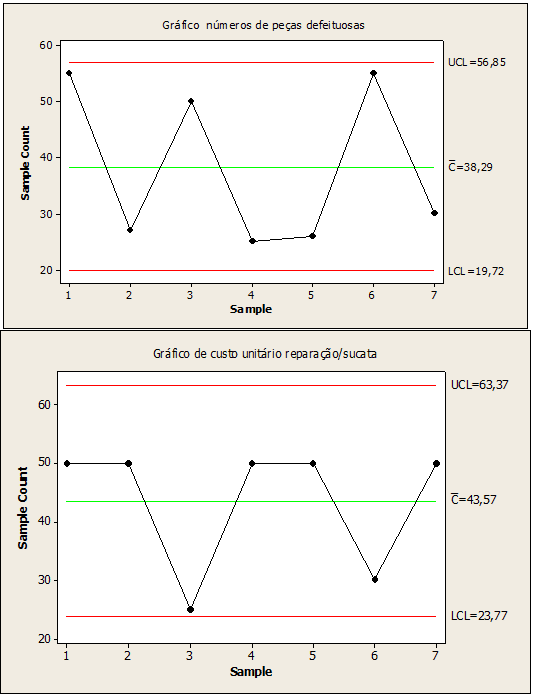
Nella figura 06, i valori utilizzati al posto dei valori dei punti fuori controllo 2,3,4,5,6,7, seguiti sono 27,50,25,26,55,30 per le parti difettose e 25 per la riparazione dei rottami a costo unitario al punto 3. Questi dati di sostituzione generati dalla tabella di controllo hanno migliorato il processo stocastico tenendo sotto controllo, riducendo la variabilità nella produzione di portali in acciaio inossidabile, mantenendo stabile la qualità del prodotto.
03) Uno stampo di estrusione viene utilizzato per produrre aste di alluminio. Il diametro delle cante è una caratteristica critica della qualità. La tabella seguente mostra i valori x e r per 20 campioni di cinque canti ciascuno. Le specifiche sulle cante sono 0,5035 +/- 0,0010 pollici. I valori dei dati sono le ultime tre cifre della misura, ovvero 34,2 viene letto come 0,50342.
a) Utilizzando tutti i dati, trovare i limiti di controllo per i grafici X e R, costruire il grafico e tracciare i dati.
b) Utilizzare i limiti dei tentativi di controllo degli articoli (a) per identificare i punti fuori controllo. Se necessario, rivedere i limiti di controllo, considerando che qualsiasi campione al di fuori dei limiti di controllo può essere eliminato.
Tabella 3: Campioni di unghie
| Campione | R | Campione | R | ||
| 1 | 34,2 | 3 | 11 | 35,4 | 8 |
| 2 | 31,6 | 4 | 12 | 34,0 | 6 |
| 3 | 31,8 | 4 | 13 | 36,0 | 4 |
| 4 | 33,4 | 5 | 14 | 37,2 | 7 |
| 5 | 35,0 | 4 | 15 | 35,2 | 3 |
| 6 | 32,1 | 2 | 16 | 33,4 | 10 |
| 7 | 32,6 | 7 | 17 | 35,0 | 4 |
| 8 | 33,8 | 9 | 18 | 34,4 | 7 |
| 9 | 34,8 | 10 | 19 | 33,9 | 8 |
| 10 | 38,6 | 4 | 20 | 34,0 | 4 |
Fonte: Montgomery (2013)
Figura 07: Campioni di barre fuori controllo
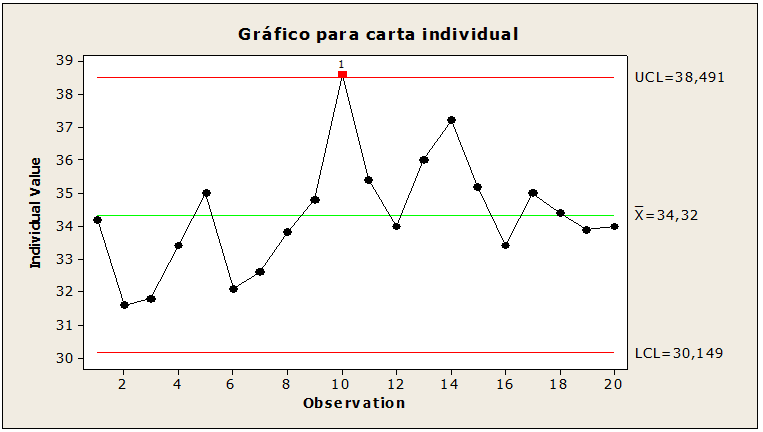
Controllo statistico per 20 campioni di cinque aste ciascuno. Interpretando la figura 07, i valori del limite superiore erano 38,49, la media 34,32, la deviazione standard 1,72, il limite inferiore 30,14 con il punto 10 del valore 38, 6 sopra il limite superiore dando indicazioni di cause speciali che possono essere corrette. La correzione a questo punto è suggerita in modo che i limiti siano regolati.
Figura 08: Campioni di unghie sotto controllo
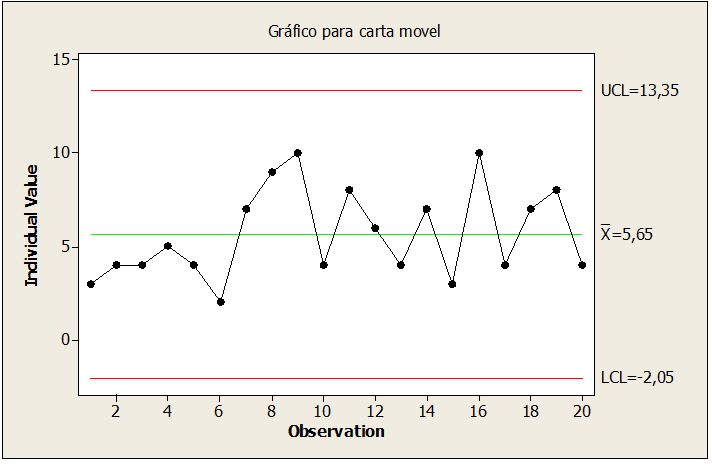
Correggendo il punto nella figura 08, il punto 10 è stato regolato, riducendo il valore del campione a 36,6, mantenendo il processo stabile e sotto controllo nella fabbricazione del diametro delle barre di alluminio.
Figura 09: Campioni di stelo con capacità di processo
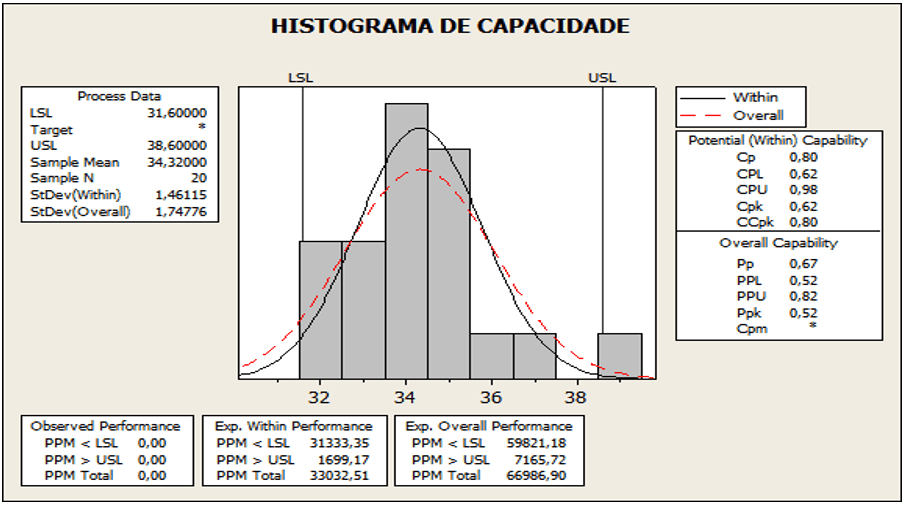
Secondo l’analisi della Figura 09, presenta il valore per Cpk pari a 0,49, media 5,65, deviazione standard 2,434 e valore p 0,025. Risultato CPk fuori dai limiti, se Ppk < CPk. La media ottenuta è stata di 5,65, con spostamento verso l’LSE. Il CPk 0,49 inferiore ai valori stabiliti che implicano 1,33 è al di fuori del limite stabile.
Figura 10: Percentuale di difetti
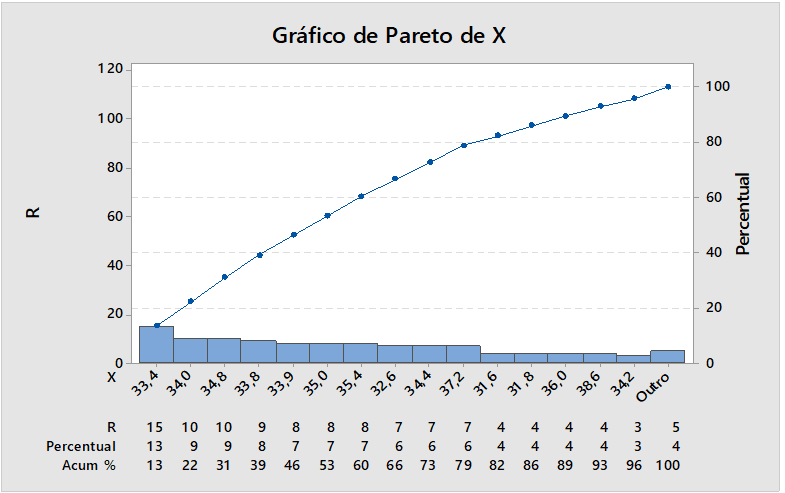
Figura 10. Il grafico di pareto fornisce la percentuale dei campioni analizzati di difettosi prodotti in questo processo, percentuale, la più grande fonte di 15 parti difettose che corrisponde a una percentuale del 13%. È necessario eliminare le variazioni.
Osservando le figure, è stato verificato che nella Figura 07, il punto 10 è al di fuori del limite di controllo, presentando anomalie nel diametro delle aste che possono essere corrette. Già nella figura 09, il cpk è fuori dai limiti. Tuttavia la figura 10, ha un difetto nelle aste. Figura successiva 08. Dopo aver interpretato, analizzato ed eliminato le cause speciali nel punto del diametro sono rimaste stabili.
La figura 11 mostra le tabelle di controllo per le medie, la deviazione standard e il numero di non conformità misurate campionando 5 pezzi in 25 lotti. Attraverso i grafici presentati possiamo osservare che esiste un punto al di fuori del limite di controllo ed è distribuito intorno alla media, così come ci ha permesso di osservare l’ordine di grandezza delle deviazioni di processo e infine ha permesso di trovare i punti di cause speciali, dove presenta un punto al di fuori del limite. Attraverso queste analisi, abbiamo scoperto che c’è variabilità della causa speciale nel punto 17 LSC, dove il punto è al di fuori del limite di controllo, che richiede correzioni e riduzione della variabilità. Questa anomalia è stata rilevata dalla tabella di controllo del software Minitab nel 1 ° test in cui il processo è stato necessario per stabilizzarsi. Quindi, per tenere sotto controllo il processo, è stato applicato il 2° test per integrare il 1° test al fine di creare una nuova tabella di controllo che abbia il processo sotto controllo.
Tre situazioni sono state raccomandate quando si costruisce il grafico dei limiti sotto controllo: rimuovere l’osservazione del valore 3.95445, modificare i valori di non conformità o costruire un nuovo grafico. Il 2° test nella Figura 12. Mostrare la correzione, il confronto e la riduzione delle variazioni nella costruzione di un nuovo grafico con il punto sotto controllo in relazione alla media, con modifica nel punto di campionamento al fine di mantenere il processo sotto controllo. Il valore di esempio 3,95445 ha modificato il valore 2,55445. Dopo aver controllato il processo, è stato possibile confrontare i risultati ottenuti con i risultati precedenti tra i processi. Rispetto ai valori del calcolo del campione nel processo sotto controllo, la media presentava il valore pari a 1,60, la deviazione standard 0,66 e l’ampiezza del valore limite 3,66. Mentre il processo fuori controllo significa pari a 1,68, deviazione standard 0,69 e ampiezza limite con valore 3,81.
Figura 11: Lettera fuori controllo
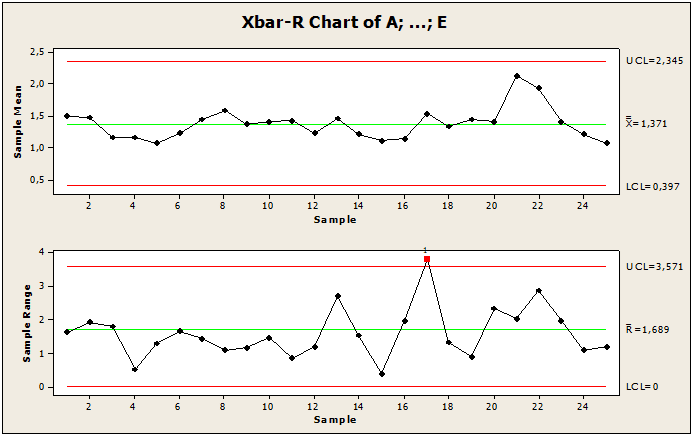
Figura 12: Lettera sotto controllo
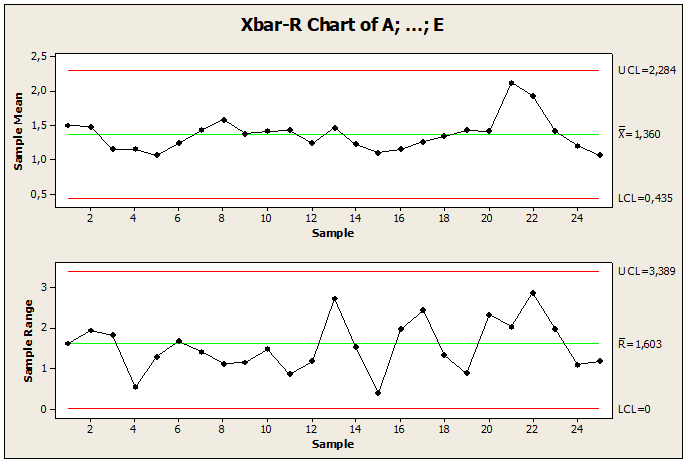
I risultati ottenuti in questo studio mostrano le carte di controllo come uno strumento efficace per ridurre la variabilità nelle applicazioni delle scienze dell’educazione trovando la stabilità del processo e migliorando la qualità.
4. CONCLUSIONE
Attraverso le carte di controllo del software Minitab, è stato possibile tracciare e analizzare i cambiamenti nella distribuzione del campione nel processo statistico informando i punti critici con variabilità nelle applicazioni delle scienze dell’educazione. Attraverso l’analisi dei grafici di controllo possiamo percepire che le applicazioni statistiche presentavano variabilità.
Il grafico è uno strumento utilizzato per controllare l’anomalia mediante test statistici e la variabilità è stata trovata in alcuni punti campione di applicazioni statistiche. Pertanto, era necessario fare inferenze nel controllo delle variabili con punti fuori controllo. È stato verificato dal 1 ° test che i sottogruppi che sono insoliti rispetto ad altri sottogruppi presentavano anomalie e c’era la necessità di applicare il 2 ° test per correggere e mantenere il processo sotto controllo.
I grafici hanno permesso di verificare le variazioni e stabilizzare le variabili tra parametri media, deviazioni standard e ampiezza. I grafici hanno permesso di approssimare i punti di campionamento al di fuori dei limiti e regolare i difetti tra i limiti, aiutando nel miglioramento continuo del processo, consentendo di percepire i difetti e controllare le cause di variazione anomala tra i parametri limitati della tabella sotto confronto dei campioni nei test di verifica.
Analizzando i grafici al fine di fissare i limiti per le ispezioni future sarebbe necessario eliminare la variabilità spaziale e dopo aver cambiato i campioni costruire un nuovo grafico in minitab diventa fattibile nell’eliminare questi punti per il calcolo dei limiti rivisti
Gli obiettivi stabiliti in questa ricerca sono stati raggiunti con successo consentendo l’uso di tecniche statistiche per identificare ed eliminare anomalie non conformi a problemi statistici. Tali tecniche hanno permesso l’inferenza nelle applicazioni ingegneristiche attraverso i campioni. Le azioni hanno ridotto il verificarsi di variabilità nel software Minitab e quindi hanno mantenuto il processo stocastico stabile e sotto controllo. Questo tema ha rivelato che è possibile raccogliere, analizzare e interpretare i dati attraverso grafici di controllo, perché attraverso questo strumento è possibile verificare l’anomalia nei problemi statistici.
Si è riscontrato che il software statistico è in grado di soddisfare le specifiche nel controllo del processo. E’ stata verificata la necessità di utilizzare Minitab per prevenire possibili cause di variabilità. Infine, con il presente studio della variabilità, è stato possibile percepire e comprendere il contributo delle risorse delle carte di controllo applicando il software nella riduzione dell’anomalia nelle applicazioni scientifiche statistiche.
RIFERIMENTI
BORTOLOTTI, S. L. V. et al. Análise da qualidade do produto final no processo de envase de azeitonas verdes. Tecnol. & Hum., Curitiba, ano 23, n. 36, jan/jun. 2009. Disponível em: https://revistas.utfpr.edu.br/rth/article/viewFile/6238/3889
CARPINETTI, L. C. R. Gestão da Qualidade, Conceitos e Técnicas. São Paulo: Atlas S.A., 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CASTRO, D. R. C. et al. A aplicabilidade dos gráficos de controle nas empresas como modelo de inspeção para a avaliação da qualidade. In: XXXII Encontro Nacional de Engenharia de Produção. Bento Gonçalves, RS, 2012. Disponível em: http://www.abepro.org.br/biblioteca/enegep2012_tn_stp_158_921_20804.pdf
CHAVES, J. B. P. Controle de Qualidade na Indústria de Alimentos. Viçosa,
MG, (s.n.), 1997.
CHAVES, J. B. P.; TEIXEIRA, M. A. Controle Estatístico de Qualidade:
inspeção por amostragem/ mapas de controle. DTA/UFV. Viçosa, MG: (s.n.), p. 162,
1997.
CORTIVO, Z. D. Aplicação do Controle Estatístico de Processo em sequências curtas de produção e análise estatística de processo através do planejamento econômico. Curitiba: Universidade Federal do Paraná, 2005.
FERREIRA, J. M.; OLIVEIRA, M. S. de. Controle estatístico da qualidade. Lavras: UFLA/FAEPE, p.87, 2008.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
HORA, H. R. M., COSTA, H. G. Tomada de decisão no MASP: uma contribuição para decisões utilizando a matriz AHP. XXIX Encontro Nacional de Engenharia de Produção. Salvador. ENEGEP, 2009.
IPEK, H. et al. The application of statistical process control. Minerals Engineering, Vol. 12, Issue 7, p. 827-835, 1999. ISSN 0892-6875. Disponível em: https://doi.org/10.1016/S0892-6875(99)00067-9.
JURAN, J. M.; GRYNA, F. M. Controle da Qualidade: Métodos Estatísticos Clássicos Aplicados à Qualidade. São Paulo, Ed. Makron, 1992.
LAGO NETO, J. C. do. O efeito da autocorrelação em gráficos de controle para variável contínua: Um estudo de caso. Florianópolis, 1999.
MAGALHÃES, M. S. de; MOURA NETO, F. D. Economic-statistical design of variable parameters non-central chi-square control chart. Production, v. 21, n. 2, p. 259–270, 2011.
MICHEL, M. H. Metodologia e Pesquisa Científica em Ciências Sociais: Um Guia Prático para Acompanhamento da Disciplina e Elaboração de Trabalhos Monográficos. São Paulo: Atlas, 2005.
MINITAB. Conheça o Minitab para Windows. 1º. ed. São Paulo: Editora Minitab
Inc., 2010.
MONTGOMERY, D. C. Estatística Aplicada e Probabilidade para Engenheiros. Tradução e revisão técnica Verônica Calado. Rio de Janeiro, LTC, 2015.
MONTGOMERY, D. C. Introdução Ao Controle Estatístico Da Qualidade. 4. ed. Rio de Janeiro: LTC, 2009.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 1997.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 4. ed. Rio de Janeiro: LTC, 2004.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 2013.
MONTGOMERY, D. C. Introdução ao controle estatístico de qualidade. Rio de Janeiro: LTC, 2016.
OLIVEIRA, T. S.; LIMA, R. H. P. Aplicação do controle estatístico de processo na mensuração da variabilidade em uma usina de etanol. Anais. INGEPRO Inovação, Gestão e Produção, v. 3, n. 6, p. 022-033, 2015.
OLIVEIRA, V. F. de. Mobilidade e acessibilidade urbana: uma análise socioespacial a partir dos bairros Jardim Morada do Sol e Conjunto Habitacional Ana Jacinta, em Presidente Prudente. Faculdade de Ciências e Tecnologia – FCT, Unesp, 2011.
PALLADINI, E. P. et al. Gestão da Qualidade: Teoria e Casos. 2. Ed. São Paulo: Atlas, 2010.
PEDRINI, D. C. Proposta de um método para aplicação de gráficos de controle de regressão no monitoramento de processos. Universidade Federal do Rio Grande do Sul: UFRGS, 2009.
PEREIRA, A.; PATRÍCIO, T. Guia prático de utilização: análise de dados para Ciências Sociais e Psicologia. 8.ª ed. Lisboa : Sílabo, 2013.
REBELATO, M. G. et al. Estudo sobre a aplicação de gráficos de controle em processos de saturação de papel. XIII SIMPEP. Bauru, SP: 2006.
RIBEIRO, J. L.; CATEN, C. T. Controle estatístico de processos: Apostila de Curso. Porto Alegre: UFRGS, 2012.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. 3 ed. São Paulo: Atlas, 1999.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
RODRIGUES, G. P. Controle Estatístico de Qualidade e de Processo na Indústria de Alimentos. Universidade Federal de Viçosa, MG, p. 152,1998.
ROSA, L. C. Introdução ao Controle Estatístico de Processos. Santa Maria, Ed. Da UFSM, 2009.
SIQUEIRA, L. G. P. Controle Estatístico de Processos – Equipe Grifo – Série Qualidade Brasil. São Paulo: Pioneira, 1997.
SOUZA, A. M., RIGÃO, M. H. Identificação de variáveis fora de controle em processos produtivos multivariados. Revista Produção, São Paulo, V.15 no.1, p.74-86, abr. 2005.
SOUZA, R. Case Research in Operations Management. EDEN Doctoral Seminar on Research Methodology in Operations Management, Brussels, Belgium, 2005.
SPIEGEL, M. R.; STEPHENS, L. J. Schaum’s esboço de teoria e problemas de estatística: Aprenda a si mesmo. 4ª ed., Rio de Janeiro: LTC, 2007.
TRIVELLATO, A. A. Aplicação das sete ferramentas básicas da qualidade no ciclo PDCA para melhoria contínua: estudo de caso numa empresa de autopeças. Trabalho de conclusão de curso, Universidade de São Paulo, 2010.
VIEIRA, S. Estatística para a qualidade: como avaliar com precisão a qualidade em produtos e serviços. Rio de Janeiro: Elsevier, 1999.
VILAÇA, A. C.; OLIVEIRA, R. C. B. Utilização do Controle Estatístico de Processo para Avaliação de Peso de Massas para Pastel. FAZU em Revista, Uberaba, n. 8, p. 137-146. 2011.
WERKEMA, M. C. C. Avaliação de sistemas de medição. 2.ed. Belo Horizonte: Werkema. 2012.
WERKEMA, M. C. C. Ferramentas estatísticas básicas para o gerenciamento de processos. Belo Horizonte: Werkema, 2006.
YIN, R. K. Estudo de caso: planejamento e métodos. 2. Ed. Porto Alegre: Bookman, 2001.
[1] Master in Ingegneria dei processi – PPGEP/ITEC-UFPA.
[2] Doutor em Engenharia de Recursos Naturais pela Universidade Federal do Pará.
Inviato: Aprile 2021.
Approvato: Giugno 2021.