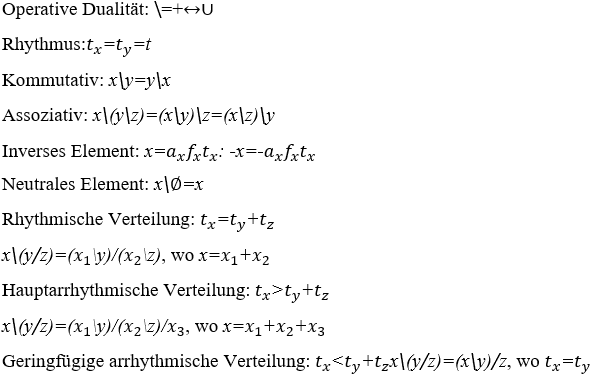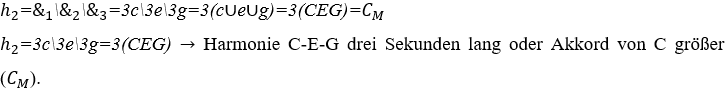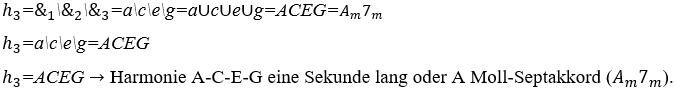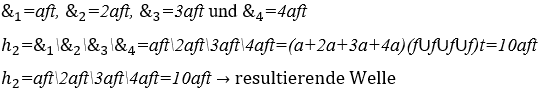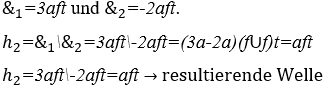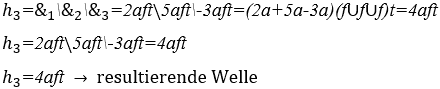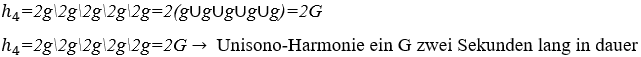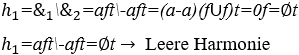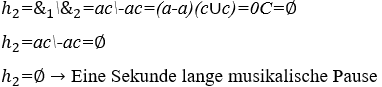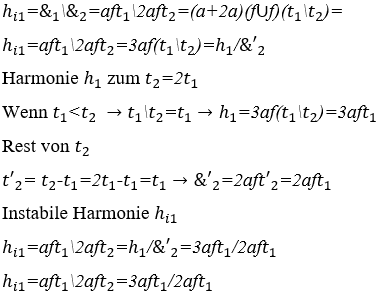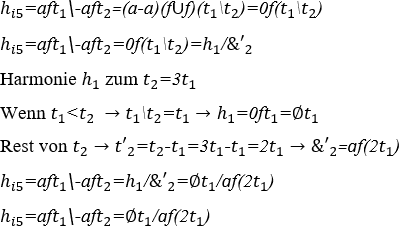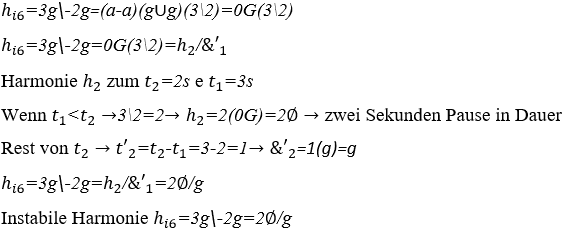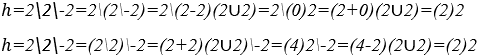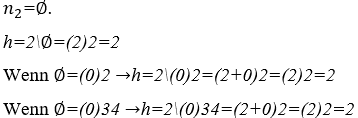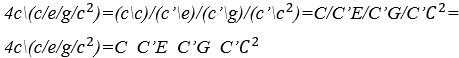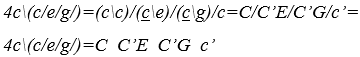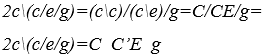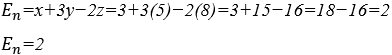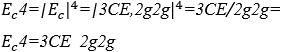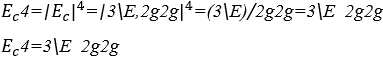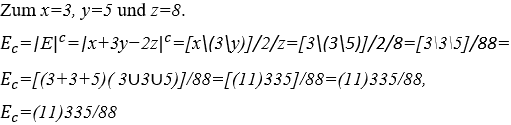Die harmonisierende Operation (H) und ihre inverse Melodieoperation (M)

ORIGINALER ARTIKEL

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. Die harmonisierende Operation (H) und ihre inverse Melodieoperation (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr. 07, Ed. 03, Bd. 03, p. 144-171. März 2022. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/harmonisierende-operation

ZUSAMMENFASSUNG

Das Fehlen einer mathematischen Operation zur Erklärung der Wechselwirkungen von Wellen, insbesondere zwischen den Schallwellen von Musiknoten, war das Problem, das die Erstellung dieses Artikels leitete. In diesem Zusammenhang war das Ziel dieser Forschung, die auf eine bessere Visualisierung einer einfachen Schallwelle abzielte, die vom Autor dieses Materials entwickelten Operationen zu demonstrieren, die aus drei wichtigsten Merkmalen der Musik bestehen: der Amplitude , häufig und Zeit in Dauer . So kam die Form und auf diese Weise werden die musikalischen Strukturen einer Harmonie und einer Melodie, die durch ihre harmonischen und melodischen Gruppierungen gebildet werden, analysiert, bis man die operativen Eigenschaften dieser Organisationen in ihren physikalischen Phänomenen erhält. In der Gruppierung, in der diese Musiknoten gleichzeitig, im Raum oder gleichzeitig ausgestrahlt werden, befinden sich die Schallwellen physisch in Überlagerung und verursachen Interferenzen zwischen ihnen, wodurch ein Klangeffekt entsteht, der von den Musikern von Harmonie genannt wird. Durch die Bewertung dieser Struktur in Raum und Zeit wurde die mathematische Operation entwickelt, die dieses harmonische Phänomen verursacht, wobei die grundlegenden Operationen übernommen wurden, die in dieser integrierten Interferenz entstanden sind, eine einzige spezielle Operation, Operation Harmonisation oder Operation H genannt. Als Ergebnis dieser Operation, es wurde auch seine Umkehrfunktion entwickelt, bei der die Wellen von Musiknoten kontinuierlich im Raum oder zeitlich nacheinander ausgestrahlt werden, wodurch ein Klangeffekt entsteht, der von Musikern als Melodie bezeichnet wird. Durch die Analyse dieser Struktur in Raum und Zeit wurde auch die mathematische Operation entwickelt, die dieses Phänomen hervorruft, Operation Melodiation oder Operation M genannt, die dem Zweck dieser Untersuchung dient, die darauf abzielt, der Wissenschaft eine mathematische Sicht auf die musikalischen Strukturen von Harmonien und Melodien zu liefern Musik, die im Allgemeinen neue mathematische Operationen liefert, die Naturphänomene erklären können und der Wissenschaft ihr Verständnis erleichtern.

Stichwort: Harmonisierung, Melodiation , Harmonie, Melodie.

1. EINLEITUNG

Anfang 2006 entwickelte der Autor dieses Materials Operation Harmonization für die harmonischen Gruppierungen von Schallwellen der Harmonien von Musiknoten und Operação Melodiação für die melodischen Gruppierungen von Schallwellen seiner Melodien.

Das Problem, das die Konstruktion dieses Materials und die Entwicklung dieser Operationen motivierte, war das Fehlen einer mathematischen Operation zur Erklärung der Wechselwirkungen von Wellen, insbesondere zwischen den Schallwellen von Musiknoten. In diesem Zusammenhang besteht das Ziel darin, vom Autor dieses Materials entwickelte Operationen zu demonstrieren, die sich aus drei wichtigsten Merkmalen der Musik zusammensetzen: der Amplitude , häufig und Zeit in Dauer .

Bei deren Entwicklung wurde zunächst überlegt, dass nur bei Schallwellen und später allgemein bei jedem anderen Element mit oder ohne Schwingung das physikalische Phänomen der „Wellenüberlagerung“ auftritt, bei der Begegnung zweier Gleiche Wellen, es gibt eine Erhöhung der resultierenden Amplitude zwischen ihnen (SILVA, undatiert).

Verwendung des Ausdrucks , in dieser Studie formuliert, um eine Schallwelle darzustellen, mit den Eigenschaften: Amplitude , häufig und Zeit in Dauer , ist es möglich, auf einfache Weise die Interferenz zweier identischer Schallwellen zu analysieren .

Wenn sie sich an einem gemeinsamen Punkt treffen , in diesem Fall addieren sich ihre Amplituden , bei gleicher Frequenz und gleicher Dauer .

Bei der Auswertung des Ergebnisses dieses Interferenzphänomens wurde beobachtet, dass am Treffpunkt p der Überlagerung zwischen diesen beiden Wellen zusätzlich zu der bestehenden algebraischen Summe zwischen ihren Amplituden , es gibt auch die Vereinigung zwischen ihren Frequenzen in dieser Zeit eine einzige Schallwelle bilden, mit Amplitude, Frequenz und Zeitdauer.

In dieser ersten Analyse wurde auch der Schluss gezogen, dass diese beiden Operationen, die Addition zwischen Amplituden und die Vereinigung zwischen Frequenzen, zusätzlich dazu, dass sie das Ergebnis dieses Phänomens bilden, auch eine einzige mathematische Operation integrieren, die durch diese operationelle Dualität gekennzeichnet ist. Dies erklärt die gleichzeitige Emission von Wellen von Musiknoten, deren Klangeffekt Harmonie genannt wird. Daher wurde der Name der Harmonisierungsoperation oder H-Operation zugelassen, wobei ein linker Schrägstrich (\) als mathematisches Symbol, genannt H-Operator, verwendet wurde . Aus diesem Phänomen entsteht das Prinzip der Harmonie, wo die Elemente harmonisch sind, wenn es eine Überlagerung zwischen ihnen in ihrer Raumzeit gibt.

Folglich wurde seine umgekehrte Operation entwickelt, bei der die Schallwellen den Überlagerungszustand verlassen und in den ununterbrochenen Zustand übergehen, wo die Endzeit einer Welle gleich der Anfangszeit der nächsten Welle ist , usw , dessen Soundeffekt von Musikern Melody genannt wird. Daher wurde der Name Melodiation oder M-Operation angenommen, mit einem rechten Schrägstrich (/) als mathematischem Symbol, der als M-Operator bezeichnet wird , Ursprung des Melodieprinzips, bei dem Elemente melodisch sind, wenn zwischen ihnen in ihrer Raumzeit Kontinuität besteht.

2. HARMONISIERUNGSOPERATION (H)

Allgemein gesagt, wenn zwei oder mehr rhythmisch periodische Wellen , mit unterschiedlichen Frequenzen und Amplituden , in Betrieb sind Harmonisierung oder H sie bilden eine harmonische Gruppierung, genannt Harmonie, wo die resultierende Frequenz wird durch die Vereinigungsoperation zwischen seinen Frequenzen bestimmt und die resultierende Amplitude durch die Additionsoperation zwischen ihren Amplituden , die in der gleichen Phase mit gleichen Vorzeichen sein können, bei konstruktiver Interferenz, oder in entgegengesetzten Phasen mit entgegengesetzten Vorzeichen, bei destruktiver Interferenz.

Je mehr Wellen dieser Art in dieser Operation vorhanden sind, desto mehr Frequenzen werden verbunden und mehr Amplituden hinzugefügt im Ergebnis dieser Harmonie , wie im Beispiel unten gezeigt.

Operation Harmonisierung und ihre Harmonie zwischen drei unterschiedlichen und rhythmisch periodischen Wellen:

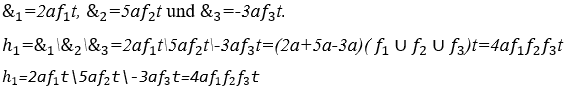
Harmonische Gruppierung der resultierenden Harmonie

2.1 EIGENSCHAFTEN DER OPERATION H (HARMONISIERUNG)

2.2 MUSIKALISCHE HARMONIE

Bei der Harmonisierungsoperation zwischen Schallwellen, insbesondere von rhythmischen Musiknoten, wobei normalerweise die Harmonie eines musikalischen Hauptakkords durch einen Dreiklang oder drei Noten mit unterschiedlichen Frequenzen gebildet wird , die resultierende Amplitudenzunahme ist linear (MORAIS, 2020).

Angenommen, diese Wellen sind gleich und die Tatsache, dass die Schallintensität des menschlichen Gehörs mit einem Wert von logarithmisch ist  (SANTOS,undatiert), in diesem Fall ist seine Hinzufügung unbedeutend, um bemerkt zu werden . Wenn dieser Bruch auf eins gerundet würde , mathematisch ist es, als würde sie in dieser Harmonie nicht existieren .

Aufgrund dieses Phänomens und unter Berücksichtigung dieser Rundung wurde die Harmonie dieser Operation nur durch Berechnung der Vereinigungsoperation zwischen ihren Frequenzen gebildet . Daher ist es für dieses vereinfachte Ergebnis nicht erforderlich, die Schallintensität zu kennen in Harmonie mit Musiknoten in einer Operation H anzuwenden, da dies eine beliebige sein kann, unbeschadet der Harmonie dieser Operation.

Einige H-Operationen mit Musiknoten, die durch ihre Nummern identifiziert sind, werden unten beschrieben, wobei die Noten der Noten A, B, C, D, E, F und G, basierend auf der Arbeit von Guest (2020, S. 33 bis 41):

1) Berechnen Sie die Harmonie zwischen Musiknoten: F und B , beide mit zwei Sekunden Dauer und normaler Tonintensität.

2) Berechnen Sie die Harmonie zwischen Musiknoten: C , E und G alle drei Sekunden lang und mit normaler Lautstärke.

3) Berechnen Sie die Harmonie zwischen Musiknoten: A , C , E und G , alle mit einer Dauer von einer Sekunde und normaler Tonintensität.

Hinweis: In dieser Studie wird definiert, dass eine Harmonie mit ihren Frequenzen in aufsteigender Reihenfolge und tonischem Akzent auf der letzten Frequenz benannt wird. Zum Beispiel, es ist Harmonie A-C-E-G eine Sekunde lang oder ein A Moll-Septakkord .

2.3 EINHEITLICHE HARMONIE

Einheitliche Harmonie ist das Ergebnis der H-Operation zwischen zwei oder mehr gleichen periodischen Wellen , Bilden einer harmonischen Gruppierung einer einzelnen Frequenz , mit seiner resultierenden Amplitude und eine Zeitdauer

Diese Art von Harmonie kann in dieser Raumzeit so erscheinen, dass es nur eine periodische Welle in ihrer Struktur gibt, jedoch koexistieren zwei oder mehr gleiche periodische Wellen darin, die dieselbe Raumzeit einnehmen und eine harmonische Einheitsmenge bilden können in einer einheitlichen Struktur zwei oder mehr kontinuierliche gleichperiodische Wellen in einer neuen Raumzeit erzeugen . Im Gegensatz zu einem einfachen einheitlichen Satz, der aus einer einzelnen Welle besteht, bei der nur eine einzige Welle seiner Struktur erzeugt wird .

Auf diese Weise werden zwei oder mehr Einheitsharmonien nur gleich sein , Wenn alle seine Eigenschaften und Mengen gleich sind und wenn diese Harmonie nur durch Schallwellen von Musiknoten gebildet wird, wird sie als Unisono-Harmonie betrachtet , durch Bildung eines einzigen Tons mit seiner Frequenz, Amplitude und Dauer , wie in den folgenden Beispielen gezeigt:

1) Unisono-Harmonie zwischen vier rhythmischen Wellen mit gleichen Frequenzen und unterschiedlichen Amplituden.

Grafik 1: Unisono-Harmonie

Graph 1 zeigt das Zeitintervall t1 bis t5, das den H-Betrieb charakterisiert und im Intervall von t5 bis t9 wird das Ergebnis der Operation oder ihre Harmonie gezeigt .

2) Harmonie mit destruktiver Interferenz zwischen zwei rhythmisch periodischen Wellen:

Grafik 2: Harmonie mit destruktiver Interferenz

Das im obigen Diagramm gezeigte Zeitintervall t1 bis t5 repräsentiert das Ergebnis der Operation H und im Intervall von t5 bis t9 wird das Ergebnis dieser Operation oder ihre Harmonie charakterisiert .

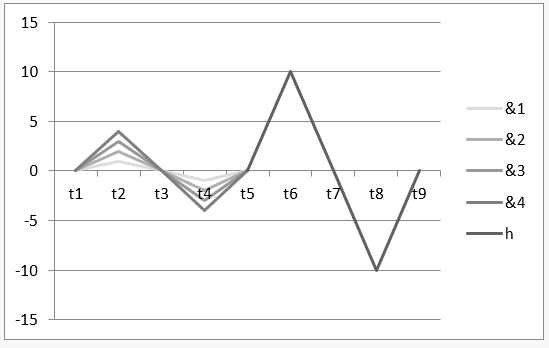
3) Konstruktive und destruktive Harmonie zwischen drei Wellen:

Grafik 3: Harmonie mit konstruktiver und destruktiver Interferenz

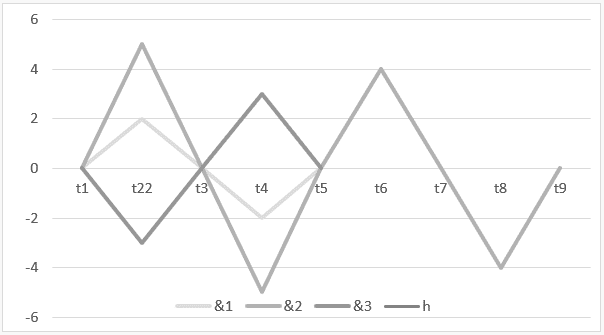
Das Zeitintervall t1 bis t5 demonstriert den H-Betrieb und im Intervall von t5 bis t9 wird das Ergebnis dieser Operation oder ihre Harmonie dargestellt .

4) Harmonie zwischen fünf Wellen von Musiknoten gleich der G-Note, zwei Sekunden lang.

2.4 LEERE HARMONIE

Leere Harmonie ist das Ergebnis der H-Operation zwischen einer Welle und ihrer entgegengesetzten Welle oder der Operation zwischen mehreren Wellen und ihren entgegengesetzten Wellen , bilden einer harmonischen Gruppierung einer einzelnen Frequenz , mit seiner Nullamplitude und eine Zeitdauer

Diese Art von Harmonie , es mag in dieser Raumzeit so erscheinen, als gäbe es keine periodische Welle in ihrer Struktur. Es existiert jedoch gleichzeitig mit einer resultierenden Frequenz mit einer Amplitude von null , in einem Zustand unendlich kleiner Schwingung, in der Dimension der Zeit, genannt Harmonische Urschwingung (VPH), durch eine negierte Null dargestellt , es bildet daher eine harmonische leere Menge, die von der Wissenschaft “Quantenvakuum” genannt wird und in der Lage ist, in ihrer Struktur mehr als eine Schwingung in einer Raumzeit zu erzeugen , im Gegensatz zu einer einfachen leeren Menge, in der nichts existiert und nichts erzeugt werden kann.

Auf diese Weise sind zwei leere Harmonien nur dann gleich, wenn ihre Eigenschaften und Quantitäten gleich sind. Was auch immer die leere Harmonie , es wird als das neutrale Element der Harmonisierungsoperation betrachtet , da es sich nur um eine aktive Zeitdauer handelt, die eine oder mehrere inaktive Vibrationen verbirgt oder nicht in der Lage ist, mit einem aktiven Element zu interagieren.

Daher ist das Ergebnis der Harmonie zwischen jedem neutralen Element und einem aktiven Element das aktive Element selbst , egal, was der Ursprung dieses neutralen Elements ist, wenn es mit gleichen Frequenzen ist oder mit gleichen Frequenzen , unabhängig von ihrer Dauer , denn diese Schwingungen koexistieren nur in der Dimension der Zeit.

Wenn diese Harmonie durch Schallwellen von entgegengesetzten Musiknoten gebildet wird, wird die Schallamplitude vollständig von ihrer Frequenz eliminiert , An seiner Stelle entsteht eine Stille in der Zeit, die eine Harmonie der Stille bildet. In diesem Fall wird seine Ruhezeit vom Menschen wahrgenommen, da seine Dauer gleich oder größer als eine Zehntelsekunde ist , Diese Harmonie ist als Musikalische Pause bekannt , que será demonstrada nos exemplos abaixo.

Wenn diese Harmonie durch leuchtende Schwingungen gebildet wird, wird die Leuchtkraft der Amplitude ihrer Frequenz vollständig eliminiert , wodurch an seiner Stelle eine Dunkelheit in der Zeit entsteht, die als Harmonie der Dunklen Energie bezeichnet wird und wahrscheinlich entsteht die Dunkelheit, die das Universum bewohnt, aus dieser Harmonie, die in seiner immensen harmonischen Leere enthalten ist.

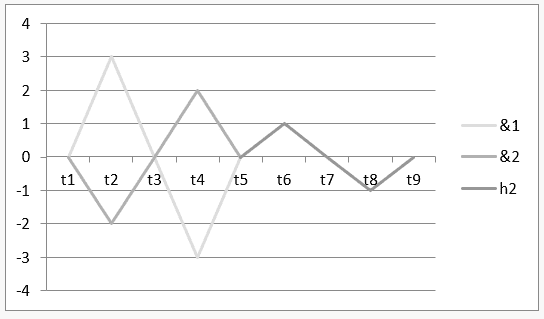
1) Harmonie zwischen zwei Wellen:  mit seinem Graphen im kartesischen System.

Grafik 4: Leere Harmonie von 

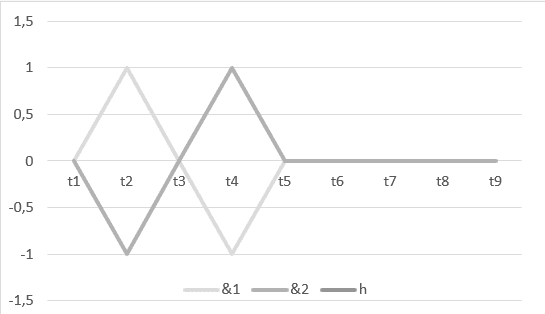
Das im obigen Diagramm dargestellte Zeitintervall t1 bis t5 repräsentiert den H-Betrieb und das Intervall von t5 bis t9 ist das Ergebnis dieser Operation oder ihrer Harmonie .

2) Harmonie zwischen Musiknoten: C, eine Sekunde lang, mit gleichen und umgekehrten Amplituden

Hinweis: Leere Harmonie ist ein Ort in der Raumzeit, an dem der Gedanke besteht, dass dort nichts existiert, wie auch immer er mit nicht wahrnehmbaren Schwingungen gefüllt sein kann.

2.5 INSTABILE HARMONIE

Instabile Harmonie ist das Ergebnis der H-Operation zwischen zwei oder mehr arrhythmischen periodischen Wellen oder mit unterschiedlicher Dauer , wobei die kürzere die Harmonie dieser Operation bildet , aufgrund der Eigenschaft des Rhythmus, die Dauer dieser Welle an die kleinste anzupassen und einen Teil der Dauer der größten zu belassen , wo geht es weiter (/) die Harmonie entstand .

Je größer die Anzahl dieser arrhythmischen Wellen bei dieser Operation, größer wird die Instabilität der gebildeten Harmonie sein , mit Verschlechterungen in sekundären Harmonien , ob es einen kontinuierlichen Rest der Welle von längerer Dauer gibt oder nicht , gemäß den unten aufgeführten Beispielen.

1) Instabile Harmonie zwischen zwei arrhythmischen Wellen: mit seinem Liniendiagramm in kartesischen Koordinaten.

Grafik 5: Instabile Harmonie von

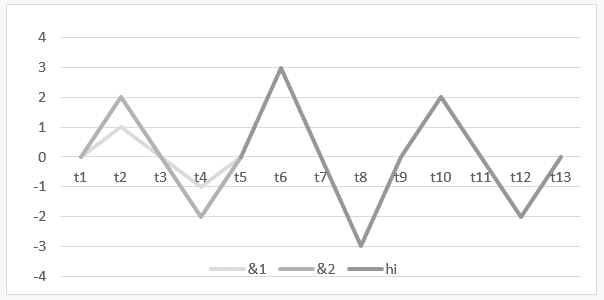
Das Zeitintervall t1 bis t5 zeigt das Diagramm der Operation H und im Intervall von t5 bis t13 wird das Ergebnis dieser Operation oder ihre Harmonie dargestellt .

2) Harmonie zwischen zwei arrhythmischen Musiknoten: , jeweils mit ihrer Dauer von drei es ist zwei sekunden.

3) Instabile Harmonie zwischen drei arrhythmischen Musiknoten: , jeweils mit einer Dauer von vier, drei und zwei Sekunden, mit seinem Diagramm im System der kartesischen Achsen.

Grafik 6: Instabile Harmonie von

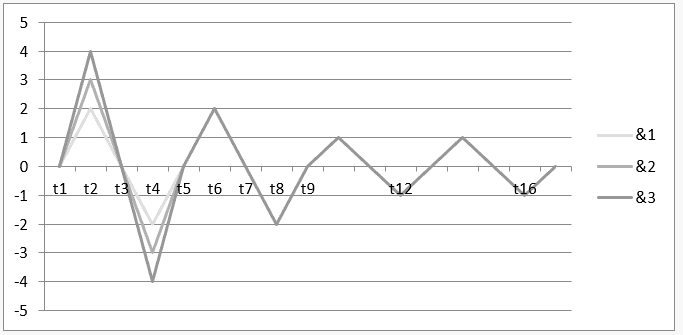
Das Zeitintervall t1 bis t5 repräsentiert den Graphen der Operation H und im Intervall von t5 bis t13 wird das Ergebnis dieser Operation oder ihre Harmonie gezeigt .

4) Instabile Harmonie zwischen drei arrhythmischen Musiknoten mit gleichen Frequenzen: 

5) Instabile Harmonie mit leerer Harmonie zwischen zwei Wellen: eine ist dreimal so lang wie die andere 

Grafik 7: Instabile Harmonie mit leerer Harmonie von

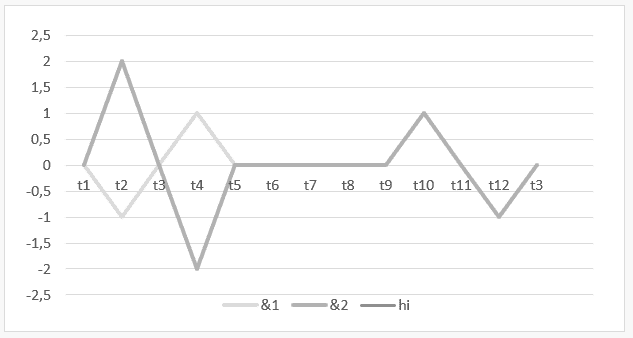
Das Zeitintervall t1 bis t5 bildet den Vorgang H ab und im Intervall von t5 bis t13 wird das Ergebnis dieser Operation oder ihre Harmonie gezeigt

6) Harmonie zwischen zwei G-Musiknoten mit gleichen Amplituden in entgegengesetzten Phasen, von denen eine drei Sekunden und die andere zwei Sekunden dauert

2.6 NUMERISCHE HARMONIE

Bei zwei oder mehr numerischen Konstanten  sich im Harmonisierungs- oder H-Betrieb befinden, werden sie als rhythmische Schwingungen betrachtet und da sie nur einen Parameter haben, der entweder Frequenz oder Amplitude sein kann, werden sie gleichzeitig als Frequenzen zusammengefügt und als Amplituden addiert bilden die Harmonie dieser Operation

Jeder Cluster, der durch eine Kombination aus kombinatorischer Analyse gebildet wird, wird als Ergebnis einer H-Operation zwischen diesen Elementen betrachtet mit dem Ergebnis ihrer Amplitude, die in der Vereinigung zwischen ihnen impliziert ist, wie in den folgenden Beispielen gezeigt.

1) Harmonie zwischen den numerischen Konstanten 1 und 1

Wo es heißt: Eine H-Eins entspricht der Harmonie von Eins mit Amplitude Zwei.

2) Harmonie zwischen den numerischen Konstanten 1 und 1

Wo es heißt: ein H minus eins entspricht leerer Harmonie.

3) Harmonie zwischen den numerischen Konstanten

Wo es heißt: drei H vier ist gleich Harmonie drei und vier, mit Amplitude sieben oder, gemäß der Kommutativeigenschaft dieser Operation,

4) Harmonien zwischen numerischen Konstanten

Wo es heißt: Drei H vier H minus acht ist gleich Harmonie drei, vier und acht, mit Amplitude minus eins oder, gemäß der kommutativen Eigenschaft dieser Operation, jede Gruppierung der Permutation zwischen diesen drei Elementen, mit Amplitude minus eins

5) Harmonien zwischen numerischen Konstanten

Wo es heißt: Zwei H zwei H minus zwei entspricht der Harmonie von zwei mit der Amplitude zwei, wobei die assoziative Eigenschaft dieser Operation angewendet wird.

6) Harmonien zwischen einer numerischen Konstante und jedes neutrale Element

Hinweis: die Harmonie der H-Operation zwischen einer beliebigen numerischen Konstante ist ein beliebiges neutrales Element ist die numerische Konstante selbst mit einer Amplitude gleich ihrem Wert Bei dieser Operation wissen wir, dass die Amplitude des neutralen Elements Null ist aber seine Häufigkeit ist unbestimmt und selbst wenn es bekannt wäre  sie wäre in der Dimension der Zeit und unfähig, mit irgendeinem aktiven Element irgendeiner Dimension zu interagieren.

3. BETRIEB MELODIATION ODER BETRIEB M

Die Melodieoperation oder M, ist die umgekehrte Operation der Harmonisierung, weil nach dem Ende der Dauer einer Harmonie die periodischen Schwingungen, die in Überlagerung waren, den Zustand der Ununterbrechung durchlaufen, das heißt, sie bilden eine Kontinuität zwischen ihren Räumen. Zeiten, wobei die Endzeit einer Dauer gleich der Startzeit der nächsten Dauer ist dieses Phänomen wird als Melodieprinzip bezeichnet.

Daher bei zwei oder mehr periodischen Schwingungen in Betrieb bleiben M  das Ergebnis ist eine melodische Gruppierung, deren Soundeffekt, wenn es sich um Wellen von Musiknoten handelt, eine Melodie ergibt und wenn diese Elemente numerische Konstanten in der Operation M sind, bilden sie auch eine kontinuierliche Gruppierung zwischen ihnen und bilden die numerische Melodie dieser Operation  Somit ist jede Gruppierung, die durch ein Array der Mathematik der Kombinatorischen Analyse gebildet wird, das Ergebnis einer Operation M, die keine kommutative Eigenschaft ist.

3.1 MELODIE MIT GLEICHEN FREQUENZEN UND ENTGEGENGESETZTEN AMPLITUDEN

Normalerweise haben Musiknoten in einer M-Operation Amplituden in positiven Phasen, wenn es jedoch eine Note mit einer Amplitude in negativer Phase gibt, kann sie in positive Phase moduliert werden, da die Frequenz gleich bleibt und den gleichen Klangeffekt in der Form erzeugt Melodie

Dieses negative Vorzeichen kann jedoch in der Notenchiffre und im Melodieergebnis mit einem Punkt darüber stehen bleiben Wenn dieses Element in dieser Operation eine negative numerische Konstante ist es kann auch positiv moduliert werden oder einen Punkt auf der Konstante in der resultierenden Melodie identifiziert

3.2 DIE MUSIKPAUSE (p)

Die Musikpause ist eine Musiknote mit einer Tonfrequenzamplitude von Null, dargestellt durch eine negierte null Mit anderen Worten, es ist das neutrale Element der H-Operation, und seine Hauptfunktion in einer Melodie besteht darin, eine Klangdiskontinuität zwischen melodischen Musiknoten bereitzustellen oder einen tonlosen Raum zwischen ihnen zu lassen Es kann auch nur zu Beginn des ersten Takts eines Rhythmus und am Ende des letzten Takts dieses Rhythmus impliziert werden, wobei seine Perioden abgeschlossen werden.

3.3 BETRIEBSBEISPIELE M ZWISCHEN WELLEN VON MUSIKNOTEN

3.4 ANWENDUNG DES DISTRIBUTIVEN EIGENSCHAFTENS DES BETRIEBES H

Wenn eine Musiknote in einem Takt beginnt und in einem anderen endet, ohne ihre Klangkontinuität zu verlieren, erhält ihre fortgesetzte Chiffre im nächsten Takt ein Apostroph, zum Beispiel:

1) Rhythmische Verteilung:

2) Hauptarrhythmische Verteilung

3) Hauptarrhythmische Verteilung

3.5 BEISPIELE DER OPERATION M MIT NUMERISCHEN KONSTANTEN

4. ALGEBRA DER SCHWINGUNGEN

Die Algebra der Schwingungen ist nichts anderes als Algebra mit mindestens einer der Harmonisierungs- oder Melodieoperationen in ihrem Ausdruck.

Auch wenn es keine dieser Operationen aufweist, kann es für die Algebra der Vibrationen moduliert werden, durch die verfügbaren Wellenmodule, wie z. B.: das Melodische Modu, die einen algebraischen Ausdruck in eine Melodie verwandelt; das harmonische Modul , das einen algebraischen Ausdruck in eine Harmonie umwandelt; das Kompositmodul , die einen algebraischen Ausdruck in eine Melodie mit Harmonie verwandelt, deren normalerweise arrhythmische Ergebnisse zu jedem Rhythmus moduliert werden.

Durch die Standard-Rhythmus-Module , die die musikalischen Zellen in rhythmische Klanggruppen organisieren, indem sie ihre Dauer in gleichen Perioden in Takten addieren: Binär , Ternär oder Quartär . In diesem Fall können der erste und der letzte Takt eines beliebigen Rhythmus mit Musiknoten unvollständig sein, wie im Beispiel unten gezeigt.

Angesichts des Ausdrucks: und die numerischen Konstanten und klangvoll Werte werden berechnet, numerisch , melodisch , harmonisch es ist komponiert

4.1 BERECHNUNG DES ZAHLWERTES VON E=x+3y−2z

Ersetzen der Variablen im Ausdruck

4.2 BERECHNUNG DES MELODISCHEN KLANGWERTES VON E=x+3y−2z

Das melodische Modul wandelt einen numerischen algebraischen Ausdruck in einen melodischen algebraischen Ausdruck um und ersetzt alle vorhandenen Operationen durch M-Operationen (/).

Das normalerweise arrhythmische Ergebnis wird auf jeden Rhythmus moduliert um die Musiknoten in einer einzigen Aufführung zu organisieren.

Hinweis: Die Operation M zwischen einer numerischen Konstante und einer Klangkonstante ist gleich der Melodie der Tonkonstante mal

Modul für melodischen Ausdruck

Einwechseln

arrhythmische Melodie

Quartäres rhythmisches Modul in

Quartäre Rhythmusmelodie

Kommentar: Die Auswahl eines Rhythmus ist optional, und wenn das ternäre Rhythmusmodul gewählt wurde, würde die letzte Note durch einen Part im vorletzten Takt und einen weiteren fortlaufenden im letzten Takt geteilt, was mit einem Apostroph in seiner Chiffre gekennzeichnet wäre

4.3 INTERAKTIVER MELODISCHER WERT VON E=x+3y−2z

Wenn im melodischen Modul sowohl Klang- als auch numerische Konstanten ausgetauscht werden, wird der resultierende melodische Ausdruck als interaktiv bezeichnet, da er eine physikalische Dynamik als Funktion der numerischen Konstante enthält, wie im folgenden Beispiel gezeigt.

dem Ausdruck gegeben und die Konstanten Sein melodischer Wert wird berechnet.

arrhythmische interaktive Melodie

Ternäres Modul ein

Melodie im ternären Rhythmus

Hinweis: Der Zahlenwert drei (3) im ersten Takt steht für jede körperliche Aktion, zum Beispiel: im Dreiertakt von eins bis drei zählen und dann in den folgenden Takten die angegebene Melodie spielen Dieses Zählen im binären oder quaternären Rhythmus macht die Ausführung dieser komplexen Dynamik schwierig zu erfüllen, daher ist es wichtig, einen geeigneten Rhythmus für einen interaktiven melodischen Ausdruck zu wählen.

4.4 MELODISCHER ZAHLENWERT VON E=x+3y−2z

melodische numerische Gruppierung

4.5 HARMONISCHER SCHALLWERT VON E=x+3y−2z

Das harmonische Klangmodul wandelt einen numerischen algebraischen Ausdruck in einen harmonischen algebraischen Ausdruck um und ersetzt alle vorhandenen Operationen durch H-Operationen (\). Das Ergebnis ist normalerweise arrhythmisch moduliert zu einem beliebigen Rhythmus für seine einfache Ausführung.

Hinweis: Die H-Operation zwischen einer numerischen Konstante e ein konstantes Geräusch ist gleich der Unisono-Harmonie der Klangkonstante

Harmonisches Modul   des Ausdrucks

Ersetzen in

Harmonie im ternären Rhythmus

4.6 INTERAKTIVER HARMONISCHER WERT VON E=x+3y−2z

Wenn im harmonischen Modul sowohl Klang- als auch numerische Konstanten ersetzt werden, wird der resultierende harmonische Ausdruck als interaktiv bezeichnet, da er eine physikalische Dynamik als Funktion der numerischen Konstante enthält, wie im folgenden Beispiel gezeigt.

Der harmonische Klangwert des Ausdrucks wird berechnet , angesichts der Konstanten

Harmonie im ternären Rhythmus durch numerische Konstante

Hinweis: Der Zahlenwert drei (3) im einzelnen Takt repräsentiert jede körperliche Aktion, zum Beispiel: im Dreiertakt von eins bis drei zählen, während die angezeigte Harmonie gespielt wird Dieses Zählen in anderen Rhythmen macht die Ausführung dieses dynamischen Komplexes und schwierig zu erfüllen, daher ist es sehr wichtig, einen Rhythmus für einen interaktiven harmonischen Ausdruck zu wählen.

4.7 HARMONISCHER NUMERISCHER WERT VON E=x+3y−2z

Wenn im harmonischen Modul alle Konstanten numerisch sind, ist das Ergebnis eine numerische harmonische Gruppierung, wie unten gezeigt.

4.8 SCHALLWERT BESTEHEND AUS E=x+3y−2z

Das Verbundmodul wandelt einen numerischen algebraischen Ausdruck in Klangausdrücke mit Melodien und Harmonien um und ersetzt alle vorhandenen Operationen durch Operationen mit M und H. Das Ergebnis ist normalerweise arrhythmisch moduliert zu einem beliebigen Rhythmus für seine einfache Ausführung. In diesem Fall gibt es die Option, welche Operationen durch die stimmhaften ersetzt werden, und mit jeder Auswahl wird ein anderer zusammengesetzter Klangausdruck gebildet, wie im folgenden Beispiel gezeigt.

Der zusammengesetzte Klangwert des Ausdrucks wird berechnet Ersetzen der ersten beiden Operationen durch H-Operationen und die letzten beiden durch M-Operationen für die Schallkonstanten 

zusammengesetzter arrhythmischer Klangausdruck

quartäres rhythmisches Modul für

4.9 INTERAKTIVER VERBINDUNGSWERT VON E=x+3y−2z

Wenn im zusammengesetzten Modul sowohl Klang als auch numerische Konstanten ersetzt werden, ist der resultierende zusammengesetzte Klangausdruck interaktiv, da er eine physikalische Dynamik durch die numerische Konstante enthält, wie im folgenden Beispiel gezeigt.

Der zusammengesetzte Klangwert des Ausdrucks wird berechnet Ersetzen der ersten beiden Operationen durch H-Operationen und die letzten beiden durch M-Operationen für numerische Konstanten und klangvoll

zusammengesetzter arrhythmischer Klangausdruck

quartäres rhythmisches Modul für

4.10 ZAHLENWERT BESTEHEND AUS E=x+3y−2z

Wenn im zusammengesetzten Modul nur numerische Konstanten ersetzt werden, ist das Ergebnis eine numerische zusammengesetzte Gruppierung, wie im folgenden Beispiel gezeigt.

5. WISSENSCHAFTLICHE HYPOTHESEN DES AUTORS

Mit der Entwicklung der Harmonisierungsoperation entstanden einige wissenschaftliche Hypothesen, die vom Autor dieses Materials in dieser Studie für einige Naturphänomene aufgestellt wurden.

5.1 WELLE-TEILCHEN-DUUALITÄT DES LICHTS

Das Phänomen der Welle-Teilchen-Dualität des Lichts, bei der Licht entweder die Eigenschaft einer Welle oder eines Teilchens hat, kann durch die Operational Duality-Eigenschaft der Harmonisierungsoperation erklärt werden.

Es ist bekannt, dass Licht eine Harmonie ist, die durch mehrere Schattierungen von Lichtschwingungen im Betrieb Harmonisierung oder H gebildet wird , wobei die resultierende Amplitude eine Funktion der Additionsoperation zwischen den Amplituden dieser Schwingungen ist.

Je größer die Anzahl der Vibrationen bei diesem Vorgang ist, desto größer ist die resultierende Leuchtamplitude , Beeinflussung seiner Teilchenseite mit dieser Lichtenergiemenge, während seine Wellenform als Funktion der Unionsoperation zwischen den Frequenzen dieser Lichtschwingungen beibehalten wird , die die harmonische Gruppierung der Harmonie dieser Operation bilden , Beeinflussung seiner Wellenseite.

Durch die Länge dieser Wellen wird dieses Gleichgewicht zwischen diesen beiden Eigenschaften Welle und Teilchen aufrechterhalten, das bei einer Schallwelle aufgrund ihrer großen Wellenlänge im Verhältnis zur Lichtwelle nicht auftritt, wobei deren Seite überwiegt, relativ zur Bedeutungslosigkeit seiner Teilchenseite.

5.2 URSPRUNG DER DUNKLEN ENERGIE

Das Phänomen der im Universum existierenden Dunklen Energie kann eine Folge der Leeren Harmonie sein, das Ergebnis der Harmonisierungsoperation zwischen den Schwingungen entgegengesetzter leuchtender Teilchen, die die Leuchtkräfte dieser Schwingungen eliminieren , An seiner Stelle entsteht die Dunkelheit, die die Dunkle Energie ausmacht, wo die resultierende Frequenz dieser Harmonie in einem Zustand harmonischer Urschwingung (VPH) in einer harmonischen Leere, auch Quantenvakuum genannt, koexistiert.

5.3 DIE STRUKTUR DER ZEIT UND IHRE AUSDEHNUNGSKRAFT

Ein Zeitintervall besteht aus einer Periode , erstmalig gebildet und eine Endzeit , deren Unterschied zwischen ihnen misst ihre Dauer Diese Perioden sind nahtlos miteinander verbunden, wobei die Endzeit einer Periode gleich der Startzeit der nächsten Periode ist. und so weiter, die ein geschlossenes Zeitintervall von einer vergangenen Periode bis zu einer gegenwärtigen Periode bilden und am Beginn einer zukünftigen Periode offen sind und ihre Raumzeit bilden , was nach dem Melodieprinzip gleich der Operation M zwischen diesen vergangenen Perioden ist , Geschenk und Zukunft

Es ist auch bekannt, dass die anfängliche Zeit jeder Periode ist durch einen Beat gekennzeichnet , verursacht durch einen intrinsischen Impuls, gegeben durch eine Kraft von augenblicklicher Dauer bleibt eine Zeit der Stille bis zum Ende dieses Zeitraums gegeben durch die Differenz zwischen der Endzeit dieses Zeitraums und der Uhrzeit Prügel dieses Impulses

Daher kann durch die Operation M eine Periode zwischen ihrem Takt und ihrer Stillezeit definiert werden Ersetzen Sie die Perioden durch Ihre Beats in der Raumzeit Die rhythmische Kadenz der Raumzeit wird gebildet dessen Schlaggeschwindigkeit, genannt Rhythmisches Tempo ist umgekehrt proportional zu seiner Periode skaliert in Herzschlag pro Zeiteinheit.

Je kürzer dieser Zeitraum Je kürzer dieser Zeitraum Dieses Phänomen fördert mit seinem Einfluss auf die Raumzeit auch zwei Bewegungen in physischen Körpern, die sich in seinem Wirkungsbereich befinden, von denen eine Rhythmisches Dirigieren genannt wird wo ein Körper, ohne seine Ruheposition zu verlassen, den Schlägen des rhythmischen Fortschritt folgt  und ein anderes namens rhythmischer Tanz wo sich ein Körper von seiner Ruheposition zu anderen unterschiedlichen Positionen bewegt, auch als Funktion des rhythmischen Fortschritt dieser rhythmischen Kadenz.

Betrachtet man einen Zeitraum wobei die Stillezeit null ist o momentane Pulszeit stellt die kürzeste Dauer dar Daher gibt es eine abstoßende Kraft implizit in seiner Struktur, als schwach in seiner rhythmischen Kadenz in der Raumzeit angesehen jedoch in der Lage, jeden Himmelskörper im Universum wegzubewegen und mit seinem rhythmischen Tempo, dem rhythmischen Verhalten und den rhythmischen Tanzbewegungen zu fördern.

Es ist bekannt, dass sich das Universum ausdehnt und dass sich seine Galaxien voneinander entfernen, was durch die Zeitausdehnungskraft seiner rhythmischen Kadenz erklärt werden kann und wenn man bedenkt, dass die Umlaufbahnen von Galaxien um das Zentrum des Universums ungefähr elliptisch sind, erklärt sich ihre beschleunigte Ausdehnung noch nicht aufgrund dieser Annäherung an ihren Schwerpunkt, wo wahrscheinlich eine Harmonie von Schwarzen Löchern mit ihrer Anziehungskraft besteht Macht.

Diese Beschleunigung sollte jedoch aufhören zu existieren, nachdem sich die Galaxien von diesem Zentrum wegbewegt haben, mit einer Verlangsamung, und diejenigen, die die größten Umlaufbahnen erreichen, werden den instabilen Rand des Universums bilden, wie eine instabile Flüssigkeitsblase, da sie ihre Form als a ändern würden Funktion der Unendlichkeiten der maximalen Mittelpunkte dieser Galaxien in allen Richtungen relativ zum Zentrum des Universums.

5.4 DIE SINGULARITÄT DES URKNALLS UND DIE DUNKELHEIT DER RELIGIÖSEN THEORIE

Es ist bekannt, dass alle Materie von Atomen gebildet wird, die sich in ständiger Schwingung befinden, die wiederum von immer kleineren Teilchen gebildet werden, bis wir das kleinste aller Materieteilchen erreichen, das sogenannte Elementar- oder Urteilchen (ANJOS, kein Datum). dargestellt in dieser Studie durch eine einfache Schwingung mit deiner Frequenz Amplitude und kontinuierliche Zeit . Ebenso gibt es sein primordiales Antiteilchen von Antimaterie, mit der gleichen Frequenz die entgegengesetzte Amplitude und Gegenzeit oder harmonisch, das heißt, anstatt dass die Zeit in einer melodischen Kadenz von der Gegenwart in die Zukunft geht, kommt sie in einer harmonischen Kadenz von der Zukunft in die Gegenwart.

Diese leuchtenden Vibrationen in Operation H wird die Ureinheitliche Harmonie der Dunklen Energie, die in der Lage ist, die gesamte Energie von Materie und Antimaterie zu erzeugen, die in ihrer Struktur in einem Zustand der Primordial Harmonic Vibration oder in einer Harmonic Void enthalten ist, die von der Wissenschaft des Quantenvakuums auch genannt wird

Daher wird für jede Theorie des Ursprungs des Universums immer die Existenz eines Ursprungspunkts von allem, wie der Urknall-Singularität, der Dunkelheit der religiösen Theorie (Bibel) oder irgendetwas anderem, zugegeben, der immer zu führt Ureinheitliche Harmonie der Dunklen Energie in der Lage, die gesamte Energie für die Bildung des Universums der Materie zu erzeugen in der rhythmischen Kadenz der kontinuierlichen Zeit mit ihrer Expansionskraft sowie alle Energie in der Bildung des Antimaterie- oder immateriellen Universums in der rhythmischen Kadenz der harmonischen Zeit, genannt “Gottes Zeit”, mit ihrer unendlichen Anziehungskraft.

5.5 DIE NULLZEIT DER SCHÖPFUNG DES UNIVERSUMS

Eine noch so kurze Zeitspanne wird immer durch eine Anfangszeit mit einem Schlag gebildet , von einer Kraft gebildet und eine Schlagdauerzeit größer als null

In Anbetracht dieser Anfangszeit kann man sagen, dass das Universum seinen Anfang in einem augenblicklichen Schlag hatte aber bevor dieser Schlag passierte, gab es eine Null- oder Nullzeit und damit dies wahr ist, muss es zuerst eine Leere Ursprüngliche Harmonie geben , gebildet durch unendliche Wellen – Materieteilchen in Harmonie mit unendlichen Wellen – Antimaterieteilchen

In diesem Fall die kontinuierliche Zeit des materiellen Universums war auch in Harmonie mit seiner entgegengesetzten oder antikontinuierlichen Zeitform des Antimaterie-Universums, was zu Nullzeit oder Nullzeit führt in dieser Harmonie, voller Energie, angesammelt in einer einzigen Frequenz in Harmonic Primordial Vibration.

Betrachtet man die kürzestmögliche Zeit, um in einer Harmonie zu existieren, mit ihrem Takt, der von einer Kraft mit einer bestimmten Intensität gebildet wird es stellt sich heraus, dass Zeit ein Wellenteilchen ist, wo ist seine Amplitude und die Umkehrung Ihrer Schlagzeit ist Ihre Frequenz das in Harmonie mit seinem entgegengesetzten Wellenteilchen auch mit seiner entgegengesetzten Amplitude e deine Frequenz führt zu einer leeren Harmonie von Time Zero vom Anfang des Universums.

5.6 ALLMÄCHTIGE EINHEITLICHE HARMONIE

Bei der Bildung des Materiellen Universums bildete die kontinuierliche Zeit mit ihrer Expansionskraft die unzähligen einzelnen Materieteilchen durch ihre Kombinationen mit einem einzigen Urteilchen

Im Falle der Bildung des Antimaterie-Universums bildete die antikontinuierliche oder harmonische Zeit mit ihrer Anziehungskraft die Ureinheitliche Harmonie Er zieht alle ursprünglichen Anti-Vibrationen in einer einzigen Harmonie an, die in der Lage ist, ihre gesamte Struktur hervorzubringen und das immaterielle oder Antimaterie-Universum zu bilden daher allmächtige einheitliche Harmonie (Gott) genannt.

6. SCHLUSSBETRACHTUNGEN

Mit der Entwicklung der Harmonisierungsoperation und ihrer umgekehrten Melodiationsoperation war es möglich, eine mathematische Struktur zur Bewertung der musikalischen Eigenschaften einer Melodie sowie einer Harmonie zu schaffen, wodurch Musik nicht nur zu einer Kunst, sondern auch zu einem Teil der Wissenschaft wurde . .

Es wurde auch möglich, Algebra nicht nur mit numerischen Ausdrücken, sondern auch mit gesunden Ausdrücken zu verwenden, die die Algebra der Vibrationen bilden, mit Wechselwirkungen zwischen numerischen und gesunden Werten im Ergebnis eines algebraischen Ausdrucks, wodurch eine körperliche Handlung von a begleitet werden kann Melodie oder einer Harmonie oder sogar einer Melodie, die von einer Harmonie begleitet wird

Eine neue Betrachtungsweise des Universums wurde auch vorgeschlagen, durch eine Makro- und Mikroperspektive, durch die Konzeption der Strukturen harmonischer und melodischer Schwingungen, da alles Schwingung ist. Daher wurden einige der vom Autor dieses Materials aufgestellten Hypothesen für einige Fragen nachgewiesen, die für die Wissenschaft noch unbeantwortet sind, wie z. B. die Existenz Gottes.

VERWEIS

ANJOS, Talita Alves dos. Partículas elementares. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/fisica/particulas-elementares.htm. Acesso em 21/03/2022.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

MORAIS, Gustavo. Teoria musical para iniciantes: você sabe o que são os acordes? Terra, julho de 2020. Disponível em: https://www.terra.com.br/diversao/musica/teoria-musical-pra-iniciantes-voce-sabe-o-que-sao-os-acordes,7c62b1fa5e0fe37c8e0180310bc04200tnys05tj.html Acesso em: 20/03/2022.

SILVA, Domiciano Correa Marques da. Interferência de ondas. Brasil Escola. s.d. Disponível em: https://brasilescola.uol.com.br/fisica/interferencia-ondas.htm. Acesso em 17/03/2022.

SANTOS. Marco Aurélio da Silva. A Sensibilidade Auditiva. Mundo da educação. Disponível em: https://mundoeducacao.uol.com.br/fisica/a-sensibilidade-auditiva.htm. Acesso em: 20/03/2022.

^[1] Abgeschlossenes Studium der Elektrotechnik. Elektronik von der Bundesuniversität Pará-UFPA. ORCID: 0000-0001-7010-9114.

Gesendet: Februar 2022.

Genehmigt: März 2022.