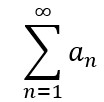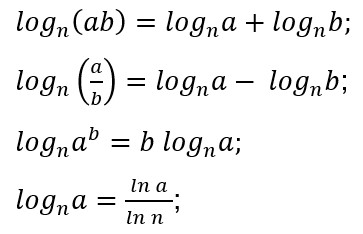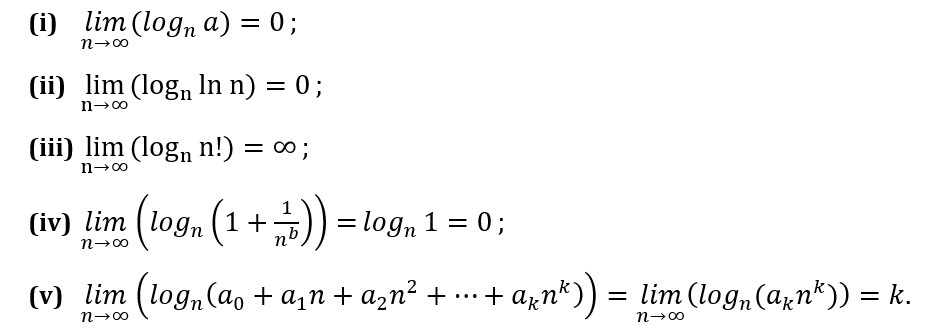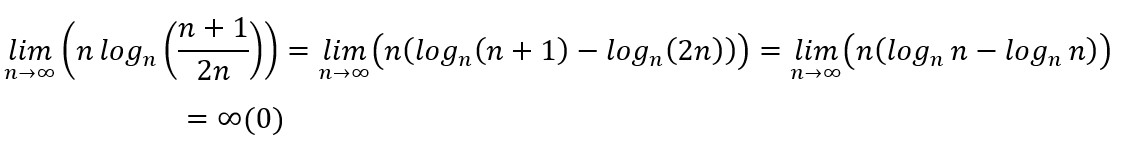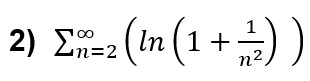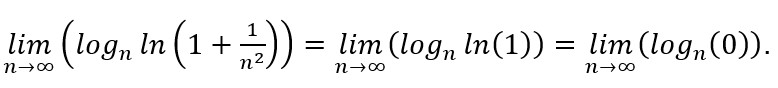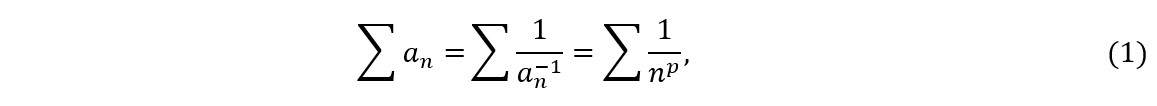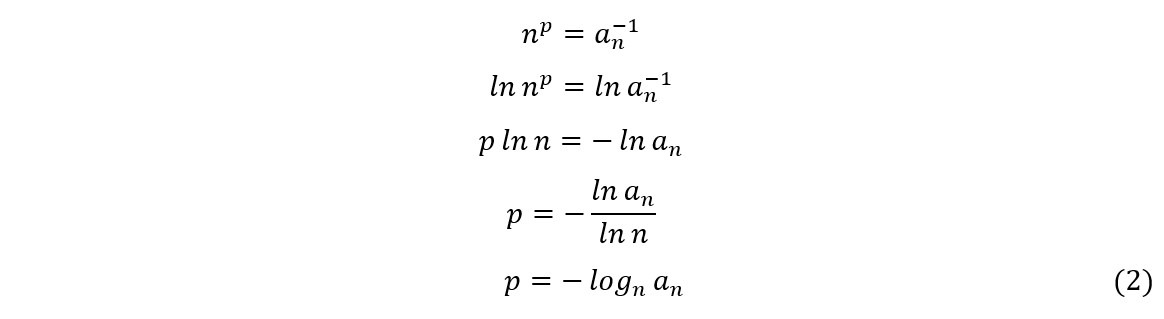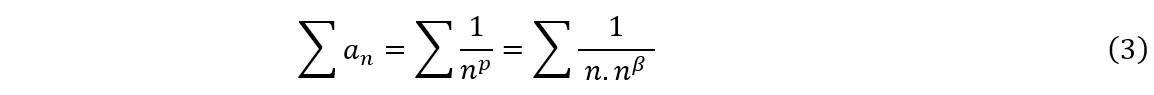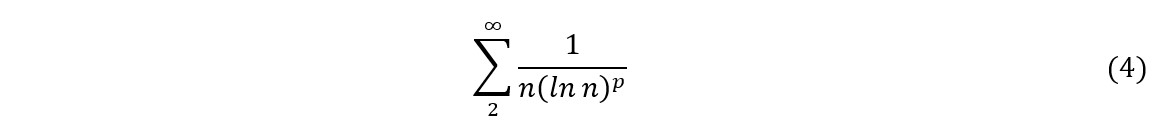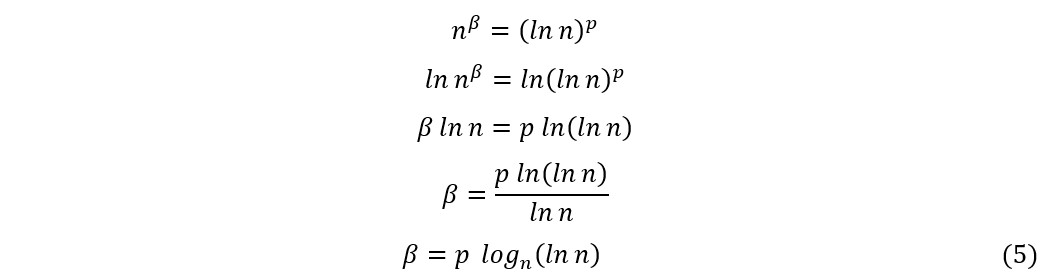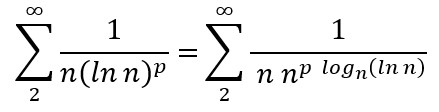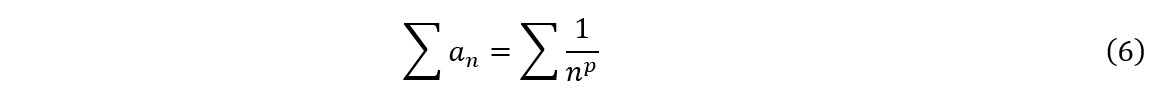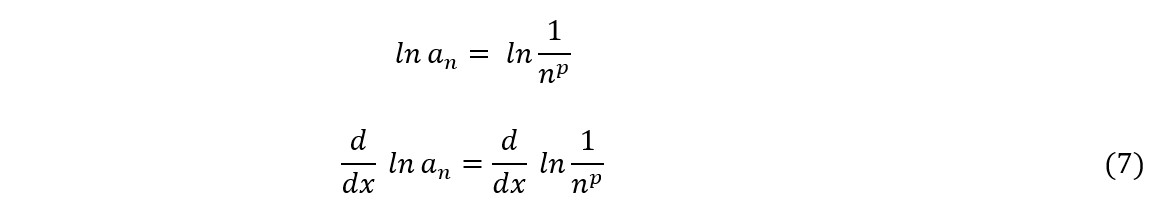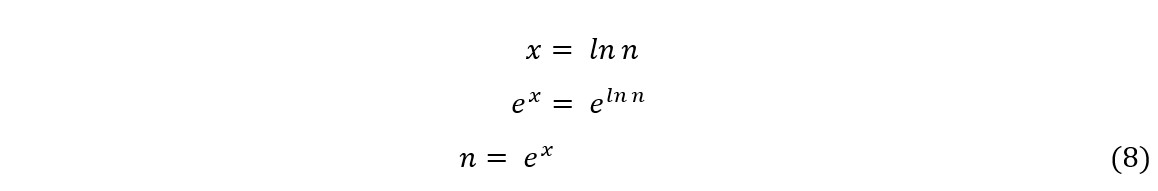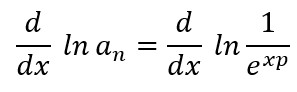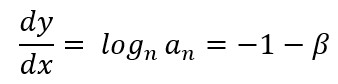Teste do logaritmo enésimo para a verificação da convergência absoluta de séries

ARTIGO ORIGINAL

MORAIS, Cláudio Marcelo ^[1]

MORAIS, Cláudio Marcelo. Teste do logaritmo enésimo para a verificação da convergência absoluta de séries. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 08, Ed. 09, Vol. 01, pp. 78-97. Setembro de 2023. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/logaritmo-enesimo, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/logaritmo-enesimo

RESUMO

Neste artigo apresento um teste de convergência absoluta para séries numéricas infinitas utilizando o conceito de logaritmo de base n indeterminada. Embora haja casos em que o presente teste seja de difícil aplicação e outros onde podem ser obtidos resultados inconclusivos, ele deve ser visto como um recurso adicional que os estudantes de matemática poderão utilizar ao lado dos testes já disponíveis para verificação da convergência absoluta de uma série.

Palavras-chave: Convergência, Séries, Teste.

1. INTRODUÇÃO

Nos cursos de cálculo, ao se deparar com o estudo de séries infinitas, o estudante é apresentado a uma variedade de testes para verificar se uma série numérica converge para um certo valor ou se ela diverge, i.e., se a soma de seus termos tenderá a um valor finito (L) ou se tenderá para mais infinito ou menos infinito, quando o número de termos (n) da série também tender ao infinito (∞).

Uma série infinita consiste em uma sequência de termos ordenados, geralmente em ordem decrescente, somados entre si. Uma série infinita, ou simplesmente uma série, pode ser expressa na forma:

Onde as reticências no final indicam que os termos da série continuam de modo que n tenda ao infinito. A série também pode ser expressa de maneira mais compacta utilizando a notação sigma:

Através da análise do termo geral  podemos saber se a série converge ou não. Para isso, foram criados inúmeros testes de convergência, tais como: teste da comparação, teste da razão, teste da integral, teste da raiz etc. (Simmons, 1996). A minha proposta neste artigo é apresentar um teste que sirva como mais uma opção ao alcance do estudante de matemática na determinação da convergência absoluta de uma série numérica infinita.

2. LOGARITMO DE BASE N

2.1 DEFINIÇÃO DE LOGARITMO ENÉSIMO

O conceito de logaritmo foi introduzido pelo matemático escocês John Napier em 1614 e pode ser considerado um dos maiores avanços científicos do século XVII, tornando mais fácil a vida de quem precisava fazer cálculos numéricos numa época em que ainda não havia máquinas calculadoras disponíveis. Nesse sentido, a sua importância chega mesmo a ser comparada com o avanço trazido pelo sistema numérico decimal desenvolvido pelos indianos (Hobson,1914). Embora o advento dos computadores e das calculadoras eletrônicas tenha mudado a forma como as pessoas fazem cálculos, o logaritmo, estudado como uma função, ainda mantém a sua importância teórica indispensável para a matemática e suas aplicações (Simmons, 1996). A função logarítmica pode ser descrita na forma

onde x é um número real positivo, denominado logaritmando, eé um número real positivo e diferente de 1, denominado base do logaritmo. O valor deacaba por nomear o tipo de logaritmo: para , temos o logaritmo de base dois, para , temos o logaritmo de base 3 e assim por diante. Os logaritmos de base 10 e de base, dada a importância que têm, recebem nomes especiais: o logaritmo de base 10 é chamado de logaritmo decimal ou logaritmo comum, enquanto chamamos de logaritmo natural, ou neperiano, ao de base , onde  é um número irracional que vale aproximadamente 2,718281828.

Definiremos o logaritmo de base, ou logaritmo enésimo, de um número, como o logaritmo de base indeterminada. Assim, seja um número real, podemos escrever

Ao contrário do que ocorre com os logaritmos de base determinada, não é possível obter o valor do logaritmo enésimo de um número, uma vez queé desconhecido. A princípio isso pode não parecer muito útil, porém o intuito aqui é o de usarmos o logaritmo enésimo para realizar operações sobre os termos gerais das séries, onde n se torna a variável indexada pelo operador sigma. Assim, tentaremos implementar um método para testar se uma série converge ou não, buscando nos beneficiar das propriedades operacionais dos logaritmos onde isso for possível.

2.2 OPERAÇÕES COM LOGARITMOS ENÉSIMOS

O logaritmo de base enésima possui as mesmas propriedades operacionais dos demais logaritmos, pois obedecem às regras do produto, do quociente, da potência e da mudança de base, como segue:

3. TESTE DE CONVERGÊNCIA

3.1 DESCRIÇÃO DO TESTE

A partir de agora vamos propor um teste para verificação da convergência absoluta de séries baseado no uso do logaritmo enésimo. Assim, dada uma série infinita de termos não-negativos, começaremos por encontrar o logaritmo enésimo do seu termo geral a_n e, caso a variável n ainda permaneça, iremos calcular o limite daquele logaritmo, com n tendendo ao infinito, se tal limite existir. Dito isto, o teste se dará da seguinte forma:

A aplicação do teste sem a necessidade do uso de limites só se dará naqueles raros casos em que o termo geral da série seja composto apenas por potências de n com expoentes numéricos. Nos demais casos, teremos que recorrer invariavelmente ao uso de limites. É interessante notar que, ao usarmos a forma log_n(a_n) em lugar da forma equivalente ln (a_n)/ln n, muitas vezes poderemos calcular o limite do termo geral aplicando as propriedades dos logaritmos, evitando cair na indeterminação do tipo ∞/∞. Entretanto, em outras ocasiões, ao calcularmos o logaritmo enésimo do termo geral, ainda assim iremos chegar a algum tipo de indeterminação, de modo a não ser possível conhecermos o valor do limite. Nestes casos será necessário aplicar a regra de L’Hopital ao logaritmo enésimo na forma equivalente ln (a_n)/ln n para eliminar a indeterminação, porém esse procedimento geralmente é trabalhoso a ponto de não ser recomendado seguir adiante, pois provavelmente um ou mais testes já conhecidos serão mais adequados para testar a convergência da série.

3.2 ALGUNS EXEMPLOS DE USO DO TESTE

3.2.1 CÁLCULO DIRETO DE log_n a_n

Nos casos mais simples, o termo geral (a_n) é composto apenas da variável n elevada a alguma potência numérica inteira ou fracionária. Dessa forma não será necessário o cálculo de nenhum limite para aplicar o teste de convergência.

3.2.2 CASOS EM QUE O LIMITE DE log_n a_n É FÁCIL DE SER CALCULADO

Vamos destacar agora alguns casos em que os limites do logaritmo enésimo do termo geral são relativamente fáceis de se calcular, i.e., vamos considerar casos onde não haja indeterminação no cálculo dos limites e onde apareça um dos seguintes resultados triviais:

Esses resultados podem ser facilmente obtidos pelo estudante, uma vez que em (i) o valor do logaritmo de uma constante (a) vai tendendo a zero à medida que n tende ao infinito. No caso (ii), onde a constante é substituída pelo logaritmo natural de n, o valor de ln n cresce muito mais lentamente que n, de modo que o logaritmo enésimo acaba por também tender a zero. No caso (iii) ocorre o contrário, uma vez que n! cresce rápido demais em relação a n, fazendo com que o logaritmo acabe por tender ao infinito. Em (iv), a fração tende a zero quando n tende ao infinito. Por fim, em (v), o termo de maior grau do polinômio determina o comportamento final do limite à medida que n tender ao infinito. Vejamos alguns exemplos:

3.2.3 ALGUNS LIMITES NOTÁVEIS

No cálculo do limite de log_n a_n é muito comum a indeterminação do tipo (∞)(0). Para lidarmos com esse tipo de indeterminação, foram listados a seguir alguns resultados que podem ser memorizados com facilidade e que nos permitirá aplicar o teste do logaritmo enésimo a um grande número de séries de maneira bastante direta. Vejamos:

No caso (i), o limite também é fácil de se obter, uma vez que n cresce assintoticamente mais rápido que , à medida em que n tende ao infinito. Assim, não sendo a=1, o que faria o logaritmo ser igual a zero para todo n, teremos o logaritmo fornecendo um sinal positivo ou negativo para o limite, conforme a seja maior ou menor que 1. Em (ii), embora o comportamento do limite possa não ser tão evidente quanto em (i), pode-se dizer que o expoente p está associado à rapidez com que o limite tende a zero, enquanto b está associado à rapidez com que o limite tende ao infinito. O mesmo raciocínio se aplica ao caso (iii). Vejamos alguns exemplos:

3.3 ALGUMAS OBSERVAÇÕES

(i) Existem casos em que a simples mudança na ordem das operações pode eliminar uma indeterminação. Vejamos um exemplo:

Numa primeira tentativa, aplicamos a propriedade do logaritmo do quociente antes de calcular o limite, chegando assim a uma indeterminação:

Por outro caminho, calculamos primeiramente o limite entre parênteses e depois usamos o resultado visto no item 3.2.3 (i) e verificamos que a série converge:

(ii) Em algumas situações, ao calcularmos o limite de , aplicando as propriedades operatórias dos logaritmos, chegaremos a log_n0 ou a alguma indeterminação, como a diferença entre infinitos, o produto de infinito por zero, o quociente entre infinitos, o quociente entre zeros ou a razão entre zero e infinito. Entretanto, isso não significa necessariamente que o limite não exista. Isso significa apenas que o teste do logaritmo enésimo não é uma forma prática para se determinar a convergência ou não da série, pois para isso, seria necessário aplicar a regra de L’Hopital ao logaritmo enésimo na sua forma ln(a_n)/ln(n), incluindo-se aí outras manipulações algébricas que se fizerem necessárias. Nestes casos, frequentemente encontraremos um teste já existente que seja menos trabalhoso de se aplicar. Por exemplo, sabemos que a série a seguir converge para aproximadamente 1,29686:

Aplicando-se o teste do logaritmo enésimo, trabalhando-se apenas com as propriedades dos logaritmos, chega-se ao seguinte resultado:

Entretanto, após aplicarmos a regra de L’Hopital a ln(a_n)/ln(n) e efetuarmos algumas operações envolvendo limites, encontramos que:

Portanto, a série converge conforme esperado. A convergência dessa série pode ser mais facilmente verificada aplicando-se o teste da comparação com limite.

4. DISCUSSÃO DO TESTE

4.1 DEDUÇÃO

O presente teste consiste basicamente em realizar o teste de comparação com a série  por intermédio do uso do logaritmo de base enésima, assim, espera-se obter uma facilidade de cálculo onde as propriedades operatórias dos logaritmos (ver secção 2.2) puderem ser utilizadas, seja através da aplicação direta daquelas propriedades, seja em conjunto com a noção de limite de uma função. Para iniciarmos a nossa dedução, vamos considerar os casos em que se é possível realizar o cálculo direto do logaritmo do termo geral (ver 3.2.1). Primeiramente vamos escrever o termo geral como o inverso de uma potência de n:

Onde n é um inteiro e p é um número real. A partir das igualdades acima, teremos:

Substituindo (2) em (1), teremos:

Como sabemos (Simmons, 1996), se p>1, a série converge. Se p≤ 1, a série diverge. Finalmente, substituindo p por — nessas desigualdades e multiplicando ambos os lados por , teremos que a série:

4.2 QUANDO O TESTE É INCONCLUSIVO

Na seção 3.2.1, vimos os casos em que log_n a_n é calculado diretamente. Porém, como vimos logo em seguida, frequentemente ainda ficaremos com a variável n após ser calculado o logaritmo enésimo do termo geral de uma dada série. O uso da noção de limite permite-nos estender a aplicabilidade do teste, pois quando calcularmos o limite do logaritmo à medida que n tende ao infinito, poderemos usar o valor desse limite como o resultado do teste para saber se a série converge ou não (ver seção 3.1). Entretanto, essa vantagem tem um certo preço, pois há casos em que esse limite nos fornece um resultado que torna o teste inconclusivo.

O fato de uma série convergir ou não, depende da rapidez com que o termo geral tende a zero (Simmons, 1996). Se ordenarmos as séries partindo daquelas que convergem mais rapidamente, para as que convergem cada vez mais lentamente, passando a seguir para as séries que divergem mais lentamente e indo em direção àquelas que divergem cada vez mais rápido, poderemos delimitar o intervalo entre as séries como o intervalo onde ocorre a transição das séries convergentes para as séries divergentes. Vamos escrever as séries desse intervalo usando um expoente auxiliar β, tal que β seja uma função de n, como segue:

Assim, se , então temos p>1 e a série converge. Se , então temos p<1 e a série diverge. Todavia, se , a convergência ou não da série dependerá da velocidade com que β tender a zero, i.e., a série convergirá desde que β tenda a zero suficientemente rápido. Por exemplo, pelo teste da integral (Simmons, 1996) pode-se verificar que a série a seguir diverge para p=1 e converge para p>1:

Calculando-se o expoente β para essa série, teremos:      

 Substituindo (5) em (3) e igualando a (4), obtemos:

Como calculado em (5) é igual a zero para todo p, concluímos que  para todo p. Mas, como sabemos, para certos valores de p a série converge e, para outros, ela diverge. Assim, podemos ver que o teste do logaritmo enésimo é inconclusivo nesses casos[3], pois tanto pode haver séries convergentes quanto divergentes para as quais o teste resulta em —1. Vejamos alguns exemplos:

5. O LOGARITMO ENÉSIMO COMO DERIVADA

Uma maneira que pode ser muito interessante para o estudante visualizar o comportamento de uma série é através do uso de gráficos com escalas logarítmicas. Nesses gráficos, as séries cujos termos gerais são formados por potências de n com expoentes exclusivamente numéricos se apresentam como retas e, quanto mais rapidamente uma série divergir, menor será a inclinação daquela reta. Assim, as séries que divergem rapidamente dão origem a retas que se aproximam mais da horizontal quando comparadas com as retas traçadas a partir das séries que divergem de modo mais lento. Por outro lado, quanto mais rapidamente a série convergir, mais inclinada será a sua reta no gráfico, i.e., ela estará mais próxima da vertical que outras que convergem mais lentamente. Já os gráficos das séries cujo termo geral apresenta expoentes que são funções da variável indexada n, de um modo geral apresentam-se inicialmente como curvas exponenciais, mas à medida que n vai tendendo ao infinito, os gráficos vão se aproximando de linhas retas. O gráfico da figura 1 a seguir foi traçado com os eixos em escala logarítmica natural e ilustra alguns exemplos do que foi dito. Nele, as séries convergentes estão indicadas com cv e as divergentes com dv. Logo à primeira vista, pode-se perceber como as duas séries mais à esquerda, com expoente n, convergem rapidamente, se aproximando da vertical, enquanto, na parte de cima, temos algumas séries que divergem.

Figura 1: Gráfico de Figura 2: Gráfico ln a_n vs. ln n para algumas séries

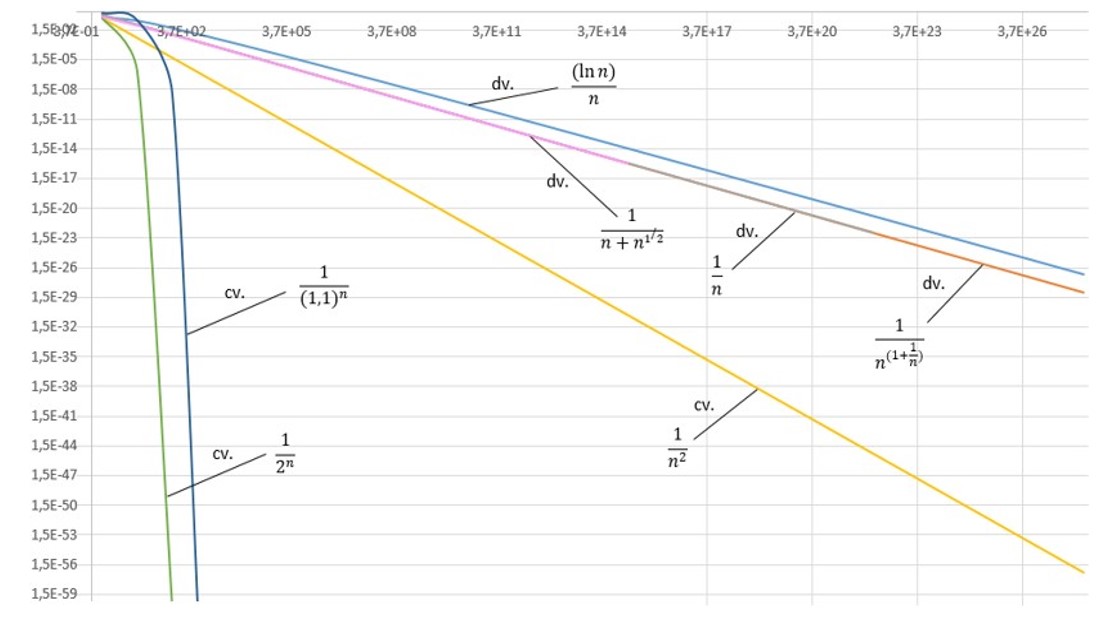
Quanto mais rapidamente a série divergir, mais próximo da horizontal será a sua reta no gráfico. Nota-se ainda como duas das séries apresentadas, contendo expoentes fracionários, divergem de maneira praticamente idêntica à série de termo geral 1/n, mostrando como o expoente fracionário influencia muito pouco o comportamento daquelas séries.  Particularmente acredito que esse tipo de visualização pode ser um instrumento útil do ponto de vista didático ao se introduzir o conceito de convergência de uma série. Vamos agora ver como o logaritmo enésimo está relacionado a este tipo de gráfico.

Na figura 2 temos o gráfico de ln a_n versus ln n, onde a curva representa a progressão dos termos de uma série à medida que n tende ao infinito e cuja forma geral já vista anteriormente é dada por:

Figura 2: Gráfico ln a_n vs. ln n

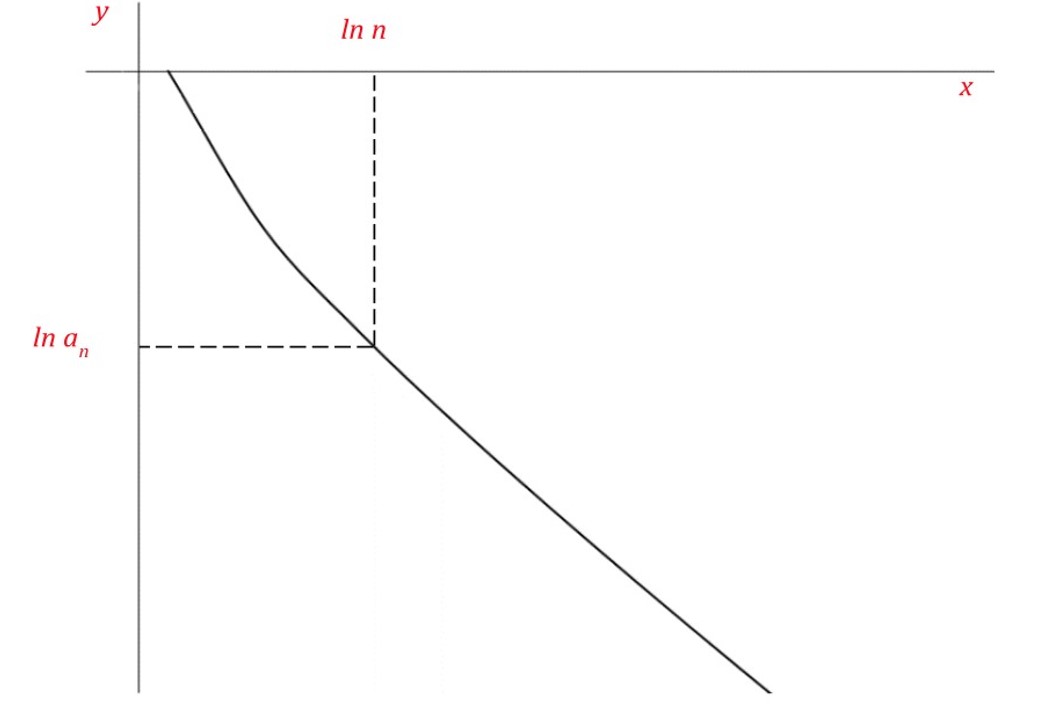
Tomando-se o termo geral e calculando a derivada do logaritmo natural de cada lado, teremos

A partir do gráfico, fazendo-se x = ln n, teremos

Substituindo (8) em (7), fica:

Finalmente, substituindo-se ln a_n por y e calculando a derivada do termo à direita, teremos:

Entretanto, já sabemos que o logaritmo enésimo do termo geral em (6) é , logo, podemos escrever:

Ou seja, o logaritmo enésimo do termo geral é igual à derivada da curva da série no gráfico de ln a_n x ln n. Se substituirmos p por 1+β, sendo β uma função de n, podemos escrever:

Ao calcularmos e encontrarmos um valor real δ, significa que o gráfico tende a uma reta com coeficiente angular . Assim, desde quenão tenda a , o logaritmo enésimo nos fornecerá o coeficiente angular da reta que se forma no gráfico ln a_n vs. ln n à medida que ln n tender ao infinito.

6. CONCLUSÃO

O uso do logaritmo de base n para saber se uma série infinita converge absolutamente ou não, pode ser uma alternativa interessante aos métodos já existentes, desde que o limite do logaritmo enésimo do termo geral da série, caso seja necessário o seu cálculo, possa ser obtido de maneira relativamente fácil. Para aplicar o teste podemos nos valer não só das propriedades operacionais dos logaritmos como também de alguns resultados básicos já conhecidos. Nos casos em que a indeterminação persista, ela poderá ser eliminada aplicando-se a regra de L’Hopital ao logaritmo enésimo do termo geral na forma ln(a_n)/ln(n), mas nesses casos geralmente o esforço não valerá à pena, pois provavelmente haverá um ou mais testes já conhecidos que podem ser utilizados para determinar a convergência de maneira mais rápida. Ao traçarmos o gráfico de uma série com os eixos em escala logarítmica natural, podemos ver que o logaritmo enésimo do termo geral em um ponto qualquer do gráfico nada mais é do que a derivada da curva naquele ponto.

REFERÊNCIAS

HOBSON, Ernest William. John Napier and the invention of logarithms. Cambridge: The University Press, 1914.

SIMMONS, George Finlay. Calculus with analytic geometry. 2. ed. New York: McGraw-Hill, 1996.

APÊNDICE – NOTA DE RODAPÉ

2. Na seção 4.2 discutiremos melhor essa condição.

3. Este caso, embora apresente apenas uma família específica de séries formada à medida que se varia o expoente p, é condição suficiente para demonstrar o caráter inconclusivo do teste quando o seu resultado, obtido por meio do limite, for . Entretanto, seria interessante mostrar que o caso n(ln n)^p, com p>1, não é uma exceção, i.e., mostrar que existem outras séries convergentes cujo logaritmo enésimo do termo geral seja , uma vez que encontrar séries que divergem é relativamente fácil.

^[1] Graduado em Física pela Universidade Federal de Minas Gerais (2000); Especialização em Instrumentação e Controle de Processos pelo Serviço Nacional de Aprendizagem Industrial-SENAI; Habilitação profissional de Técnico em Eletrônica pelo Instituto Monitor S/C Ltda. ORCID: 0009-0001-4633-3914. Currículo Lattes: http://lattes.cnpq.br/9333737637565760.

Enviado: 10 de julho, 2023.

Aprovado: 23 de agosto, 2023.