Jogos pedagógicos como proposta de intervenção no ensino das funções exponenciais

ARTIGO ORIGINAL

QUARESMA, Marli Pantoja ^[1], FRANÇA, Elma de Jesus ^[2], COSTA, Bruno Sebastião Rodrigues da ^[3]

QUARESMA, Marli Pantoja. FRANÇA, Elma de Jesus. COSTA, Bruno Sebastião Rodrigues da. Jogos pedagógicos como proposta de intervenção no ensino das funções exponenciais. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 01, Vol. 05, pp. 131-147. Janeiro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/proposta-de-intervencao

RESUMO

O presente artigo tem como objetivo apresentar alguns jogos para auxiliar no ensino do conteúdo de Função Exponencial, como alternativas facilitadoras para o processo de ensino e aprendizagem, com o intuito de contribuir de forma positiva com as habilidades propostas na Base Nacional Comum Curricular (BNCC), a qual está inserida no processo em questão. Por meio dos jogos, existe a possibilidade de os alunos despertarem interesse pelos conteúdos propostos em sala de aula, proporcionando uma aula com mais entusiasmo e dinamismo, contribuindo assim com a prática docente. Neste sentido, o problema de pesquisa surgiu a partir da seguinte questão: Os jogos pedagógicos para o ensino de Matemática são eficientes para proporcionar uma aprendizagem produtiva e significativa para o aluno no que tange ao conteúdo das funções exponenciais? Para tal, é interessante adotar essas práticas como objetos permanentes de estudo, implementação e ampliação da capacidade de criação e articulação com uma proposta que valorize uma educação de qualidade. Dessa forma, apresenta-se neste artigo uma sequência de atividades lúdicas para alunos do 1° ano do Ensino Médio, a fim de auxiliar no conteúdo de Função Exponencial de forma dinâmica, facilitando o processo de ensino e aprendizagem. A proposta metodológica foi embasada por meio de pesquisas bibliográficas e observações de vivências profissionais no período de 2018-2020. Como resultado ficou constatado que os jogos lúdicos para o Ensino da Matemática, como proposta de intervenção, são eficientes, pois é atrativa na medida em que proporciona uma proximidade significativa com a aprendizagem dos alunos para o aprendizado do conteúdo de Funções Exponenciais.

Palavras-chave: Ensino e Aprendizagem, Funções Exponenciais, Jogos.

1. INTRODUÇÃO

Ao longo dos anos, o ensino de Matemática vem proporcionando aos alunos diversas metodologias de aprendizado, uma delas é a ludicidade. Diante disso, é importante apresentar os conteúdos por meio dessa metodologia, considerando as habilidades relativas aos processos de investigação, de construção de modelos e de resolução de problemas que o aluno necessita adquirir ao longo das atividades a serem desenvolvidas, assim como os conhecimentos subsunções que o aluno possui.

Segundo Moreira (1999) o processo ideal de aquisição de conhecimento ocorre quando uma nova ideia se relaciona aos conhecimentos prévios do estudante, motivado por situações que faça sentido. Com isso o aluno amplia, avalia, atualiza e reconfigura a informação anterior transformando-a em nova.

Mas o que se percebe é que muitas vezes os conteúdos são trabalhados somente por meio de aulas expositivas, sem o auxílio de um material pedagógico que contribua e facilite o aprendizado do aluno. No entanto, por intermédio dos jogos é possível contribuir para um processo de aprendizagem mais efetivo no desenvolvimento dos alunos durante seu aprendizado, pois proporciona um clima propício à aprendizagem como ressalta as autoras Modesto e Rubio (2014, p.4) o lúdico, ferramenta importante na mediação do conhecimento, estimula a criança enquanto trabalha com material concreto, jogos.

É essencial o acompanhamento do educador para promover o processo de ensino e aprendizagem com qualidade, que desperte o interesse do aluno em seu processo de construção do conhecimento. Para tanto, realizou-se a pesquisa bibliográfica e observações durante à vivência profissional no período de 2018-2020, o embasamento teórico adveio de obras de autores como D’Ambrósio (2003), Turrioni (2004), Montibeller (2003) e Brasil (1996) que subsidiaram o desenvolvimento da pesquisa. O problema de pesquisa surgiu a partir da seguinte questão: Os jogos pedagógicos para o ensino de Matemática são eficientes para proporcionar uma aprendizagem produtiva e significativa para aluno no que tange ao conteúdo das funções exponenciais?

O trabalho tem como objetivo apresentar alguns jogos como proposta para ensinar o conteúdo de Função Exponencial, como alternativa facilitadora para o processo de ensino e aprendizagem, uma vez que estes podem contribuir efetivamente com o processo de desenvolvimento do aluno, facilitando a compreensão dos conteúdos apresentados. Nessa perspectiva:

Os jogos constituem uma forma interessante de propor problemas, pois permitem que estes sejam apresentados de modo atrativo e favorecem a criatividade na elaboração de estratégias de resolução e busca de soluções. Propiciam a simulação de situações-problema que exigem soluções vivas e imediatas, o que estimula o planejamento das ações (BRASIL, 1998, p. 47).

Segundo D’Ambrosio (2003), entende-se que o jogo é da natureza do ser humano, pois do seu nascimento até o início da sua vida escolar, ele aprende a brincar, e é através da brincadeira que o professor, como mediador para o conhecimento, poderá facilitar o processo de ensino e aprendizagem dos alunos, oportunizando o relacionamento do jogo com o conteúdo estudado.

No que diz respeito ao tema sugerido é importante adotar essas práticas como objetos permanentes de estudo, implementação e ampliação da capacidade de criação e articulação com uma proposta que valorize a educação em todos os aspectos metodológicos. Mas para se atingir os objetivos é preciso um comprometimento em conjunto da equipe que faz parte da escola, explorando novas possibilidades de modo a produzir um ensino significativo e de qualidade para a vida dos alunos.

Nessa perspectiva, com o presente artigo propomos trabalhar as Funções Exponenciais por meio de jogos como uma proposta de intervenção, contribuindo assim com o processo de aprendizagem do aluno. Visto que, os jogos proporcionam aos alunos, o interesse pelos conteúdos ensinados, levando-os a participar das aulas com mais entusiasmo.

Diante disso, percebemos que o baixo rendimento dos alunos, mensurados através de avaliações externas, como PROVA BRASIL[4], o Sistema de Avaliação da Educação Básica (SAEB)[5] e Exame Nacional do Ensino Médio (ENEM)[6], além dos fatores extra escolares como condição social e escolaridades dos pais podem interferir diretamente no rendimento dos alunos, o que nos desafia a desenvolver e incentivar os educadores a utilizar os jogos pedagógicos como proposta de intervenção no ensino de Função Exponencial contribuindo assim com o ensino e aprendizagem dos alunos.

Utilizar jogos como instrumento pedagógico não se restringe a trabalhar com jogos prontos, nos quais as regras e os procedimentos já estão determinados; mas, principalmente, estimular a criação, de jogos relacionados com os temas abordados no contexto da sala de aula (BRASIL, 2006, p.28).

Dessa forma, apresenta-se neste artigo uma sequência de atividades, com o intuito de favorecer a compreensão de Função Exponencial de maneira facilitadora e dinâmica, no qual as habilidades referentes aos objetos de conhecimentos sejam alcançadas, facilitando assim o aprendizado do aluno.

2. DESENVOLVIMENTO

Durante as vivências nos espaços de sala de aula, percebe-se que os alunos apresentam dificuldades no conteúdo do componente curricular de Matemática, dado que, essas aulas são ministradas segundo Vitti (1999, p.19) sem o apoio de um instrumento pedagógico concreto que desperte no aluno o interesse de compreender o que o professor está apresentando. Pois os instrumentos como o material concreto facilita o aprendizado e a compreensão. Nesse sentido, Turrioni (2004) afirma que:

O material concreto exerce um papel fundamental na aprendizagem, facilitando a observação e a análise, além de desenvolver o raciocínio lógico, crítico e científico, é fundamental para o ensino experimental e é excelente para auxiliar ao aluno na construção de seus conhecimentos (TURRIONI, 2004, p.66).

Diante disso, entende – se que a Matemática está presente no cotidiano e desempenha papel importante na vida das pessoas, ajudando a resolver inúmeras situações. Pois, ao longo da história da humanidade o ser humano construiu seus conceitos matemáticos por meio da utilização de objetos como pedra, sementes e palitos.

Isso evidencia a utilização do conceito matemático no dia a dia das pessoas, no qual já era presenciado em épocas passadas, sem a utilização de tais conceitos, ou seja, o homem usava instrumentos que possibilitava a compreensão de números, e dessa forma conseguia se organizar e atingir seus objetivos.

Os jogos matemáticos desenvolvem o raciocínio dos alunos e suas habilidades, levam a compreender e entender a matemática como uma disciplina prazerosa, pois com os jogos os alunos encontram equilíbrio entre o real e o imaginário, ampliando assim os seus conhecimentos (MONTIBELLER, 2003, p. 23).

Segundo a Lei de Diretrizes e Bases (LDB) 9394/96 o ensino da Matemática nas escolas não deve se distanciar dos seus principais objetivos, entre os quais está a construção da cidadania, o preparo para o mundo do trabalho e o desenvolvimento cognitivo.

Por essa razão, os jogos com seu caráter lúdico se tornam importante para o ser humano em qualquer idade. Propiciar situações com jogos é instigar no prazer, no desafio e no melhor desempenho dos alunos nas aulas de matemática.

Segundo alguns estudiosos, a aprendizagem é um processo integrado que provoca uma transformação qualitativa na estrutura mental daquele que aprende. O processo de construção do conhecimento se dá em base sólida de acordo com a afetividade que se tem perante o objeto de estudo e o desconhecido, pressupondo-se que todo desconhecido é novo e o novo tem que associar-se ao já aprendido, modificando-o e aumentando-o (PERRENNOUD, 2002, p. 35).

Portanto se faz necessário buscar alternativas que facilite a aprimore o aprendizado do educando, facilitando assim o processo de internalização dos objetos de conhecimentos nas diferentes etapas do processo de ensino e aprendizagem. Corroborando com o nosso pensamento, o autor Borin (1996, p.9) destaca que a introdução de jogos nas aulas de matemática é a possibilidade de diminuir bloqueios apresentados por muitos de nossos estudantes que temem a Matemática e sentem-se incapacitados para aprendê-la.

3. APRESENTAÇÃO DAS ESTRATÉGIAS LÚDICAS

Ao longo de décadas os jogos foram modificando as suas dinâmicas, e materiais utilizados com o intuito de contribuir para o processo de ensino e aprendizagem da Matemática, podemos usar como exemplo o conteúdo de Função Exponencial, tornando as aulas dinâmicas, motivadoras e facilitadoras.

3.1 O DOMINÓ COMO ESTRATÉGIA INTRODUTÓRIA PARA O ENSINO DE POTÊNCIA

No Brasil, o jogo do dominó, teria chegado com os portugueses no século XVI, transformando – se em entretenimento para os escravos. O dominó comumente possui 28 peças. No entanto, existem dominós com figuras, mais usados pelas crianças, facilitando o desempenho do jogo.

A riqueza desse material lúdico permite o seu aproveitamento como recurso pedagógico em diferentes níveis. Assim, este material, favorece uma série de desempenhos em um contexto educacional como o raciocínio lógico e aritmético dos alunos.  Como o dominó é uma atividade lúdica, compete ao professor investigar o conhecimento que seus alunos têm sobre o mesmo, pois ao jogar se constrói o contexto das descobertas, que poderá ser utilizada em recursos complementares, auxiliando o professor em sala de aula.

Sendo assim, as interações permitem momentos de comunicação e de construção de informações trabalhadas durante as aulas teóricas. A aprendizagem por meio de jogos, como dominó da potenciação, permite que o educando faça da aprendizagem uma ação interessante e prazerosa. Os jogos estão em correlação direta com o pensamento matemático. Pois, nos jogos temos regras, instruções, operações, definições, deduções, desenvolvimento, utilização de preceitos e operacionalizações (BORIN, 1996).

3.1.1 CONFECÇÃO DO JOGO

Para a produção dos jogos de dominós foi recortado 28 peças retangulares para cada jogo em E.V.A e assim se fez nas demais.

Para o primeiro jogo separou – se as 28 peças, e com a régua traçou – se uma linha vertical sobre cada peça, onde de um lado escreveram – se os valores de potenciação e do outro a base e seus expoentes.

Figura 1: Confeccionando o Dominó

Para o segundo jogo com 28 peças também se traçou uma linha vertical para colocar valores das bases e das propriedades como: produto de potência, quociente de potência, potência de uma potência e potência de um produto, e do outro lado a determinação dos cálculos das propriedades de potência.

Figura 2: Confeccionando o Dominó

Fonte: Acervo de pesquisa, 2020.

3.1.2 MANIPULAÇÃO DO JOGO

Os jogos de dominós, não seguiram a mesma estrutura do Dominó tradicional, visto que se fez necessário utilizar entre 2 a 4 participantes para praticar o jogo.

A seguir apresentaremos as regras, que serão válidas para os dois jogos:

Com as 28 peças, sobre uma superfície com as informações numéricas para baixo, o mesmo deve ser distribuído ao acaso pelos participantes.

1- Cada um dos dois alunos retira sete peças sem que o seu adversário as veja.

Observação: As demais peças restantes continuavam sobre a superfície, caso um dos jogadores não tenha os valores a peça a ser encaixada de ambos os lados, poderá comprar as peças restantes até encontrar o valor referente.

2- O jogo começa quando os participantes decidem no “par ou ímpar”, quem deve iniciar o mesmo.

Figura 3: Praticando o jogo de dominó da Potência

Para auxiliar no jogo, propõe-se o uso da calculadora como instrumento de facilitação. Visto que, os Parâmetros Curriculares Nacional (PCN)[7], no que tange o ensino da Matemática incentivam o uso da calculadora na sala de aula, pois além de ser um instrumento motivador, leva o estudante a perceber a importância do uso das tecnologias disponíveis na sociedade contemporânea. A calculadora pode, então, tornar – se um recurso didático facilitador na aprendizagem.

Outro documento regulamentador para o ensino da educação, a Base Nacional Comum Curricular (BNCC)[8], ressalta que a calculadora deve estar presente nas aulas de matemática, porém é imprescindível que esteja incorporado a situações que possibilitam reflexões, colaborando para a organização e formalização de conceitos matemáticos. Desse modo, o professor deve usar esse instrumento sempre que for favorável para o processo de ensino e aprendizagem do aluno.

Por isso as metodologias e novas propostas de ensino, surgem com o objetivo de propor metodologias inovadoras do ensino deste componente curricular, inclusive com a utilização de materiais concretos e tecnologias.

Neste contexto, o uso da calculadora, por meio de atividades permite ao estudante explorar esta ferramenta, investigar propriedades, verificar resultados, tomar decisões em contextos variados, pode ser tomado como uma dessas “novas” abordagens, embora, ainda hoje, o uso de tecnologia, na sala de aula, assusta muitos professores (OLIVEIRA, 1999; FEDALTO, 2006; GUINTHER, 2009). Entretanto, o desenvolvimento das tecnologias ocorre de forma muito rápida e a escola deve se antecipar ao que será o mundo de amanhã. É impossível conceber uma escola cuja finalidade maior seja dar continuidade ao passado. Nossa obrigação primordial é preparar gerações para o futuro (D’AMBRÓSIO, 1986, p. 42).

Figura 4: Utilizando a Calculadora no jogo de dominó da potência

Dessa forma, o jogo de dominó tem como objetivo estimular os alunos a aprender os cálculos de potenciação e utilizar a calculadora como instrumento auxiliar durante o jogo, dado que a potenciação gera números grandes, para demonstrar como a multiplicação é feita na potenciação.

Na opinião de D’Ambrósio (1996, p.33) uma vez aceita a calculadora sem restrições, estaria desfeito o nó górdio da Educação Matemática. Pelo fato de alguns não aceitarem a calculadora na sala de aula. No entanto, o que se observa é que a calculadora pode se tornar um recurso facilitador no decorrer do desenvolvimento das atividades com a potenciação.

3.2 A FUNÇÃO EXPONENCIAL E A LENDA DO XADREZ

A história nos conta que o jogo de xadrez foi criado no século VI d.C. por um homem considerado muito inteligente. Segundo a história, este homem deslocou-se até Pataliputra para expor sua criação ao imperador.

A lenda nos conta que o imperador ficou tão deslumbrado com o jogo que era tão difícil e tão bonito, que ofereceu ao criador qualquer coisa que ele quisesse no império como recompensa. Ao enaltecer a generosidade do imperador, o criador disse que tudo que desejava era uma quantidade de arroz para sustentar sua família. Como a bondade do imperador estava exacerbada por conta da criação, o inventor fez uma contraproposta propôs então que usassem o tabuleiro para determinar a quantidade de arroz que receberia.

Então, o inventor sugeriu que o imperador colocasse um único grão de arroz no primeiro quadrado do tabuleiro, dois no segundo, quatro no terceiro e assim por diante, nesse sentido é possível notar que cada espaço recebia o dobro de grãos de arroz que recebeu o anterior. Enquanto os grãos foram sendo colocados no tabuleiro, o imperador começou a perceber que algo estava errôneo. Depois de 32 quadrados, já havia dado ao criador cerca de 4 bilhões de grãos de arroz. Deste ponto em diante, o imperador começou a ter cautela. Afinal, sua generosidade poderia lhe custar caro demais, a partir da segunda metade do tabuleiro, a duplicação de grãos de arroz para cada quadrado começou a disparar, chegando a trilhões.

Em termos práticos, para que cumprisse com o compromisso, o imperador deveria ser proprietário de arrozais que cobrissem duas vezes a extensão da Terra, incluindo os mares.

Figura 5: Representação do tabuleiro & xadrez

A lenda do imperador e do autor do tabuleiro de xadrez é apropriado para explicar o poder do crescimento exponencial e para acentuar o ponto em que os números começam a se tornar enormes, sendo inconcebíveis, por essa razão a importância do uso da calculadora, como um recurso metodológico na resolução de tais problemas matemáticos.

3.2.1 O XADREZ COMO MATERIAL CONCRETO NA SALA DE AULA

A utilização de materiais concretos na sala de aula, contribuem para uma aprendizagem de maneira leve e divertida, estimulando o aluno a fazer questionamentos, a criar hipóteses e a encontrar soluções. O autor Turrioni (2004) defende que:

Se usufruído conforme as regras em sala de aula, com propósito e finalidade, o instrumento manipulável pode tornar-se um grande aliado do professor, auxiliando no ensino e contribuindo para que o aluno tenha uma aprendizagem significativa, mesmo porque ele exerce um papel importante na aprendizagem. Facilita a observação e a análise, desenvolve o raciocínio lógico, crítico e científico, é fundamental e é excelente para auxiliar ao aluno na construção de seus conhecimentos (TURRIONI, 2004, p. 78).

Com isso, dentre muitos jogos utilizados como material auxiliador no ensino e aprendizagem do aluno, o xadrez se destaca principalmente nas séries do Ensino do Médio por facilitar no ensino da Função Exponencial.

Segundo Moura (1994) o jogo é o elemento externo que irá atuar internamente no sujeito, possibilitando-o a chegar a uma nova estrutura de pensamento. Portanto a utilização do tabuleiro do jogo de xadrez como material concreto no conteúdo de Função Exponencial objetiva explorar os conceitos do tabuleiro com o da matemática.

Vale ressaltar que a relação do xadrez que envolve a Matemática mais especificamente ao conteúdo da Função Exponencial, está ligada ao fato do tabuleiro ser composto por 8 linhas e 8 colunas resultando em 64 casas jogáveis, valor obtido pela multiplicação de 8 com 8 ou 8 ao quadrado. As casas recebem “nomes” formados pela junção de uma letra (A a H referentes às colunas) e um número (1 a 8 referente às linhas).

A partida de xadrez é disputada em um tabuleiro de casa claras e escuras, sendo que no início, cada enxadrista controla dezesseis peças de diferentes formatos e características, o objetivo do jogo é conquistar o “rei” de seu adversário.

Conforme Sá (2019) como uma das possibilidades de proporcionar momentos de um conteúdo de matemática estudado é a utilização de jogos. Então nada impede que a realização de uma ou mais atividades de redescoberta, ou conceituação sejam utilizados jogos para que os estudantes pratiquem de maneira lúdica o conhecimento adquirido por meio do ensino de matemática por atividades.

Nesse sentido, o jogo do xadrez tem caráter lúdico e pedagógico e possibilita um trabalho interdisciplinar e permite ao aluno desenvolver o raciocínio e as estratégias para solução de problemas, apreender as técnicas do jogo, e noções de cálculos e geometria, melhorar a interação na relação professor – aluno, estimular a autoestima dos alunos, desenvolver a capacidade de raciocínio lógico e criatividade de forma lúdica, aprimorar no aspecto moral o autocontrole, a paciência, a perseverança, o respeito aos outros e honestidade, compreender e solucionar problemas pela análise do contexto geral em que estão inseridos, a melhoria do poder de concentração, a realização de atividade de lazer sadia e educativa.

Nota – se que o jogo do xadrez traz diversos benefícios no processo de ensino aprendizagem e relacionado a Matemática tem um valor relevante, pois sua dinâmica de jogos e estratégias facilitam o desenvolvimento intelectual do aluno.

3.3 FUNÇÕES EXPONENCIAIS E A TORRE DE HANÓI

A torre de Hanói, refere – se a um instrumento pedagógico e estratégico iminentemente rico no desenvolvimento do raciocínio combinatório e das capacidades de processamento de contagem, cuja utilização pode contribuir para que os estudantes formulem e/ou ampliem suas estratégias cognitivas de resolução de problemas.

O objetivo deste jogo consiste em transportar todos os discos da haste para outra utilizando o mínimo possível de movimentos, respeitando as seguintes regras:

1- Transferir um disco de cada vez, o qual deverá ser o do topo de uma das três hastes.

2- Cada disco nunca poderá ser colocado sobre outro de diâmetro menor. Ou seja, é um quebra-cabeça que consiste em uma base contendo basicamente três pinos, em um dos quais são dispostos alguns discos.

Nesta atividade o aluno desenvolve o cognitivo, podendo ser aplicado em pequenos grupos ou individualmente além de proporcionar possibilidades de implementação de habilidades matemáticas que se baseiam em suas regras. Por possuir regras de fácil assimilação, esta atividade pode ser desenvolvida em todas as etapas do ensino básico.

Figura 6: Torre de Hanói

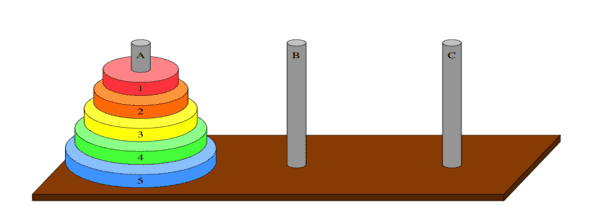
Com esse procedimento o aluno deve movimentar todos os discos do pino A para o pino C seguindo as regras determinadas:

1- Apenas um disco pode ser movido de cada vez.

2- O disco de diâmetro maior jamais poderá ficar embaixo de um dos discos que possui diâmetro menor.

Com isso, o aluno precisa estar atento a cada mudança dos discos.

Na Função Exponencial, a partir de uma série de tentativas, pode-se introduzir ou deduzir que o número mínimo de movimentos do jogo é 2ⁿ -1, na qual n representa a quantidade de discos utilizados e, a partir disso, o estudante pode ir variando esta quantidade e descobrindo o número mínimo de jogadas em cada caso.

Com essa estratégia o aluno compreenderá a conceito de uma Função Exponencial observando a quantidade de discos e a contagem de movimentos utilizados para transportar os discos de um pino para o outro, além de desenvolver a atenção e o raciocínio logico, aprendendo assim de maneira significativa as habilidades que necessita adquirir com este objeto de conhecimento.

Ao se utilizar um jogo com finalidades educacionais, este deve ter objetivos de aprendizagem bem definidos e ensinar conteúdos disciplinares, ou promover o desenvolvimento de estratégias ou habilidades importantes para ampliar a capacidade cognitiva e intelectual dos alunos. (GROS, 2003, apud SAVI E ULBRICHT, 2008)

Portanto, por meio deste jogo, pode – se explicar os objetos de conhecimento necessários para o aluno, bem como proporcionar o desenvolvimento de suas habilidades, associando à capacidade cognitiva dos alunos.

4. CONSIDERAÇÕES FINAIS

O presente artigo buscou apresentar alguns jogos para se trabalhar o conteúdo de Funções Exponenciais como alternativas facilitadoras para o processo de ensino e aprendizagem, pois muitos alunos do 1° ano do Ensino Médio relatam imensas dificuldades em compreender e entender como chegar ao resultado de uma função.

Neste sentido, os jogos lúdicos como proposta de intervenção para o ensino da Matemática é um suporte para o professor, pois este tem uma responsabilidade grande, de levar a comunidade escolar a perceber a importância de integrar os jogos em suas aulas, pois estes materiais poderão proporcionar um aprendizado satisfatório para o conteúdo de funções exponenciais.

Percebe-se que a inclusão do jogo no processo de ensino e aprendizagem da Matemática é uma alternativa que contribuirá para tal procedimento, mediante a participação efetiva e transformadora do professor na ação desencadeada pelo jogo, pois neste processo de assimilação do conhecimento, os jogos lúdicos podem favorecer estímulos para o desenvolvimento, criando um ambiente que estimula a capacidade de comunicação, fortalecendo as relações interpessoais, de liderança e de trabalho em equipe.

Neste viés, o uso de estratégias lúdicas no ensino da Matemática tem como finalidade, fazer com que os alunos aprendam tal conteúdo de forma prazerosa e dinâmica, por meio de jogos, como o dominó da potência, o xadrez e a torre de Hanói. Para tal, estes devem ser planejados e organizados durante todo o processo de planejamento da aula, podendo ser utilizados para introduzir, fixar os conteúdos, garantindo assim que o aluno adquira as habilidades matemáticas relevantes para o desenvolvimento do processo de ensino e aprendizagem.

Assim, através das observações de vivencias profissionais no período de 2018-2020, ficou constatado que os jogos lúdicos para o Ensino da Matemática como proposta de intervenção são eficientes, pois é atrativa na medida em que proporciona uma proximidade significativa com a aprendizagem dos alunos no conteúdo das funções exponenciais e dessa forma a aprendizagem faz sentido no cotidiano do aluno que precisa se apropriar de inúmeros conhecimentos disponibilizados no ambiente escolar.

REFERÊNCIAS

BORIN, J. Jogos e resolução de problemas: uma estratégia para as aulas de matemática. 6.ed. São Paulo: IME/USP, 1996.

BRASIL, Ministério da Educação. Orientações curriculares para o ensino médio: Linguagens, códigos e suas tecnologias / Secretaria de Educação Básica. Volume Linguagens, códigos e suas tecnologias. Brasília: MEC/SEMTEC, 2002.

_______, Ministério da Educação. Parâmetros Curriculares Nacionais. Brasília: 1998.

_______. Base Nacional Comum Curricular (BNCC). Educação é a Base. Brasília, MEC/CONSED/UNDIME, 2017.

_______. Lei de Diretrizes e Bases da Educação Nacional, Lei número 9394/96. Brasília: MEC, 1996.

_______. Ministério da Educação. Secretaria da Educação Média e Tecnológica. Parâmetros Curriculares Nacionais – Ciências da Natureza, Matemática e suas Tecnologias. Brasília: MEC; SEMTEC, 1997.

D´AMBROSIO, Ubiratan. Um brasileiro no Congresso Internacional de Matemáticos de 1900. Revista Brasileira de História da Matemática, v. 3, 2003.

__________, ________. Da realidade à ação: reflexões sobre Educação e Matemática. São Paulo: Summus: Unicamp, 1986.

__________, ________. Educação Matemática. Da teoria à prática.17 Ed. Campinas – São Paulo: Papiras, 1996. Disponível em:  http://www.docplayer.com,br./414669-por-que-se-ensina-matemática.html. Acessado em 13 de jun de 2020.

FEDALTO, D.L. O Imprevisto Futuro das Calculadoras nas Aulas de Matemática no Ensino Médio. Dissertação de Mestrado em Educação. Curitiba. 2006.

Futuro exponencial: Disponível em: http://Xadrez | Compreendendo o pensamento exponencial com a lenda… (futuroexponencial.com). Acessado em 22 de nov de 2020.

GUINTER, A. Uma experiência com calculadoras numa 6ª série do Ensino Fundamental. Informação e Tecnologia, Campinas, 2009. Disponível em: http://www.revista.unicamp.br/infotec/artigos/ariovaldo.html. Acessado em 27 de jun de 2020.

MODESTO, Monica Cristina; RUBIO, Juliana de Alcântara Silveira. A importância da ludicidade na construção do conhecimento. Revista Eletrônica Saberes da Educação, v. 5, n. 1, p. 1-16, 2014.

MONTIBELLER, Lílian.  O brinquedo na constituição do sujeito e como elemento precursor da escrita.  IN Sérgio Antônio da S.  Leite (org.), Alfabetização e Letramento- Contribuições para as Práticas Pedagógicas. Campinas, SP: Editora Komedi, 2003.

MOREIRA, M.A. e MASINI, E.F.S. Aprendizagem significativa: a teoria de aprendizagem de David Ausbebel. São Paulo: Editora Moraes, 1982.

MOURA, M. O. A séria busca no jogo: do Lúdico na Matemática. In: A Educação Matemática em Revista. São Paulo: SBEM– SP, 1994.

OLIVEIRA, J.C.G. A visão dos professores de Matemática do Estado do Paraná em relação ao uso de calculadoras nas aulas de Matemática. Tese de doutorado. Campinas, SP. 1999.

PCN+ Ensino Médio: orientações educacionais complementares aos Parâmetros Curriculares Nacionais. Vol. Linguagens, códigos e suas tecnologias. Brasília: MEC/ SEMTEC, 2002.

PERRENNOUD, Philippe. A formação dos professores no século XXI. As competências para ensinar no século XXI – Porto Alegre: Artmed Editora, 2002.

SÁ, Pedro Franco de. Possibilidades do ensino de matemática por atividades. Matemática-Estudo e ensino. Matemática-Formação de profissional– IFPA, Campus Belém, SINEPEM, v.7, Coleção I, p.1- 65, 2019.

SAVI, R.; ULBRICHT, V. R. Jogos Digitais Educacionais: Desafios e benefícios. CINTEDUFRGS. Novas tecnologias na educação, v.6, 2008.

TAROUCO, L. Avaliação de Objetos de Aprendizagem, 2004. Disponível em: http://penta2.ufrgs.br/edu/objetosaprendizagem/.

TURRIONI, A. M. S. O Laboratório de Educação Matemática na Formação Inicial de Professores. 163f. Dissertação de Mestrado em Educação Matemática – Instituto de Geociências e Ciências Exatas-Campus Rio Claro, Rio Claro, 2004.

VITTI, C. M. Matemática com prazer, a partir da história e da geometria. 2ª Ed.  Piracicaba – São Paulo. Editora UNIMEP. 1999.

APÊNDICE – REFERÊNCIA NOTA DE RODAPÉ

4. São avaliações diagnósticas em larga escala, com o intuito de avaliar a qualidade do ensino que o sistema brasileiro oferece, por meio de testes padronizados e questionários socioeconômicos.

5. São testes de matemática e de língua portuguesa, que tem como ênfase a resolução de problemas e a leitura, no qual são definidos nas Matrizes de referência do sistema de avaliação da educação básica.

6. Avalia o desempenho escolar dos estudantes ao término da educação básica.

7. Material desenvolvido, com a finalidade de servir como ponto inicial para o trabalho do professor, o qual norteará as atividades realizadas na sala de aula.

8. É um documento que norteia as escolas das redes de ensino públicas e privadas, o qual serve como referência obrigatória para elaboração dos currículos escolares e propostas pedagógicas para o ensino básico no Brasil.

^[1] Graduação.

^[2] Graduação.

^[3] Orientador.

Enviado: Julho, 2021.

Aprovado: Janeiro, 2022.