DUTRA, Francisco de Assis Souza. [1]
DUTRA, Francisco de Assis Souza. Aprendendo Sistemas Lineares com Equações de Primeiro Grau Através da Aplicabilidade em Sala de Aula. Revista Científica Multidisciplinar Núcleo do Conhecimento. Edição 05. Ano 02, Vol. 01. pp 799-806, Julho de 2017. ISSN:2448-0959
Resumo
O jogo trabalhado e abordado em salas do 7o ano de uma escola municipal de Caicó/RN teve o intuito de fazer com que os alunos interagissem em aula e resolvessem os sistemas lineares com equação do primeiro grau com duas variáveis de forma mais satisfatória e prazerosa, de modo que, pudesse brotar curiosidade nos mesmos, ao mesmo tempo em que trabalhassem a concentração desabrochando a capacidade intelectual na hora da aula quando fossem resolver tais atividades propostas pelos professores. Isso, também, teve o intuito de fazer com que o ambiente em sala de aula fugisse um pouco do tradicional trazendo para os alunos uma forma inovadora de absorver o conhecimento ao mesmo tempo em que eles davam sustento ao interesse, mesmo que, isso fosse, apenas, momentâneo. Em função disso, eles puderam interagir entre si e com os professores. Isso pôde trazer, então, para eles uma noção de trabalho em equipe já que a proposta de resolução das equações foi para ser em grupo, sendo que, por falta de concentração, interação, curiosidade e, principalmente, aplicabilidade alguns desses mesmos alunos costumavam atrapalhar as aulas e, por causa disso a consequência era que, o resultado das aulas era pouco eficaz, por não haver vontade satisfatória de participarem das tarefas. Portanto daremos mais ênfase sobre esse trabalho e veremos que o aprendizado pode ser satisfatório quando se trabalha atividades de forma aplicadas, a fim de, fazer despertar interesse pelo conhecimento didático da matemática.
Palavras-Chave: Jogo, Alunos, Professores, Aplicabilidade.
Introdução
Os sistemas de equações lineares são de suma importância para a resolução de cálculos matemáticos já que são usados no cotidiano em diversos campos de trabalho, além do ambiente doméstico em casos peculiares nos quais a pessoa não esteja portando alguma calculadora. Caso a pessoa tenha uma boa noção de sua aplicação, isso pode facilitar o raciocínio, a fim de, se chegar a um resultado mais rápido e eficaz de uma resolução matemática.
Atualmente as equações são usadas, entre outras coisas, para calcular circuitos elétricos na eletrônica, em projetos residuais, prediais e industriais na engenharia elétrica, para determinar o lucro de uma firma, para calcular a taxa de uma aplicação financeira, para fazer a previsão do tempo, etc. A palavra “equação” vem do latim equatione, equacionar, que quer dizer igualar, pesar, igualar em peso. E a origem primeira da palavra “equação” vem do árabe adala, que significa “ser igual a“, de novo a ideia de igualdade[2]. Por serem desconhecidos, esses valores são representados por letras.
Resolver sistemas de equações estimula o raciocínio e ajuda a encontrar soluções rápidas para os problemas complexos, mas algumas equações não são assim tão simples de resolver. Elas exigem dos alunos concentração e bom raciocínio.
Sabendo dessa complexidade e dessa aplicabilidade, mas tendo conhecimento da dificuldade de concentração e da ausência de interesse de alguns alunos pelos assuntos da matemática, de modo que, para resolver sistemas de equações é preciso: ler com atenção os problemas propostos, levantar dados, fazer a tradução do enunciado para a linguagem das equações, usar letras, símbolos e ter aplicação. Foi utilizado um jogo que já veio com as soluções dadas dentro de pequenos envelopes. Isso foi o suficiente para despertar o interesse e curiosidade dos mesmos, tendo em vista que as soluções para os problemas equacionais estavam dentro de envelopes, onde só era preciso abrir, pegar os pares ordenados que estavam escritos em bilhetes e substituí-los nas equações até encontrar o par ordenado correspondente, de forma que, entre vários bilhetes contidos dentro de cada envelope, apenas, um bilhete continha o par ordenado correto. Assim, essa busca pelo bilhete que continha a resposta correta fez com que eles fixassem a concentração no que estavam fazendo, já que isso fez surgir neles a curiosidade de achar a resposta correta para tais equações.
Sistemas de equações lineares de primeiro grau e suas aplicações.
Primeiramente devemos abordar o conceito de expressões algébricas que são aquelas em que a variável aparece apenas submetida às chamadas operações algébricas: adição, subtração, multiplicação, divisão e potenciação.
A equação é um tipo de expressão algébrica formada por um sinal de igualdade que demostra que duas coisas são iguais. A igualdade separa membros formados por números e letras (incógnitas, variáveis, etc…). Uma variável é uma letra que sempre representa um número. Não é tomada como equação uma estrutura algébrica formada, apenas, por números. É preciso haver incógnitas.
Por exemplo:
3 + 12 = 15 não é uma expressão algébrica.
Segundo STELING (2011, p.15) “antes que o uso dos símbolos tivesse êxito, os problemas eram escritos na forma de expressões longas e prolixas”.
Por exemplo:
O numero de pipocas mais duas vezes o números de sorvetes é igual a 18.
Traduzindo para a linguagem das equações, isso significa: . Assim o numero de pipocas representa a variável x e o numero de sorvetes representa a variável y.
Ainda segundo STELING (2011, pag.15) “de fato o uso de sinais e operações foi um grande progresso” Sabe-se que os egípcios deram esse grande passo e foi a partir disso que se pôde calcular operações mais complexas. Mas no decorrer da história das expressões algébricas, foram em outras civilizações que também houve prosseguimentos e ascensões das expressões algébricas.
Segundo PERUZZO (2013, p.6) “tratando-se de equações algébricas, os mesopotâmios foram além dos egípcios. Resolviam sistemas com duas equações lineares com duas variáveis de maneira semelhante ao processo atual (Subtração ou soma)”.
Por exemplo:
No cotidiano essas equações são bastante aplicadas:
Por exemplo:

Na figura 1, temos uma situação que encontramos nas atividades em sala de aula, mas isso também está sujeito a ocorrer em situações inusitadas do dia a dia.
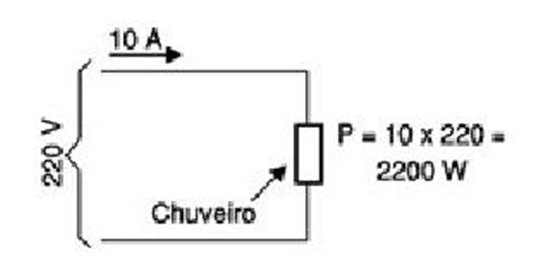
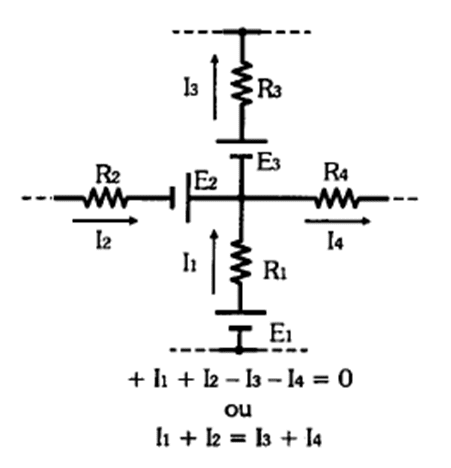
Nas figuras 2 e 3 temos exemplos de aplicações de sistemas de equações no campo da eletrônica.
Na figura 2, não se sabe qual é a potencia(P) do chuveiro elétrico, mas sabe-se qual o valor da corrente elétrica (A) e da tensão (V), então sabendo de todas essas informações basta usar uma simples equação e usando a letra P como incógnita, podemos achar facilmente o valor equivalente da potencia elétrica do chuveiro.
Já na figura 3, segundo a lei de Kirchhoff citada por MARKUS (2001,p. 43) “A soma das correntes elétricas em um nó é igual à zero ou a soma das correntes que chegam a esse nó é igual à soma das correntes que saem desse nó”. Então em casos de circuitos onde não se saiba o valor de algumas dessas correntes, basta usar a lei de Kirchhoff e aplicar o sistema de equações lineares para achar o valor das correntes elétricas (I) desejadas. Este exemplo dado foi de um circuito simples, mas há casos de circuitos mais complexos, onde a aplicação de sistemas equacionais é fundamental para o desenvolvimento do cálculo.
Assim, apesar dos sistemas de equações do primeiro grau já terem sidos trabalhados pelos mesopotâmicos e outras civilizações, nos dias atuais é notória a prática do seu uso.
Aprendizado e aplicações no ambiente escolar
No decorrer do seu trajeto acadêmico o aluno deverá ganhar ferramentas para ser capaz de resolver diversos tipos de equações. Entretanto, para que o mesmo adquira a capacidade de resolver tais expressões algébricas é preciso ter um notório saber das quatro operações: adição, subtração, divisão e multiplicação. Também é interessante ter uma noção de praticidade e da importância do assunto. O professor deve passar para o mesmo que o assunto terá aplicabilidade não só dentro de sala de aula, como também fora dela.
Para isso, é preciso que a escola ofereça uma boa estrutura, oferecendo laboratórios e aulas de campo, do contrário a responsabilidade de apresentar a aplicabilidade dos assuntos matemáticos fica toda em cima do professor. Sendo assim, os jogos matemáticos tornam-se uma saída para trazer aplicação matemática para dentro da escola.
Sabendo disso, os bolsistas do PIBID de uma escola municipal de Caicó/RN fizeram a aplicação de um jogo envolvendo equações lineares. Entretanto, usou-se uma forma básica para que os alunos descobrissem as soluções, já lhes dando variadas respostas contidas em envelopes, de modo que eles deveriam substituir os pares ordenados nos sistemas de equações.
Mesmo que isso tenha sido bem básico, percebeu-se que por ser algo diferente do que se via nas aulas escritas em quadro, acabou gerando mais interesse dos alunos pela atividade prática.
Segundo FELICETTE e MARTINS GIRAFFA (2012) “Assegura-se que para haver aprendizagem de um determinado assunto matemático é necessário que o aluno tenha certo nível de desenvolvimento cognitivo a respeito, isto é, são necessários conhecimentos estruturados em aprendizagens anteriores. Isto significa que as situações de jogo atuam como elementos estimuladores do desenvolvimento cognitivo, pois podem envolver tanto aprendizagens anteriores como novas podendo, assim, serem considerados os jogos como atividades pedagógicas no ensino da Matemática”.
Segundo MOURA (1994) citado por FELICETTE e MARTINS GIRAFFA (2012), “a importância está nas possibilidades de aproximação do aluno com o conhecimento científico, pois lhe permite viver virtualmente problemas que o homem enfrenta ou enfrentou”.
Portanto, sabendo de tudo isso, o jogo dos sistemas das equações aplicado naquela escola foi criado de uma forma que os alunos pudessem praticar as equações de forma diferente, colocando a prática como forma de aprendizado coletivo e satisfatório.
Metodologias e materiais.
Segundo John Von Neumann (apud FALCÂO, 2013, P.1) citado por FELICETTE e MARTINS GIRAFFA (2012), “jogo é toda e qualquer interação entre dois ou mais sujeitos dentro de um conjunto de regras”.
Segundo FELICETTE e MARTINS GIRAFFA (2012) “vive-se implicitamente ou explicitamente jogando. Decorre daí, o interesse natural do ser humano por jogos, independentemente da faixa etária em que se encontra. Os jogos envolvem desafios, onde a superação dos mesmos dá-se mediante respeito às regras existentes em cada jogo”.
Ainda segundo FELICETTE e MARTINS GIRAFFA (2012) “considerando os jogos como atividades de interação, com características desafiadoras e que acompanham o desenvolvimento da humanidade, sendo apreciados por ela e fazendo-se presentes em diferentes contextos e sobre diferentes enfoques, infere-se que estes podem contribuir para um ensino da matemática mais dinâmico e atraente ao aluno. A partir de atividades lúcidas com os jogos, os alunos estarão sendo instigados à participação, à crítica, à busca do novo, à perda do medo e desenvolvendo atitudes de respeito e cooperação entre os participantes (DOHME,2013). Logo o fato de que as pessoas aprendem através dos jogos é evidente”. Decorrendo, daí que os jogos podem ser utilizados pelo professor em sala de aula, intervindo para um melhor aprendizado da matemática.
Os jogos no ensino da matemática desencadeiam desafios e possibilitam ao educando o desenvolvimento da análise de situações, a criação de estratégias próprias para a resolução de problemas, pois exige a busca de novas maneiras de pensar. O jogo também desenvolve habilidades de tomada de decisão, de trabalho em grupo de saber e perder e, ainda estimula a concentração e atenção.
Portanto, a praticabilidade com jogos, requer do professor um cuidado na preparação de materiais, exigindo atenção para as diferentes fases e possibilidades do jogo e, principalmente, a adequação do jogo ao nível de conhecimento do aluno, afim de que este não se esmoreça diante das dificuldades apresentadas.
Jogo
A aplicação do jogo nas turmas do 7o ano foi dividida em três etapas, tais que, cada etapa continha um sistema linear de equações para cada grupo. A turma foi dividida em três grupos e cada grupo recebeu três envelopes, de modo que, cada envelope representava cada etapa. Dentro de cada envelope tinha cinco pares ordenados, mas apenas um desses pares ordenados representava a solução correta para a equação dada naquela determinada etapa. Assim, pulava de etapa quando achasse a solução correspondente à equação.


Na figura 4 temos os exercícios propostos divididos em grupos de três e divididos em três etapas.
Na figura 5 temos os envelopes contendo as respectivas soluções correspondentes a cada sistema de duas equações do 1o grau e de duas variáveis embaralhadas com soluções incorretas e divididos, também, em três etapas.
Quando os grupos conseguiam achar o par ordenado correspondente substituindo o mesmo nas incógnitas (x,y) das equações, pulavam de etapa e, depois acabavam deparando-se com equações mais complicadas do que as anteriores. E dai, terminava aquele que encontrasse todos os pares ordenados correspondentes de cada sistema linear das equações que foram trabalhadas e divididas por etapas.
Resultados e discussões
Os resultados obtidos durante a aplicação do jogo mostraram que boa parte dos alunos gosta de matemática. Conforme o decorrer da aplicação, percebemos que muitos estavam interessados, e os que não estavam, passaram a interagir ao ver que as aulas saíam do cotidiano e fluíam de forma dinâmica. Como pôde ser percebido em sala, o nível de alguns alunos ainda não está coerente com o ano em que estudam. Houve a preocupação de que o jogo não fosse levado apenas na brincadeira, e sim, como um exercício mental trabalhado com o objetivo de promover a interação professor-aluno e estimular o aprendizado através do raciocínio do aluno de forma lúdica.
Considerações finais
Portanto, esta aplicação, ministrada em sala de aula fez com que os alunos trabalhassem os sistemas lineares de equações de forma lúdica e agradável. Isso fez com que eles absorvessem as informações de uma forma diferente, pois se viu prazer em tentar resolver as equações através do jogo e, assim, gerando interesse na maioria. A partir desse interesse, essa maioria conseguiu entender e resolver as equações e ainda facilitou o trabalho do professor dentro da sala de aula.
Referencias
Peruzzo, Jucimar. Evolução dos métodos de resolução de Equações Agébricas / Jucimar Peruzzo, Irani (SC):2013. 129p.
Felicetti, Vera Lucia Matofobia: auxiliando a enfrentar este problema no contexto escolar [recurso eletrônico] / Vera Lucia Felicetti, Lucia Maria Martins Giraffa. – Dados eletrônicos – Porto Alegre: EDIPUCRS, 2012.
GABBI, Gilberto G. O romance das equações algébricas / Gilberto G. Garbi, – 3.ed ver. E ampl. – São Paulo: Editora Livraria da Física, 2009
STERLING, Mary Jane Algebra I Para Leigos / Mary Jane Sterling – Rio de Janeiro: ALTA BOOKS, 2011
MARKUS, Otávio. Circuitos Elétricos: Corrente Contínua e Corrente Alternada. São Paulo. Editora Erica LTDA, p.43, 2001
A origem das equações do 1º grau. Disponível em:http://brasilescola.uol.com.br/matematica/sistema-duas-equacoes.htm. Acesso em 07 abr. 2017.
Sistemas de duas equações. Disponível em: http://www.matematiques.com.br/conteudo.php?id=582. Acesso em 07 abr. 2017.
Sistema de equações lineares: Disponível em:https://pt.slideshare.net/RafaelFloyd/sistemas-de-equaes-lineares-23064456. Acesso em 07 abr. 2017.
Fundamentos de Eletroeletrônica. Disponível em: https://pt.slideshare.net/ccirro/apostila-eletricidade-vol-1Acesso em 07 abr. 2017.
[1] UFRN/CERES, Caicó
[2] Mais informações sobre a origem das equações do 1º grau você encontra em: http://www.matematiques.com.br/conteudo.php?id=582



3 respostas
Muito bom!
Parabéns! Esse tipo de atividade favorece à criança um ambiente agradável, motivador, planejado e enriquecido, buscando um meio de aprendizagem prazeroso.
O jogo educativo sem dúvidas exerce grande influência para o ensino aprendizagem da matemática!