ARTIGO ORIGINAL
NETO, Zacarias Carvalho de Araújo [1], COÊLHO, Saul Mark Lima [2]
NETO, Zacarias Carvalho de Araújo. COÊLHO, Saul Mark Lima. O ensino de sistemas lineares usando registros de representação semiótica. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 06, Vol. 10, pp. 107-121. Junho de 2019. ISSN: 2448-0959
RESUMO
Este artigo tem como objetivo geral investigar se os alunos da graduação em Matemática do IFPI Campus Angical compreendem a resolução de sistemas lineares 2×2 e 3×3 a partir de uma abordagem que favorece a conversão e o tratamento de registro de representação aliados a um ambiente computacional. Os objetivos específicos consistem em verificar se os alunos da graduação conseguem fazer a conversão do registro da língua natural em registro algébrico e do registro algébrico em registro gráfico. Além disso, verificou-se se conseguem fazer o tratamento algébrico pelo método de escalonamento e examinou-se a influência do software winplot na aprendizagem do conteúdo em questão. A pesquisa consta da aplicação e análise de duas atividades exploratórias, em que foram abordadas a língua natural, algébrica, gráfica e o tratamento algébrico com e sem o uso do software winplot. Na análise de dados fez-se a analise a priori e a posteriori comparando os resultados esperados em cada questão e as respostas dos alunos. O embasamento teórico foi estudado a partir da Teoria dos Registros de Representação Semiótica de Raymond Duval. Nesta investigação observou-se que o uso do software winplot pode facilitar a compreensão de sistemas lineares.
Palavras-chave: sistemas lineares, registros de representação semiótica, software winplot.
INTRODUÇÃO
A proposta deste trabalho consistiu na representação algébrica, língua natural e gráfica com o uso do recurso do software winplot em sistemas de equações lineares 2×2 e 3×3, como forma de atingir uma aprendizagem significativa. Além disso, foi abordado o tratamento algébrico por meio do método de escalonamento.
A importância de pesquisar este tema foi de contribuir com a melhoria do processo de ensino aprendizagem de sistemas lineares. Os professores limitam-se ao livro didático, e não abordam todos os registros de representação semiótica, principalmente no conteúdo de sistemas lineares 3×3. Esta postura resulta em um ensino baseado na mecanização de processos sem compreensão.
O objetivo geral desta pesquisa é investigar se os alunos da graduação em Matemática conseguem compreender a resolução de sistemas lineares 2×2 e 3×3 a partir de uma abordagem que favorece a conversão e o tratamento de registro de representação aliados a um ambiente computacional.
Os objetivos específicos foram: averiguar se os alunos da graduação conseguem fazer a conversão do registro da língua natural em registro algébrico; verificar se os discentes conseguem fazer a conversão do registro algébrico em registro gráfico; reconhecer se os mesmos conseguem fazer o tratamento algébrico pelo método de escalonamento; examinar a influência do software winplot na aprendizagem de sistemas lineares.
Os autores utilizados para embasar este trabalho foram: Allevato (2007), Batista (2004), Battaglioli (2008), Brasil (2005), Cervo (2007), Dante (2006), Duval (2009), Iezzi (2006), Machado (1996), Silva (2005) e Oliveira (2013). Todos foram de grande relevância, mas o foco da investigação foi fundamentado nos Registros de Representação Semiótica de Raymond Duval.
1. OS REGISTROS DE REPRESENTAÇÃO SEMIÓTICA NO ENSINO DE SISTEMAS LINEARES COM O USO DO WINPLOT
Neste tópico há um breve resumo do conteúdo de sistemas lineares com sua definição, representação, métodos de resolução e classificação. Em seguida, observam-se os diversos Registros de Representação Semiótica e das vantagens do software winplot.
1.1 SISTEMAS LINEARES
Sistema linear é um conjunto de m equações lineares e n incógnitas. De acordo com Iezzi et. al. (2006), os chineses foram os primeiros a resolver sistemas lineares idêntico ao método de Gauss ou escalonamento empregando um método sistemático.
Segundo Silva (2005, p. 220) um sistema linear de m equações com n incógnitas, é representado por um conjunto de equações lineares do tipo:
As formas de obter o conjunto verdade de um sistema são os métodos da adição, substituição, regra de Cramer e o escalonamento.
Na resolução dos sistemas 2×2 a regra de Cramer é muito prática, mas no caso dos sistemas formados por três ou mais equações o método do escalonamento é o mais indicado, por ser um processo menos trabalhoso.
Segundo Iezzi (2006), a conhecida regra de Cramer é uma descoberta do escocês Colin Maclaurin (1698-1746) e data aproximadamente de 1729, embora só tenha sido publicada em 1750.
Os sistemas podem ser classificados quanto ao número de soluções em Sistema Possível Determinado (SPD), Sistema Possível e Indeterminado (SPI), e Sistema Impossível (SI). Dante (2006, p. 269) explica que:
Em um sistema linear 2×2, se as duas equações forem totalmente proporcionais, o sistema é indeterminado (SPI). Se as duas equações tiverem apenas os coeficientes das mesmas incógnitas em ambas as equações proporcionais (e os termos independentes não estiverem na mesma proporção), o sistema é impossível (SI). Se as duas equações não tiverem os coeficientes das mesmas incógnitas em ambas as equações proporcionais o sistema é determinado (SPD).
Nos sistemas lineares a classificação pode ser feita observando as equações, além disso, também podemos classificá-los fazendo a construção dos gráficos e observando as posições relativas das retas, no caso dos sistemas lineares 2×2, e dos planos nos sistemas lineares 3×3.
1.2 OS REGISTROS DE REPRESENTAÇÃO SEMIÓTICA
O embasamento teórico foi estudado a partir da Teoria dos Registros de Representação Semiótica de Raymond Duval (2009), assim utilizada devido à importância da diversidade de registros e a articulação entre eles nas atividades matemáticas.
Duval (2003) relaciona a aprendizagem da matemática com os processos de semiósis e noésis. Entende-se por semiósis a apreensão ou produção de uma representação semiótica, e por noésis, a apreensão conceitual de um objeto. Segundo o autor, “não há noésis sem semiósis”, isto é, não se adquire conhecimento de um objeto sem se utilizar dos sistemas de representação semiótica.
A fim de desenvolver as atividades e atingir objetivos, esta pesquisa foi realizada com a mobilização simultânea de registros de representação por ser apontada por Duval (2003) como fator indispensável para a compreensão do objeto matemático. Para o autor, essa compreensão e a originalidade da atividade matemática supõe a coordenação de ao menos dois registros de representação semiótica. As representações semióticas passam por dois tipos de transformações que são diferentes: os tratamentos e as conversões.
Duval (2009) define um tratamento como uma transformação que se efetua no interior de um mesmo registro, aquele onde as regras de funcionamento são utilizadas; um tratamento mobiliza então apenas um registro de representação. Por exemplo:![]() . Em (1) temos uma representação decimal com um tratamento decimal e em (2) a representação é fracionária com um tratamento fracionário. Em relação ao tema deste trabalho, os sistemas lineares, utilizou-se o tratamento ao propor a resolução de um problema por meio do método de escalonamento.
. Em (1) temos uma representação decimal com um tratamento decimal e em (2) a representação é fracionária com um tratamento fracionário. Em relação ao tema deste trabalho, os sistemas lineares, utilizou-se o tratamento ao propor a resolução de um problema por meio do método de escalonamento.
Para Duval (2009) a conversão é, ao contrário, uma transformação que faz passar de um registro a outro. Por exemplo: Um certo número somado ao seu sucessor e adicionado de 4 unidades é igual a 15. (1),![]() (2). Em (1) tem-se uma representação em língua natural, em (2) este registro é convertido da língua natural para o registro simbólico algébrico. Nesta pesquisa, usou-se a conversão ao propor a resolução de problemas cujo objetivo era: a mudança de registro da língua natural em linguagem algébrica e a mudança do registro algébrico para o gráfico.
(2). Em (1) tem-se uma representação em língua natural, em (2) este registro é convertido da língua natural para o registro simbólico algébrico. Nesta pesquisa, usou-se a conversão ao propor a resolução de problemas cujo objetivo era: a mudança de registro da língua natural em linguagem algébrica e a mudança do registro algébrico para o gráfico.
Uma investigação feita por Battaglioli (2008) sobre esse tema destaca a importância da exploração do registro gráfico na resolução dos sistemas lineares, uma vez que tal método poderá colaborar para que os alunos tenham maior facilidade, não só para entender o conjunto solução de um sistema linear, mas também para classificá-lo e discuti-lo quando necessário.
A maioria dos alunos do Ensino Médio e até mesmo da graduação não conseguem fazer a conversão dos registros, seja da língua natural para o algébrico ou do algébrico para o gráfico, limitam-se apenas a mecanização de processos sem compreensão. Duval (2009, p. 34) reforça:
mudar a forma de uma representação se revela ser, para muitos alunos nos diferentes níveis de ensino, uma operação difícil e, por vezes, mesmo impossível. Tudo se passa como se a compreensão que a grande maioria dos estudantes tivesse de um conteúdo ficasse limitada à forma de representação utilizada.
Nos livros didáticos a conversão em diferentes registros é pouco abordada, e prioriza a conversão do registro da língua natural para o algébrico. O livro é de extrema importância no cotidiano escolar, por isso a maioria dos professores têm-se apoiado exclusivamente neste recurso. Contudo cabe ao docente buscar novos métodos de ensino para melhorar a aprendizagem de Matemática.
1.3 O SOFTWARE WINPLOT
O software educacional winplot é um programa gráfico, que permite a construção e animação de gráficos em duas dimensões 2D e em três dimensões 3D por meio de diferentes tipos de equações (explícitas, implícitas, paramétricas, polar e outras). Este foi desenvolvido pelo professor Richard Parris “Rick”, por volta de 1985.
Segundo Batista (2004), o winplot foi considerado como sendo bastante coerente com as propostas do Programa Nacional do Livro Didático para o Ensino Médio (2005), contribuindo para a construção do conhecimento e permitindo estabelecer conjecturas a partir da visualização da movimentação dos gráficos, aspecto fundamental para o desenvolvimento da resolução das atividades proposta nesta pesquisa.
Outros fatores significativos à escolha do software winplot: ser de fácil manuseio; ocupar pouca memória no computador; possibilitar movimento dos planos e ser um programa de domínio público.
Em relação à construção de aprendizagem com ajuda de ambientes informatizados, Allevato (2007, p. 79) afirma:
Em ambientes informatizados de ensino, verifica-se com frequência uma forma de aprendizagem segundo a perspectiva do construtivismo, qual seja aquela que se constrói sobre a própria experiência. Não raro, a depender das atividades realizadas e do modo como são realizadas, os estudantes vivenciam experiências de aprendizagem mais significativas e intensas do que é possível apenas com lápis e papel.
Nesta pesquisa, pretendeu-se investigar como o uso do software winplot pode interferir na compreensão dos alunos, pois possibilita a conversão do registro algébrico para o registro gráfico.
Assim, o estudo com auxílio de ambientes computacionais pode proporcionar uma visão mais apurada das mudanças de registos. Para Oliveira (2013) os ambientes virtuais são ferramentas que permitem desenvolver a criatividade, no entanto, ele orienta que o professor deve se atentar para a escolha do tipo de mídia a ser usada para que não haja perda na aprendizagem em matemática.
2. METODOLOGIA
Este estudo foi desenvolvido através de uma pesquisa experimental. Para Cervo (2007) pesquisa experimental é aquela em que a manipulação das variáveis proporciona o estudo das relações entre as causas e os efeitos de determinado fenômeno.
A pesquisa ocorreu no Instituto Federal de Educação, Ciência e Tecnologia do Piauí (IFPI), Campus Angical, com a participação de vinte e quatro alunos do 4º módulo da licenciatura em Matemática do turno noite. A pesquisa contou ainda com a participação do professor da disciplina de Núcleos Temáticos 2, também orientador deste trabalho. Os participantes foram escolhidos pelo fato de o orientador ministrar aula nesta turma, e os mesmos terem visto este conteúdo no Ensino Médio e na disciplina Elementos da Matemática, ministrada no primeiro período do referido curso.
Como instrumentos para coleta de dados foram utilizadas duas atividades, abordando os sistemas lineares 2×2 e 3×3. A primeira atividade foi aplicada em sala de aula, no dia 19/03/2019 e a segunda atividade foi realizada em laboratório de informática, no dia 29/03/2019, como mostra o quadro 01:
Quadro 01 – Descrição das atividades realizadas

Para resolver a 1ª atividade, os licenciandos utilizaram lápis e régua, e a 2ª atividade teve o auxílio do software winplot, possibilitando a visualização das posições relativas das retas no espaço bidimensional 2D e dos planos no espaço tridimensional 3D.
A conversão é abordada nesta pesquisa de três formas distintas:
1º. Do registro da língua natural como registro de partida e o registro algébrico como registro de chegada, como observado no quadro 02:
Quadro 02 – Exemplo da passagem de um registro a outro

2º. Do registro algébrico para registro de tabelas e registro gráfico, como podemos ver no quadro 03:
Quadro 03 – Exemplo da passagem de um registro a outro
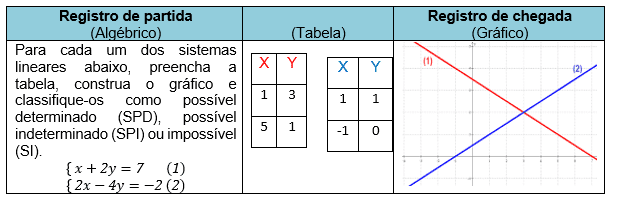
3º. Do registro algébrico para o registro gráfico, como mostra o quadro 04:
Quadro 04 – Exemplo da passagem de um registro a outro
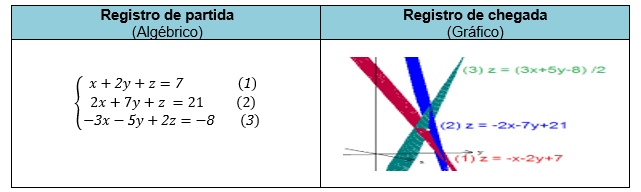
Desta forma, a mudança de registro poderá contribuir para a compreensão do conteúdo em estudo: os sistemas lineares.
A análise a priori consiste na elaboração de atividade experimental da ação em sala de aula. Para isto, foram elaborados, no mês de novembro/2013, os dois questionários a serem aplicados.
A análise a posteriori é o conjunto de resultados que se pode tirar da exploração dos dados recolhidos durante a experimentação.
3. RESULTADOS E DISCUSSÕES
Nesta investigação analisou-se as resoluções dos questionários feitas pelos alunos, e foram comparados os dados coletados com a análise a priori. A validação deste estudo foi realizada a partir da comparação entre a análise a priori e a análise a posteriori.
3.1 ANÁLISE A PRIORI E A ANÁLISE A POSTERIOR DA PARTE A1 E B1
Para desenvolver a parte A1 e B1 foram disponibilizadas pelo professor da turma três aulas, em classe, com duração de cinquenta minutos cada uma das aulas.
Os alunos receberam uma atividade, contendo quatro questões que deveriam ser desenvolvidas individualmente durante as três aulas.
A primeira questão da parte A1 a priori tinha como objetivo verificar o desempenho dos alunos quanto à conversão do registro da língua natural para o registro algébrico, como pode ser observado no quadro 05:
Quadro 05 – Parte A1 sobre sistema linear 2×2

Esperava-se que os alunos fizessem essa conversão mobilizando conhecimentos prévios e realizando tratamentos que lhes possibilitassem chegar a uma resposta quanto ao número de notas de cada tipo.
Para que os alunos desenvolvessem a estratégia escolhida, seria necessário: usar letras como incógnitas específicas; conhecer os tratamentos numéricos e algébricos no conjunto dos números reais; elaborar uma resposta que satisfizesse à pergunta proposta no problema.
Segundo Brasil (2005) podem ser utilizadas diferentes linguagens para representar os conteúdos: símbolos matemáticos, língua natural, desenhos, gráficos, ícones. Esse tratamento diversificado é apontado, atualmente, como um fator muito importante para a compreensão dos conceitos e procedimentos matemáticos.
Na análise a posteriori verificou-se que 50% dos alunos haviam realizado a conversão do registro da língua natural para o registro algébrico.
A segunda questão da parte A1 a priori tinha como objetivo verificar o desempenho dos alunos quanto à conversão do registro algébrico para o de tabela e para o registro gráfico, e classificar cada sistema de acordo com o tipo de solução, como é visto no quadro 06:
Quadro 06 – Parte A1 sobre sistema linear 2×2
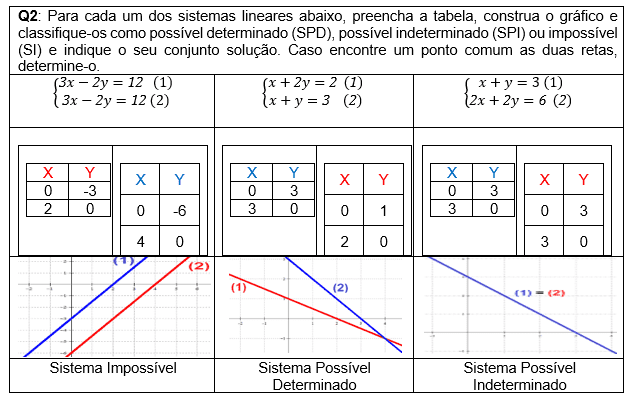
A conversão do registro algébrico como registro de partida para o registro gráfico, como registro de chegada, é possível quando os alunos utilizam o registro de tabela, e assim, efetuam as conversões para o registro gráfico. Desta forma, é necessário atribuir valores para uma das incógnitas e calcular os valores correspondentes da outra incógnita. Obter, portanto, pelo menos dois pares ordenados (x, y) para construir a reta que caracteriza cada equação.
Esperava-se que os alunos preenchessem as tabelas, construíssem os gráficos e classificassem os sistemas lineares em: sistema impossível (letra a), sistema possível determinado (letra b) e sistema possível indeterminado (letra c).
Para Machado (1996) uma das causas das dificuldades que os alunos enfrentam na disciplina Álgebra Linear é a passagem do registro algébrico para o gráfico e vice-versa. Ela destaca a importância de se abordar essas conversões de registros antes do ensino superior, caso contrário, os discentes continuarão resolvendo sistemas sem dar sentido algum a eles.
Na análise a posteriori observou-se que somente 39% dos alunos, em média nos três itens, realizaram a conversão do registro algébrico para o de tabela e para o registro gráfico. Além disso, 71% dos alunos tiveram dificuldade em classificar o sistema linear 2×2.
A primeira questão da parte B1 a priori tinha como objetivo verificar, o desempenho dos alunos quanto à conversão do registro da língua natural para o registro algébrico como mostra o quadro 07:
Quadro 07 – Parte B1 sobre sistema linear 3×3

Esperava-se que os alunos fizessem a conversão do registro da língua natural para o registro algébrico, mobilizando conhecimentos prévios e realizando tratamentos que lhes possibilitassem chegar a uma resposta quanto ao preço de cada item.
Na análise a posteriori constatou-se que 62% dos alunos haviam realizado a conversão do registro da língua natural para o registro algébrico.
A segunda questão da parte B1 a priori tinha como objetivo investigar se os alunos faziam o tratamento algébrico ao usarem o método de escalonamento, como podemos ver no quadro 08:
Quadro 08 – Parte B1 sobre sistema linear 3×3

Esperava-se que os alunos fizessem o escalonamento dos sistemas classificando estes em Sistema Possível Determinado, Sistema Possível Indeterminado e Sistema Impossível respectivamente.
Na análise a posteriori somente 21% dos alunos, em média nos três itens, realizaram o tratamento do registro algébrico. Neste sentido, 79% dos alunos não aprenderam a escalonar um sistema linear 3×3.
3.2 ANÁLISE A PRIORI E A ANÁLISE A POSTERIOR DA PARTE A2 E B2
Na atividade 2 os alunos foram para o laboratório de informática e receberam duas questões que deveriam ser desenvolvidas individualmente no computador com o auxílio do software winplot.
A primeira questão da parte A2 a priori tinha como objetivo verificar o desempenho dos alunos quanto à conversão do registro algébrico para o registro gráfico, e classificar cada sistema de acordo com o gráfico, como observado no quadro 09:
Quadro 09 – Parte A2 sobre sistema linear 2×2
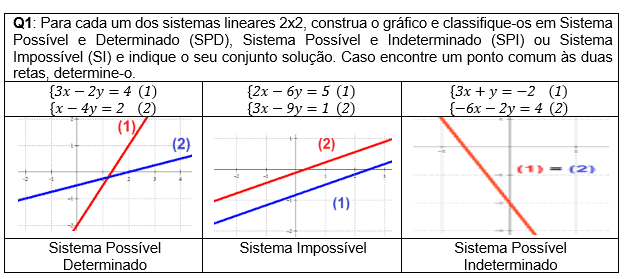
Os discentes deveriam isolar a variável y para colocar a informação no programa winplot, obtendo assim a reta de cada equação.
Na análise a posteriori verificamos que 48% dos alunos realizaram a conversão do registro algébrico para o registro gráfico.
A primeira questão da parte B2 a priori tinha como objetivo verificar o desempenho dos alunos quanto à conversão do registro algébrico para o registro gráfico, e classificar cada sistema de acordo com o gráfico, como mostra o quadro 10:
Quadro 10 – Parte B2 sobre sistema linear 3×3
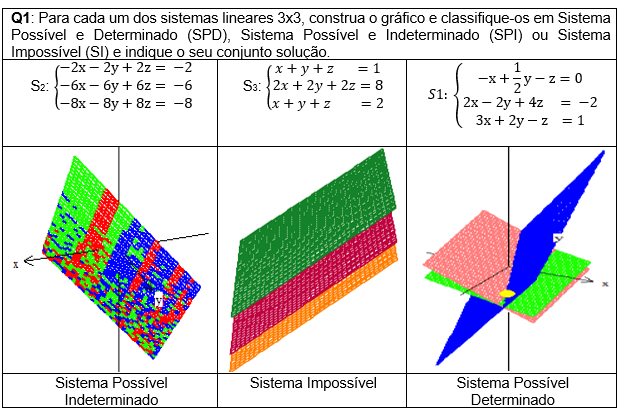
Os discentes deveriam isolar a variável z para colocar a informação no programa winplot, obtendo assim o plano de cada equação.
A conversão do registro algébrico como registro de partida para o registro gráfico como registro de chegada é possível com o uso do winplot, pois este proporciona possibilidades de exploração e experimentação pelo movimento dos eixos (x, y, z), facilitando a visualização e a compreensão do posicionamento dos planos.
Na análise a posteriori averiguamos que 55% dos alunos, em média nos três itens, realizaram a conversão do registro algébrico para o registro gráfico.
CONSIDERAÇÕES FINAIS
Na análise da questão 1 (parte A1 e parte B1) constatou-se que 56%, em média, dos discentes sabem fazer a conversão do registro da língua natural em registro algébrico.
As atividades elaboradas necessitavam de conhecimentos prévios, isto causou algumas dificuldades para determinados alunos. Na questão 2 (parte A1) 61% destes não fizeram a conversão do registro algébrico em registro gráfico.
A aplicação das atividades também revelou o grau de dificuldade dos estudantes em relação ao tratamento de um sistema pelo método do escalonamento, pois 79% destes não sabiam escalonar os sistemas lineares 3×3 da questão 2 (parte B1).
No confronto entre a atividade (questão 2 – parte A1) feita em sala, com lápis e régua, e a executada com o uso do software winplot (questão 1 – parte A2) percebeu-se uma ampliação de 39% para 48% de conversão do registro algébrico para o gráfico nos sistemas lineares 2×2.
A exploração e experimentação no espaço tridimensional 3D melhorou a visualização e compreensão dos graduandos, sobre a classificação (SPD, SPI ou SI) de um sistema linear 3×3. Assim, na questão 1 (parte B2) constatou-se que 55% destes fizeram a conversão do registro algébrico para o gráfico nos sistemas lineares 3×3.
Vale ressaltar que, mediante a dificuldade da representação gráfica dos três planos no espaço tridimensional, foi essencial o uso da ferramenta computacional em nossa pesquisa. Na fala de um dos sujeitos “o uso do software winplot é vantajoso, pois facilita a visualização dos gráficos dos sistemas lineares facilitando o entendimento do conteúdo não ficando tão abstrato”. (SUJEITO IV, 2014).
Nos livros didáticos a conversão em diferentes registros é pouco abordada, isto demonstra a limitação deste recurso, pois os planos das equações estão em 3D, e é difícil visualizar no plano do papel algo na terceira dimensão.
Nesta investigação cuja proposta favorece a conversão e o tratamento de registros de representação, esperamos dar a nossa contribuição para aprendizagem dos graduandos no tema em questão e incentivar outros estudos deste tema nas pesquisas em Educação Matemática.
REFERÊNCIAS
ALLEVATO, N. S. G. Aspectos Emergentes da Utilização do Computador na Educação Matemática. In: ALLEVATO N. S. G. e FRANZONI M. (Org.) Reflexões sobre a Formação de Professores e o ensino de Ciências e Matemática. Campinas: Alínea, 2007.
ANDRADE, A. A; SANTOS, B.C.A. Um cenário das pesquisas envolvendo a teoria dos registros de representação semiótica em edições do sipem. Revista REnCiMa, v. 10, n.1, p. 228-245, 2019
BATISTA, S. C. F. Softmat: Um repositório de softwares para matemática do Ensino Médio – Um instrumento em prol de posturas mais conscientes na seleção de softwares educacionais – UENF: Dissertação de Mestrado, 2004.
BATTAGLIOLI, C. S. M. Sistemas Lineares na segunda série do Ensino Médio: Um olhar sobre os livros didáticos – PUCSP: Dissertação de Mestrado, 2008.
BRASIL. Secretaria da Educação Média e Tecnológica. Programa Nacional dos
Livros Didáticos para o Ensino Médio – Matemática (PNLEM). Brasília: MEC, 2005.
CERVO, A. L. et. al. Metodologia científica. 6. ed. São Paulo: Pearson Prentice Hall, 2007.
DANTE, L. R. Matemática. 1. ed. São Paulo: Ática, 2006.
DUVAL, R. Registros de Representações Semióticas e Funcionamento Cognitivo da Compreensão em Matemática. In: Machado, S. D. A. (Org.) Aprendizagem em Matemática, Registros de Representações Semióticas. Campinas: Papirus. (Coleção Papirus Educação) p. 11-33, 2003.
_____________. Semiósis e Pensamento Humano: Registros semióticos e aprendizagens intelectuais (Fascículo I). 1. ed. São Paulo: Livraria da Física, 2009.
IEZZI, G. et. al. Matemática: ciência e aplicações. 4. ed. São Paulo: Atual, 2006.
MACHADO, S. D. A. O Universitário principiante x Significado dos Sistemas de Equações in Anais do IV EPEM – p. 241-248. São Paulo: SBEM, 1996.
OLIVEIRA, Franciele Martins de. O uso da sala de informática nas aulas de matemática no ensino fundamental: percepções de um grupo de professores. UNIJUÍ – Universidade Regional do Noroeste do Estado do Rio Grande do Sul, 2013, p. 07.
REIS, E. F; REHFELDT, M. J. Software phet e matemática: possibilidade para o ensino e aprendizagem da multiplicação. Revista REnCiMa, v. 10, n.1, p. 194-208, 2019.
SILVA, C. X. Matemática aula por aula. 2. ed. renov. São Paulo: FTD, 2005.
[1] Especialista, Graduado em Matemática e Graduado em História.
[2] Professor do IFPI Campus Angical. Graduação: licenciatura plena em matemática; Especialização em Educação.
Enviado: Dezembro, 2018.
Aprovado: Junho, 2019.
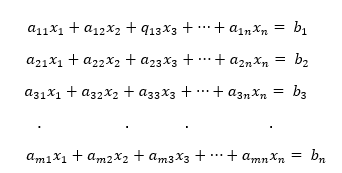


Uma resposta
Otimo! Artigo Top!