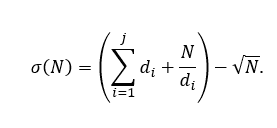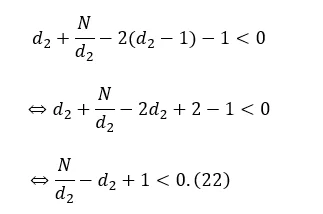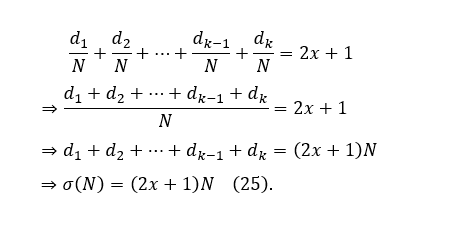ARTIGO ORIGINAL
FERNANDES, Hiller Alves [1]
FERNANDES, Hiller Alves. Números s-perfeitos ímpares. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 08, Ed. 03, Vol. 02, pp. 96-107. Março de 2023. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/numeros-s-perfeitos, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/numeros-s-perfeitos
RESUMO
A teoria dos números é um campo da matemática que possui diversos problemas em aberto. Um número natural N é dito S-perfeito se a soma de todos os seus divisores positivos for igual a SN, isto é, em notação matemática σ(N)=SN. Um problema muito antigo é o da existência de números perfeitos ímpares. De modo geral, se sabe pouco sobre números S-perfeitos ímpares. Então, o intuito deste artigo é demonstrar e investigar certas propriedades sobre os números S-perfeitos ímpares, em especial, com S ímpar. Inicialmente, será realizada uma breve introdução sobre o tema. Em seguida, há 4 lemas que visam dar suporte e entendimento ao leitor para demonstrações posteriores. Logo após, será apresentado um teorema que é a pedra angular do artigo. Por fim, tem-se duas consequências em forma de corolários e uma breve conclusão da discussão.
Palavras-chave: Números s-perfeitos, Números perfeitos ímpares, Teoria dos números.
1. INTRODUÇÃO
A soma dos divisores positivos de N é denotada por σ(N). Um número inteiro positivo é S-perfeito se σ(N)=SN. Para S=2, é dito que N é perfeito. O presente artigo tem como objetivo mostrar um teorema inédito e original e dois corolários decorrentes dele. O problema central é sobre a existência de números S-perfeitos ímpares com S ímpar, que é uma generalização do problema sobre a existência de números perfeitos ímpares. As demonstrações dos resultados são dadas por redução ao absurdo ou contradição.
Um artigo recentemente sobre temas correlatos da teoria dos números foi publicado Poulkas em 2021. Seu artigo possui uma demonstração que prova a inexistência de números perfeitos ímpares. O mais interessante do artigo é que sua demonstração é simples, e se vale tão somente da matemática elementar. O ponto central é o fato dos divisores de N virem em pares. Além disso, sua demonstração se dá pela redução ao absurdo. Se os divisores formam pares, pode-se modificar a forma como trata-se a soma de todos os divisores positivos. De modo que, 
(POULKAS, 2021).
Também neste artigo, um dos pontos centrais é o fato dos divisores de N virem em pares. Contudo, como será demonstrado no lema [3], se N é um S-perfeito com N e S ímpares, então N é um quadrado perfeito. Logo, 
, pois o lado direito soma duas vezes a 
. Então, o argumento necessita de uma pequena correção. Esta ligeira modificação está exposta no lema [4].
2. DEMONSTRAÇÕES
Lema [1]: seja N,S ∈ N. Se N é um número S-perfeito, então, existem pelo menos dois números primos distintos que dividem N.
Demonstração: seja N um inteiro positivo S-perfeito, isto é, σ(N)=SN, suponha-se, por absurdo, que N=pª com p, α ∈ N ∪{0} e p primo. Logo:
Contudo, 
, mas 
. Contradição, portanto, N tem pelo menos dois divisores primos distintos.
Lema [2]: seja N∈ N tal que N não é um quadrado perfeito, então, N tem uma quantidade par de divisores positivos, e a soma de seus divisores positivos pode ser dada por:
Demonstração: seja 
o conjunto de todos os divisores positivos de N, então 
. Ao definir 
, o par de divisores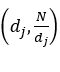 
é bem definido. O par de divisores (1,N) é o par trivial. Como N não é um quadrado perfeito, segue que 
para todo 
. Portanto,
Como queria-se demonstrar. Além disso, N tem um número par de divisores, pois há 
pares distintos com 
para todo 
.
Lema [3]: Sejam 
tais que ambos são ímpares e 
. Se N é um número S-perfeito, então N é um quadrado perfeito.
Demonstração: suponha, por absurdo, que N>0 é um inteiro ímpar S-perfeito, mas não é um quadrado perfeito. Em outras palavras, 
. Então, pelo Lema [2] N, possui uma quantidade par de divisores ímpares, consequentemente, 
é par. Mas, por hipótese, é ímpar, contradição. Portanto, N é um quadrado perfeito.
Lema [4]: seja 
tal que N é quadrado perfeito, então, a soma de seus divisores positivos pode ser dada por:
Demonstração: seja 
o conjunto de todos os divisores positivos de N, então, 
. Ao definir 
, o par de divisores 
é bem definido. Contudo, para algum j, tem-se 
pois N é um quadrado perfeito. Para não somar duas vezes sua raiz quadrada, basta subtrair 
após a realização da soma de todos os pares de divisores:
Teorema [1]: não existe número inteiro positivo ímpar S-perfeito com S ímpar.
Demonstração: seja k um número inteiro positivo, suponha, por absurdo, que 
é um número S-perfeito com S ímpar, isto é, σ(N)=SN com S e N ímpares. Pelo Lema [3], N é um quadrado perfeito. Então, pelo Lema [4]:
Extraindo o par trivial de divisores obtém-se:
Pode-se substituir 
por 
em (5). Existe 
tal que S=2s+1, logo:
Seja D o conjunto dos divisores positivos de N, pelo Lema [1], N não é primo. isso implica que 
, isto é, o conjunto dos divisores positivos não triviais de N não é vazio. Portanto, pelo princípio da boa ordenação, existe um elemento em D que é o elemento mínimo, isto é, 
tal que para todo
com 
tem-se 
, Por convenção, 
. Além disso, 
é primo. De fato, se é composto, então existe 
tal que 
e, portanto, 
, mas 
contradição. Extraindo o par de divisores 
obtém-se:
Observe que 
é par, então existe 
tal que 
. Substituindo 
por 
em (7) obtém-se:
Multiplicando toda a equação (9) por 
tem-se:
Observe que a equação (10) pode ser tratada como uma equação do segundo grau. Para descobrir o valor de 
, basta aplicar a fórmula resolutiva da equação do segundo grau. Logo:
Portanto:
Com maior exatidão
Como
, portanto, 
é um quadrado perfeito. Note que:
Caso contrário, 
. Além disso:
De fato, pois:
Subtraindo a equação (15) de (16), tem-se:
Por comodidade, 
Logo:
Por outro lado, 
. Logo:
Porém, 
, como demonstrado na equação (18). Consequentemente, 
. Portanto:
(20)
A equação (8) diz que 
substituindo em (20), obtém-se:
Substituindo 
por 
, em (20), tem-se:
Contudo, 
. Contradição, pois, em (22), tem-se 
. Portanto, não existe N inteiro positivo e ímpar S-perfeito com S ímpar.
Como observação: seja o conjunto M tal que 
, então 
. Note que 
e que
. O elemento mínimo de 
Além disso, 
.
Corolário [1]: a soma dos inversos dos divisores positivos de N não pode ser ímpar se N também é ímpar.
Demonstração: suponha, por absurdo, que a soma dos inversos dos divisores positivos de N ímpar é ímpar. Então:
Com x,k ϵ N ∪ {0} . Por outro lado, para cada 
, existe um 
tal que:
(24)
Aplicando o conceito exposto na equação acima e utilizando a propriedade comutativa da divisão, segue que:
O que é uma contradição com o Teorema [1]. Portanto, a soma dos inversos dos divisores positivos de N não pode ser ímpar se N também é ímpar.
Corolário [2]: a soma dos inversos dos divisores positivos de N não pode ser um inteiro positivo se 
com N ímpar, 
.
Demonstração: suponha, por absurdo, que a soma dos inversos dos divisores positivos de N é um inteiro positivo com 
ímpar. Pelo corolário [1], sabe-se que essa soma não pode ser ímpar. Portanto, precisa ser par. Logo:
Com 
. Por outro lado, para cada 
, existe um 
tal que:
Aplicando o conceito exposto na equação acima e utilizando a propriedade comutativa da divisão, segue que:
Portanto, a soma dos divisores positivos de N é par. Mas isso é um absurdo, pois a soma dos divisores positivos de um quadrado ímpar é ímpar. Consequentemente, a soma não pertence aos inteiros positivos, visto que todo número inteiro ou é par ou é ímpar.
3. CONSIDERAÇÕES FINAIS
Os resultados apresentados são inéditos e originais. A teoria dos números é famosa por conter problemas de fácil entendimento, mas extremamente difíceis de demonstrar. Tais problemas são fantásticos, principalmente quando as soluções são, de certa forma, simples, por usar matemática elementar, mas de extrema elegância.
O ponto central do artigo é investigar a existência de números naturais ímpares e S-perfeitos com S ímpar. Pelo Teorema [1], é provado que tais números com essa propriedade não existem. A demonstração se vale de um artifício que é somar os divisores por pares do tipo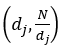 
e realizar uma ligeira correção, pois N é um quadrado perfeito.
Além disso, há duas consequências decorrentes do Teorema [1]: a primeira é que a soma dos inversos dos divisores positivos de N não pode ser ímpar se N também é ímpar. Em outras palavras, tal soma só pode ser um inteiro par ou um racional. A segunda consequência é que a soma dos inversos dos divisores positivos de N não pode ser um inteiro positivo se 
com N ímpar, 
. São racionais e não inteiros. Resultados impressionantes e de cunho teórico.
REFERÊNCIA
POULKAS, Demetrius Chr. Very original proofs of two famous problems: “are there any odd perfect numbers?” (unsolved until to date) and “Fermat’s last theorem: a new proof of theorem (less than one and a half pages) and Its generalization”.
Advances in Pure Mathematics, v. 11, n. 11, p. 891-928, 2021.
[1] Mestrando em Matemática – (UFVJM), especialista em Matemática financeira e Estatística – (UCAM) e Licenciatura em Matemática – (UNIUBE). ORCID: 0000-0001-6957-6209. CURRÍCULO LATTES: 8992771071815999.
Enviado: 29 de Dezembro, 2022.
Aprovado: 01 de Março, 2023.
