ARTIGO ORIGINAL
ARANTES, Gabriel Costa Vieira [1]
ARANTES, Gabriel Costa Vieira. Sobre a finitude dos números primos gêmeos com base no teorema dos números primos. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 11, Vol. 13, pp. 189-196. Novembro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/numeros-primos, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/numeros-primos
RESUMO
Os números primos distantes duas unidades um do outro são chamados de gêmeos. O conjunto dos números primos é comumente simbolizado por ![]() . A Conjectura dos Números Primos Gêmeos afirma que existem infinitos pares de números primos p, q
. A Conjectura dos Números Primos Gêmeos afirma que existem infinitos pares de números primos p, q ![]() que são gêmeos. Na Matemática, conjecturas são hipóteses comumente aceitas, mas que ainda não foram rigorosamente demonstradas (ou contrariadas). Neste artigo, objetiva-se demonstrar que a Conjectura dos Primos Gêmeos é falsa. Isto será feito através do raciocínio por redução ao absurdo. Esta demonstração será baseada no famoso Teorema dos Números Primos.
que são gêmeos. Na Matemática, conjecturas são hipóteses comumente aceitas, mas que ainda não foram rigorosamente demonstradas (ou contrariadas). Neste artigo, objetiva-se demonstrar que a Conjectura dos Primos Gêmeos é falsa. Isto será feito através do raciocínio por redução ao absurdo. Esta demonstração será baseada no famoso Teorema dos Números Primos.
Palavras-chave: Conjectura, Primos gêmeos, Teorema dos números primos, Finitude.
INTRODUÇÃO
Considere que ![]() é o conjunto dos números primos. Dados dois números primos p, q
é o conjunto dos números primos. Dados dois números primos p, q ![]() tais que q > p, eles serão chamados de gêmeos quando a distância entre ambos for de exatamente duas unidades (RIBENBOIM, 2020). Em notação algébrica, tem-se q = p + 2. A Conjectura dos Primos Gêmeos afirma que existem infinitos pares de números primos p, q
tais que q > p, eles serão chamados de gêmeos quando a distância entre ambos for de exatamente duas unidades (RIBENBOIM, 2020). Em notação algébrica, tem-se q = p + 2. A Conjectura dos Primos Gêmeos afirma que existem infinitos pares de números primos p, q ![]() que cumprem a propriedade apresentada no parágrafo anterior. Na Matemática, uma conjectura é uma hipótese ainda não demonstrada, ou seja, é factível de ser contrariada, por mais que pareça ser verdadeira. Neste artigo, será demonstrado que a Conjectura dos Números Primos Gêmeos é falsa, e, portanto, o conjunto destes números deve ser FINITO. Para realizar tal demonstração, nos basearemos no famoso Teorema dos Números Primos, decorrente dos estudos iniciais de Carl Friedrich Gauss sobre a função
que cumprem a propriedade apresentada no parágrafo anterior. Na Matemática, uma conjectura é uma hipótese ainda não demonstrada, ou seja, é factível de ser contrariada, por mais que pareça ser verdadeira. Neste artigo, será demonstrado que a Conjectura dos Números Primos Gêmeos é falsa, e, portanto, o conjunto destes números deve ser FINITO. Para realizar tal demonstração, nos basearemos no famoso Teorema dos Números Primos, decorrente dos estudos iniciais de Carl Friedrich Gauss sobre a função ![]() de contagem dos números primos. Este teorema afirma que a imagem desta função, denotada por
de contagem dos números primos. Este teorema afirma que a imagem desta função, denotada por ![]() , tende para x/ln(x) à medida em que a variável independente x
, tende para x/ln(x) à medida em que a variável independente x ![]() tende ao infinito (SANTOS, 2020).
tende ao infinito (SANTOS, 2020).
DESENVOLVIMENTO
Eis a definição da função de contagem dos números primos, até um certo número x ![]() :
:
Quando ![]() , temos a aproximação de Gauss para a função
, temos a aproximação de Gauss para a função ![]() dada por:
dada por:
Esta aproximação consiste no famoso Teorema dos Números Primos, devidamente provado pelos matemáticos Atle Selberg e Paul Erdos em 1949.
Dados dois números primos p, q ![]() , eles serão chamados de primos gêmeos quando ocorrer:
, eles serão chamados de primos gêmeos quando ocorrer:
Note também que, sempre que dois números primos p, q ![]() são gêmeos, tem-se o seguinte:
são gêmeos, tem-se o seguinte:
Pois se p, q ![]() são gêmeos, então certamente eles são números primos consecutivos em
são gêmeos, então certamente eles são números primos consecutivos em ![]() .
.
Teorema: O conjunto dos números primos gêmeos é finito, isto é, limitado.
Vamos supor, por hipótese de absurdo, que existam infinitos pares de números primos p, q ![]() que sejam gêmeos, tais que q = p + 2. Então, fazendo
que sejam gêmeos, tais que q = p + 2. Então, fazendo ![]() , teríamos o seguinte:
, teríamos o seguinte:
A partir daí, seguindo o raciocínio de absurdo, poderíamos afirmar que:
E aqui jaz a nossa contradição, pois na verdade se tem:
Vamos provar este resultado logo abaixo:
Portanto, até este momento, podemos concluir que:
 Vamos fazer uma pausa para determinar o resultado do limite que consta no numerador:
Vamos fazer uma pausa para determinar o resultado do limite que consta no numerador:
Como verificamos que a indeterminação é do tipo 0/0, podemos utilizar a Regra de L’Hôpital:
Deste modo, obtivemos o seguinte resultado:
 Isto posto, podemos prosseguir com o nosso desenvolvimento anterior:
Isto posto, podemos prosseguir com o nosso desenvolvimento anterior:
Com isto, concluímos finalmente que se tem:
Mas a nossa suposição inicial de que existem infinitos números primos p, q ![]() que sejam gêmeos, tais que q = p + 2, nos conduziu ao seguinte absurdo:
que sejam gêmeos, tais que q = p + 2, nos conduziu ao seguinte absurdo:
Logo, nossa suposição inicial é falsa, o que significa que NÃO EXISTEM infinitos números primos p, q ![]() que sejam gêmeos. Logo, o conjunto dos primos gêmeos é FINITO. Mais um resultado que corrobora com este fato é o seguinte: não existe nenhum número primo p
que sejam gêmeos. Logo, o conjunto dos primos gêmeos é FINITO. Mais um resultado que corrobora com este fato é o seguinte: não existe nenhum número primo p ![]() que satisfaz a equação que havíamos obtido, também através da hipótese de absurdo:
que satisfaz a equação que havíamos obtido, também através da hipótese de absurdo:
De fato, esta equação admite somente um par de soluções complexas, quando p ![]() . Veja:
. Veja:
Isto também configura uma contradição, pois a suposição de que p ![]() é um dos pilares fundamentais da nossa demonstração. O par de soluções complexas exibidas acima não pode ser obtido analiticamente, apenas numericamente, por isso a aproximação. Também devido a este fato, utilizou-se o site de inteligência artificial WolframAlpha para obter tais soluções.
é um dos pilares fundamentais da nossa demonstração. O par de soluções complexas exibidas acima não pode ser obtido analiticamente, apenas numericamente, por isso a aproximação. Também devido a este fato, utilizou-se o site de inteligência artificial WolframAlpha para obter tais soluções.
CONSIDERAÇÕES FINAIS
Existem alguns artigos científicos com possíveis demonstrações da validade da Conjectura dos Primos Gêmeos, que se baseiam em outros teoremas ou conjecturas. Um grande exemplo é o artigo do pesquisador Adecio da Silva Santos, onde ele demonstra a validade da Conjectura dos Primos Gêmeos com base na Conjectura de Andrica (SANTOS, 2019). O presente artigo científico é provavelmente o primeiro que consiste em uma possível demonstração da não-validade da Conjectura dos Números Primos Gêmeos, contrariando o seu enunciado. A convicção do autor neste resultado se fundamenta no pilar do famoso Teorema dos Números Primos, baseado nos estudos iniciais de Gauss sobre a função de contagem dos números primos ![]() e devidamente demonstrado por Selberg e Erdos em 1949, a partir do qual foi construído todo o raciocínio de redução ao absurdo que conduziu à contradição da Conjectura dos Primos Gêmeos. Assim como toda demonstração, esta somente será validada e reconhecida pelas organizações internacionais da Matemática após uma rigorosa análise, que deve ser conduzida por uma equipe credenciada de matemáticos. Até que este momento ocorra, a demonstração apresentada neste artigo permanece como possível candidata à solução da Conjectura dos Números Primos Gêmeos.
e devidamente demonstrado por Selberg e Erdos em 1949, a partir do qual foi construído todo o raciocínio de redução ao absurdo que conduziu à contradição da Conjectura dos Primos Gêmeos. Assim como toda demonstração, esta somente será validada e reconhecida pelas organizações internacionais da Matemática após uma rigorosa análise, que deve ser conduzida por uma equipe credenciada de matemáticos. Até que este momento ocorra, a demonstração apresentada neste artigo permanece como possível candidata à solução da Conjectura dos Números Primos Gêmeos.
REFERÊNCIAS
RIBENBOIM, Paulo. Números Primos: velhos mistérios, novos recordes. 3ª Edição. Coleção Matemática Universitária. 317 páginas. IMPA. Rio de Janeiro. 2020.
SANTOS, Adecio da Silva. Demonstração da Conjectura de Andrica para todos os primos gêmeos. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 04, Vol. 06, PP. 18-24. Abril de 2019. ISSN: 2448-0959. Disponível em: DOI: 10.32749/nucleodoconhecimento.com.br/matematica/primos-gemeos. Acesso em: 20 jun. 2022.
SANTOS, José Plínio de Oliveira. Introdução à Teoria dos Números. 3ª Edição. Coleção Matemática Universitária. 128 páginas. IMPA. Rio de Janeiro. 2020.
[1] Especialista Lato Sensu (Pós-Graduação) em Ensino de Estatística pela UFN, Licenciado em Física pela PUC Goiás, Licenciado em Química pela PUC Goiás. ORCID: 0000-0001-6298-1906.
Enviado: Julho, 2022.
Aprovado: Novembro, 2022.


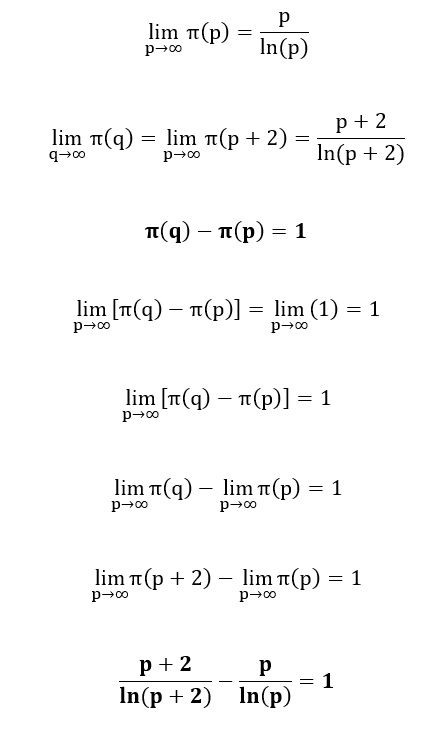











4 respostas
Muito bom artigo, poucos tentam por esse ponto de vista de negar uma conjectura. Esse teorema dos números primos é muito intrigante tambem, tanto pra provar como pra falsear.
Mas infelizmente a comunidade matemática tem muito previlégios para uns.
Vou compartilhar pois achei curioso o Artigo..
Deano Mendes, muito obrigado pelo seu comentário! Estou muito empolgado com minhas recentes investigações sobre os números primos. De fato, o Teorema dos Números Primos é fascinante, permitindo diversas demonstrações por redução ao absurdo, como a que está presente neste artigo. Agradeço muito pelo incentivo, ao compartilhar o meu artigo! Grande abraço.
Prezado Sr Gabriel Costa Vieira Arantes, interessante sua explanação e demonstração, peço minhas sinceras desculpas a todos(as) aqui presente desta Revista Científica, dentro de sua explanação e demonstração encontrei alguns pontos negativos ao afirmar que existe números primos gêmeos!!! com base em suas fórmulas apresentada na inicial: “Eis a definição da função de contagem dos números primos, até um certo número x Equação”, prove com números sua afirmação os números primos gêmeos e qual o valor de π usado em suas demonstrações?; como já é sabido de tempos passados que este enigmático número de π , conforme relato do grande pensador e matemático Arquimedes de Siracusa, “No que diz respeito à obtenção do número, estima-se que em 250 A.E.C.(Antes Era de Cristo); Arquimedes obteve uma aproximação de π calculando o perímetro de dois hexágonos, um inscrito e outro circunscrito numa circunferência. Ao aumentar o número de lados do polígono, até chegar aos 96 lados, conseguiu uma aproximação igual a esta fração de números inteiros(22:7=3,1428571428571428571428571428571)”(Fonte site de Matemáticas), de tempos passados ele foi dito como um número transcendente e irracional, ocorre que um Brasileiro com um Polígono de 1134 lados dentro de uma Circunferência de 360º graus obteve uma razão de números inteiros, afirmando cientificamente com uma obra cientifica publicada: ” A ousadia do π ser racional”. que na era atual padronizou este enigmático número de π para ser Racional e Irreversível(3,15), Três inteiros e quinze centésimos finito depois da vírgula, dentro deste número enigmático com 100% de total precisão, sancionei uma lei que deverá ser respeitada sempre, está Lei diz: “Não pode ser aproximado, Não pode ser arredondado, Não pode ser simplificado, Não pode ser Fatorado; tem que ser 100% exato com total precisão” nas resoluções onde ele estiver presente…. com relação aos números primos, onde um Brasileiro afirma cientificamente que alguns números não são primos como todos(as) vem relatando de tempos passados, com uma simples PA(Progressão Aritmética), desvendei seus enigmas, onde afirmo cientificamente que não são primos e nem primos gêmeos: segue os números relatados a seguir: 2; 19; 41; 59; 61; 79; 101; 139; 179; 181; 199; 239; 241; 281; 359; 401; 419; 421; 439; 461; 479; 499; 521; 541; 599; 601; 619; 641; 659; 661; 701; 719; 739; 761; 821; 839; 859; 881; 919; 941; 1019; 1021; 1039; 1061; 1181; 1201; 1259; 1279; 1301; 1319; 1321; 1361; 1381; 1399; 1439; 1459; 1481; 1499; 1559; 1579; 1601; 1619; 1621; 1699; 1721; 1741; 1759; 1801; 1861; 1879; 1901; 1979; e mais alguns…… sendo assim “A Hipótese de Rielmann perde totalmente sua força” o autor Sr Sidney Silva.
Prezado nobre amigo Gabriel Costa Vieira Arantes, interessante sua pergunta, pois com uma simples PA(Progressão Aritmética) padronizei duas fórmulas: vejamos como ficaria pegar um número primo e dividir ou seja usar a fatoração ou a decomposição de números primos para ser fatorado do menor para o maior e do maior para o menor, assim será considerado um número primo:
esse número é primo 12280616105497 e somente pode ser dividido e fatorado somente pelos números 1867; 1871; 1873; 1877 que também são primos vejamos como fica minha tese:
do menor para o maior:
12280616105497 1867
6577726891 1871
3515621 1873
1877 1877
1
Agora irei fatorar com números primos do maior para o menor:
12280616105487 1877
6542683061 1873
3493157 1871
1867 1867
1
Provando minha tese que o numeral 2, 19 e outros já citados acima não são primos, e os primos gêmeos não existe. lendo este número primo teremos; (Doze Trilhões, Duzentos e Oitenta Bilhões, Seiscentos e Dezesseis Milhões, Cento e Cinco Mil Quatrocentos e Oitenta e Sete.), com esta simples fórmula cheguei na casa dos 92 Nonilhões, e é Finito…. Sr Sidney Silva.
o primeiro numero primo seria o numeral três( 3): vejamos como ficaria minha tese e teoria:
3*5*7*11*13*17= 255255 vejamos como fica pela minha definição de números primos:
Do menor para o maior:
255255 3
85085 5
17017 7
2431 11
221 13
17 17
1
Agora do maior para o menor:
255255 17
15015 13
1155 11
105 7
15 5
3 3
1
Prova que os valores fatorados somente com números primos; será considerado números primos, pois foi dividido somente com os números primos existente dentro da minha tese e teoria…porém haverá um único numero primo que será dividido por ele mesmo e o resultado será 1, classificando como os verdadeiros números primos………esse é meu conceito e a definição para os números primos…….meu cordial abraço Sr Sidney Silva.
interessante sua explanação e demonstração, simples e de fácil aprendizado aos seus alunos(as) com meu respeito a todos(as) aqui presente neste singelo canal, tenho um conceito sobre o que é números primos:
“Pra ser um número primo terá que dividir somente pelo número primo, sendo do menor para o maior, e do maior para o menor, só assim poderá ser um número primo exato e finito” essa Lei é aplicada no momento em que for feita a Fatoração ou a decomposição de números primos”…. ao contrário que todos(as) vem relatando em tempos passados, usando uma teoria já obsoleta para os tempos atuais, Sr Sidney Silva. Porém não é possível esta sequência, pois tem alguns números que não são primos e os primos gêmeos não existe…..