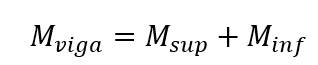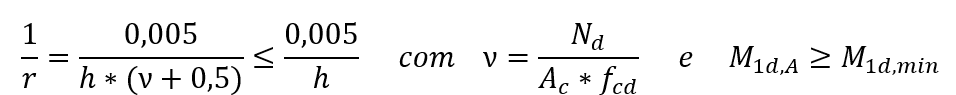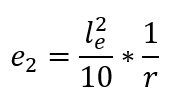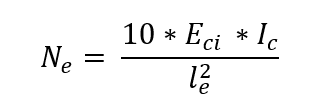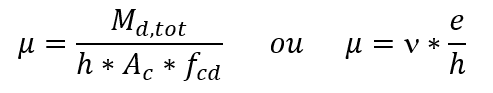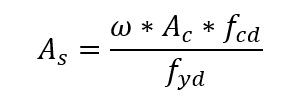Comparación de dimensionamiento y modelado de columnas

ARTÍCULO ORIGINAL

CARVALHAES, Daniely Silva ^[1], CARVALHAES, Daniel José ^[2], QUARESMA, Wanessa Mesquita Godoi ^[3]

CARVALHAES, Daniely Silva. CARVALHAES, Daniel José. QUARESMA, Wanessa Mesquita Godoi. Comparación de dimensionamiento y modelado de columnas. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 05, Ed. 05, Vol. 04, págs. 121 a 146. Mayo de 2020. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/ingenieria-civil/modelado-de-columnas

RESUMEN

La búsqueda de la reducción del tiempo en la elaboración de proyectos se convierte en una necesidad, junto con la indigencia de entender problemas recurrentes en el uso de estructuras de hormigón armado como patologías. Por lo tanto, uniendo los dos problemas, el tiempo y el análisis, se hace imperativo estudiar formas de modelar y analizar las estructuras en el software común de desarrollo de proyectos. El objetivo es modelar un edificio y comparar un elemento estructural, analizando las cargas y dimensiones realizadas por el software TQS®. Este proceso se debe al modelado en el software TQS del edificio ejemplo de José Milton de Araújo (2014). Se observó que el proceso de modelado en comparación con el proceso numérico presenta una diferencia significativa debido al hecho de hacer el análisis del edificio completo, siendo así fiable el modelado realizado en el software, lo que permite un estudio previo de toda la estructura.

Palabras clave: Pilares, tamaño, modelado, experimental, TQS.

1. INTRODUCCIÓN

Bastos (2006, p. 07) presenta hormigón armado siendo “la unión de hormigón simple y un material resistente a la tracción (envuelto por hormigón) de tal manera que ambos resisten conjuntamente los esfuerzos de solicitud”, es decir, el hormigón armado es el resultado del hormigón simple más refuerzo más adherencia.

Para Piancastelli (1997), el hormigón armado está sujeto a cambios en el tiempo, ya que es un material no inerte, gracias a las interacciones entre sus elementos constitutivos (cemento, arena, grava, agua y acero), interacciones entre estos elementos y agentes externos como gases, sales, bases, ácidos y otros, y con materiales que se le añaden (aditivos y adiciones minerales).

Durante mucho tiempo el hormigón se consideró un material duradero, debido a trabajos antiguos todavía en buen estado, pero el deterioro temprano de las estructuras actuales nos lleva a las razones de las patologías concretas (BRANDÃO y PINHEIRO, 1999). Esto se debe a las nuevas tecnologías, para hacer las estructuras esbeltas y más ligeras, del proceso de planificación y producción de las estructuras.

Los pilares son elementos generalmente alineados verticalmente en su eje, en los que las fuerzas de compresión normales son preponderantes (ABNT NBR 6118, 2014), su estudio es uno de los controles esenciales, con respecto al dimensionamiento, el mal funcionamiento de un pilar de una estructura puede comprometer la funcionalidad y causar accidentes graves. Siendo responsables de la transmisión de cargas verticales, los pilares están generalmente sujetos, en particular, a la condición de flexión-compresión, por lo tanto, la necesidad de considerar los efectos de segundo orden y el análisis de estabilidad del pilar en su conjunto.

Los pilares se dimensionan de acuerdo con los esfuerzos externos que solicitan el cálculo, que conforman las fuerzas normales (N_d), los momentos en llamas (M_dx y M_dy) y las fuerzas de corte (V_dx y V_dy) siendo horizontales. NBR 6118, en la versión de 2003, particularmente en el racionamiento de los pilares, la norma insertó varias modificaciones, como el valor de la excentricidad accidental, una cubierta de hormigón más grande, un nuevo método en el cálculo del límite de esbelta que hace referencia a la contemplación o no de los momentos flóricos del segundo orden y, sobre todo, con la consideración del momento mínimo deflector, y puede sustituir el momento deflector como resultado de la excentricidad accidental. La versión 2014 añadió la comprobación mínima del momento del fletor, hecha a partir de la comparación de una envoltura robusta, que incluye la envoltura mínima con el segundo orden.

2. CÁLCULO Y DIMENSIONAMIENTO DE PILARES POR ABACOS

2.1 CLASIFICACIÓN DE PILARES

Los pilares se clasifican según su posición en la estructura, puede ser intermedio, final o esquina. Esta clasificación le permite considerar los esfuerzos de solicitud en cada situación calculada. (FUSCO,1981)

Figura 1 – Posición de los pilares en los edificios.

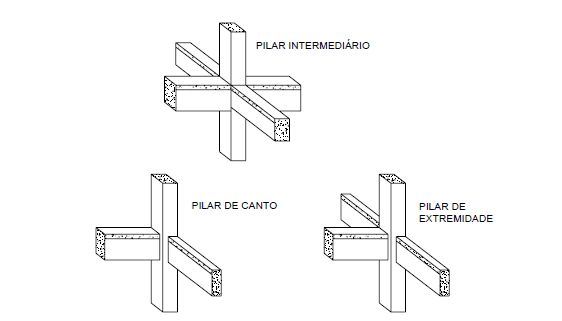
Los pilares intermedios se someten predominantemente a las fuerzas de compresión axial, porque los momentos de flema son de poca intensidad, en cuanto a las acciones verticales (variables permanentes y normales). A menos que los intervalos de las vigas continuas que se basan en estos pilares se consideren diferentes, los momentos finales de lanzamiento transmitidos a los pilares se ignoran. Por lo tanto, se admite el pilar intermedio sometido a una compresión centrada en la situación del proyecto, es decir, la excentricidad inicial, en el dimensionamiento de las áreas de los refuerzos transversales y longitudinales, se considera igual a cero.

Los pilares de las extremidades están sometidos a fuerzas de compresión normales y a la acción de los momentos propagados por las vigas, que tienen sus extremidades externas apoyadas en estos pilares. En las vigas transversales al eje de la viga interrumpida, no se tienen en cuenta los momentos. Por lo tanto, se considera la columna de extremidad sujeta a flexión normal compuesta, teniendo en cuenta, por lo tanto, la excentricidad inicial en uno de los pedidos locales de la sección transversal de la columna.

Pilares de esquina además de ser sometidos a la fuerza de accionamiento normal, uno debe considerar los momentos transmitidos por las vigas, de las cuales los planos medios son perpendiculares a las caras de los pilares, y se interrumpen en los bordes de la columna. En la situación de diseño, se considera la columna de esquina enviada a la flexión oblicua compuesta, con excentricidades que son iniciales según los ejes coordinados locales.

Los pilares, aunque su clasificación por su posición en la estructura es muy habitual, también se clasifican en cuanto al tipo de solicitud que se presenta el pilar. Es decir, pilares sometidos a flexión compuesta normal, pilares sometidos a flexión compuesta oblicua y pilares sometidos a compresión centrada.

2.2 ÍNDICE DE BANDAS

El índice de esbeltez de las columnas de hormigón armado es la relación entre la longitud equivalente (l_e) de la columna y el radio de rotación (i) de la sección. (NBR 6118, 2014)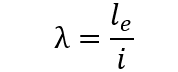
La clasificación de los pilares depende de los límites de esbeltez y factores adicionales, como la excentricidad relativa, la forma del diagrama de los momentos y las condiciones de unión de los extremos. Estos factores se consideran utilizando el coeficiente de λ₁.

Para los pilares cortos NBR 6118 (2014) (λ ≤ λ₁), los efectos de segundo orden podrían ignorarse ya que los índices de referencia son más altos que los índices de delgadez. Pilares medianos delgados (λ₁ <λ ≤ 90) que son aquellos para los que se pueden considerar los efectos de segundo orden, mediante un proceso aproximado, como el método de columna estándar con curvatura aproximada. Las columnas delgadas (90 <λ ≤ 140) son aquellas para las que es posible considerar el método de columna estándar junto con los diagramas M – N – 1 / r. Pilares muy esbeltos (140 <λ ≤ 200) que requieren, para verificar el estado límite de inestabilidad, los métodos exactos a considerar. La NBR 6118 no permite el diseño y construcción de un pilar con un índice de esbeltez (λ) mayor a 200. En el caso de postes con resistencia normal menor a 0.10.f_cd.A_c, este límite puede excederse.

2.3 EXCENTRICIDADES

En los pilares, las excentricidades ocurren no sólo por las peticiones iniciales sobre los pilares, sino también por factores adicionales como los efectos del segundo orden, la fluencia de las imperfecciones concretas y geométricas.

Es necesario obtener las excentricidades relacionadas con el tipo de columna analizada para realizar su acotación. Este punto presenta los criterios para la obtención de estas excentricidades en pilares por separado, de acuerdo con la norma NBR 6118, 2014.

2.3.1 EXCENTRICIDAD INICIAL DE 1ER ORDEN

Sabemos que las vigas y los pilares componen gantries tridimensionales, de modo que los pilares están sometidos a flexión oblicua compuesta y, en consecuencia, presentan excentricidades iniciales en dos direcciones principales. En los proyectos que consideran procesos simplificados para la definición de los esfuerzos de solicitud son el momento fletor, la fuerza normal y la fuerza de corte, por ejemplo, el caso de viga continua presentado en NBR 6118 (2014), se admite que las excentricidades iniciales surgen en los pilares de esquina y fin. Recordando que las excentricidades no se consideran para los pilares intermedios.

Las excentricidades del 1er orden son dadas por las expresiones:

N_d sería la fuerza de cálculo solicitante;

M_d,A y M_d,B los momentos de cálculo solicitantes en los extremos de la columna.

La excentricidad más alta en valor absoluto se adopta para e_i,A.

Cuando no se calculan los valores exactos de los esfuerzos de solicitud en la estructura, es posible adoptar la forma estática indicada en la Figura 2, con el fin de obtener los momentos de la gripe en los soportes extremos, como la simplificación.

Figura 2 – Modelo considerado en casos de soporte extremo de vigas continuas.

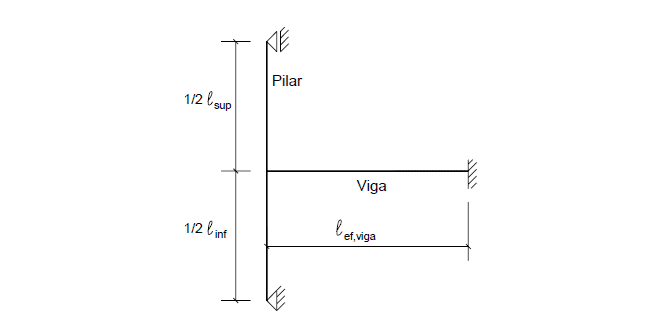
Los momentos de solicitud en las ramas superior e inferior del pilar se obtienen mediante: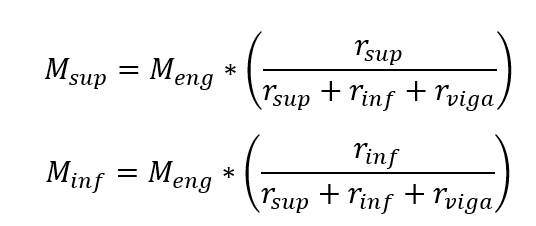

Siendo, M_eng el momento de ajuste perfecto en el tranvía analizado (fin de la viga) de la viga.

Los coeficientes de rigidez de las ramas superior e inferior de la columna y en la sección de viga se definen por las relaciones entre momentos de inercia y intervalos, de acuerdo con las siguientes expresiones: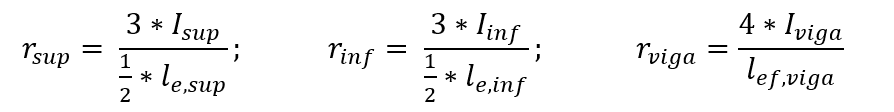El momento del fletor en la viga se determina mediante la siguiente expresión, teniendo en cuenta el equilibrio del nodo.

La longitud equivalente de l_e columna se puede determinar mediante la expresión: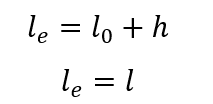siendo que:

l_o distancia entre las caras internas de los elementos estructurales, supuestamente horizontales, que unen la columna.

h la altura de la sección transversal de la columna, conocida en el plano de la estructura.

l la distancia entre los ejes de los elementos estructurales a los que está unido el pilar.

Los intervalos efectivos de las vigas se pueden calcular mediante la expresión: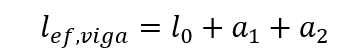

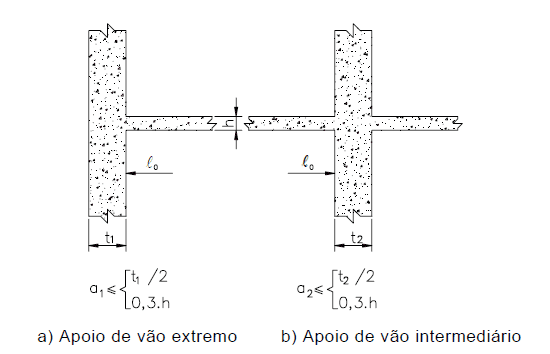
Los valores de a₁ y a₂, en cada extremo del intervalo, se pueden calcular mediante los valores apropiados de a_i, indicados en la Figura 3, siendo:

a₁ igual al valor más bajo entre (t₁/2 y 0,3 * h).

a₂ igual al valor más bajo entre (t₂/2 y 0,3 * h).

Figura 3 – Ir vigas efectivas.

2.3.2 FORMA DE EXCENTRICIDAD

Para ajustar la posición de los elementos estructurales en función del diseño arquitectónico, los diseñadores estructurales deben hacer que las caras internas o externas de las vigas sean compatibles con las de los pilares que los reciben. Cuando esto sucede, los ejes de las vigas no pasan a través del centro de gravedad de la sección de la columna (figura 4), por lo que las excentricidades emergentes llamadas excentricidades de forma (AGUIAR. 2000).

Figura 4 – Excentricidad de la forma en pilares.

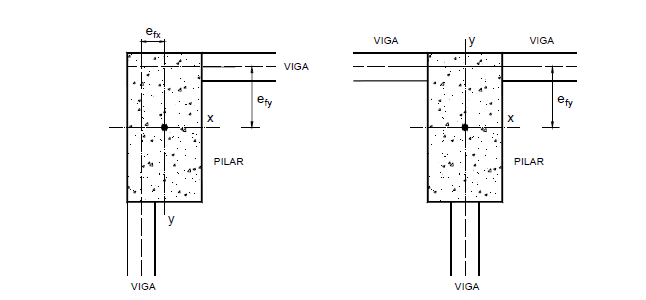
Las excentricidades de la forma, cuando se realizan los proyectos y estructuras de los edificios, no se tienen en cuenta en el dimensionamiento, sin la ayuda de programas informáticos elaborados para este fin. El momento fletor generado por las excentricidades a nivel de cada piso es nivelado por un par, causando, en cada piso, pares de fuerzas del mismo orden de magnitud y direcciones contrarias, que se cancelan. Los programas computacionales elaborados para el análisis estructural y el dimensionamiento con comprobaciones de apertura de grietas y los criterios de los últimos estados límite y desplazamientos con los parámetros de los estados de límites de servicio, tienen en cuenta estas excentricidades de la forma.

2.3.3 ECCENTRICIDAD ACCIDENTAL

NBR 6118 (2014) prevé el cálculo de una excentricidad accidental (e_a), teniendo en cuenta las situaciones de imperfección local debidas a la construcción de los pilares, puede ser por la desintegración del eje de columna.

Según NBR 6118 (2014), en las estructuras reticuladas normales, se admite que el efecto de las imperfecciones locales se resuelve si se considera el valor del momento total mínimo. En el caso de la flexión compuesta oblicua, el valor mínimo del momento debe respetarse necesariamente por separado en cada una de las direcciones principales.

2.3.4 EXCENTRICIDAD DE SEGUNDO ORDEN

Los efectos locales de segundo orden se pueden calcular por métodos aproximados o mediante el método general. Sólo se tienen en cuenta los efectos del segundo orden para los pilares delgados de la mediana, utilizando el método de columna estándar con curvatura aproximada y la columna estándar con rigidez aproximada. Las medianas representan la mayoría de las ocurrencias en las estructuras actuales de los edificios, y los casos de pilares con índices delgados superiores a 90 son inusuales.

• Método de pilar estándar con curvatura aproximada

En el dimensionamiento de pilares con λ ≤ 90, con sección constante y refuerzo simétrico y constante en todo su eje. Este método sólo se utiliza en el caso de la flexión compuesta normal. La no linealidad física se toma mediante una expresión cercana a la curvatura en la sección transversal que expresa el valor de momento de flexión más alto teniendo en cuenta los momentos de primer y segundo orden. El momento total máximo en el pilar, es decir, la suma de los momentos de primer orden con los momentos de 2^o orden, se calcula mediante la expresión: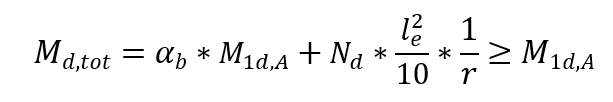

Siendo

α_b es un coeficiente que depende de la distribución de momentos en el pilar.

M_1d,A el valor de cálculo del momento de 1er orden MA;

h la altura de la sección de la columna en la dirección analizada;

ν la fuerza adimensional normal;

f_cd el cálculo de la resistencia a la compresión del hormigón;

M_1d,min el primer momento mínimo de pedido.

Por lo tanto, a partir de la segunda entrega de la expresión anterior, se deduce que la excentricidad de 2o orden (e₂) asume la siguiente expresión:

2.3.5 EXCENTRICIDAD CAUSADA POR FLUIDEZ

Según NBR 6118 (2014) la excentricidad generada por la fluidez del hormigón e_c debe calcularse en pilares con λ > 90, es decir, pilares delgados y esbeltos. No se tienen en cuenta los efectos de la fluidez en pilares con índices de esbeltez inferiores a 90.

Aunque el análisis preciso de los efectos de la fluidez es un trabajo complejo, NBR 6118 aporta una expresión simplificada para el cálculo de la excentricidad e_c , lo siguiente: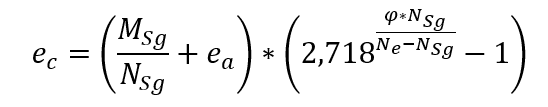Siendo

M_Sg y N_sg los esfuerzos necesarios en el pilar tomado de la combinación casi permanente;

e_a y excentricidad accidental;

φ el coeficiente de fluidez.

E_ci 5,600-* f_ck^0.5 es el módulo inicial de elasticidad del hormigón;

I_c el momento de inercia de la sección del pilar;

l_e longitud equivalente de la pata de columna.

La excentricidad calculada debe añadirse a la excentricidad del 1er orden. La Figura 5 muestra la excentricidad del segundo orden.

Figura 5 – Excentricidades iniciales y de segundo orden en pilares.

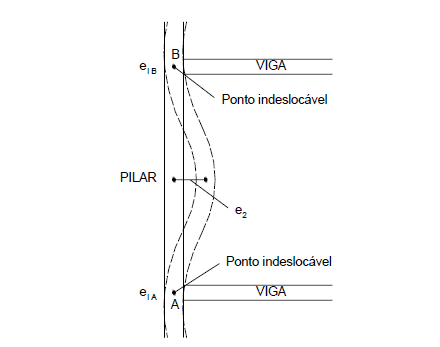
Las secciones finales no implican los efectos del segundo orden y deben considerarse únicamente en la sección intermedia.

2.4 CALCULACION DE REINFORCEMENTO LONGITUDINAL CON LA AYUDA DE ABACU

En el dimensionamiento manual de los pilares, los abaci son indispensables, ya que aportan la rápida definición de la tasa de refuerzo, por lo que no es necesario aplicar las ecuaciones teóricas de la Flexion Compuesta Normal u Oblicua. Además, los abaci permiten elegir fácilmente varios arreglos de armadura en la sección transversal. Los Abaci de Venturini y Rodrigues (2000) para la Flexión Compuesta Normal y de Pinheiro (1994) para la Flexión Compuesta Oblicua sólo deben utilizarse en el dimensionamiento de pilares con hormigones del Grupo de Resistencia I (fck ≤ 50 MPa), ya que fueron elaborados con algunos parámetros numéricos donde no se aplican a los concretos del Grupo II.

2.4.1 FLEXIÓN COMPUESTA NORMAL

Para Venturini y Rodrigues (2000) Normal Composite Flexion, la figura 6 muestra la notación de la aplicación del ábaco. La excentricidad (e) es paralela a la distancia d ‘, entre el centro de la barra de esquina y la cara de la sección. En general, hay d ‘= c + Φt + Φλ / 2, con c = revestimiento de hormigón, Φt = diámetro del estribo y Φλ = diámetro de la barra longitudinal.

Figura 6 – Notación para la flexión compuesta normal.

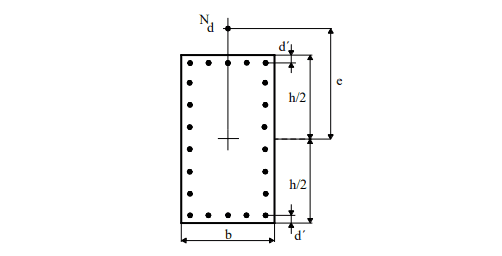
Las ecuaciones utilizadas para la construcción de abaci fueron señaladas en la publicación de Venturini y Rodrigues (2000). La definición del refuerzo longitudinal se inicia calculando los esfuerzos dimensionales n (ni) y μ (mi). El valor adimensional n se definió en la siguiente ecuación:

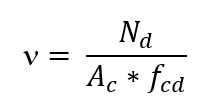El valor de μ, dependiendo del momento o excentricidad del fletor, es:

Siendo

N_d la fuerza normal del cálculo;

A_c el área de la sección transversal del pilar;

f_cd la fuerza de cálculo del hormigón a la compresión (f_ck/γ_c);

M_{d, tot} el momento total fletor momento de cálculo;

(h) el tamaño del pilar en la dirección considerada;

y excentricidad en la dirección considerada.

Una vez elegida una distribución constructiva para la armadura en la columna, se define el ábaco a utilizar, en función del tipo de acero y del valor de la relación d ‘/ h. En el ábaco, con el par ν y μ, se obtiene la tasa mecánica ω. El refuerzo se calcula mediante la expresión:

2.4.2 FLEXIÓN DE COMPUESTOS OBLICUOS

Para Oblique Composite Flexion de Pinheiro (1994), la notación aplicada en el uso de ábacos se muestra en la figura 7. Sin embargo, las distancias d’_x y d’_y tienen la misma interpretación que d ’, cada una en una dirección del pilar.

Figura 7 – Notación para la flexión compuesta normal.

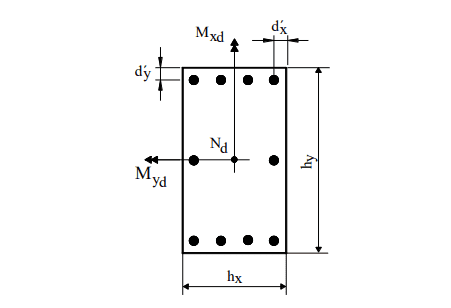
La determinación del refuerzo comienza calculando los esfuerzos dimensionales y μ, con μ de acuerdo con las dos direcciones principales de la columna: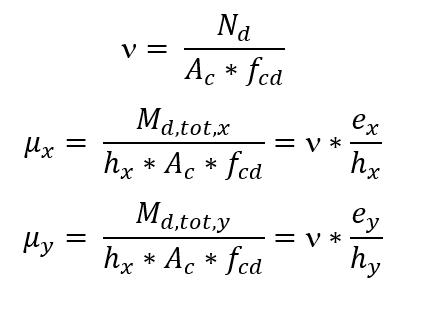 Una vez elegida una distribución constructiva para el refuerzo en la columna, se define el ábaco a utilizar, dependiendo de los valores de las relaciones d’_x/h_x y d’y/h_y y del tipo de acero. En el ábaco, con el trío , se obtiene la velocidad mecánica . El esqueleto se calcula con la siguiente ecuación:

2.5 DETALLE DE LOS PILARES DE HORMIGÓN ARMADO

NBR 6118, 2014 determina que la dimensión de la sección transversal de la columna no debe ser inferior a 19 cm. Esta recomendación tiene como objetivo evitar comportamientos inaceptables para los elementos estructurales y permitir condiciones de construcción adecuadas.

Sin embargo, para casos especiales, se permite que el tamaño de columna más pequeño sea entre 19 cm y 12 cm. Para estos casos, es necesario multiplicar los esfuerzos de cálculo final aplicados en el diseño de las columnas por un coeficiente adicional γ_n, según la imagen 8.

Figura 8 – Valores del coeficiente adicional γ_n.

En primer lugar, la tasa geométrica de refuerzo longitudinal de la columna se define por la siguiente relación: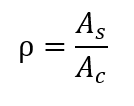

Siendo

A_s suma de las áreas de la sección transversal de las barras longitudinales.

A_c el área de sección transversal del pilar.

El área mínima de refuerzo longitudinal, depende de la intensidad de la solicitud debido a la resistencia normal del acero, se determina por la siguiente expresión: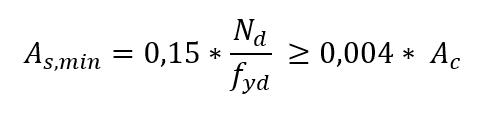 Por lo tanto, la tasa de refuerzo geométrico mínimo es igual a 0,4%.

El área de refuerzo máxima posible en los pilares debe ser del 8% del área transversal, teniendo en cuenta la superposición del refuerzo en las regiones de empalme, es decir: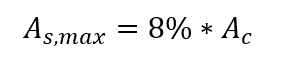

El diámetro mínimo de las barras longitudinales no será inferior a 10 mm y no excederá de 1/8 del tamaño más pequeño de la sección de columna.

Para una concreción adecuada es necesario que el hormigón tenga un mínimo de espacio para atravesar entre los refuerzos longitudinales. Por lo tanto, se imponen limitaciones al espacio libre entre las barras del refuerzo longitudinal (a_L), que debe ser igual o mayor que el superior de los siguientes valores:

• 20 mm;
• La medida de diámetro de la barra, viga o manguito adoptado en la costura;
• 1.2 en su lugar el diámetro máximo del agregado;

El espaciado máximo entre los ejes de las barras de refuerzo también es limitado, y debe ser menor o igual al doble del tamaño más pequeño de la columna, sin exceder 400 mm.

El diámetro de los estribos (φ_t) en los pilares no será inferior a 5 mm o 1/4 del diámetro de la barra longitudinal.

Con el fin de garantizar el posicionamiento de las barras de refuerzo longitudinal y, además, hacer imposible reducir las barras longitudinales y utilizar el refuerzo de costura en las regiones de costura, se requieren espasmos máximos entre los estribos (medidos en la dirección del eje de la columna), siendo inferior o igual al inferior de los siguientes valores:

• 200 mm;
• dimensión de sección más pequeña;
• 24 φ para el acero CA-25 y 12o para acero CA-50, φ es el diámetro de la barra longitudinal;

Cuando exista la posibilidad de pandeo de las barras en la superficie, se deben tomar medidas para evitarlo.

3. MODELADO DE SOFTWARE CAD/TQS

Una de las formas de tener un cálculo estructural detallando, en hormigón armado, más rápido y más preciso (con menos redondeo), es a través del uso de software, uno de ellos se llama TQS, utiliza la plataforma CAD para su funcionamiento. Con TQS podemos obtener los cálculos de esfuerzos y flechas en la estructura, las dimensiones y detalles de los refuerzos en función de las peticiones y el trazado de todo el material necesario, todo ello de acuerdo a lo que el profesional lanzó en la plataforma de dibujo. El TQS hace que todo esto se acotante y detalla de acuerdo con los estándares actuales.

Los sistemas TQS tienen recursos que hacen del desarrollo de proyectos estructurales un proceso altamente productivo. Desde la concepción hasta la emisión de la planta, todos los pasos están automatizados. Sus principales productos son TQS (hormigón reforzado y pretensado), Alvest (albañilería estructural), PREO (prefabricado) y SISEs (geotécnico).

Adaptado a las últimas revisiones regulatorias (NBR 6118/2014, NBR 15200:2012, NBR 15.575:2013, NBR 9062:2006, NBR 15812:2010, NBR 15961:2011. Cada versión de los sistemas TQS se somete a rigurosas pruebas, tanto operativamente como en relación con sus resultados. También están disponibles materiales educativos para todos sus productos, tales como TQS paso a paso, trazado, escaleras paso a paso, Alvest paso a paso (TQS, 2020).

3.1 VERSIÓN ESTRUCTURAL EN TQS/CAD SOFTWARE

La estructura hecha para el análisis fue el ejemplo completo del libro Proyecto Estructural de Edificios de Hormigón Reforzado, de José Milton de Araújo (2014). Para el modelado en el software se lanzaron los pilares, las vigas, las losas, las escaleras, las cargas de pared, secuencialmente en el orden descrito.

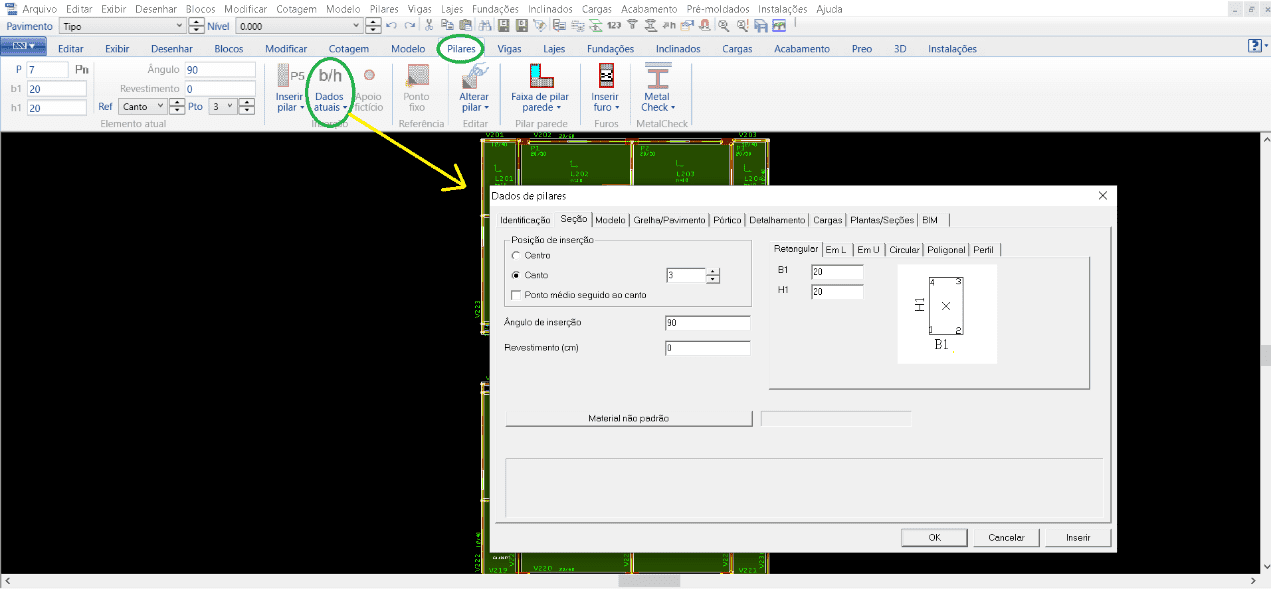
Para los pilares, se siguieron los siguientes pasos: Después de abrir el modelo estructural, la pestaña “Pillars” está activa, se debe abrir la ventana “Datos actuales” (figura 9), donde aparecerán todos los datos para la inserción de la columna, colocando las dimensiones, el número de identificación, la posición de inserción, la determinación de dónde nace y muere el pilar, entre otras informaciones. Al final de todas las ediciones relevantes, se incluyen todos los pilares necesarios.

Figura 9 – Ventana TQS/CAD en la pestaña “Pilares”.

Para la construcción de vigas en el software CAD/TQS, el proceso es el siguiente:

Después de definir todos los pilares, pasamos a la liberación de las vigas. Inicialmente debe activar el menú “Vigas”, donde todos los comandos con los siguientes comandos son específicos de la liberación de las vigas.

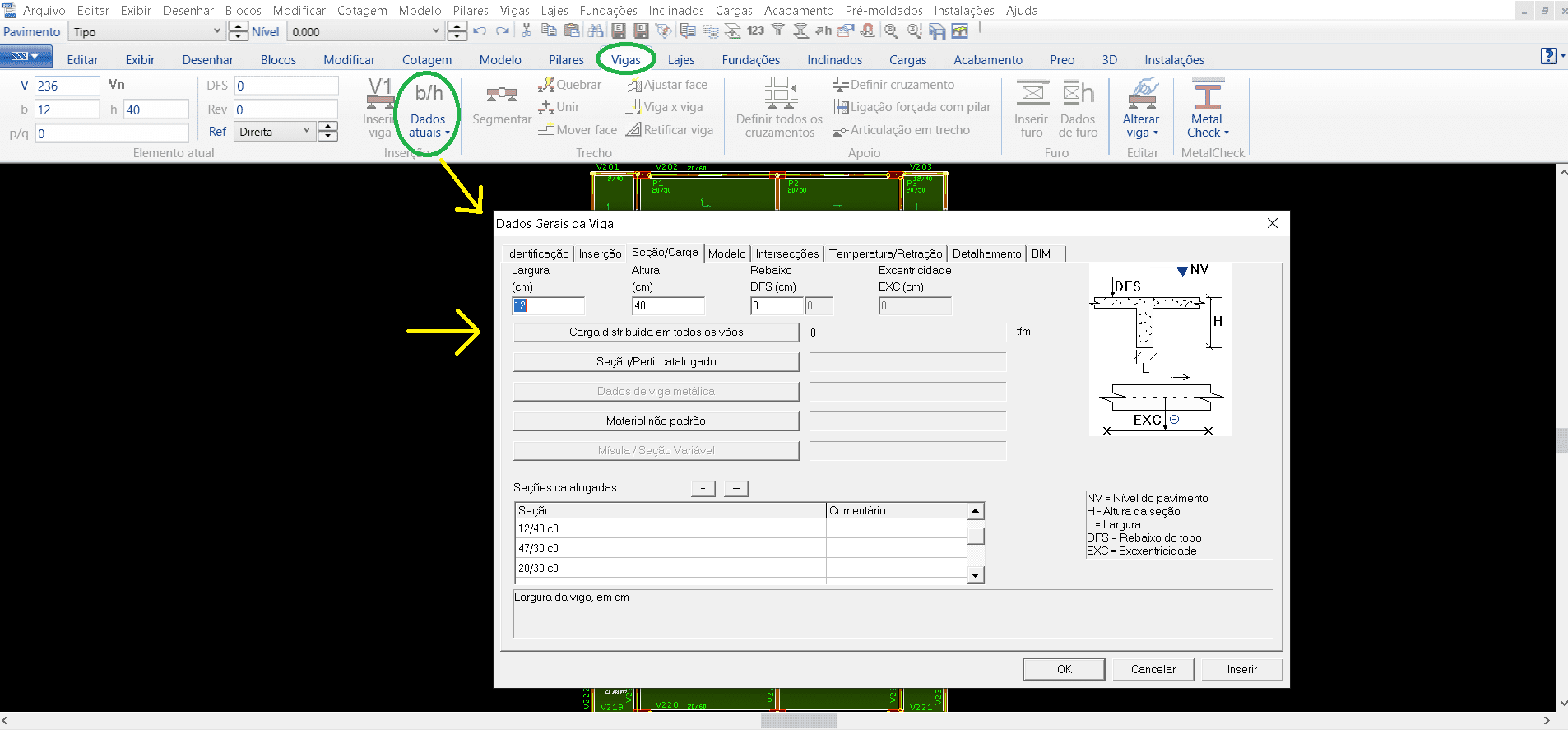
Dentro de la pestaña “Vigas” debe seleccionar el comando de “Datos actuales” (figura 10), donde se abrirá una ventana de los datos generales de las vigas, colocando así toda la información necesaria para la liberación de cada viga. Información como el número de identificación de cada viga, su cubierta, las cargas que esta viga actuará sobre los pilares, como el permanente y accidental, su sección. Después de todo este proceso de detalle, podemos insertar la viga, colocando en el punto inicial y luego en el punto final, por lo general estos puntos de inserción son los vértices de los pilares ya insertados previamente, repitiendo el mismo procedimiento hasta colocar todas las vigas necesarias.

Figura 10 – Ventana TQS/CAD en la pestaña “Vigas”.

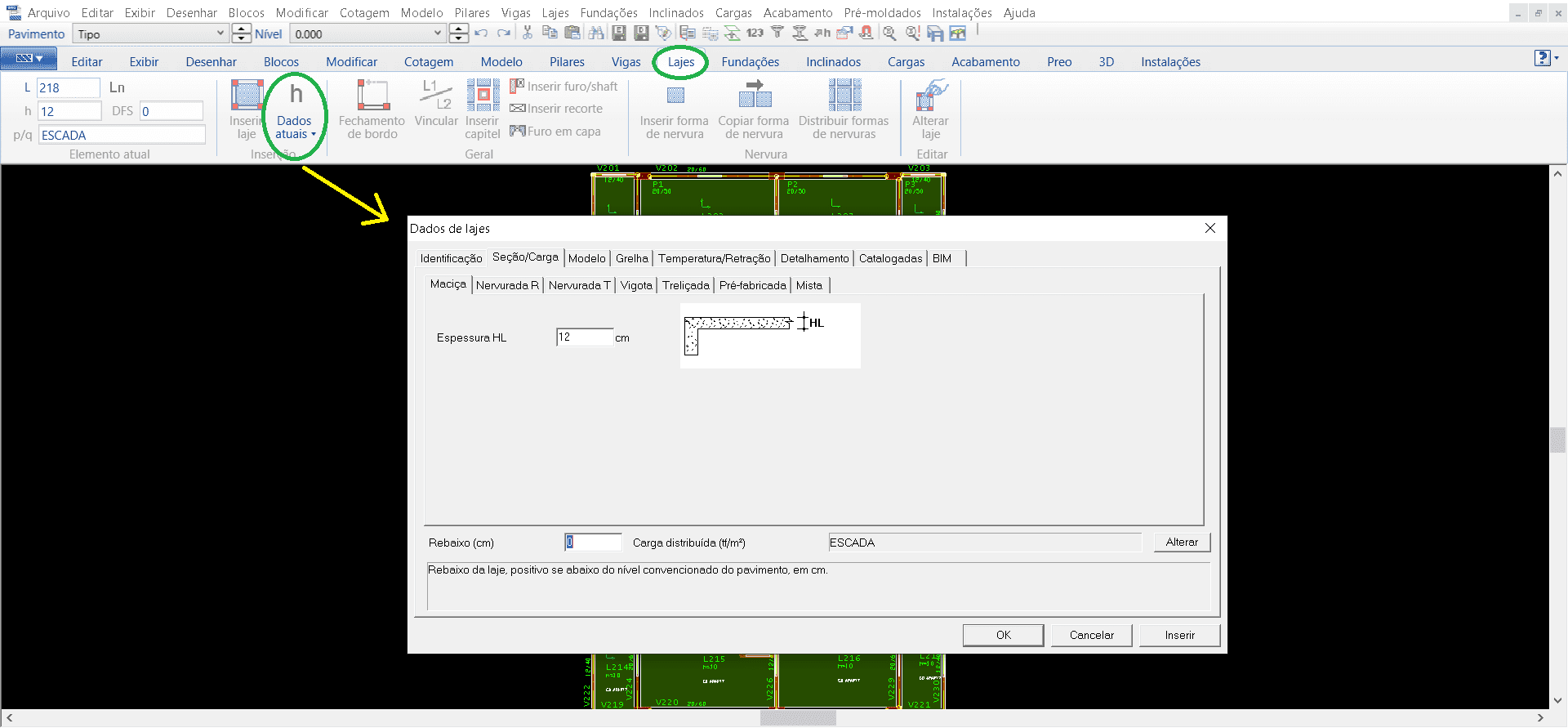
Tras las vigas lanzadas, pasamos a las losas, siguiendo los mismos procedimientos que los dos anteriores en “Losas” seleccionando “Datos actuales” para identificar el tipo de losa y su espesor (imagen 11).

Figura 11 – Ventana TQS/CAD en la pestaña “Losas”.

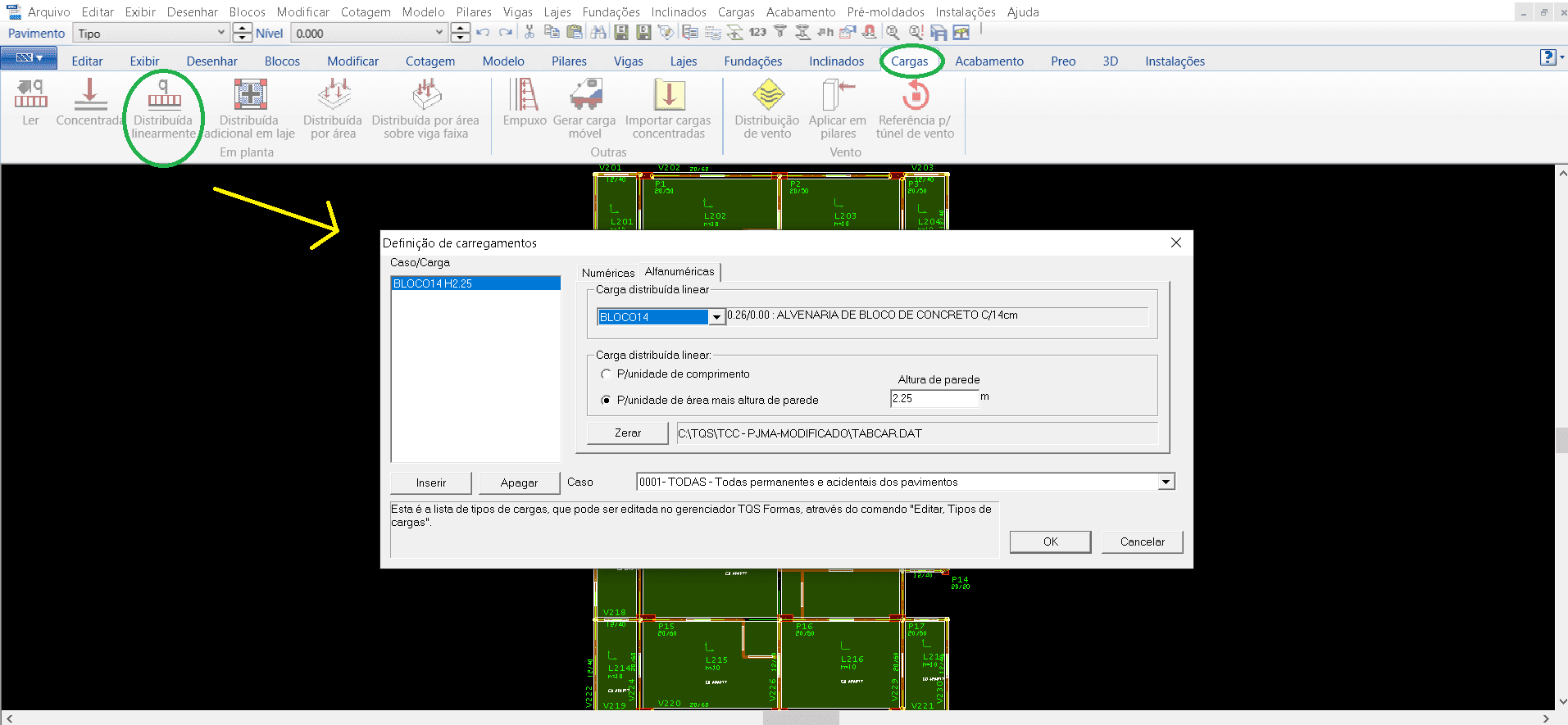
Para la contabilización de cargas de muro sigue la misma línea de procedimientos. En la ventana “Cargas” selecciona la pestaña “Distribuido linealmente”, luego abre una ventana para la selección del tipo de carga, para el modelado en cuestión se insertó el bloque 14 (albañilería de bloque de hormigón 14 cm) y la altura del muro determinado (imagen 12).

Fuente: Figura 12 – Ventana TQS/CAD en la pestaña “Cargas”.

Por lo tanto, al finalizar el lanzamiento de todos los elementos necesarios en los pisos, debemos guardar los datos definidos hasta ahora en el menú “Archivo” en el comando “Guardar el modelo estructural”.

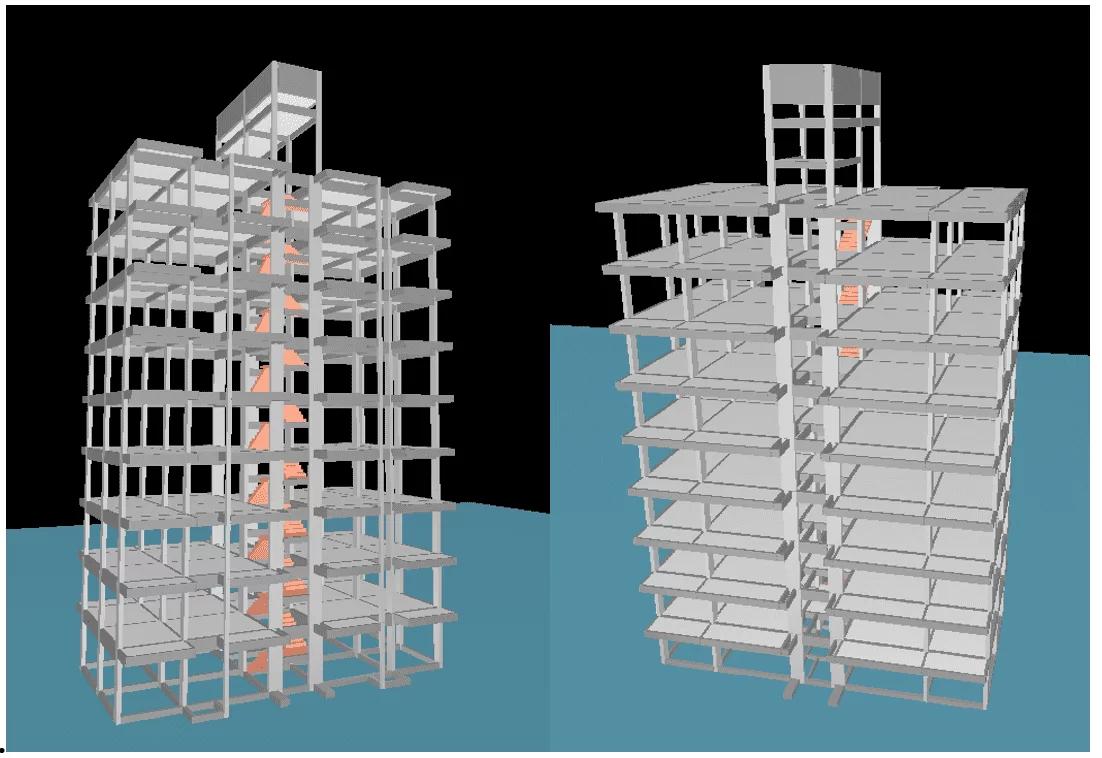
Figura 13 – Creación de ejemplo 3D, TQS/CAD

Usando el visor tridimensional tenemos la idea concreta de cómo sería el edificio de ejemplo (figura 13).

La aplicación P-Calc es una calculadora TQS que comprueba los pilares de hormigón armado sujetos a flexión compuesta oblicua individual (TQS, 2020).

Las principales características de P-Calc son:

• Verificación de los pilares sometidos a flexión compuesta, normal u oblicua, en relación con el último límite de estado de ruptura e inestabilidad;
• Análisis de pilares con hormigón de alta resistencia (fck > 50 MPa);
• Esfuerzo normal x diagrama de interacción del momento deflector (FCO y FCN);
• Resultados gráficos para tensiones y deformaciones en la sección;
• Evaluación de los efectos locales del segundo orden adoptando la no linealidad geométrica y física, según ABNT NBR 6118;
• Envelomycista de momentos mínimos;
• Memoria de cálculo en formato PDF;

4. PRESENTACIÓN Y ANÁLISIS DE RESULTADOS

En este tema se presentan las comparaciones entre las referencias de los elementos estudiados. Se dividió en subtemas para los principales elementos de un proyecto estructural. Se destaca que las referencias estudiadas fueron la base del proyecto del libro “PROJETO ESTRUTURAL DE EDIFÍCIOS DE CONCRETO ARMADO” de JOSÉ MILTON DE ARAÚJO, 3^a edición, modelado, calculado y detallado en el TQS. Para las otras pruebas, algunos elementos se compararon con otras herramientas de cálculo como Pcalc y Bending Abaci para los datos de los pilares.

4.1 MODELADO Y DIMENSIONAMIENTO COMPARATIVO – PILAR

Tras el modelado y dimensionamiento de los pilares, según el tema 3, se comparó el principal esfuerzo, sección y área de acero entre las referencias estudiadas para los dos pilares (P2 y P5) según el resumen de las tablas 01 y 02.

Cuadro 1 – Presentación de los resultados en comparación con el pilar 2

Elementos	Esfuerzos característicos (tf)	Sección (cm x cm)	Zona de acero (cm2)
Araujo (2014)	71,4	20 x 50	6ϕ20 (18,90)
TQS	66,2	20 x 50	8ϕ20 (25,20)
Pcalc*	71,4	20 x 50	10ϕ20 (31,50)
Pcalc*	66,2	20 x 50	10ϕ20 (31,50)
Ábacus- Flexion normal*	71,4	20 x 50	6ϕ20 (18,90)
Ábacus- Flexion normal*	66,2	20 x 50	4ϕ20 (12,60)

*Solución de pilar estándar con curvatura aproximada.

Fuente: Autor, 2020.

Se puede observar, analizando las comparaciones para el pilar P2 que el dimensionamiento del Araújo (2014) en relación con el TQS muestra un aumento del 33,33% en la zona siderúrgica, teniendo en cuenta que Araújo presenta una fuerza normal un 7,85% mayor, ya en relación con el PCalc, hubo un incremento del 66,67%, correlacionándolos con la misma carga.

Es interesante notar que estos mismos valores en relación con el dimensionamiento de la columna estándar con curva aproximada utilizando la Flexion Abaci Normal (VENTURINI y RODRIGUES, 2000), se separaron en dos grupos de cargas porque el modelado realizado en el TQS difiere del estudio de carga de Araújo (2014) por lo que tenemos las figuras 14 y 15.

Figura 14 – Comparación entre TQS x Pcalc x Abaci para el pilar 2

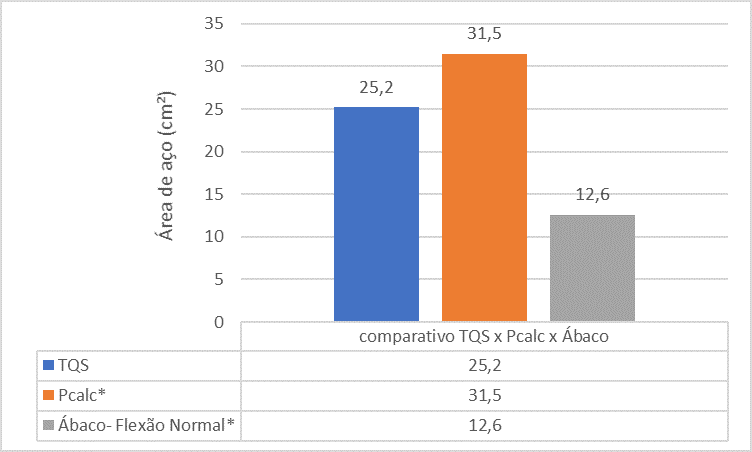
El análisis comparativo entre las referencias muestra que el área de acero de la columna P2 encontrada por la herramienta TQS es más pequeña que el área de acero encontrada por Pcalc y Abaci. Esto se debe al hecho del análisis monolítico realizado en el programa.

Figura 15 – Comparación entre Araújo (2014) x Pcalc x Abacos para Pilar 2

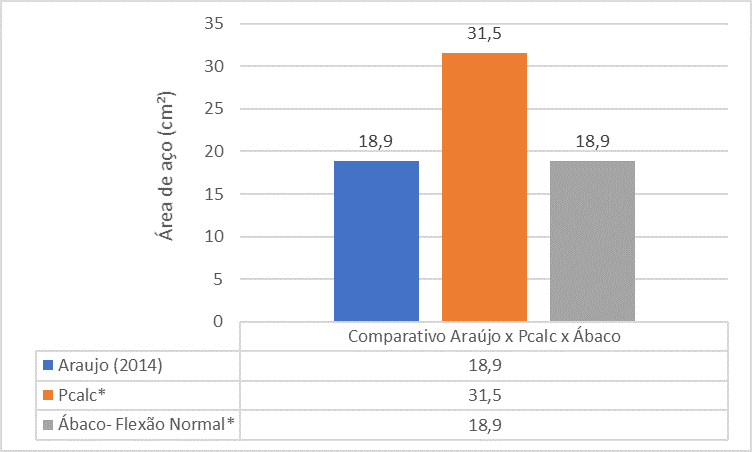
El análisis comparativo entre las referencias muestra que la superficie de acero del pilar P2 encontrada por el libro de Araújo (2014) es mucho menor que la zona de acero encontrada por The PCalc y Abacus.

El pilar P2 es una columna final, soporte intermedio para la viga V202, en la dirección x, sin tener en cuenta estos momentos transmitidos. En la dirección y tenemos el haz V 227, esto fue considerado los momentos transmitidos en el pilar. A partir de este análisis, el momento de ajuste perfecto (M_eng) fue cálculo, momento de inercia de haz (I_vig), coeficiente de rigidez del haz (r_vig), momento de inercia de los pilares (I_p), coeficiente de rigidez de los pilares (r_p) y momentos iniciales en los pilares (M_p), a partir de los cálculos, se obtienen los momentos reducidos, pero dividir la gran diferencia entre ellos, se consideraron cero y tamaño de la sección en flexo – compresión normal en la dirección.

Para la fuerza normal en el eje x tenemos el índice de esbeltez (λ_x) excentricidades iniciales (e_ia), excentricidad accidental (e_ax), excentricidad mínima (e_{1x, min}), excentricidad inicial en la sección intermedia (e_ix), excentricidad de segundo orden (e_2x) y excentricidad de fluidez (e_cx). La sesión crítica fue en la sesión de extremidades, utilizando las mesas de área de acero se puede armar la sesión con 6 barras de 20 mm, adoptando un área de acero total igual a 18,85 cm².

Cuadro 2 – Presentación de los resultados en comparación con el pilar 5

Elementos	Esfuerzos característicos (tf)	Sección (cm x cm)	Zona de acero (cm2)
Araujo (2014)	112,2	20 x 50	10ϕ16 (20,00)
TQS	141,5	20 x 50	8ϕ25 (40,00)
Pcalc*	112,2	20 x 50	12ϕ20 (37,80)
Pcalc*	141,5	20 x 50	12ϕ25 (60,00)
Ábacus- Flexion normal*	112,2	20 x 50	8ϕ25 (40,00)
Ábacus- Flexion normal*	141,5	20 x 50	11ϕ25 (55,00)

*Solución de pilar estándar con curvatura aproximada.

Fuente: Autor, 2020.

Se puede observar, analizando las comparaciones para el pilar P5 que, El dimensionamiento de Araújo (2014) en relación con el TQS muestra un aumento del 100% en la superficie siderúrgica, teniendo en cuenta que Araújo tiene una resistencia normal un 26,11% inferior, ya en relación con el PCalc, hubo un aumento del 89% en relación con la carga de Araújo, y del 50% en relación con la carga del TQS, hubo un aumento del 89% en relación con la carga de araújo, y del 50% en relación con la carga del TQS , mostrando que cuanto mayor sea el aumento de la carga, mayor será la divergencia de las áreas de acero. Se puede decir que esta divergencia se debe al hecho de presentar el siguiente error para la resolución del pilar P5 en el Pcalc, para Araújo (2014) en el último estado límite (ELU): El pilar no presta atención a la verificación del momento mínimo. El pilar con la carga de TQS en el Pcalc genera el siguiente error de 5,89% >.max a 4,00%.

Es interesante notar que estos mismos valores en relación con el dimensionamiento de la columna estándar con curva aproximada utilizando la Curva de Flexión Normal (VENTURINI y RODRIGUES, 2000), se separaron en dos grupos de cargas porque el modelado realizado en el TQS difiere del estudio de carga de Araújo (2014) por lo que tenemos las figuras 16 y 17.

Figura 16 – Comparación entre TQS x Pcalc x Abaci para el pilar 5

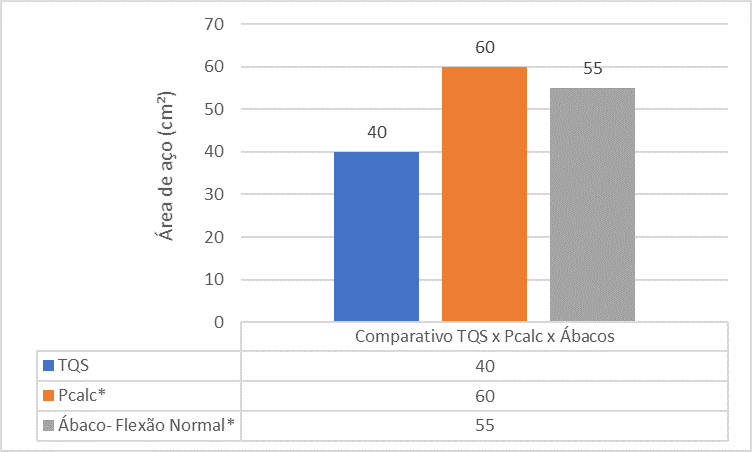
El análisis comparativo entre las referencias muestra que el área de acero del pilar P5 encontrada por la herramienta TQS es más pequeña que la zona de acero encontrada por el Pcalc y Abaci. Esto se debe al hecho del análisis monolítico realizado en el programa.

Figura 17 – Comparación entre Araújo (2014) x Pcalc x Abacos para Pilar 5

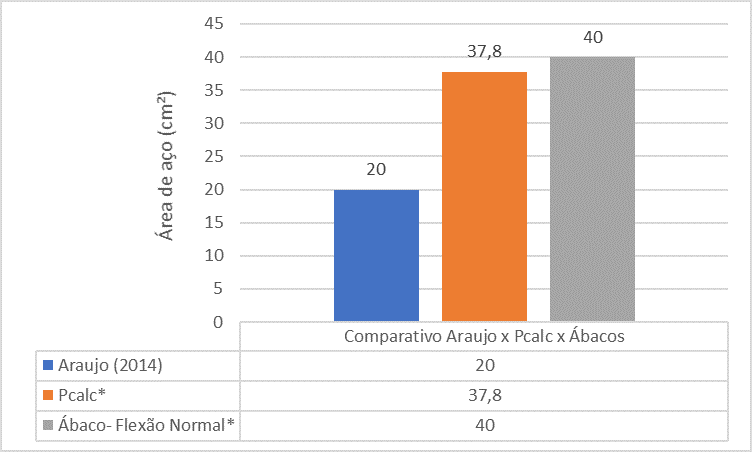
El análisis comparativo entre las referencias muestra que el área de acero del pilar P5 encontrada por el libro de Araújo (2014) es mucho más pequeña que la zona de acero encontrada por The PCalc y Abacus.

El pilar P5 es un pilar intermedio, con los vanos y cargas de vigas V204 y V227, no difieren entre sí, por lo que uno puede ignorar los momentos iniciales transmitidos por estas vigas. A partir de este análisis, el cálculo se realizó en el eje Y, porque era el índice de esbeltez más alto (λ_x) encontrado, de excentricidad (e_y), dada por la suma de excentricidad de primer orden (e_1x), excentricidad de segundo orden (e_2x) y excentricidad de fluidez (e_cy). Usando las mesas de área de acero la sesión puede ser armada con 10 barras de 16 mm, adoptando un área de acero total igual a 20.00 cm2.

5. CONCLUSIÓN

Observó que la comparación entre los métodos es importante para elegir la mejor herramienta para su uso en el dimensionamiento de pilares.

Reproduciendo el modelado del edificio de Araújo en el TQS, se notó una diferencia de carga, y para estas cargas se percibe que la herramienta TQS en modo predeterminado está cerca del dimensionamiento de la herramienta PCalc y Abaci para pilares intermedios.

En los pilares finales del araújo muestra una menor variación de las respuestas en relación con Abaci y PCalc.

Por lo tanto, el análisis comparativo entre los métodos de cálculo es diferente debido al hecho de que el análisis monolítico de la estructura realizado en la herramienta TQS, diferente de los otros métodos que presentan el análisis segmentado de los elementos con formas de cálculo simplificadas.

REFERENCIAS

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 1978.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2003.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2014.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15200. Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro, — Procedimento, 2012.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15575. Edificações habitacionais – Desempenho. Rio de Janeiro, — Procedimento, 2013.

ABNT (Associação Brasileira de Normas Técnicas). NBR 9062. Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, — Procedimento, 2006.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15812. Alvenaria estrutural – Blocos cerâmicos. Rio de Janeiro, — Procedimento, 2010.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15961. Alvenaria estrutural – Blocos de concreto. Rio de Janeiro, — Procedimento, 2011.

AGUIAR, E.A.B. Projeto de pilares de concreto de alto desempenho. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2000.

ARAUJO, José Milton de. Projeto estrutural de edifícios de concreto armado. 3. ed. Rio Grande: Editora Dunas, 2014.

BASTOS, Paulo S. dos Santos. Fundamentos do Concreto Armado. Universidade Estadual Paulista. Bauru, São Paulo. 2006.

BRANDÃO, A. M. S.; PINHEIRO, L. M. Qualidade e durabilidade das estruturas de concreto armado: aspectos relativos ao projeto. Cadernos de Engenharia de Estruturas. EESC. Universidade de São Paulo. São Carlos, 1999.

CARVALHO, Roberto Chust.; FIGUEIREDO FILHO, Jasson Rodrigues de. Pilares de concreto armado. p.9-25. Notas de aula – Universidade Federal de São Carlos, 2002

FUSCO, P.B. Estruturas de concreto – solicitações normais, editora Guanabara, São Paulo, 1986.

PIANCASTELLI, E. M. Patologia, Recuperação e Reforço de Estruturas de Concreto Armado. Apostila para Curso de Extensão, Ed. Depto. Estruturas da Escola de Engenharia da UFRG, Belo Horizonte, 1997

PINHEIRO, L.M.; BARALDI, L.T.; POREM, M.E. Concreto Armado: Ábacos para flexão oblíqua. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1994.

TQS, Calculadora P-Calc, Pilares de concreto, 2020. Disponível em: <https://www.tqs.com.br/apps/p-calc/ejm1se496l>

TQS, Sobre a TQS, 2020.Disponível em: <https://www.tqs.com.br/about>

VENTURINI, Wilson Sérgio; RODRIGUES, Rogério de Oliveira. Dimensionamento de peças retangulares de concreto armado solicitadas à flexão reta. San Carlos, Departamento de Ingeniería Estructural, Escuela de Ingeniería de San Carlos – USP, 1987 (reimpreso.2000)

^[1] Licenciado en Ingeniería Civil.

^[2] Graduado en Ingeniería Civil.

^[3] Máster en Geotecnia y Construcción Civil. Graduación en Ingeniería Civil. Graduación en Ingeniería Agrícola.

Enviado: Mayo, 2020.

Aprobado: Mayo, 2020.