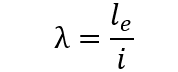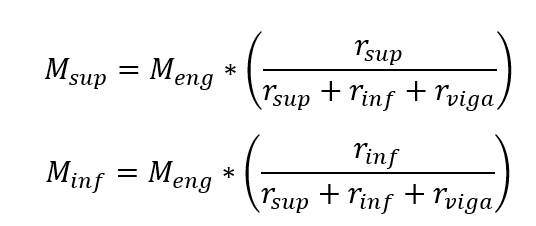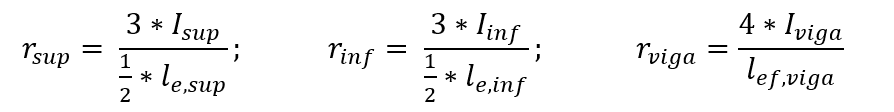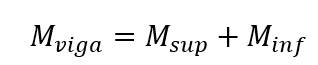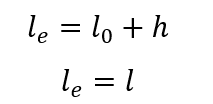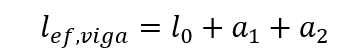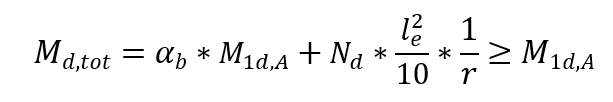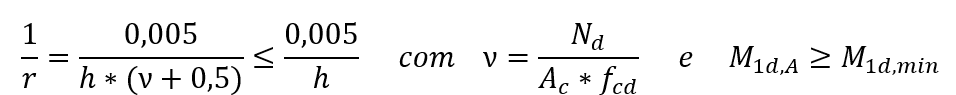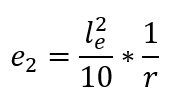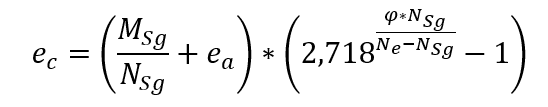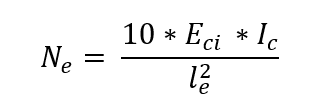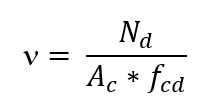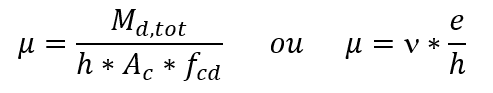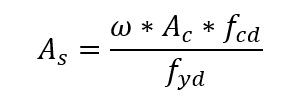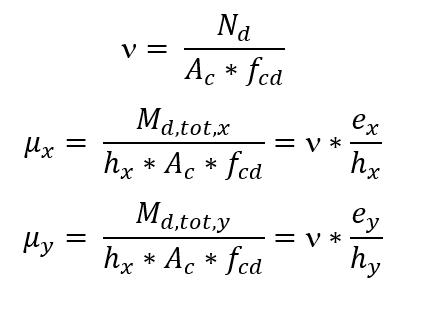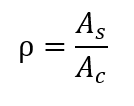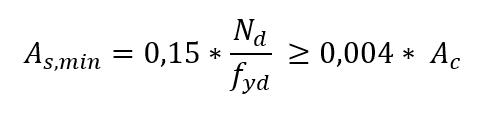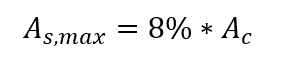Comparativo de dimensionamento e modelagem de pilares

ARTIGO ORIGINAL

CARVALHAES, Daniely Silva ^[1], CARVALHAES, Daniel José ^[2], QUARESMA, Wanessa Mesquita Godoi ^[3]

CARVALHAES, Daniely Silva. CARVALHAES, Daniel José. QUARESMA, Wanessa Mesquita Godoi. Comparativo de dimensionamento e modelagem de pilares. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 05, Vol. 04, pp. 121-146. Maio de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/modelagem-de-pilares, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-civil/modelagem-de-pilares

RESUMO

A busca pela redução do tempo na elaboração de projetos se torna uma necessidade, juntamente com a indigência do entendimento de problemas recorrentes no uso de estruturas em concreto armado como as patologias. De tal modo, unindo as duas problemáticas, tempo e análise, se torna imperativo estudar formas de modelar e analisar as estruturas em softwares usuais de desenvolvimento de projetos. Objetiva-se modelar um edifício e comparar um elemento estrutural, analisando as cargas e dimensionamentos feitos pelo software TQS®. Esse processo se dá pela modelagem no software TQS do edifício exemplo de José Milton de Araújo (2014). Observou-se que o processo de modelagem em comparação com o processo numérico apresenta diferença significativa pelo fato de fazer a análise do edifício completo, assim sendo confiável a modelagem realizada no software o que permite um estudo prévio de toda estrutura.

Palavras-Chave: Pilares, dimensionamento, modelagem, experimental, TQS.

1. INTRODUÇÃO

Bastos (2006, p. 07) apresenta o concreto armado sendo “a união do concreto simples e de um material resistente à tração (envolvido pelo concreto) de tal modo que ambos resistam solidariamente aos esforços solicitantes”, isto é o concreto armado é o resultado do concreto simples mais armadura mais a aderência.

Para Piancastelli (1997), o concreto armado se sujeita a alterações ao longo do tempo, por ser um material não inerte, graças a interações entre seus elementos constitutivos (cimento, areia, brita, água e aço), interações entre esses elementos e agentes externos como gases, sais, bases, ácidos e outros, e com materiais que lhe são acrescentados (aditivos e adições minerais).

Por um grande espaço de tempo o concreto foi considerado um material durável, devido a obras antigas ainda estar em bom estado, porém a deterioração precoce de estruturas atuais nos encaminha aos porquês das patologias do concreto (BRANDÃO e PINHEIRO, 1999). Isso se deve as novas tecnologias, para deixar as estruturas mais esbeltas e leves, do processo de planejamento e produção das estruturas.

Pilares são elementos usualmente alinhados verticalmente em seu eixo, em que forças normais de compressão são preponderantes (ABNT NBR 6118, 2014), o seu estudo é uma das verificações essenciais, quanto ao dimensionamento, o mau funcionamento de um pilar de uma estrutura pode comprometer a funcionalidade e provocar graves acidentes. Sendo responsáveis pela transmissão de cargas verticais, os pilares estão geralmente sujeitos, em particular, à condição de flexo-compressão, portanto a necessidade da consideração de efeitos de segunda ordem e de análise de estabilidade do pilar como um todo.

Os pilares são dimensionados de acordo com os esforços externos solicitantes de cálculo, que compõem as forças normais (N_d), os momentos fletores (M_dx e M_dy) e as forças cortantes (V_dx e V_dy) sendo de ação horizontal. A NBR 6118, na versão de 2003, particularmente em ralação aos pilares, a norma inseriu diversas modificações, como no valor da excentricidade acidental, um cobrimento maior de concreto, um novo método no cálculo da esbeltez limite referente à contemplação ou não dos momentos fletores de 2ª ordem e, sobretudo, com a consideração do momento fletor mínimo, podendo substituir o momento fletor em consequência da excentricidade acidental. A versão de 2014 adicionou a verificação do momento fletor mínimo, feita a partir da comparação de uma envoltória resistente, que inclua a envoltória mínima com 2ª ordem.

2. CÁLCULO E DIMENSIONAMENTO DE PILARES POR ÁBACOS

2.1 CLASSIFICAÇÃO DOS PILARES

Os pilares são classificados conforme a sua posição na estrutura, ele pode ser intermediário, de extremidade ou de canto. Essa classificação permite considerar os esforços solicitantes em cada situação calculada. (FUSCO,1981)

Figura 1 – Posição dos pilares em edifícios.

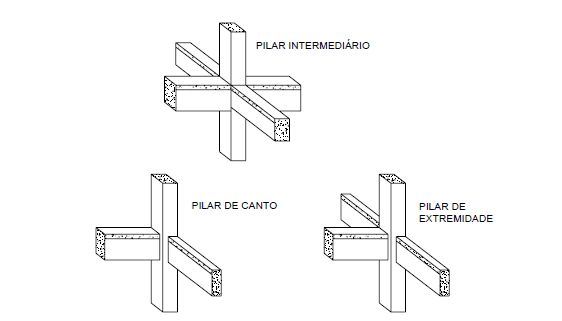
Pilares intermediários são submetidos predominante ás forças axiais de compressão, pois os momentos fletores são de pouca intensidade, quanto somente às ações verticais (as permanentes e as variáveis normais). A não ser que os vãos das vigas contínuas que se apoiam nesses pilares sejam considerados diferentes, desconsideram-se os momentos fletores finais transmitidos aos pilares. Portanto, admite-se o pilar intermediário submetido a uma compressão centrada em situação de projeto, isto é a excentricidade inicial, no dimensionamento das áreas das armaduras transversal e longitudinal, é considerada igual a zero.

Os pilares de extremidade estão submetidos às forças normais de compressão e a ação de momentos propagados pelas vigas, que têm suas extremidades externas apoiadas nesses pilares. Nas vigas transversais ao eixo da viga interrompida, não são considerados os momentos. Portanto, considera-se o pilar de extremidade sujeito à flexão normal composta, considerando-se, portanto, excentricidade inicial em uma das ordenadas locais da seção transversal do pilar.

Pilares de canto além de submetidos à força normal de compressão atuante, deve-se considerar os momentos transmitidos pelas vigas, da qual os planos médios são perpendiculares às faces dos pilares, e são interrompidas nas bordas do pilar. Na situação de projeto, considera-se o pilar de canto submetido à flexão oblíqua composta, com excentricidades inicias segundo os eixos coordenados locais.

Os pilares, embora sua classificação pela sua posição na estrutura ser muito usual, também são classificados quanto ao tipo de solicitação que o pilar está submetido. Ou seja, pilares submetidos a flexão composta normal, pilares submetidos a flexão composta oblíqua e pilares submetidos a compressão centrada.

2.2 ÍNDICE DE ESBELTEZ

O índice de esbeltez dos pilares de concreto armado é a razão entre o comprimento equivalente (l_e) do pilar e o raio de giração (i) da seção. (NBR 6118, 2014)

A classificação dos pilares depende dos limites de esbeltez e de fatores adicionais, tais como a excentricidade relativa, da forma do diagrama de momentos fletores e as condições de vinculação das extremidades. Esses fatores são considerados por meio do coeficiente λ₁.

Para NBR 6118 (2014) pilares curtos (λ ≤ λ₁) os efeitos de segunda ordem poderiam ser desconsiderados pois os índices de referência são maiores que os índices de esbeltez. Pilares medianamente esbeltos (λ₁ < λ ≤ 90) que são aqueles para os quais podem ser considerados, por processo aproximado, os efeitos de segunda ordem, como o método do pilar-padrão com curvatura aproximada. Pilares esbeltos (90 < λ ≤ 140) são aqueles para os quais é possível considerar o método do pilar-padrão junto a diagramas de M – N – 1/r. Pilares muito esbeltos (140 < λ ≤ 200) que exigem, para a verificação do estado de limite de instabilidade, a consideração dos métodos exatos. A NBR 6118 não permite que se projete e construa pilar com índice de esbeltez (λ) maior do que 200. Em caso de postes com força normal menor do que 0,10.f_cd.A_c, esse limite pode ser ultrapassado.

2.3 EXCENTRICIDADES

Nos pilares, as excentricidades acontecem não apenas por causa das solicitações iniciais atuantes nos pilares, mas também por conta de fatores adicionais como os efeitos de 2ª ordem, a fluência do concreto e as imperfeições geométricas.

É preciso obter as excentricidades relacionadas ao tipo de pilar analisado para fazer seu dimensionamento. Neste item apresentam-se os critérios para a obtenção dessas excentricidades em pilares separadamente, de acordo com a norma NBR 6118, 2014.

2.3.1 EXCENTRICIDADE INICIAL DE 1ª ORDEM

Sabemos que as vigas e os pilares compõem pórticos tridimensionais, de maneira que os pilares ficam submetidos a flexão oblíqua composta e, consequentemente, apresentam excentricidades iniciais em duas direções principais. Em projetos que se consideram processos simplificados para a definição dos esforços solicitantes são eles momento fletor, força normal e força cortante, por exemplo, o caso de viga contínua apresentado na NBR 6118 (2014), admite-se que as excentricidades iniciais surgem nos pilares de canto e nos de extremidade. Lembrando que as excentricidades não são consideradas para os pilares intermediários.

As excentricidades de 1ª ordem são dadas pelas expressões:

N_d  seria a força solicitante de cálculo;

M_d,A e M_d,B os momentos solicitantes de cálculo nas extremidades do pilar.

Adota-se a maior excentricidade em valor absoluto para e_i,A.

Quando não for calculado valores exatos dos esforços solicitantes na estrutura, permite-se adotar a forma estática indicado na figura 2, para a obter dos momentos fletores nos apoios extremos, como simplificação.

Figura 2 – Modelo considerado nos casos de apoio extremos de vigas continuas.

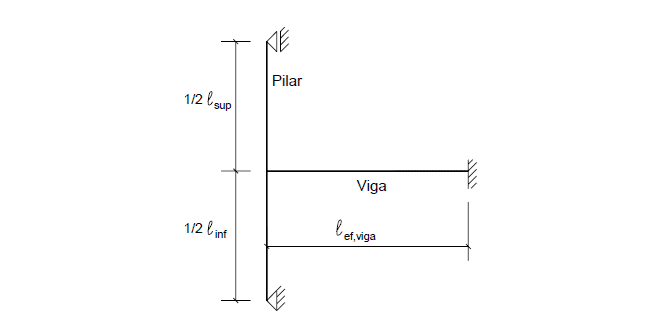
Os momentos solicitantes nos tramos superior e inferior do pilar são obtidos por:

Sendo, M_eng o momento de engastamento perfeito no tramo analisado (tramo de extremidade) da viga.

Os coeficientes de rigidez dos tramos superior e inferior do pilar e no tramo da viga, são definidos pelas relações entre momentos de inércia e vãos, conforme as expressões a seguir:

O momento fletor na viga é determinado pela expressão seguinte, considerando o equilíbrio do nó.

O comprimento equivalente l_e do pilar pode ser determinado pela expressão:

sendo que:

l_o a distância entre as faces internas dos elementos estruturais, supostos horizontais, que vinculam o pilar.

h a altura da seção transversal do pilar, conhecida no plano da estrutura.

l a distância entre os eixos dos elementos estruturais aos quais o pilar está vinculado.

Já os vãos efetivos das vigas podem ser calculados pela expressão:

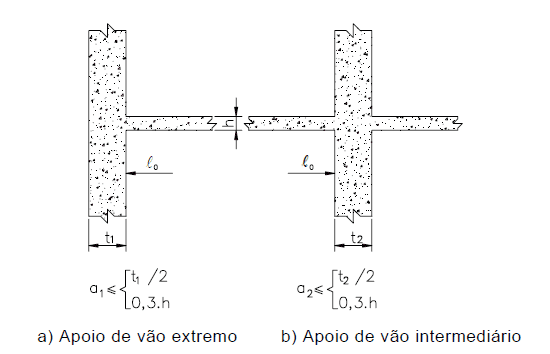
Os valores de a₁ e a₂, em cada extremidade do vão, podem ser calculados pelos valores apropriados de a_i, indicado na figura 3, sendo:

a₁ igual ao menor valor entre (t₁/2 e 0,3 * h).

a₂ igual ao menor valor entre (t₂/2 e 0,3 * h).

Figura 3 – Vão efetivo de vigas.

2.3.2 EXCENTRICIDADE DE FORMA

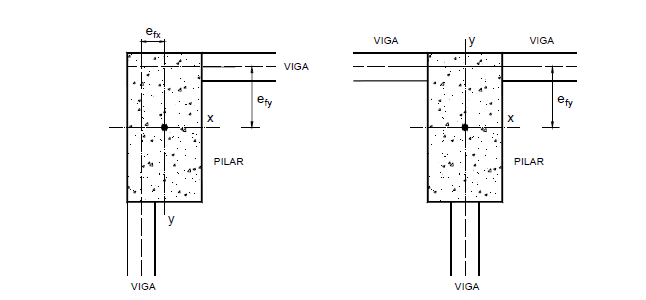
Para ajustar a posição dos elementos estruturais em função do projeto arquitetônico, os projetistas estruturais precisam compatibilizar as faces internas ou externas das vigas com as dos pilares que as recebem. Quando isso acontece os eixos das vigas não passam pelo centro de gravidade da seção do pilar (figura 4), surgindo assim excentricidades denominadas excentricidades de forma (AGUIAR. 2000).

Figura 4 – Excentricidade de forma em pilares.

As excentricidades de forma, quando feito os projetos e estruturas de edifícios, não são consideradas no dimensionamento, sem a ajuda de programas computacionais elaborados para este fim. O momento fletor gerado pelas excentricidades no nível de cada andar é nivelado por um binário, provocando, em cada piso, pares de forças de mesma ordem de grandeza e de sentidos contrários, que se anulam. Programas computacionais elaborados para análise estrutural e dimensionamento com verificações de aberturas de fissuras e os critérios dos estados limites últimos e deslocamentos com os parâmetros dos estados limites de serviço, levam em conta essas excentricidades de forma.

2.3.3 EXCENTRICIDADE ACIDENTAL

A NBR 6118 (2014) prevê o cálculo de uma excentricidade acidental (e_a), levando em conta as situações de imperfeição local por decorrência da construção dos pilares, podem ser pelo desaprumo do eixo do pilar.

De acordo com a NBR 6118 (2014), nas estruturas reticuladas usuais, admite-se que o efeito das imperfeições locais se encontra resolvido caso for considerado o valor do momento total mínimo. No caso de flexão composta oblíqua, o valor do momento mínimo necessariamente tem que ser respeitado, separadamente, em cada uma das direções principais.

2.3.4 EXCENTRICIDADE DE SEGUNDA ORDEM

Os efeitos locais de segunda ordem podem ser calculados por métodos aproximados ou pelo método geral. Somente é considerada os efeitos de 2ª ordem para os pilares medianamente esbeltos, utilizando o método do pilar padrão com curvatura aproximada e o de pilar padrão com rigidez aproximada. Os pilares medianamente esbeltos representam a maior parte das ocorrências em estruturas atuais de edifícios, sendo que os casos de pilares com índices de esbeltez superiores que 90 são incomuns.

• Método do pilar padrão com curvatura aproximada

No dimensionamento de pilares com λ ≤ 90, com seção constante e armadura simétrica e constante no decorrer do seu eixo. Este método empregasse somente ao caso de flexão composta normal. A não-linearidade física é tida por uma expressão próxima da curvatura na seção transversal que expressa maior valor de momento fletor considerando os momentos de primeira e segunda ordens. O momento total máximo no pilar, isto é, a soma dos momentos de 1ª ordem com os momentos de 2ª ordem, é calculado pela expressão:

Sendo

α_b um coeficiente que depende da distribuição de momentos no pilar.

M_1d,A  o valor de cálculo do momento de 1ª ordem M_A;

h a altura da seção do pilar na direção analisada;

ν a força normal adimensional;

f_cd a resistência a compressão de cálculo do concreto;

M_1d,min  o momento de 1ª ordem mínimo.

Dessa forma, começando da segunda parcela da expressão anterior, deduz-se que a excentricidade de 2.ª ordem (e₂) assume a seguinte expressão:

2.3.5 EXCENTRICIDADE CAUSADA PELA FLUÊNCIA

Segundo a NBR 6118 (2014) a excentricidade gerada pela fluência do concreto e_c deve ser calculada em pilares com λ > 90, isto é, pilares esbeltos e muitos esbeltos. São desprezados os efeitos da fluência em pilares com índices de esbeltez menores que 90.

Embora a analise precisa dos efeitos da fluência seja um trabalho complexo, a NBR 6118 traz uma expressão simplificada para o cálculo da excentricidade e_c, aprestada a seguir:

Sendo

M_Sg e N_sg os esforços solicitantes no pilar retirados da combinação quase permanente;

e_a a excentricidade acidental;

φ o coeficiente de fluência.

E_ci = 5.600⋅* f_ck^0,5 é o módulo de elasticidade inicial do concreto;

I_c o momento de inércia da seção do pilar;

l_e o comprimento equivalente do tramo do pilar.

A excentricidade e_c calculada precisa ser somada à excentricidade de 1.ª ordem. Na figura 5 está exemplificada a excentricidade de segunda ordem.

Figura 5 – Excentricidades iniciais e de segunda ordem em pilares.

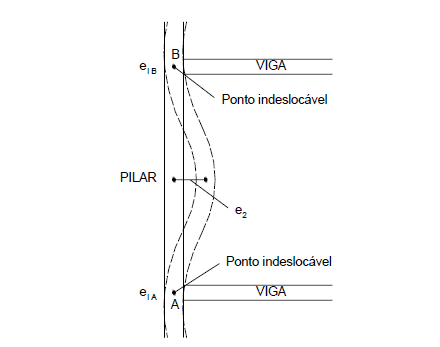
As seções de extremidade não envolvem os efeitos de 2ª ordem, devendo ser considerada apenas na seção intermediária.

2.4 CÁLCULO DA ARMADURA LONGITUDINAL COM AUXÍLIO DE ÁBACO

No dimensionamento manual dos pilares, os ábacos são indispensáveis, pois, trazem a rápida definição da taxa de armadura, não fazendo necessário aplicar as equações teóricas da Flexão Composta Normal ou Oblíqua. Além do que, os ábacos permitem a fácil escolha de diversos arranjos de armadura na seção transversal. Os ábacos de Venturini e Rodrigues (2000) para a Flexão Composta Normal e de Pinheiro (1994) para a Flexão Composta Oblíqua, devem ser utilizados somente no dimensionamento de pilares com concretos do Grupo I de resistência (fck ≤ 50 MPa), pois foram elaborados com alguns parâmetros numéricos onde não se aplicam aos concretos do Grupo II.

2.4.1 FLEXÃO COMPOSTA NORMAL

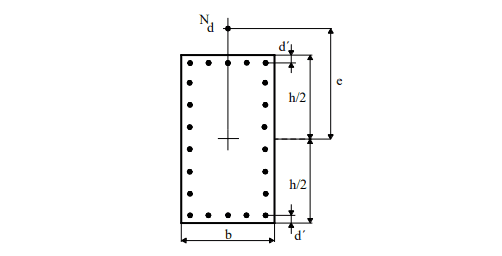
Para a Flexão Composta Normal de Venturini e Rodrigues (2000), a figura 6, mostra a notação da aplicação dos ábacos. A excentricidade (e) é paralela à distância d’, entre o centro da barra do canto e a face da seção. De modo geral tem-se d’ = c + Φt + Φλ/2, com c = cobrimento de concreto, Φt = diâmetro do estribo e Φλ = diâmetro da barra longitudinal.

Figura 6 – Notação para a flexão Composta normal.

Foram apontadas na publicação de Venturini e Rodrigues (2000) as equações utilizadas para a construção dos ábacos. É iniciada a definição da armadura longitudinal, pelo cálculo dos esforços adimensionais n (ni) e μ (mi). O valor adimensional n foi definido na equação seguinte:

O valor de μ, em função do momento fletor ou da excentricidade, é:

Sendo

N_d a força normal de cálculo;

A_c a área da seção transversal do pilar;

f_cd a resistência de cálculo do concreto à compressão (f_ck/γ_c);

M_d,tot  o momento fletor total de cálculo;

h a dimensão do pilar na direção considerada;

e a excentricidade na direção considerada.

Escolhida uma distribuição construtiva para a armadura no pilar, define-se o ábaco a ser usado, em função do tipo de aço e do valor da relação d’/h. No ábaco, com o par ν e μ, obtém-se a taxa mecânica ω. A armadura é calculada pela expressão:

2.4.2 FLEXÃO COMPOSTA OBLÍQUA

Para a Flexão Composta Oblíqua de Pinheiro (1994) mostra-se, na figura 7, a notação aplicada na utilização dos ábacos. As distâncias d’_x e d’_y têm a mesma interpretação de d’, porém, cada uma em uma direção do pilar.

Figura 7 – Notação para a flexão Composta normal.

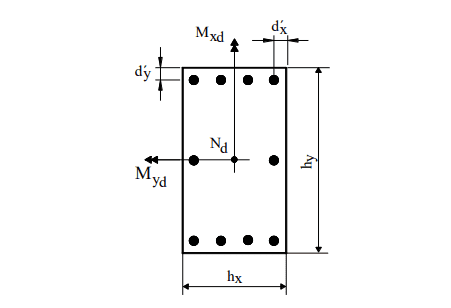
A determinação da armadura tem início pelo cálculo dos esforços adimensionais ν e μ, com μ segundo as duas direções principais do pilar:

Escolhida uma distribuição construtiva para a armadura no pilar, define-se o ábaco a ser usado, em função dos valores das relações d’_x/h_x e d’_y/h_y e do tipo de aço. No ábaco, com o trio (ν, μ_x, μ_y), obtém-se a taxa mecânica ω. A armadura é calculada com a equação a seguir:

2.5 DETALHAMENTO DE PILARES DE CONCRETO ARMADO

A NBR 6118, 2014 determina que a dimensão da seção transversal do pilar não deve ser menor que 19 cm. Esta recomendação tem como objetivo evitar um comportamento inaceitável para os elementos estruturais e possibilitar condições apropriadas de construção.

Porém, para casos especiais, autoriza-se que a menor dimensão do pilar esteja entre 19cm e 12cm. Para estes casos, é necessário multiplicar os esforços finais de cálculo aplicados no dimensionamento dos pilares por um coeficiente adicional γ_n, de acordo com a imagem 8.

Figura 8 – Valores do coeficiente adicional γ_n.

Primeiramente é definido a taxa geométrica de armadura longitudinal do pilar pela seguinte relação:

Sendo,

A_s a soma das áreas das seções transversais das barras longitudinais.

A_c a área da seção transversal do pilar.

A área mínima de armadura longitudinal, depende da intensidade da solicitação em virtude da força normal e da resistência do aço, é determinada pela seguinte expressão:

Logo, a taxa mínima geométrica de armadura é igual a 0,4%.

A área de armadura máxima possível em pilares deve ser de 8% da área da seção transversal, considerando a sobreposição de armadura em regiões de emenda, ou seja:

O diâmetro mínimo das barras longitudinais não deve ser inferior a 10 mm e não pode ser superior a 1/8 da menor dimensão da seção do pilar.

Para uma concretagem apropriada é necessário que o concreto tenha um mínimo de espaço para percorrer entre as armaduras longitudinais. Em razão disso impõem-se limitações ao espaçamento livre entre as barras da armadura longitudinal (a_L), o qual precisa ser igual ou superior ao maior dos valores a seguir:

• 20 mm;
• A medida do diâmetro da barra, do feixe ou da luva adotada na emenda;
• 1,2 vez o diâmetro máximo do agregado;

O espaçamento máximo entre os eixos das barras da armadura é também limitado, precisando ser inferior ou igual a duas vezes a menor dimensão do pilar, sem ultrapassar 400mm.

O diâmetro dos estribos (φ_t) em pilares não pode ser inferior a 5 mm ou 1/4 do diâmetro da barra longitudinal.

Com a finalidade de garantir o posicionamento das barras da armadura longitudinal e, além disso, impossibilitar a flambagem das barras longitudinais e usar de armadura de costura nas regiões de emendas, são exigidos espaçamentos máximos entre os estribos (medido na direção do eixo do pilar), sendo inferior ou igual ao menor dos seguintes valores:

• 200 mm;
• menor dimensão da seção;
• 24 φ para aço CA-25 e 12φ para aço CA-50, onde φ é o diâmetro da barra longitudinal;

Quando existir a possibilidade de flambagem das barras sobre a superfície, devem ser tomadas medidas para evitá-la.

3. MODELAGEM EM SOFTWARE CAD/TQS

Uma das formas de ter um detalhamento de cálculo estrutural, em concreto armado, mais rápido e preciso (com menos arredondamentos), é através da utilização de softwares, um deles se chama TQS, ele utiliza a plataforma CAD para seu funcionamento. Com o TQS podemos obter os cálculos dos esforços e flechas na estrutura, os dimensionamentos e detalhamentos das armaduras em função das solicitações e a plotagem de todo material necessário, tudo de acordo com o que o profissional lançou na plataforma de desenho. O TQS faz todo esse dimensionamento e detalhamento conforme nas normas vigentes.

Os sistemas TQS possuem recursos que tornam a elaboração de projetos estruturais um processo altamente produtivo. Desde a concepção até a emissão das plantas, todas as etapas são automatizadas. Seus principais produtos são o TQS (concreto armado e protendido), Alvest (alvenaria estrutural), PREO (pré-moldados) e SISEs (geotecnia).

Adaptados à mais recentes revisões normativas (NBR 6118/2014, NBR 15200:2012, NBR 15.575:2013, NBR 9062:2006, NBR 15812:2010, NBR 15961:2011. Cada versão dos sistemas TQS são rigorosamente testadas, tanto operacionalmente quanto em relação aos seus resultados. São disponibilizados ainda, material didático para todos os seus produtos, como TQS passo-a-passo, plotagem, escadas passo-a-passo, Alvest passo-a-passo (TQS, 2020).

3.1 LANÇAMENTO ESTRUTURAL NO SOFTWARE TQS/CAD

A estrutura feita para análise foi o exemplo completo, do livro Projeto Estrutural de Edifícios de Concreto Armado, de José Milton de Araújo (2014). Para a modelagem no software foram lançados os pilares, as vigas, as lajes, as escadas, as cargas de parede, sequencialmente na ordem descrita.

Para os pilares foram seguidos os seguintes passos: Após abertura do Modelo Estrutural, ativa-se a aba de “Pilares”, deve-se abrir a janela de “Dados atuais” (figura 9), onde aparecerá todos dados para inserção do pilar, colocando então as dimensões, número de identificação, posição de inserção, determinação onde o pilar nasce e morre, entre outras informações. Ao finalizar todas as edições pertinentes então faz-se a inserção de todos pilares necessários.

Figura 9 – Janela TQS/CAD na aba de “Pilares”.

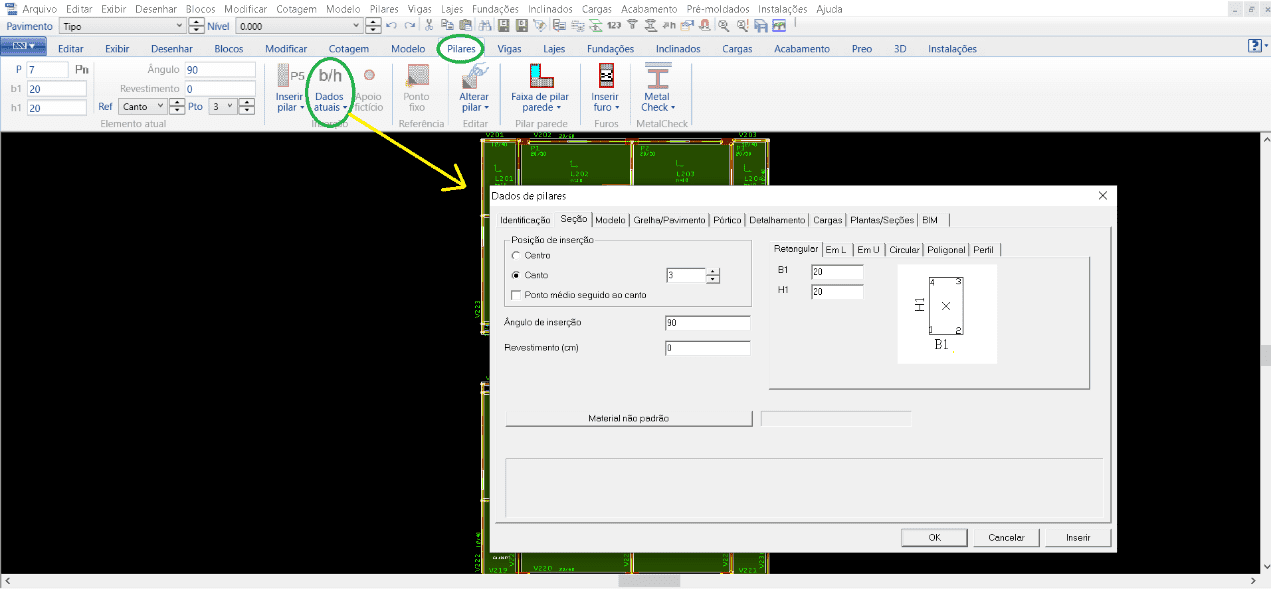
Para a construção das vigas no software CAD/TQS, o processo é o seguinte:

Após a definição de todos os pilares, passamos para o lançamento das vigas. Inicialmente deve-se ativar o menu “Vigas”, onde todos com comandos seguintes são específicos para o lançamento das vigas.

Dentro da aba de “Vigas” deve-se selecionar o comando de “Dados atuais” (figura 10), onde abrirá uma janela dos dados gerais das vigas, colocando assim todas as informações necessárias para o lançamento de cada viga. Informações essas como o número de identificação de cada viga, o seu cobrimento, as cargas que essa viga vai atuar nos pilares, como as permanentes e acidentais, sua seção. Terminado todo esse processo de detalhamento, podemos então inserir a viga, colocando no ponto inicial depois no ponto final, geralmente esses pontos de inserção são os vértices dos pilares já inseridos anteriormente, repetindo o mesmo procedimento até colocar todas as vigas necessárias.

Figura 10 – Janela TQS/CAD na aba de “Vigas”.

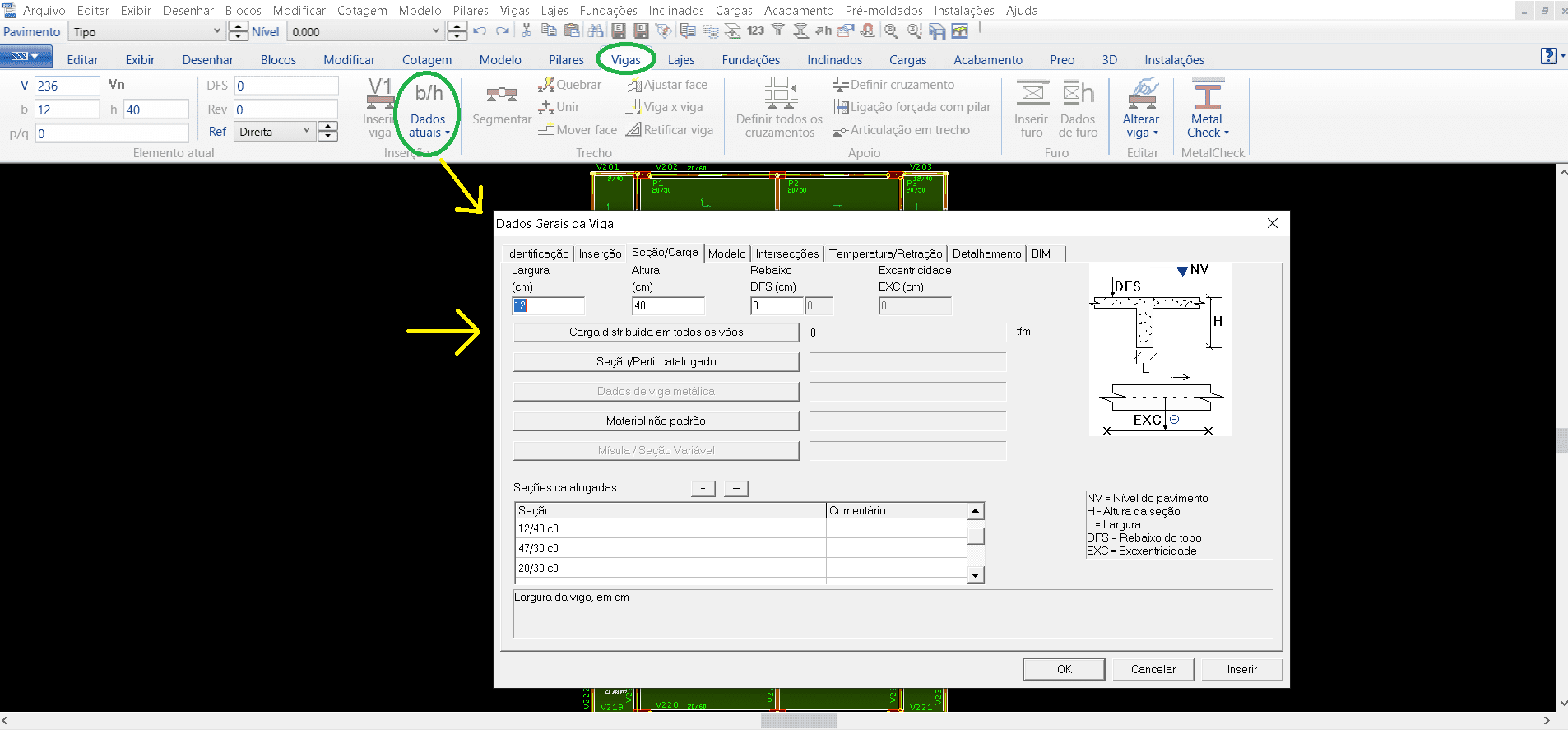
Após as vigas lançadas passamos para as lajes, seguindo mesmos procedimentos dos anteriores na aba “Lajes” selecionando “Dados atuais” coloca-se a identificação, tipo de laje e a sua espessura (imagem 11).

Figura 11 – Janela TQS/CAD na aba de “Lajes”.

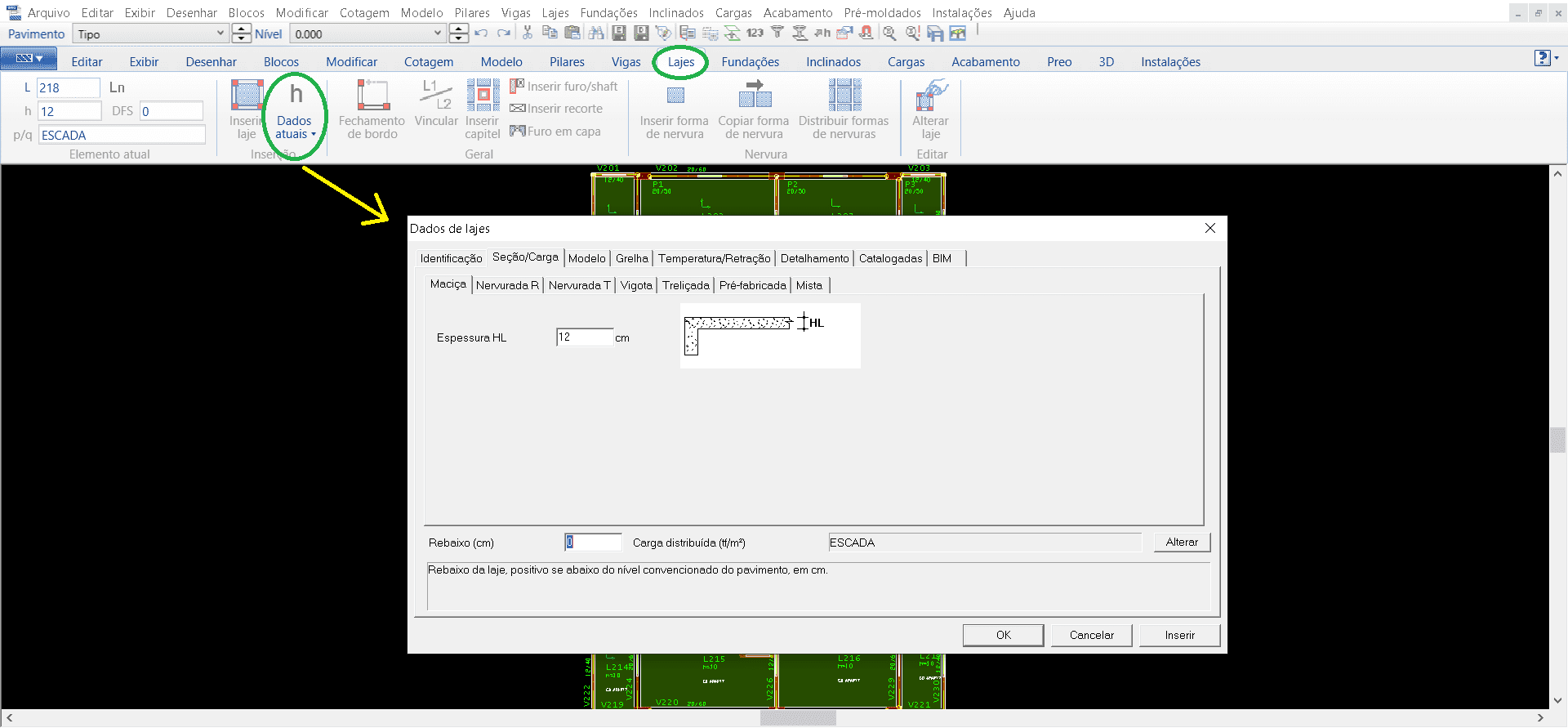
Para o lançamento das cargas de parede segue a mesma linha de procedimentos. Na janela “Cargas” seleciona a aba “Distribuída linearmente”, abrindo então uma janela para a seleção do tipo da carga, para a modelagem em questão foi inserido bloco 14 (alvenaria de bloco de concreto 14 cm) e a altura da parede determinada (imagem 12).

Fonte: Figura 12 – Janela TQS/CAD na aba de “Cargas”.

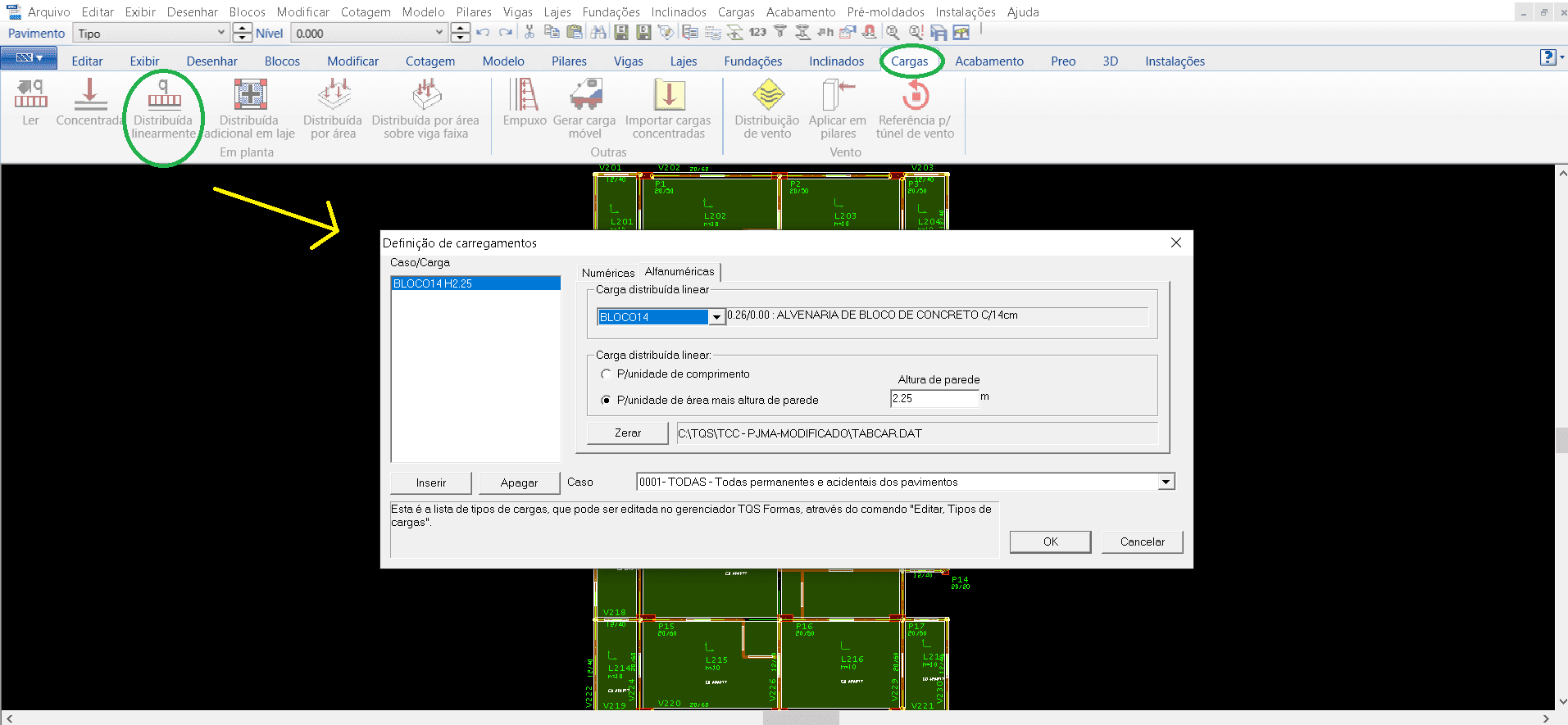
Assim, ao terminar o lançamento de todos os elementos necessários nos pavimentos, devemos salvar os dados definidos até aqui no menu “Arquivo” no comando “Salvar o modelo estrutural”.

Figura 13 – Edifício exemplo 3D, TQS/CAD

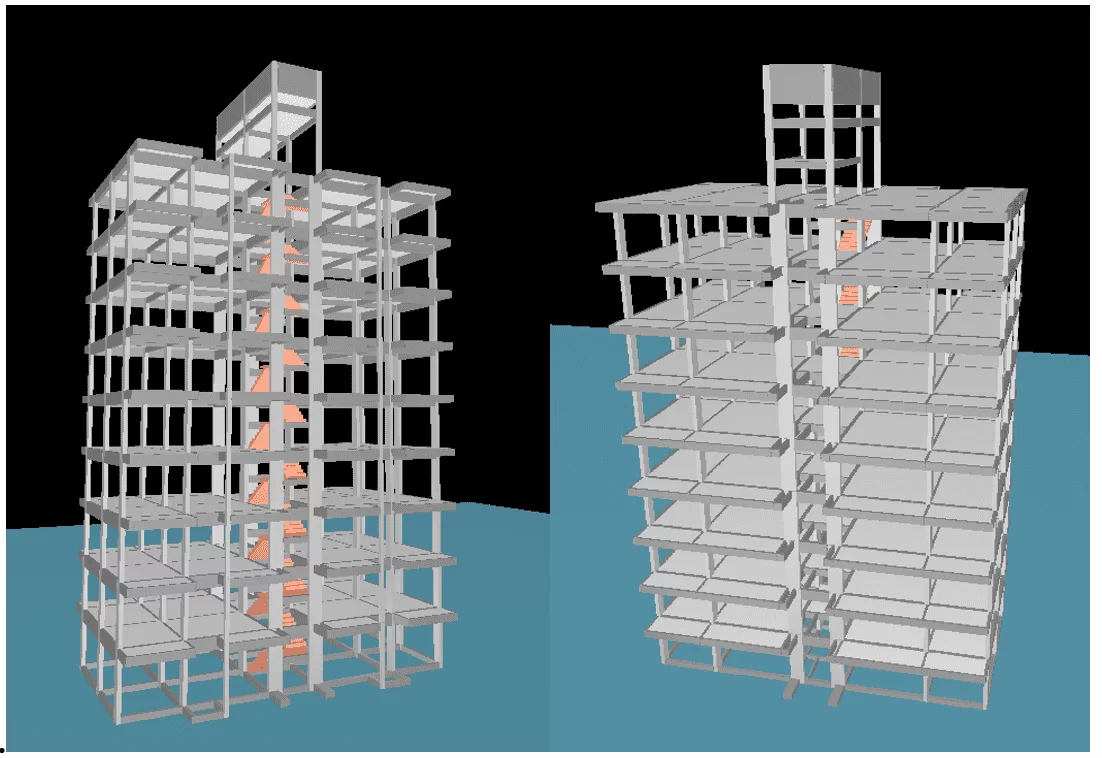
Utilizando o visualizador tridimensional temos a ideia concreta de como seria o edifício exemplo (figura 13).

O aplicativo P-Calc é uma calculadora da TQS que faz uma verificação de pilares de concreto armado sujeitos à flexão composta oblíqua individual (TQS, 2020).

As principais características do P-Calc são:

• Verificação de pilares submetidos a flexão composta, normal ou oblíqua, em relação ao estado limite último de ruptura e instabilidade;
• Análise de pilares com concretos de resistência elevada (fck > 50 MPa);
• Diagrama de interação Esforço normal x Momento fletor (FCO e FCN);
• Resultados gráficos para tensões e deformações na seção;
• Avaliação dos efeitos locais de 2ª ordem adotando a não linearidade geométrica e física, de acordo com a norma ABNT NBR 6118;
• Envoltória de momentos mínimos;
• Memória de cálculo em formato PDF;

4. APRESENTAÇÃO E ANÁLISE DOS RESULTADOS

Este tópico apresenta os comparativos entres os referenciais para os elementos estudados. Foi dividido em subtópicos para os elementos principais de um projeto estrutural. Ressalta-se que os referenciais estudados foram a base do projeto do livro “PROJETO ESTRUTURAL DE EDIFÍCIOS DE CONCRETO ARMADO” do JOSÉ MILTON DE ARAÚJO, 3ª edição, modelado, calculado e detalhado no TQS. Para contra prova alguns elementos foram comparados com outras ferramentas de cálculo como Pcalc e o Ábacos de Flexão para os dados dos pilares.

4.1 COMPARATIVO DE MODELAGEM E DIMENSIONAMENTO – PILAR

Após a modelagem e dimensionamento dos pilares, conforme tópico 3, realizou-se o comparativo do esforço principal, seção e área de aço entre as referências estudadas para os dois pilares (P2 e P5) conforme resumo nos quadros 01 e 02.

Quadro 1 – Apresentação dos resultados comparados para o pilar 2

Elementos	Esforços característicos (tf)	Seção (cm x cm)	Área de aço (cm²)
Araujo (2014)	71,4	20 x 50	6ϕ20 (18,90)
TQS	66,2	20 x 50	8ϕ20 (25,20)
Pcalc*	71,4	20 x 50	10ϕ20 (31,50)
Pcalc*	66,2	20 x 50	10ϕ20 (31,50)
Ábaco- Flexão Normal*	71,4	20 x 50	6ϕ20 (18,90)
Ábaco- Flexão Normal*	66,2	20 x 50	4ϕ20 (12,60)

*Solução por pilar-padrão com curvatura aproximada.

Fonte: Autor, 2020.

Pode-se observar, analisando os comparativos para o pilar P2 que, o dimensionamento de Araújo (2014) em relação ao TQS mostra um aumento de 33,33% na área de aço, levando em consideração que Araújo apresenta uma força normal 7,85% maior, já em relação ao PCalc, houve um aumento de 66,67%, correlacionando-os com a mesma carga.

É interessante observar que esses mesmos valores em relação ao dimensionamento de pilar-padrão com curva aproximada utilizando os Ábacos de Flexão Normal (VENTURINI e RODRIGUES, 2000), foi separado em dois grupos de cargas pois, a modelagem feita no TQS difere do levantamento de carga de Araújo (2014) então assim, temos as figuras 14 e 15.

Figura 14 – Comparativo entre TQS x Pcalc x Ábacos para o Pilar 2

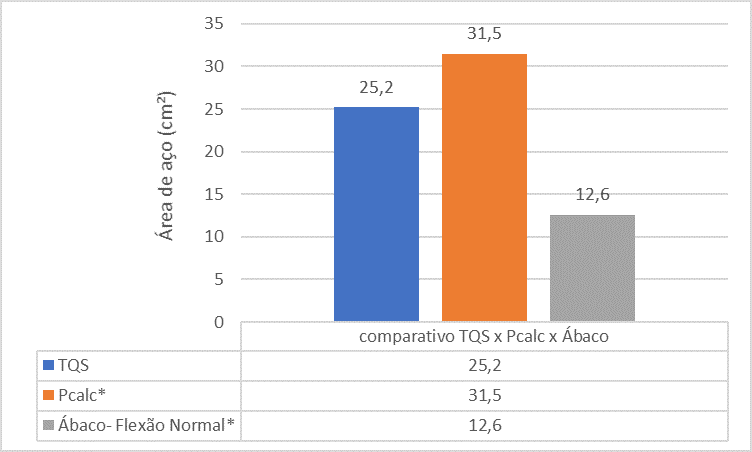
A análise comparativa entre os referenciais apresenta que a área de aço do pilar P2 encontrada pela ferramenta TQS é menor que a área de aço encontrada pelo Pcalc e Ábacos. Isso se deve ao fato da análise monolítica feita no programa.

Figura 15 – Comparativo entre Araújo (2014) x Pcalc x Ábacos para o Pilar 2

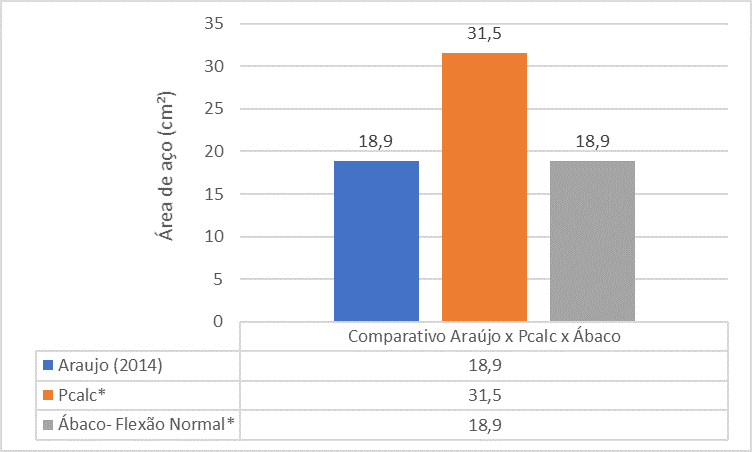
A análise comparativa entre os referenciais apresenta que a área de aço do pilar P2 encontrada pelo livro de Araújo (2014) é bem menor que a área de aço encontrada pelo PCalc e Ábacos.

O pilar P2 é um pilar de extremidade, apoio intermediário para a viga V202, na direção x, desconsiderando esses momentos transmitidos. Já na direção y temos a viga V 227, essa sim foi considerada os momentos transmitidos no pilar. A partir dessa análise foi feito o cálculo do momento de engastamento perfeito (M_eng) , momento de inercia da viga (I_vig), coeficiente de rigidez da viga (r_vig), momento de inercia dos pilares(I_p),coeficiente de rigidez dos pilares(r_p) e momentos iniciais nos pilares(M_p), a partir dos cálculos, obtém-se os momentos reduzidos, porem divido a grande diferença entra eles, foram considerados zero e dimensionar a seção em flexo -compressão normal na direção x.

Para a força normal no eixo x, temos o índice de esbeltez (λ_x) excentricidades iniciais (e_ia), excentricidade acidental (e_ax), excentricidade mínima (e_1x,min), excentricidade inicial ne seção intermediaria (e_ix), excentricidade de segunda ordem (e_2x) e excentricidade de fluência (e_cx). A sessão crítica foi na sessão da extremidade, empregando as tabelas de área de aço a sessão pode ser armada com 6 barras de 20 mm, adotando uma área total de aço igual a 18,85 cm².

Quadro 2 – Apresentação dos resultados comparados para o pilar 5

Elementos	Esforços característicos (tf)	Seção (cm x cm)	Área de aço (cm²)
Araujo (2014)	112,2	20 x 50	10ϕ16 (20,00)
TQS	141,5	20 x 50	8ϕ25 (40,00)
Pcalc*	112,2	20 x 50	12ϕ20 (37,80)
Pcalc*	141,5	20 x 50	12ϕ25 (60,00)
Ábaco- Flexão Normal*	112,2	20 x 50	8ϕ25 (40,00)
Ábaco- Flexão Normal*	141,5	20 x 50	11ϕ25 (55,00)

*Solução por pilar-padrão com curvatura aproximada.

Fonte: Autor, 2020.

Pode-se observar, analisando os comparativos para o pilar P5 que, o dimensionamento de Araújo (2014) em relação ao TQS mostra um aumento de 100% na área de aço, levando em consideração que Araújo apresenta uma força normal 26,11% menor, já em relação ao PCalc, houve um aumento de 89%  em relação a carga de Araújo, e 50% em relação a carga do TQS, mostrando que quanto maior o aumento da carga maior é divergência das áreas de aço. Pode-se dizer que essa divergência se deve ao fato de apresentar o seguinte erro para a resolução do pilar P5 no Pcalc, para Araujo (2014) no Estado limite último (ELU): O pilar não atente a verificação quanto ao momento mínimo. Já o Pilar com a carga do TQS no Pcalc gera o seguinte erro ρs = 5.89% > ρs.max = 4.00%.

É interessante observar que esses mesmos valores em relação ao dimensionamento de pilar-padrão com curva aproximada utilizando os Ábacos de Flexão Normal (VENTURINI e RODRIGUES, 2000), foi separado em dois grupos de cargas pois, a modelagem feita no TQS difere do levantamento de carga de Araújo (2014) então assim, temos as figuras 16 e 17.

Figura 16 – Comparativo entre TQS x Pcalc x Ábacos para o Pilar 5

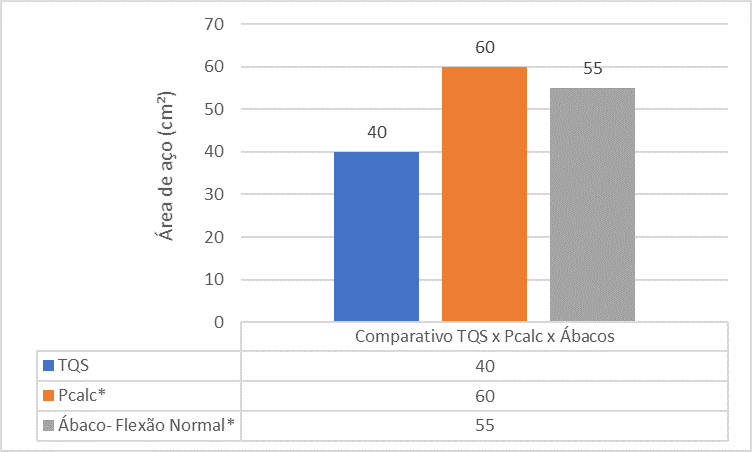
A análise comparativa entre os referenciais apresenta que a área de aço do pilar P5 encontrada pela ferramenta TQS é menor que a área de aço encontrada pelo Pcalc e Ábacos. Isso se deve ao fato da análise monolítica feita no programa.

Figura 17 – Comparativo entre Araújo (2014) x Pcalc x Ábacos para o Pilar 5

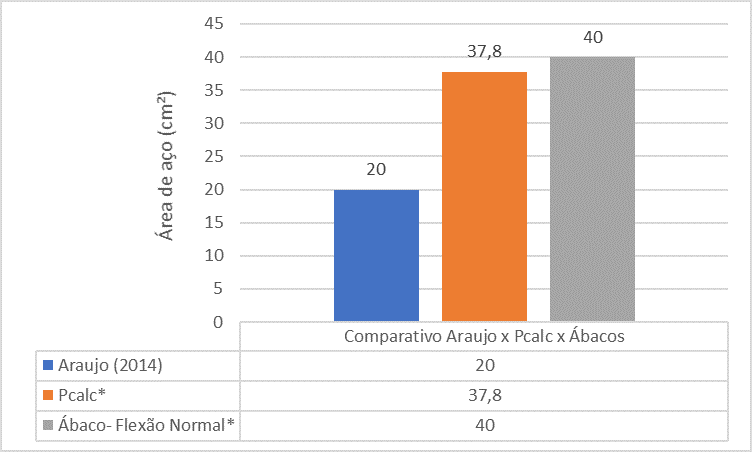
A análise comparativa entre os referenciais apresenta que a área de aço do pilar P5 encontrada pelo livro de Araújo (2014) é bem menor que a área de aço encontrada pelo PCalc e Ábacos.

O pilar P5 é um pilar intermediário, com os vãos e as cargas das vigas V204 e V227, não diferem entre si, por isso podem-se desprezar os momentos iniciais transmitidos por essas vigas. A partir dessa análise foi feito o cálculo no eixo y, pois foi o maior índice de esbeltez (λ_x) encontrado, da excentricidade (e_y), dado pela soma da excentricidade de primeira ordem (e_1x), da excentricidade de segunda ordem (e_2x) e excentricidade de fluência (e_cy). Empregando as tabelas de área de aço a sessão pode ser armada com 10 barras de 16 mm, adotando uma área total de aço igual a 20,00 cm².

5. CONCLUSÃO

Observou que o comparativo entre os métodos é importante para a escolha da melhor ferramenta para uso no dimensionamento de pilares.

Reproduzindo a modelagem do prédio de Araújo no TQS percebeu-se uma diferença de carga, e para estas cargas percebe-se que a ferramenta TQS em modo default se mostra próxima do dimensionamento para a ferramenta PCalc e Ábacos para pilares intermediários.

Já em pilares de extremidade Araújo mostra uma menor variação das respostas em relação ao Ábacos e PCalc.

Assim, a análise comparativa entre os métodos de cálculo mostra-se diferente devido ao fato da análise monolítica da estrutura feita na ferramenta TQS, diferente dos outros métodos que apresenta análise segmentada dos elementos com formas de cálculo simplificada.

REFERÊNCIAS

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 1978.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2003.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2014.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15200. Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro, — Procedimento, 2012.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15575. Edificações habitacionais – Desempenho. Rio de Janeiro, — Procedimento, 2013.

ABNT (Associação Brasileira de Normas Técnicas). NBR 9062. Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, — Procedimento, 2006.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15812. Alvenaria estrutural – Blocos cerâmicos. Rio de Janeiro, — Procedimento, 2010.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15961. Alvenaria estrutural – Blocos de concreto. Rio de Janeiro, — Procedimento, 2011.

AGUIAR, E.A.B. Projeto de pilares de concreto de alto desempenho. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2000.

ARAUJO, José Milton de. Projeto estrutural de edifícios de concreto armado. 3. ed. Rio Grande: Editora Dunas, 2014.

BASTOS, Paulo S. dos Santos. Fundamentos do Concreto Armado. Universidade Estadual Paulista. Bauru, São Paulo. 2006.

BRANDÃO, A. M. S.; PINHEIRO, L. M. Qualidade e durabilidade das estruturas de concreto armado: aspectos relativos ao projeto. Cadernos de Engenharia de Estruturas. EESC. Universidade de São Paulo. São Carlos, 1999.

CARVALHO, Roberto Chust.; FIGUEIREDO FILHO, Jasson Rodrigues de. Pilares de concreto armado. p.9-25. Notas de aula – Universidade Federal de São Carlos, 2002

FUSCO, P.B. Estruturas de concreto – solicitações normais, editora Guanabara, São Paulo, 1986.

PIANCASTELLI, E. M. Patologia, Recuperação e Reforço de Estruturas de Concreto Armado. Apostila para Curso de Extensão, Ed. Depto. Estruturas da Escola de Engenharia da UFRG, Belo Horizonte, 1997

PINHEIRO, L.M.; BARALDI, L.T.; POREM, M.E. Concreto Armado: Ábacos para flexão oblíqua. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1994.

TQS, Calculadora P-Calc, Pilares de concreto, 2020. Disponível em: <https://www.tqs.com.br/apps/p-calc/ejm1se496l>

TQS, Sobre a TQS, 2020.Disponível em: <https://www.tqs.com.br/about>

VENTURINI, Wilson Sérgio; RODRIGUES, Rogério de Oliveira. Dimensionamento de peças retangulares de concreto armado solicitadas à flexão reta. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1987 (reimpresso.2000)

^[1] Graduanda em Engenharia Civil.

^[2] Graduando em Engenharia Civil.

^[3] Mestrado em Geotecnia e Construção Civil. Graduação em Engenharia Civil. Graduação em Engenharia Agrícola.

Enviado: Maio, 2020.

Aprovado: Maio, 2020.