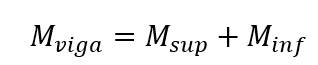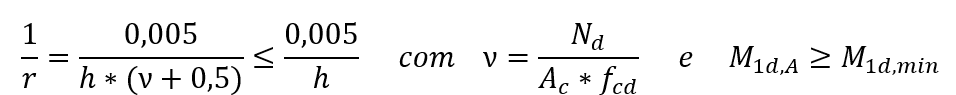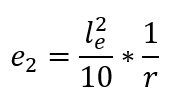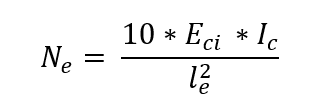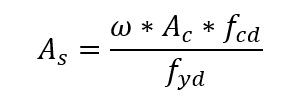ORIGINALER ARTIKEL
CARVALHAES, Daniely Silva [1], CARVALHAES, Daniel José [2], QUARESMA, Wanessa Mesquita Godoi [3]
CARVALHAES, Daniely Silva. CARVALHAES, Daniel José. QUARESMA, Wanessa Mesquita Godoi. Vergleich der Dimensionierung und Modellierung von Spalten. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 05, Vol. 04, S. 121-146. Mai 2020. ISSN: 2448-0959, Zugriffsverbindung: https://www.nucleodoconhecimento.com.br/bauingenieurwesen/modellierung-von-spalten
ZUSAMMENFASSUNG
Die Suche nach zeitverkleinerung bei der Ausarbeitung von Projekten wird zur Notwendigkeit, zusammen mit der Empörung, wiederkehrende Probleme bei der Verwendung von Stahlbetonstrukturen wie Pathologien zu verstehen. Wenn man also die beiden Probleme, Zeit und Analyse, vereint, wird es unerlässlich, Wege zu untersuchen, um die Strukturen in der gemeinsamen Software der Projektentwicklung zu modellieren und zu analysieren. Ziel ist es, ein Gebäude zu modellieren und ein Strukturelement zu vergleichen, indem die Lasten und Abmessungen der TQS® analysiert werden. Dieser Prozess ist auf die Modellierung in der TQS-Software des Beispielgebäudes von José Milton de Araújo (2014) zurückzuführen. Es wurde beobachtet, dass der Modellierungsprozess im Vergleich zum numerischen Prozess einen signifikanten Unterschied aufgrund der Tatsache der Analyse des gesamten Gebäudes darstellt, wodurch die in der Software durchgeführte Modellierung zuverlässig ist, was eine vorherige Untersuchung der gesamten Struktur ermöglicht.
Schlüsselwörter: Säulen, Dimensionierung, Modellierung, Experimentell, TQS.
1. EINFÜHRUNG
Bastos (2006, S. 07) präsentiert Stahlbeton als “die Vereinigung von einfachem Beton und einem zugfesten Material (durch Beton) in einer Weise, dass beide sich gemeinsam den ersuchenden Bemühungen widersetzen”, das heißt, der Stahlbeton ist das Ergebnis des einfachen Betons plus Bewehrung plus Haftung.
Für Piancastelli (1997) kann sich Stahlbeton im Laufe der Zeit ändern, da er ein nicht inertes Material ist, dank Wechselwirkungen zwischen seinen Bestandteilen (Zement, Sand, Kies, Wasser und Stahl), Wechselwirkungen zwischen diesen Elementen und äußeren Einflüssen wie Gasen, Salzen, Basen, Säuren und anderen sowie mit Materialien, die ihm zugesetzt werden (Additive und Mineralzusätze).
Lange Zeit galt der Beton aufgrund alter Noch in gutem Zustand als langlebiges Material, aber die frühe Verschlechterung der aktuellen Strukturen führt uns zu den Gründen konkreter Pathologien (BRANDÃO und PINHEIRO, 1999). Dies ist auf die neuen Technologien, um die Strukturen schlank und leichter zu machen, des Prozesses der Planung und Produktion der Strukturen.
Säulen sind Elemente, die in der Regel vertikal in ihrer Achse ausgerichtet sind, in denen normale Kompressionskräfte überwiegen (ABNT NBR 6118, 2014), ihre Studie ist eine der wesentlichen Prüfungen, was die Dimensionierung betrifft, kann die Fehlfunktion einer Säule einer Struktur die Funktionalität beeinträchtigen und schwere Unfälle verursachen. Da die Säulen für die Übertragung vertikaler Lasten verantwortlich sind, unterliegen sie in der Regel insbesondere der Flexokompressionsbedingung, daher die Notwendigkeit, Effekte zweiter Ordnung und eine Stabilitätsanalyse der Säule als Ganzes zu berücksichtigen.
Die Säulen werden gemäß den externen Berechnungsbemühungen dimensioniert, die die Normalkräfte (Nd), die Biegemomente (Mdx und Mdy) und die Scherkräfte (Vdx und Vdy) umfassen, die horizontal wirken. Mit dem NBR 6118 wurden in der Fassung von 2003, insbesondere in Bezug auf die Säulen, verschiedene Änderungen eingeführt, z. B. der Wert der zufälligen Exzentrizität, eine größere Betondeckung, eine neue Methode zur Berechnung der schlanken Grenze hinsichtlich der Betrachtung oder Nichtberücksichtigung der Biegemomente 2. Ordnung und vor allem unter Berücksichtigung des minimalen Biegemoments das Biegemoment durch versehentliche Exzentrizität ersetzen können. In der Version 2014 wurde die Überprüfung des minimalen Biegemoments hinzugefügt, die aus dem Vergleich eines widerstandsfähigen Umschlags hervorgeht, der den minimalen Umschlag mit 2. Ordnung enthält.
2. BERECHNUNG UND DIMENSIONIERUNG VON PILLARS VON ABACOS
2.1 KLASSIFIZIERUNG DER SÄULEN
Die Säulen werden nach ihrer Position in der Struktur klassifiziert, es kann Zwischen-, Ende- oder Ecke sein. Diese Klassifizierung ermöglicht es Ihnen, die anfordernden Anstrengungen in jeder berechneten Situation zu berücksichtigen. (FUSCO,1981)
Abbildung 1: Position der Pfeiler in Gebäuden.
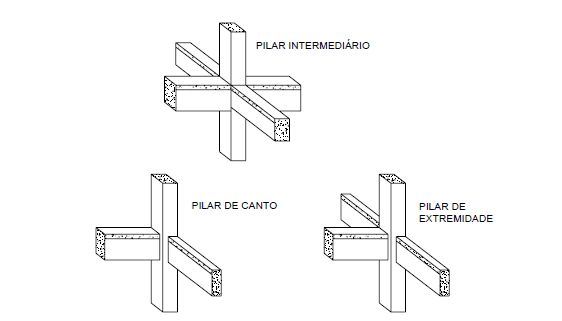
Zwischensäulen sind vorwiegend axialen Druckkräften ausgesetzt, da die Biegemomente von geringer Intensität sind, da nur die vertikalen Einwirkungen (die permanenten und die normalen Variablen). Sofern die Spannweiten der durchgehenden Träger, die auf diesen Säulen ruhen, nicht als unterschiedlich angesehen werden, werden die auf die Säulen übertragenen endgültigen Biegemomente nicht berücksichtigt. Daher ist die in der Konstruktionssituation zentrierte Drucksäule zulässig, dh die anfängliche Exzentrizität bei der Bemaßung der Quer- und Längsbewehrungsbereiche wird als gleich Null angesehen.
Die Extremitätssäulen sind normalen Kompressionskräften und der Wirkung von Momenten ausgesetzt, die von den Strahlen propagiert werden, die ihre äußeren Extremitäten auf diesen Säulen stützen. In den Strahlen quer zur Achse des unterbrochenen Strahls werden Momente nicht berücksichtigt. Daher wird die Extremitätssäule, die einer zusammengesetzten Normalbeugung unterliegt, berücksichtigt, wobei die anfängliche Exzentrizität in einem der lokal geordneten des Querschnitts der Säule berücksichtigt wird.
Eckpfeiler neben der normalen Betätigungskraft, sollte man die Momente durch die Balken übertragen, von denen die mittleren Ebenen senkrecht zu den Flächen der Säulen sind, und an den Rändern der Säule unterbrochen werden. In der Konstruktionssituation wird die Ecksäule berücksichtigt, die der verbundigen Schrägbiegung unterzogen wird, mit Exzentrizitäten, die nach den lokalen koordinierten Achsen initial sind.
Die Säulen werden, obwohl ihre Einstufung nach ihrer Position in der Struktur sehr üblich ist, auch nach der Art des Antrags, den die Säule gestellt wird, klassifiziert. Das heißt, Säulen, die der normalen Verbundflexion unterworfiert werden, Säulen, die der schrägen Verbundflexion unterworfiert werden, und Säulen, die der zentrierten Kompression unterzogen werden.
2.2 GÜRTELINDEX
Der Schlankheitsindex von Stahlbetonsäulen ist das Verhältnis zwischen der äquivalenten Länge (le) der Säule und dem Drehradius (i) des Abschnitts. (NBR 6118, 2014)
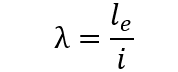
Die Klassifizierung der Säulen hängt von den Schlankheitsgrenzen und zusätzlichen Faktoren ab, wie der relativen Exzentrizität, der Form des Biegemomentdiagramms und den Bindungsbedingungen der Extremitäten. Diese Faktoren werden durch den Koeffizienten λ1 berücksichtigt.
Für kurze Säulen NBR 6118 (2014) (λ ≤ λ1) könnten die Effekte zweiter Ordnung ignoriert werden, da die Referenzindizes höher sind als die Schlankheitsindizes. Mittlere schlanke Säulen (λ1 <λ ≤ 90), bei denen die Effekte zweiter Ordnung durch einen ungefähren Prozess wie die Standardsäulenmethode mit ungefährer Krümmung berücksichtigt werden können. Schlanke Säulen (90 <λ ≤ 140) sind solche, für die es möglich ist, die Standardspaltenmethode zusammen mit M – N – 1 / r-Diagrammen zu betrachten. Sehr schlanke Säulen (140 <λ ≤ 200), die zur Überprüfung des Zustands der Instabilitätsgrenze die genauen zu berücksichtigenden Methoden erfordern. NBR 6118 erlaubt nicht die Konstruktion und den Bau einer Säule mit einem Schlankheitsindex (λ) von mehr als 200. Bei Pfosten mit einer normalen Festigkeit von weniger als 0,10 fcd.Ac kann diese Grenze überschritten werden.
2.3 EXZENTRIK
In den Säulen entstehen Exzentrizitäten nicht nur aufgrund der anfänglichen Anforderungen an die Säulen, sondern auch wegen zusätzlicher Faktoren wie den Auswirkungen der 2. Ordnung, dem Kriechen von Beton und geometrischen Unvollkommenheiten.
Es ist notwendig, die Exzentrizitäten zu erhalten, die sich auf den Typ der analysierten Spalte beziehen, um ihre Dimensionierung zu machen. Dieser Artikel stellt die Kriterien für die Herstellung dieser Exzentrizitäten in Säulen getrennt, nach dem NBR 6118, 2014 Standard.
2.3.1 ANFÄNGLICHE EXZENTRIZITÄT DER 1. ORDNUNG
Wir wissen, dass die Balken und Säulen dreidimensionale Gantries bilden, so dass die Säulen einer zusammengesetzten schrägen Beugung ausgesetzt sind und somit anfängliche Exzentrizitäten in zwei Hauptrichtungen darstellen. In Projekten, die vereinfachte Verfahren zur Definition der Anforderungsbemühungen als Fletormoment, Normalkraft und Schnittkraft betrachten, z. B. der in NBR 6118 (2014) dargestellte Dauerstrahlfall, wird eingeräumt, dass die anfänglichen Exzentrizitäten in den Eck- und Endsäulen entstehen. Daran erinnern, dass Exzentrizitäten für Zwischensäulen nicht berücksichtigt werden.
Die Exzentrizitäten der 1. Ordnung werden durch die Ausdrücke gegeben:
Nd wäre die ersuchende Kraft für die Berechnung;
Md,A und Md,B die anfordernden Berechnungsmomente am Ende der Spalte.
Die höchste Exzentrizität des absoluten Wertes wird für ei,A angenommen.
Wenn die genauen Werte der anfragenden Anstrengungen in der Struktur nicht berechnet werden, ist es möglich, die statische Form in Abbildung 2 zu übernehmen, um die Momente des Flusses in den extremen Stützen zu erhalten, wie z. B. Vereinfachung.
Abbildung 2: Modell, das bei extremer Unterstützung von kontinuierlichen Strahlen berücksichtigt wird.
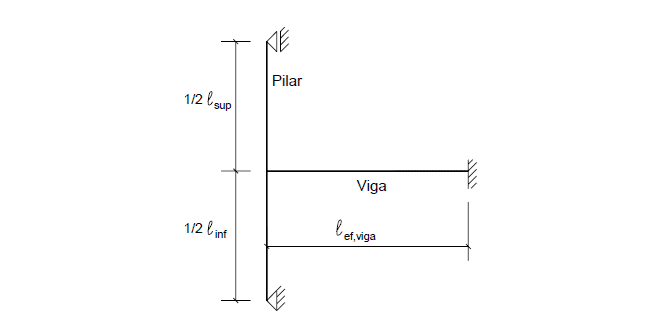
Die nachfragenden Momente in den oberen und unteren Zweigen der Säule werden ermittelt durch: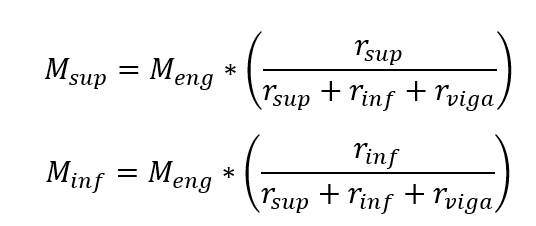
Als, Meng der perfekte Einstellung Moment in der analysierten Straßenbahn (Ende des Balkens) des Balkens.
Die Steifigkeitskoeffizienten der oberen und unteren Zweige der Säule und im Balkenabschnitt werden durch die Beziehungen zwischen Trägheitsmomenten und Spannweiten nach den folgenden Ausdrücken definiert: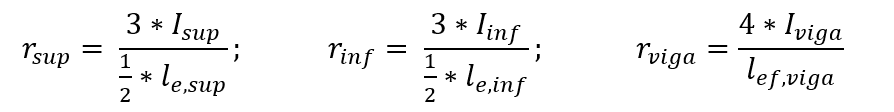 Das Fletormoment auf dem Strahl wird durch den folgenden Ausdruck unter Berücksichtigung des Gleichgewichts des Knotens bestimmt.
Das Fletormoment auf dem Strahl wird durch den folgenden Ausdruck unter Berücksichtigung des Gleichgewichts des Knotens bestimmt.
Die äquivalente Länge der Spalte kann durch den Ausdruck bestimmt werden:
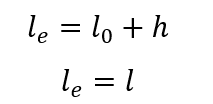
dass:
lo der Abstand zwischen den Innenflächen der Strukturelemente, die horizontal sein sollen und die Säule verbinden.
h die Höhe des Querschnitts der Säule, bekannt auf der Ebene der Struktur.
l der Abstand zwischen den Achsen der Strukturelemente, mit denen die Säule verbunden ist.
Die effektiven Spannen der Träger können durch den Ausdruck berechnet werden: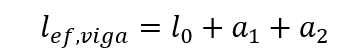
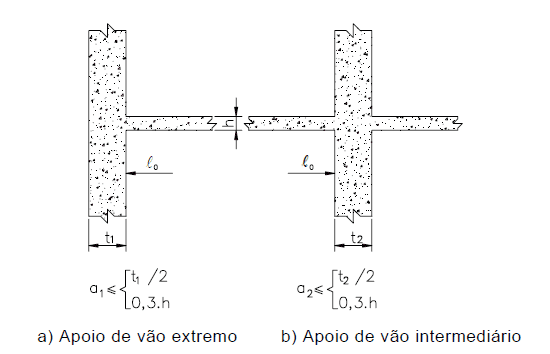
Die Werte von a1 und a2 an jedem Ende der Spanne können anhand der in Abbildung 3 angegebenen entsprechenden Werte von ai berechnet werden:
a1 gleich dem niedrigsten Wert zwischen (t1/2 und 0,3 * h).
a2 gleich dem niedrigsten Wert zwischen (t2/2 und 0,3 * h).
Abbildung 3: Gehen Sie effektive Strahlen.
2.3.2 FORM EXZENTRIZITÄT
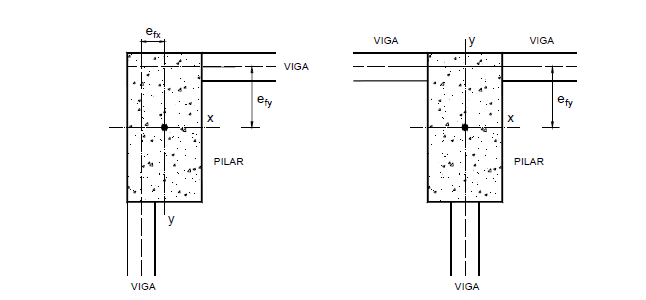
Um die Position der Strukturelemente in Abhängigkeit von der architektonischen Gestaltung anzupassen, müssen Die Statiker die Innen- oder Außenflächen der Balken mit denen der Säulen, die sie erhalten, kompatibel machen. Wenn dies geschieht, passieren die Achsen der Balken nicht den Schwerpunkt des Abschnitts der Säule (Abbildung 4), wodurch exzentrische Eigenschaften genannt werden, die Exzentrizitäten der Form genannt werden (AGUIAR. 2000).
Abbildung 4 – Exzentrizität der Form in Säulen.
Die Exzentrizitäten der Form, wenn die Projekte und Strukturen von Gebäuden getan werden, werden nicht in der Dimensionierung berücksichtigt, ohne die Hilfe von Computerprogrammen für diesen Zweck ausgearbeitet. Der Fletormoment, der durch Exzentrizitäten auf der Ebene jedes Bodens erzeugt wird, wird durch ein Drehmoment nivelliert, das auf jeder Etage Kräfte paare in der gleichen Größenordnung und entgegengesetzte richtungen verursacht, die sich aufheben. Berechnungsprogramme für die Strukturanalyse und Dimensionierung mit Rissöffnungsprüfungen und den Kriterien der letzten Grenzzustände und Verschiebungen mit den Parametern der Dienstgrenzenzustände berücksichtigen diese Formalitäten.
2.3.3 VERSEHENTLICHE EXZENTRIZITÄT
NBR 6118 (2014) sieht die Berechnung einer zufälligen Exzentrizität (ea) vor, unter Berücksichtigung der Situationen der lokalen Unvollkommenheit aufgrund der Konstruktion der Säulen, kann durch den Zerfall der Säulenachse sein.
Nach NBR 6118 (2014) wird in den normalen netzgebundenen Strukturen zugegeben, dass die Wirkung lokaler Unvollkommenheiten behoben wird, wenn der Wert des minimalen Gesamtmoments berücksichtigt wird. Bei schräger Verbundflexion muss der Minimale Momentwert in jeder Hauptrichtung unbedingt separat eingehalten werden.
2.3.4 EXZENTRITÄT ZWEITER ORDNUNG
Lokale Effekte zweiter Ordnung können mit ungefähren Methoden oder nach der allgemeinen Methode berechnet werden. Berücksichtigt werden nur die Effekte der 2. Ordnung für die mittleren schlanken Säulen, wobei die Standardsäulenmethode mit ungefährer Krümmung und die Standardspalte mit ungefährer Steifigkeit verwendet werden. Die Mediane stellen die meisten Vorkommen in aktuellen Gebäudestrukturen dar, und die Fälle von Säulen mit schlanken Indizes über 90 sind ungewöhnlich.
- Standard-Säulenverfahren mit ungefährer Krümmung
In der Dimensionierung von Säulen mit λ ≤ 90, mit konstantem Schnitt und symmetrischer und konstanter Verstärkung über die gesamte Achse. Diese Methode wird nur bei normaler Verbundflexion angewendet. Die physikalische Nichtlinearität wird von einem Ausdruck in der Nähe der Krümmung im Querschnitt genommen, der den höchsten Biegemomentwert unter Berücksichtigung der Momente erster und zweiter Ordnung ausdrückt. Das maximale Gesamtmoment in der Säule, d.a. die Summe der Momente der ersten Ordnung mit den Momenten der 2. Ordnung, wird durch den Ausdruck berechnet: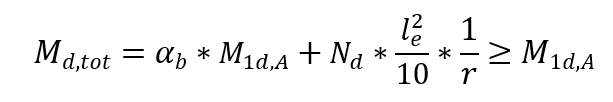
αb ein Koeffizient, der von der Verteilung der Momente in der Spalte abhängt.
M1d,A der Berechnungswert des Moments der 1. Ordnung MA;
h die Höhe des Säulenabschnitts in der analysierten Richtung;
• die normale Maßkraft;
fcd die Druckfestigkeit der konkreten Berechnung;
M1d, min moment der Mindestbestellung 1. Ordnung.
So wird ausgehend von der zweiten Folge des vorherigen Ausdrucks daraus geschlossen, dass die Exzentrizität der 2. Ordnung (e2) den folgenden Ausdruck annimmt:
2.3.5 EXZENTRIZITÄT DURCH FLUENCY
Die Exzentrizität, die durch die Fließfähigkeit von Ec-Beton entsteht, muss laut NBR 6118 (2014) in Pfeilern mit λ > 90, also schlanken und vielen schlanken Säulen, berechnet werden. Die Auswirkungen der Fließfähigkeit auf Säulen mit Schlankheitsindizes unter 90 werden nicht berücksichtigt.
Obwohl die genaue Analyse der Auswirkungen der Fließfähigkeit eine komplexe Arbeit ist, bringt NBR 6118 einen vereinfachten Ausdruck für die Berechnung der Exzentrizität ec, wie folgt: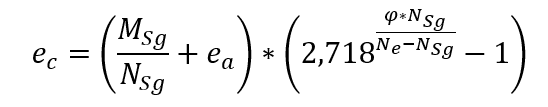 sein
sein
MSg und Nsg die ersuchenden Bemühungen in der Säule aus der fast dauerhaften Kombination genommen;
ea und zufällige Exzentrizität;
φ den Fließkoeffizienten.
Eci = 5.600-* fck0.5 ist der anfangs elastizierte Modul des Betons;
Ic das Trägheitsmoment des Säulenabschnitts;
le die äquivalente Länge des Säulenbeins.
Die berechnete ec-Exzentrizität muss der Exzentrizität der 1. Ordnung hinzugefügt werden. Abbildung 5 zeigt die Exzentrizität der zweiten Ordnung.
Abbildung 5: Exzentrizitäten erster und zweiter Ordnung in Säulen.
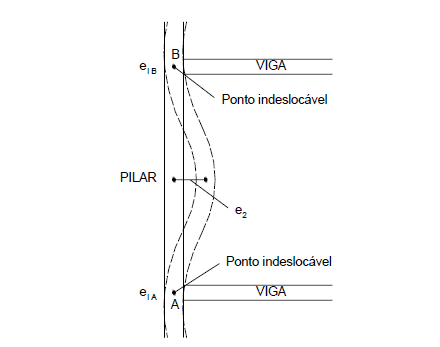
Die Endabschnitte beinhalten nicht die Auswirkungen der 2. Ordnung und sollten nur im Zwischenabschnitt berücksichtigt werden.
2.4 BERECHNUNG DER LONGITUDINALEN ARMATUR MIT ABACUS-HILFE
Bei der manuellen Bemaßung der Säulen sind die Abakusse unverzichtbar, da sie eine schnelle Definition der Bewehrungsrate ermöglichen, so dass die theoretischen Gleichungen der normalen oder schrägen Verbundflexion nicht angewendet werden müssen. Darüber hinaus ermöglichen die Abakusse die einfache Auswahl mehrerer Verstärkungsanordnungen im Querschnitt. Venturini und Rodrigues (2000) für Normal Composite Flexion und Pinheiro (1994) für Oblique Composite Flexion sollten nur für die Konstruktion von Säulen mit festem Beton der Gruppe I (fck ≤ 50 MPa) verwendet werden mit einigen numerischen Parametern ausgearbeitet, bei denen sie nicht für Betone der Gruppe II gelten.
2.4.1 NORMALCOMPOSITE BENDING
Für Venturini und Rodrigues (2000) Normal Composite Flexion zeigt Abbildung 6 die Notation der Abakusanwendung. Die Exzentrizität (e) ist parallel zum Abstand d ‘zwischen der Mitte der Eckstange und der Fläche des Abschnitts. Im Allgemeinen gibt es d ‘= c + Φt + Φλ / 2 mit c = Betondeckung, Φt = Bügeldurchmesser und Φλ = Durchmesser des Längsstabs.
Abbildung 6 : Notation für normale Verbundflexion.
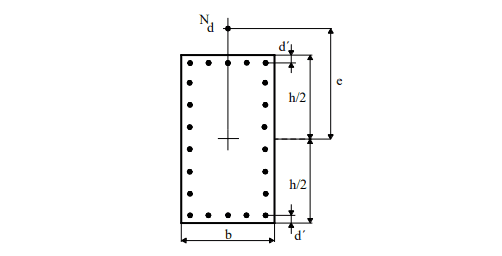
Die Gleichungen, die für den Bau von Abaci verwendet wurden, wurden in der Veröffentlichung von Venturini und Rodrigues (2000) hervorgehoben. Die Definition der Längsverstärkung wird durch Berechnung der Maßanstrengungen n (ni) und μ (mi) eingeleitet. Der adimensionale Wert n wurde in der folgenden Gleichung definiert: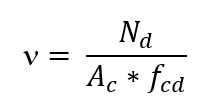
Der Wert von μ, abhängig vom Fletormoment oder der Exzentrizität, ist: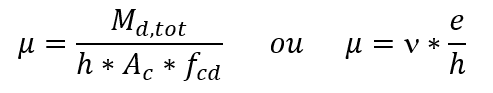
Sein
Nd die normale Kraft der Berechnung;
Ac den Bereich des Querschnitts der Säule;
fcd die Berechnungsstärke des Betons zur Kompression (fck/γc);
Md, tot das gesamte Fletor-Moment der Berechnung;
h die Größe der Säule in der betrachteten Richtung;
und Exzentrizität in die betrachtete Richtung.
Nachdem eine konstruktive Verteilung für die Bewehrung in der Säule gewählt wurde, wird der zu verwendende Abakus in Abhängigkeit von der Stahlsorte und dem Wert des d ‘/ h-Verhältnisses definiert. Im Abakus wird mit dem Paar ν und μ die mechanische Rate ω erhalten. Die Bewehrung wird berechnet durch den Ausdruck:
2.4.2 OBLIQUE COMPOUND FLEXION
Für Pinheiroes Oblique Composite Flexion (1994) zeigt Abbildung 7 die Notation, die bei der Verwendung von abaci angewendet wird. Die Entfernungen d’x und d’y haben jedoch die gleiche Interpretation von d’, jedoch jeweils in eine Richtung der Säule.
Abbildung 7 : Notation für normale Verbundflexion.
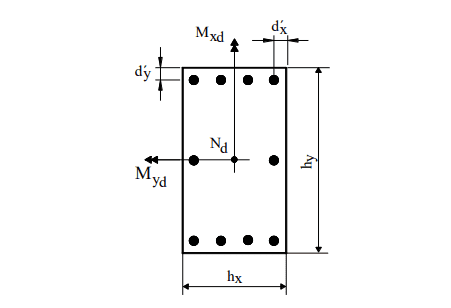
Die Bestimmung der Bewehrung beginnt mit der Berechnung der Maßanstrengungen ν und μ, wobei μ nach den beiden Hauptrichtungen der Säule: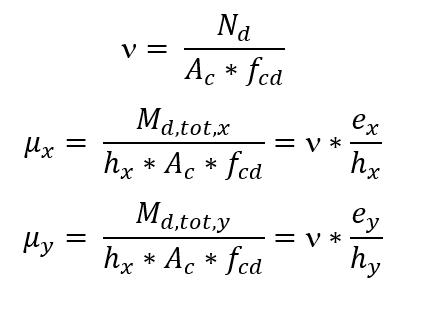 Sobald eine konstruktive Verteilung für die Verstärkung auf der Säule gewählt ist, wird der zu verwendende Abakus definiert, abhängig von den Werten der Verhältnisse d’x/hx und d’y/hy und der Art des Stahls. Im Abakus wird mit dem Trio (ν, μx, μy) man erhält die mechanische Rate ω. Die Bewehrung wird mit folgender Gleichung berechnet:
Sobald eine konstruktive Verteilung für die Verstärkung auf der Säule gewählt ist, wird der zu verwendende Abakus definiert, abhängig von den Werten der Verhältnisse d’x/hx und d’y/hy und der Art des Stahls. Im Abakus wird mit dem Trio (ν, μx, μy) man erhält die mechanische Rate ω. Die Bewehrung wird mit folgender Gleichung berechnet:
2.5 DETAILLIERUNG VON STAHLBETONPFEILERN
NBR 6118, 2014 legt fest, dass die Dimension des Querschnitts der Säule nicht weniger als 19 cm betragen sollte. Diese Empfehlung zielt darauf ab, inakzeptables Verhalten bei Bauteilen zu vermeiden und angemessene Baubedingungen zu ermöglichen.
In Sonderfällen darf die kleinste Größe der Säule jedoch zwischen 19cm und 12cm liegen. Für diese Fälle ist es notwendig, die endgültigen Berechnungsbemühungen, die bei der Dimensionierung der Säulen angewendet werden, mit einem zusätzlichen Koeffizienten gemäß Bild 8 zu multiplizieren.
Abbildung 8 – Werte des zusätzlichen Koeffizienten Yn.

Zunächst wird die geometrische Rate der Längsverstärkung der Säule durch das folgende Verhältnis definiert: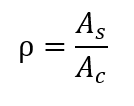
Sein
As die Summe der Bereiche der Querschnitte der Längsstäbe.
Ac den Querschnittbereich der Säule.
Die minimale Längesfläche, die von der Intensität des Antrags aufgrund der normalen Festigkeit und Festigkeit des Stahls abhängt, wird durch den folgenden Ausdruck bestimmt: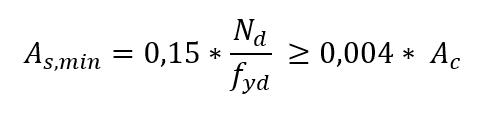
Daher beträgt die minimale geometrische Bewehrungsrate 0,4%.
Die maximal mögliche Bewehrungsfläche in Stützen muss 8% der Querschnittsfläche betragen, unter Berücksichtigung der Bewehrungsüberlappung in Spleißbereichen, dh:
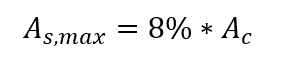 Der Mindestdurchmesser der Längsstäbe darf nicht weniger als 10 mm betragen und darf 1/8 der kleinsten Größe des Säulenabschnitts nicht überschreiten.
Der Mindestdurchmesser der Längsstäbe darf nicht weniger als 10 mm betragen und darf 1/8 der kleinsten Größe des Säulenabschnitts nicht überschreiten.
Für das richtige Betonieren ist es notwendig, dass der Beton ein Minimum an Raum hat, um zwischen den Längsverstärkungen zu durchqueren. Daher werden Einschränkungen für den freien Abstand zwischen den Balken der Längsverstärkung (aL) auferlegt, der gleich oder größer als der höhere der folgenden Werte sein muss:
- 20 mm;
- Die Durchmessermessung der Stange, des Balkens oder der Hülse in der Naht;
- 1.2 stattdessen der maximale Durchmesser des Aggregats;
Der maximale Abstand zwischen den Achsen der Bewehrungsstäbe ist ebenfalls begrenzt und muss kleiner oder gleich der doppelten Größe der Säule sein, ohne 400 mm zu überschreiten.
Der Durchmesser der Bügel (φt) in Säulen darf nicht weniger als 5 mm oder 1/4 des Durchmessers der Längsstange betragen.
Um die Positionierung der Längsverstärkungsstäbe zu gewährleisten und darüber hinaus die Längsstangen nicht zu versenken und Nahtverstärkung in den Nahtbereichen zu verwenden, sind maximale Abstände zwischen den Steigbügeln (gemessen in Richtung der Säulenachse) erforderlich, die kleiner oder gleich dem niedrigeren der folgenden Werte sind:
- 200 mm;
- kleinere Schnittdimension;
- 24 φ für CA-25-Stahl und 12 φ für CA-50-Stahl, wobei φ der Durchmesser der Längsstange ist;
Wenn die Möglichkeit besteht, die Stäbe an der Oberfläche zu knicken, sollten Maßnahmen ergriffen werden, um dies zu vermeiden.
3. CAD/TQS SOFTWARE MODELLING
Eine der Möglichkeiten, eine strukturelle Berechnung Detaillierung, in Stahlbeton, schneller und genauer (mit weniger Rundung), ist durch den Einsatz von Software, eine von ihnen heißt TQS, verwendet es die CAD-Plattform für seinen Betrieb. Mit TQS können wir die Berechnungen der Anstrengungen und Pfeile in der Struktur, die Abmessungen und Details der Verstärkungen in Abhängigkeit von den Anforderungen und der Darstellung aller notwendigen Materialien erhalten, alles nach dem, was der Profi auf der Zeichenplattform gestartet hat. Das TQS macht all diese Dimensionierung und Detaillierung nach aktuellen Standards.
TQS-Systeme verfügen über Ressourcen, die die Entwicklung von Strukturprojekten zu einem hochproduktiven Prozess machen. Von der Empfängnis bis zur Anlagenemission werden alle Schritte automatisiert. Seine Hauptprodukte sind TQS (verstärkter und spannbelasteter Beton), Alvest (Strukturmauerwerk), PREO (Fertigteil) und SISEs (Geotechnik).
Angepasst an die neuesten regulatorischen Überprüfungen (NBR 6118/2014, NBR 15200:2012, NBR 15.575:2013, NBR 9062:2006, NBR 15812:2010, NBR 15961:2011. Jede Version von TQS-Systemen wird sowohl operativ als auch in Bezug auf ihre Ergebnisse rigoros getestet. Ebenfalls verfügbar sind Lehrmaterial für alle seine Produkte, wie Schritt-für-Schritt-TQS, Plotten, Schritt-für-Schritt-Treppen, Alvest Schritt für Schritt (TQS, 2020).
3.1 STRUKTURELLE RELEASE IN TQS/CAD SOFTWARE
Die für die Analyse angefertigte Struktur war das vollständige Beispiel des Buches “Strukturprojekt für Stahlbetonbauten” von José Milton de Araújo (2014). Für die Modellierung in der Software wurden die Säulen, die Balken, die Platten, die Treppen, die Wandlasten, sequenziell in der beschriebenen Reihenfolge gestartet.
Für die Säulen wurden folgende Schritte befolgt: Nach dem Öffnen des Strukturmodells ist die Registerkarte “Säulen” aktiv, das Fenster “Aktuelle Daten” muss geöffnet werden (Abbildung 9), wo alle Daten zum Einfügen der Spalte angezeigt werden, und dann die Dimensionen, die Identifikationsnummer, die Einfügeposition, die Bestimmung, wo die Säule geboren wird und stirbt, unter anderem Informationen platzieren. Am Ende aller relevanten Ausgaben sind dann alle notwendigen Säulen enthalten.
Abbildung 9: TQS/CAD-Fenster in der Registerkarte “Säulen”.
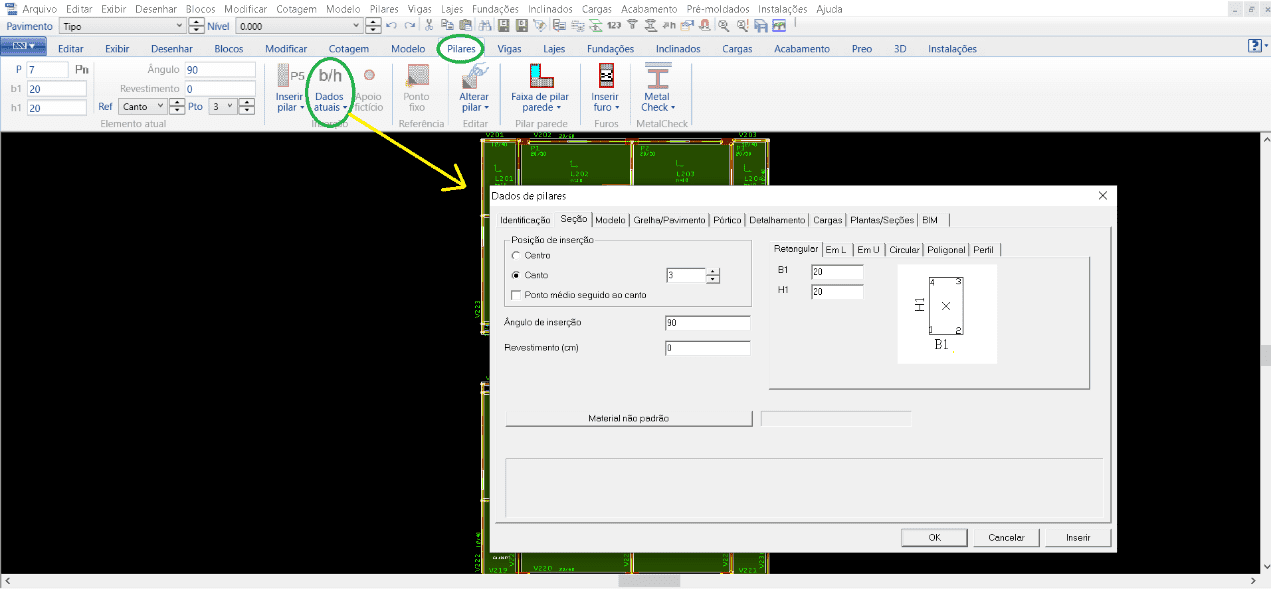
Für den Bau von Trägern in CAD/TQS-Software ist der Prozess wie folgt:
Nachdem wir alle Säulen definiert haben, gehen wir zur Freigabe der Balken über. Zunächst müssen Sie das Menü “Beams” aktivieren, in dem alle mit den folgenden Befehlen spezifisch für die Freigabe der Balken sind.
Innerhalb der Registerkarte “Beams” müssen Sie den Befehl “Aktuelle Daten” (Abbildung 10) auswählen, wo Sie ein Fenster der allgemeinen Daten der Träger öffnen und so alle Informationen platzieren, die für die Freigabe jedes Balkens erforderlich sind. Informationen wie die Identifikationsnummer jedes Balkens, seine Abdeckung, die Lasten, die dieser Strahl auf die Säulen einwirken wird, wie z. B. den dauerhaften und zufälligen Abschnitt. Nach all diesem Detaillierungsprozess können wir dann den Balken einfügen, am Startpunkt dann am Endpunkt platzieren, in der Regel sind diese Einfügepunkte die Scheitelpunkte der bereits eingefügten Säulen, die das gleiche Verfahren wiederholen, bis alle notwendigen Balken platziert werden.
Abbildung 10 – TQS/CAD-Fenster in der Registerkarte “Beams”.
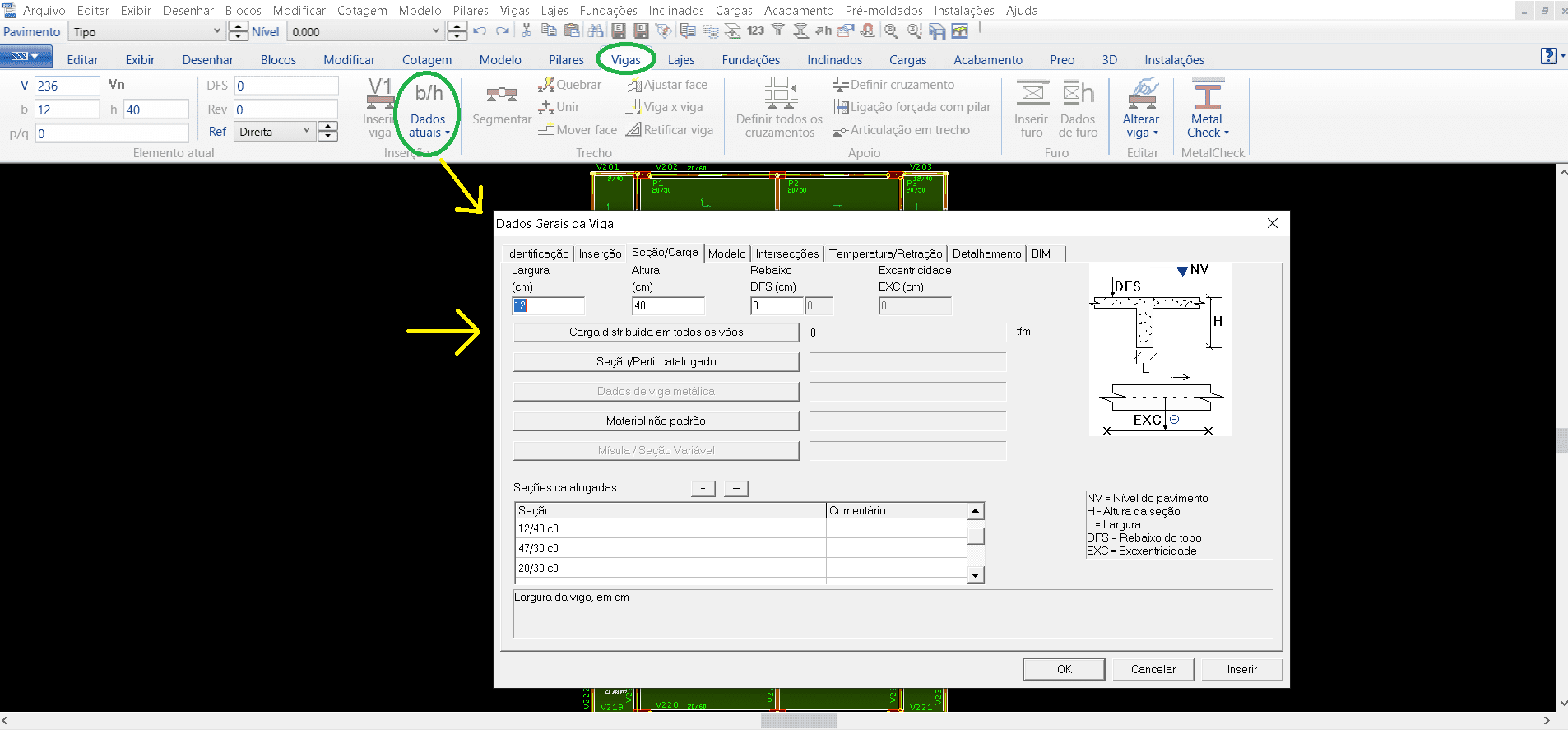
Nachdem die Balken freigegeben sind, bewegen wir uns zu den Platten, nach den gleichen Verfahren wie die vorherigen in der Registerkarte “Platten” Auswahl “Aktuelle Daten” setzt die Identifizierung, Art der Platte und ihre Dicke (Bild 11).
Abbildung 11 – TQS/CAD-Fenster auf der Registerkarte “Platten”.
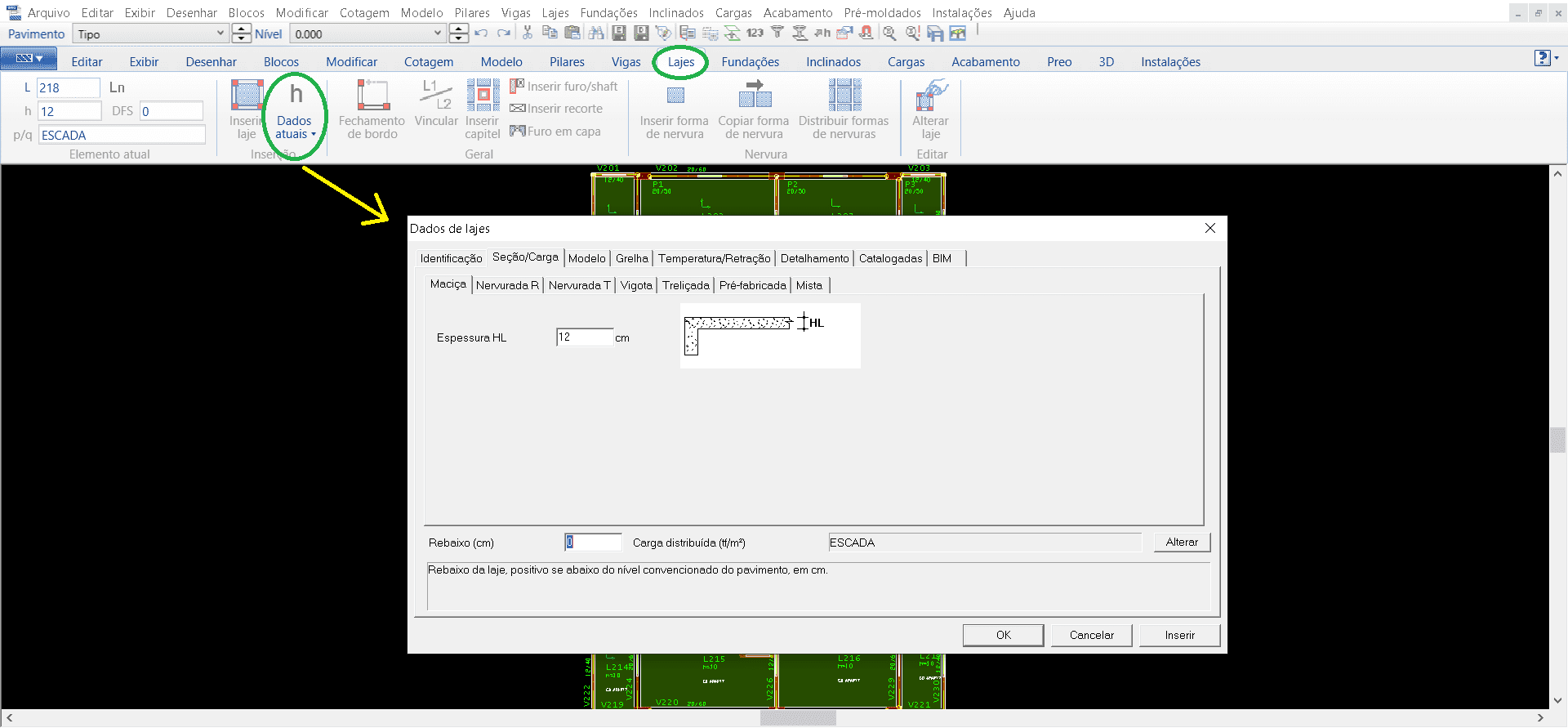
Für die Buchung von Wandladungen folgt die gleiche Linie von Verfahren. Im Fenster “Loads” wählt die Registerkarte “Linear verteilt” und öffnet dann ein Fenster für die Auswahl der Lastart, für die fragliche Modellierung wurde Block 14 (BetonblockMauerwerk 14 cm) und die Höhe der Wand bestimmt (Bild 12).
Quelle: Abbildung 12 – TQS/CAD-Fenster auf der Registerkarte “Loads”.
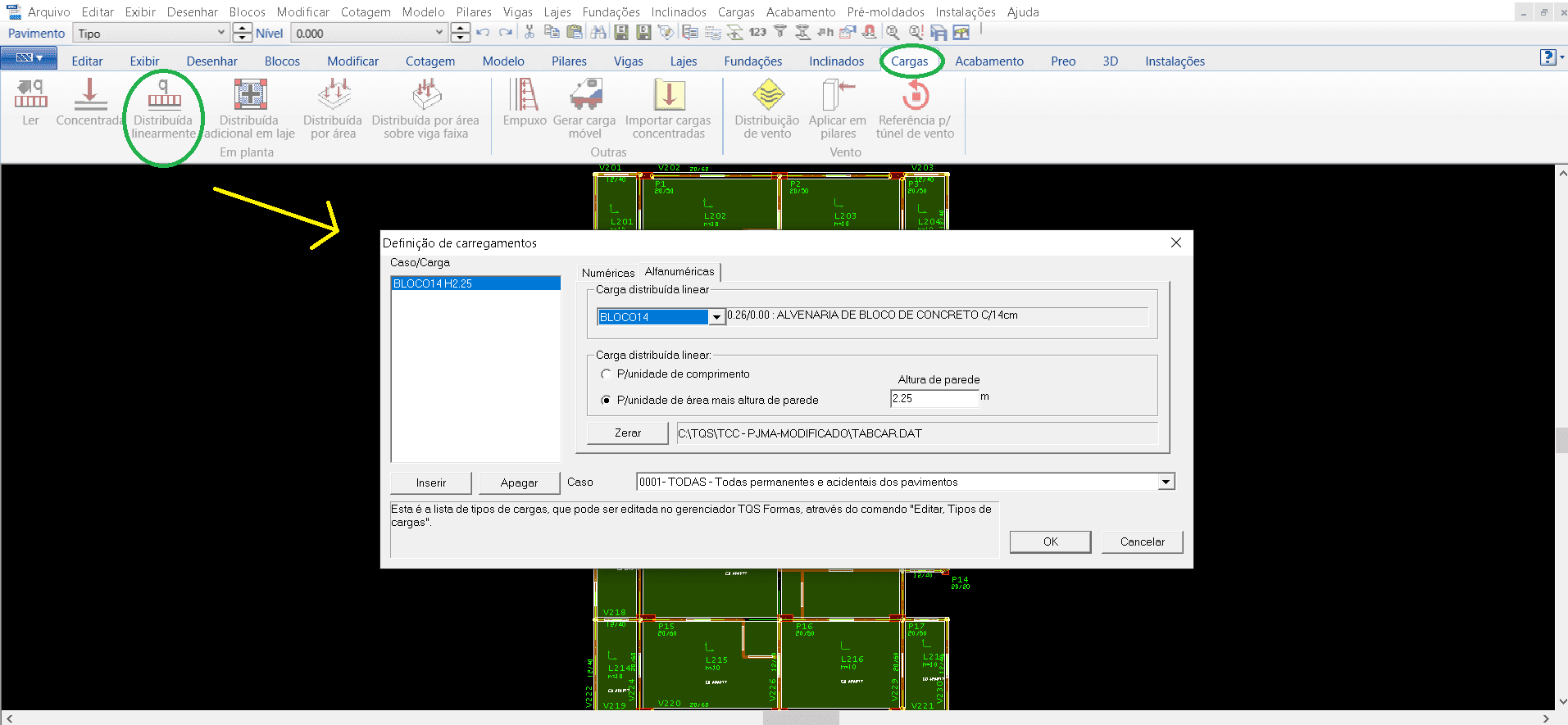
Daher müssen wir beim Beenden der Freigabe aller notwendigen Elemente in den Etagen die bisher im Menü “Datei” definierten Daten im Befehl “Speichern des Strukturmodells” speichern.
Abbildung 13 – 3D-Beispielgebäude, TQS/CAD
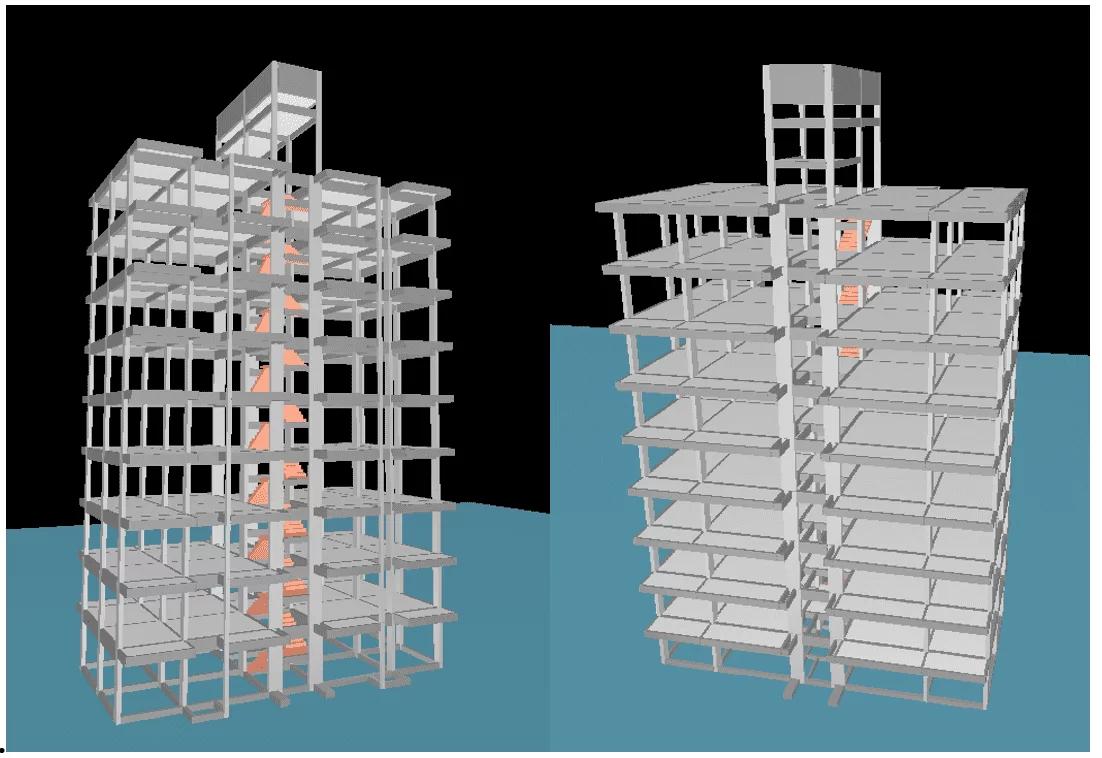
Quelle: Autor, 2020.
Mit dem dreidimensionalen Betrachter haben wir die konkrete Vorstellung davon, wie das Beispielgebäude aussehen würde (Abbildung 13).
Die P-Calc-Anwendung ist ein TQS-Rechner, der Stahlbetonsäulen überprüft, die einer individuellen schrägen Verbundbiegung unterliegen (TQS, 2020).
Die Hauptmerkmale von P-Calc sind:
- Überprüfung der Säulen, die der zusammengesetzten Beugung, normal oder schräg, in Bezug auf den letzten Grenzzustand von Bruch und Instabilität unterzogen werden;
- Analyse von Säulen mit hochfestem Beton (fck > 50 MPa);
- Normalaufwand x Deflektormoment Interaktionsdiagramm (FCO und FCN);
- Grafische Ergebnisse für Spannungen und Verformungen im Abschnitt;
- Bewertung der lokalen Wirkungen der 2. Ordnung unter Annahme der geometrischen und physikalischen Nichtlinearität, ABNT abnt NBR 6118;
- Umhüllung von minimalen Momenten;
- Berechnungsspeicher im PDF-Format;
4. PRÄSENTATION UND ANALYSE DER ERGEBNISSE
In diesem Thema werden die Vergleiche zwischen den Referenzen für die untersuchten Elemente dargestellt. Es wurde in Unterthemen für die Hauptelemente eines Strukturprojekts unterteilt. Es wird betont, dass die untersuchten Referenzen die Grundlage für das Projekt des Buches “PROJETO ESTRUTURAL DE EDIFÍCIOS DE CONCRETO ARMADO” von JJOSÉ MILTON DE ARAÚJO, 3. Auflage, modelliert, berechnet und detailliert in der TQS waren. Bei den anderen Tests wurden einige Elemente mit anderen Berechnungswerkzeugen wie Pcalc und Bending Abaci für die Daten der Säulen verglichen.
4.1 VERGLEICHENDE MODELLIERUNG UND GRÖSSE – SÄULE
Nach der Modellierung und Dimensionierung der Pfeiler wurden nach Thema 3 hauptaufwand, Abschnitt und Stahlbereich zwischen den für die beiden Säulen (P2 und P5) untersuchten Referenzen gemäß der Zusammenfassung in den Tabellen 01 und 02 verglichen.
Tabelle 1 – Darstellung der Ergebnisse gegenüber Säule 2
| Elemente | Charakteristische Anstrengungen (tf) | Abschnitt (cm x cm) |
Stahlfläche (cm2) |
| Araujo (2014) | 71,4 | 20 x 50 | 6ϕ20 (18,90) |
| TQS | 66,2 | 20 x 50 | 8ϕ20 (25,20) |
| Pcalc* | 71,4 | 20 x 50 | 10ϕ20 (31,50) |
| Pcalc* | 66,2 | 20 x 50 | 10ϕ20 (31,50) |
| Abacus- Normale Flexion* | 71,4 | 20 x 50 | 6ϕ20 (18,90) |
| Abacus- Normale Flexion* | 66,2 | 20 x 50 | 4ϕ20 (12,60) |
*Standard-Säulenlösung mit ungefährer Krümmung.
Quelle: Autor, 2020.
Bei der Analyse der Vergleiche für die P2-Säule ist festzustellen, dass die Bemaßung des Araújo (2014) im Vergleich zum TQS einen Anstieg um 33,33 % im Stahlbereich zeigt, wobei zu berücksichtigen ist, dass Arajo eine um 7,85 % höhere Normalkraft darstellt, und zwar bereits im Vergleich zum PCalc, dass ein Anstieg um 66,67 % zu verzeichnen ist, der mit der gleichen Belastung korreliert.
Es ist interessant festzustellen, dass dieselben Werte in Bezug auf die Dimensionierung der Standardspalte mit ungefährer Kurve mit der Normal Flexion Abaci (VENTURINI und RODRIGUES, 2000) in zwei Lastgruppen unterteilt wurden, da die im TQS durchgeführte Modellierung von der Belastungserhebung von Araújo (2014) abweicht, so dass wir die Zahlen 14 und 15 haben.
Abbildung 14 – Vergleich zwischen TQS x Pcalc x Abaci für Säule 2
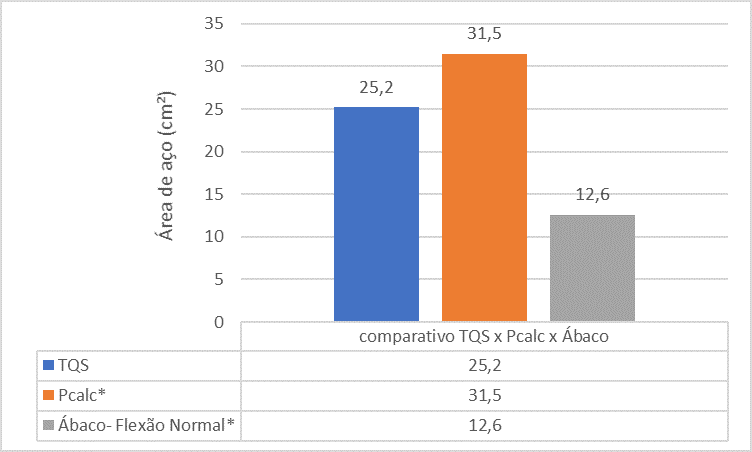
Die vergleichende Analyse zwischen den Referenzen zeigt, dass die Stahlfläche der P2-Säule, die vom TQS-Werkzeug gefunden wurde, kleiner ist als die Stahlfläche, die von Pcalc und Abaci gefunden wurde. Dies ist auf die Tatsache der monolithischen Analyse im Programm gemacht.
Abbildung 15 – Vergleich zwischen Araújo (2014) x Pcalc x Abacos für Pilar 2
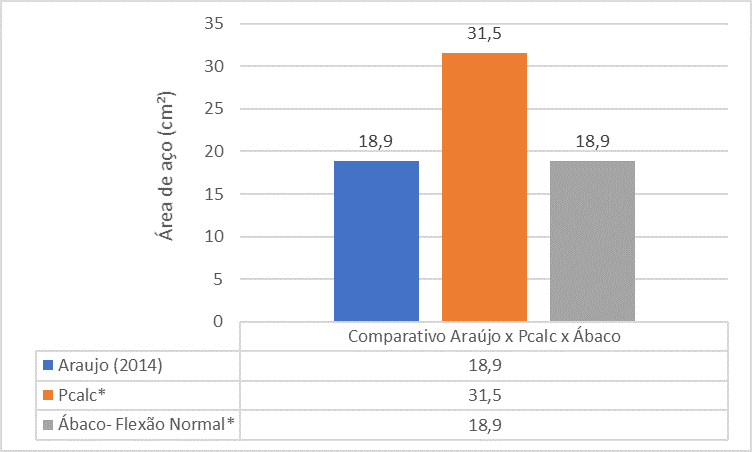
Die vergleichende Analyse zwischen den Referenzen zeigt, dass die Stahlfläche der P2-Säule, die in Araújo Buch (2014) gefunden wurde, viel kleiner ist als die Stahlfläche, die von The PCalc und Abacus gefunden wurde.
Die P2-Säule ist eine Endsäule, eine Zwischenstütze für den Strahl V202 in x-Richtung, wobei diese übertragenen Momente nicht berücksichtigt werden. In y-Richtung haben wir den Strahl V 227, dies wurde als die in der Säule übertragenen Momente angesehen. Aus dieser Analyse ergibt sich die Berechnung des perfekten Einstellmoments (Meng), des Strahlträgheitsmoments (Ivig), des Strahlsteifigkeitskoeffizienten (rvig), des Säulenträgheitsmoments (Ip), des Säulenneifigkeitskoeffizienten (rp) und Anfangsmomente in den Säulen (Mp), aus den Berechnungen werden die reduzierten Momente erhalten, aber geteilt durch den großen Unterschied zwischen ihnen wurden sie als Null betrachtet und den Abschnitt in Biegung dimensioniert – normale Kompression in x-Richtung.
Für die Normalkraft auf der x-Achse haben wir die anfänglichen Exzentrizitäten (eia) des Schlankheitsindex (λx), die zufällige Exzentrizität (eax), die minimale Exzentrizität (e1x, min), die anfängliche Exzentrizität im Zwischenabschnitt (eix) und die Exzentrizität zweiter Ordnung (eix). e2x) und Fließfähigkeitsexzentrizität (ecx). Die kritische Sitzung fand in der Extremitätssitzung statt. Unter Verwendung der Stahlflächentabellen kann die Sitzung mit 6 20-mm-Stäben bewaffnet werden, wobei eine Gesamtstahlfläche von 18,85 cm² angenommen wird.
Tabelle 2 – Darstellung der Ergebnisse gegenüber Säule 5
| Elemente | Charakteristische Anstrengungen (tf) | Abschnitt (cm x cm) |
Stahlfläche (cm2) |
| Araujo (2014) | 112,2 | 20 x 50 | 10ϕ16 (20,00) |
| TQS | 141,5 | 20 x 50 | 8ϕ25 (40,00) |
| Pcalc* | 112,2 | 20 x 50 | 12ϕ20 (37,80) |
| Pcalc* | 141,5 | 20 x 50 | 12ϕ25 (60,00) |
| Abacus- Normale Flexion* | 112,2 | 20 x 50 | 8ϕ25 (40,00) |
| Abacus- Normale Flexion* | 141,5 | 20 x 50 | 11ϕ25 (55,00) |
*Standard-Säulenlösung mit ungefährer Krümmung.
Quelle: Autor, 2020.
Bei der Analyse der Vergleiche für die P5-Säule kann beobachtet werden, dass die Dimensionierung von Araújo (2014) in Bezug auf das TQS eine 100% ige Zunahme der Stahlfläche zeigt, wobei berücksichtigt wird, dass Araújo eine um 26,11% niedrigere Normalkraft aufweist In Bezug auf den PCalc gab es einen Anstieg von 89% in Bezug auf die Last von Araújo und 50% in Bezug auf die Last des TQS, was zeigt, dass die Divergenz der Stahlflächen umso größer ist, je größer der Anstieg der Last ist. Es kann gesagt werden, dass diese Abweichung auf die Tatsache zurückzuführen ist, dass für Araújo (2014) im endgültigen Grenzzustand (ELU) der folgende Fehler für die Auflösung der P5-Säule im Pcalc vorliegt: Die Säule achtet nicht auf die Überprüfung des Mindestmoments. Die Säule mit der Last des TQS im Pcalc erzeugt den folgenden Fehler: ρs = 5,89%> ρs.max = 4,00%.
Es ist interessant festzustellen, dass dieselben Werte in Bezug auf die Konstruktion von Standard-Abutments mit ungefähren Kurven unter Verwendung des Normal Flexion Abacus (VENTURINI und RODRIGUES, 2000) in zwei Lastgruppen unterteilt wurden, da sich die im TQS durchgeführte Modellierung vom Anheben von unterscheidet Araújo Ladung (2014), dann haben wir die Abbildungen 16 und 17.
Abbildung 16 – Vergleich zwischen TQS x Pcalc x Abaci für Säule 5
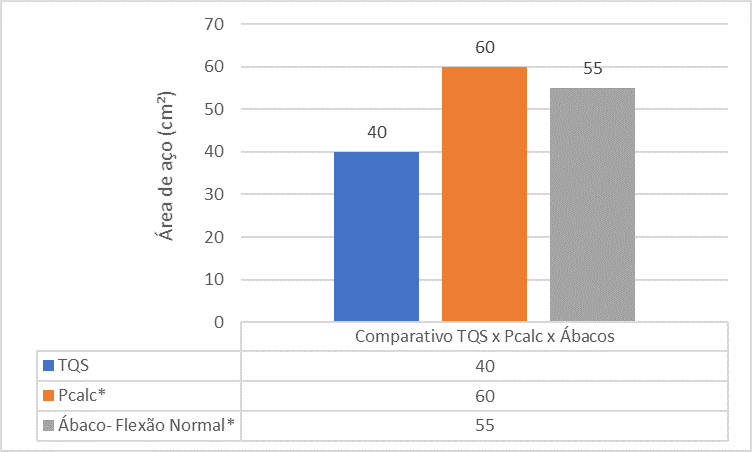
Die vergleichende Analyse zwischen den Referenzen zeigt, dass die Stahlfläche der P5-Säule, die vom TQS Werkzeug gefunden wurde, kleiner ist als die Stahlfläche, die von Pcalc und Abaci gefunden wurde. Dies ist auf die Tatsache der monolithischen Analyse im Programm gemacht.
Abbildung 17 – Vergleich zwischen Araújo (2014) x Pcalc x Abacos für Pilar 5
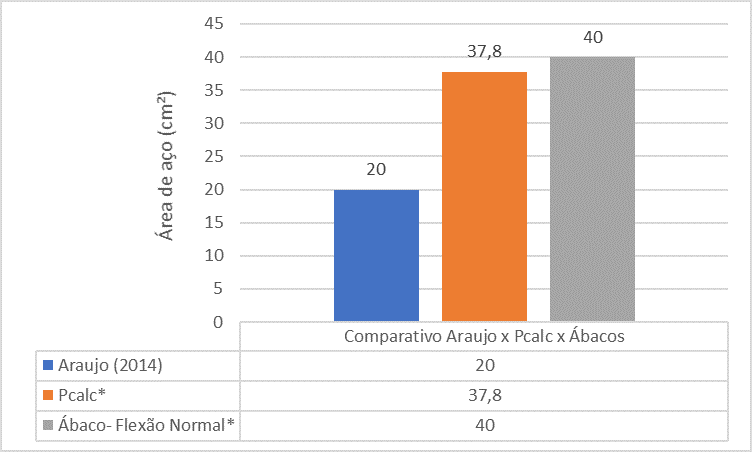
Die vergleichende Analyse zwischen den Referenzen zeigt, dass die Stahlfläche der P5-Säule, die in Araújo Buch (2014) gefunden wurde, viel kleiner ist als die Stahlfläche, die von The PCalc und Abacus gefunden wurde.
Die P5-Säule ist eine Zwischensäule, bei der sich die Spannweiten und Belastungen der Träger V204 und V227 nicht unterscheiden, sodass die von diesen Trägern übertragenen Anfangsmomente vernachlässigt werden können. Basierend auf dieser Analyse wurde die Berechnung auf der y-Achse durchgeführt, da es sich um den höchsten gefundenen Schlankheitsindex (λx) handelte, die Exzentrizität (ey), gegeben durch die Summe der Exzentrizität erster Ordnung (e1x), der Exzentrizität zweiter Ordnung (e2x) und Kriechexzentrizität (ecy). Mithilfe der Stahlflächentische kann die Sitzung mit 10 Balken von 16 mm bewaffnet werden, wobei eine Gesamtstahlfläche von 20,00 cm² angenommen wird.
5. FAZIT
Er stellte fest, dass der Vergleich zwischen den Methoden wichtig für die Wahl des besten Werkzeugs für die Verwendung in der Dimensionierung von Säulen ist.
Bei der Reproduktion der Modellierung des Gebäudes von Araújo im TQS wurde ein Lastunterschied festgestellt, und für diese Lasten wird wahrgenommen, dass das TQS-Werkzeug im Standardmodus nahe an der Dimensionierung für das Werkzeug PCalc und Abaci für Zwischensäulen liegt.
In ara-jo zeigen die Endsäulen eine kleinere Variation der Antworten in Bezug auf Abaci und PCalc.
Die vergleichende Analyse zwischen den Berechnungsmethoden unterscheidet sich daher dadurch, dass sich die monolithische Analyse der im TQS-Tool vorgenommenen Struktur von den anderen Methoden unterscheidet, die eine segmentierte Analyse der Elemente mit vereinfachten Berechnungsformularen darstellt.
REFERENZEN
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 1978.
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2003.
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2014.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15200. Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro, — Procedimento, 2012.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15575. Edificações habitacionais – Desempenho. Rio de Janeiro, — Procedimento, 2013.
ABNT (Associação Brasileira de Normas Técnicas). NBR 9062. Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, — Procedimento, 2006.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15812. Alvenaria estrutural – Blocos cerâmicos. Rio de Janeiro, — Procedimento, 2010.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15961. Alvenaria estrutural – Blocos de concreto. Rio de Janeiro, — Procedimento, 2011.
AGUIAR, E.A.B. Projeto de pilares de concreto de alto desempenho. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2000.
ARAUJO, José Milton de. Projeto estrutural de edifícios de concreto armado. 3. ed. Rio Grande: Editora Dunas, 2014.
BASTOS, Paulo S. dos Santos. Fundamentos do Concreto Armado. Universidade Estadual Paulista. Bauru, São Paulo. 2006.
BRANDÃO, A. M. S.; PINHEIRO, L. M. Qualidade e durabilidade das estruturas de concreto armado: aspectos relativos ao projeto. Cadernos de Engenharia de Estruturas. EESC. Universidade de São Paulo. São Carlos, 1999.
CARVALHO, Roberto Chust.; FIGUEIREDO FILHO, Jasson Rodrigues de. Pilares de concreto armado. p.9-25. Notas de aula – Universidade Federal de São Carlos, 2002
FUSCO, P.B. Estruturas de concreto – solicitações normais, editora Guanabara, São Paulo, 1986.
PIANCASTELLI, E. M. Patologia, Recuperação e Reforço de Estruturas de Concreto Armado. Apostila para Curso de Extensão, Ed. Depto. Estruturas da Escola de Engenharia da UFRG, Belo Horizonte, 1997
PINHEIRO, L.M.; BARALDI, L.T.; POREM, M.E. Concreto Armado: Ábacos para flexão oblíqua. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1994.
TQS, Calculadora P-Calc, Pilares de concreto, 2020. Disponível em: <https://www.tqs.com.br/apps/p-calc/ejm1se496l>
TQS, Sobre a TQS, 2020.Disponível em: <https://www.tqs.com.br/about>
VENTURINI, Wilson Sérgio; RODRIGUES, Rogério de Oliveira. Dimensionamento de peças retangulares de concreto armado solicitadas à flexão reta. Sao Carlos, Institut für Bauingenieurwesen, School of Engineering of Séo Carlos – USP, 1987 (reprinted.2000)
[1] Studium der Bauingenieurwissenschaften.
[2] Abschluss in Bauingenieurwesen.
[3] Master in Geotechnik und Bauwesen. Abschluss in Bauingenieurwesen. Abschluss in Agrartechnik.
Eingesandt: Mai 2020.
Genehmigt: Mai 2020.