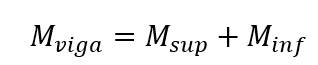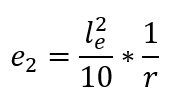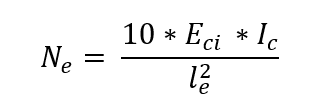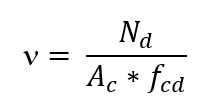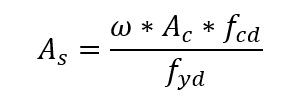ARTICOLO ORIGINALE
CARVALHAES, Daniely Silva [1], CARVALHAES, Daniel José [2], QUARESMA, Wanessa Mesquita Godoi [3]
CARVALHAES, Daniely Silva. CARVALHAES, Daniel José. QUARESMA, Wanessa Mesquita Godoi. Confronto tra dimensionamento e modellazione di colonne. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 05, Vol. 04, pp. 121-146. maggio 2020. ISSN: 2448-0959, Link di accesso: https://www.nucleodoconhecimento.com.br/ingegneria-civile/modellazione-di-colonne
RIEPILOGO
La ricerca della riduzione dei tempi di elaborazione dei progetti diventa una necessità, insieme all’indigenza di comprendere problemi ricorrenti nell’uso di strutture in cemento armato come patologie. Così, unendo i due problemi, il tempo e l’analisi, diventa imperativo studiare modi di modellare e analizzare le strutture nel software comune di sviluppo del progetto. L’obiettivo è quello di modellare un edificio e confrontare un elemento strutturale, analizzando i carichi e le dimensioni realizzati dal software TQS®. Questo processo è dovuto alla modellazione nel software TQS dell’edificio di esempio di José Milton de Araújo (2014). È stato osservato che il processo di modellazione rispetto al processo numerico presenta una differenza significativa a causa del fatto di fare l’analisi dell’edificio completo, essendo così affidabile la modellazione eseguita nel software, che consente un precedente studio dell’intera struttura.
Parole chiave: Pilastri, dimensionamento, modellazione, sperimentale, TQS.
1. INTRODUZIONE
Bastos (2006, p. 07) presenta il cemento armato come “l’unione di calcestruzzo semplice e di un materiale resistente alla trazione (avvolto dal calcestruzzo) in modo tale che entrambi resistano congiuntamente agli sforzi richiesto”, cioè il cemento armato è il risultato del semplice calcestruzzo più rinforzo più adesione.
Per Piancastelli (1997), il cemento armato è soggetto a cambiamenti nel tempo, perché è un materiale non inerte, grazie alle interazioni tra i suoi elementi costitutivi (cemento, sabbia, ghiaia, acqua e acciaio), alle interazioni tra questi elementi e agenti esterni come gas, sali, basi, acidi e altri, e con materiali che vi si aggiungono (additivi e aggiunte minerali).
Per molto tempo il calcestruzzo è stato considerato un materiale durevole, a causa di vecchie opere ancora in buone condizioni, ma il deterioramento precoce delle strutture attuali ci porta alle ragioni di patologie concrete (BRANDÃO e PINHEIRO, 1999). Ciò è dovuto alle nuove tecnologie, per rendere le strutture sottili e leggere, del processo di pianificazione e produzione delle strutture.
I pilastri sono elementi solitamente allineati verticalmente nel suo asse, in cui le normali forze di compressione sono preponderanti (ABNT NBR 6118, 2014), il loro studio è uno dei controlli essenziali, per quanto riguarda il dimensionamento, il malfunzionamento di un pilastro di una struttura può compromettere la funzionalità e causare gravi incidenti. Essendo responsabili della trasmissione dei carichi verticali, i pilastri sono generalmente soggetti, in particolare, alla condizione di flessoco compressione, pertanto la necessità di prendere in considerazione gli effetti del secondo ordine e l’analisi della stabilità del pilastro nel suo complesso.
Le colonne sono dimensionate in funzione degli sforzi di calcolo esterni, che comprendono le forze normali (Nd), i momenti flettenti (Mdx e Mdy) e le forze di taglio (Vdx e Vdy) essendo di azione orizzontale. La NBR 6118, nella versione 2003, in particolare in relazione ai pilastri, la norma ha introdotto diverse modifiche, come nel valore dell’eccentricità accidentale, un maggiore rivestimento in calcestruzzo, un nuovo metodo per il calcolo del limite di snello rispetto alla contemplazione o meno dei momenti flettenti 2 ° ordine e, soprattutto, con considerazione del momento flettente minimo, potendo sostituire il momento flettente per eccentricità accidentale. Nella versione 2014 è stata aggiunta la verifica del momento flettente minimo, effettuata dal confronto di una busta resistente, che comprende la busta minima con il 2 ° ordine.
2. CALCOLO E DIMENSIONAMENTO DEI PILASTRI DA PARTE DEGLI ABACOS
2.1 CLASSIFICAZIONE DEI PILASTRI
I pilastri sono classificati in base alla loro posizione nella struttura, può essere intermedio, finale o angolo. Questa classificazione consente di considerare gli sforzi necessari in ogni situazione calcolata. (FUSCO, 1981)
Figura 1 – Posizione dei pilastri negli edifici.
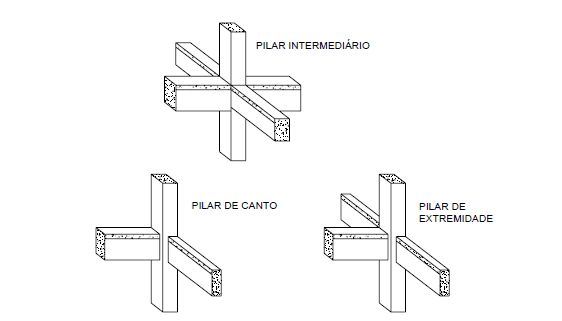
I pilastri intermedi sono prevalentemente sottoposti a forze di compressione assiale, perché i momenti catarro sono di poca intensità, così come solo alle azioni verticali (variabili permanenti e normali). A meno che le campate delle travi continue che si basano su questi pilastri non siano considerate diverse, i momenti finali di lancio trasmessi ai pilastri non vengono presi in considerazione. Pertanto, viene ammesso il pilastro intermedio sottoposto a compressione centrata sulla situazione del progetto, cioè l’eccentricità iniziale, nel dimensionamento delle aree dei rinforzi trasversali e longitudinali, è considerata uguale a zero.
I pilastri delle estremità sono sottoposti a normali forze di compressione e all’azione dei momenti propagati dalle travi, che hanno le loro estremità esterne sostenute su questi pilastri. Nelle travi trasversali all’asse del fascio interrotto, i momenti non sono considerati. Pertanto, la colonna di estremità soggetta a flessione normale composita è considerata, considerando, quindi, l’eccentricità iniziale in uno dei locali ordinati della sezione trasversale della colonna.
Pilastri angolari oltre ad essere sottoposti a normale forza di azionamento, si dovrebbero considerare i momenti trasmessi dalle travi, da cui i piani centrali sono perpendicolari alle facce dei pilastri, e vengono interrotti ai bordi della colonna. Nella situazione di progettazione, viene considerata la colonna d’angolo sottoposta a piegatura obliqua composita, con eccentricità iniziali in base agli assi coordinati locali.
I pilastri, sebbene la loro classificazione in base alla loro posizione nella struttura sia molto usuale, sono anche classificati per quanto riguarda il tipo di richiesta di presentare il pilastro. Cioè, pilastri sottoposti alla normale flessione composita, pilastri sottoposti a flessione composita obliqua e pilastri sottoposti a compressione centrata.
2.2 INDICE DI CINTURA
L’indice di snellezza dei pilastri in cemento armato è il rapporto tra la lunghezza equivalente (le) della colonna e il raggio di rotazione (i) della sezione. (NBR 6118, 2014)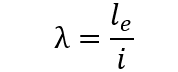
La classificazione dei pilastri dipende dai limiti di snellezza e da fattori aggiuntivi, come l’eccentricità relativa, la forma del diagramma dei momenti e le condizioni di legame delle estremità. Questi fattori sono considerati usando il coefficiente λ1.
Per i pilastri corti NBR 6118 (2014) (λ ≤ λ1) gli effetti del secondo ordine potrebbero essere ignorati perché gli indici di riferimento sono superiori agli indici di snellezza. Pilastri sottili mediani (λ1 < λ ≤ 90) che sono quelli per i quali gli effetti del secondo ordine possono essere considerati per processo approssimativo, come il metodo a pilastri standard con curvatura approssimativa. I pilastri sottili (90 < λ ≤ 140) sono quelli per i quali è possibile considerare il metodo standard a pilastri accanto ai diagrammi di M – N – 1/r. Pilastri molto sottili (140 < λ ≤ 200) che richiedono, per la verifica dello stato limite di instabilità, la considerazione dei metodi esatti. NBR 6118 non consente la progettazione e la costruzione di un pilastro con un indice di snellezza (λ) maggiore di 200. In caso di pali con forza normale inferiore a 0,10.fcd.Ac, quel limite può essere superato.
2.3 ECCENTRICITÀ
Nei pilastri, le eccentricità si verificano non solo a causa delle richieste iniziali sui pilastri, ma anche a causa di fattori aggiuntivi come gli effetti del 2 ° ordine, lo scorrimento di imperfezioni concrete e geometriche.
È necessario ottenere le eccentricità relative al tipo di colonna analizzata per dimensionarne il dimensionamento. Questa voce presenta i criteri per ottenere queste eccentricità nei pilastri separatamente, secondo lo standard NBR 6118, 2014.
2.3.1 ECCENTRICITÀ INIZIALE DEL 1° ORDINE
Sappiamo che le travi e i pilastri compongono gantries tridimensionali, in modo che i pilastri siano sottoposti a flessione obliqua composita e, di conseguenza, presentino eccentricità iniziali in due direzioni principali. Nei progetti che considerano processi semplificati per la definizione di sforzi richiedenti sono il momento fletor, la forza normale e la forza di taglio, ad esempio, il caso della trave continua presentato in NBR 6118 (2014), si ammette che le eccentricità iniziali sorgono nei pilastri angolo e fine. Ricordando che le eccentricità non sono considerate per i pilastri intermedi.
Le eccentricità del primo ordine sono date dalle espressioni:

Nd sarebbe la forza richiedente per il calcolo;
Md,A e Md,B i momenti di calcolo richiedenti alle estremità della colonna.
La più alta eccentricità in valore assoluto è adottata per ei,A.
Quando non vengono calcolati i valori esatti degli sforzi richiesto nella struttura, è possibile adottare la forma statica indicata nella figura 2, al fine di ottenere i momenti dell’influenza nei supporti estremi, come la semplificazione.
Figura 2 – Modello considerato in caso di supporto estremo di travi continue.
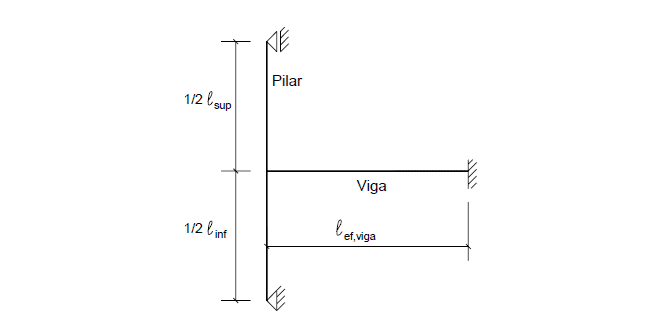
I momenti richiesti nei rami superiore e inferiore del pilastro sono ottenuti da:
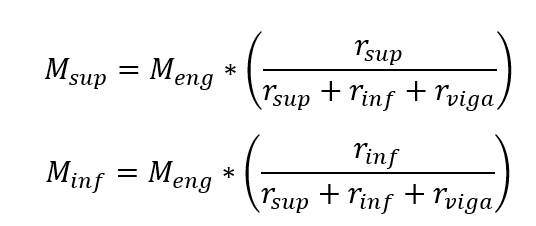 Essendo, Meng il momento di impostazione perfetto nel tram analizzato (fine della trave) della trave.
Essendo, Meng il momento di impostazione perfetto nel tram analizzato (fine della trave) della trave.
I coefficienti di rigidità dei rami superiore e inferiore della colonna e nella sezione del fascio sono definiti dalle relazioni tra momenti di inerzia e campate, secondo le seguenti espressioni: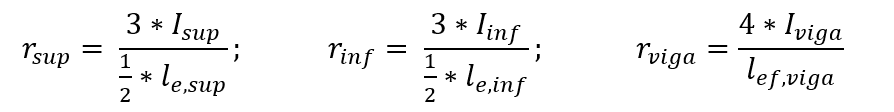 Il momento fletor sulla trave è determinato dalla seguente espressione, considerando l’equilibrio del nodo.
Il momento fletor sulla trave è determinato dalla seguente espressione, considerando l’equilibrio del nodo.
La lunghezza equivalente le dell’abutment può essere determinata dall’espressione:
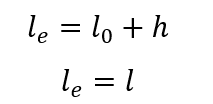
essendo che:
lo distanza tra le facce interne degli elementi strutturali, supposti orizzontali, che collegano il pilastro.
h l’altezza della sezione trasversale della colonna, nota al piano della struttura.
l la distanza tra gli assi degli elementi strutturali a cui è collegato il pilastro.
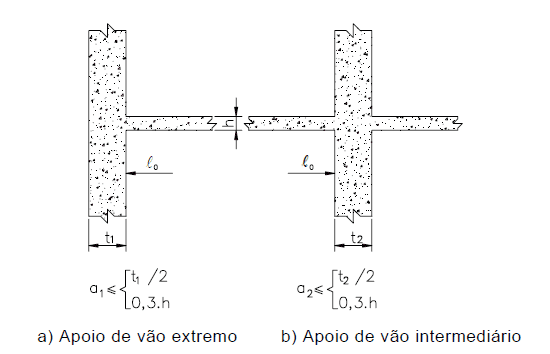
Le campate effettive delle travi possono essere calcolate dall’espressione: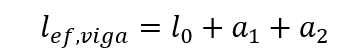 I valori di a1 e a2, ad ogni estremità dell’intervallo, possono essere calcolati in base ai valori appropriati dell’intelligenza artificiale, indicati nella figura 3, essendo:
I valori di a1 e a2, ad ogni estremità dell’intervallo, possono essere calcolati in base ai valori appropriati dell’intelligenza artificiale, indicati nella figura 3, essendo:
a1 uguale al valore più basso compreso tra (t1/2 e 0,3 * h).
a2 uguale al valore più basso compreso tra (t2/2 e 0,3 * h).
Figura 3 – Vai travi efficaci.
2.3.2 ECCENTRICITÀ DELLA FORMA
Per regolare la posizione degli elementi strutturali in funzione della progettazione architettonica, i progettisti strutturali devono rendere le facce interne o esterne delle travi compatibili con quelle dei pilastri che le ricevono. Quando ciò accade, gli assi delle travi non passano attraverso il centro di gravità della sezione della colonna (figura 4), emergendo così eccentricità chiamate eccentricità di forma (AGUIAR. 2000).
Figura 4 – Eccentricità della forma nei pilastri.
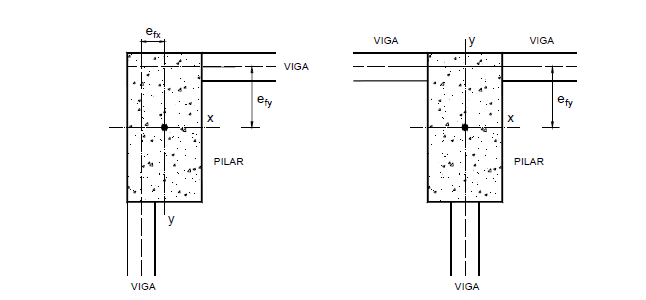
Le eccentricità della forma, al termine dei progetti e delle strutture degli edifici, non sono considerate nel dimensionamento, senza l’aiuto di programmi per computer elaborati a questo scopo. Il momento fletor generato dalle eccentricità a livello di ogni piano è livellato da una coppia, causando, su ogni piano, coppie di forze dello stesso ordine di grandezza e direzioni contrarie, che si annullano. I programmi computazionali elaborati per l’analisi strutturale e il dimensionamento con controlli di apertura delle crepe e i criteri degli ultimi stati limite e spostamenti con i parametri degli stati dei limiti di servizio, tengono conto di queste eccentricità di forma.
2.3.3 ECCENTRICITÀ ACCIDENTALE
NBR 6118 (2014) prevede il calcolo di un’eccentricità accidentale (ea), tenendo conto delle situazioni di imperfezione locale dovute alla costruzione dei pilastri, può essere dovuto alla disintegrazione dell’asse delle colonne.
Secondo NBR 6118 (2014), nelle normali strutture reticolate, si ammette che l’effetto delle imperfezioni locali si risolve se si considera il valore del momento totale minimo. Nel caso della flessione composita obliqua, il valore minimo del momento deve necessariamente essere rispettato separatamente in ciascuna delle direzioni principali.
2.3.4 ECCENTRICITÀ DI SECONDO ORDINE
Gli effetti locali di secondo ordine possono essere calcolati con metodi approssimativi o con il metodo generale. Vengono considerati solo gli effetti del secondo ordine per i pilastri sottili mediani, utilizzando il metodo della colonna standard con curvatura approssimativa e la colonna standard con rigidità approssimativa. Le mediane rappresentano la maggior parte degli eventi nelle attuali strutture degli edifici e i casi di pilastri con indici sottili superiori a 90 sono insoliti.
- Metodo a pilastri standard con curvatura approssimativa
Quando si progettano pilastri con λ ≤ 90, con sezione costante e armatura simmetrica e costante lungo il proprio asse. Questo metodo viene utilizzato solo in caso di flessione composita normale. La non linearità fisica è considerata un’espressione prossima alla curvatura nella sezione trasversale che esprime il valore del momento flettente più elevato considerando i momenti del primo e del secondo ordine. Il momento massimo totale nel pilastro, ovvero la somma dei momenti del 1 ° ordine e dei momenti del 2 ° ordine, è calcolato dall’espressione:
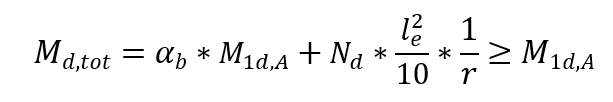 Essere:
Essere: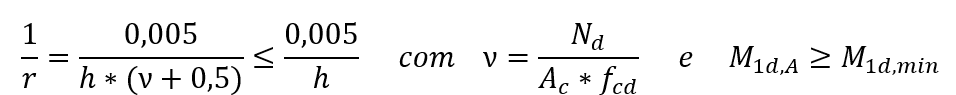
αb un coefficiente che dipende dalla distribuzione dei momenti nella colonna.
M1d, A il valore di calcolo del momento del 1 ° ordine MA;
h l’altezza della sezione della colonna nella direzione analizzata;
ν la normale forza adimensionale;
fcd la resistenza alla compressione del calcolo del calcestruzzo;
M1d,min il primo momento minimo di ordine.
Quindi, a partire dalla seconda parte dell’espressione precedente, si deduce che l’eccentricità di 2 ° ordine (e2) assume la seguente espressione:
2.3.5 ECCENTRICITÀ CAUSATA DALLA FLUIDITÀ
Secondo NBR 6118 (2014) l’eccentricità generata dallo scorrimento del calcestruzzo ec deve essere calcolata su colonne con λ > 90, cioè colonne sottili e molto sottili. Gli effetti dello scorrimento vengono trascurati nelle colonne con indici di snellezza inferiori a 90.
Sebbene l’analisi precisa degli effetti di scorrimento sia un compito complesso, NBR 6118 fornisce un’espressione semplificata per il calcolo dell’eccentricità ec, come mostrato di seguito: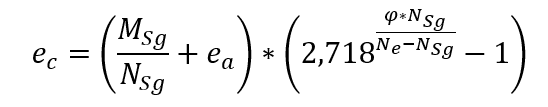
Essere:
MSg e Nsg gli sforzi sollecitanti sul pilastro presi dal binomio quasi permanente;
ea eccentricità accidentale;
φ coefficiente di fluidità.
Eci = 5.600⋅ * fck0.5 è il modulo elastico iniziale del calcestruzzo;
Ic il momento d’inerzia della sezione della colonna;
le leggere la lunghezza equivalente della sezione della colonna.
L’eccentricità e il calcolo devono essere aggiunti all’eccentricità del 1 ° ordine. La figura 5 mostra l’eccentricità del secondo ordine.
Figura 5 – Eccentricità iniziale e di secondo ordine nei pilastri.
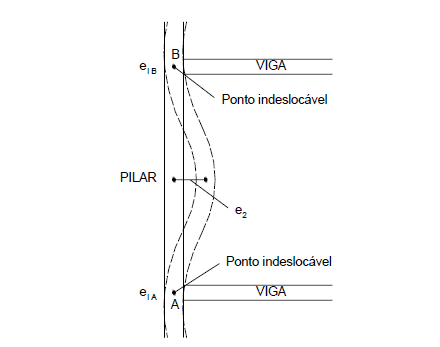
Le sezioni finali non comportano gli effetti del secondo ordine e devono essere considerate solo nella sezione intermedia.
2.4 CALCOLO DEL RINFORZO LONGITUDINALE CON L’AUSILIO DI ABACUS
Nel dimensionamento manuale dei pilastri, gli abaci sono indispensabili, perché portano la rapida definizione del tasso di rinforzo, rendendo non necessario applicare le equazioni teoriche della flessione composita normale o obliqua. Inoltre, gli abaci consentono una facile scelta di vari arrangiamenti di armatura nella sezione trasversale. Gli Abaci di Venturini e Rodrigues (2000) per la flessione composita normale e Pinheiro (1994) per la flessione composita obliqua dovrebbero essere utilizzati solo nel dimensionamento di pilastri con calcestruzzi del Gruppo di Resistenza I (fck ≤ 50 MPa), in quanto elaborati con alcuni parametri numerici in cui non si applicano ai calcestruzzi del Gruppo II.
2.4.1 NORMALE PIEGATURA COMPOSITA
Per Venturini e Rodrigues (2000) Normal Composite Flexion, la figura 6 mostra la notazione dell’applicazione abaco. L’eccentricità (e) è parallela alla distanza d ‘, tra il centro della barra d’angolo e la faccia della sezione. In generale, esiste d ‘= c + Φt + Φλ / 2, con c = copriferro, Φt = diametro staffa e Φλ = diametro della barra longitudinale.
Figura 6 – Notazione per la flessione composita normale.
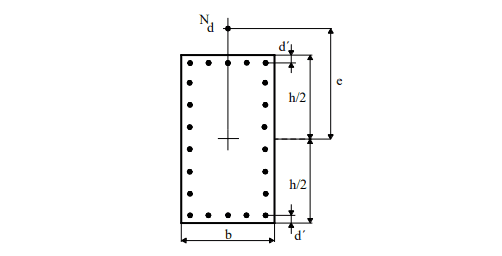
Le equazioni utilizzate per la costruzione degli abaci sono state evidenziate nella pubblicazione di Venturini e Rodrigues (2000). La definizione del rinforzo longitudinale viene avviata calcolando gli sforzi dimensionali n (ni) e μ (mi). Il valore adimensionale n è stato definito nella seguente equa Essere:
Il valore della μ, a seconda del momento del fletor o dell’eccentric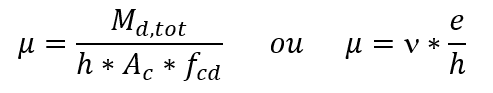 ità, è:
ità, è:
Nd Trovare la forza di calcolo normale;
Ac l’area della sezione trasversale del pilastro;
fcd la resistenza alla compressione del calcestruzzo alla compressione (fck / γc);
Md,tot il momento flettente totale di calcolo;
h le dimensioni del pilastro nella direzione considerata;
eccentricità nella direzione considerata.
Una volta scelta una distribuzione costruttiva per il rinforzo sulla colonna, viene definito l’abaco da utilizzare, a seconda del tipo di acciaio e del valore del rapporto d’/h. Nell’abaco, con la coppia ν e μ, si ottiene la velocità meccanica ω. L’armatura viene calcolata dall’espressione:
2.4.2 FLESSIONE COMPOSTA OBLIQUA
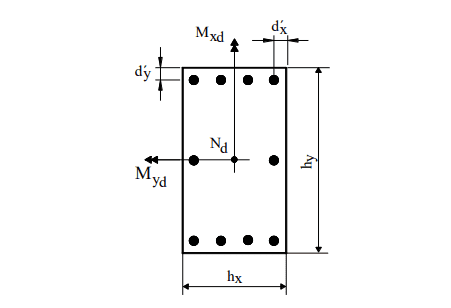
Per la flessione composita obliqua di Pinheiro (1994) la figura 7 mostra la notazione applicata nell’uso di abaci. Le distanze d’x e d’y hanno la stessa interpretazione di d’, tuttavia, ognuna in una direzione del pilastro.
Figura 7 – Notazione per la flessione composita normale.
La determinazione del rinforzo inizia calcolando gli sforzi dimensionali ν e μ, con μ secondo le due direzioni principali della colonna: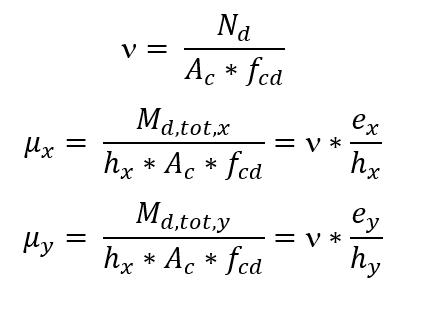 Una volta scelta una distribuzione costruttiva per il rinforzo sulla colonna, viene definito l’abaco da utilizzare, a seconda dei valori dei rapporti d’x/hx e d’y/hy e del tipo di acciaio. Nell’abaco, con il trio (ν, μx, μy), si ottiene la velocità meccanica ω. L’armatura viene calcolata con la seguente equazione:
Una volta scelta una distribuzione costruttiva per il rinforzo sulla colonna, viene definito l’abaco da utilizzare, a seconda dei valori dei rapporti d’x/hx e d’y/hy e del tipo di acciaio. Nell’abaco, con il trio (ν, μx, μy), si ottiene la velocità meccanica ω. L’armatura viene calcolata con la seguente equazione:
2.5 DETTAGLI DEI PILASTRI IN CEMENTO ARMATO
NBR 6118, 2014 determina che la dimensione della sezione trasversale della colonna non deve essere inferiore a 19 cm. Questa raccomandazione mira ad evitare comportamenti inaccettabili per gli elementi strutturali e a consentire condizioni di costruzione appropriate.
Tuttavia, per casi particolari, la dimensione più piccola della colonna può essere compresa tra 19 cm e 12 cm. Per questi casi, è necessario moltiplicare gli sforzi di calcolo finale applicati nel dimensionamento dei pilastri per un coefficiente γn aggiuntivo, secondo l’immagine 8.
Figura 8 – Valori del coefficiente addi aggiuntivo γn.

In primo luogo, la velocità geometrica di rinforzo longitudinale della colonna è definita dal seguente rapporto: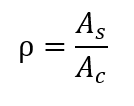 Essere,
Essere,
As la somma delle aree della sezione trasversale delle barre longitudinali.
Ac l’area della sezione trasversale del pilastro.
L’area minima di rinforzo longitudinale, dipende dall’intensità della richiesta dovuta alla normale resistenza e resistenza dell’acciaio, è determinata dalla seguente espressione: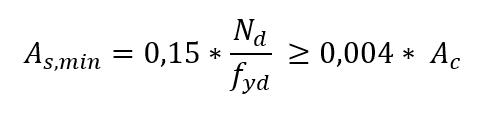 Per tanto, la velocità minima di rinforzo geometrico è pari allo 0,4%.
Per tanto, la velocità minima di rinforzo geometrico è pari allo 0,4%.
L’area massima di rinforzo possibile sui pilastri dovrebbe essere l’8% dell’area trasversale, considerando la sovrapposizione di rinforzi nelle regioni di giunzione, vale a dire: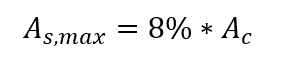 Il diametro minimo delle barre longitudinali non deve essere inferiore a 10 mm e non deve superare 1/8 della dimensione più piccola della sezione della colonna.
Il diametro minimo delle barre longitudinali non deve essere inferiore a 10 mm e non deve superare 1/8 della dimensione più piccola della sezione della colonna.
Per una corretta concrezione è necessario che il calcestruzzo abbia un minimo di spazio per attraversare tra i rinforzi longitudinali. Pertanto, vengono imposte limitazioni alla spaziatura libera tra le barre del rinforzo longitudinale (aL), che deve essere uguale o maggiore del più alto dei seguenti valori:
- 20 mm;
- La misurazione del diametro della barra, della trave o del manicotto adottata nella cucitura;
- 1.2 invece il diametro massimo dell’aggregato;
Anche la spaziatura massima tra gli assi delle barre di rinforzo è limitata e deve essere inferiore o uguale al doppio della dimensione più piccola della colonna, senza superare i 400 mm.
Il diametro delle staffe (φt) nei pilastri non deve essere inferiore a 5 mm o 1/4 del diametro della barra longitudinale.
Al fine di garantire il posizionamento delle barre longitudinali di rinforzo e, inoltre, rendere impossibile contrastare le barre longitudinali e utilizzare il rinforzo della cucitura nelle regioni di cucitura, sono necessarie interlinee massime tra le staffe (misurate nella direzione dell’asse della colonna), essendo inferiori o uguali al più basso dei seguenti valori:
- 200 mm;
- dimensione della sezione più piccola;
- 24 φ per l’acciaio CA-25 e 12 φ per l’acciaio CA-50, dove φ è il diametro della barra longitudinale;
Qualora vi sia la possibilità di instabilità delle barre sulla superficie, è necessario adottare misure per evitarlo.
3. MODELLAZIONE SOFTWARE CAD/TQS
Uno dei modi per avere dettagli di calcolo strutturale, in cemento armato, più veloci e precisi (con meno arrotondamenti), è attraverso l’utilizzo di software, uno di questi si chiama TQS, utilizza la piattaforma CAD per il suo funzionamento. Con il TQS possiamo ottenere i calcoli degli sforzi e delle frecce nella struttura, il dimensionamento e il dettaglio dei rinforzi secondo le richieste e la tracciatura di tutto il materiale necessario, il tutto secondo quanto lanciato dal professionista sulla piattaforma di progettazione. TQS esegue tutto questo dimensionamento e dettaglio in conformità alle normative vigenti.
I sistemi TQS hanno risorse che rendono lo sviluppo di progetti strutturali un processo altamente produttivo. Dall’ideazione all’emissione dell’impianto, tutti i passaggi sono automatizzati. I suoi prodotti principali sono TQS (cemento armato e precompresso), Alvest (muratura strutturale), PREO (prefabbricato) e SISE (geotecnica).
Adattato alle ultime recensioni normative (NBR 6118/2014, NBR 15200:2012, NBR 15.575:2013, NBR 9062:2006, NBR 15812:2010, NBR 15961:2011. Ogni versione dei sistemi TQS è rigorosamente testata, sia operativamente che in relazione ai loro risultati. Sono disponibili anche materiale didattico per tutti i suoi prodotti, come TQS passo-passo, plottaggio, scale passo-passo, Alvest passo dopo passo (TQS, 2020).
3.1 RILASCIO STRUTTURALE NEL SOFTWARE TQS/CAD
La struttura fatta per l’analisi è stato l’esempio completo del libro Structural Project of Reinforced Concrete Buildings, di José Milton de Araújo (2014). Per la modellazione nel software sono stati lanciati i pilastri, le travi, le lastre, le scale, i carichi a parete, in sequenza nell’ordine descritto.
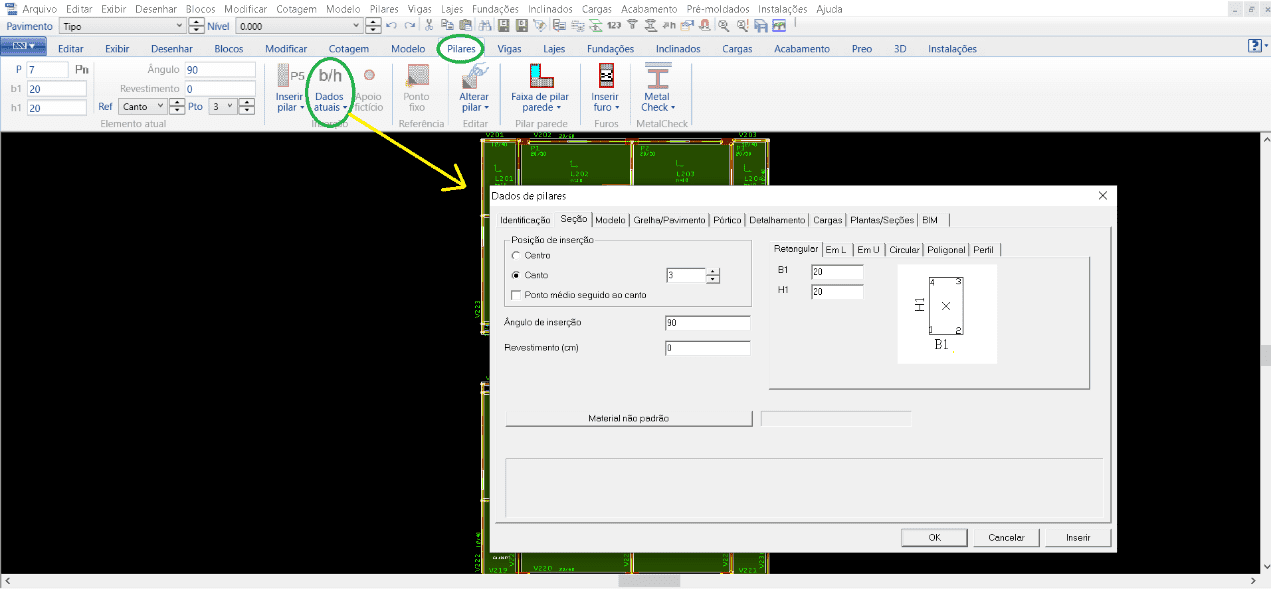
Per i pilastri sono stati seguiti i seguenti passaggi: dopo aver aperto il Modello Strutturale, è attiva la scheda “Pilastri”, deve essere aperta la finestra “Dati correnti” (figura 9), dove appariranno tutti i dati per l’inserimento della colonna, quindi posizionando le dimensioni, il numero di identificazione, la posizione di inserimento, la determinazione in cui il pilastro nasce e muore, tra le altre informazioni. Alla fine di tutte le edizioni pertinenti, quindi, sono inclusi tutti i pilastri necessari.
Figura 9 – Finestra TQS/CAD nella scheda “Pilastri”.
Per la costruzione di travi nel software CAD/TQS, il processo è il seguente:
Dopo aver definito tutti i pilastri, passiamo al rilascio delle travi. Inizialmente è necessario attivare il menu “Travi”, dove tutti con i seguenti comandi sono specifici per il rilascio delle travi.
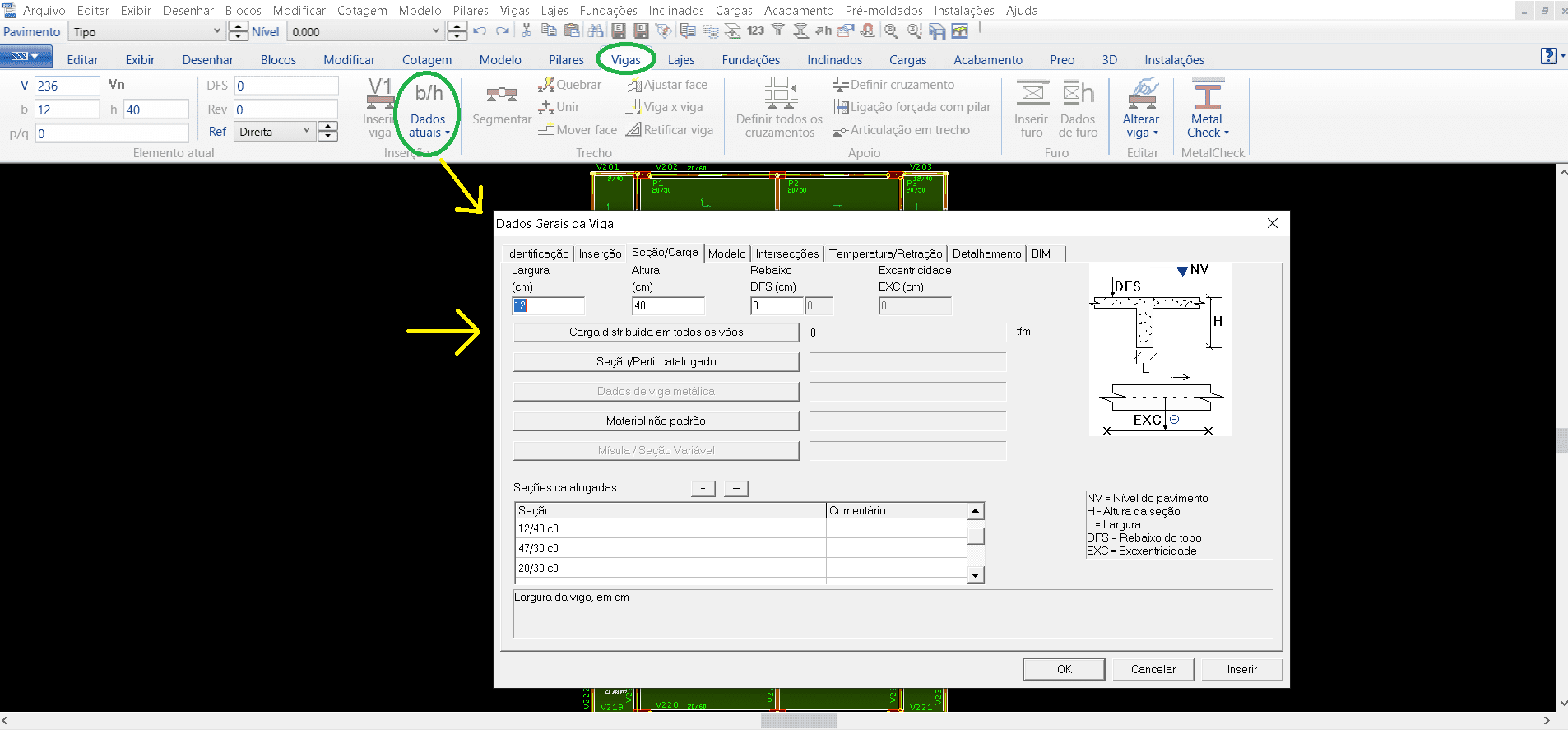
All’interno della scheda “Travi” è necessario selezionare il comando “Dati correnti” (figura 10), dove si aprirà una finestra dei dati generali delle travi, posizionando così tutte le informazioni necessarie per il rilascio di ogni trave. Informazioni come il numero di identificazione di ogni trave, il suo coperchio, i carichi che questa trave agirà sui pilastri, come il permanente e accidentale, la sua sezione. Dopo tutto questo processo di dettaglio, possiamo quindi inserire la trave, posizionando al punto di partenza poi al punto finale, di solito questi punti di inserimento sono i vertici dei pilastri già inseriti in precedenza, ripetendo la stessa procedura fino a posizionare tutte le travi necessarie.
Figura 10 – Finestra TQS/CAD nella scheda “Travi”.
Dopo le travi rilasciate ci spostiamo sulle lastre, seguendo le stesse procedure delle precedenti nella scheda “Lastre” selezionando “Dati correnti” si inserisce l’identificazione, il tipo di lastra e il suo spessore (immagine 11).
Figura 11 – Finestra TQS/CAD nella scheda “Lastre”.
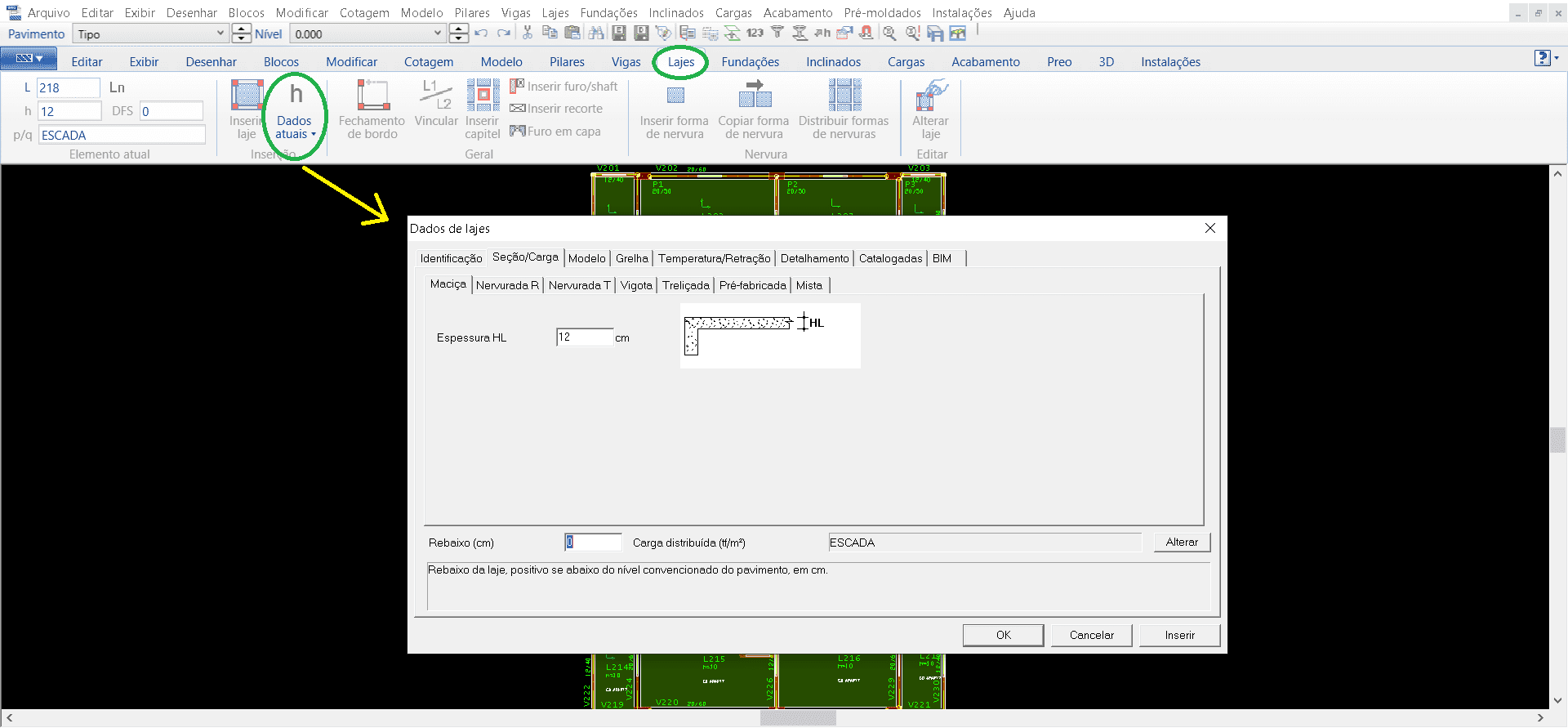
Per la registrazione dei carichi a parete segue la stessa linea di procedure. Nella finestra “Carichi” seleziona la scheda “Distribuito linearmente”, quindi aprendo una finestra per la selezione del tipo di carico, per la modellazione in questione è stato inserito il blocco 14 (muratura a blocchi di cemento 14 cm) e l’altezza della parete determinata (immagine 12).
Fonte: Figura 12 – Finestra TQS/CAD nella scheda “Carichi”.
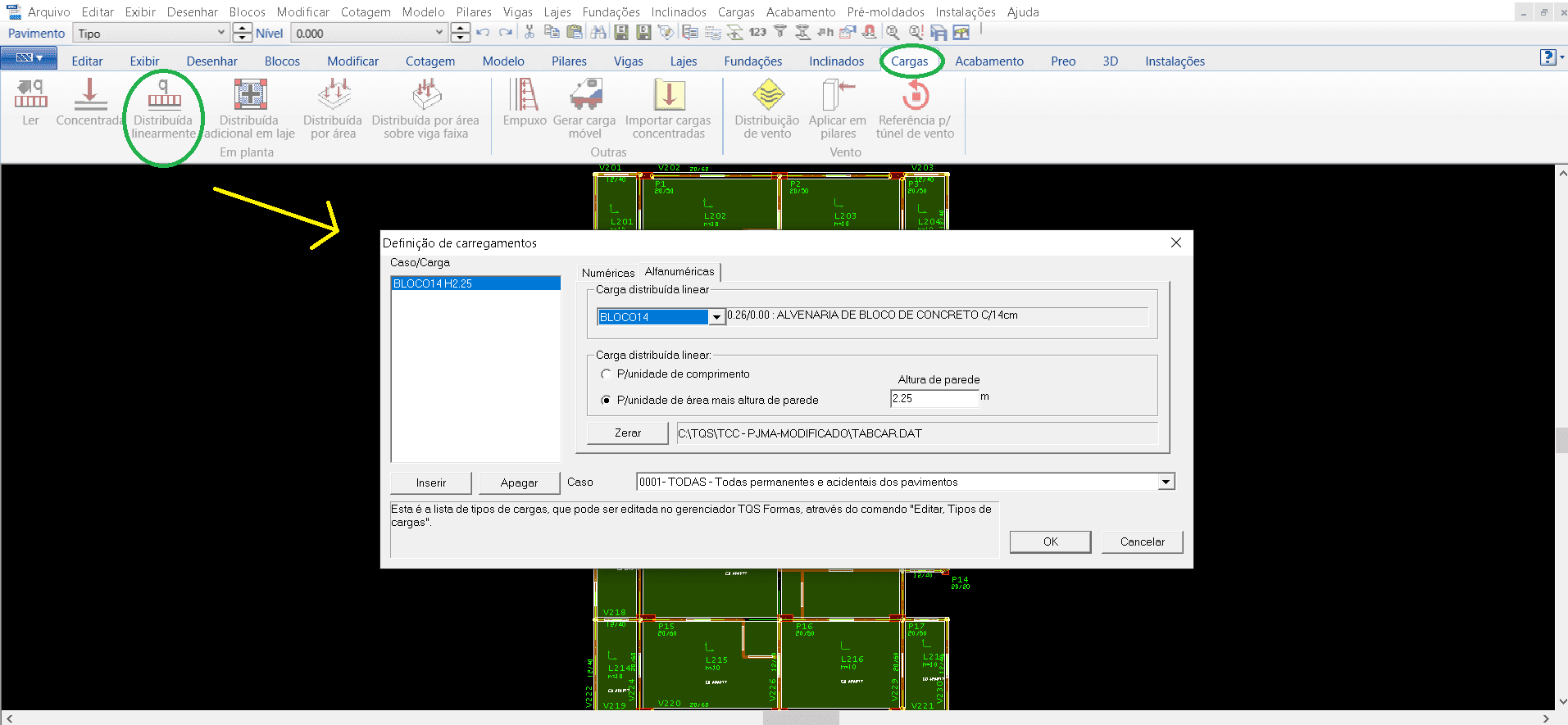
Pertanto, al termine del rilascio di tutti gli elementi necessari nei pavimenti, è necessario salvare i dati definiti finora nel menu “File” nel comando “Salva il modello strutturale”.
Figura 13 – Edificio di esempio 3D, TQS/CAD
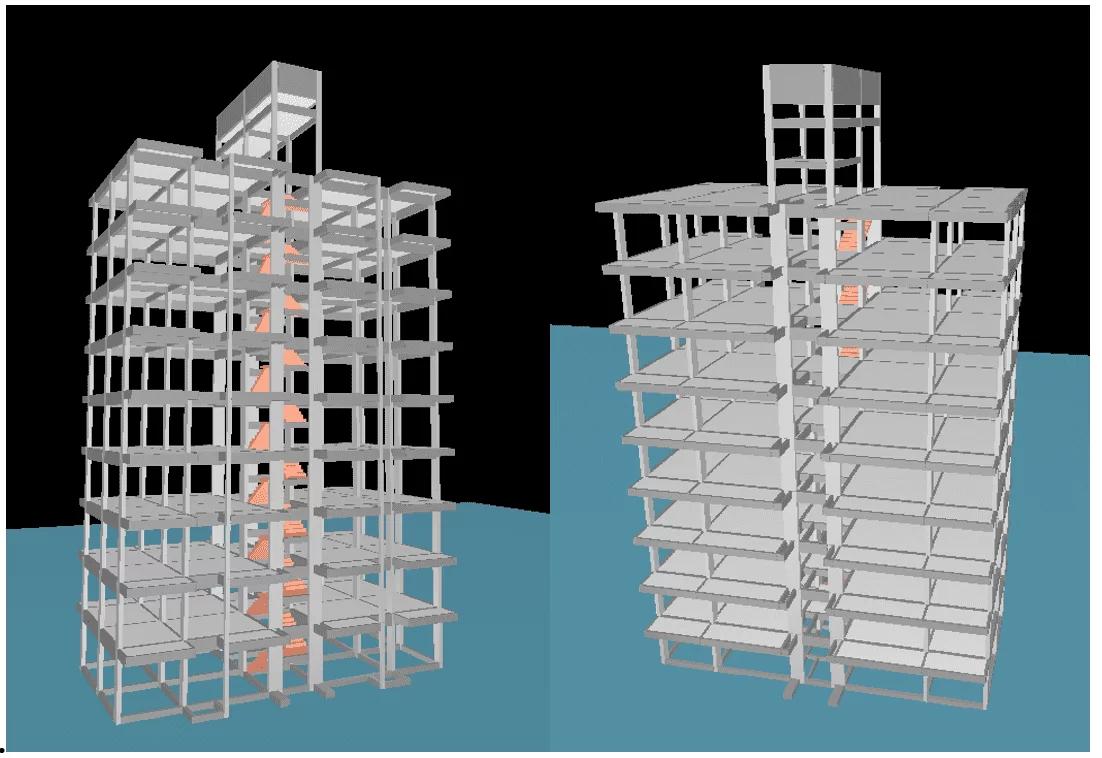
Fonte: Autore, 2020.
Usando lo spettatore tridimensionale abbiamo l’idea concreta di come sarebbe l’edificio di esempio (figura 13).
L’applicazione P-Calc è una calcolatrice TQS che controlla pilastri in cemento armato soggetti a piegatura composita individuale obliqua (TQS, 2020).
Le caratteristiche principali di P-Calc sono:
- Verifica dei pilastri sottoposti a flessione composita, normale o obliqua, in relazione all’ultimo stato limite di rottura e instabilità;
- Analisi di pilastri con calcestruzzo ad alta resistenza (fck > 50 MPa);
- Schema di interazione del momento deflettore x sforzo normale (FCO e FCN);
- Risultati grafici per sollecitazioni e deformazioni nella sezione;
- Valutazione degli effetti locali di 2 ° ordine adottando la non linearità geometrica e fisica, secondo ABNT NBR 6118;
- Avvolgente dei momenti minimi;
- Memoria di calcolo in formato PDF;
4. PRESENTAZIONE E ANALISI DEI RISULTATI
Questo argomento presenta i confronti tra i riferimenti per gli elementi studiati. È stato diviso in sottoargomenti per gli elementi principali di un progetto strutturale. Si sottolinea che i riferimenti studiati sono stati alla base del progetto del libro “PROJETO ESTRUTURAL DE EDIFÍCIOS DE CONCRETO ARMADO” di JOSÉ MILTON DE ARAÚJO, 3a edizione, modellato, calcolato e dettagliato nel TQS. Per gli altri test, alcuni elementi sono stati confrontati con altri strumenti di calcolo come Pcalc e Bending Abaci per i dati dei pilastri.
4.1 MODELLAZIONE E DIMENSIONAMENTO COMPARATO – PILASTRO
Dopo la modellazione e il dimensionamento dei pilastri, secondo l’argomento 3, lo sforzo principale, la sezione e l’area dell’acciaio sono stati confrontati tra i riferimenti studiati per i due pilastri (P2 e P5) secondo l’abstract nelle tabelle 01 e 02.
Tabella 1 – Presentazione dei risultati rispetto al secondo pilastro
| Elementi | Sforzi caratteristici (tf) | Sezione (cm x cm) |
Zona siderurgica (cm²) |
| 2014 – Araujo | 71,4 | 20 x 50 | 6ϕ20 (18,90) |
| TQS | 66,2 | 20 x 50 | 8ϕ20 (25,20) |
| Pcalc* | 71,4 | 20 x 50 | 10ϕ20 (31,50) |
| Pcalc* | 66,2 | 20 x 50 | 10ϕ20 (31,50) |
| Abaco- Flessione normale* | 71,4 | 20 x 50 | 6ϕ20 (18,90) |
| Abaco- Flessione normale* | 66,2 | 20 x 50 | 4ϕ20 (12,60) |
*Soluzione a pilastri standard con curvatura approssimativa.
Fonte: Autore, 2020.
Si può osservare, analizzando i confronti per il pilastro P2 che il dimensionamento araújo (2014) in relazione al TQS mostra un aumento del 33,33% nell’area siderurgica, tenendo conto del fatto che Araújo presenta una forza normale superiore del 7,85%, già in relazione al PCalc, c’è stato un aumento del 66,67%, correlandoli con lo stesso carico.
È interessante notare che questi stessi valori in relazione al dimensionamento della colonna standard con curva approssimativa utilizzando il Normal Flexion Abaci (VENTURINI e RODRIGUES, 2000), sono stati separati in due gruppi di carichi perché la modellazione eseguita nel TQS differisce dall’indagine sul carico di Araújo (2014), quindi abbiamo le cifre 14 e 15.
Figura 14 – Confronto tra TQS x Pcalc x Abaci per il pilastro 2
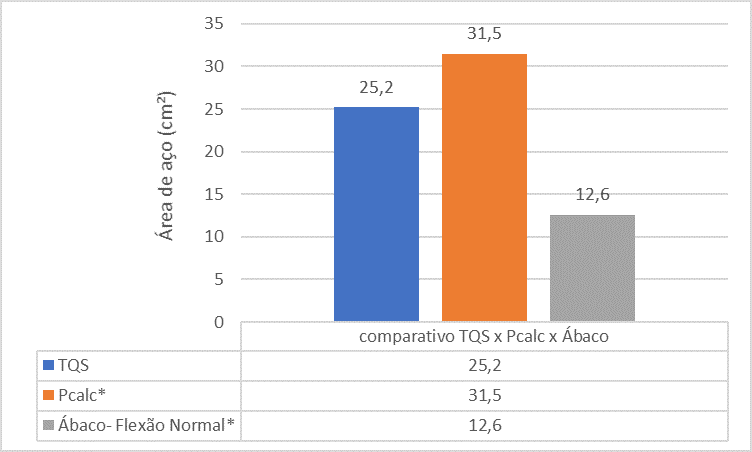
L’analisi comparativa tra i riferimenti mostra che l’area siderurgica della colonna P2 trovata dall’utensile TQS è inferiore alla superficie siderurgica trovata dai Pcalc e dagli Abaci. Ciò è dovuto al fatto che l’analisi monolitica fatta nel programma.
Fig. 15 – Confronto tra Araújo (2014) x Pcalc x Abacos per Pilar 2
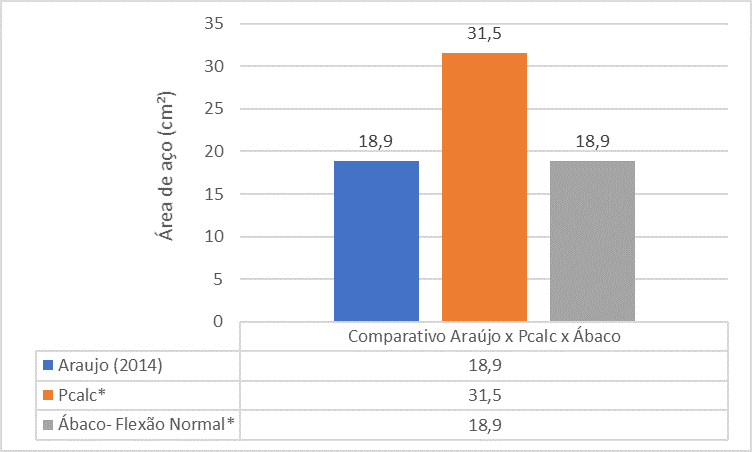
L’analisi comparativa tra i riferimenti mostra che l’area in acciaio del pilastro P2 trovata dal libro di Araújo (2014) è molto più piccola dell’area siderurgica trovata da PCalc e Abacus.
La colonna P2 è una colonna terminale, supporto intermedio per la trave V202, nella direzione x, trascurando questi momenti trasmessi. Nella direzione y, abbiamo il fascio V 227, questo è stato considerato i momenti trasmessi nel pilastro. Da questa analisi, il calcolo del momento di presa perfetta (Meng), momento di inerzia della trave (Ivig), coefficiente di rigidità della trave (rvig), momento di inerzia della colonna (Ip), coefficiente di rigidità della colonna (rp) e momenti iniziali nei pilastri (Mp), dai calcoli si ottengono i momenti ridotti, ma divisi per la grande differenza tra loro sono stati considerati nulli e dimensionando la sezione in flessione – compressione normale in direzione x.
Per la forza normale sull’asse x, abbiamo l’indice di snellezza (λx) eccentricità iniziale (eia), eccentricità accidentale (eax), eccentricità minima (e1x,min), eccentricità iniziale ne sezione intermedia (eix), eccentricità di secondo ordine (e2x) ed eccentricità di fluidità (ecx). La sessione critica è stata nella sessione finale, impiegando i tavoli dell’area in acciaio la sessione può essere armata con 6 barre da 20 mm, adottando un’area in acciaio totale pari a 18,85 cm².
Tabella 2 – Presentazione dei risultati rispetto al pilastro 5
| Elementi | Sforzi caratteristici (tf) | Sezione (cm x cm) |
Zona siderurgica (cm²) |
| Araujo (2014) | 112,2 | 20 x 50 | 10ϕ16 (20,00) |
| Tqs | 141,5 | 20 x 50 | 8ϕ25 (40,00) |
| Pcalc* | 112,2 | 20 x 50 | 12ϕ20 (37,80) |
| Pcalc* | 141,5 | 20 x 50 | 12ϕ25 (60,00) |
| Abaco- Flessione normale* | 112,2 | 20 x 50 | 8ϕ25 (40,00) |
| Abaco- Flessione normale* | 141,5 | 20 x 50 | 11ϕ25 (55,00) |
*Soluzione a pilastri standard con curvatura approssimativa.
Fonte: Autore, 2020.
Può essere osservato, analizzando i confronti per il pilastro P5 che, il dimensionamento di Araújo (2014) in relazione al TQS mostra un aumento del 100% della zona siderurgica, tenendo conto del fatto che Araújo ha una resistenza normale inferiore del 26,11%, già in relazione al PCalc, c’è stato un aumento dell’89% rispetto al carico di Araújo e del 50% rispetto al carico del TQS , dimostrando che maggiore è l’aumento del carico, maggiore è la divergenza delle zone siderurgiche. Si può dire che questa divergenza è dovuta al fatto di presentare il seguente errore per la risoluzione del pilastro P5 nel Pcalc, per Araújo (2014) nell’ultimo stato limite (ELU): il pilastro non presta attenzione alla verifica del momento minimo. Il pilastro con il carico TQS nel Pcalc genera il seguente errore ρs = 5,89% > ρs.max = 4,00%.
È interessante notare che questi stessi valori in relazione al dimensionamento della colonna standard con curva approssimativa utilizzando le normali abace di flessione (VENTURINI e RODRIGUES, 2000), sono stati separati in due gruppi di carichi perché la modellazione eseguita nel TQS differisce dall’indagine sul carico di Araújo (2014), quindi abbiamo le cifre 16 e 17.
Figura 16 – Confronto tra TQS x Pcalc x Abaci per il pilastro 5
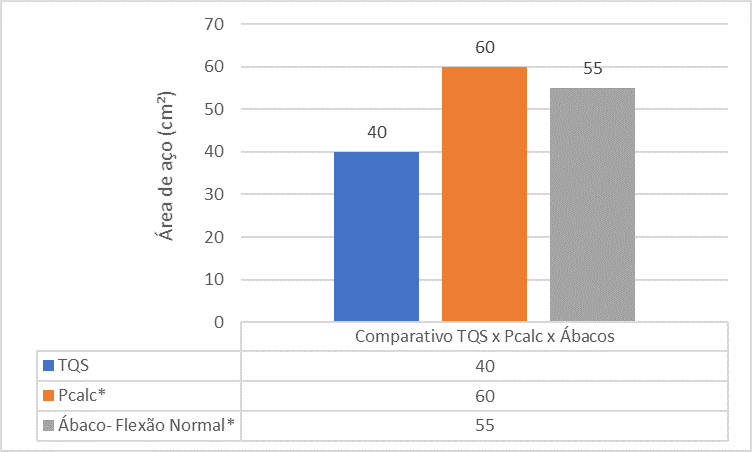
L’analisi comparativa tra i riferimenti mostra che l’area siderurgica del pilastro P5 trovata dall’utensile TQS è inferiore alla superficie siderurgica riscontrata dai Pcalc e dagli Abaci. Ciò è dovuto al fatto che l’analisi monolitica fatta nel programma.
Fig. 17 – Confronto tra Araújo (2014) x Pcalc x Abacos per Pilar 5
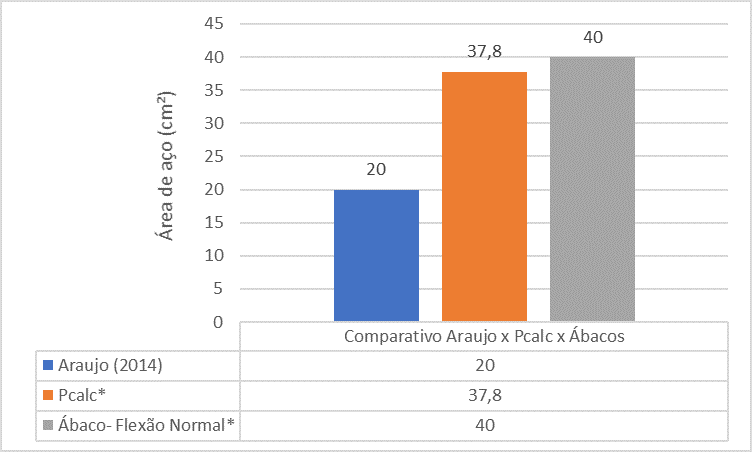
L’analisi comparativa tra i riferimenti mostra che l’area in acciaio del pilastro P5 trovata dal libro di Araújo (2014) è molto più piccola dell’area siderurgica trovata da PCalc e Abacus.
Il pilastro P5 è un pilastro intermedio, con le campate e i carichi delle travi V204 e V227, non differiscono, quindi si possono trascurare i momenti iniziali trasmessi da queste travi. In base a questa analisi, il calcolo è stato effettuato sull’asse y, in quanto era il più alto indice di snellezza (λx) trovato, l’eccentricità (ey), data dalla somma dell’eccentricità del primo ordine (e1x), dell’eccentricità del secondo ordine (e2x) ed eccentricità di scorrimento (ecy). Utilizzando i tavoli area acciaio, la seduta può essere armata con 10 barre da 16 mm, adottando una superficie totale in acciaio pari a 20,00 cm².
5. CONCLUSIONE
Ha osservato che il confronto tra i metodi è importante per scegliere lo strumento migliore per l’uso nel dimensionamento dei pilastri.
Riproducendo la modellazione dell’edificio di Araújo nel TQS, è stata notata una differenza di carico, e per questi carichi si percepisce che lo strumento TQS in modalità predefinita è vicino al dimensionamento per lo strumento PCalc e Abaci per i pilastri intermedi.
Nei pilastri finali di Araújo mostra una minore variazione delle risposte in relazione ad Abaci e PCalc.
Pertanto, l’analisi comparativa tra i metodi di calcolo è diversa a causa del fatto che l’analisi monolitica della struttura effettuata nello strumento TQS, diversa dagli altri metodi che presenta l’analisi segmentata degli elementi con forme di calcolo semplificate.
RIFERIMENTI
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 1978.
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2003.
ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2014.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15200. Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro, — Procedimento, 2012.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15575. Edificações habitacionais – Desempenho. Rio de Janeiro, — Procedimento, 2013.
ABNT (Associação Brasileira de Normas Técnicas). NBR 9062. Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, — Procedimento, 2006.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15812. Alvenaria estrutural – Blocos cerâmicos. Rio de Janeiro, — Procedimento, 2010.
ABNT (Associação Brasileira de Normas Técnicas). NBR 15961. Alvenaria estrutural – Blocos de concreto. Rio de Janeiro, — Procedimento, 2011.
AGUIAR, E.A.B. Projeto de pilares de concreto de alto desempenho. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2000.
ARAUJO, José Milton de. Projeto estrutural de edifícios de concreto armado. 3. ed. Rio Grande: Editora Dunas, 2014.
BASTOS, Paulo S. dos Santos. Fundamentos do Concreto Armado. Universidade Estadual Paulista. Bauru, São Paulo. 2006.
BRANDÃO, A. M. S.; PINHEIRO, L. M. Qualidade e durabilidade das estruturas de concreto armado: aspectos relativos ao projeto. Cadernos de Engenharia de Estruturas. EESC. Universidade de São Paulo. São Carlos, 1999.
CARVALHO, Roberto Chust.; FIGUEIREDO FILHO, Jasson Rodrigues de. Pilares de concreto armado. p.9-25. Notas de aula – Universidade Federal de São Carlos, 2002
FUSCO, P.B. Estruturas de concreto – solicitações normais, editora Guanabara, São Paulo, 1986.
PIANCASTELLI, E. M. Patologia, Recuperação e Reforço de Estruturas de Concreto Armado. Apostila para Curso de Extensão, Ed. Depto. Estruturas da Escola de Engenharia da UFRG, Belo Horizonte, 1997
PINHEIRO, L.M.; BARALDI, L.T.; POREM, M.E. Concreto Armado: Ábacos para flexão oblíqua. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1994.
TQS, Calculadora P-Calc, Pilares de concreto, 2020. Disponível em: <https://www.tqs.com.br/apps/p-calc/ejm1se496l>
TQS, Sobre a TQS, 2020.Disponível em: <https://www.tqs.com.br/about>
VENTURINI, Wilson Sérgio; RODRIGUES, Rogério de Oliveira. Dimensionamento de peças retangulares de concreto armado solicitadas à flexão reta. São Carlos, Dipartimento di Ingegneria Strutturale, Scuola di Ingegneria di São Carlos – USP, 1987 (ristampato.2000)
[1] Laureato in Ingegneria Civile.
[2] Laurea in Ingegneria Civile.
[3] Laurea magistrale in Geotecnica e Edilizia Civile. Laurea in Ingegneria Civile. Laurea in Ingegneria Agraria.
Inviato: Maggio, 2020.
Approvato: maggio 2020.