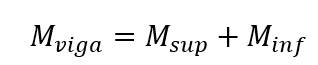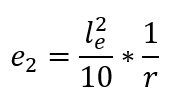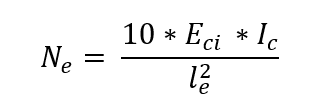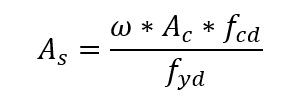Comparaison de dimensionnement et modélisation de colonnes

ARTICLE ORIGINAL

CARVALHAES, Daniely Silva ^[1], CARVALHAES, Daniel José ^[2], QUARESMA, Wanessa Mesquita Godoi ^[3]

CARVALHAES, Daniely Silva. CARVALHAES, Daniel José. QUARESMA, Wanessa Mesquita Godoi. Comparaison de dimensionnement et modélisation de colonnes. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 05, Vol. 04, pp. 121-146. mai 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/travaux-publics/modelisation-de-colonnes ‎

RÉSUMÉ

La recherche de la réduction du temps dans l’élaboration des projets devient une nécessité, ainsi que l’indigence de comprendre les problèmes récurrents dans l’utilisation de structures en béton armé telles que les pathologies. Ainsi, en unissant les deux problèmes, le temps et l’analyse, il devient impératif d’étudier les méthodes de modélisation et d’analyse des structures dans le logiciel commun de développement de projet. L’objectif est de modéliser un bâtiment et de comparer un élément structurel, en analysant les charges et les dimensions du logiciel TQS®. Ce processus est dû à la modélisation dans le logiciel TQS de l’exemple de construction de José Milton de Araújo (2014). Il a été observé que le processus de modélisation par rapport au processus numérique présente une différence significative en raison du fait de faire l’analyse du bâtiment complet, étant ainsi fiable la modélisation effectuée dans le logiciel, ce qui permet une étude antérieure de l’ensemble de la structure.

Mots-clés: Piliers, dimensionnement, modélisation, expérimental, TQS.

1. INTRODUCTION

Bastos (2006, p. 07) présente le béton armé comme étant « l’union d’un béton simple et d’un matériau résistant à la tensile (enveloppé par du béton) de telle sorte que les deux résistent conjointement aux efforts demandés », c’est-à-dire que le béton armé est le résultat du béton simple plus du renforcement plus de l’adhérence.

Pour Piancastelli (1997), le béton armé est sujet à changement au fil du temps, car il s’agit d’un matériau non inerte, grâce aux interactions entre ses éléments constitutifs (ciment, sable, gravier, eau et acier), aux interactions entre ces éléments et les agents externes tels que les gaz, les sels, les bases, les acides et autres, et avec les matériaux qui y sont ajoutés (additifs et ajouts minéraux).

Pendant longtemps, le béton a été considéré comme un matériau durable, en raison d’anciens travaux encore en bon état, mais la détérioration précoce des structures actuelles nous conduit à des pathologies concrètes (BRANDÃO et PINHEIRO, 1999). Cela est dû aux nouvelles technologies, pour rendre les structures minces et plus légères, du processus de planification et de production des structures.

Les piliers sont des éléments généralement alignés verticalement dans son axe, dans lesquels les forces de compression normales sont prépondérantes (ABNT NBR 6118, 2014), leur étude est l’un des contrôles essentiels, en ce qui concerne la dimension, le dysfonctionnement d’un pilier d’une structure peut compromettre la fonctionnalité et causer des accidents graves. Étant responsables de la transmission des charges verticales, les piliers sont généralement soumis, en particulier, à l’état de flexo-compression, d’où la nécessité de tenir compte des effets de second ordre et de l’analyse de stabilité du pilier dans son ensemble.

Les piliers sont dimensionnés en fonction des efforts externes demandant le calcul, qui composent les forces normales (N_d), les moments enflammés (M_dx et M_dy) et les cutforces (V_dx et V_dy) étant horizontaux. NBR 6118, dans la version 2003, notamment dans le rationnement des piliers, la norme a inséré plusieurs modifications, telles que la valeur de l’excentricité accidentelle, une couverture en béton plus grande, une nouvelle méthode dans le calcul de la finesse limite se référant à la contemplation ou non des moments flasques du 2ème ordre et, surtout, avec l’examen du moment minimum de déflecteur, et peut remplacer le moment de déflecteur à la suite d’une excentricité accidentelle. La version 2014 a ajouté le chèque minimum moment fletor, faite à partir de la comparaison d’une enveloppe robuste, qui comprend l’enveloppement minimum avec 2ème ordre.

2. CALCUL ET DIMENSION DES PILIERS PAR ABACOS

2.1 CLASSIFICATION DES PILIERS

Les piliers sont classés en fonction de leur position dans la structure, il peut être intermédiaire, extrémité ou coin. Cette classification vous permet d’examiner les efforts de demande dans chaque situation calculée. (FUSCO, 1981)

Figure 1 – Position des piliers dans les bâtiments.

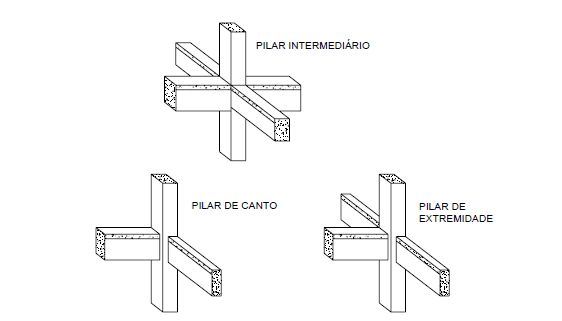
Les piliers intermédiaires sont principalement soumis à des forces de compression axiales, parce que les moments de flegme sont de peu d’intensité, comme seulement aux actions verticales (variables permanentes et normales). À moins que les travées des faisceaux continus qui sont basés sur ces piliers ne soient considérées comme différentes, les derniers moments de aventure transmis aux piliers ne sont pas pris en compte. Par conséquent, le pilier intermédiaire soumis à une compression centrée sur la situation du projet est admis, c’est-à-dire que l’excentricité initiale, dans la dimensionnement des zones des renforts transversaux et longitudinals, est considérée comme égale à zéro.

Les piliers d’extrémité sont soumis à des forces de compression normales et à l’action de moments propagés par les faisceaux, dont les extrémités externes sont soutenues sur ces piliers. Dans les faisceaux transversaux vers l’axe du faisceau interrompu, les moments ne sont pas pris en compte. Par conséquent, la colonne d’extrémité soumise à la flexion normale composite est considérée, considérant, par conséquent, l’excentricité initiale dans l’un des locaux commandés de la section transversale de la colonne.

Piliers d’angle en plus d’être soumis à une force d’actionnement normale, il faut tenir compte des moments transmis par les faisceaux, à partir de laquelle les plans du milieu sont perpendiculaires aux faces des piliers, et sont interrompus aux bords de la colonne. Dans la situation de conception, la colonne d’angle soumise à la flexion oblique composite est considérée, avec des excentricités qui sont initiales selon les axes coordonnés locaux.

Les piliers, bien que leur classification par leur position dans la structure soit très habituelle, sont également classés quant au type de demande que le pilier est soumis. C’est-à-dire les piliers soumis à la flexion composite normale, les piliers soumis à la flexion composite oblique et les piliers soumis à la compression centrée.

2.2 INDEX D’ESBELTEZ

L’indice de minceur des piliers en béton armé est le rapport entre la longueur équivalente (l_e) de la colonne et le rayon de rotation (i) de la section. (NBR 6118, 2014)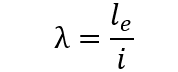

La classification des poteaux dépend des limites d’élancement et de facteurs supplémentaires, tels que l’excentricité relative, la forme du diagramme des moments de flexion et les conditions de liaison des extrémités. Ces facteurs sont considérés par le coefficient λ₁.

Pour les piliers courts NBR 6118 (2014) (λ ≤ λ1), les effets du second ordre pourraient être ignorés car les indices de référence sont supérieurs aux indices de minceur. Piliers élancés moyens (λ1 <λ ≤ 90) qui sont ceux pour lesquels les effets du second ordre peuvent être considérés, au moyen d’un processus approché, comme la méthode standard des colonnes à courbure approximative. Les colonnes élancées (90 <λ ≤ 140) sont celles pour lesquelles il est possible de considérer la méthode des colonnes standard avec les diagrammes M – N – 1 / r. Piliers très élancés (140 <λ ≤ 200) qui nécessitent, pour vérifier l’état limite d’instabilité, les méthodes exactes à considérer. NBR 6118 ne permet pas la conception et la construction d’un pilier avec un indice d’élancement (λ) supérieur à 200. Dans le cas de poteaux de résistance normale inférieure à 0,10.f_cd.A_c, cette limite peut être dépassée.

2.3 EXCENTRICITÉS

Dans les piliers, les excentricités se produisent non seulement en raison des demandes initiales sur les piliers, mais aussi en raison de facteurs supplémentaires tels que les effets du 2ème ordre, le fluage des imperfections concrètes et géométriques.

Il est nécessaire d’obtenir les excentricités liées au type de colonne analysée pour en faire sa dimension. Cet article présente les critères d’obtention de ces excentricités en piliers séparément, selon la norme NBR 6118, 2014.

2.3.1 EXCENTRICITÉ INITIALE DU 1ER ORDRE

Nous savons que les poutres et les piliers composent des portiques tridimensionnels, de sorte que les piliers sont soumis à une flexion oblique composite et, par conséquent, présentent des excentricités initiales dans deux directions principales. Dans les projets qui envisagent des processus simplifiés pour la définition des efforts demandés sont fletor moment, force normale et force de coupe, par exemple, le boîtier de faisceau continu présenté dans NBR 6118 (2014), il est admis que les excentricités initiales apparaissent dans le coin et les piliers finaux. Se souvenant que les excentricités ne sont pas prises en compte pour les piliers intermédiaires.

Les excentricités du 1er ordre sont données par les expressions _:

Nd serait la force de calcul demandeuse;

M_d,A et M_d,B les moments de calcul demandeurs aux extrémités de la colonne.

La plus grande excentricité en valeur absolue est adoptée pour e_i,A.

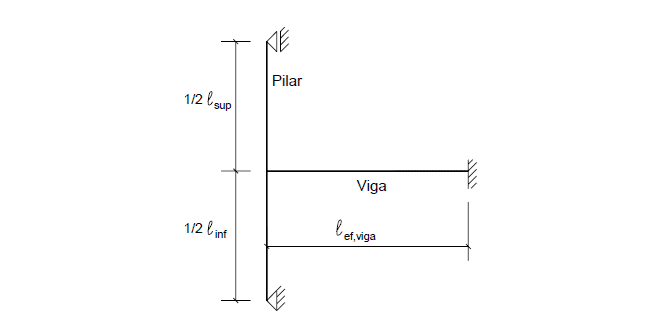
Lorsque les valeurs exactes des efforts demandés dans la structure ne sont pas calculées, il est possible d’adopter la forme statique indiquée à la figure 2, afin d’obtenir les moments de la grippe dans les supports extrêmes, comme la simplification.

Figure 2 – Modèle considéré en cas de soutien extrême des faisceaux continus.

Les moments de demande dans les branches supérieures et inférieures du pilier sont obtenus par :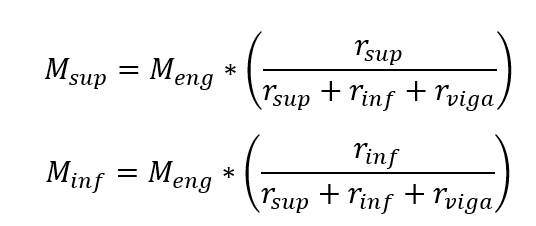

Puisque M_eng est le moment de prise parfait dans la section analysée (section d’extrémité) de la poutre.

Les coefficients de rigidité des branches supérieure et inférieure de la colonne et de la section du faisceau sont définis par les relations entre les moments d’inertie et les travées, selon les expressions suivantes :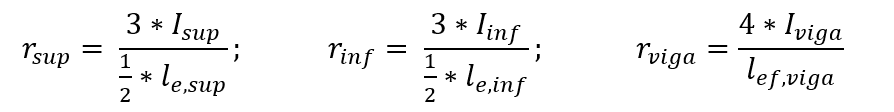

Le moment de flexion dans la poutre est déterminé par l’expression suivante, en tenant compte de l’équilibre du nœud.

La longueur équivalente l_e du pilier peut être déterminée par l’expression:

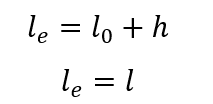
étant que:

l_o distance entre les faces internes des éléments de structure, supposés horizontaux, qui relient le poteau.

h la hauteur de la section transversale de la colonne, connue au plan de la structure.

l la distance entre les axes des éléments structurels auxquels le pilier est lié.

Les travées efficaces des faisceaux peuvent être calculées par l’expression :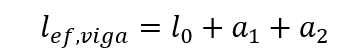

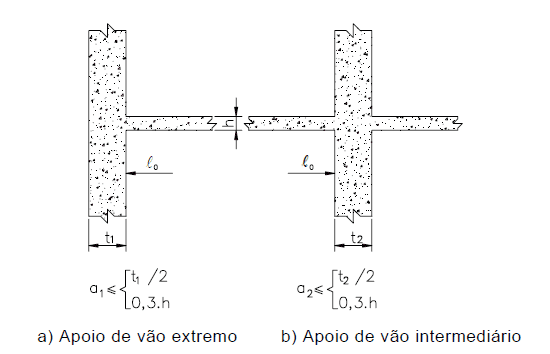
Les valeurs de a₁ et a_2, à chaque extrémité de la travée, peuvent être calculées par les valeurs appropriées d’a_i, indiquées à la figure 3, étant :

a₁ égal à la plus petite valeur entre (t₁ / 2 et 0,3 * h).

a₂ égal à la plus petite valeur entre (t₂ / 2 et 0,3 * h).

Figure 3 – Aller poutres efficaces.

2.3.2 EXCENTRICITÉ DE FORME

Pour ajuster la position des éléments structurels en fonction de la conception architecturale, les concepteurs structuraux doivent rendre les faces internes ou externes des poutres compatibles avec celles des piliers qui les reçoivent. Lorsque cela se produit, les axes des faisceaux ne passent pas par le centre de gravité de la section de la colonne (figure 4), émergeant ainsi des excentricités appelées excentricités de forme (AGUIAR. 2000).

Figure 4 – Excentricité de la forme dans les piliers.

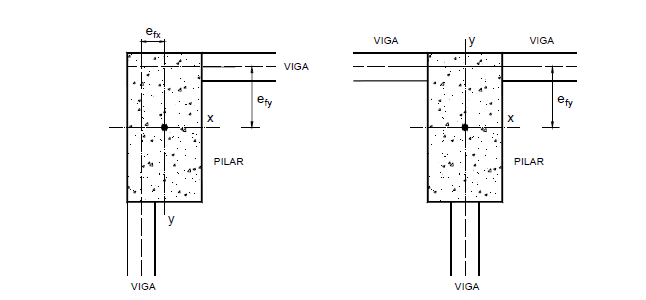
Les excentricités de la forme, lorsqu’elles sont faites les projets et les structures des bâtiments, ne sont pas prises en compte dans la dimension, sans l’aide de programmes informatiques élaborés à cet effet. Le moment fletor généré par les excentricités au niveau de chaque étage est nivelé par un couple, provoquant, à chaque étage, des paires de forces du même ordre de grandeur et des directions contraires, qui s’annulent. Les programmes informatiques élaborés pour l’analyse structurelle et la dimensionnement avec des contrôles d’ouverture des fissures et les critères des derniers états de limite et des déplacements avec les paramètres des états limites de service, prennent en compte ces excentricités de forme.

2.3.3 EXCENTRICITÉ ACCIDENTELLE

Le NBR 6118 (2014) prévoit le calcul d’une excentricité accidentelle (e_a), en tenant compte des situations d’imperfection locale dues à la construction des colonnes, elles peuvent être dues à la non rectitude de l’axe des colonnes.

Selon NBR 6118 (2014), dans les structures réticulées normales, il est admis que l’effet des imperfections locales est résolu si l’on considère la valeur du moment total minimum. Dans le cas de la flexion composite oblique, la valeur minimale du moment doit nécessairement être respectée séparément dans chacune des directions principales.

2.3.4 EXCENTRICITÉ DE DEUXIÈME ORDRE

Les effets locaux de second ordre peuvent être calculés par des méthodes approximatives ou par la méthode générale. Seuls les effets du 2ème ordre pour les piliers minces médians sont pris en compte, en utilisant la méthode de colonne standard avec courbure approximative et la colonne standard avec rigidité approximative. Les médianes représentent la plupart des occurrences dans les structures actuelles des bâtiments, et les cas des piliers avec des index minces supérieurs à 90 sont peu fréquents.

• Méthode de pilier standard avec courbure approximative

Lors de la conception de poteaux avec λ ≤ 90, avec une section constante et un ferraillage symétrique et constant le long de son axe. Cette méthode n’est utilisée que dans le cas d’une flexion composite normale. La non-linéarité physique est prise pour une expression proche de la courbure dans la section transversale qui exprime la valeur de moment de flexion la plus élevée compte tenu des moments du premier et du second ordre. Le moment total maximum dans le pilier, c’est-à-dire la somme des moments du 1er ordre et des moments du 2ème ordre, est calculé par l’expression:
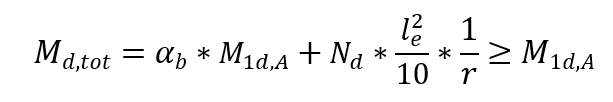Étant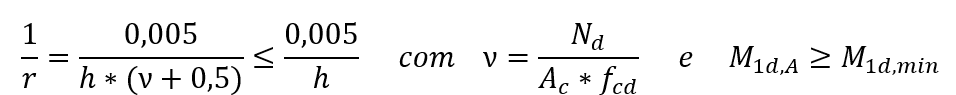
α_b un coefficient qui dépend de la distribution des moments dans la colonne.

M_1d,A la valeur de calcul du moment de 1ère commande MA ;

h la hauteur de la section de colonne dans la direction analysée;

ν la force dimensionnelle n_ormale;

f_cd la résistance à la compression du calcul du béton;

M_1d,min le 1er moment minimum de commande.

Ainsi, à partir de la deuxième tranche de l’expression précédente, on en déduit que l’excentricité du 2ème ordre (e₂) suppose l’expression suivante:

2.3.5 EXCENTRICITÉ CAUSÉE PAR LA FLUIDITÉ

Selon NBR 6118 (2014), l’excentricité générée par le fluage du béton et c doit être calculée sur des poteaux de λ > 90, c’est-à-dire des poteaux élancés et nombreux. Les effets du fluage sont négligés dans les colonnes avec des indices d’élancement inférieurs à 90.

Bien que l’analyse précise des effets de la maîtrise soit une œuvre complexe, NBR 6118 apporte une expression simplifiée pour le calcul de l’excentricité e_c, ce qui suit :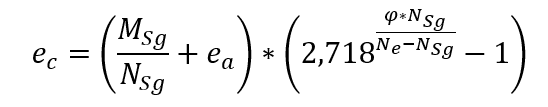Être

M_Sg et N_sg les efforts demandés dans le pilier tiré de la combinaison presque permanente;

e_a et excentricité accidentelle;

φ le coefficient de fluidité.

E_ci = 5 600.* f_ck^0.5 est le modulus initial de l’élasticité du béton;

I_c le moment d’inertie de la section pilier;

l_e la longueur équivalente de la section de colonne.

L’excentricité c_alculée ec doit être ajouté à l’excentricité du 1er ordre. La figure 5 montre l’excentricité du deuxième ordre.

Figure 5 – Excentricités initiales et de second ordre dans les piliers.

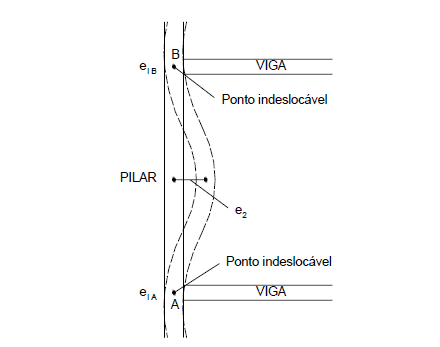
Les sections de fin n’impliquent pas les effets du 2ème ordre et ne devraient être considérées que dans la section intermédiaire.

2.4 CALCUL DU RENFORCEMENT LONGITUDINAL À L’AIDE D’ABACUs

Dans le dimensionnement manuel des colonnes, les abaques sont indispensables, car ils apportent la définition rapide du taux de ferraillage, rendant inutile l’application des équations théoriques de la Flexion Composite Normale ou Oblique. De plus, les abaques permettent le choix aisé de plusieurs dispositions de renforcement dans la section transversale. Les abaques de Venturini et Rodrigues (2000) pour la flexion composite normale et Pinheiro (1994) pour la flexion composite oblique, ne doivent être utilisés que dans la conception de colonnes avec du béton de résistance du groupe I (fck ≤ 50 MPa), en l’état. élaborés avec certains paramètres numériques lorsqu’ils ne s’appliquent pas aux bétons du groupe II.

2.4.1 FLEXION COMPOSITE NORMALE

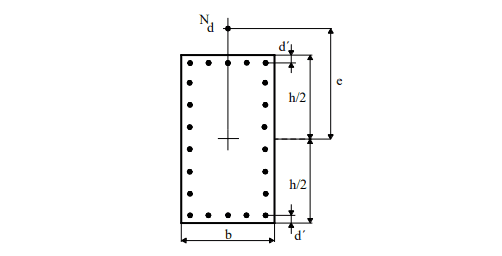
Pour Venturini et Rodrigues (2000) Flexion composite normale, la figure 6 montre la notation de l’application abaque. L’excentricité (e) est parallèle à la distance d ‘, entre le centre de la barre d’angle et la face du profilé. En général, il y a d ‘= c + Φt + Φλ / 2, avec c = couverture de béton, Φt = diamètre de l’étrier et Φλ = diamètre de la barre longitudinale.

Figure 6 – Notation pour flexion composite normale.

Les équations utilisées pour la construction de l’abaci ont été soulignées dans la publication de Venturini et Rodrigues (2000). La définition du renforcement longitudinal est initiée par le calcul des efforts dimensionnels n (ni) et μ (mi). La valeur adimensionnelle n a été définie dans l’équation suivante :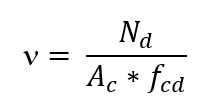

La valeur de μ, selon le moment fletor ou l’excentricité, est :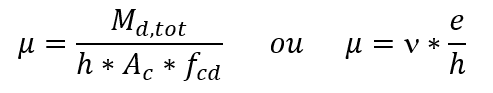

Être

N_d la force normale de calcul;

A_c la zone de la coupe transversale du pilier;

f_cd la force de calcul du béton à la compression (f_ck/γ_c);

M_d,tot le moment fletor total de calcul;

h la taille du pilier dans la direction considérée;

et l’excentricité dans la direction considérée.

Une fois qu’une distribution constructive est choisie pour le renforcement sur la colonne, le boulier à utiliser est défini, selon le type d’acier et la valeur du rapport d’/h. Dans le boulier, avec la paire ν et μ, le taux mécanique ω est obtenu. L’armature est calculée par l’expression :

2.4.2 FLEXION COMPOSÉE OBLIQUE

Pour Pinheiro Oblique Composite Flexion (1994) figure 7 montre la notation appliquée dans l’utilisation de l’abaci. Les distances d’_x et d’_y ont la même interprétation de d’, cependant, chacun dans une direction du pilier.

Figure 7 – Notation pour flexion composite normale.

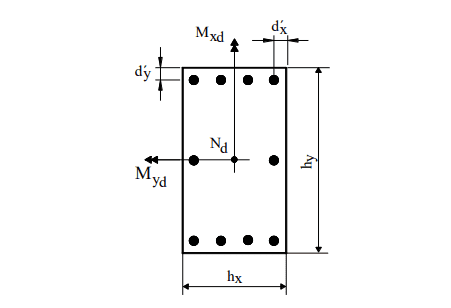
La détermination du renforcement commence par le calcul des efforts dimensionnels ν et μ, avec μ selon les deux directions principales de la colonne :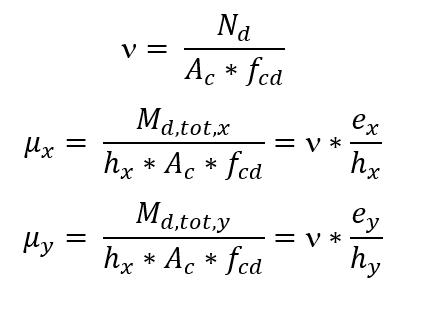Une fois qu’une distribution constructive pour le renforcement sur la colonne est choisie, le boulier à utiliser est défini, en fonction des valeurs des ratios d’_x/h_x et d’_y/h_y et du type d’acier. Dans le boulier, avec le trio (ν, μx, μ_y), le taux mécanique ω est obtenu. L’armature est calculée avec l’équation suivante :

2.5 DÉTAIL DES PILIERS EN BÉTON ARMÉ

NBR 6118, 2014 détermine que la dimension de la section transversale de la colonne ne doit pas être inférieure à 19 cm. Cette recommandation vise à éviter les comportements inacceptables pour les éléments structurels et à permettre des conditions de construction appropriées.

Cependant, pour les cas spéciaux, la plus petite taille de la colonne est autorisée à être entre 19cm et 12cm. Dans ces cas, il est nécessaire de multiplier les efforts de calcul finaux appliqués dans le dimensionnement des piliers par un coefficient supplémentaire de γ_n, selon l’image 8.

Figure 8 – Valeurs du coefficient additionnel γ_n.

Tout d’abord, le taux géométrique de renforcement longitudinal de la colonne est défini par le rapport suivant :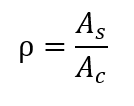

Être,

A_s la somme des zones des sections transversales des barres longitudinales.

A_c la zone transversale du pilier.

La zone minimale de renforcement longitudinal, dépend de l’intensité de la demande due à la force normale et la force de l’acier, est déterminée par l’expression suivante: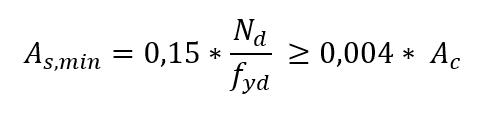Par conséquent, le taux minimum de renforcement géométrique est égal à 0,4 %.

La zone maximale de renforcement possible sur les piliers devrait être de 8 % de la zone transversale, compte tenu du chevauchement du renforcement dans les régions épissantes, c’est-à-dire :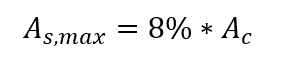

Le diamètre minimum des barres longitudinales ne doit pas être inférieur à 10 mm et ne doit pas dépasser 1/8 de la plus petite taille de la section de colonne.

Pour une bétonnage adéquate, il est nécessaire que le béton dispose d’un minimum d’espace pour traverser entre les renforts longitudinals. Par conséquent, des limitations sont imposées à l’espacement libre entre les barres du renforcement longitudinal (a_L), qui doit être égal ou supérieur à la plus élevée des valeurs suivantes :

• 20 mm;
• La mesure du diamètre de la barre, du faisceau ou du manchon adopté dans la couture;
• 1,2 au lieu du diamètre maximum de l’agrégat;

L’espacement maximal entre les axes des barres de renfort est également limité, et doit être inférieur ou égal à deux fois la plus petite taille de la colonne, sans dépasser 400mm.

Le diamètre des étriers (φt) _dans les piliers ne doit pas être inférieur à 5 mm ou 1/4 du diamètre de la barre longitudinale.

Afin d’assurer le positionnement des barres de renforcement longitudinales et, en outre, de rendre impossible de contredir les barres longitudinales et d’utiliser le renforcement de la couture dans les régions de couture, un espacement maximal entre les étriers (mesuré dans le sens de l’axe de la colonne) sont nécessaires, étant inférieurs ou égaux à la baisse des valeurs suivantes :

• 200 mm;
• dimension de section plus petite;
• 24 φ pour l’acier CA-25 et 12 φ pour l’acier CA-50, où φ est le diamètre de la barre longitudinale;

Lorsqu’il est possible de faire flamber les barres à la surface, des mesures devraient être prises pour l’éviter.

3. MODÉLISATION LOGICIELLE CAD/TQS

Une des façons d’avoir un calcul structurel détaillant, en béton armé, plus rapide et plus précis (avec moins d’arrondi), est par l’utilisation de logiciels, l’un d’eux est appelé TQS, il utilise la plate-forme CAD pour son fonctionnement. Avec TQS, nous pouvons obtenir les calculs des efforts et des flèches dans la structure, les dimensions et les détails des renforts en fonction des demandes et le traçage de tout le matériel nécessaire, le tout en fonction de ce que le professionnel a lancé sur la plate-forme de dessin. Le TQS fait tout cela dimensionnant et détaillant selon les normes actuelles.

Les systèmes TQS ont des ressources qui font du développement de projets structurels un processus très productif. De la conception à l’émission de l’usine, toutes les étapes sont automatisées. Ses principaux produits sont TQS (béton armé et prétresse), Alvest (maçonnerie structurale), PREO (préfabriqué) et SISEs (géotechnique).

Adapté aux dernières revues réglementaires (NBR 6118/2014, NBR 15200:2012, NBR 15.575:2013, NBR 9062:2006, NBR 15812:2010, NBR 15961:2011. Chaque version des systèmes TQS est rigoureusement testée, tant sur le plan opérationnel que par rapport à leurs résultats. Du matériel éducatif pour tous ses produits, comme TQS étape par étape, traçage, escaliers étape par étape, Alvest étape par étape (TQS, 2020).

3.1 LIBÉRATION STRUCTURELLE DANS LE LOGICIEL TQS/CAD

La structure faite pour analyse est l’exemple complet du livre Structural Project of Reinforced Concrete Buildings, de José Milton de Araújo (2014). Pour la modélisation dans le logiciel ont été lancés les piliers, les poutres, les dalles, les escaliers, les charges murales, séquentiellement dans l’ordre décrit.

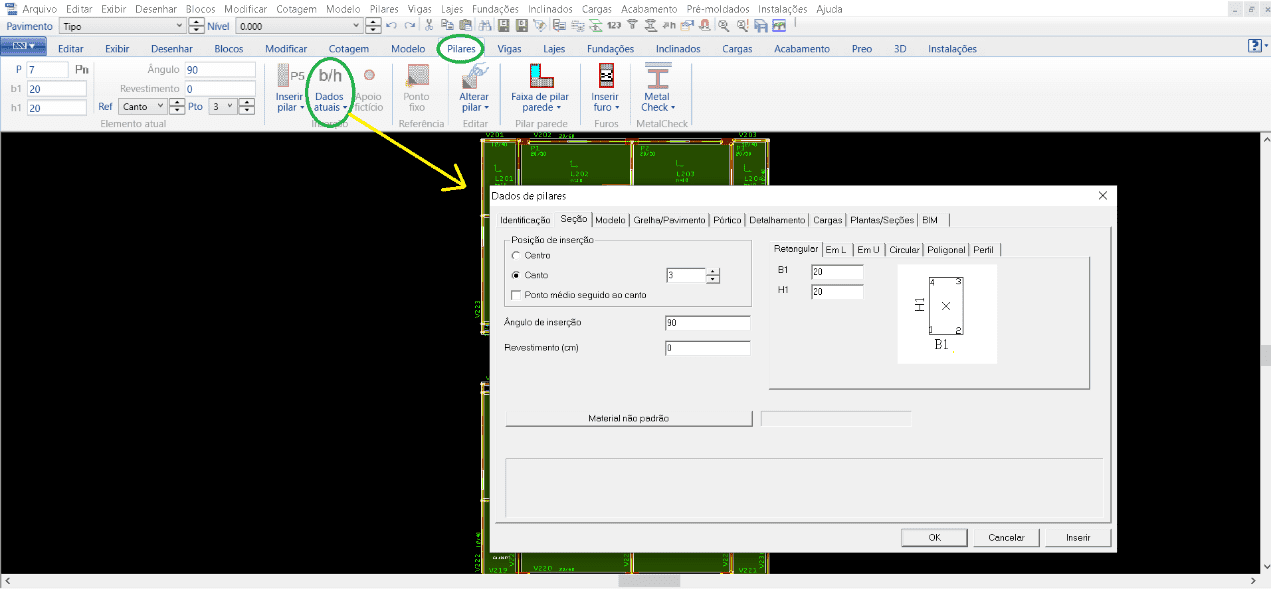
Pour les piliers, les étapes suivantes ont été suivies : après l’ouverture du modèle structurel, l’onglet « Piliers » est actif, la fenêtre « Données actuelles » doit être ouverte (figure 9), où toutes les données apparaîtront pour l’insertion de la colonne, puis placer les dimensions, le numéro d’identification, la position d’insertion, déterminer où le pilier est né et meurt, entre autres informations. À la fin de toutes les éditions pertinentes, donc, tous les piliers nécessaires sont inclus.

Figure 9 – Fenêtre TQS/CAD dans l’onglet « Piliers ».

Pour la construction de poutres dans le logiciel CAD/TQS, le processus est le suivant :

Après avoir défini tous les piliers, nous passons à la libération des poutres. Initialement, vous devez activer le menu « Faisceaux », où tous avec les commandes suivantes sont spécifiques à la libération des faisceaux.

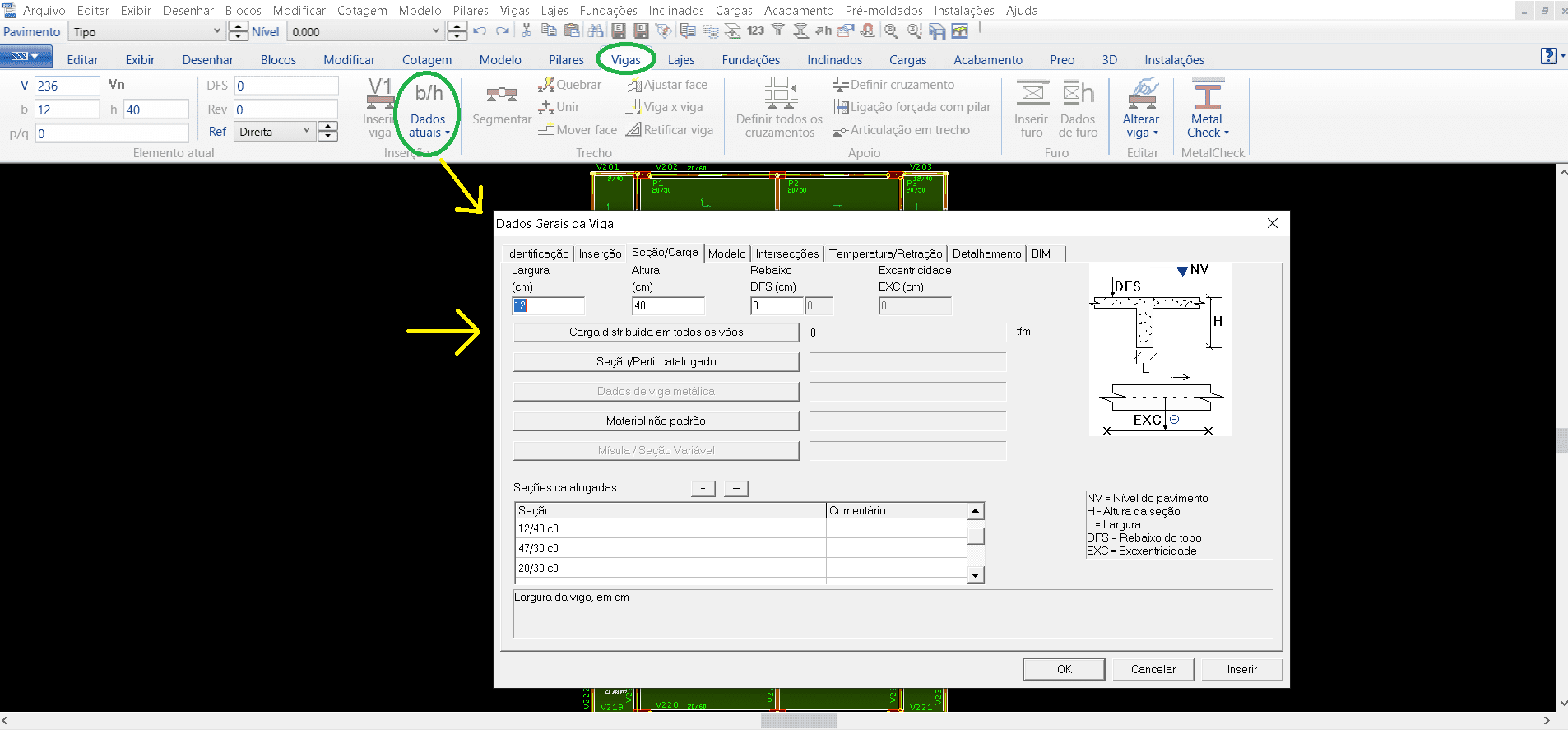
Dans l’onglet « Faisceaux », vous devez sélectionner la commande de « Données actuelles » (figure 10), où vous ouvrirez une fenêtre des données générales des faisceaux, plaçant ainsi toutes les informations nécessaires à la libération de chaque faisceau. Informations telles que le numéro d’identification de chaque faisceau, son couvercle, les charges que ce faisceau agira sur les piliers, tels que le permanent et accidentelle, sa section. Après tout ce processus de détail, nous pouvons ensuite insérer le faisceau, plaçant au point de départ puis au point final, généralement ces points d’insertion sont les vertices des piliers déjà insérés précédemment, répétant la même procédure jusqu’à placer tous les faisceaux nécessaires.

Figure 10 – Fenêtre TQS/CAD dans l’onglet « Poutres ».

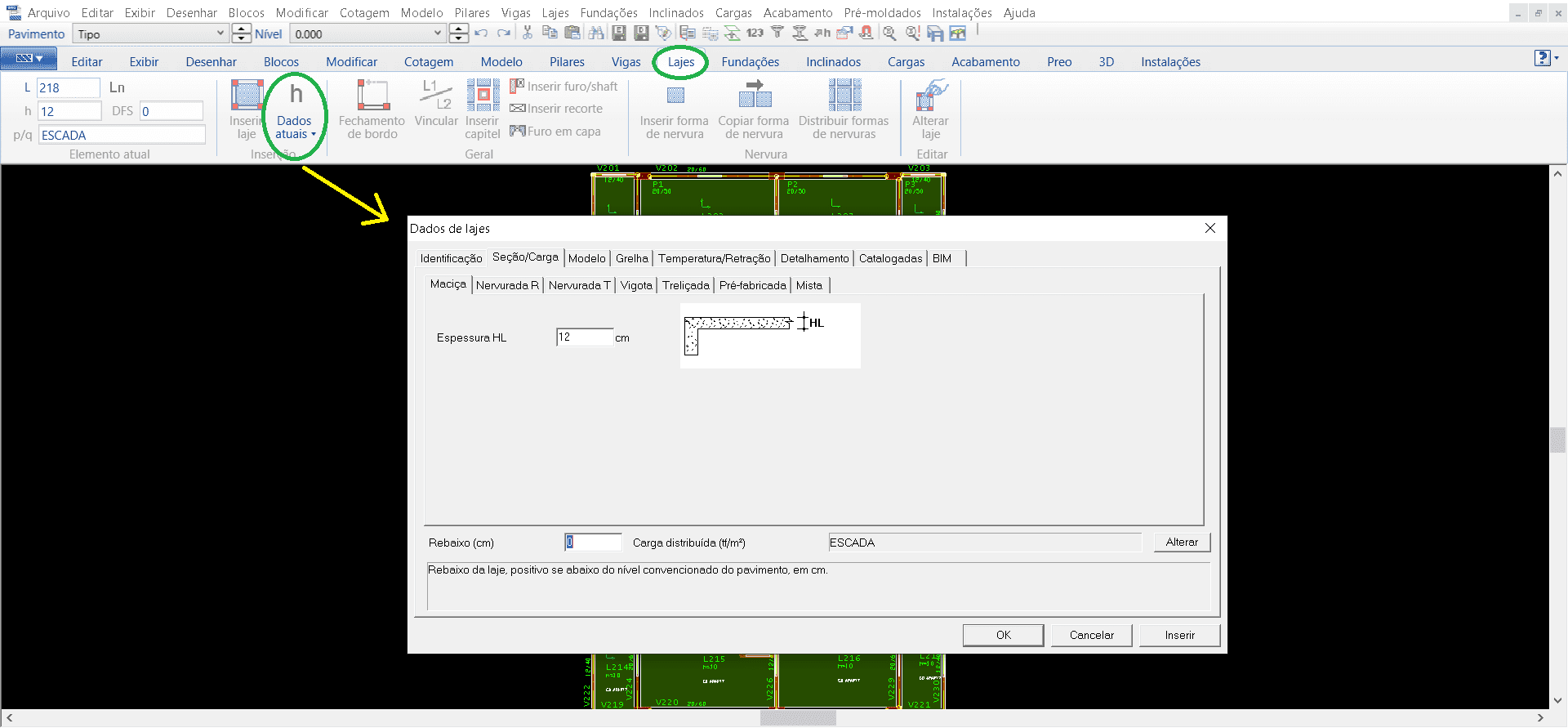
Après la libération des poutres, nous nous déplaçons vers les dalles, suivant les mêmes procédures que les précédentes dans l’onglet « Dalles » sélectionnant « Données actuelles » met l’identification, le type de dalle et son épaisseur (image 11).

Figure 11 – Fenêtre TQS/CAD dans l’onglet « Dalles ».

Pour l’affichage des charges murales suit la même ligne de procédures. Dans la fenêtre ” Charges ” sélectionne l’onglet « Distribué linéairement », puis l’ouverture d’une fenêtre pour le choix du type de charge, pour la modélisation en question a été inséré bloc 14 (maçonnerie bloc de béton 14 cm) et la hauteur du mur déterminé (image 12).

Source : Figure 12 – Fenêtre TQS/CAO dans l’onglet « Charges ».

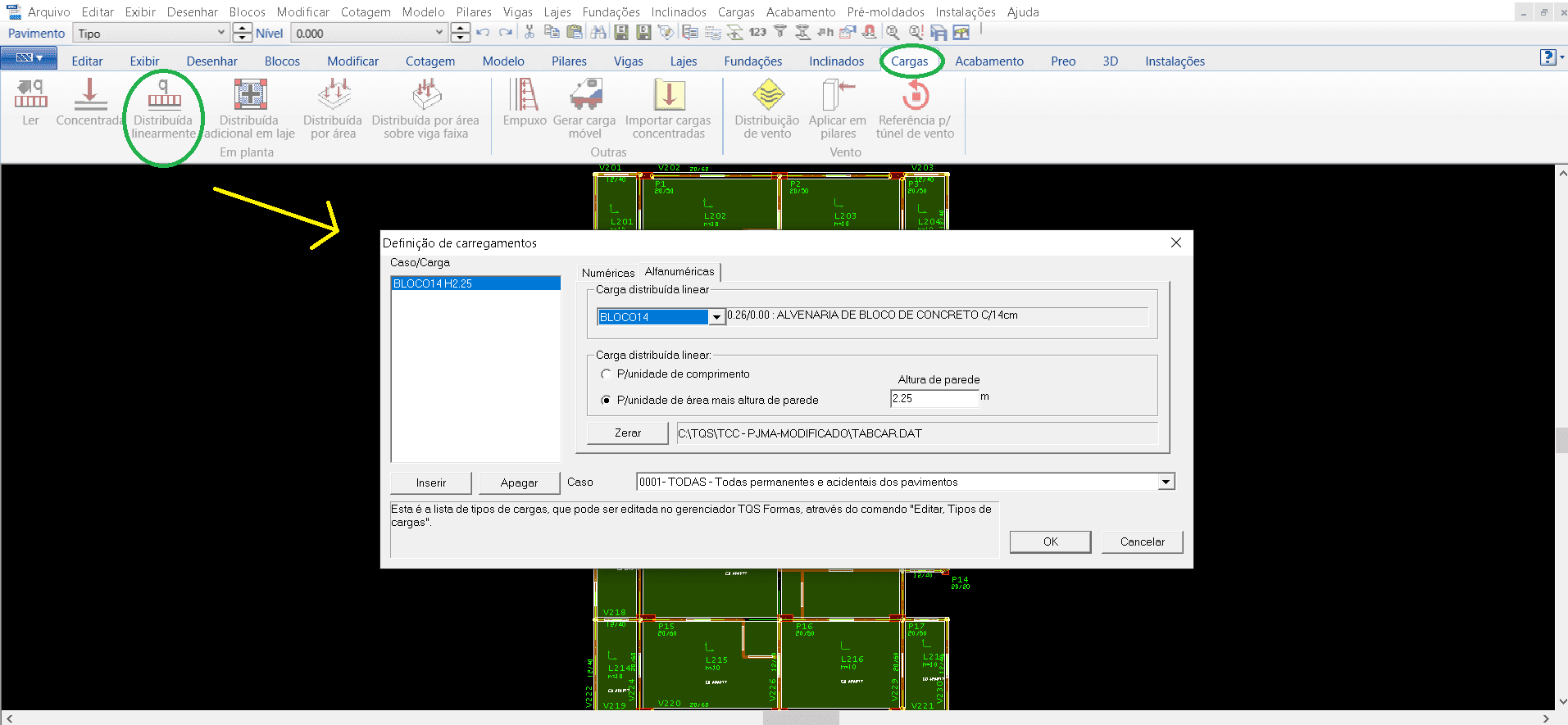
Ainsi, lors de la finition de la version de tous les éléments nécessaires dans les planchers, nous devons enregistrer les données définies jusqu’à présent dans le menu « Fichier » dans la commande « Enregistrer le modèle structurel ».

Figure 13 – Bâtiment d’exemple 3D, TQS/CAD

En utilisant le spectateur tridimensionnel, nous avons l’idée concrète de ce à quoi ressemblerait le bâtiment d’exemple (figure 13).

L’application P-Calc est une calculatrice TQS qui vérifie les piliers en béton armé soumis à une flexion composite oblique individuelle (TQS, 2020).

Les principales caractéristiques de P-Calc sont:

• Vérification des piliers soumis à la flexion composite, normale ou oblique, par rapport à la dernière limite d’état de rupture et d’instabilité;
• Analyse des piliers avec béton à haute résistance (fck > 50 MPa);
• Diagramme normal d’interaction de moment d’effort x déflecteur (FCO et FCN);
• Résultats graphiques pour les contraintes et les déformations dans la section;
• Évaluation des effets locaux du 2e ordre en adoptant la non-ligne géométrique et physique, selon ABNT NBR 6118;
• Envelomyciste de moments minimes;
• Mémoire de calcul en format PDF;

4. PRÉSENTATION ET ANALYSE DES RÉSULTATS

Ce sujet présente les comparaisons entre les références pour les éléments étudiés. Il a été divisé en sous-utopiques pour les principaux éléments d’un projet structurel. Il est souligné que les références étudiées ont été à la base du projet du livre « PROJETO ESTRUTURAL DE EDIFÍCIOS DE CONCRETO ARMADO » de JOSÉ MILTON DE ARAÚJO, 3ème édition, modélisé, calculé et détaillé dans le TQS. Pour les autres tests, certains éléments ont été comparés à d’autres outils de calcul tels que Pcalc et Bending Abaci pour les données des piliers.

4.1 MODÉLISATION ET DIMENSIONNEMENT COMPARATIFS – PILIER

Après modélisation et dimension des piliers, selon le sujet 3, l’effort principal, la section et la surface d’acier ont été comparés entre les références étudiées pour les deux piliers (P2 et P5) selon l’abstrait dans les tableaux 01 et 02.

Tableau 1 – Présentation des résultats par rapport au pilier 2

Éléments	Efforts caractéristiques (tf)	Section (cm x cm)	Superficie en acier (cm²)
Araujo (2014)	71,4	20 x 50	6ϕ20 (18,90)
TQS	66,2	20 x 50	8ϕ20 (25,20)
Pcalc*	71,4	20 x 50	10ϕ20 (31,50)
Pcalc*	66,2	20 x 50	10ϕ20 (31,50)
Abacus- Flexion normale*	71,4	20 x 50	6ϕ20 (18,90)
Abacus- Flexion normale*	66,2	20 x 50	4ϕ20 (12,60)

*Solution de pilier standard avec courbure approximative.

Source: Auteur, 2020.

On peut observer, en analysant les comparaisons pour le pilier P2 que la dimension araújo (2014) par rapport à la TQS montre une augmentation de 33,33% dans la zone sidérurgique, en tenant compte du fait qu’Araújo présente une force normale 7,85% plus élevée, déjà par rapport au PCalc, il y a eu une augmentation de 66,67%, les corrélant avec la même charge.

Il est intéressant de noter que ces mêmes valeurs par rapport au dimensionnement de la colonne standard avec courbe approximative à l’aide de la Flexion Normale Abaci (VENTURINI et RODRIGUES, 2000), ont été séparées en deux groupes de charges parce que la modélisation effectuée dans le TQS diffère de l’enquête de charge d’Araújo (2014) donc nous avons les chiffres 14 et 15.

Figure 14 – Comparaison entre TQS x Pcalc x Abaci pour le pilier 2

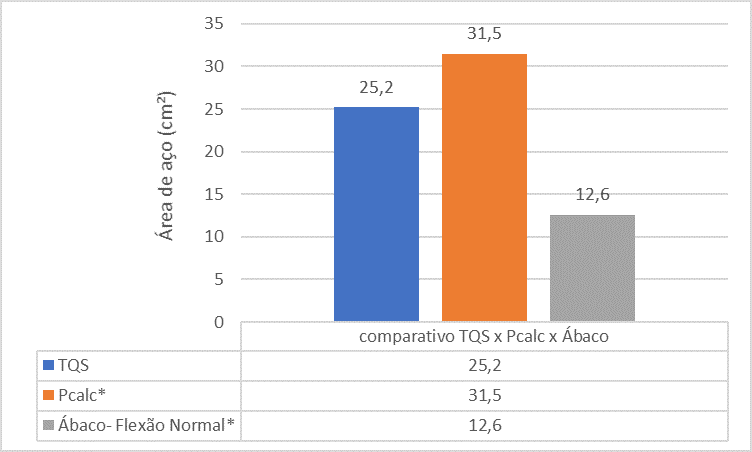
L’analyse comparative entre les références montre que la surface en acier de la colonne P2 trouvée par l’outil TQS est plus petite que la surface d’acier trouvée par le Pcalc et l’Abaci. Cela est dû au fait de l’analyse monolithique effectuée dans le programme.

Figure 15 – Comparaison entre Araújo (2014) x Pcalc x Abacos pour Pilar 2

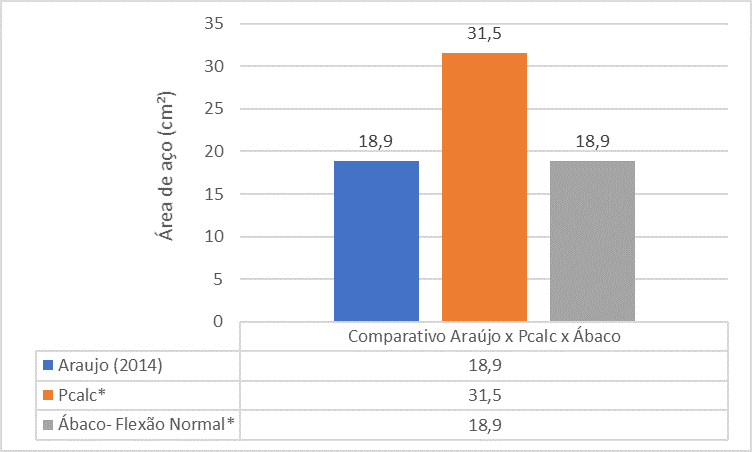
L’analyse comparative entre les références montre que la surface sidérurgique du pilier P2 trouvée par le livre d’Araújo (2014) est beaucoup plus petite que la surface sidérurgique trouvée par Le PCalc et Abacus.

Le pilier P2 est une colonne d’extrémité, support intermédiaire pour le faisceau V202, dans la direction x, sans tenir compte de ces moments transmis. Dans la direction y nous avons faisceau V 227, cela a été considéré comme les moments transmis dans le pilier. De cette analyse, le moment de réglage parfait (M_eng) a été le calcul, le moment d’inercia de faisceau (I_vig), le coefficient de rigidité de faisceau (r_vig), le moment d’inercia des piliers (I_p), le coefficient de rigidité des piliers (r_p) et les premiers instants dans les piliers (M_p), des calculs, les moments réduits sont obtenus, mais divisent la grande différence entre eux, ont été considérés comme zéro et la taille de la section dans la compression flexo-normale dans la direction x.

Pour une force normale sur l’axe x, nous avons l’indice de minceur (λ_x) excentricités initiales (e_ia), excentricité accidentelle (e_ax), excentricité minimale (e_1x,min), excentricité initiale ne section intermédiaire (e_ix), excentricité de second ordre (e_2x) et excentricité de la fluidité (e_cx). La séance critique a été à la fin de la session, en utilisant les tables de surface d’acier de la session peut être armé de 6 barres de 20 mm, en adoptant une surface totale en acier égale à 18,85 cm².

Tableau 2 – Présentation des résultats par rapport au pilier 5

Éléments	Efforts caractéristiques (tf)	Section (cm x cm)	Superficie en acier (cm²)
Araujo (2014)	112,2	20 x 50	10ϕ16 (20,00)
TQS	141,5	20 x 50	8ϕ25 (40,00)
Pcalc*	112,2	20 x 50	12ϕ20 (37,80)
Pcalc*	141,5	20 x 50	12ϕ25 (60,00)
Abacus- Flexion normale*	112,2	20 x 50	8ϕ25 (40,00)
Abacus- Flexion normale*	141,5	20 x 50	11ϕ25 (55,00)

*Solution de pilier standard avec courbure approximative.

Source: Auteur, 2020.

On peut l’observer, en analysant les comparaisons pour le pilier P5 qui, La dimension d’araújo (2014) par rapport au TQS montre une augmentation de 100% de la surface sidérurgique, compte tenu du fait qu’Araújo a une force normale inférieure de 26,11%, déjà par rapport au PCalc, il y a eu une augmentation de 89% par rapport à la charge d’Araújo, et de 50% par rapport à la charge du TQS , montrant que plus l’augmentation de la charge est élevée, plus la divergence des zones sidérurgiques est grande. On peut dire que cette divergence est due au fait de présenter l’erreur suivante pour la résolution du pilier P5 dans le Pcalc, pour Araujo (2014) dans le dernier état limite (ELU): Le pilier ne prête pas attention à la vérification du moment minimum. Le pilier avec la charge TQS dans le Pcalc génère les erreurs suivantes = 5,89% > ρs.max = 4,00%.

Il est intéressant de noter que ces mêmes valeurs par rapport au dimensionnement de la colonne standard avec courbe approximative à l’aide des abaces flexion normales (VENTURINI et RODRIGUES, 2000), ont été séparées en deux groupes de charges parce que la modélisation effectuée dans le TQS diffère de l’enquête de charge d’Araújo (2014) donc nous avons les figures 16 et 17.

Figure 16 – Comparaison entre TQS x Pcalc x Abaci pour le pilier 5

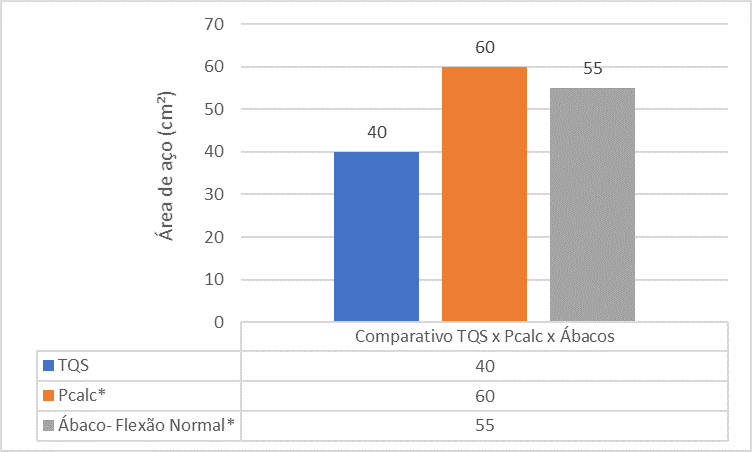
L’analyse comparative entre les références montre que la surface d’acier du pilier P5 trouvée par l’outil TQS est plus petite que la surface sidérurgique trouvée par le Pcalc et l’Abaci. Cela est dû au fait de l’analyse monolithique effectuée dans le programme.

Figure 17 – Comparaison entre Araújo (2014) x Pcalc x Abacos pour Pilar 5

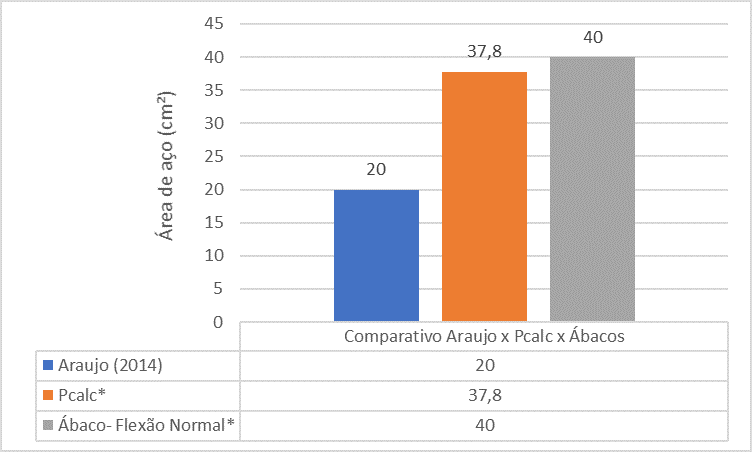
L’analyse comparative entre les références montre que la surface en acier du pilier P5 trouvée par le livre d’Araújo (2014) est beaucoup plus petite que la surface sidérurgique trouvée par Le PCalc et Abacus.

Le pilier P5 est un pilier intermédiaire, avec les travées et les charges des poutres V204 et V227, ne diffèrent pas les uns des autres, de sorte que l’on peut ignorer les premiers moments transmis par ces faisceaux. À partir de cette analyse, le calcul a été fait sur l’axe y, parce qu’il s’agissait de l’indice de minceur le plus élevé (λ_x) trouvé, de l’excentricité (e_y), donnée par la somme de l’excentricité de premier ordre (e_1x), de l’excentricité de second ordre (e_2x) et de l’excentricité de la fluidité (e_cy). À l’aide des tables en acier, la séance peut être armée de 10 barres de 16 mm, adoptant une surface totale en acier égale à 20,00 cm².

5. CONCLUSION

Il a observé que la comparaison entre les méthodes est importante pour choisir le meilleur outil à utiliser dans le dimensionnement des piliers.

En reproduisant la modélisation du bâtiment d’Araújo dans le TQS, une différence de charge a été remarquée, et pour ces charges, il est perçu que l’outil TQS en mode par défaut est proche de la dimension de l’outil PCalc et Abaci pour les piliers intermédiaires.

Dans les piliers finaux araújo montre une plus petite variation des réponses par rapport à Abaci et PCalc.

Ainsi, l’analyse comparative entre les méthodes de calcul est différente en raison du fait que l’analyse monolithique de la structure faite dans l’outil TQS, différente des autres méthodes qui présente une analyse segmentée des éléments avec des formulaires de calcul simplifiés.

RÉFÉRENCES

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 1978.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2003.

ABNT (Associação Brasileira de Normas Técnicas). NBR 6118. Projeto de estruturas de concreto — Procedimento, 2014.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15200. Projeto de estruturas de concreto em situação de incêndio. Rio de Janeiro, — Procedimento, 2012.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15575. Edificações habitacionais – Desempenho. Rio de Janeiro, — Procedimento, 2013.

ABNT (Associação Brasileira de Normas Técnicas). NBR 9062. Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, — Procedimento, 2006.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15812. Alvenaria estrutural – Blocos cerâmicos. Rio de Janeiro, — Procedimento, 2010.

ABNT (Associação Brasileira de Normas Técnicas). NBR 15961. Alvenaria estrutural – Blocos de concreto. Rio de Janeiro, — Procedimento, 2011.

AGUIAR, E.A.B. Projeto de pilares de concreto de alto desempenho. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2000.

ARAUJO, José Milton de. Projeto estrutural de edifícios de concreto armado. 3. ed. Rio Grande: Editora Dunas, 2014.

BASTOS, Paulo S. dos Santos. Fundamentos do Concreto Armado. Universidade Estadual Paulista. Bauru, São Paulo. 2006.

BRANDÃO, A. M. S.; PINHEIRO, L. M. Qualidade e durabilidade das estruturas de concreto armado: aspectos relativos ao projeto. Cadernos de Engenharia de Estruturas. EESC. Universidade de São Paulo. São Carlos, 1999.

CARVALHO, Roberto Chust.; FIGUEIREDO FILHO, Jasson Rodrigues de. Pilares de concreto armado. p.9-25. Notas de aula – Universidade Federal de São Carlos, 2002

FUSCO, P.B. Estruturas de concreto – solicitações normais, editora Guanabara, São Paulo, 1986.

PIANCASTELLI, E. M. Patologia, Recuperação e Reforço de Estruturas de Concreto Armado. Apostila para Curso de Extensão, Ed. Depto. Estruturas da Escola de Engenharia da UFRG, Belo Horizonte, 1997

PINHEIRO, L.M.; BARALDI, L.T.; POREM, M.E. Concreto Armado: Ábacos para flexão oblíqua. São Carlos, Departamento de Engenharia de Estruturas, Escola de Engenharia de São Carlos – USP, 1994.

TQS, Calculadora P-Calc, Pilares de concreto, 2020. Disponível em: <https://www.tqs.com.br/apps/p-calc/ejm1se496l>

TQS, Sobre a TQS, 2020.Disponível em: <https://www.tqs.com.br/about>

VENTURINI, Wilson Sérgio; RODRIGUES, Rogério de Oliveira. Dimensionamento de peças retangulares de concreto armado solicitadas à flexão reta. São Carlos, Department of Structural Engineering, School of Engineering of São Carlos – USP, 1987 (réimprimé.2000)

^[1] Diplômé en génie civil.

^[2] Diplômé en génie civil.

^[3] Maîtrise en géotechnique et construction civile. Diplôme en génie civil. Diplôme en génie agricole.

Envoyé : Mai 2020.

Approuvé : mai 2020.