ORIGINAL ARTICLE
RAMOS, Gilberto Pereira [1]
RAMOS, Gilberto Pereira. Proposal for Teaching Polar Coordinates with the help of GrafEq Software. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 09, Vol. 04, p. 35-75. September 2020. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/education/polar-coordinates
ABSTRACT
This work aims to present a proposal for the introduction and exploration of the main concepts present in the study of polar coordinates, which is part of the content of the High School Mathematics course according to the PCNs[2]. This proposal was elaborated from the verification, through preliminary studies, of the existence of difficulties related to the understanding and learning of the concepts associated with this theme. Considering the importance of studying polar coordinates in the school curriculum and in understanding natural phenomena and in the various areas of science, the activities that make up this proposal are based on the ideas that learning takes place through a process of knowledge construction . In addition, believing that the contextualization of contents contributes to the significant learning of mathematics, this work proposes a sequence of activities that, based on real problems, intends to explore the main concepts present in the study of the polar coordinate system. To help students solve problems and explore these concepts, we use GrafEq software. We believe that this proposal can contribute to improving the quality of mathematics teaching and more specifically to the teaching of polar coordinates. In addition, this work can serve as an inspiration to mathematics teachers for the creation of new teaching methodologies.
Keywords: GrafEq, teaching, mathematics, coordinates, polars.
1. INTRODUCTION
The topic of mathematical software is quite challenging and the increasing use of computational means as a tool for mathematics education makes it of great relevance to the teaching-learning process nowadays. In addition to this motivating factor, I was also led to think about the subject when studying the subject Informatics in Education, one of the subjects of the curriculum of the Mathematics course at the Universidade Estácio de Sá, where some tools to aid the teaching and learning of mathematics were presented. When researching more on the subject, I discovered the GrafEq tool, which helps in the visual treatment of mathematical algebraic concepts and structures. I was interested in working on the theme ‘polar coordinates’ because it is still not very present in high school classes and because I did not find in my research the relationship between the proposed content and the appropriate tool. Therefore, I introduce this work taking this teaching approach with impetus and the fact that this teaching proposal is in line with the guidelines of the PCNs.
The Ministry of Education (MEC) through the document entitled “National curriculum parameters – High School (PCNEM) – Volume 2”, Chapter 3, guides teachers and schools on how to deal with mathematical content, methodologies to be used, use of technology, organization curriculum and political-pedagogical project.
With this, we will propose some content that can be developed in order to complement the mathematical training of students. After searching in Mathematics Education article databases, such as Bolema and Revemat, and on the Internet, no polar coordinate approaches were found using the GrafEq mathematical software version 2.13, which served as a motivating factor for the elaboration of this work.
2. HOW TO FAVOR THE TEACHING-LEARNING PROCESS IN THE CLASSROOM?
The question that generates the motivation of this work is the following: “Given the difficulty of learning the mathematical content ”transformation of Cartesian coordinate systems into a polar coordinate system“, how can we favor the teaching-learning process in the classroom? ?” The present work starts from the premise that there is a difficulty in learning algebraic mathematical content regarding the transformations of the Cartesian system into polar coordinate systems, and seeks to propose an approach that aims to facilitate this learning and that it intends to be answered in this work. This theme, although foreseen in the PCNs, is still absent in high school classes, appearing only at the university in the first periods of the exact sciences and related subjects. Making transformations has always been a problem in the teaching of mathematics, because once the student gets used to a universe, mathematics comes and takes him to another with more possibilities.
The student is challenged to expand the abstraction, is led to novelty and this generates discomfort. The concept of coordinate system transformations is widely used in mathematics and forms the basis of computer systems, with emphasis on Linear Algebra in Computer Graphics.
In order to find the answer to this question, this work carries out a bibliographical research based on the theories of constructivist-interactionist learning, the use of educational software as a didactic resource and finally proposes the use in the classroom of the GrafEq 2.13 mathematical software as an aid in the teaching the content of polar coordinate systems.
3. MATHEMATICAL EDUCATION AND COMPUTATIONAL TECHNOLOGY
It is true to say that information and communication technologies have been increasingly introduced in education, which requires students to have a new vision and attitude in the ways of conceiving and working with the proposed problems, requiring new cognitive strategies to solve them a problem. It is also necessary to mention the importance of teacher training in this process. For Valente (1999, p. 19) “the issue of teacher training is shown to be of fundamental importance in the process of introducing information technology into education, demanding innovative solutions and new approaches that underlie the training courses”.
Stahl (2008, p. 307), mentions that “education requires a different approach in which the technological component cannot be ignored”. Teachers need to understand that society’s entry into the information age requires skills that have not been developed at school, and that the ability of new technologies to provide individual and independent knowledge acquisition implies a more demanding curriculum, challenges the traditional curriculum and the prevailing educational philosophy, and it is up to them to carry out the necessary changes (STAHL, 2008).
According to Papert (1994), the teaching of mathematics can free itself from the pedagogy of training and turn to the formation of man as a thinking and creative being. Mathematical software appears as a proposal for a complementary means for the teaching-learning process.
According to Vieira (1999), educational software can also be classified according to the student’s level of learning as:
- Sequential – where the objective is the transfer of information, presentation of contents and passive posture of the student;
- Relational – where the objective is to acquire certain skills, it allows the student to relate to other facts or other information;
- Creative – where it is related to the creation of new mental schemes, enabling interaction between people and technology, a more participatory and active posture of the student.
Mathematics education is strongly influenced by technological advances, since ICT resources can help with students’ learning difficulties, in addition to proposing a new dynamic in mathematics teaching. Students in general have difficulties in relation to the learning process, often caused by lack of motivation or classes unrelated to everyday life. Considering these factors, this work analyzed the use of GrafEq 2.13 mathematical software as an aid in mathematics learning, having as content proposal the concept of polar coordinates, presenting it as an alternative to make classes more pleasant for students.
In the words of Baranauskas et al. (1999) computer technology has changed the practice of almost all activities, from scientific to business to business. And educational content and practice also follow this trend. We can say that the creation of computer systems for educational purposes has followed the history and evolution of computers.
“The great challenge is to find options that will contribute to overcoming the difficulties encountered by teachers and students in the teaching and learning of Mathematics” (SOUZA, 2001, p. 24).
Pedagogically speaking, the use of computerized environments, using educational software previously evaluated by the teacher, accompanied by constructive and evolutionary didactics, can be an interesting solution to the various learning problems at different levels. (MAGEDANZ, 2004)
For the teacher, the use of educational software enables a greater understanding of the contents by the students distinguishing those that lend themselves more to work aimed at testing knowledge from those that seek to get the student to interact with the program in order to build knowledge. (PCN, BRAZIL, 1997)
The choice of GrafEq 2.13 software was due to the fact that it is a free program, with easy access, in which it is possible to build graphs and geometric figures using equations, inequalities and numerical intervals, using Cartesian or polar coordinates.
A motivating factor was also the fact that there are still no published articles relating the use of the GrafEq 2.13 mathematical software with the concept of transformations in polar coordinates. “In constructions with GrafEq, the concepts of function, equation, inequality and their graphic representations are necessary, […]” (GRAVINA; BASSO, 2012, p. 113).
As a consequence, it becomes a good alternative for the teaching-learning process, due to all the possibilities and functions that this program provides. According to Valente (1994 and 1999), the use of the computer in education aims at its integration in the process of learning curricular concepts in all modalities and levels of education, being able to play a role of facilitator between the student and the construction of his knowledge.
The author defends the importance of opening the mind to new computational approaches in order to improve the quality of the classes taught. It also seeks through this work to propose a way to be explored by the teacher in the visual treatment of mathematical concepts and structures for a better presentation of mathematical content for students.
4. MATERIALS AND METHODS
This work consists of a bibliographical research about the learning theories that support the theme, as well as the investigative study of the GrafEq 2.13 mathematical software, its potential and its application in the teaching of mathematics for the content of polar coordinate systems. The research also addresses the means of working with educational software as a didactic resource in mathematics classes.
According to Fonseca (2002) apud Gerhardt and Silveira (2009),
A pesquisa bibliográfica é feita a partir do levantamento de referências teóricas já analisadas, e publicadas por meios escritos e eletrônicos, como livros, artigos científicos, páginas de web sites. Qualquer trabalho científico inicia-se com uma pesquisa bibliográfica, que permite ao pesquisador conhecer o que já se estudou sobre o assunto. Existem porém pesquisas científicas que se baseiam unicamente na pesquisa bibliográfica, procurando referências teóricas publicadas com o objetivo de recolher informações ou conhecimentos prévios sobre o problema a respeito do qual se procura a resposta (FONSECA, 2002, p. 32 apud GERHARDT e SILVEIRA, 2009, p. 37).
When conjecturing the theme, the research started looking for materials/articles that could serve as a basis and reference for the research project, with this it was possible to identify which are the important points to be worked on during the research, as well as the structure that the work should follow. This provided the student researcher with a theoretical contribution in order to base their work. The bibliographic research was based on studies about the use of educational software in the teaching of mathematics.
In this way, a search was made for scientific articles, dissertations and websites that dealt with the topic in question. From the reading of the materials considered relevant for the work, the theoretical foundation was constituted. The results obtained will be presented in four stages, in which we will, at first, talk about the theories of learning that support the theme, what are educational software, then about their use as a didactic resource in the teaching of mathematics, and finally, how to work with the GrafEq 2.13 mathematical software to help teach the content of polar coordinate systems for secondary and higher education.
This work and research proposal intends to establish an action plan that favors the teaching-learning process in the classroom for the specific theme “learning in polar coordinates”.
All activities can be developed with some knowledge about functions and content exposed in elementary school. In addition, knowledge is also related to numerical sets, representation of points in the Cartesian plane and basic rules of algebra.
The teacher, in turn, should learn the main commands of the GrafEq software, which can be done by reading some tutorials available on the internet and which will be referenced later.
We know that the methodology used in the classroom to teach mathematical content is one of the most important resources to ensure that the student effectively learns them.
The development of the first activity using GrafEq aims to build a circle in both Cartesian and Polar systems. The student will be able with this example to have an intuitive notion of the polar system and will see how easy this transformation is.
To carry out the second activity, we propose another problem-situation. In this situation, the objective is to know the general equation of the spiral and build its graph.
The third activity will be developed with the aim of exploring and introducing the study of a category of curves called rosacea, knowing its general equation and building its graph.
The fourth activity presents a category of curves called cardioids, which are so named because they are shaped like a heart.
In the first two problems, students will have the opportunity to discuss the graphic representation of situations and thus develop their creativity and criticality.
Next, we will begin to explore the graphic representation of different types of functions in polar coordinates, with the objective of making the student perceive the relationship between the law of formation and its graphic representation, highlighting the property that characterizes this type of function and some important aspects related to their coefficients.
By allowing the computer to generate a graphic on the screen through the tool, and being able to modify this graphic as many times as you want and test possibilities, the activity becomes more pleasant and enriching for the student, as it provides opportunities for discovery.
5. ABOUT THE GRAFEQ SOFTWARE
Grafeq software is a software that works with equations and inequalities, in Cartesian and polar coordinates. This Canadian software generates graphs of equations and inequalities of plane figures based on a generalized form of interval arithmetic developed by Jeff Tupper. “Tupper’s arithmetic”, as it is called, is masterfully exposed in his thesis Graphing Equations with Generalized Interval Arithmetic (available on his personal page). Using GrafEq4 does not require any knowledge of interval arithmetic, but it is interesting to read Tupper’s beautiful work as an important example of how abstraction and mathematical sophistication can produce practical results.
6. A PROPOSAL FOR THE TEACHING OF POLAR COORDINATES
In this chapter we present a didactic sequence aiming to use different activities for the introduction and development of the study of polar coordinates for students of the 3rd year of high school. The questions present in this proposal aim to ensure that the student is part of the knowledge construction process. The teacher thus has the role of leading the activities, and doing them in a way that involves the students through debates and questioning, which, we believe, will lead to the scalable development of the concepts that surround the study of polar coordinates and their applications.
7. POLAR COORDINATES
According to the excerpt taken from the Book Cálculo Vetorial e Geometria Analítica, according to the author, we have the following definition for polar coordinates:
Dado o par ordenado 
de números reais, com 
, o par 
, com 
, é dito uma representação de em coordenadas polares. Costuma-se dizer, embora 
esteja definido apenas a menos de um múltiplo inteiro de 
, que 
são as “coordenadas polares” de . (ACKER, 2016, p.103)
Example:
Figure 1 – Cartesian coordinates and polar coordinates
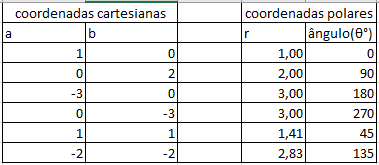
Figure 2 – example chart of Cartesian coordinates
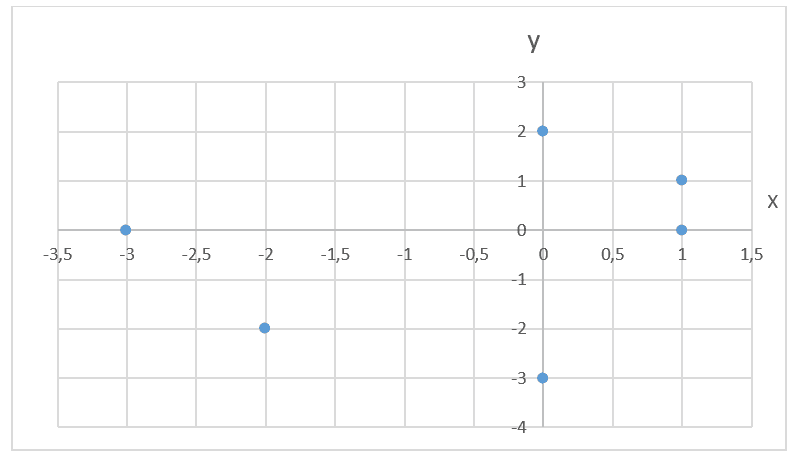
Figure 3 – example graphic of polar coordinates
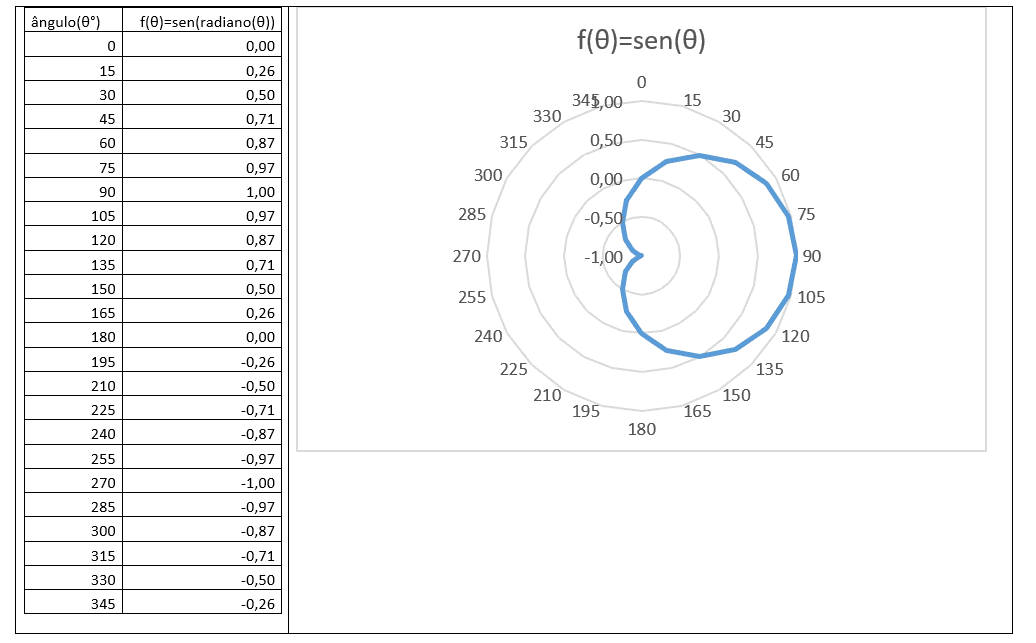
Figure 4 – polar axis
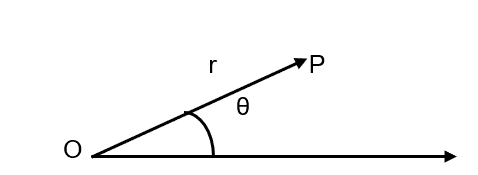
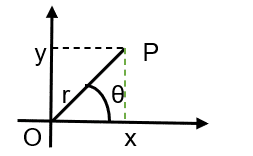
The fixed point O is called the pole, and the ray is called the polar axis.
It is worth remembering that the same point 
does not refer only to an ordered pair, but to a class of ordered pairs.
Example 1: 
Figure 5 – example 1
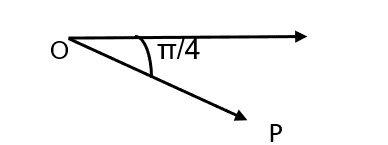
We denote P by 
, for
positive, if 
, that is, we consider
. So, 
is the symmetric of 
in relation to the pole.
Figure 6 – symmetry
Example 2: 
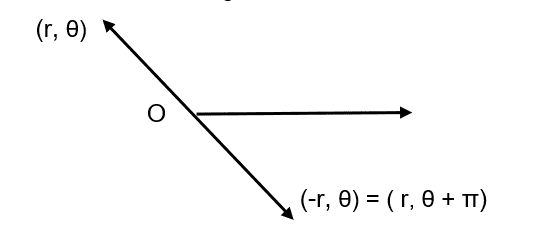
Figure 7 – example 2
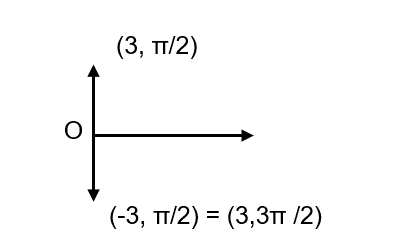
Note that an angle θ can be represented by 
, for every integer k. Thus, 
Example. 
8. CHANGE OF COORDINATES
Let us consider a point P in the plane, we can represent this point in Cartesian coordinates by 
or by 
, in polar coordinates. For simplicity, let’s consider the point O coinciding with the origin of the Cartesian system and the non-negative part of the x axis will represent the ray.
Performing the transformation from polar coordinates to Cartesian coordinates.
Given a point P with polar coordinates 
.
For 
and 
.
We obtain the following relations on the right triangle OPx.
Figure 8 – change of coordinates
and
b) Performing the transformation from Cartesian coordinates to polar coordinates
Given a point P, with Cartesian coordinates 
. As we saw above, considering P with coordinates 
, we have the relations 
and 
.
Since 
= r², we have that 
If 
, that is, 
then we can take any.
If 
is such that 
and sin 
.
Example:
If P has polar coordinates 
, then 
and 
.
With this, 
and 
, hence it follows that P has Cartesian coordinates
Example:
With P having Cartesian coordinates 
then 
, that is, 
Since cos 
and sin 
, then 
.
So it turns out that P has polar coordinates: 
9. FIRST ACTIVITY
The first activity in our sequence seeks to introduce students to an intuitive idea of the concept of polar coordinates.
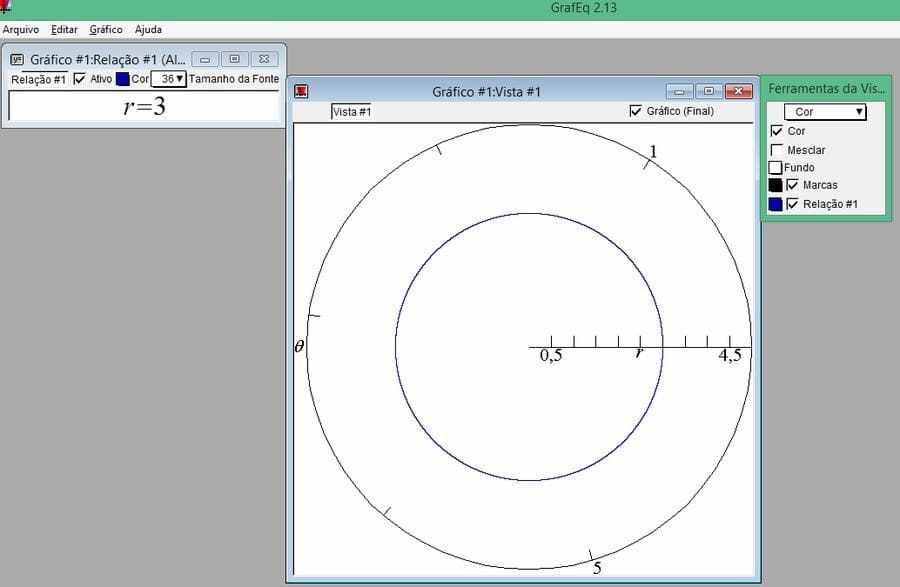
Example. The circle with center at the origin and radius 3 has Cartesian equation
. As 
and 
, then 
, that is, 
is the polar equation of this circumference.
Using GrafEq to plot the quoted circle in both coordinate systems:
In the Cartesian coordinate system:
Figure 9 – Circumference of radius r = 3
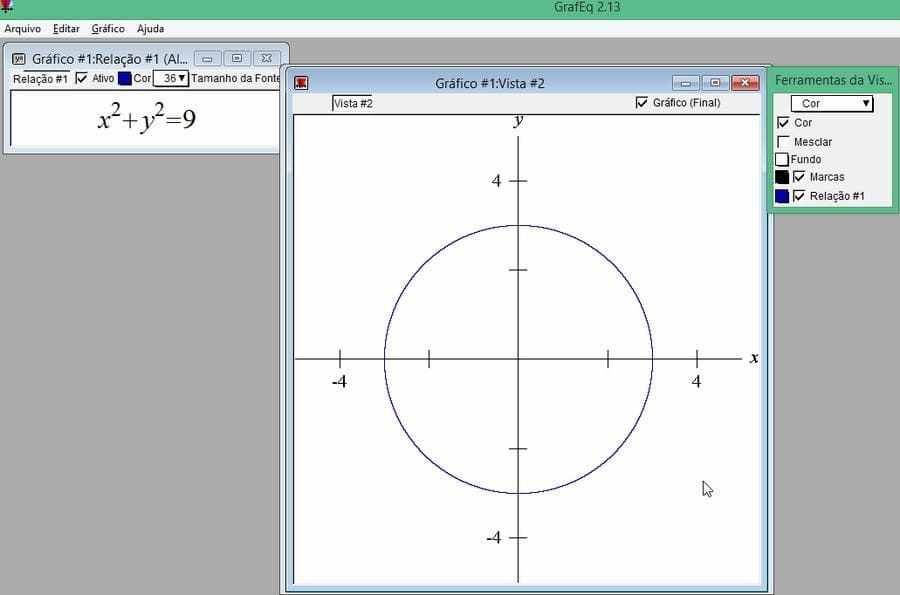
Figure 10 – Circumference of radius r = 3, in polar coordinates.
10. SECOND ACTIVITY
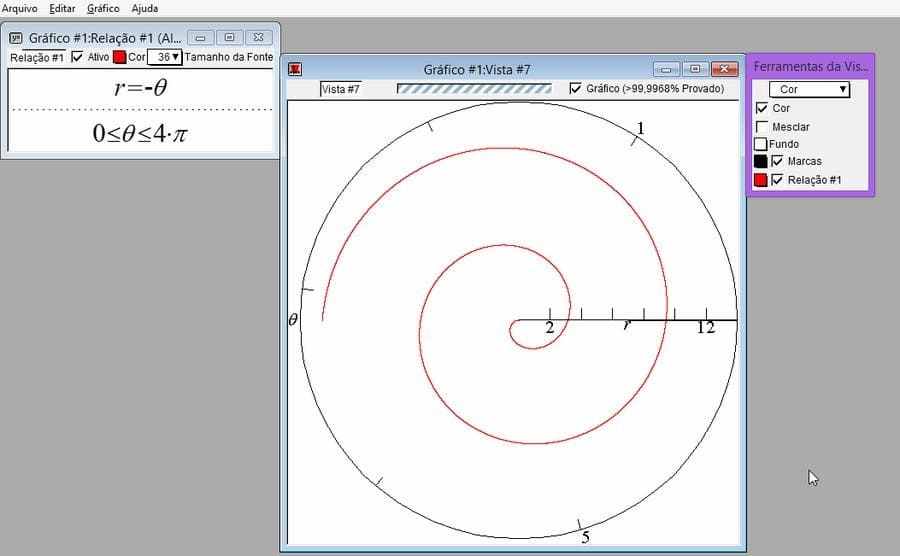
Solve in polar coordinates the graph of 
.
The graph of 
concerns the points 
where 
, that is, all points P, where we have the distance from P to the pole equal to the angle
itself, in radians, between the segment OP and the polar axis. The general equation of the spiral will be given by 
, where 
and a integer.
Using GrafEq plot the graphs of 
and 
, for 
.
Response:
Tooltip: Configuring GrafEq for Polar Style:
Figure 11-New View menu item
Figure 12-Caption
Tip: Double clicking on the formula opens the quick buttons box.
Figure 13-Quick buttons
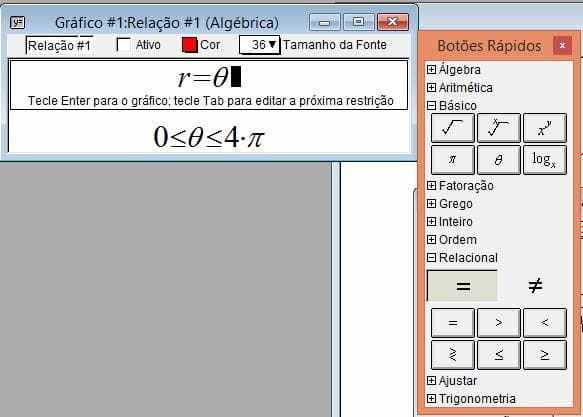
Figure 14-Solution 1-a
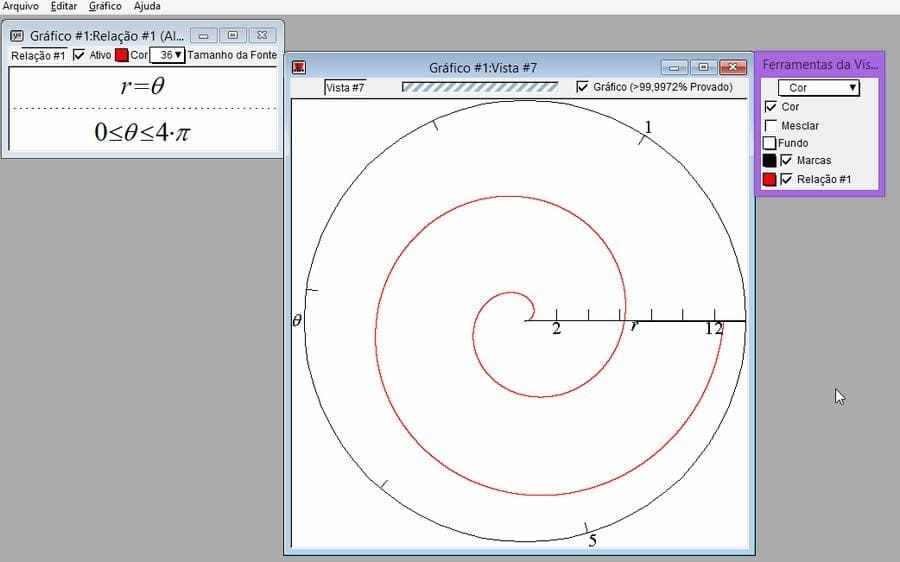
Figure 15-Solution 1-b
11. THIRD ACTIVITY
Using GrafEq, solve in polar coordinates the graph of 
Solution:
Figure 16-Rosacea
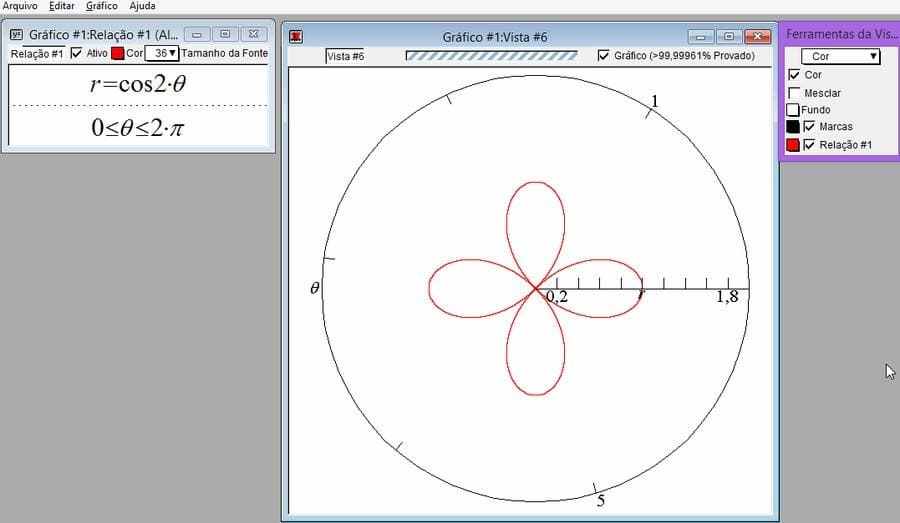
Note that every equation of the type 
or 
for any integer and positive n, represents the set of curves of type rosettes.
12. FOURTH ACTIVITY
Knowing the Cardioids
Using GrafEq, solve the graph of 
, 
Figure 17-Cardioid
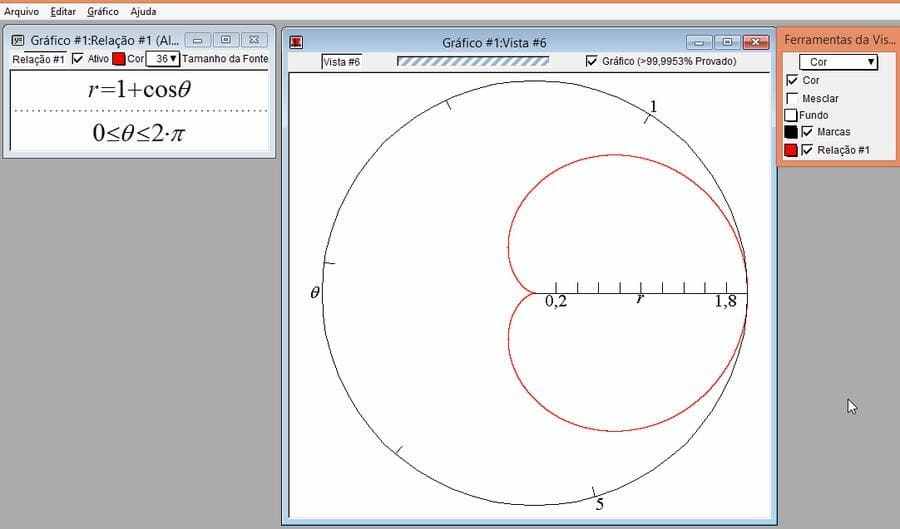
Note that every equation of the type 
or
represents a set of cardioid-like curves, so called because they have the shape of a heart.
13. FINAL CONSIDERATIONS
The present work had the objective of elaborating a proposal for the introduction of exploration of concepts present in the study of polar coordinates with a focus on the learning of high school students and perhaps the first year of higher education in the exact sciences chairs.
We believe that the proposal presented here meets these needs and can contribute to the appropriation of mathematical knowledge by students. This belief can be based on the methodological choices and on the approach in which the activities were designed. The choice of software and the problem solving methodology allowed a greater exploration of the aspects involved in the study of polar coordinate systems in an attractive and significant way.
This proposal is an approach to teaching polar coordinates subject to corrections and adaptations. During the structuring of activities, we realized that a simple problem-situation could generate a great opportunity for the development of the school contents discussed here. So, we understand that many of the suggested and expected changes for the teaching of mathematics can arise from simple ideas added to the teacher’s disposition to face new challenges and try to experiment with new methodologies and differentiated strategies.
Nowadays, more and more schools are taking advantage of computers and information and communication technologies. The teacher, in this context, must seek to prepare himself to use these resources in order to take advantage of teaching and also to contribute as a mediator in the teaching-learning process and ensure that these strategies promote the learning of new knowledge. Our proposal fits perfectly into this perspective.
Finally, we hope that this work can contribute to the teaching of mathematics with a focus on teaching polar coordinates. And in addition to offering teachers a new methodology for teaching polar coordinates, our proposal also aims to provide a moment of reflection on pedagogical practice and the search for alternatives to improve education through mathematics.
14. REFERENCES
ALMEIDA, FJ; Fonseca Junior, F.M. Projetos e ambientes inovadores. Brasília: Secretaria de Educação a Distância – Seed/ Proinfo- Ministério da Educação, 2000.
ACKER, Felipe. Cálculo Vetorial e Geometria Analítica: Livro 1: O Plano. Instituto de Matemática, UFRJ, Rio de Janeiro, 2016. Disponível em http://www.im.ufrj.br/cvga/problemas/exercicios/oplanolista1.pdf. Acesso em 03 de Setembro de 2020.
BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais – Ensino Médio. Brasília. Ministério da Educação, 2002.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 3.ed. Belo Horizonte: Autêntica, 2007.
CAMPOS, Márcia de Borba. Construtivismo. Disponível em http://penta.ufrgs.br / marcia/piaget.htm Acesso em 28 de Setembro de 2016.
DUARTE, Sinara. Fazendo as pazes com o bicho papão: A Matemática e o SL. In: Revista Espírito Livre, n.002, p. 74-78, maio. 2009. 89 p.
GERHARDT, T. E. & SILVEIRA, D. T. Métodos de pesquisa. 1. ed. Porto Alegre: UFRGS, 2009.
GRAVINA, Maria Alice. . . [et al.]. Matemática, Mídias Digitais e Didática: tripé para a formação de professores. Porto Alegre: Evangraf, 2012.
MAGEDANZ, Adriana. Computador: Ferramenta de trabalho no Ensino (de Matemática). 2004. 14f. Curso de Pós-Graduação Lato Sensu. Especialização em ensino de Matemática – UNIVATES – Centro Universitário, Lajeado, 2004. Disponível em http://ensino.univates.br/magedanza/pos/artigo_final_adriana_magedanz.pdf Acesso em 29 de Setembro de 2016.
PAPERT, Seymour. A máquina das crianças: repensando a escola na era digital. Porto Alegre: Artes Médicas, 1994.
PIAGET, Jean. Seis estudos de psicologia. Trad. Maria Alice Magalhães D’Amorim e Paulo Sérgio Lima Silva. Rio de Janeiro: Forense, 1964.
STAHL, Marimar M. A formação de professores para o uso das novas tecnologias de comunicação e informação. In: CANDAU, Vera Maria (org). Magistério: construção cotidiana. 6 ed. Petrópolis, RJ: Vozes, 2008. p. 292-317.
SILVA, José Orlando. FERNANDES, Natal Lania Roque. Tecnologias da Informação e Comunicação na Educação de Jovens e Adultos. Disponível em http://portal.mec.gov.br/setec/arquivos/pdf3/tcc_tecnologias.pdf. Acesso em 29 de Setembro de 2016.
VALENTE, José Armando (org). O computador na sociedade do conhecimento. Campinas: UNICAMP/NIED, 1999.
VIEIRA, F. (1999) Avaliação de software Educativo: Reflexões para uma análise Criteriosa.
APPENDIX – FOOTNOTE
2. National Curriculum Parameters.
[1] Bachelor in Informatics/Computer Science – UFRJ. Degree in Mathematics – Estácio de Sá University – UNESA – RJ. MBA in IT Management – Polytechnic School of UFRJ.
Sent: August, 2020.
Approved: September, 2020.
