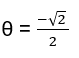ARTICLE ORIGINAL
RAMOS, Gilberto Pereira [1]
RAMOS, Gilberto Pereira. Proposition d’enseignement des coordonnées polaires à l’aide du Software GrafEq. Revista Científica Multidisciplinar Núcleo do Conhecimento. Année 05, Éd. 09, Vol. 04, p. 35-75. Septembre 2020. ISSN : 2448-0959, lien d’accès: https://www.nucleodoconhecimento.com.br/education-fr/coordonnees-polaires
RÉSUMÉ
Ce travail vise à présenter une proposition d’introduction et d’exploration des principaux concepts présents dans l’étude des coordonnées polaires, qui fait partie du contenu du cours de Mathématiques du Lycée selon les PCNs[2]. Cette proposition a été élaborée à partir de la vérification, par des études préalables, de l’existence de difficultés liées à la compréhension et à l’apprentissage des concepts associés à ce thème. Compte tenu de l’importance de l’étude des coordonnées polaires dans le programme scolaire et dans la compréhension des phénomènes naturels et dans les différents domaines scientifiques, les activités qui composent cette proposition sont basées sur l’idée que l’apprentissage se fait à travers un processus de construction des connaissances. De plus, estimant que la contextualisation des contenus contribue à l’apprentissage significatif des mathématiques, ce travail propose une séquence d’activités qui, basée sur des problèmes réels, entend explorer les principaux concepts présents dans l’étude du système de coordonnées polaires. Pour aider les élèves à résoudre des problèmes et à explorer ces concepts, nous utilisons le Software GrafEq. Nous pensons que cette proposition peut contribuer à améliorer la qualité de l’enseignement des mathématiques et plus spécifiquement de l’enseignement des coordonnées polaires. De plus, ce travail peut servir d’inspiration aux professeurs de mathématiques pour la création de nouvelles méthodologies d’enseignement.
Mots clés : GrafEq, Enseignement, Mathématiques, Coordonnées, Polaires.
1. INTRODUCTION
Le sujet des Software mathématiques est assez difficile et l’utilisation croissante des moyens de calcul comme outil pour l’enseignement des mathématiques le rend d’une grande pertinence pour le processus d’enseignement-apprentissage de nos jours. En plus de ce facteur de motivation, j’ai également été amené à réfléchir au sujet lors du cours d’informatique dans l’éducation, l’un des sujets du programme du cours de mathématiques de l’Universidade Estácio de Sá, où certains outils d’aide à l’enseignement et à l’apprentissage des mathématiques ont été présentés. En approfondissant mes recherches sur le sujet, j’ai découvert l’outil GrafEq, qui aide au traitement visuel des concepts et des structures algébriques mathématiques. J’étais intéressé à travailler sur le thème ‘coordonnées polaires’ car il est encore peu présent dans les classes de lycée et car je n’ai pas trouvé dans mes recherches le rapport entre le contenu proposé et l’outil approprié. Par conséquent, j’introduis ce travail en prenant cette approche pédagogique avec impulsion et le fait que cette proposition pédagogique est adéquate aux orientations des PCN.
Le Ministère de l’Éducation nationale (MEC) à travers le document intitulé “Paramètres du curriculum national – Lycée (PCNEM) – Volume 2”, chapitre 3, guide les enseignants et les écoles sur la manière d’aborder le contenu mathématique, les méthodologies à utiliser, l’utilisation de la technologie, organisation curriculaire et projet politico-pédagogique.
Sur ce, nous proposerons quelques contenus qui pourront être développés afin de compléter la formation mathématique des étudiants. Après une recherche dans les bases de données d’articles sur l’enseignement des mathématiques, telles que Bolema et Revemat, et sur Internet, aucune approche de coordonnées polaires n’a été trouvée à l’aide du Software mathématique GrafEq version 2.13, ce qui a servi de facteur de motivation pour l’élaboration de ce travail.
2. COMMENT FAVORISER LE PROCESSUS D’ENSEIGNEMENT-APPRENTISSAGE EN CLASSE ?
La question qui génère la motivation de ce travail est la suivante : “Compte tenu de la difficulté d’apprentissage du contenu mathématique “transformation des systèmes de coordonnées cartésiennes en un système de coordonnées polaires”, comment peut-on favoriser le processus d’enseignement-apprentissage en classe ? ?” Le présent travail part du postulat qu’il y a une difficulté à apprendre le contenu mathématique algébrique concernant les transformations du système cartésien en systèmes de coordonnées polaires, et cherche à proposer une approche qui vise à faciliter cet apprentissage et qui entend répondre dans ce travailler. Ce thème, bien que prévu dans les PCN, est encore absent dans les classes du secondaire, n’apparaissant qu’à l’université dans les premières périodes des sciences exactes et matières apparentées. Faire des transformations a toujours été un problème dans l’enseignement des mathématiques, car une fois que l’élève s’est habitué à un univers, les mathématiques viennent l’emmener dans un autre avec plus de possibilités.
L’étudiant est mis au défi d’élargir l’abstraction, est amené à la nouveauté et cela génère un malaise. Le concept de transformations de systèmes de coordonnées est largement utilisé en mathématiques et constitue la base des systèmes informatiques, en mettant l’accent sur l’algèbre linéaire en infographie.
Afin de trouver la réponse à cette question, ce travail réalise une recherche bibliographique basée sur les théories de l’apprentissage constructiviste-interactionniste, l’utilisation des Softwares pédagogiques comme ressource didactique et propose enfin l’utilisation en classe du Software mathématique GrafEq 2.13 comme aide à l’enseignement du contenu des systèmes de coordonnées polaires.
3. ENSEIGNEMENT MATHÉMATIQUE ET TECHNOLOGIE INFORMATIQUE
Il est vrai de dire que les technologies de l’information et de la communication sont de plus en plus introduites dans l’enseignement, ce qui oblige les élèves à avoir une nouvelle vision et attitude dans les façons de concevoir et de travailler avec les problèmes proposés, nécessitant de nouvelles stratégies cognitives pour résoudre un problème. Il faut également mentionner l’importance de la formation des enseignants dans ce processus. Pour Valente (1999, p. 19) « la question de la formation des enseignants se révèle être d’une importance fondamentale dans le processus d’introduction des technologies de l’information dans l’éducation, exigeant des solutions innovantes et de nouvelles approches qui sous-tendent les cours de formation ».
Stahl (2008, p. 307), mentionne que « l’éducation nécessite une approche différente dans laquelle la composante technologique ne peut être ignorée ». Les enseignants doivent comprendre que l’entrée de la société dans l’ère de l’information nécessite des compétences qui n’ont pas été développées à l’école, et que la capacité des nouvelles technologies à fournir une acquisition de connaissances individuelle et indépendante implique un programme plus exigeant, remet en question le programme traditionnel et la philosophie éducative dominante , et c’est à eux d’opérer les changements nécessaires (STAHL, 2008).
Selon Papert (1994), l’enseignement des mathématiques peut s’affranchir de la pédagogie de l’apprentissage et se tourner vers la formation de l’homme en tant qu’être pensant et créateur. Le Software mathématique apparaît comme une proposition de médium complémentaire pour le processus d’enseignement-apprentissage.
Selon Vieira (1999), les Softwares éducatifs peuvent également être classés selon le niveau d’apprentissage de l’élève comme suit :
- Séquentiel – où il vise le transfert d’informations, la présentation de contenus et la posture passive de l’étudiant;
- Relationnel – où il vise à acquérir certaines compétences, permet à l’élève de se rapporter à d’autres faits ou à d’autres informations;
- Créatif – où il est lié à la création de nouveaux schémas mentaux, permettant une interaction entre les personnes et la technologie, une posture plus participative et active de l’étudiant.
L’enseignement des mathématiques est fortement influencé par les avancées technologiques, puisque les ressources TIC peuvent venir en aide aux difficultés d’apprentissage des élèves, en plus de proposer une nouvelle dynamique dans l’enseignement des mathématiques. Les étudiants ont en général des difficultés par rapport au processus d’apprentissage, souvent causées par un manque de motivation ou des cours sans rapport avec la vie quotidienne. Compte tenu de ces facteurs, ce travail a analysé l’utilisation du Software mathématique GrafEq 2.13 comme aide à l’apprentissage des mathématiques, ayant comme proposition de contenu le concept de coordonnées polaires, le présentant comme une alternative pour rendre les cours plus agréables pour les élèves.
Selon les termes de Baranauskas et al. (1999) la technologie informatique a changé la pratique de presque toutes les activités, du scientifique au commercial en passant par le commercial. Et les contenus et pratiques pédagogiques suivent également cette tendance. On peut dire que la création de systèmes informatiques à des fins éducatives a suivi l’histoire et l’évolution des ordinateurs.
« Le grand défi est de trouver des options qui contribueront à surmonter les difficultés rencontrées par les enseignants et les élèves dans l’enseignement et l’apprentissage des mathématiques » (SOUZA, 2001, p. 24).
Sur le plan pédagogique, l’utilisation d’environnements informatisés, utilisant des Softwares pédagogiques préalablement évalués par l’enseignant, accompagnés d’une didactique constructive et évolutive, peut être une solution intéressante aux différents problèmes d’apprentissage à différents niveaux. (MAGEDANZ, 2004)
Pour l’enseignant, l’utilisation de software pédagogiques permet une meilleure compréhension des contenus par les élèves, Quant aux softwares pédagogiques, il est essentiel que l’enseignant apprenne à les choisir en fonction des objectifs qu’il veut atteindre et de sa propre conception du savoir et de l’apprentissage, en distinguant ceux qui se prêtent davantage à des travaux visant à tester des connaissances de ceux qui cherchent à amener l’étudiant à interagir avec le programme afin de construire des connaissances. (PCN, BRASIL, 1997)
Le choix du software GrafEq 2.13 a été dû au fait qu’il s’agit d’un programme gratuit, d’accès facile, dans lequel il est possible de construire des graphiques et des figures géométriques à l’aide d’équations, d’inéquations et d’intervalles numériques, en utilisant des coordonnées cartésiennes ou polaires.
Un facteur de motivation a également été le fait qu’il n’y a toujours pas d’articles publiés concernant l’utilisation du software mathématique GrafEq 2.13 avec le concept de transformations en coordonnées polaires. « Dans les constructions avec GrafEq, les notions de fonction, d’équation, d’inégalité et leurs représentations graphiques sont nécessaires, […] » (GRAVINA ; BASSO, 2012, p. 113).
En conséquence, il devient une bonne alternative pour le processus d’enseignement-apprentissage, en raison de toutes les possibilités et fonctions que ce programme offre. Selon Valente (1994 et 1999), l’utilisation de l’ordinateur dans l’éducation vise à son intégration dans le processus d’apprentissage des concepts curriculaires dans toutes les modalités et tous les niveaux d’enseignement, pouvant jouer un rôle de facilitateur entre l’élève et la construction de sa connaissance.
L’auteur défend l’importance d’ouvrir l’esprit aux nouvelles approches computationnelles afin d’améliorer la qualité des cours dispensés. Il cherche également à travers ce travail à proposer une voie à explorer par l’enseignant dans le traitement visuel des concepts et des structures mathématiques pour une meilleure présentation des contenus mathématiques aux élèves.
4. MATÉRIAUX ET MÉTHODES
Ce travail consiste en une recherche bibliographique sur les théories d’apprentissage qui soutiennent le thème, ainsi que l’étude d’investigation du software mathématique GrafEq 2.13, son potentiel et son application dans l’enseignement des mathématiques pour le contenu des systèmes de coordonnées polaires. La recherche porte également sur les moyens de travailler avec des softwares éducatifs comme ressource didactique dans les cours de mathématiques.
Selon Fonseca (2002) apud Gerhardt et Silveira (2009),
A pesquisa bibliográfica é feita a partir do levantamento de referências teóricas já analisadas, e publicadas por meios escritos e eletrônicos, como livros, artigos científicos, páginas de web sites. Qualquer trabalho científico inicia-se com uma pesquisa bibliográfica, que permite ao pesquisador conhecer o que já se estudou sobre o assunto. Existem porém pesquisas científicas que se baseiam unicamente na pesquisa bibliográfica, procurando referências teóricas publicadas com o objetivo de recolher informações ou conhecimentos prévios sobre o problema a respeito do qual se procura a resposta (FONSECA, 2002, p. 32 apud GERHARDT e SILVEIRA, 2009, p. 37).
Lors de la conjecture du thème, la recherche a commencé à chercher des matériaux/articles qui pourraient servir de base et de référence pour le projet de recherche, avec cela il a été possible d’identifier quels sont les points importants à travailler au cours de la recherche, ainsi que les structure que le travail doit suivre. Cela a fourni à l’étudiant chercheur un apport théorique afin de soutenir son travail. La recherche bibliographique s’est appuyée sur des études portant sur l’utilisation de softwares éducatifs dans l’enseignement des mathématiques.
Ainsi, une recherche d’articles scientifiques, de thèses et de sites Web traitant du sujet en question a été effectuée. A partir de la lecture des matériaux jugés pertinents pour le travail, le fondement théorique a été constitué. Les résultats obtenus seront présentés en quatre étapes, au cours desquelles nous parlerons, dans un premier temps, des théories de l’apprentissage qui soutiennent le thème, de ce que sont les softwares éducatifs, puis de leur utilisation comme ressource didactique dans l’enseignement des mathématiques, et enfin , comment travailler avec le software mathématique GrafEq 2.13 pour aider à enseigner le contenu des systèmes de coordonnées polaires pour l’enseignement secondaire et supérieur.
Cette proposition de travail et de recherche vise à établir un plan d’action favorisant le processus d’enseignement-apprentissage en classe pour le thème spécifique « apprentissage en coordonnées polaires ».
Toutes les activités peuvent être développées avec quelques connaissances sur les fonctions, les contenus exposés à l’école élémentaire. De plus, la connaissance est également liée aux ensembles numériques, à la représentation des points dans le plan cartésien et aux règles de base de l’algèbre.
L’enseignant, à son tour, doit apprendre les principales commandes du software GrafEq, ce qui peut se faire en lisant quelques tutoriels disponibles sur internet et qui seront référencés plus tard.
Nous savons que la méthodologie utilisée en classe pour enseigner le contenu mathématique est l’une des ressources les plus importantes pour s’assurer que l’élève l’apprend efficacement.
Le développement de la première activité utilisant GrafEq vise à construire un cercle dans les systèmes cartésien et polaire. L’étudiant pourra avec cet exemple avoir une notion intuitive du système polaire et verra à quel point cette transformation est facile.
Pour réaliser la deuxième activité, nous proposons une autre situation-problème. Dans cette situation, l’objectif est de connaître l’équation générale de la spirale et de construire son graphique.
La troisième activité sera développée dans le but d’explorer et d’introduire l’étude d’une catégorie de courbes appelées rosettes, en connaissant son équation générale et en construisant son graphe.
La quatrième activité présente une catégorie de courbes appelées cardioïdes, ainsi nommées parce qu’elles ont la forme d’un cœur.
Dans les deux premiers problèmes, les élèves auront l’occasion d’aborder la représentation graphique de situations et ainsi développer leur créativité et leur criticité.
Ensuite, nous commencerons à explorer la représentation graphique de différents types de fonctions en coordonnées polaires, dans le but de faire percevoir à l’étudiant la relation entre la loi de formation et sa représentation graphique, en mettant en évidence la propriété qui caractérise ce type de fonction et certains aspects importants liés à leurs coefficients.
En permettant à l’ordinateur de générer un graphique à l’écran grâce à l’outil, et en pouvant modifier ce graphique autant de fois que l’on veut et tester les possibilités, l’activité devient plus agréable et enrichissante pour l’élève, car elle offre des opportunités de découverte.
5. À PROPOS DU SOFTWARE GRAFEQ
Le software Grafeq est un software qui travaille avec des équations et des inégalités, en coordonnées cartésiennes et polaires. Ce software canadien génère des graphiques d’équations et d’inégalités de figures planes basés sur une forme généralisée d’arithmétique d’intervalle développée par Jeff Tupper. « L’arithmétique de Tupper », comme on l’appelle, est magistralement exposée dans sa thèse Graphing Equations with Generalized Interval Arithmetic (disponible sur sa page personnelle). L’utilisation de GrafEq4 ne nécessite aucune connaissance de l’arithmétique des intervalles, mais il est intéressant de lire le beau travail de Tupper comme un exemple important de la façon dont l’abstraction et la sophistication mathématique peuvent produire des résultats pratiques.
6. UNE PROPOSITION POUR L’ENSEIGNEMENT DES COORDONNÉES POLAIRES
Dans ce chapitre nous présentons une séquence didactique visant à utiliser différentes activités pour l’introduction et le développement de l’étude des coordonnées polaires pour les élèves de la 3e année du secondaire. Les questions présentes dans cette proposition visent à s’assurer que l’étudiant fait partie du processus de construction des connaissances. L’enseignant a donc pour rôle de diriger les activités, et de les faire de manière à impliquer les élèves à travers des débats et des questionnements, ce qui, selon nous, conduira au développement évolutif des concepts qui entourent l’étude des coordonnées polaires et de leurs applications.
7. COORDONNÉES POLAIRES
D’après l’extrait tiré du livre Cálculo Vetorial e Geometria Analítica, selon l’auteur, nous avons la définition suivante pour les coordonnées polaires :
coordonnees-polaires
de números reais, com 
, o par 
, com 
, é dito uma representação de em coordenadas polares. Costuma-se dizer, embora 
esteja definido apenas a menos de um múltiplo inteiro de 
, que 
são as “coordenadas polares” de . (ACKER, 2016, p.103)
Exemple:
Figure 1 – Coordonnées cartésiennes et coordonnées polaires
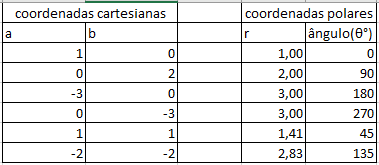
Figure 2 – exemple de carte de coordonnées cartésiennes
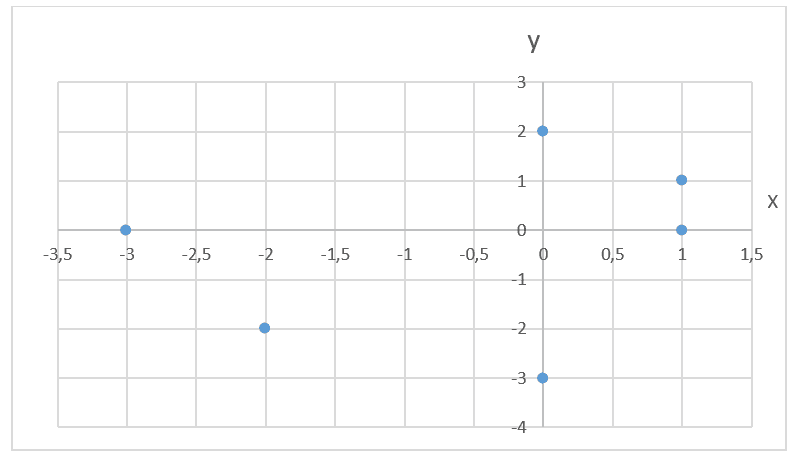
Figure 3 – exemple graphique de coordonnées polaires
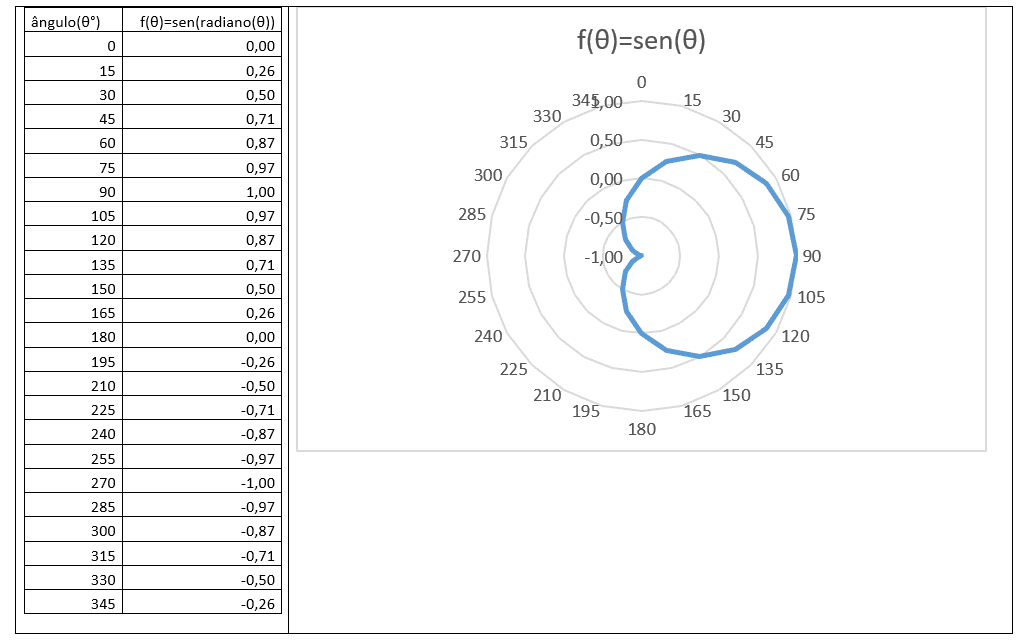
Figure 4 – axe polaire
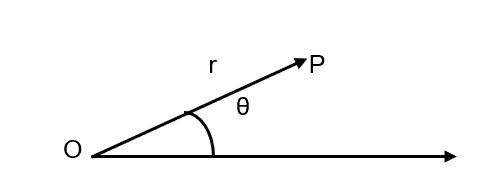
Le point fixe O s’appelle le pôle et le rayon s’appelle l’axe polaire.
Il est bon de rappeler qu’un même point 
ne se réfère pas seulement à un couple ordonné, mais à une classe de couples ordonnés.
Exemple 1 : 
Figure 5 – exemple 1
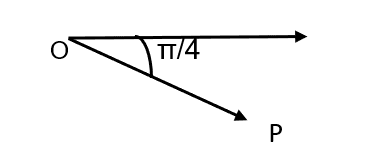
On note P par 
, pour 
positif, si 
, c’est-à-dire que l’on considère 
. Ainsi, 
est le symétrique de 
par rapport au pôle.
Figure 6 – symétrie
Exemple 2 : 
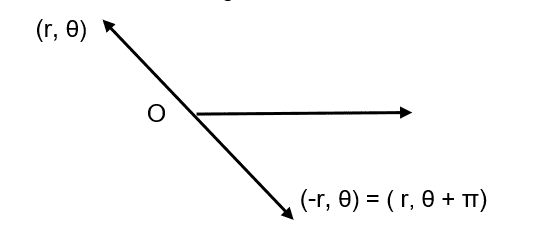
Illustration 7 – exemple 2
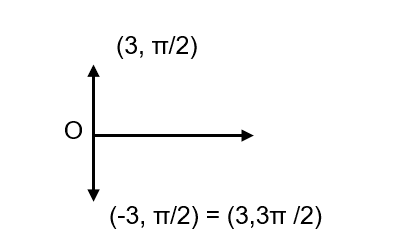
Notez qu’un angle θ peut être représenté par 
, pour tout entier k. Ainsi, 
Exemple. 
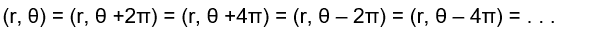
8. CHANGEMENT DE COORDONNEES
Considérons un point P dans le plan, on peut représenter ce point en coordonnées cartésiennes par 
ou par 
, en coordonnées polaires. Pour simplifier, considérons le point O coïncidant avec l’origine du système cartésien et la partie positive de l’axe x représentera le rayon.
- Effectuer la transformation des coordonnées polaires aux coordonnées cartésiennes.
Soit un point P de coordonnées polaires 
.
Pour 
et 
On obtient les relations suivantes sur le triangle rectangle OPx.
Figure 8 – changement de coordonnées
et 
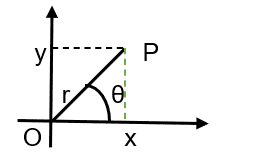
b) Exécution de la transformation de coordonnées cartésien pour les coordonnées polaire.
Soit un point P, de coordonnées cartésiennes
. Comme on l’a vu plus haut, en considérant P de coordonnées 
, on a les relations 
et 
Puisque 
, nous avons 
.
Si 
, c’est-à-dire 
, alors nous pouvons en prendre n’importe lequel.
Si 
est tel que 
et sin 
.
Exemple:
Si P a pour coordonnées polaires 
, alors 
et 
.
Avec cela, 
et 
, d’où il s’ensuit que P a des coordonnées cartésiennes 
Exemple:
Avec P de coordonnées cartésiennes 
alors 
, soit 
Puisque cos 
et sin 
, alors
.
Il s’avère donc que P a pour coordonnées polaires : 
9. PREMIÈRE ACTIVITÉ
La première activité de notre séquence vise à initier les élèves à une idée intuitive du concept de coordonnées polaires.
Exemple. Le cercle de centre à l’origine et de rayon 3 a l’équation cartésienne 
. Comme 
et , alors 
, c’est-à-dire que 
est la polaire équation de cette circonférence.
Utilisation de GrafEq pour tracer le cercle cité dans les deux systèmes de coordonnées :
Dans le système de coordonnées cartésien :
Figure 9 – Circonférence du rayon
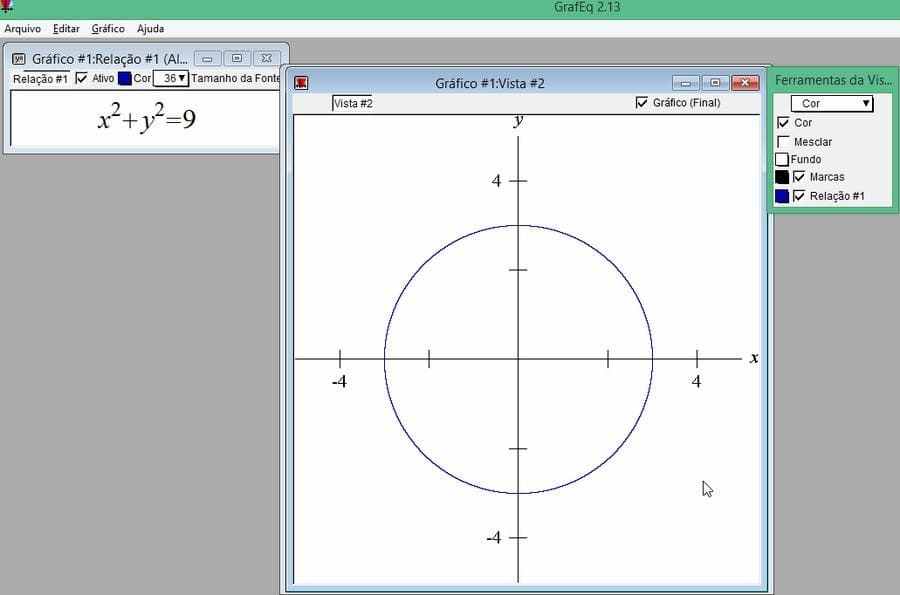
Figure 10 – Circonférence de rayon r = 3, en coordonnées polaires.
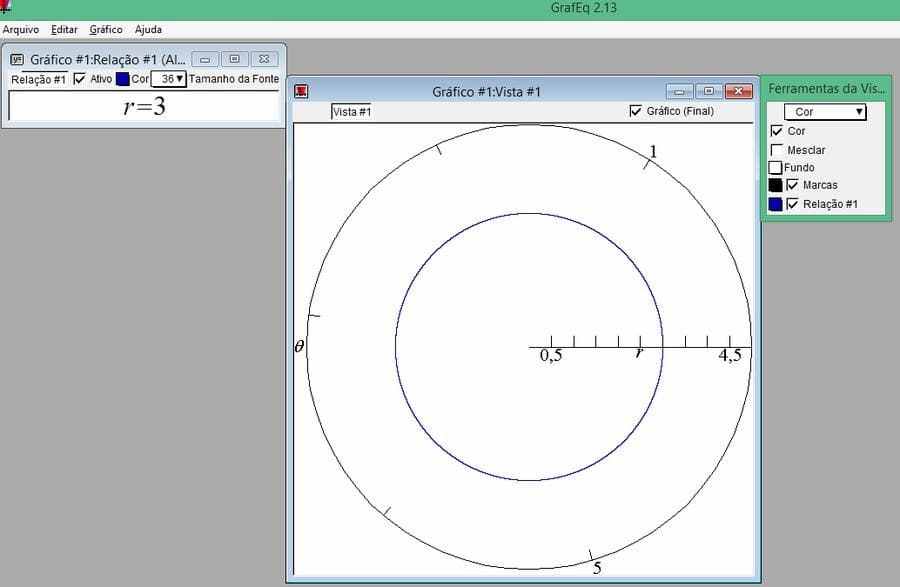
10. DEUXIÈME ACTIVITÉ
Résoudre en coordonnées polaires le graphe de 
.
Le graphe de
concerne les points 
où 
, c’est-à-dire tous les points P, où l’on a la distance de P au pôle égale à l’angle
lui-même, en radians, entre les segment OP et l’axe polaire. L’équation générale de la spirale sera donnée par 
, où 
et un entier.
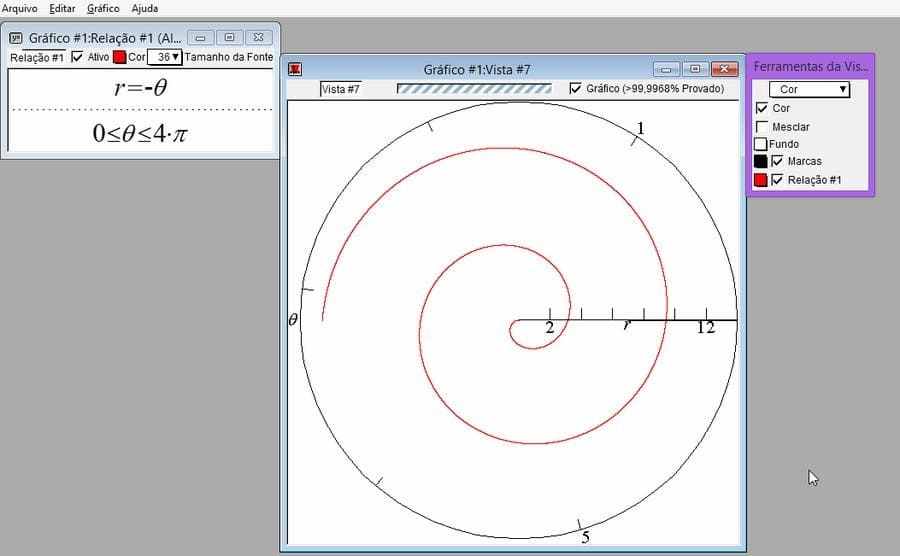
À l’aide de GrafEq, tracez les graphiques de 
et 
, pour 
.
Réponse:
Info-bulle : Configuration de GrafEq pour le style polaire :
Figure 11-élément de menu Nouvelle vue
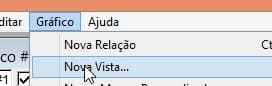
Figure 12-Légende
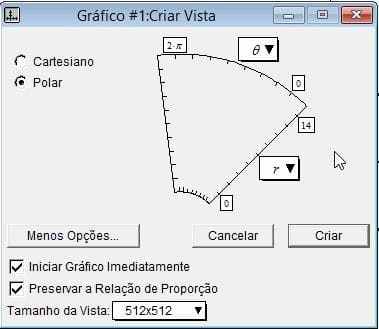
Astuce : un double-clic sur la formule ouvre la boîte des boutons rapides.
Figure 13-Boutons rapides
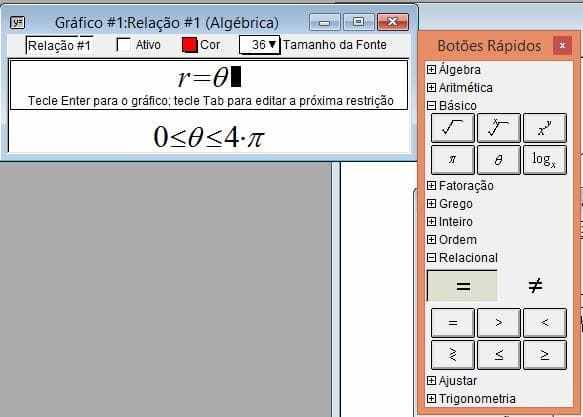
Figure 14-Solution 1-a
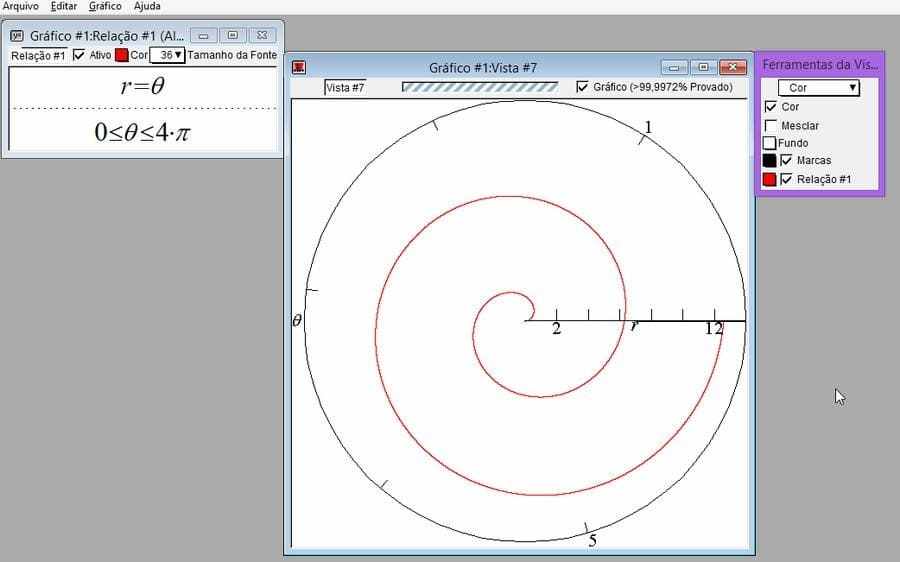
Figure 15-Solution 1-b
11. TROISIÈME ACTIVITÉ
A l’aide de GrafEq, résolvez en coordonnées polaires le graphe de 
La solution:
Figure 16-Rosacée
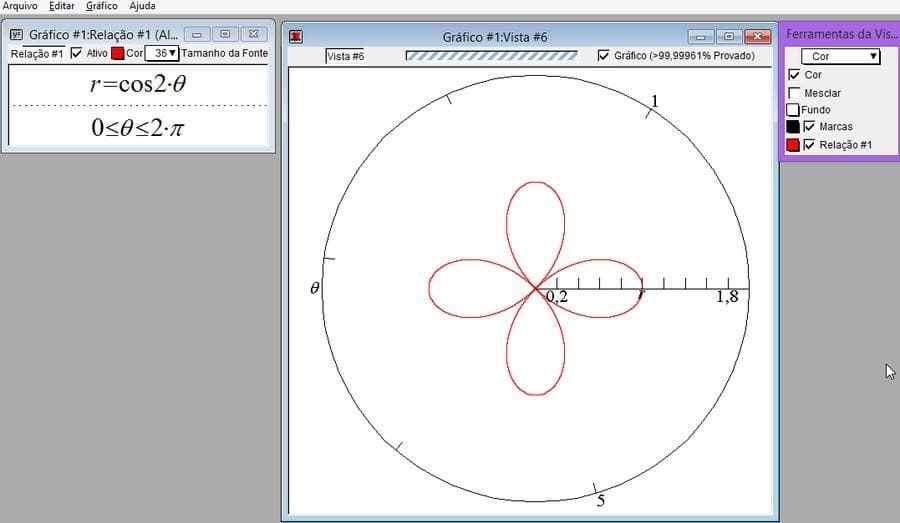
Notez que toute équation du type 
ou
pour tout entier et n positif, représentent l’ensemble des courbes du type rosacée.
12. QUATRIÈME ACTIVITÉ
Connaître les cardioïdes
À l’aide de GrafEq, résolvez le graphique de 
, 
Figure 17-cardioïde
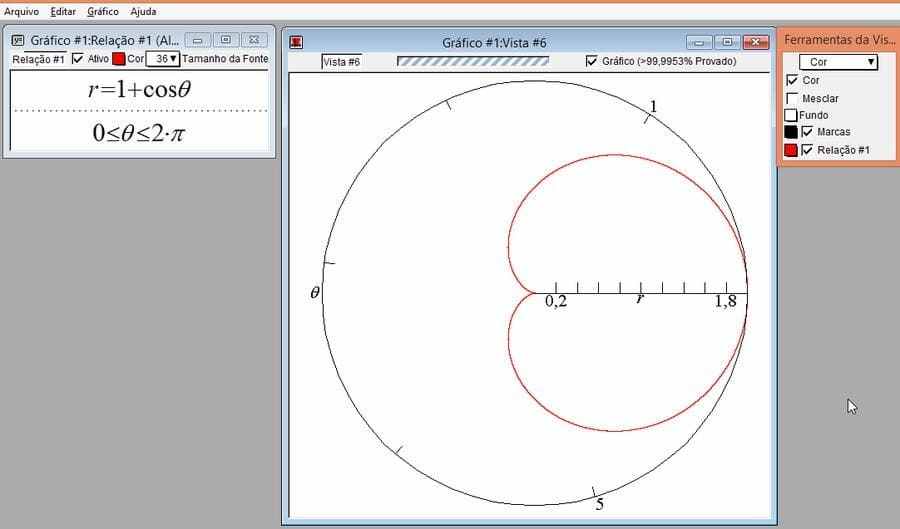
Notez que toute équation du type
ou 
représente un ensemble de courbes de type cardioïde, ainsi appelées parce qu’elles ont la forme d’un cœur.
13. CONSIDÉRATIONS FINALES
Le présent travail visait à élaborer une proposition pour l’introduction et l’exploration des concepts présents dans l’étude des coordonnées polaires avec un accent sur l’apprentissage des élèves du secondaire et peut-être la première année de l’enseignement supérieur dans les matières de sciences exactes.
Nous pensons que la proposition présentée ici répond à ces besoins et peut contribuer à l’appropriation des connaissances mathématiques par les élèves. Cette croyance peut être fondée sur les choix méthodologiques et sur l’approche dans laquelle les activités ont été conçues. Le choix du software et la méthodologie de résolution de problèmes ont permis une plus grande exploration des aspects impliqués dans l’étude des systèmes de coordonnées polaires d’une manière attrayante et significative.
Cette proposition est une approche d’enseignement des coordonnées polaires sous réserve de corrections et d’adaptations. Lors de la structuration des activités, nous nous sommes rendus compte qu’une simple situation-problème pouvait générer une belle opportunité pour le développement des contenus scolaires abordés ici. Ainsi, nous comprenons que bon nombre des changements suggérés et attendus pour l’enseignement des mathématiques peuvent découler d’idées simples ajoutées à la disposition de l’enseignant à faire face à de nouveaux défis et à essayer d’expérimenter de nouvelles méthodologies et des stratégies différenciées.
De nos jours, de plus en plus d’écoles tirent parti des ordinateurs et des technologies de l’information et de la communication. L’enseignant, dans ce contexte, devrait chercher à se préparer à utiliser ces ressources afin de tirer profit de l’enseignement et aussi de contribuer en tant que médiateur dans le processus d’enseignement-apprentissage et de s’assurer que ces stratégies favorisent l’apprentissage de nouvelles connaissances. Notre proposition s’inscrit parfaitement dans cette perspective.
Enfin, nous espérons que ce travail pourra contribuer à l’enseignement des mathématiques en mettant l’accent sur l’enseignement des coordonnées polaires. Et en plus d’offrir aux enseignants une nouvelle méthodologie d’enseignement des coordonnées polaires, notre proposition vise également à offrir un moment de réflexion sur la pratique pédagogique et la recherche d’alternatives pour améliorer l’enseignement par les mathématiques.
14. RÉFÉRENCES
ALMEIDA, FJ; Fonseca Junior, F.M. Projetos e ambientes inovadores. Brasília: Secretaria de Educação a Distância – Seed/ Proinfo- Ministério da Educação, 2000.
ACKER, Felipe. Cálculo Vetorial e Geometria Analítica: Livro 1: O Plano. Instituto de Matemática, UFRJ, Rio de Janeiro, 2016. Disponível em http://www.im.ufrj.br/cvga/problemas/exercicios/oplanolista1.pdf. Acesso em 03 de Setembro de 2020.
BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais – Ensino Médio. Brasília. Ministério da Educação, 2002.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 3.ed. Belo Horizonte: Autêntica, 2007.
CAMPOS, Márcia de Borba. Construtivismo. Disponível em http://penta.ufrgs.br / marcia/piaget.htm Acesso em 28 de Setembro de 2016.
DUARTE, Sinara. Fazendo as pazes com o bicho papão: A Matemática e o SL. In: Revista Espírito Livre, n.002, p. 74-78, maio. 2009. 89 p.
GERHARDT, T. E. & SILVEIRA, D. T. Métodos de pesquisa. 1. ed. Porto Alegre: UFRGS, 2009.
GRAVINA, Maria Alice. . . [et al.]. Matemática, Mídias Digitais e Didática: tripé para a formação de professores. Porto Alegre: Evangraf, 2012.
MAGEDANZ, Adriana. Computador: Ferramenta de trabalho no Ensino (de Matemática). 2004. 14f. Curso de Pós-Graduação Lato Sensu. Especialização em ensino de Matemática – UNIVATES – Centro Universitário, Lajeado, 2004. Disponível em http://ensino.univates.br/magedanza/pos/artigo_final_adriana_magedanz.pdf Acesso em 29 de Setembro de 2016.
PAPERT, Seymour. A máquina das crianças: repensando a escola na era digital. Porto Alegre: Artes Médicas, 1994.
PIAGET, Jean. Seis estudos de psicologia. Trad. Maria Alice Magalhães D’Amorim e Paulo Sérgio Lima Silva. Rio de Janeiro: Forense, 1964.
STAHL, Marimar M. A formação de professores para o uso das novas tecnologias de comunicação e informação. In: CANDAU, Vera Maria (org). Magistério: construção cotidiana. 6 ed. Petrópolis, RJ: Vozes, 2008. p. 292-317.
SILVA, José Orlando. FERNANDES, Natal Lania Roque. Tecnologias da Informação e Comunicação na Educação de Jovens e Adultos. Disponível em http://portal.mec.gov.br/setec/arquivos/pdf3/tcc_tecnologias.pdf. Acesso em 29 de Setembro de 2016.
VALENTE, José Armando (org). O computador na sociedade do conhecimento. Campinas: UNICAMP/NIED, 1999.
VIEIRA, F. (1999) Avaliação de software Educativo: Reflexões para uma análise Criteriosa.
ANNEXE – NOTE DE BAS
2. Paramètres du curriculum national.
[1] Licence en Informatique/Informatique – UFRJ. Licence en Mathématiques – Université Estácio de Sá – UNESA – RJ. MBA en Informatique de Gestion – Ecole Polytechnique de l’UFRJ.
Envoyé : Août 2020.
Approuvé : Septembre 2020.
