ARTICLE ORIGINAL
LIMA, Elielson Magalhães [1], MAGALHÃES, Jessica Bruna Ribeiro Wercelens [2], SILVA JÚNIOR, Justino Nogueira da [3], SILVA NETO, João Ferreira da [4]
LIMA, Elielson Magalhães. Et al. Robotique et enseignement des mathématiques: construire un simple feu de signalisation dans la classe. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 12, Vol. 18, p. 67-77. décembre 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/education-fr/signalisation
RÉSUMÉ
Le but de cet article est de montrer quelques possibilités de l’utilisation de la robotique dans les classes de mathématiques, décrivant la construction et le fonctionnement d’un simple feu de circulation. Considérant que les actions utilisant des outils technologiques permettent un apprentissage significatif pour les élèves, nous développons une séquence d’activités utilisant la robotique, à travers une planification didactique-pédagogique différente de celle utilisée traditionnellement dans la pratique scolaire. Mis au défi par les problèmes inhérents à la construction du simple feu de circulation, les élèves ont cherché à s’améliorer, à développer des concepts mathématiques et à réduire leurs difficultés. Nous avons donc constaté que l’utilisation de la robotique dans les cours de mathématiques peut contribuer à l’amélioration de l’apprentissage. Toutefois, face aux propositions naissantes de cette utilisation, nous savons qu’il est nécessaire d’investir dans des œuvres qui traitent de ce thème, en particulier dans la formation des enseignants.
Mots-clés: Robotique, Éducation, Mathématiques, Apprentissage.
INTRODUCTION
À l’heure actuelle, il existe de nombreux défis à relever pour enseigner les mathématiques, dont le manque d’enthousiasme des élèves en classe est notoire, car il est présent dans les différents niveaux d’éducation (OLIVEIRA, 2007). En accord avec cet auteur, nous comprenons qu’il est nécessaire d’investir dans des méthodologies d’enseignement dans le but d’insuffler et de provoquer l’attention et la participation des étudiants, réduisant leur manque d’enthousiasme.
Dans ce scénario, l’utilisation de la robotique en classe peut être configurée comme une proposition privilégiée pour instigation et défier les élèves, l’expansion de l’apprentissage des mathématiques et la réduction de leurs difficultés d’apprentissage. Comme Mill (2013) l’affirme à juste titre, l’utilisation de la robotique comme ressource didactique permet aux étudiants d’accroître leur créativité, de les rapprocher des connaissances mathématiques et de permettre le développement des compétences de ce secteur et d’autres.
Avec la présence de plus en plus forte des technologies de l’information et de la communication dans la société, les tendances éducatives ont indiqué l’utilisation de ces outils dans les propositions actuelles pour l’enseignement des mathématiques. Dans ce contexte, le but de cet article est de montrer certaines possibilités d’utilisation de la robotique dans les classes de mathématiques, décrivant la construction et le fonctionnement d’un simple feu de circulation.
Grâce à une planification didactique-pédagogique différente de celle utilisée traditionnellement dans la pratique scolaire, nous avons développé une séquence d’activités utilisant la robotique. Nous croyons que les actions qui utilisent ces artefacts technologiques permettent un apprentissage significatif pour les élèves dans la mesure où ils élargissent les possibilités d’interaction enseignant-élève dans la construction de connaissances mathématiques.
ROBOTIQUE ÉDUCATIVE ET LE KIT MODELIX
L’évolution des technologies de l’information et de la communication a été de plus en plus rapide, puisque «[…] nous vivons dans une société où des changements se sont produits dans une rapidité jamais vue auparavant » (SILVA NETO, 2012). Pour accompagner ces transformations sociales, il est nécessaire que les établissements d’enseignement non seulement installent des équipements technologiques, mais intègrent le corps professoral et l’étudiant à la pratique qui utilise ces technologies dans les processus éducatifs (VELOSO, 2011). Selon cet auteur, la robotique éducative peut offrir un environnement d’enseignement et d’apprentissage motivant avec des informations théoriques et pratiques qui favorisent le développement d’activités partagées entre les élèves et les enseignants. En outre, l’utilisation de la robotique permet la création d’un environnement d’apprentissage agréable, où l’étudiant peut exprimer ses idées en construisant et en testant des prototypes.
Dans ce contexte, l’utilisation de la robotique éducative sert à créer et à améliorer des pratiques pédagogiques visant à accroître le potentiel des étudiants, à ajouter des connaissances mathématiques et à permettre leur application dans la compréhension de la réalité (CRUZ, 2007). La robotique éducative ou la robotique pédagogique “[…] devraient être définies comme l’assemblage de modèles et de systèmes robotiques dans le but d’apprendre des concepts scientifiques […] par ceux qui effectuent l’assemblage de tels systèmes ” (ATTROT; AYROSA, 2002).
Pour Almeida (2008), le terme « robotique éducative » est utilisé dans la caractérisation d’environnements d’apprentissage qui rassemblent des matériaux de rebut ou des kits d’assemblage composés de diverses pièces, moteurs et capteurs contrôlables par ordinateur et par logiciel. Ces environnements nous permettent de programmer, d’une certaine façon, le fonctionnement de modèles qui sont utilisés pour enseigner différents domaines de la connaissance.
Nous comprenons que l’utilisation de ces environnements, imprégnée par la production d’assemblages variés, peut contribuer au développement des compétences et des compétences nécessaires pour les étudiants, en élargissant leur autonomie et leur créativité. Parmi les outils robotiques éducatifs, nous avons choisi le kit éducatif modelix, car il est considéré comme le premier entièrement développé au Brésil. Il a une architecture très similaire à arduino, l’un des matériels les plus répandus dans le monde.
Arduino est un outil largement utilisé pour enseigner la robotique à différents niveaux d’éducation. Il se compose d’un microcontrôleur; pièces mécaniques – engrenages, poulies, vis et tiges -; composants électroniques – capteurs et écran LCD -; moteurs; boutons; balises et lumières sonores. Les prototypes fabriqués à partir de ces matériels peuvent être contrôlés par infrarouge, télécommande ou bluetooth et leurs horaires sont basés sur l’utilisation de débitcharts.
Le travail avec le kit modelix a une base méthodologique dans l’approche curriculaire STEAM – Science, Technology, Engineering, Art and Mathematics, ou, en portugais, Science, Technologie, Ingénierie, Arts et Mathématiques. Cette approche méthodologique favorise la multidisciplinarité des zones connectées dans les projets qui fournissent l’utilisation des mathématiques pour créer des prototypes d’ingénierie et d’arts, élargissant ainsi la curiosité des élèves (SANTOS, 2005).
L’approche STEAM répond aux exigences de la Base nationale des programmes communs (2017), car elle accroît la critique des élèves en développant les compétences nécessaires aux assemblées les plus diverses. Dans les perspectives mathématiques, il est possible d’utiliser des algorithmes, en établissant des schémas et des procédures essentiels pour les constructions, de la conception de l’idée, à la préparation de l’objet, à sa programmation (GAROFALO, 2019).
LA CONSTRUCTION DU FEU DE CIRCULATION SIMPLE DANS LA SALLE DE CLASSE
Pour montrer certaines possibilités d’utiliser la robotique dans les classes de mathématiques, nous avons prévu une séquence d’activité dans laquelle nous choisissons d’utiliser le kit éducatif modelix – un cabinet où vous pouvez trouver un arsenal de pièces et de composants qui sont destinés à l’enseignement de la robotique. Une fois ce kit éducatif choisi, nous avons développé une série d’activités dans une école publique municipale à Arapiraca, Alagoas.
Malgré la trousse éducative présente à l’école, nous n’avons pas trouvé de modèles d’activités d’enseignement et d’apprentissage disponibles pour guider les enseignants. Comme il n’y a pas toujours un enseignant ayant des compétences pour travailler avec la robotique éducative, nous avons cherché à développer une proposition qui favoriserait la multidisciplinarité des domaines liés aux mathématiques, en élargissant la curiosité et la créativité des élèves.
La séquence d’activités a été développée avec les élèves des dernières années de l’école primaire de la dite école qui ont participé au programme Novo Mais Educação[5]. En ce qui concerne les mathématiques, la communauté scolaire a constaté que les plus grandes difficultés des élèves étaient liées aux algorithmes d’opérations de base et à la résolution de problèmes. Afin d’atténuer ces difficultés, nous avons développé des cours de robotique éducative pour les étudiants qui participent au programme. Ces classes ont cherché à envisager la culture numérique de compétence (BRASIL, 2017) qui englobe la compréhension, l’utilisation et la création de la technologie numérique d’une manière critique, significative et éthique.
Les activités ont été développées deux fois par semaine – les lundis et mardis – avec dix élèves qui ont fréquenté la 7e à la 9e année de l’école primaire. Avec cette classe, nous avons fait une séquence d’activités dans laquelle nous avons développé un algorithme de fonctionnement d’un feu de circulation, puis nous avons utilisé les outils modelix pour l’écrire. Les étapes de l’algorithme sont indiquées dans le graphique 1.
Tableau 1 : algorithme de fonctionnement d’un simple sémaphore
| Étape 1 | Vert clair, éteignez le feu jaune et rouge pendant 30 secondes. |
| Étape 2 | Après 30 secondes : Éteignez le feu vert pendant 15 secondes, allumez la lumière jaune pendant 15 secondes et tournez au rouge pendant 15 secondes. |
| Étape 3 | Après 15 secondes : Éteignez le feu vert pendant 30 secondes, éteignez la lumière jaune pendant 30 secondes et tournez au rouge pendant 30 secondes. |
| Étape 4 | Après 30 secondes: revenir à la première étape, créant ainsi un cycle infini. |
Source: auteurs
Après avoir enregistré l’algorithme du fonctionnement du sémaphore, nous leur avons demandé de développer un algorithme pour le microcontrôleur modelix selon la figure 1.
Figure 1 – Microcontrôleur Modelix

En manipulant le microcontrôleur en groupes, nous avons développé un algorithme tel que montré dans le graphique 2.
Tableau 2 : algorithme pour microcontrôleur
| Étape 1 | Allumez la LED rouge 30 secondes (sortie 9), éteignez la LED jaune (sortie 10) et la LED rouge (sortie 11) pendant 30 secondes. |
| Étape 2 | Éteignez la LED rouge 15 secondes (sortie 9), allumez la LED jaune (sortie 10) pendant 15 secondes et éteignez la LED rouge (sortie 11) pendant 15 secondes. |
| Étape 3 | Après 15 secondes : Éteignez le feu vert pendant 30 secondes, éteignez la lumière jaune pendant 30 secondes et tournez au rouge pendant 30 secondes. |
| Étape 4 | Après 30 secondes: revenir à la première étape, la création d’une boucle infinie. |
Source: auteurs
Avec l’élaboration d’algorithmes, nous commençons à construire des flowcharts, qui sont des moyens graphiques de représenter un algorithme. La programmation du microcontrôleur se fait à l’aide de débitcharts qui exécutent les fonctions prédéfinis d’une manière ordonnée. Dans la figure 2, nous avons le flowchart qui vous permet d’effectuer la fonctionnalité du sémaphore.
Figure 2: Flowchart
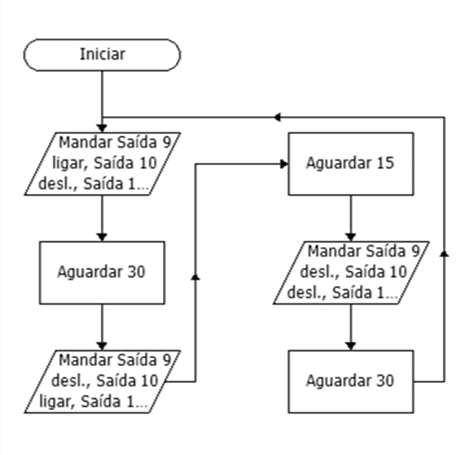
La programmation de microcontrôleur a un simulateur de débit qui indique l’erreur. Ceci, lorsqu’il est identifié par la vérification du débit, est corrigé, ce qui permet au microcontrôleur de faire le test final.
DISCUSSION ET RÉSULTATS
En ce qui concerne cette activité aux mathématiques scolaires, des problèmes ont été proposés sur le volume de trafic. Le volume est la quantité de véhicules n qui traversent l’emplacement ainsi-va étudié dans une période prédéfini t temps pendant quelques secondes, comme l’équation montre: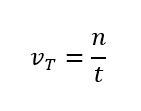 Par cette équation, il est possible de déterminer le nombre maximum de véhicules circulant dans une direction donnée d’une intersection, en connaissant le temps maximum pour le feu vert (t1 secondes), pour le signal jaune (t2 secondes) et pour le signal rouge (t3 secondes). Toutefois, cette équation n’a pas été initialement mise à disposition, visant à comprendre les concepts qu’elle implique. Pour ce faire, nous avons demandé aux élèves de résoudre certains problèmes de volume de trafic, comme suit.
Par cette équation, il est possible de déterminer le nombre maximum de véhicules circulant dans une direction donnée d’une intersection, en connaissant le temps maximum pour le feu vert (t1 secondes), pour le signal jaune (t2 secondes) et pour le signal rouge (t3 secondes). Toutefois, cette équation n’a pas été initialement mise à disposition, visant à comprendre les concepts qu’elle implique. Pour ce faire, nous avons demandé aux élèves de résoudre certains problèmes de volume de trafic, comme suit.
Premier problème.
Quel est le volume de trafic lorsque 30 véhicules traversent un feu de circulation au feu vert, dont le temps maximum est de 60 secondes?
Solution:
Être vt = volume de trafic et remplacé les valeurs maximales, nous avons: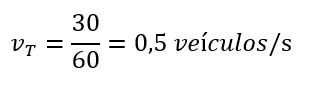
Ce problème a été pensé pour deux raisons principales : la proximité de la situation réelle et le résultat étant un nombre décimal. En fait, il y avait plusieurs questions dans la classe : « Qu’est-ce qu’un demi-véhicule? » Par conséquent, il y a eu une discussion qui a permis de mieux comprendre le concept de proportionnalité, surtout lorsque les élèves ont expliqué qu’ils comprenaient que, toutes les deux secondes, un véhicule traversait le feu de circulation.
Deuxième problème.
Sachant que le temps maximum du signal jaune du feu de circulation du problème 1 est de 15 secondes, quelle est la quantité maximale de véhicules qui peuvent passer?
Solution:
Compte tenu n2 le nombre maximum de véhicules qui peuvent passer dans le signal jaune et t2 le temps maximum de ce signal, nous avons:
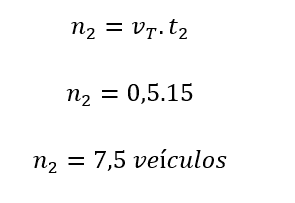 Dans le problème 2, il a été possible de discuter du fait que les quantités de véhicules n et le temps t sont directement proportionnels, tandis que les quantités de volume de trafic vt et de temps t sont inversement proportionnelles. Nous avons également discuté de la décision de s’arrêter ou de passer pendant la lumière jaune. En particulier, les élèves ont compris que sept véhicules décideraient correctement de passer, tandis qu’un huitième véhicule pourrait causer un accident s’il ne décidait pas de s’arrêter.
Dans le problème 2, il a été possible de discuter du fait que les quantités de véhicules n et le temps t sont directement proportionnels, tandis que les quantités de volume de trafic vt et de temps t sont inversement proportionnelles. Nous avons également discuté de la décision de s’arrêter ou de passer pendant la lumière jaune. En particulier, les élèves ont compris que sept véhicules décideraient correctement de passer, tandis qu’un huitième véhicule pourrait causer un accident s’il ne décidait pas de s’arrêter.
Problème 3.
Sachant que le temps maximum de signalisation rouge du feu de circulation 1 problème est de 45 secondes, quelle est la quantité maximale de véhicules qui ne peuvent pas?
Solution:
Nous savons que pendant les feux rouges les véhicules doivent s’arrêter et il est possible de savoir combien doivent le faire. Étant le nombre de véhicules qui s’arrêtent et est le temps maximum du feu rouge, nous avons:
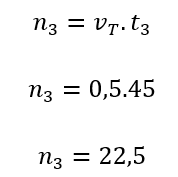 Comme dans les problèmes précédents, le nombre décimal qui en a résulté a généré des questions qui ont permis de réfléchir sur le paradigme de l’exactitude mathématique. Lors de la résolution de ce dernier problème, par exemple, nous avons discuté de ce que ce média représenterait qui pourrait être lié à une attente minimale ou à une avancée accélérée du signal jaune. Il convient de noter que ce débat a atteint des questions éthiques liées à l’éducation routière, dépassant les objectifs mathématiques initialement énoncés.
Comme dans les problèmes précédents, le nombre décimal qui en a résulté a généré des questions qui ont permis de réfléchir sur le paradigme de l’exactitude mathématique. Lors de la résolution de ce dernier problème, par exemple, nous avons discuté de ce que ce média représenterait qui pourrait être lié à une attente minimale ou à une avancée accélérée du signal jaune. Il convient de noter que ce débat a atteint des questions éthiques liées à l’éducation routière, dépassant les objectifs mathématiques initialement énoncés.
De ces problèmes, il a été possible de discuter de certains concepts mathématiques, en particulier la raison et la proportionnalité. Nous pouvons affirmer que l’activité avec l’utilisation de la robotique a permis d’encourager l’étudiant à développer la compréhension des concepts mathématiques, en plus d’élargir leurs connaissances dans d’autres domaines.
CONSIDÉRATIONS FINALES
Ayant l’intention de montrer certaines possibilités de l’utilisation de la robotique dans les classes de mathématiques, nous sommes basés sur des études sur le sujet, principalement dans l’élaboration et l’exécution d’algorithmes pour l’exécution des tâches. Dans ce contexte, nous avons élaboré l’activité de construction d’un simple feu de circulation afin que les étudiants, à l’aide d’instrumentations robotiques, développent des concepts mathématiques.
Confrontés aux problèmes inhérents à la construction du simple feu de circulation, les élèves ont cherché à s’améliorer, développant leur créativité et leur critique. Dans nos activités, nous avons remarqué qu’il y avait un espace pour les échanges de connaissances, permettant à l’élève de réduire ses difficultés initiales et d’être incité à apprendre les mathématiques.
Nous pouvons dire que l’utilisation de la robotique dans les cours de mathématiques peut contribuer à l’amélioration de l’apprentissage. Toutefois, face aux propositions naissantes de cette utilisation, nous savons qu’il est nécessaire d’investir dans des œuvres qui traitent de ce thème, en particulier dans la formation des enseignants.
RÉFÉRENCES
ALMEIDA, M. A. Possibilidades da robótica educacional para a educação matemática. Dia a dia Educação. Curitiba – PR. 2008. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/363-4.pdf. Acesso em 7, jan. 2020.
ATTROT, W.; AYROSA, P. P. da S. Aplicações da Robótica no Ensino de Ciência da Computação. Artigo para SBC 2002. Londrina, 2002.
ALVES, E.M.S. Ludicidade e o Ensino de Matemática. (2006). Papirus Editora.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, DF: MEC/CNE, 2017.
CRUZ, M.E.J.K.; LUX, B.: HAETIGER, W.: ENGELMANN, E. H. C.; HORN, F. Formação Prática do Licenciando em Computação para Trabalho com Robótica Educativa. São Paulo: XVIII Simpósio Brasileiro de Informática na Educação, 2007.
GAROFALO, D. Como levar o STEAM para a sala de aula. Nova Escola, 25, jun. de 2019. Disponível em: https://novaescola.org.br/conteudo/18021/como-levar-o-steam-para-a-sala-de-aula. Acesso em: 19, jun. 2020.
MILL, D.; CÉSAR, D. Estudo sobre dispositivos robóticos na educação: sobre a exploração do fascínio humano pela robótica no ensino-aprendizagem. In: MILL,D.(Org). Escritos sobre educação: Desafios e Possibilidades para ensinar e aprender com as tecnologias emergentes. São Paulo: Paulus, 2013. Cap. 10, p. 269-294.
OLIVEIRA, R. A robótica na aprendizagem da matemática: um estudo com alunos do 8º ano da escolariadade. Madeira/Protugal, 2007. Dissertação (Mestrado em Matemática para o Ensino), Universidade da Madeira, Madeira/ Portugal.
SANTOS, C.F.; MENEZES, C.S.A Aprendizagem da Física no Ensino Fundamental em um Ambiente de Robótica Educacional. São Leopoldo: Workshop de Informática na Educação/ XXV Congresso da Sociedade brasileira de Computação, 2005.
SILVA NETO, J. F. Concepções sobre a formação continuada de professores de matemática em Alagoas. Dissertação de Mestrado, Universidade Federal de Pernambuco, Programa de Pós-Graduação em Educação Matemática e Tecnológica, Recife, 2012.
VELLOSO, R. V. Educação e tecnologia em diálogo na cena contemporânea. Ponto de Acesso, Salvador, v.5, n. 2, p. 03-19, ago., 2011.
ANNEXE – RÉFÉRENCE DE RÉFÉRENCE
5. Ce programme intègre les actions du Plan de développement de l’éducation (PDE) qui vise officiellement à améliorer les indices éducatifs grâce à l’expansion de la journée scolaire et la conception de l’éducation intégrale. Plus précisément pour cette communauté scolaire, le programme Novo Mais Educação a organisé en 2019 des ateliers d’alphabétisation et de mathématiques visant à réhéguer certaines difficultés des élèves.
[1] Doctorant en éducation, maîtrise en mathématiques, troisième cycle en mathématiques et statistiques, diplômé en mathématiques baccalauréat.
[2] Troisième cycle en physiologie de l’exercice et en biomécanique, diplômé en éducation physique.
[3] Troisième cycle en mathématiques, diplômé en mathématiques baccalauréat.
[4] Doctorant en éducation, maîtrise en mathématiques et éducation technologique, spécialiste des programmes d’enseignement des mathématiques, diplôme en mathématiques.
Soumis : décembre 2020.
Approuvé : décembre 2020.


