ORIGINAL ARTICLE
LIMA, Elielson Magalhães [1], MAGALHÃES, Jessica Bruna Ribeiro Wercelens [2], SILVA JÚNIOR, Justino Nogueira da [3], SILVA NETO, João Ferreira da [4]
LIMA, Elielson Magalhães. Et al. Robotics and the Teaching of Mathematics: Building a simple traffic light in the classroom. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 12, Vol. 18, pp. 67-77. December 2020. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/education/traffic-light
SUMMARY
The aim of this article is to show some possibilities of the use of robotics in mathematics classes, describing the construction and operation of a simple traffic light. Considering that actions that use technological tools allow a significant learning for students, we develop a sequence of activities using robotics, through didactic-pedagogical planning different from that conventionally used in school practice. Challenged by the problems inherent to the construction of the simple traffic light, the students sought to improve themselves, developing mathematical concepts and reducing their difficulties. We found, therefore, that the use of robotics in mathematics classes can contribute to the improvement of learning. However, in the face of incipient proposals of this use, we know that it is necessary to invest in works that discuss this theme, especially in teacher education.
Keywords: Robotics, Education, mathematics, learning.
INTRODUCTION
Currently, there are many challenges to teach mathematics, of which the lack of enthusiasm of students in the classroom is notorious, because it is present in the various levels of education (OLIVEIRA, 2007). Agreeing with this author, we understand that it is necessary to invest in teaching methodologies with the objective of instigating and provoking the attention and participation of students, reducing their lack of enthusiasm.
In this scenario, the use of robotics in the classroom can be configured as a privileged proposal to instigate and challenge students, expanding mathematics learning and reducing their learning difficulties. As Mill (2013) rightly states, the use of robotics as a didactic resource allows students to increase creativity, bringing them closer to mathematical knowledge and enabling the development of skills of this and other areas.
With the increasingly strong presence of information and communication technologies in society, educational trends have indicated the use of these tools in current proposals for mathematics teaching. In view of this, the aim of this article is to show some possibilities of the use of robotics in mathematics classes, describing the construction and operation of a simple traffic light.
Through didactic-pedagogical planning different from that conventionally used in school practice, we developed a sequence of activities using robotics. We believe that actions that use these technological artifacts allow meaningful learning for students to the extent that they expand the possibilities of teacher-student interaction in the construction of mathematical knowledge.
EDUCATIONAL ROBOTICS AND THE MODELIX KIT
The evolution of information and communication technologies has been increasingly rapid, since “[…] we live in a society in which changes have occurred in a rapidity never seen before” (SILVA NETO, 2012). To accompany these social transformations, it is necessary that educational institutions not only install technological equipment, but integrate the faculty and student to practice that uses such technologies in educational processes (VELOSO, 2011). According to this author, educational robotics can offer a motivating teaching and learning environment with theoretical and practical information that favors the development of activities shared between students and teachers. In addition, the use of robotics allows the creation of a pleasant learning environment, where the student can express their ideas by building and testing prototypes.
In this context, the use of educational robotics serves to create and improve pedagogical practices aimed at raising the potential of students, adding mathematical knowledge and enabling their application in understanding reality (CRUZ, 2007). Educational robotics or pedagogical robotics “[…] should be defined as the assembly of models and robotic systems with the purpose of learning scientific […] concepts by those who perform the assembly of such systems” (ATTROT; AYROSA, 2002).
For Almeida (2008), the term “educational robotics” is used in the characterization of learning environments that bring together scrap materials or assembly kits composed of various parts, motors and sensors controllable by computer and software. These environments allow us to program, in some way, the functioning of models that are used for teaching different areas of knowledge.
We understand that the use of these environments, permeated by the production of varied assemblies, can contribute to the development of skills and competencies necessary for students, expanding their autonomy and creativity. Among the educational robotics tools, we chose the modelix educational kit, because it is considered the first fully developed in Brazil. It has an architecture very similar to arduino, one of the most widespread hardware in the world.
Arduino is a widely used tool for teaching robotics at various levels of education. It consists of a microcontroller; mechanical parts – gears, pulleys, screws and rods -; electronic components – sensors and LCD display -; engines; buttons; beacons and sound lights. Prototypes made from these hardware can be controlled by infrared, remote control or bluetooth and their schedules are based on the use of flowcharts.
The work with the modelix kit has methodological basis in the curricular approach STEAM – Science, Technology, Engineering, Art and Mathematics, or, in Portuguese, Ciências, Tecnologia, Engenharia, Artes and Matemática. This methodological approach promotes the multidisciplinarity of connected areas in projects that provide the use of mathematics to create engineering and arts prototypes, expanding students’ curiosity (SANTOS, 2005).
The STEAM approach meets the requirements of the National Common Curriculum Base (2017), as it increases the criticality of students by developing the skills needed by the most diverse assemblies. Within the mathematical perspectives, it is possible to make use of algorithms, establishing essential patterns and procedures for constructions, from the conception of the idea, through the preparation of the object, to its programming (GAROFALO, 2019).
THE CONSTRUCTION OF THE SIMPLE TRAFFIC LIGHT IN THE CLASSROOM
To show some possibilities of using robotics in mathematics classes, we have planned a sequence of activity in which we choose to use the modelix educational kit – a cabinet where you can find an arsenal of parts and components that are intended for the teaching of robotics. Once this educational kit was chosen, we developed a sequence of activities in a municipal public school in Arapiraca, Alagoas.
Despite the educational kit present at the school, we did not find models of teaching and learning activities available to guide teachers. As there is not always a teacher with skills to work with educational robotics, we sought to develop a proposal that would promote the multidisciplinarity of areas related to mathematics, expanding the curiosity and creativity of students.
The sequence of activities was developed with students from the final years of the elementary school of the said school who participated in the Novo Mais Educação[5]. With regard to mathematics, the school community found that the students’ greatest difficulties were related to basic operations algorithms and problem solving. In order to alleviate these difficulties, we developed educational robotics classes for students who participate in the program. These classes sought to contemplate the competence digital culture (BRASIL, 2017) that encompasses the understanding, use and creation of digital technology in a critical, meaningful and ethical way.
The activities were developed twice a week – Mondays and Tuesdays – together with ten students who attended the 7th to 9th grade of elementary school. With this class, we did a sequence of activities in which we developed an algorithm of how a traffic light works and then we used the modelix tools to write it. The algorithm steps are indicated in Chart 1.
Table 1: algorithm of operation of a simple semaphore
| Step 1 | Light green, turn off Yellow and Red Light for 30 seconds. |
| Step 2 | After 30 seconds: Turn off green light for 15 seconds, turn on Yellow Light for 15 seconds and turn red for 15 seconds. |
| Step 3 | After 15 seconds: Turn off green light for 30 seconds, turn off Yellow Light for 30 seconds, and turn red for 30 seconds. |
| Step 4 | After 30 seconds: go back to the first step, thus creating an infinite cycle. |
Source: authors
After recording the algorithm of how the semaphore works, we asked them to develop an algorithm for microcontroller modelix according to Figure 1.
Figure 1 – Modelix microcontroller
Source: removed from the www.modelix.com.br
By manipulating the microcontroller into groups, we developed an algorithm as shown in Chart 2.
Table 2: algorithm for microcontroller
| Step 1 | Turn on red LED 30 seconds (Exit 9), turn off yellow LED (Output 10) and red LED (Output 11) for 30 seconds. |
| Step 2 | Turn off red LED 15 seconds (Exit 9), turn on yellow LED (Output 10) for 15 seconds and turn off red LED (Output 11) for 15 seconds. |
| Step 3 | After 15 seconds: Turn off green light for 30 seconds, turn off yellow light for 30 seconds and turn red for 30 seconds. |
| Step 4 | After 30 seconds: go back to the first step, creating an infinite loop. |
Source: authors
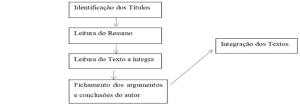
With the elaboration of algorithms, we start to build flowcharts, which are graphical ways of representing an algorithm. The programming of the microcontroller is done using flowcharts that perform the predefined functions in an orderly manner. In Figure 2 we have the flowchart that allows you to perform the functionality of the semaphore.
Figure 2: Flowchart
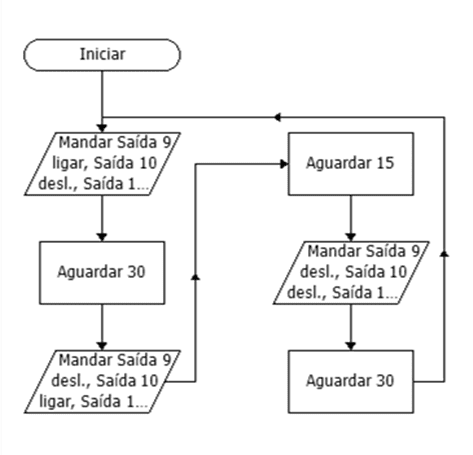
Source: authors
The microcontroller programming has a flowchart simulator that indicates error. This, when identified by the flowchart check, is corrected, allowing an upload for the microcontroller to do the final test.
DISCUSSION AND RESULTS
Relating this activity to school mathematics, problems were proposed on traffic volume. Volume is the amount of n vehicles that traverse so-going location studied in a predefined t time period for seconds, as the equation shows: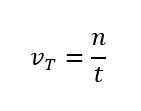
By this equation, it is possible to determine the maximum number of vehicles traveling in a given direction of an intersection, knowing the maximum time for the green light (t1 seconds), for the yellow signal (t2 seconds) and for the red signal (t3 seconds). However, this equation was not initially made available, aiming at understanding the concepts it involves. To do this, we asked students to resolve some problems with traffic volume, as follows.
Problem one.
What is the volume of traffic when 30 vehicles cross a traffic light at the green light, whose maximum time is 60 seconds?
Solution:
Being vt = traffic volume and replaced the maximum values, we have: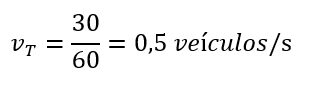
This problem was thought for two main reasons: proximity to the actual situation and the result being a decimal number. In fact, there were several questions in the class: “what would be half a vehicle?” Therefore, there was a discussion that made it possible to better understand the concept of proportionality, especially when the students explained their understanding that, every 2 seconds, a vehicle crossed the traffic light.
Problem two.
Knowing that the maximum time of the yellow signal of the traffic light of Problem 1 is 15 seconds, what is the maximum amount of vehicles that can pass?
Solution:
Considering n2 the maximum number of vehicles that can pass in the yellow signal and t2 the maximum time of this signal, we have: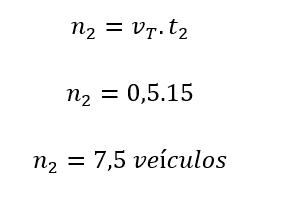
In Problem 2, it was possible to discuss that the quantities of n vehicles and time t are directly proportional, while the quantities of traffic volume vt and time t are inversely proportional. We also discussed the decision to stop or pass during the yellow light. In particular to this problem, the students understood that seven vehicles would correctly decide to pass, while an eighth vehicle could cause an accident if it did not decide to stop.
Problem three.
Knowing that the maximum red signal time of the problem 1 traffic light is 45 seconds, what is the maximum amount of vehicles that cannot?
Solution:
We know that during the red light vehicles must stop and it is possible to find out how many need to do this. Being the number of vehicles that stop and is the maximum time of the red light, we have: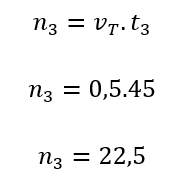
As in previous problems, the resulting decimal number generated questions that made it possible to reflect on the paradigm of mathematical accuracy. During the resolution of this last problem, for example, we discussed what this medium would represent that could be related minimum wait or an accelerated advance in the yellow signal. It is worth noting that this debate reached ethical issues related to traffic education, exceeding the mathematical objectives initially outlined.
From these problems, it was possible to discuss some mathematical concepts, especially reason and proportionality. We can affirm that the activity with the use of robotics made it possible to encourage the student to develop the understanding of mathematical concepts, in addition to expanding their knowledge in other areas.
FINAL CONSIDERATIONS
Intending to show some possibilities of the use of robotics in mathematics classes, we are based on studies on the subject, mainly in the elaboration and execution of algorithms for performing tasks. In this context, we elaborated the activity of building a simple traffic light so that students, using roboticinstruments, develop mathematical concepts.
Challenged by the problems inherent to the construction of the simple traffic light, the students sought to improve themselves, developing their creativity and criticality. In our activities, we noticed that there was a space for knowledge exchanges, allowing the student to reduce his initial difficulties and be instigated to learn mathematics.
We can say that the use of robotics in mathematics classes can contribute to the improvement of learning. However, in the face of incipient proposals of this use, we know that it is necessary to invest in works that discuss this theme, especially in teacher education.
REFERENCES
ALMEIDA, M. A. Possibilidades da robótica educacional para a educação matemática. Dia a dia Educação. Curitiba – PR. 2008. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/363-4.pdf. Acesso em 7, jan. 2020.
ATTROT, W.; AYROSA, P. P. da S. Aplicações da Robótica no Ensino de Ciência da Computação. Artigo para SBC 2002. Londrina, 2002.
ALVES, E.M.S. Ludicidade e o Ensino de Matemática. (2006). Papirus Editora.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, DF: MEC/CNE, 2017.
CRUZ, M.E.J.K.; LUX, B.: HAETIGER, W.: ENGELMANN, E. H. C.; HORN, F. Formação Prática do Licenciando em Computação para Trabalho com Robótica Educativa. São Paulo: XVIII Simpósio Brasileiro de Informática na Educação, 2007.
GAROFALO, D. Como levar o STEAM para a sala de aula. Nova Escola, 25, jun. de 2019. Disponível em: https://novaescola.org.br/conteudo/18021/como-levar-o-steam-para-a-sala-de-aula. Acesso em: 19, jun. 2020.
MILL, D.; CÉSAR, D. Estudo sobre dispositivos robóticos na educação: sobre a exploração do fascínio humano pela robótica no ensino-aprendizagem. In: MILL,D.(Org). Escritos sobre educação: Desafios e Possibilidades para ensinar e aprender com as tecnologias emergentes. São Paulo: Paulus, 2013. Cap. 10, p. 269-294.
OLIVEIRA, R. A robótica na aprendizagem da matemática: um estudo com alunos do 8º ano da escolariadade. Madeira/Protugal, 2007. Dissertação (Mestrado em Matemática para o Ensino), Universidade da Madeira, Madeira/ Portugal.
SANTOS, C.F.; MENEZES, C.S.A Aprendizagem da Física no Ensino Fundamental em um Ambiente de Robótica Educacional. São Leopoldo: Workshop de Informática na Educação/ XXV Congresso da Sociedade brasileira de Computação, 2005.
SILVA NETO, J. F. Concepções sobre a formação continuada de professores de matemática em Alagoas. Dissertação de Mestrado, Universidade Federal de Pernambuco, Programa de Pós-Graduação em Educação Matemática e Tecnológica, Recife, 2012.
VELLOSO, R. V. Educação e tecnologia em diálogo na cena contemporânea. Ponto de Acesso, Salvador, v.5, n. 2, p. 03-19, ago., 2011.
APPENDIX – FOOTNOTE REFERENCE
5. This program integrates the actions of the Education Development Plan ( PDE ) that officially aims to improve educational indexes through the expansion of the school day and the conception of Integral Education. Specifically to this school community, the Novo Mais Educação program held literacy and mathematics workshops in 2019 aimed at reathing some of the students’ difficulties.
[1] PhD student in education, Master in Mathematics, Postgraduate in Mathematics and statistics, Graduated in Mathematics Bachelor’s Degree.
[2] Postgraduate in Exercise Physiology and Biomechanics, Graduated in Physical Education Degree.
[3] Postgraduate in Mathematics, Graduated in Mathematics Bachelor’s Degree.
[4] PhD student in Education, Master in Mathematics and Technological Education, Specialist in Mathematics Teaching Programming, Degree in Mathematics.
Submitted: December, 2020.
Approved: December, 2020.
