ORIGINALER ARTIKEL
LIMA, Elielson Magalhães [1], MAGALHÃES, Jessica Bruna Ribeiro Wercelens [2], SILVA JÚNIOR, Justino Nogueira da [3], SILVA NETO, João Ferreira da [4]
LIMA, Elielson Magalhães. Et al. Robotik und Mathematikunterricht: Aufbau einer einfachen Ampel im Klassenzimmer. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 12, Vol. 18, S. 67-77. Dezember 2020. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/bildung-de/ampel
ZUSAMMENFASSUNG
Das Ziel dieses Artikels ist es, einige Möglichkeiten des Einsatzes von Robotik in Mathematik-Klassen aufzuzeigen, die den Bau und Betrieb einer einfachen Ampel beschreiben. Wenn man bedenkt, dass Maßnahmen, die technologische Werkzeuge nutzen, den Schülern ein signifikantes Lernen ermöglichen, entwickeln wir eine Abfolge von Aktivitäten mit Robotik, durch didaktisch-pädagogische Planung, die sich von der konventionell in der Schulpraxis üblichen unterscheidet. Herausgefordert durch die Probleme, die mit dem Bau der einfachen Ampel verbunden sind, versuchten die Schüler, sich zu verbessern, mathematische Konzepte zu entwickeln und ihre Schwierigkeiten zu reduzieren. Wir haben daher festgestellt, dass der Einsatz von Robotik in Mathematikkursen zur Verbesserung des Lernens beitragen kann. Angesichts der beginnenden Vorschläge für diese Verwendung wissen wir jedoch, dass es notwendig ist, in Werke zu investieren, die dieses Thema diskutieren, insbesondere in die Lehrerausbildung.
Schlagworte: Robotik, Bildung, Mathematik, Lernen.
EINFÜHRUNG
Derzeit gibt es viele Herausforderungen, Mathematik zu unterrichten, von denen der Mangel an Enthusiasmus der Schüler im Klassenzimmer berüchtigt ist, weil es in den verschiedenen Bildungsstufen vorhanden ist (OLIVEIRA, 2007). In Übereinstimmung mit diesem Autor verstehen wir, dass es notwendig ist, in Lehrmethoden zu investieren, mit dem Ziel, die Aufmerksamkeit und Die Teilnahme der Schüler anzuregen und zu provozieren, um ihren Mangel an Enthusiasmus zu verringern.
In diesem Szenario kann der Einsatz von Robotik im Klassenzimmer als privilegierter Vorschlag konfiguriert werden, um Schüler anzuzetteln und herauszufordern, das Mathematiklernen zu erweitern und ihre Lernschwierigkeiten zu verringern. Wie Mill (2013) zu Recht feststellt, ermöglicht der Einsatz von Robotik als didaktische Ressource den Schülern, ihre Kreativität zu steigern, sie dem mathematischen Wissen näher zu bringen und die Entwicklung von Fähigkeiten in diesem und anderen Bereichen zu ermöglichen.
Angesichts der zunehmenden Präsenz von Informations- und Kommunikationstechnologien in der Gesellschaft haben Bildungstrends den Einsatz dieser Instrumente in aktuellen Vorschlägen für den Mathematikunterricht angedeutet. Vor diesem Hintergrund ist es das Ziel dieses Artikels, einige Möglichkeiten des Einsatzes von Robotik in Mathematikklassen aufzuzeigen und den Bau und Betrieb einer einfachen Ampel zu beschreiben.
Durch eine didaktisch-pädagogische Planung, die sich von der konventionell in der Schulpraxis üblichen unterscheidet, haben wir eine Abfolge von Aktivitäten mit Robotik entwickelt. Wir glauben, dass Aktionen, die diese technologischen Artefakte nutzen, sinnvolles Lernen für Die Schüler in dem Maße ermöglichen, dass sie die Möglichkeiten der Interaktion zwischen Lehrern und Schülern bei der Konstruktion von mathematischem Wissen erweitern.
EDUCATIONAL ROBOTICS UND DAS MODELIX KIT
Die Entwicklung der Informations- und Kommunikationstechnologien ist immer rasanter geworden, da “[…] wir in einer Gesellschaft leben, in der Veränderungen in einer nie zuvor gesehenen Geschwindigkeit stattgefunden haben” (SILVA NETO, 2012). Um diese gesellschaftlichen Transformationen zu begleiten, ist es notwendig, dass Bildungseinrichtungen nicht nur technologische Ausrüstung installieren, sondern die Fakultät und studenten in die Praxis integrieren, die solche Technologien in Bildungsprozessen verwendet (VELOSO, 2011). Laut diesem Autor kann pädagogische Robotik eine motivierende Lehr- und Lernumgebung mit theoretischen und praktischen Informationen bieten, die die Entwicklung von Aktivitäten begünstigt, die zwischen Schülern und Lehrern geteilt werden. Darüber hinaus ermöglicht der Einsatz von Robotik die Schaffung einer angenehmen Lernumgebung, in der die Schüler ihre Ideen durch den Bau und das Testen von Prototypen zum Ausdruck bringen können.
In diesem Zusammenhang dient der Einsatz von pädagogischer Robotik dazu, pädagogische Praktiken zu schaffen und zu verbessern, die darauf abzielen, das Potenzial der Studierenden zu erhöhen, mathematisches Wissen hinzuzufügen und ihre Anwendung im Verständnis der Realität zu ermöglichen (CRUZ, 2007). Pädagogische Robotik oder pädagogische Robotik “[…] sollte definiert werden als die Montage von Modellen und Robotersystemen mit dem Ziel, wissenschaftliche […] Konzepte von denen zu erlernen, die die Montage solcher Systeme durchführen” (ATTROT; AYROSA, 2002).
Für Almeida (2008) wird der Begriff “pädagogische Robotik” bei der Charakterisierung von Lernumgebungen verwendet, die Schrottmaterialien oder Montagesätze aus verschiedenen Teilen, Motoren und Sensoren zusammenbringen, die durch Computer und Software steuerbar sind. Diese Umgebungen ermöglichen es uns, in gewisser Weise die Funktionsweise von Modellen zu programmieren, die für den Unterricht verschiedener Wissensbereiche verwendet werden.
Wir verstehen, dass die Nutzung dieser Umgebungen, die von der Produktion unterschiedlicher Baugruppen durchdrungen sind, zur Entwicklung von Fähigkeiten und Kompetenzen beitragen kann, die für die Schüler notwendig sind, und ihre Autonomie und Kreativität zu erweitern. Unter den pädagogischen Robotik-Tools haben wir uns für das modelix-Bildungskit entschieden, da es als das erste voll entwickelte in Brasilien gilt. Es hat eine Architektur sehr ähnlich wie arduino, eine der am weitesten verbreiteten Hardware in der Welt.
Arduino ist ein weit verbreitetes Werkzeug für den Unterricht von Robotik auf verschiedenen Bildungsstufen. Es besteht aus einem Mikrocontroller; mechanische Teile – Zahnräder, Riemenscheiben, Schrauben und Stäbe -; elektronische Komponenten – Sensoren und LCD-Anzeige -; Motoren; Tasten; Baken und Soundlichter. Prototypen aus dieser Hardware können per Infrarot, Fernbedienung oder Bluetooth gesteuert werden und ihre Zeitpläne basieren auf der Verwendung von Flussdiagrammen.
Die Arbeit mit dem modelix-Kit basiert auf methodischen Grundlagen im Lehrplanansatz STEAM – Science, Technology, Engineering, Art and Mathematics, oder in Portugiesisch in Naturwissenschaften, Technologie, Ingenieurwesen, Kunst und Mathematik. Ein solcher methodischer Ansatz fördert die Multidisziplinarität von Bereichen, die in Projekten miteinander verbunden sind, in denen mithilfe von Mathematik Prototypen von Ingenieurwesen und Kunst erstellt werden, was die Neugier der Studenten erhöht (SANTOS, 2005).
Der STEAM-Ansatz erfüllt die Anforderungen der National Common Curriculum Base (2017), da er die Kritikalität der Schüler erhöht, indem er die Fähigkeiten entwickelt, die von den unterschiedlichsten Versammlungen benötigt werden. Innerhalb der mathematischen Perspektiven ist es möglich, Algorithmen zu nutzen, wesentliche Muster und Verfahren für Konstruktionen zu etablieren, von der Konzeption der Idee über die Vorbereitung des Objekts bis hin zu seiner Programmierung (GAROFALO, 2019).
DER BAU DER EINFACHEN AMPEL IM KLASSENZIMMER
Um einige Möglichkeiten der Robotik in Mathematik-Klassen zu zeigen, haben wir eine Abfolge von Aktivitäten geplant, in denen wir uns entscheiden, das modelix-Bildungskit zu verwenden – ein Schrank, in dem Sie ein Arsenal von Teilen und Komponenten finden können, die für den Unterricht der Robotik bestimmt sind. Sobald dieses Pädagogische Kit ausgewählt wurde, entwickelten wir eine Reihe von Aktivitäten in einer kommunalen öffentlichen Schule in Arapiraca, Alagoas.
Trotz des an der Schule vorhandenen Pädagogischen Kits haben wir keine Modelle für Lehr- und Lernaktivitäten gefunden, die Lehrern zur Verfügung standen. Da es nicht immer einen Lehrer mit Fähigkeiten gibt, mit pädagogischer Robotik zu arbeiten, haben wir versucht, einen Vorschlag zu entwickeln, der die Multidisziplinarität von Bereichen im Zusammenhang mit Mathematik fördern und die Neugier und Kreativität der Schüler erweitern würde.
Die Abfolge der Aktivitäten wurde mit Schülern aus den letzten Jahren der Grundschule der besagten Schule entwickelt, die am Novo Mais Educação Programm [5]. In Bezug auf Mathematik stellte die Schulgemeinschaft fest, dass die größten Schwierigkeiten der Schüler mit grundlegenden Operationsalgorithmen und Problemlösung zusammenhängten. Um diese Schwierigkeiten zu lindern, haben wir pädagogische Robotik-Kurse für Schüler entwickelt, die am Programm teilnehmen. Diese Klassen versuchten, die Kompetenz digitale Kultur (BRASIL, 2017) zu betrachten, die das Verständnis, die Nutzung und die Schaffung digitaler Technologie auf kritische, sinnvolle und ethische Weise umfasst.
Die Aktivitäten wurden zweimal pro Woche – montags und dienstags – zusammen mit zehn Schülern entwickelt, die die 7. bis 9. Klasse der Grundschule besuchten. Mit dieser Klasse haben wir eine Reihe von Aktivitäten durchgeführt, in denen wir einen Algorithmus entwickelt haben, wie eine Ampel funktioniert, und dann die modelix-Tools verwendet haben, um sie zu schreiben. Die Algorithmusschritte sind in Diagramm 1 dargestellt.
Tabelle 1: Betriebsalgorithmus eines einfachen Semaphors
| Schritt 1 | Hellgrün, Schalten Sie Gelb- und Rotlicht für 30 Sekunden aus. |
| Schritt 2 | Nach 30 Sekunden: Schalten Sie grünes Licht für 15 Sekunden aus, schalten Sie Gelblicht für 15 Sekunden ein und drehen Sie 15 Sekunden lang rot. |
| Schritt 3 | Nach 15 Sekunden: Schalten Sie grünes Licht für 30 Sekunden aus, schalten Sie Gelblicht für 30 Sekunden aus, und drehen Sie 30 Sekunden lang rot. |
| Schritt 4 | Nach 30 Sekunden: Gehen Sie zurück zum ersten Schritt, wodurch ein unendlicher Zyklus entsteht. |
Quelle: Autoren
Nachdem wir den Algorithmus der Funktionsweise des Semaphors aufgezeichnet hatten, baten wir sie, einen Algorithmus für Mikrocontroller-Modellix gemäß Abbildung 1 zu entwickeln.
Abbildung 1: Modelix-Mikrocontroller

Indem wir den Mikrocontroller in Gruppen manipulieren, haben wir einen Algorithmus entwickelt, wie in Diagramm 2 dargestellt.
Tabelle 2: Algorithmus für Mikrocontroller
| Schritt 1 | Schalten Sie die rote LED 30 Sekunden ein (Exit 9), schalten Sie die gelbe LED (Ausgang 10) und die rote LED (Ausgang 11) 30 Sekunden lang aus. |
| Schritt 2 | Schalten Sie die rote LED 15 Sekunden aus (Exit 9), schalten Sie die gelbe LED (Ausgang 10) für 15 Sekunden ein und schalten Sie die rote LED (Ausgang 11) für 15 Sekunden aus. |
| Schritt 3 | Nach 15 Sekunden: Schalten Sie grünes Licht für 30 Sekunden aus, schalten Sie gelbes Licht für 30 Sekunden aus und drehen Sie 30 Sekunden lang rot. |
| Schritt 4 | Nach 30 Sekunden: Gehen Sie zurück zum ersten Schritt, und erstellen Sie eine Endlosschleife. |
Quelle: Autoren
Mit der Ausarbeitung von Algorithmen beginnen wir, Flussdiagramme zu erstellen, die grafische Möglichkeiten zur Darstellung eines Algorithmus darstellen. Die Programmierung des Mikrocontrollers erfolgt über Flussdiagramme, die die vordefinierten Funktionen geordnet ausführen. In Abbildung 2 haben wir das Flussdiagramm, mit dem Sie die Funktionalität des Semaphors ausführen können.
Abbildung 2: Flussdiagramm
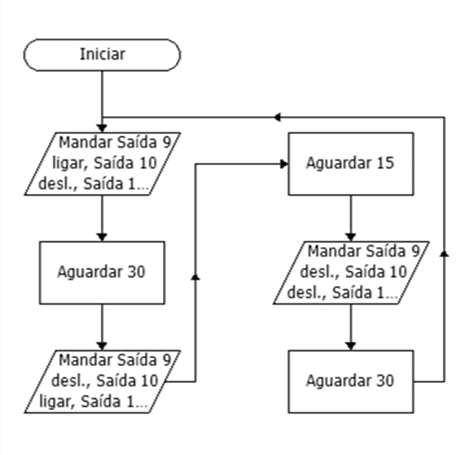
Quelle: Autoren
Die Mikrocontroller-Programmierung verfügt über einen Flussdiagrammsimulator, der auf Einen Fehler hinweist. Dies wird, wenn es durch die Flussdiagrammprüfung identifiziert wird, korrigiert, sodass ein Upload für den Mikrocontroller den letzten Test machen kann.
DISKUSSION UND ERGEBNISSE
In Bezug auf diese Tätigkeit auf Schulmathematik wurden Probleme auf das Verkehrsaufkommen vorgeschlagen. Volumen ist die Menge der n Fahrzeuge, die so-going Ort in einem vordefinierten t Zeitraum für Sekunden untersucht durchlaufen, wie die Gleichung zeigt: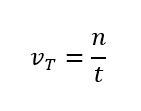 Durch diese Gleichung ist es möglich, die maximale Anzahl von Fahrzeugen zu bestimmen, die in einer bestimmten Richtung einer Kreuzung fahren, da sie die maximale Zeit für das grüne Licht (t1 Sekunden), für das gelbe Signal (t2 Sekunden) und für das rote Signal (t3 Sekunden) kennen. Diese Gleichung wurde jedoch zunächst nicht zur Verfügung gestellt, um die damit umfängs verstandenen Konzepte zu verstehen. Um dies zu tun, haben wir die Kursteilnehmer gebeten, einige Probleme mit dem Verkehrsaufkommen wie folgt zu lösen.
Durch diese Gleichung ist es möglich, die maximale Anzahl von Fahrzeugen zu bestimmen, die in einer bestimmten Richtung einer Kreuzung fahren, da sie die maximale Zeit für das grüne Licht (t1 Sekunden), für das gelbe Signal (t2 Sekunden) und für das rote Signal (t3 Sekunden) kennen. Diese Gleichung wurde jedoch zunächst nicht zur Verfügung gestellt, um die damit umfängs verstandenen Konzepte zu verstehen. Um dies zu tun, haben wir die Kursteilnehmer gebeten, einige Probleme mit dem Verkehrsaufkommen wie folgt zu lösen.
Problem eins.
Wie hoch ist das Verkehrsaufkommen, wenn 30 Fahrzeuge an der grünen Ampel eine Ampel überqueren, deren maximale Zeit 60 Sekunden beträgt?
Lösung:
Da vt = Verkehrsaufkommen und ersetzt die Maximalwerte, haben wir: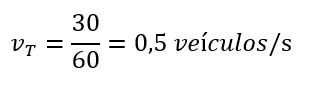 Dieses Problem wurde aus zwei Hauptgründen betrachtet: Nähe zur tatsächlichen Situation und das Ergebnis ist eine Dezimalzahl. Tatsächlich gab es in der Klasse mehrere Fragen: “Was wäre ein halbes Fahrzeug?” Daher gab es eine Diskussion, die es ermöglichte, das Konzept der Verhältnismäßigkeit besser zu verstehen, vor allem, wenn die Schüler ihr Verständnis erklärten, dass alle 2 Sekunden ein Fahrzeug die Ampel überquerte.
Dieses Problem wurde aus zwei Hauptgründen betrachtet: Nähe zur tatsächlichen Situation und das Ergebnis ist eine Dezimalzahl. Tatsächlich gab es in der Klasse mehrere Fragen: “Was wäre ein halbes Fahrzeug?” Daher gab es eine Diskussion, die es ermöglichte, das Konzept der Verhältnismäßigkeit besser zu verstehen, vor allem, wenn die Schüler ihr Verständnis erklärten, dass alle 2 Sekunden ein Fahrzeug die Ampel überquerte.
Problem zwei.
Wohl wissend, dass die maximale Zeit des gelben Signals der Ampel von Problem 1 15 Sekunden beträgt, was ist die maximale Anzahl an Fahrzeugen, die passieren können?
Lösung:
Unter Berücksichtigung von n2 die maximale Anzahl von Fahrzeugen, die im gelben Signal passieren können und t2 die maximale Zeit dieses Signals, haben wir: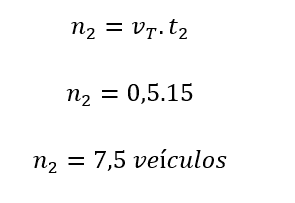
In Problem 2 konnte erörtert werden, daß die Mengen der n Fahrzeuge und die Zeit t direkt proportional sind, während die Mengen des Verkehrsaufkommens vt und der Zeit t umgekehrt proportional sind. Wir haben auch die Entscheidung diskutiert, während der gelben Ampel zu stoppen oder zu passieren. Insbesondere bei diesem Problem verstanden die Schüler, dass sieben Fahrzeuge richtig entscheiden würden, zu passieren, während ein achtes Fahrzeug einen Unfall verursachen könnte, wenn es sich nicht entschließt, anzuhalten.
Problem drei.
Wohl wissend, dass die maximale rote Signalzeit der Problem-1-Ampel 45 Sekunden beträgt, was ist die maximale Anzahl von Fahrzeugen, die das nicht können?
Lösung:
Wir wissen, dass während der Rotlichtampel Fahrzeuge anhalten müssen, und es ist möglich herauszufinden, wie viele dies tun müssen. Da die Anzahl der Fahrzeuge, die anhalten und ist die maximale Zeit der roten Ampel, habenwir: 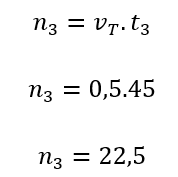
Wie bei früheren Problemen erzeugte die resultierende Dezimalzahl Fragen, die es ermöglichten, über das Paradigma der mathematischen Genauigkeit nachzudenken. Bei der Lösung dieses letzten Problems haben wir beispielsweise darüber diskutiert, was dieses Medium bedeuten würde, das mit einer minimalen Wartezeit oder einem beschleunigten Fortschritt des gelben Signals zusammenhängen könnte. Es ist erwähnenswert, dass diese Debatte ethische Fragen im Zusammenhang mit der Verkehrserziehung erreicht hat und die ursprünglich skizzierten mathematischen Ziele überstieg.
Aus diesen Problemen konnten einige mathematische Konzepte, insbesondere Vernunft und Verhältnismäßigkeit, diskutiert werden. Wir können bestätigen, dass die Aktivität mit dem Einsatz von Robotik es ermöglichte, den Schüler zu ermutigen, das Verständnis von mathematischen Konzepten zu entwickeln, zusätzlich zur Erweiterung ihres Wissens in anderen Bereichen.
ABSCHLIEßENDE ÜBERLEGUNGEN
In der Absicht, einige Möglichkeiten des Einsatzes von Robotik in Mathematik-Klassen zu zeigen, basieren wir auf Studien zu diesem Thema, vor allem in der Ausarbeitung und Ausführung von Algorithmen für die Durchführung von Aufgaben. In diesem Zusammenhang haben wir die Arbeit des Aufbaus einer einfachen Ampel ausgearbeitet, damit die Schüler mit Hilfe von Roboterinstrumenten mathematische Konzepte entwickeln können.
Herausgefordert durch die Probleme, die mit dem Bau der einfachen Ampel verbunden sind, versuchten die Schüler, sich zu verbessern und ihre Kreativität und Kritikalität zu entwickeln. In unseren Aktivitäten bemerkten wir, dass es einen Raum für Wissensaustausch gab, der es dem Schüler ermöglichte, seine anfänglichen Schwierigkeiten zu reduzieren und dazu angestiftet zu werden, Mathematik zu lernen.
Wir können sagen, dass der Einsatz von Robotik in Mathematikklassen zur Verbesserung des Lernens beitragen kann. Angesichts der beginnenden Vorschläge für diese Verwendung wissen wir jedoch, dass es notwendig ist, in Werke zu investieren, die dieses Thema diskutieren, insbesondere in die Lehrerausbildung.
REFERENZEN
ALMEIDA, M. A. Possibilidades da robótica educacional para a educação matemática. Dia a dia Educação. Curitiba – PR. 2008. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/363-4.pdf. Acesso em 7, jan. 2020.
ATTROT, W.; AYROSA, P. P. da S. Aplicações da Robótica no Ensino de Ciência da Computação. Artigo para SBC 2002. Londrina, 2002.
ALVES, E.M.S. Ludicidade e o Ensino de Matemática. (2006). Papirus Editora.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, DF: MEC/CNE, 2017.
CRUZ, M.E.J.K.; LUX, B.: HAETIGER, W.: ENGELMANN, E. H. C.; HORN, F. Formação Prática do Licenciando em Computação para Trabalho com Robótica Educativa. São Paulo: XVIII Simpósio Brasileiro de Informática na Educação, 2007.
GAROFALO, D. Como levar o STEAM para a sala de aula. Nova Escola, 25, jun. de 2019. Disponível em: https://novaescola.org.br/conteudo/18021/como-levar-o-steam-para-a-sala-de-aula. Acesso em: 19, jun. 2020.
MILL, D.; CÉSAR, D. Estudo sobre dispositivos robóticos na educação: sobre a exploração do fascínio humano pela robótica no ensino-aprendizagem. In: MILL,D.(Org). Escritos sobre educação: Desafios e Possibilidades para ensinar e aprender com as tecnologias emergentes. São Paulo: Paulus, 2013. Cap. 10, p. 269-294.
OLIVEIRA, R. A robótica na aprendizagem da matemática: um estudo com alunos do 8º ano da escolariadade. Madeira/Protugal, 2007. Dissertação (Mestrado em Matemática para o Ensino), Universidade da Madeira, Madeira/ Portugal.
SANTOS, C.F.; MENEZES, C.S.A Aprendizagem da Física no Ensino Fundamental em um Ambiente de Robótica Educacional. São Leopoldo: Workshop de Informática na Educação/ XXV Congresso da Sociedade brasileira de Computação, 2005.
SILVA NETO, J. F. Concepções sobre a formação continuada de professores de matemática em Alagoas. Dissertação de Mestrado, Universidade Federal de Pernambuco, Programa de Pós-Graduação em Educação Matemática e Tecnológica, Recife, 2012.
VELLOSO, R. V. Educação e tecnologia em diálogo na cena contemporânea. Ponto de Acesso, Salvador, v.5, n. 2, p. 03-19, ago., 2011.
ANHANG – FUßNOTEN-REFERENZ
5. Dieses Programm integriert die Maßnahmen des Bildungsentwicklungsplans (PDE), der offiziell darauf abzielt, die Bildungsindizes durch die Ausweitung des Schultages und die Konzeption der Integralen Bildung zu verbessern. Speziell für diese Schulgemeinschaft veranstaltete das Novo Mais Educação-Programm im Jahr 2019 Alphabetisierungs- und Mathematik-Workshops, um einige der Schwierigkeiten der Schüler zu lösen.
[1] Doktorand in Bildung, Master in Mathematik, Postgraduate in Mathematik und Statistik, Abschluss in Mathematik Bachelor-Abschluss.
[2] Postgraduate in Exercise Physiology and Biomechanics, Graduateed in Physical Education Degree.
[3] Postgraduate in Mathematics, Graduated in Mathematics Bachelor es Degree.
[4] Doktorand in Bildung, Master in Mathematik und technologische Rundbildung, Spezialist für Mathematik Lehre Programmierung, Abschluss in Mathematik.
Eingereicht: Dezember 2020.
Genehmigt: Dezember 2020.


