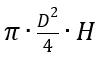ARTICOLO ORIGINALE
RASI, José Roberto [1], CAUNETTO, Donizete [2], BROETTO, Jonathan Figueiredo [3]
RASI, José Roberto. CAUNETTO, Donizete. BROETTO, Jonathan Figueiredo. Serbatoio metallico per serbatoio d’acqua in Brasile: uno studio dell’applicazione parziale dell’API 650. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 05, Vol. 01, pp. 33-62. maggio 2020. ISSN: 2448-0959, Collegamento di accesso: https://www.nucleodoconhecimento.com.br/ingegneria-civile/serbatoio-metallico
RIEPILOGO
Con la crescente domanda di riserve idriche e la mancanza di standard tecnici per i serbatoi metallici in Brasile, diversi produttori di serbatoi hanno parzialmente utilizzato API 650 per dimensionare e verificare questi serbatoi. In questo lavoro sono stati effettuati studi per verificare l’applicazione parziale e integrale dell’API 650, metodo 1 piede, attraverso il dimensionamento di 7 serbatoi metallici con lo stesso volume in funzione di diversi rapporti altezza/diametro (H/D). Analizza le sollecitazioni circonferenziali in entrambi i casi e il dimensionamento previsto nell’API 650 e determina i rapporti altezza/diametro più economici per lo stoccaggio dell’acqua.
Parole chiave: serbatoio metallico, standard API 650, dimensionamento, ottimizzazione.
1. INTRODUZIONE
I serbatoi cilindrici sono strutture comunemente utilizzate per lo stoccaggio di acqua, rifiuti industriali, rifiuti petrolchimici, oli, cereali e così via (HECKE, 2010).
Secondo Barros (2010), sono attrezzature per caldaie pesanti, soggette a pressione approssimativamente atmosferica, di solito nell’intervallo da 0 a 0,5 psi e destinate principalmente allo stoccaggio di petrolio e suoi derivati.
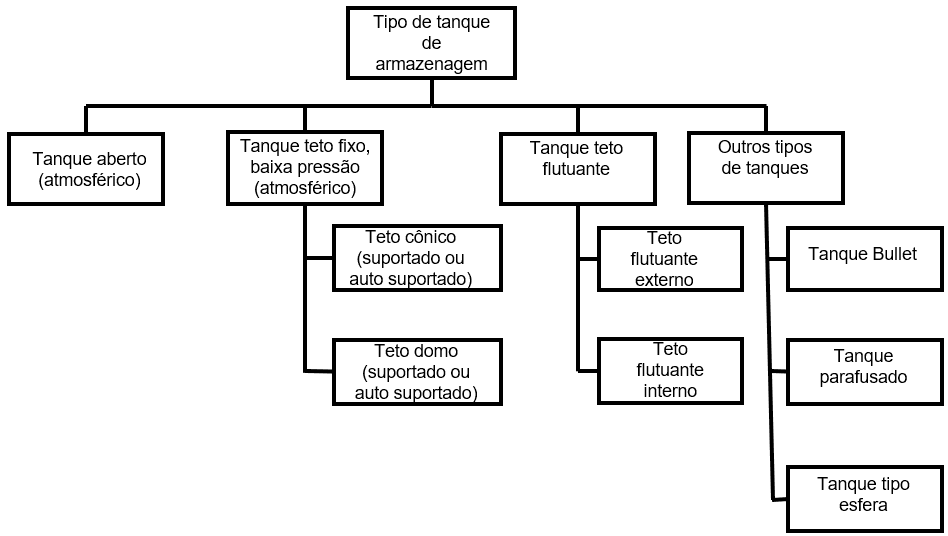
Roncetti (2011) afferma che c’è stato un aumento della domanda di stoccaggio della rinfusa liquida in varie attività economiche e anche l’aumento della domanda di attività intermedie come servizi igienico-sanitari, trattamento dei rifiuti, refrigerazione e altri processi di produzione, dove è necessario immagazzinare granei liquidi. La figura 1 illustra i vari tipi di serbatoi di stoccaggio comunemente utilizzati dalle industrie (KUAN, 2009).
Figura 1 – Tipi di serbatoi di stoccaggio.
La progettazione e la costruzione di serbatoi cilindrici atmosferici comporta una serie di cure speciali e richiede la conoscenza di standard tecnici e materiali adatti a ogni tipo di applicazione, perché guasti in queste apparecchiature possono causare grandi perdite finanziarie o addirittura perdite di vite umane (NUNES, 2013).
In Brasile, esiste uno standard per la costruzione di queste attrezzature. Lo standard NBR 7821 – Serbatoi saldati per lo stoccaggio di petrolio e derivati – pubblicato dall’Associazione brasiliana di standard tecnici (ABNT). Tuttavia, lo standard più utilizzato nei settori in generale è l’American Regulatory Standard API 650 – Welded Steel Tanks for Oil Storage – dell’American Petroleum Institute (API), entrambi destinati alla riserva di petrolio e derivati (SATO, 2015).
Secondo Barros (2010), API 650 copre le specifiche su materiale, progettazione, produzione, assemblaggio e collaudo di serbatoi di stoccaggio verticali, cilindrici, nonburati, con la costruzione saldata superiore chiusa o aperta, con varie dimensioni e capacità, per il servizio non refrigerato, con una temperatura massima di progettazione di 260 ° C e una pressione interna approssimativamente atmosferica (non superiore a 2,5 psig).
Secondo Azzumi e Guzey (2015), in conformità con API 650, i tre metodi per determinare lo spessore del serbatoio dei serbatoi cilindrici di stoccaggio in acciaio progettati in conformità con API 650 sono:
Il metodo a un piede (1FM), il metodo VDM (Variable Design Point Method) e l’analisi lineare. Abbiamo confrontato i progetti di conchiglie sulla base di questi tre metodi per diverse proprietà del serbatoio: diametro, altezza e tensione consentite.
Il metodo di un piede (1FM), che si basa su ” teoria della membrana ”. Lo spessore richiesto della piastra di peeling per ogni corsa di buccia viene calcolato utilizzando la sollecitazione circonferenziale in un punto di 0,3 m (1 piede) sopra la cucitura orizzontale della saldatura inferiore del ferrule della casseruola a causa della pressione idrostatica del liquido immagazzinato. Il 1FM viene utilizzato con successo per la maggior parte dei carri armati. Tuttavia, i progetti basati su 1FM possono diventare conservativi e proibitivi per serbatoi di diametro maggiore. Pertanto, API 650 limita l’applicabilità di questo metodo a serbatoi fino a 61 m (200 piedi) di diametro.
Il secondo metodo per calcolare lo spessore richiesto della piastra del guscio è il metodo VDM (Variable Design Point) che si basa anche sulla “teoria delle membrane”. Il VDM fu proposto da Zick e McGrath nel 1968 e successivamente adottato dall’API 650 come metodo raffinato per calcolare lo spessore richiesto della piastra dello scafo, specialmente per serbatoi di diametro superiore a 61 m (200 piedi). Il VDM tiene conto della restrizione fornita dalle piastre inferiori del serbatoio per la prima esecuzione del ferrule e della restrizione fornita da ogni ferrule inferiore per il percorso ferrule superiore. Il VDM utilizza una distanza variabile invece di una distanza fissa di 0,3 m (1 piede), come utilizzato in 1FM, sopra la saldatura circonferenziale (cucitura) per ogni runof run, per calcolare la massima sollecitazione circonferenziale dovuta alla pressione idrostatica.
Il terzo metodo fornito nell’API 650 è il calcolo dello spessore del guscio utilizzando l’analisi lineare. In questo approccio, le condizioni limite per l’analisi dovrebbero essere un momento plastico correlato alla resa della piastra sotto il guscio e al movimento radiale totalmente limitato al fondo del guscio. API 650 non descrive uno specifico metodo di analisi lineare. In questo studio, abbiamo sviluppato un nuovo metodo utilizzando la teoria della corteccia fine per eseguire un’analisi lineare dello spessore della corteccia di calcolo. In questo metodo, stiamo usando l’esatta rigidità – relazioni di flessibilità e funzioni esatte della forma originate dalla cosiddetta soluzione “guscio corto” delle equazioni che governano dalla teoria della buccia elastica fine.
C’erano poche informazioni letterarie per il calcolo di un serbatoio metallico per la riserva d’acqua e la mancanza di standard tecnici specifici per i serbatoi saldati per lo stoccaggio dell’acqua in Brasile.
A causa della mancanza di una norma tecnica specifica, è stato utilizzato come parametro di calcolo per i serbatoi metallici destinati alla riserva idrica, API 650 nella sua interezza o solo parzialmente, specificamente per quanto riguarda la determinazione degli spessori delle coste dell’acqua e le sollecitazioni ammissibili, poiché i criteri di sicurezza per gli incendi e le esplosioni del materiale immagazzinato non si approcherebbero sull’acqua.
2. MATERIALE E METODO
L’obiettivo principale di questo lavoro è quello di verificare la progettazione di serbatoi metallici aperti, senza tetto, con lo stesso volume e H/D diversi, secondo l’API 650, con il metodo a un piede (1FM), in due fasi, la prima considerando solo gli spessori calcolati dall’equazione descritta al punto 5.6.3.2 di tale norma;
Dove:
 td =spessore del progetto, in mm;
td =spessore del progetto, in mm;
D = diametro nominale del serbatoio, in m;
H = livello di progettazione liquida, in m;
G = peso liquido specifico nel caso dell’acqua: 1;
AC = sovrascrizione alla corrosione, specificata dall’acquirente, in mm;
Sd = tensione ammissibile (tabella 5-2 API 650), in Mpa.
E nella seconda fase, oltre al controllo dello spessore calcolato dall’equazione 1, vengono adottati anche gli spessori minimi, come descritto al punto 5.6.1.1 e mostrato nella tabella 1.
Tabella 1 – Spessori minimi dei trefoli

Come obiettivo complementare, determinare l’intervallo di rapporto H/D che è il più economicamente sostenibile, con il peso più basso di costruzione del serbatoio saldato.
Il criterio per determinare la relazione tra l’altezza (H) e il diametro (D) dei modelli è il volume del serbatoio, mantenuto costante, con 660,00 m³ e diametro massimo inferiore a 15,00 m secondo il punto 5.6.1.1 – API 650, mostrato nella tabella 1. Di conseguenza, per il volume costante (V0) e considerato i rapporti altezza / diametro (H / D) tra 0,25 e 4,0.
Definito: H = altezza del cilindro; D = diametro e V= volume =
Le dimensioni dei diametri, delle altezze e delle proporzioni tra di essi sono descritte nella tabella 2 e nella figura 2.
Tabella 2 – Rapporti altezza/diametro in volume costante di 660,00 m³

Figura 2 – Modelli geometrici di serbatoi cilindrici studiati

L’acciaio utilizzato è l’ASTM A36, caratterizzato da un modulo di elasticità (E) pari a 205.000 Mpa, rapporto di Poisson (µ) pari a 0,30, densità (γ) di 77.000 N / mm³, sforzo di snervamento fy = 250 .00 Mpa e ultima tensione fu = 400.00 Mpa. Secondo la tabella 5-2 Permissible Plate Materials and Allowable Stresses dell’API 650, la sollecitazione consentita per l’acciaio ASTM A36 è 160,00 Mpa (tabella 3).
Tabella 3 – Materiali piatti consentiti e sollecitazioni ammissibili
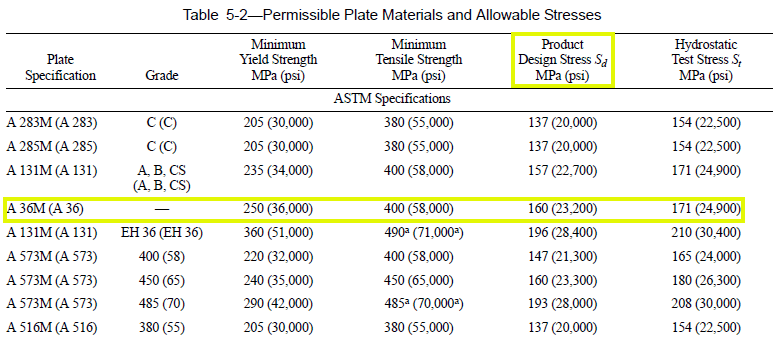
Fonte: API 650 (2007) – modificata dall’autore.
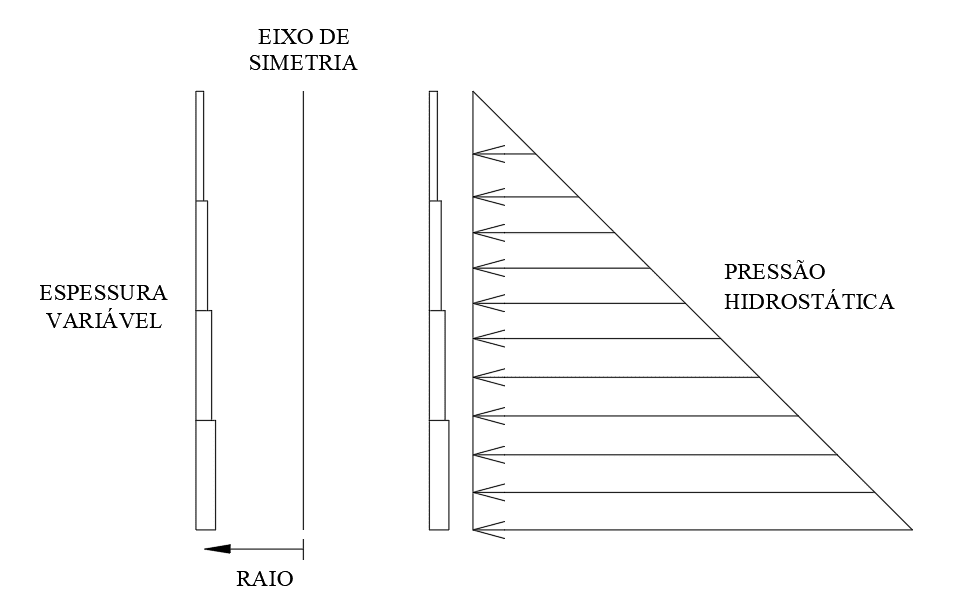
Lo spessore delle piastre del corpo del serbatoio è considerato variabile lungo l’altezza del serbatoio (figura 3).
Figura 3 – Variazione della piastra lungo l’altezza del serbatoio
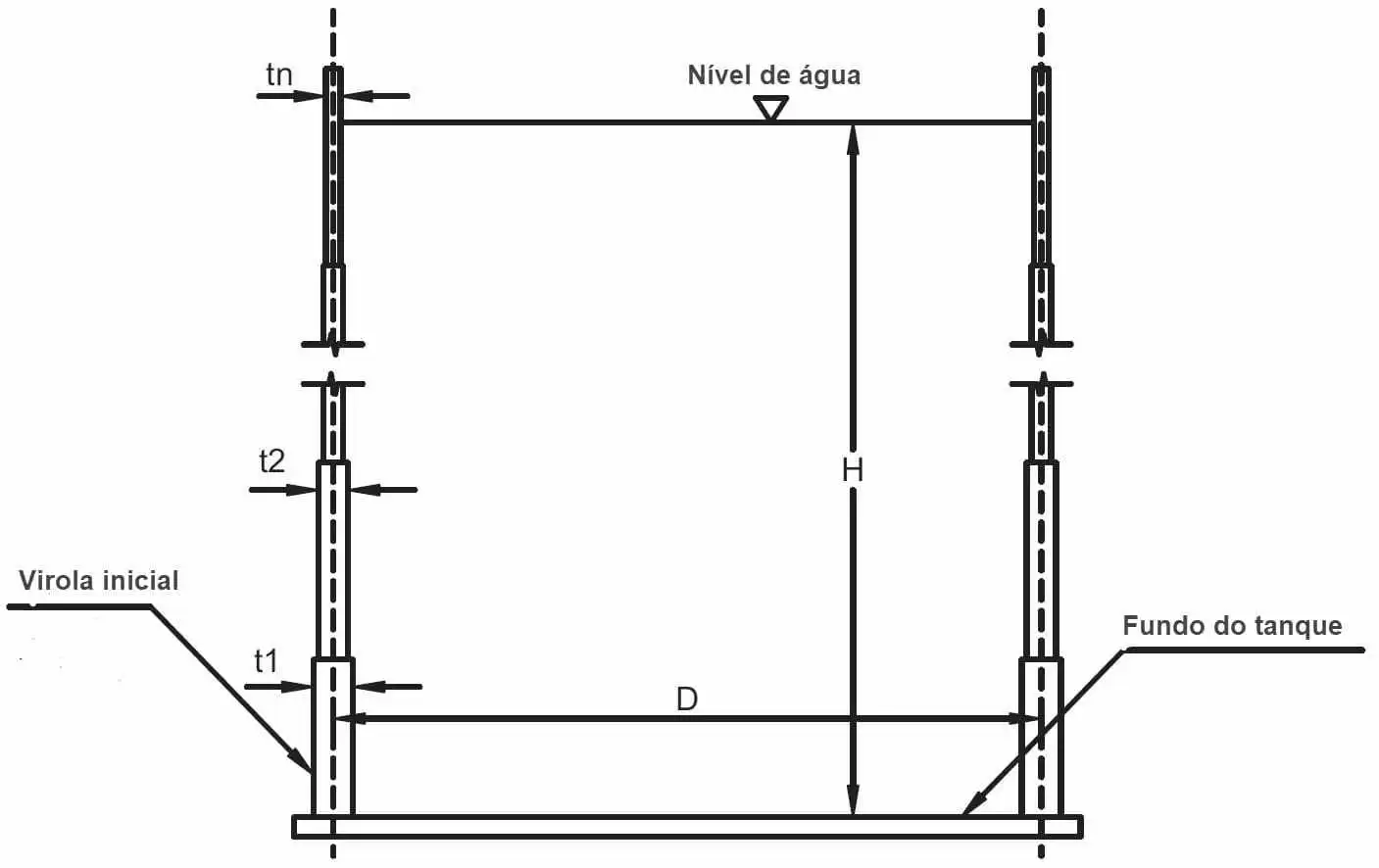
Considerando l’assenza di attrito dovuta al materiale immagazzinato (acqua), le condizioni del serbatoio sono completamente piene, la mancata applicazione del vento e le condizioni dello spessore delle piastre dei corpi dei serbatoi (virolas), risulta solo 1 (uno) caso di analisi (figura 4):
Figura 4 – Serbatoio con spessore della parete liquido e variabile sull’altezza
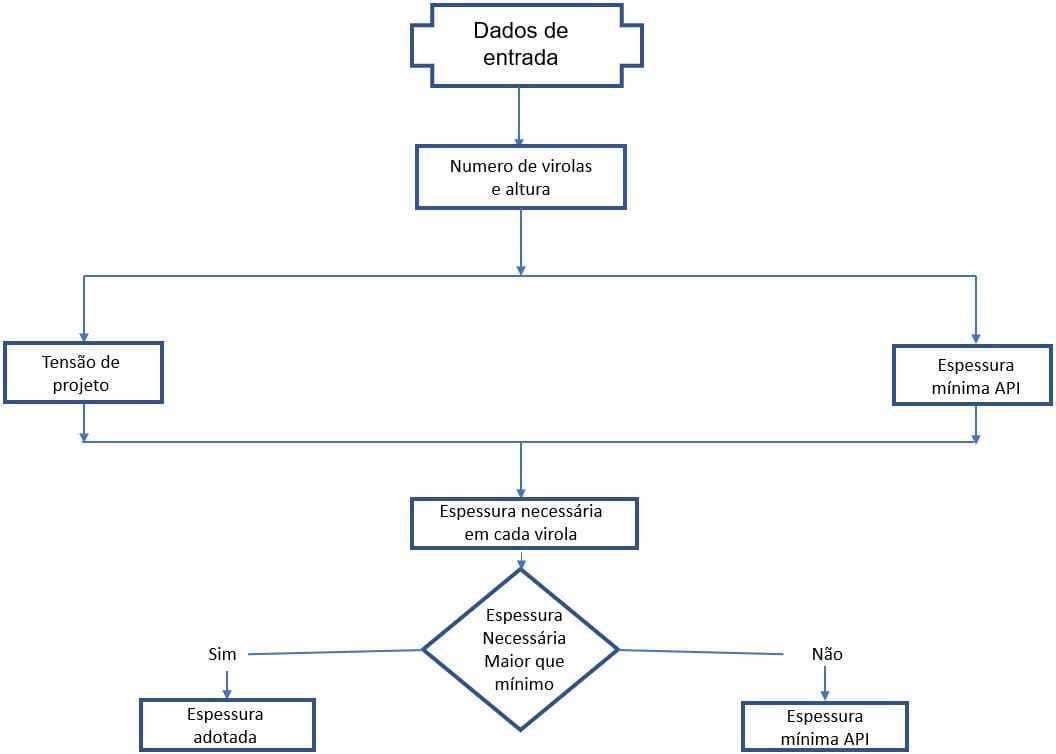
Il flussodi calcolo degli spessori dei mani di guerra dei serbatoi saldati esula dal diagramma mostrato nella figura 5.
Figura 5 – Diagramma di flusso del calcolo degli spessori delle lattine d’acqua delle cisterne
Fonte: L’autore stesso
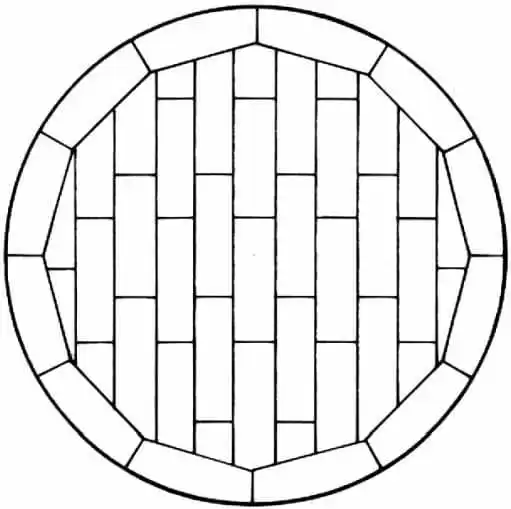
I pesi dei 7 serbatoi proposti in questo lavoro sono stati calcolati in due fasi. Il primo passo ha calcolato il peso dei fondi del serbatoio, considerando i fondi con piastre anulari (Figura 6), secondo la voce 5.4.1 di API 650 (Botton Plates), che prescrive lo spessore minimo di 6,00 mm (1/4). La sovrapposizione delle lastre di circa il 2,26% è stata considerata nel peso dei fondi del serbatoio.
Figura 6 – Disposizione tipica delle piastre inferiori con piastre anulari.
Sono stati presi in considerazione anche i pesi dei profili dell’angolo di rinforzo del bordo superiore, come specificato nella tabella 4 prescritta nella voce API 650 5.1.5.9 – Roof and Top-Angle Joints“, sovrapposti all’ultimo anello (ferrule) del lato, con patta orizzontale rivolta verso il lato esterno del serbatoio.
Prospetto 4 – Rinforzo del bordo superiore del lato.

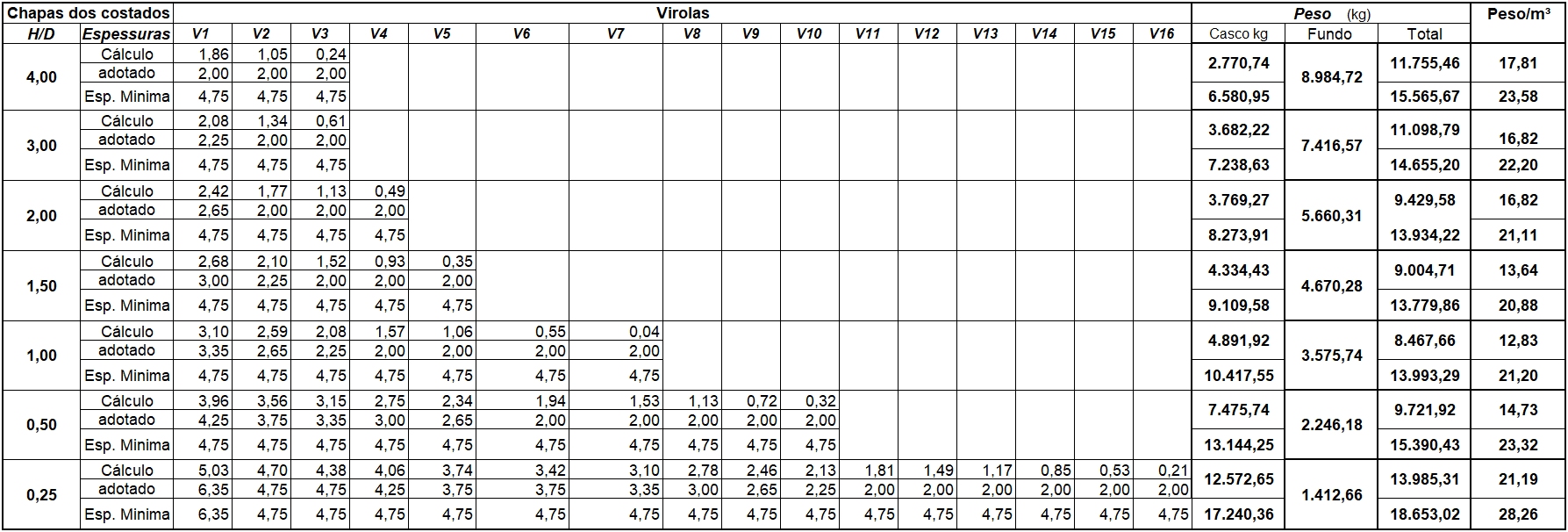
Il peso dei trefoli è stato determinato dopo aver determinato lo spessore di ciascuna piastra che compone le lattine d’acqua dei serbatoi per ciascun rapporto H/D, considerando gli spessori calcolati solo con l’equazione 1 e gli spessori considerando gli spessori minimi prescritti dall’API 650 (tabella 5). È stato utilizzato il metodo di un piede (1FM), con un’efficienza di saldatura di 1,00 (100%) e senza considerare la sovrascrienza da corrosione e le forze risultanti dall’azione dei venti non sono state applicate. Gli spessori utilizzati per il dimensionamento delle virolas erano (in millimetri): 2,00; 2,25; 2,65; 3,00; 3,35; 3,75; 4,25; 4,75 e 6,35, tutti con una larghezza di 1.500,00 mm.
Prospetto 5 – Spessore della piastra dei trefoli e dei pesi delle cisterne studiate.
3. ANALISI DEL METODO DEGLI ELEMENTI FINITI
Per l’analisi con il metodo FINITE ELEMENT MEF) dei 7 serbatoi con una capacità di 660,00 m³ e dimensioni descritte nella tabella 2, è stato utilizzato il software AUTODESK SIMULATION MECHANICAL 2018, con discretizzazione della rete in 150 x 150 mm (Figure 7 e 8).
Figura 7 – Discretizzazione del serbatoio H/D 1.00 – diametro e altezza 9,43m.
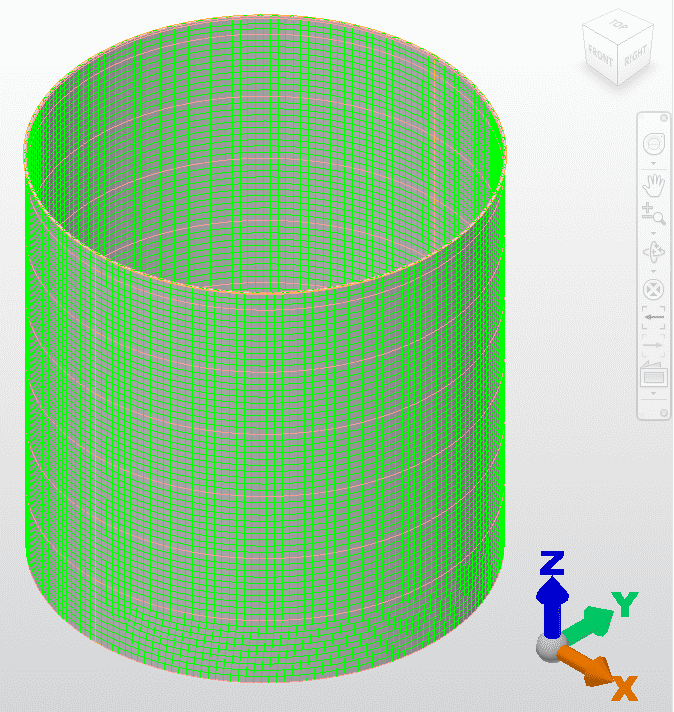
Figura 8 – Applicazione del serbatoio di carico dell’acqua H/D 1.00

Fonte: L’autore stesso
4. RISULTATI
Seguire i risultati dell’analisi utilizzando i metodi agli elementi finiti – MEF, dei 7 serbatoi proposti, utilizzando il software AUTODESK SIMULATION MECHANICAL 2018
4.1 SERBATOIO H/D = 4,00 – DIAMETRO14,98 M E ALTEZZA 3,75 M
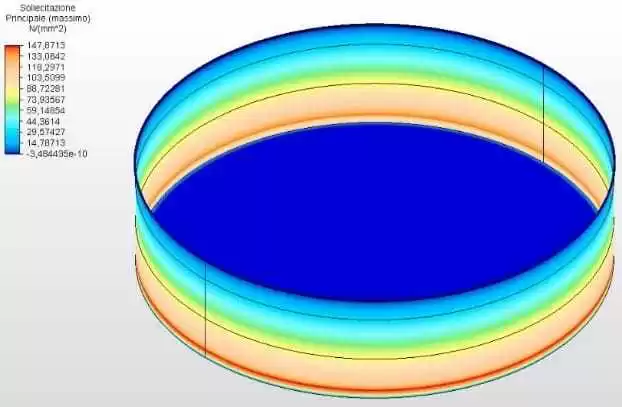
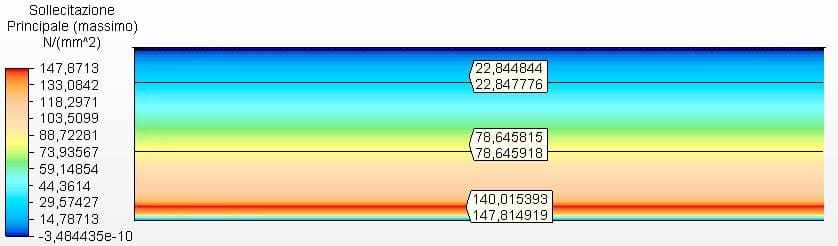
Le figure 9 e 10 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come 2,00 mm. La tensione massima di vibe 1 era di 147,81 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 9 – Sollecitazioni circonferenziali H/D 4.00 in 3D – spessori calcolati
Fonte: L’autore stesso
Figura 10 – Sollecitazioni circonferenziali H/D 4.00 in 2D – spessori calcolati
Fonte: L’autore stesso
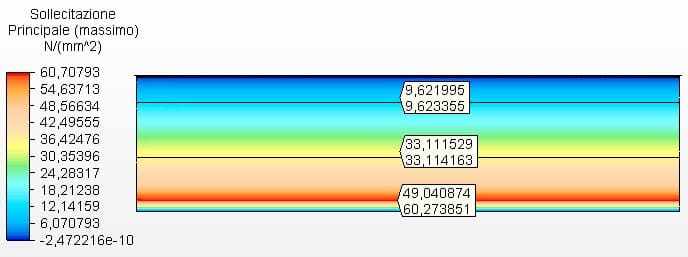
La figura 11 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, nel caso 4,75 mm. La tensione massima era di 60,27 MPa.
Figura 11 – Sollecitazioni circonferenziali H/D 4.00 negli spessori dei minimi 2D
Fonte: L’autore stesso
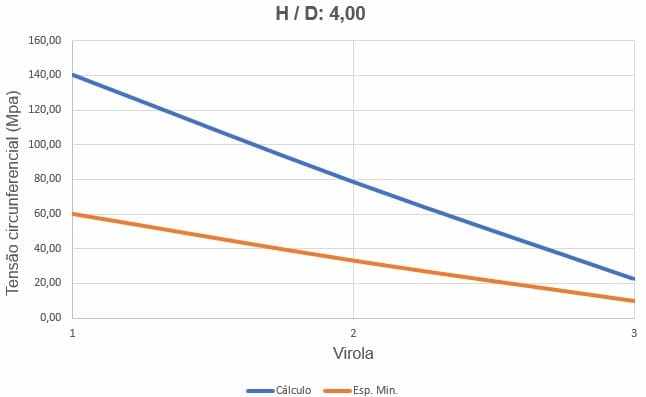
La figura 12 mostra le curve delle sollecitazioni circonferenziali, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 12 – Curve delle circonferenze del serbatoio H/D 4.00
4.2 SERBATOIO H/D = 3,00 – DIAMETRO 13,61 M E ALTEZZA 4,54 M
Le figure 13 e 14 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come ferrule 1 con 2,25 mm e l’altro con 2,00 mm. La tensione massima della virule 1 era di 146,67 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 13 – Tensioni circonferenziali H/D 3.00 in 3D – spessori calcolati
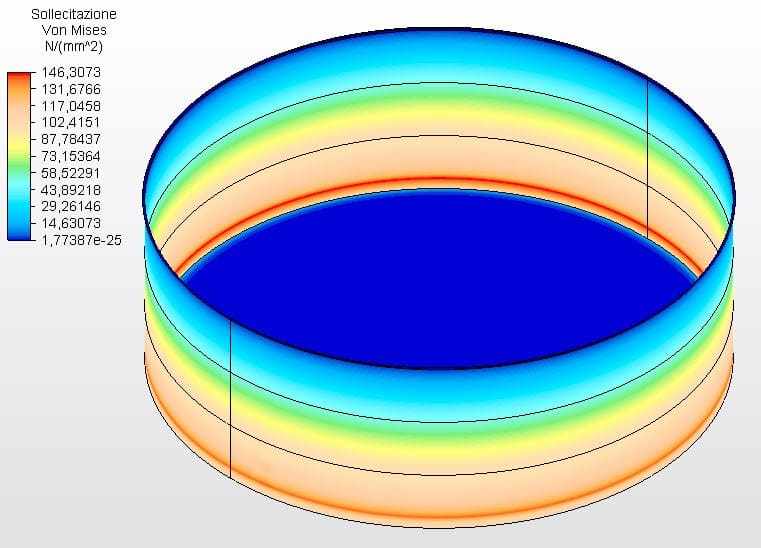
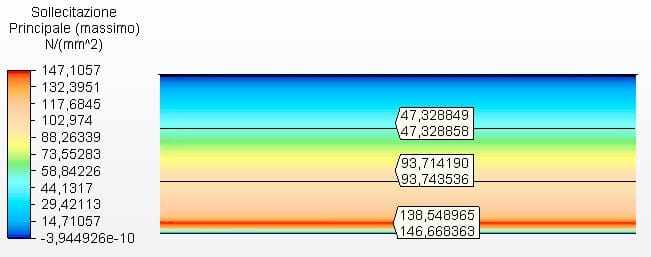
Figura 14 – Sollecitazioni circonferenziali H/D 3.00 in 2D – spessori calcolati
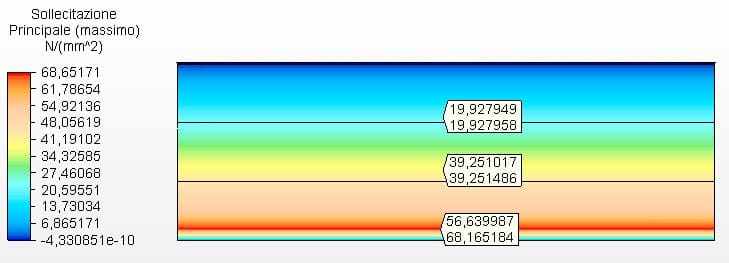
La figura 15 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, in questo caso 4,75 mm. La tensione massima era di 68,17 MPa.
Figura 15 – Sollecitazioni circonferenziali H/D 3.00 negli spessori dei minimi 2D
Fonte: L’autore stesso
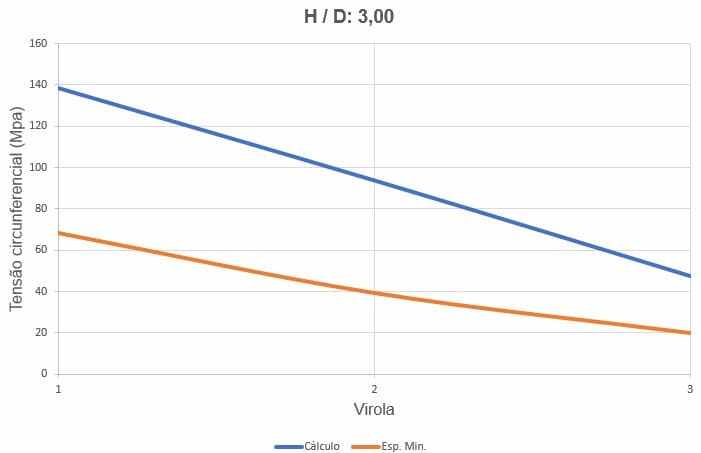
La figura 16 mostra le curve delle sollecitazioni circonferenziali, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 16 – Curve delle sollecitazioni circonferenziali del serbatoio H/D 3.00
Fonte: L’autore stesso
4.3 SERBATOIO H/D = 2,00 – DIAMETRO 11,89 M E ALTEZZA 5,94 M
Le figure 17 e 18 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come ferrule 1 con 2,65 mm e l’altro con 2,00 mm. L’atmosfera massima 1 tensione era di 144,65 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 17 – Sollecitazioni circonferenziali H/D 2.00 in 3D – spessori calcolati
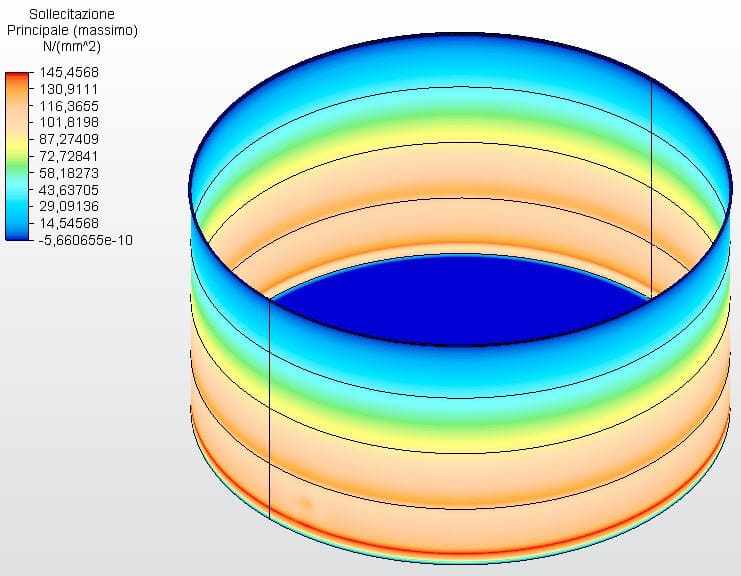
Fonte: L’autore stesso
Figura 18 – Sollecitazioni circonferenziali H/D 2.00 in 2D – spessori calcolati
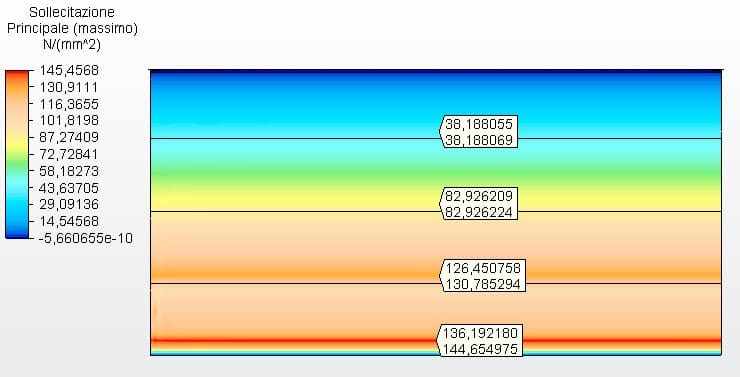
Fonte: L’autore stesso
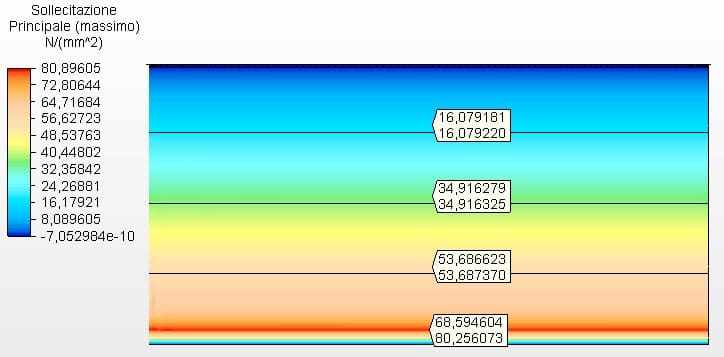
La figura 19 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, nel caso di 4,75 mm. La tensione massima era di 80,26 MPa.
Figura 19 – Sollecitazioni circonferenziali H/D 2.00 negli spessori dei minimi 2D
Fonte: L’autore stesso
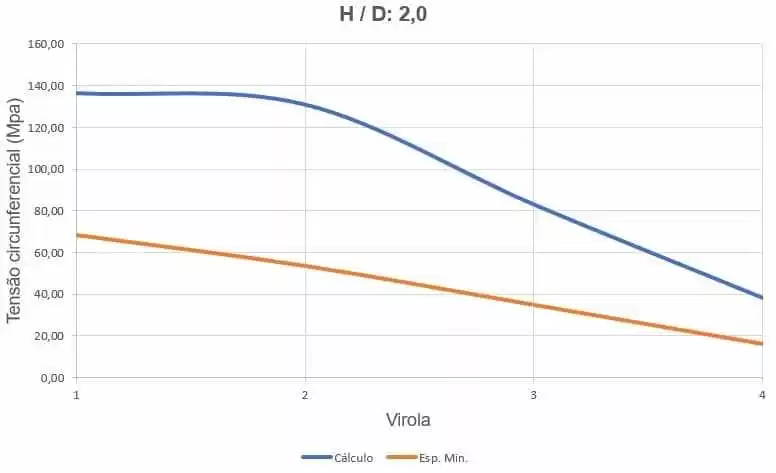
La figura 20 mostra le curve delle sollecitazioni circonferenziali, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 20 – Curve delle sollecitazioni circonferenziali del serbatoio H/D 2.00
Fonte: L’autore stesso
4.4 SERBATOIO H/D = 1,00 – DIAMETRO 9,43 M E ALTEZZA 9,43 M
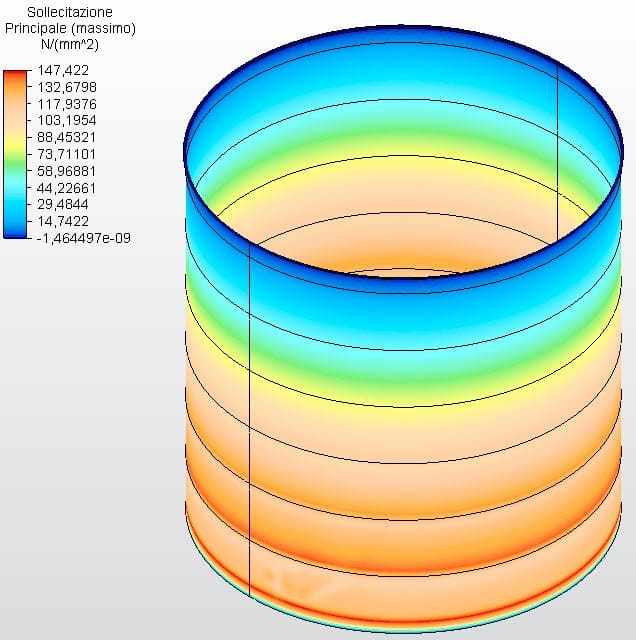
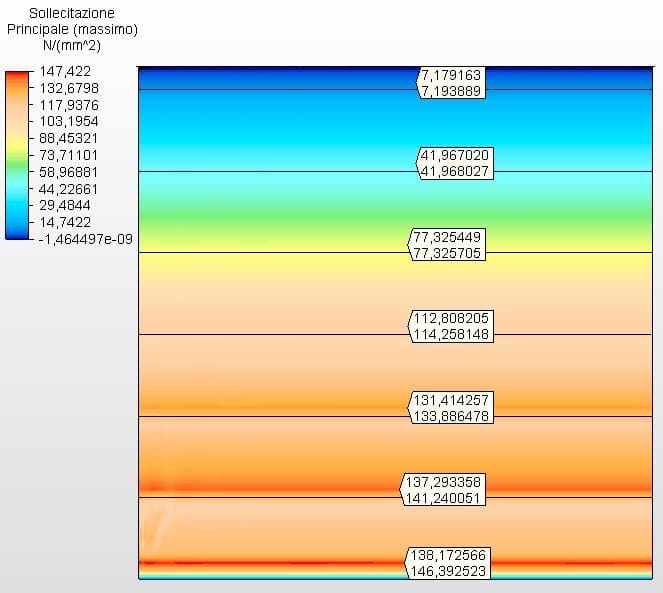
Le figure 21 e 22 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come ferrule 1 con 3,35 mm, ferrule 2 con 2,65 mm, ferrule 3 con 2,25 mm e l’altro con 2,00 mm. La tensione massima di vibe 1 era di 146,39 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 21 – Sollecitazioni circonferenziali H/D 1,00 in 3D – spessori calcolati
Fonte: L’autore stesso
Figura 22 – Sollecitazioni circonferenziali H/D 1.00 in 2D – spessori calcolati
Fonte: L’autore stesso
La figura 23 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, in questo caso 4,75 mm. La tensione massima era di 104,02 MPa.
Figura 23 – Sollecitazioni circonferenziali H/D 1.00 negli spessori dei minimi 2D
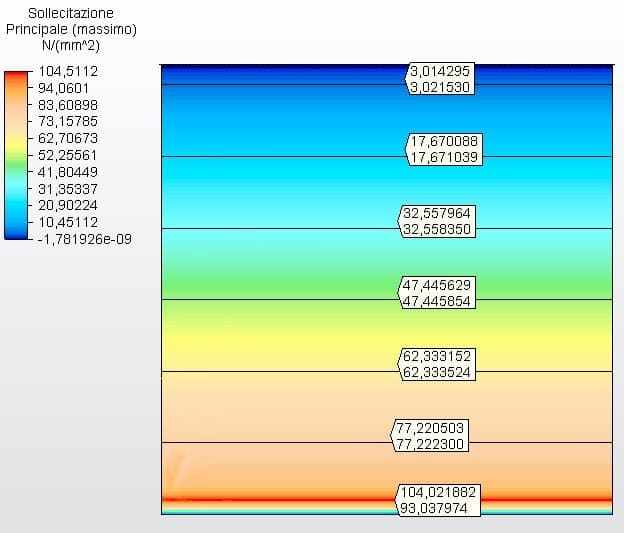
Fonte: L’autore stesso
La figura 24 mostra le curve di sollecitazione circonferenziale, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 24 – Curve di sollecitazioni circonferenziali del serbatoio H/D 1.00
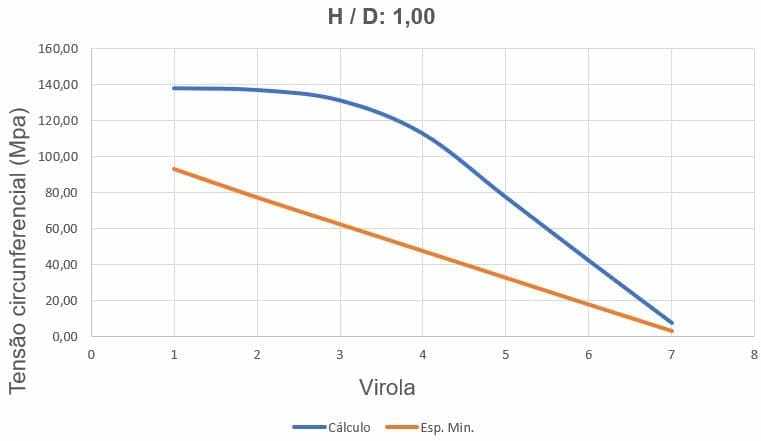
Fonte: L’autore stesso
4,5 SERBATOIO H/D = 0,50 – DIAMETRO 7,49 M E ALTEZZA 14,98 M
Le figure 25 e 26 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come ferrule 1 con 4,25 mm, ferrule 2 con 3,75 mm, ferrule 3 con 3,35 mm, ferrule 4 con 3,00, ferrule 5 con 2,65 mm e l’altro con 2,00 mm. L’atmosfera massima 1 tensione era di 146,86 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 25 – Tensioni circonferenziali H/D 0,50 in 3D – spessori calcolati
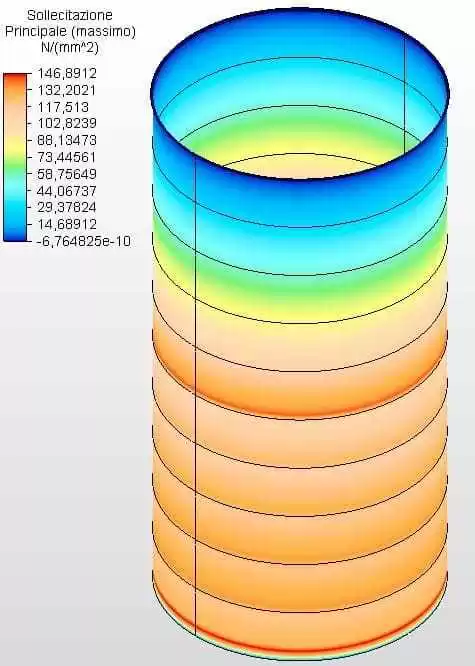
Figura 26 – Sollecitazioni circonferenziali H/D 0,50 in 2D – spessori calcolati

Fonte: L’autore stesso
La figura 27 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, nel caso 4,75 mm. La tensione massima era di 132,09 MPa.
Figura 27 – Tensioni circonferenziali H/D 0,50 negli spessori dei minimi 2D
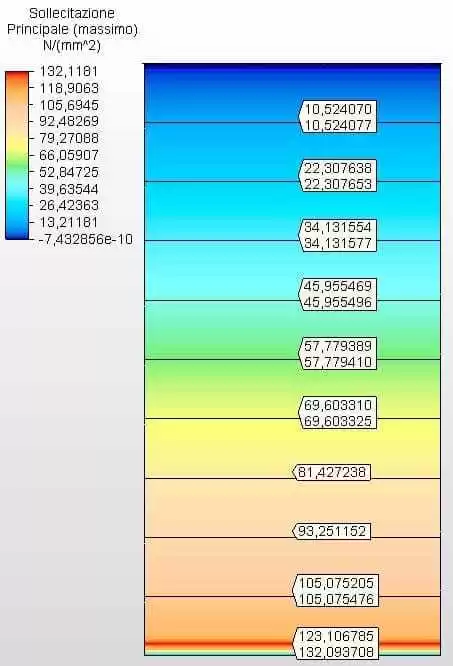
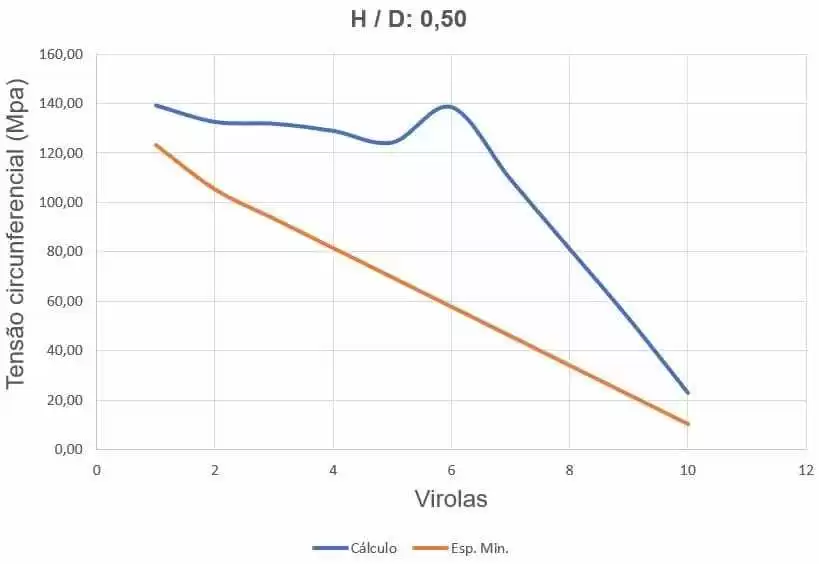
figura 28 mostra le curve delle sollecitazioni circonferenziali, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 28 – Curve delle sollecitazioni circonferenziali del serbatoio H/D 0,50
Fonte: L’autore stesso
4.6 SERBATOIO H/D = 0,25 – DIAMETRO 5,94 M E ALTEZZA 23,77 M
Le figure 29 e 30 mostrano le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati secondo l’equazione 1 e assunti come ferrule 1 con 6,35 mm, ferrule 2 con 4,75 mm, ferrule 3 con 4,25 mm, ferrule 4 con 4,25, ferrule 5 con 3,75 mm, ferrule 6 con 3,75 mm, ferrule 7 con 3,35 mm, ferrule 8 con 3,00 mm , ferrule 9 con 2,65 mm, ferrule 10 con 2,25 mm e l’altro con 2,00 mm. L’atmosfera massima 1 tensione era di 129,72 Mpa, inferiore alla sollecitazione ammissibile dell’acciaio ASTM A36 di 160,00 Mpa, secondo la tabella 5-2 dell’API 650.
Figura 29 – Sollecitazioni circonferenziali H/D 0,25 in 3D – spessori calcolati
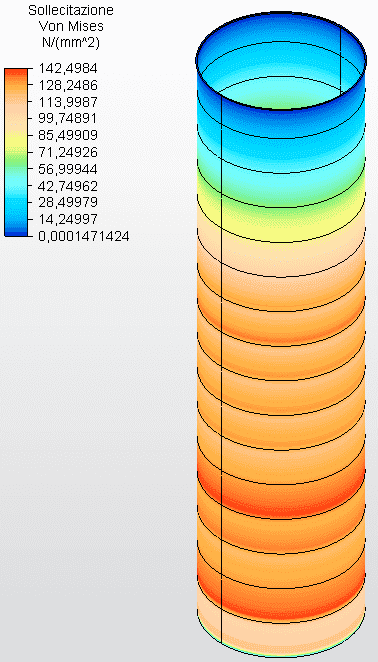
Fonte: L’autore stesso
Figura 30 – Sollecitazioni circonferenziali H/D 0,25 in 2D – spessori calcolati
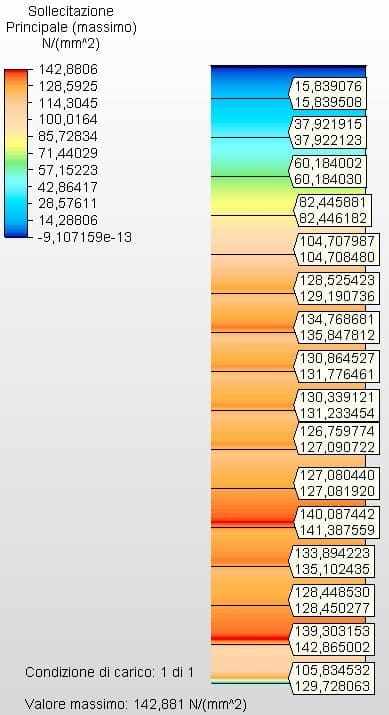
Fonte: L’autore stesso
La figura 31 mostra le sollecitazioni circonferenziali con gli spessori del serbatoio calcolati in base agli spessori minimi di API 650, in questo caso 6,35 mm. La tensione massima era di 129,72 MPa.
Figura 31 – Sollecitazioni circonferenziali H/D 0,25 negli spessori dei minimi 2D

Fonte: L’autore stesso
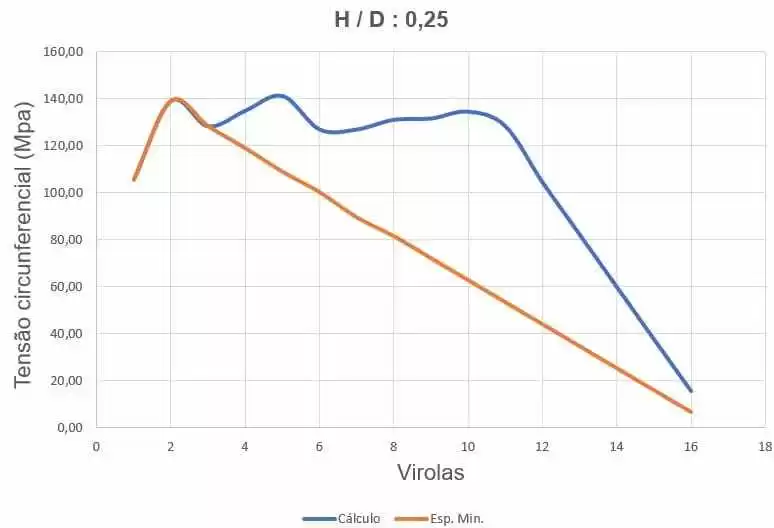
La figura 32 mostra le curve delle sollecitazioni circonferenziali, a seconda dello spessore delle ferrules e dell’altezza di carico dell’acqua.
Figura 32 – Curve delle circonferenze del serbatoio H/D 0,25
4.7 CURVA A BANDA H/D A PESO PIENO OTTIMALE
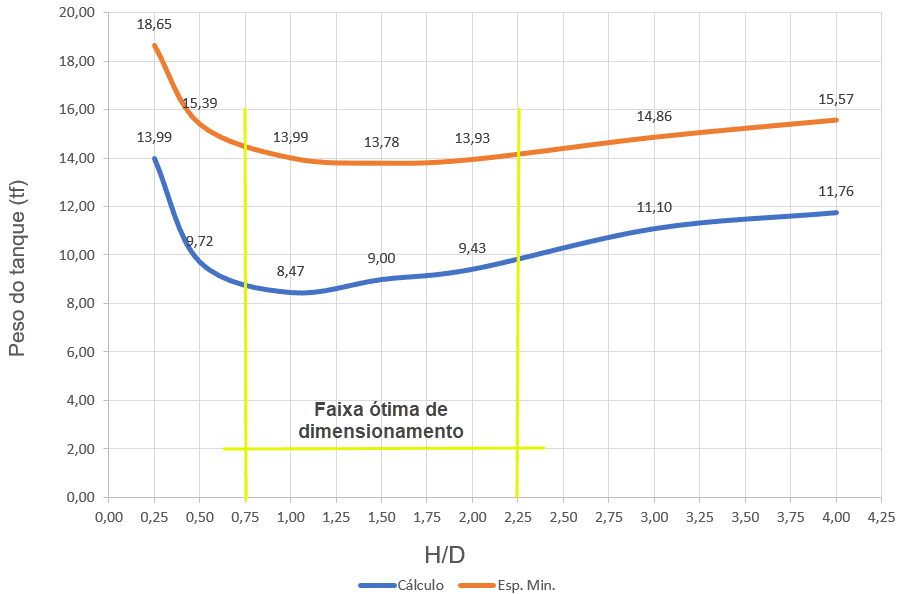
La figura 33 mostra le curve di peso tipiche in funzione dell’H/D, per i serbatoi per senzatetto, di spessori variabili, dimensionate secondo la prescrizione dell’API 650, con applicazione dell’equazione 1 (curva rossa) e degli spessori minimi (curva blu).
L’intervallo ottimale, per entrambi i criteri di dimensionamento, è compreso tra H/D = 0,75 a H/D = 2,25.
Figura 33 – Curve di peso tipiche dei serbatoi per senzatetto in funzione del rapporto H/D.
Fonte: L’autore stesso
5. CONCLUSIONE
Dai risultati presentati, si conclude che è possibile, per la riserva d’acqua, stabilire rapporti H/D ottimali che puntino ad un peso minimo del serbatoio, anche considerando i 2 criteri di dimensionamento, cioè spessori con solo l’applicazione dell’equazione 1 e spessori tenendo conto degli spessori minimi prescritti dall’API 650.
Per il dimensionamento delle cisterne metalliche per la riserva d’acqua, qualora non si applichino i criteri di sicurezza per gli incendi e le esplosioni, l’impiego del dimensionamento con solo gli spessori determinati dall’equazione 1 può essere accettabile, in quanto le sollecitazioni di circonferenza determinate dal MEF (Metodo degli elementi finiti) sono sempre state inferiori alle sollecitazioni ammissibili stabilite nella tabella 5-2 dell’API 650.
RIFERIMENTI
AMERICAN PETROLEUM INSTITUTE. API Standard 650: Welded steel tanks for oil storage. 12 th ed. Washington DC, 20013.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7821 – Tanques soldados para armazenamento de petróleo e derivados. Rio de Janeiro. 1983.
AZZUMI, E., GUZEY, S. Comparison of the shell design methods for cylindrical liquid storage tanks. Engineering Structures 101. 2015.
BARROS, S. M. Tanques de armazenamento. Universidade Petrobras. Rio de Janeiro. 2010.
HECKE, M. B. Elementos finitos aplicados à engenharia de estruturas. Reservatórios cilíndricos e silos metálicos. Universidade Federal do Paraná. Curitiba. 2010.
KUAN, S. Y. Design, Construction and Operation of the Floating Roof Tank. University of Soutthern Queensland. Queensland. 2009.
NUNES, C. P. Uma metodologia de projetos de tanques atmosféricos verticais para armazenamento de petróleo e seus derivados. Monografia. Escola de Engenharia da Universidade Federal do Rio Grande do Sul. Porto Alegre. 2013.
RONCETTI, L. Otimização estrutural e econômica de tanques de armazenamento construídos em aço. Anais do 66º Congresso Anual da Associação Brasileira de Metalurgia e Materiais – ABM. São Paulo. 2011.
SATO, A. K. Projeto de um tanque de armazenamento atmosférico com teto flutuante para estocagem de gasolina. Trabalho de graduação. Faculdade de Engenharia do Campus de Guaratinguetá, UNESP. Guaratinguetá, 2015.
ZICK L.P., MCGRATH R.V. Design of large diameter cylindrical shells. Proc. Division Refining, AMERICAM PETROLEUM INSTITUTE. New York. 1968.
[1] Laurea magistrale in Strutture e Edilizia Civile; Specializzazione in Costruzioni Industriali; Specializzazione in Ingegneria Ambientale; Specializzazione in Ingegneria della Sicurezza; Ingegnere civile e ingegnere operativo meccanico.
[2] Specializzazione in Ingegneria Strutturale e Ingegneria Civile.
[3] Ingegnere civile.
Inviato: Aprile, 2020.
Approvato: maggio 2020.