ARTIGO ORIGINAL
RODRIGUES, Rosimeire dos Santos [1], SABIÃO, Roseline Martins [2]
RODRIGUES, Rosimeire dos Santos. SABIÃO, Roseline Martins. A história da matemática e a importância da geometria. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 06, Vol. 01. pp. 96-110 Junho de 2019. ISSN: 2448-0959
RESUMO
O presente estudo refere-se ao estudo da Matemática e, mais explicitamente, à Geometria, ciência que faz parte desta disciplina. A história da matemática se enleia na história da geometria desde os primórdios da História do homem. É na busca pelos fatos que compõem a existência deste conhecimento que se revela em todos os lugares e profissões exercidas pelo homem que foi realizada uma pesquisa qualitativa bibliográfica, baseada na filosofia utilizada por muitos estudiosos, e mostrou que os autores estudados relacionam até mesmo a natureza ás formas geométricos numa forma de tornar mais fácil e compreensível o estudo de diversas ciências. Realizou-se ainda uma pesquisa em sites como Scielo, Bireme, Lilacs ou portais educacionais e pode-se perceber a geometria beneficia às crianças no que se refere ao lúdico que transforma a aprendizagem em uma maneira divertida de aprender. Além disso, teve como objetivos a obtenção do saber e as áreas empregadas e qual é a utilização diária desta ciência. É essencial saber relacionar a Geometria a métodos práticos dentro do objetivo de se fazer uma aprendizagem significativa.
Palavras chave: Geometria, ciência, profissões, aprendizagem.
1. INTRODUÇÃO
Este trabalho de conclusão de curso tem por objetivo mostrar a importância da Matemática na vida do ser humano desde seu surgimento ao longo da história e lado a lado a ela destacar o valor da geometria no contexto da vida humana.
A Matemática surgiu quando o homem sentiu necessidade de contar os objetos que ele possuía, de saber seus lucros e perdas. Todavia, esta ciência sofisticou- se quando passou a utilizar-se da Geometria.
Este artigo de conclusão de curso disponibiliza-se a analisar a Matemática trabalhando ladeada pela Geometria em suas tarefas simultâneas. Esta colaboração nasceu nos primórdios da história do homem e vem sendo construída pouco a pouco durante a passagem do tempo.
A Matemática surgiu da necessidade de contar, de reunir, de juntar as conquistas feitas e a Geometria surge das formas existentes: um punhado de bolinhas, ou frutas. Assim, vão surgindo formatos de bolas, de barquinhos que vão se sofisticando.
Neste contexto, elaborado pelo dia a dia, a Geometria passa a lado a lado com a Matemática e vice-versa, conduzindo ao crescimento do conhecimento elaborado pelo homem e chegando até às mais recentes tecnologias.
Desta forma, este trabalho de conclusão de curso é uma pesquisa qualitativa, visando a conhecer o universo imenso das artes matemáticas aliadas às artes geométricas formando um todo rico, dinâmico, criativo. Os recursos obtidos para a execução deste foi possibilitado por uma bibliografia de autores atinentes a estas ciências e a leituras em sites e portais que apresentem o tema como o Scielo, o Bireme e outros que envolvam esta temática.
A apresentação deu-se da seguinte forma: Em primeiro lugar mostrou-se ―A História da Matemática‖ e a ―Importância da Geometria, seguido pela ―Geometria e as Profissões. Destacou-se também a Geometria e a aprendizagem.
2. A HISTÓRIA DA MATEMÁTICA E A IMPORTÂNCIA DA GEOMETRIA
2.1 PEQUENA HISTÓRIA DA MATEMÁTICA
A rotina do homem exigiu a presença da Matemática em todos os momentos através de coisas que nem ao menos se percebe; cálculos são feitos a todo instante. Neste contexto, Montrezol et al. (2015, sp), destacam que há Matemática na compra do supermercado, no troco, nos dias da semana, na temperatura dos dias, entre outros. Muitas vezes, sem métodos simples de calcular, como a calculadora, o que tornava os modos de contar mais complicados. Para tanto, são as profissões que dependem desta ciência que vêm evoluindo sempre.
A Matemática tem uma evolução que remonta à Pré-História e à Antiguidade; e os registros existentes revelam que esta origem ocorreu entre o ano de 3000 a. C a 2400 a.C. Desta forma, pode ser considerada necessária e aliada aos problemas do dia a dia, os quais fizeram o seu surgimento. Nota-se que a contagem dos objetos, as medidas de comprimento e de áreas fizeram com que fossem obtidos conceitos cada vez mais perfeitos (ANDRE, 2011).
Os textos eram feitos em escrita cuneiforme e datados desde mais ou menos 3000 a.C e encontrados na Mesopotâmia. Antes da criação da escrita, já conheciam ―os dias e anos, além de saber os sistemas de subtração, adição, multiplicação e divisão‖ (ANDRE, 2011), como sugere o mesmo autor. Na China, é inventado o ábaco, primeiro instrumento mecânico para calcular. São criadas as tabuadas e o cálculo de área é desenvolvido, enfatiza André (2011).
A necessidade mais remota que se tem da matemática refere-se à necessidade de contar e às regras para calcular equações simples de primeiro grau, adições e subtrações de frações, medições de superfícies e volumes, e problemas de aritmética. Na época que esta ciência surge estão constantes do Papiro de Rhind, de 1600 a.C. (PACIEVITCH, 2008). Assim sendo, a Matemática foi ficando mais sofisticada quando as civilizações começaram a usar a aritmética e a Geometria. Elas eram utilizadas na astronomia, em construções e cálculos financeiros.
Segundo Montrezol et al. (2015), a Matemática, como já foi referido acima, foi ampliando seus espaços em diversas áreas e conduzindo conhecimentos obtidos no transcorrer da História, fazendo com que outros saberes fossem construídos. Ele lembra:
Tales de Mileto, filósofo e matemático da Grécia Antiga, foi quem trouxe o ―Teorema de Tales‖, iniciando com a matemática dedutiva.
Através de seus Teoremas saíram às definições de ângulo reto, triângulo isósceles e seus ângulos, ângulos opostos e ângulos congruentes. Tales tirou conclusões a partir da observação de sombras. Mediu a altura de uma pirâmide do Egito apenas vendo o comprimento de sua sombra. (MONTREZOL et al, 2015)
Outra descoberta importante é o Teorema de Pitágoras, criado em 550 a.C. Nele, faz-se a análise do triângulo retângulo, em que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Ainda no setor de descobertas, mais ou menos no ano 500 d. C., foram criados pelos hindus o sistema numérico decimal e o conceito do número zero.
Ao realizar a procura das leis eternas do universo, ―Pitágoras dedicou-se à Geometria, à Aritmética, à Astronomia e à Música (que eram os quatro caminhos para a sabedoria) — depois quatro artes liberais, ou “Quadrivium” (CARVALHO,2012, p.02).
O Pitágoras atribui-se o célebre teorema que estabelece a relação entre os catetos e a hipotenusa do triângulo-retângulo. Tem-se como certo de que os agrimensores babilônios, caldeus e egípcios já o conhecessem, destaca o autor acima referido. Desta forma, de Pitágoras nascido na ilha de Samos, próxima à costa jônica (c.570 a.C.) e morto em Crotona, no sul da Itália (c. 500 a.C) que a Geometria teve impulso.
A Geometria como ramo matemático surgiu enquanto atividade empírica dos povos antigos para atender as suas necessidades da época, sendo suas primeiras sistematizações realizadas pelos gregos que muito contribuíram para esse ramo do saber. Platão, Eudoxo e muitos outros deram à Geometria um caráter especial, encarando-a como um ramo de destaque da ciência Matemática. (CARVALHO, 2012, p. 02)
Euclides foi quem sistematizou os Elementos, importantes conhecimentos que os estudiosos anteriores criando um caráter axiomático-dedutivo ao conhecimento geométrico da época, destaca o autor supracitado. Muitos foram os que contribuíram para a evolução da geometria: Descartes com a Geometria analítica. Depois da contribuição grega, passa-se a várias outras, que impulsionaram mais o desenvolvimento da Geometria enquanto ramo matemático. Descarte gerou
a Geometria Analítica, Poncelet e Chasles, introduzindo novas concepções, que contribuíram para o surgimento da Geometria Projetiva; Cayley introduziu elementos imaginativos às descobertas de Poncelet e Chasles, que foram posteriormente desenvolvidos e unificados por Felix Klein. (PIAGET & GARCIA, 1987).
Também foi Euclides, nascido por volta de 295 a.C. e que estudou em Atenas, teve grande parte de sua vida em Alexandria, que fundou a escola de Matemática. A ele também se atribui a ―sistematização clara e rigorosa de toda a Matemática da antiguidade — da geometria à teoria das proporções, passando pela teoria dos números irracionais‖, além de ter escrito o livro ―Os Elementos‖. (CARVALHO, 2012, p. 03)
Neste contexto, percebe-se que os fundamentos da geometria ainda eram intuitivos (ponto e reta), mas passaram a ser entendidos como objetos geométricos, como bem destaca o autor acima. Platão (Atenas, c. 428 – 348 a.C.), enfatiza Carvalho:
… acreditava que existe uma verdade eterna que pode ser descoberta pelo pensamento humano consegue descobrir (ou “reencontrar”) uma lei geométrica, que era uma formulação do teorema de Pitágoras (um quadrado construído sobre a diagonal de um quadrado, tem o dobro da área de outro quadrado, construído sobre um dos lados). (CARVALHO, 2012, p, 04).
“Sem dúvida, a geometria é, nas matemáticas gregas, o ramo que deu prova de tal perfeição que se transformou, durante vários séculos, no próprio paradigma da ciência”. (PIAGET & GARCIA, 1987, p.91). E ainda ressalta que
Cerca de 2 mil anos mais tarde, ou seja, em meados do século XVIII, Immanuel Kant (1724-1804) retomou esse pensamento para afirmar que existe um conhecimento eterno e independente (que ele chama conhecimento sintético a priori), do qual nossas intuições de espaço e tempo seriam exemplos concretos. Para Kant, toda a verdade sobre o espaço está na geometria de Euclides. (CARVALHO, 2012, p, 04).
Para o filósofo Kant (1999), a sede principal do conhecimento matemático se encontra na sensibilidade; a intuição sensível humana é a base fundamental do conhecimento geométrico puro.
Kant (1999) caracteriza o papel distintivo na geometria da intuição pura do espaço em termos do que ele chama de ―construção na intuição pura‖, e ilustra este papel com exemplos de construção geométrica extraídos dos Elementos de Euclides. Assim, é natural que, para elucidar a concepção de Kant (1999), volte-se para os recentes trabalhos.
Descartes (2001) foi aficionado do vigor, da clareza e da disciplina metódica. Tal pode ser constatado que possui um ponto de arranque: a dúvida universal, método e critério da verdade.
Duvidando de todos os conhecimentos adquiridos, duvidando da sua própria existência, Descarte chega à evidência de uma verdade que não pode negar: o seu próprio pensar, a realidade do sujeito pensante que se torna assim no arquétipo da ideia clara e distinta –. «penso, logo existo». (GALVÂO, 2008, 01)
Grande matemático, inventor da geometria analítica, restaurador do interesse pela metafísica na sua época, os problemas e questões por ele levantados abriram caminho a um dos períodos mais florescentes da ciência e da reflexão filosófica.
3. A GEOMETRIA E AS PROFISSÕES
Como entender a Geometria nas profissões variadas? O conhecimento que se tem é de que muitas profissões como na arte e na ciência utilizam geometria. Para isso, deve-se entender a geometria como uma palavra que vem do grego geo (terra e metron medir). ―Geometria em geral relaciona-se com a posição e a forma dos objetos no espaço‖ (BARRETT, 2011, p. 02).
A Geometria então acontece desde a época que os egípcios antigos construíam as pirâmides. Atualmente, engenheiros, artistas e diversas profissões têm utilizado dessa ciência para melhorar o projeto e a função de construções, trabalhos artísticos e objetos comuns e com sucesso, desta forma, muitas profissões a utilizam para medir, organizar e investigar as formas das coisas diuturnamente.
A Geometria tem múltiplas divisões, dentre elas, destaca-se a geometria Analítica, muito usada em vários campos de estudos. Os principais desses são as:
Engenharias (Produção, Elétrica, Mecânica etc.,), Geografia, Cartografia e a Astronomia (Distanciamento de meteoros e cometas). Entre as ciências ainda se destacam a Arquitetura, as ciências exatas, […], de um atleta ou de um técnico. Percebe-se, desta maneira, que é grande a importância da Geometria, quando utilizada na organização do pensamento.
Descartes (2001) desenvolveram os sistemas de coordenadas, atualmente conhecidas como coordenadas cartesianas. A Geometria Analítica estuda a localização de pontos no plano ou no espaço e as relações decorrentes de diferentes localizações esse tipo de estudo serve ainda, na elaboração de jogos atuando no princípio da Computação Gráfica que organiza projetos e simulações para áreas já citadas.
O engenheiro eletricista faz a associação da Eletrotécnica e da Geometria Analítica e compõe os sistemas de automação e controle de consumo da energia nas indústrias. Para executar o trabalho muitas empresas elaboram gráficas e planilhas, e fazem a discriminação dos funcionários, materiais, frequência ao trabalho, horas trabalhadas, número de máquinas utilizadas etc. Além disso, a Geometria Analítica planeja ―a distribuição elétrica de uma região, utilizando o conhecimento fundamental da Geometria ele limita a proximidade das redes de transmissão, tudo representado geometricamente e através de equações‖. (B. JULIANA et al 2013) (BLOG).
Muitas aplicações geométricas que ocorrem, exigem um pensamento da geometria para se obtiver a solução.
Outros exemplos de áreas de atuação da Geometria encontram-se na: Engenharia de produção, com a função de aperfeiçoar processos. Outro exemplo seria a Engenharia, em que o engenheiro elabora e acompanha as etapas de projetos de construção de prédios (comerciais e industriais), estradas, pontes, viadutos, obras fluviais e outros tipos de construção. Outro exemplo; é a arquitetura, área que compõe o projeto arquitetônico, a supervisão e a execução de obras de arquitetura e as área correlatas ao controle e desenho do espaço habitado, como o urbanismo, o paisagismo e diversas formas de design, conforme orienta o Portal Só Matemático (2013).
Assim, o desafio seguinte do mundo de constantes e rápidos efeitos dos avanços tecnológicos é o preparo das novas gerações e a ― Geometria é um componente da Matemática extremamente importante na composição destes
conhecimentos científicos e tecnológicos, dos quais os cidadãos devem se apropriar (KUENZER, 2005, p. 01).
A Matemática, portanto, participa de muitas profissões. E a Geometria também faz parte desta composição. Na área da administração, pode-se destacar o fato de solicitar muito planejamento, ordem, controle, fazendo com que seja essencial que o administrador tenha habilidade com números, com as formas que surgem nas inúmeras tabelas e gráficos. Muitas vezes, ―ele deverá preparar orçamentos para projetos, planejar e controlar pesquisas, dentre outras atividades‖. (PORTAL SOMATEMATICA, 2013).
Na Agronomia também faz necessária à presença da Geometria porque nela estão presentes os cálculos dos componentes químicos destinados à fertilização, à divisão, ao dimensionamento e formato das áreas a serem trabalhadas e/ou planejadas. (PORTAL SOMATEMATICA, 2013)
Não menos importante é a Geometria para a Arquitetura, visto que é importante no desenvolver o estudo do arquiteto que orienta ―a construção de casas, edifícios, reformas, restaurações e no planejamento de bairros e cidades‖, faz sobressair o Portal Somatematica, (2013). E revelando mais o referido Portal destaca que a Arquitetura é uma união das ciências exatas, humanas e arte, pois exige aptidões múltiplas. O formato variado das salas, campos esportivos, ginásios olímpicos dentre outros edifícios partindo do arredondado até formatos mais exóticos, conforme o referido Portal.
Não é diferente o uso da Geometria nas artes cinematográficas; muitas animações que são apresentadas utilizam a Geometria, através do movimento dos atores na representação de seus personagens, até o cenário de fundo podem ser criados por softwares que combinam diversas formas geométricas. Os programas para computadores codificam informações como posição, movimento, cor e textura de cada pixel.
Encontram-se recursos geométricos nos diversos tipos de engenharia de conformidade com o seu tipo de estudo e de trabalho (engenharia civil, engenharia elétrica etc.), enfatiza a equipe que compõe o Portal Só Matemático, (2013).
É usada ainda, cabe ressaltar, nas mais diversas obras que fazem parte da construção civil, sistemas de telecomunicações, criação de dispositivos mecânicos, desenvolvimento de máquinas, entre outros.
Outro setor que tem presente esta face da Geometria em sua atuação é a Geografia. Os geógrafos utilizam-na junto à Matemática em diversas situações. (PORTAL SOMATEMATICA, 2013)
O geólogo utiliza de diversos princípios da Geometria para escavar, conhecer e avaliar os segredos do solo e das pedras.
Portanto, verifica-se que todas as ciências tem um grau de importância elevada e necessitam da Matemática e, principalmente da Geometria para executar suas tarefas durante o dia a dia. Isso porque ela se encontra presente por todos os lugares e por tudo o que vemos.
4. A GEOMETRIA E A APRENDIZAGEM
O uso da Geometria ocorre de maneira mais ou menos intensa dependendo das atividades executadas. Usa-se esta ciência de uma forma despercebida. No dia a dia, sugere José Neto (2007), algumas atividades requerem seu uso mais intenso, outras menos, mas, frequentemente, é usada, ainda que sem perceber. Até mesmo em jogos a geometria analítica é bastante usada. Como exemplo, pode-se ser citado o Batalha Naval que visualiza o plano cartesiano. O autor José Neto (2007) enfatiza que:
A Geometria é de extrema importância no cotidiano das pessoas, pois desenvolve o raciocínio visual e, sem essa habilidade, elas dificilmente conseguirão resolver as diferentes situações devida que forem geometrizadas; também não poderão se utilizar da Geometria como fator de compreensão e resolução de questões de outras áreas de conhecimento humano. A Geometria torna a leitura interpretativa do mundo mais completa, a comunicação das ideias se amplia e a visão de Matemática torna-se fácil de entender (JOSÉ NETO, 2007, 01).
Desta forma, Passos (2000, sp) destaca que ―o conhecimento básico da geometria é fundamental para os indivíduos interagirem em seu meio‖, e este conhecimento precisam de ―conceitos de geometria, suas propriedades e relações simples, os quais deveriam ser introduzidos nas séries iniciais, para que, na sequência do ensino fundamental‖, sugere o autor.
Este esclarecimento é necessário para a compreensão dos fundamentos da geometria. Passos (2000, sp) ainda evidencia que ― professores dessas séries·.
precisam conhecer as ideias fundamentais da geometria e as diferentes maneiras de propiciar contextos favoráveis que levem os alunos à sua aprendizagem‖.
Neste contexto, pode-se verificar que as ideias geométricas infantis ―podem ser desenvolvidas a partir de atividades de ordenação, classificação de modelos de figuras planas e de sólidos‖ destaca Passos (2000, sp) (ver exercícios abaixo). Do mesmo modo,
…quando elas constroem modelos usando varetas, manipulam formas geométricas no computador, fazem dobraduras, ou quando usam espelhos para investigar eixos de simetria, podem constatar importantes propriedades geométricas (Passos, 2000, sp).
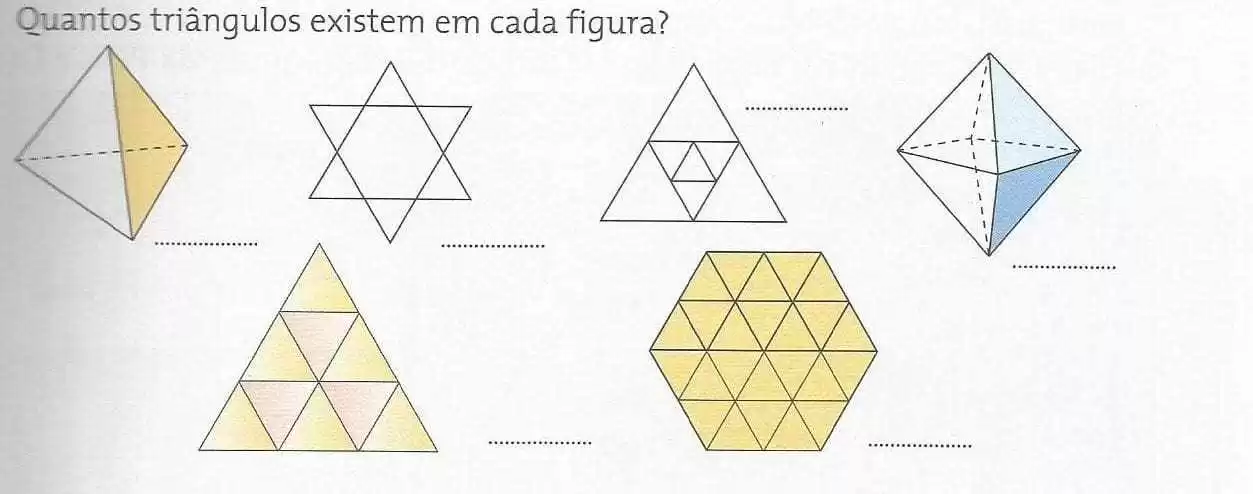
Então, na formulação de problemas, as crianças participam, criam situações novas, importantes e que explicitam saberes matemático. A geometria é um instrumento essencial para a descrição – inter-relação do homem; e é parte da matemática intuitiva, concreta. E completa que a geometria é um dos ramos da matemática o qual pode estimular o interesse pelo aprendizado desta ciência, pois pode revelar a realidade a qual rodeia o aluno, dando oportunidades de desenvolver habilidades criativas. (NOGUEIRA, 2009).
Qual é o molde do cilindro?

O ensino da geometria precisa voltar-se para a elaboração de ―problemas abertos (com mais de uma resposta e/ou com diferentes formas de resolução), com caráter dinâmico, que propiciem um processo de busca e investigação para resolvê- los‖ (NOGUEIRA, 2009). Assim ocorreria o envolvimento da imaginação criativa e das fantasias infantis e os aprendizes, sentir-se-iam interessados e motivados.
Muitas aplicações geométricas ocorrem que exigem um pensamento da geometria para se obtiver a solução.
Deste modo, é imprescindível centralizar as atividades em sala de aula, ao colocar ―alternativas adequadas para a minimização ou superação dos problemas de aprendizagem no conteúdo específico de Geometria Espacial‖, destaca Verona & Lopes, (2003, p. 03).
…de recursos como vídeo, laboratório e resolução de problemas práticos e contextualizados, a fim de despertar o interesse pelo conhecimento geométrico e assim, desenvolver e melhorar suas habilidades matemáticas para solucionar problemas no seu ambiente familiar ou de trabalho.
Sabe-se também que diversos alunos provenientes da escola pública não irão frequentar a Universidade, mas participarão do mercado de trabalho. Neste contexto, vê-se a importância ―criar uma forma para articular o saber teórico com o fazer prático a fim de formar alunos com melhor desempenho de suas capacidades, principalmente no que diz respeito à Matemática e em especial a Geometria‖.
Ao agregar o conhecimento prático à sistematização de conceitos formais, houve a necessidade de criar modelos para as figuras e formas geométricas, motivando os estudos sobre áreas e volumes, provocando a partir disso, uma busca de um melhor entendimento das formas espaciais. (VERONA & LOPES, 2003, p. 3)
O desafio seguinte deste mundo de constantes efeitos, dos avanços tecnológicos faz com que as novas gerações e a Geometria, como componente da Matemática muito importante para estes conhecimentos científicos e tecnológicos, formando o saber a ser adquirido pelo homem.
5. CONSIDERAÇÕES FINAIS
Fica evidente que o uso da Geometria preconizado nos conteúdos de Matemática do Ensino Fundamental a está intimamente ligado com os outros aspectos da escola como um todo, quando se pensa em interdisciplinaridade e contextualização. A maioria dos professores sente dificuldades em conduzir as atividades de resolução de problemas na sala de aula.
Hoje, depara-se com tarefas geométricas nas lides da cozinha até a evolução crescente das tecnologias.
Na sala de aula, múltiplas são as atividades a serem desempenhadas pelo professor diligente. Lança-se a ideia e o aluno elabora seu pensamento com criatividade e dinamismo.
Sendo assim, é necessário desenvolver por um lado, materiais que tirem partido do uso da Geometria e, por outro, formar professores para o uso delas. Incentivar a formação de professores para a introdução ao uso da tecnologia na sala de aula.
REFERÊNCIAS
André, P. Resumo da História da matemática. 2001. Disponível em: http://www.resumoescolar.com.br/matematica/resumo-da-historia-da-matematica/ ACESSADO EM 24/05/2016.·.
BARRETTS O NEILL Elementos de Geometria Diferencial download na http://www.4shared.com/office/k_6rhNf9/elementos_de_geometria_diferen.html. ACESSADO EM 13/08/2016.
CARVALHO, Joaquim Francisco de. Evolução do pensamento matemático, das origens aos nossos dias. 2012. Artigos e Ensaios. Disponível em: http://cienciaecultura.bvs.br/scielo.php?pid=S00097252012000200021&script=sci_arttext. Acessado em: 12/07/2016.
DESCARTES, RA. Geometria. Trad. Emídio Cesar de Queiroz Lopes. Lisboa: Editorial Prometeu 2001.
EUCLIDES. Os Elementos. 300 a.C. Disponível em http://www.matematica.br/historia/euclides.html. acessado em 12/07/2016.
JOSE NETO. A geometria é de extrema importância na vida das pessoas. 2015. http://docslide.com.br/documents/a-geometria-e-de-extrema-importancia-no-cotidiano-das-pessoas.html. Acessado em 23/09/2016.
KANT, I. Crítica da Razão Pura. São Paulo: Ed. Nova Cultura, 1999. (os pensadores).
JULIANA, b et al. Profissões que envolvem geometria analítica. 2013. Disponível em http://mundoestatistica.blogspot.com.br/2013/12/curiosidades- profissoes-que-envolvem.html. Acessado em: 22/08/2016.
KUENZER, Acácia. Ensino Médio: Construindo uma proposta para os que vivem do trabalho, 4° ed, São Paulo: Cortez, 2005.
MONTREZOL Ale. A historia da matemática. Disponível em: http://multiplicandoideiasmatematicas.blogspot.com.br/. Acessado em: 09/07/2016.
NASCIMENTO, A. mania de calcular: Geometria. 2015. Disponível em http://maniadecalcular.blogspot.com.br/search/label. Acessado em: 19/08/2016.
NOGUEIRA, Vandira Loiola. Uso da Geometria no Cotidiano. 2009. Disponível em: htttp://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/1850-8.pdf. Acessado em 12/04/2016.
PACIEVITCH. Thais. História da Matemática. Infoescola, 2008. Disponível em:
http://www.infoescola.com/a história da matemática. Acessado em 12/07/2016.
PASSOS, C.M.B. Representações, interpretações e prática pedagógica: Geometria na sala de aula. Tese de doutorado (Universidade Estadual de Campinas– (Faculdade de educação). 2000.
PIAGET, J. & GARCIA, R. Psicogêneses e História das Ciências. Ciência Nova, Nº 6,
VERONA V. A & LOPES, MRM. Geometria Espacial Numa Perspectiva Contextualizada 2009 EPREM X ENCONTRO PARANAENSE DE MATEMATICA. DISPONIVEL EM http://www.unicentro.br/editora/. ACESSADO EM 28/08/2016.
[1] Graduanda do Curso de Matemática e Especialista em Docência e Didática do Ensino Superior.
[2] Especialista em Língua Portuguesa, Artes, Linguística e Docência e Didática do Ensino Superior.
Enviado: Abril, 2018.
Aprovado: Junho, 2019.