ARTIGO ORIGINAL
ARANTES, Gabriel Costa Vieira [1], LELIS, Bárbara Costa [2], POTIGUARA, Camila Gonçalves [3], ARANTES, João Marcos Silva [4], SOUZA, Lethícia Pires de [5], OLIVEIRA JUNIOR, Vilmar de [6], LOPES, Yasmin Moreira [7]
ARANTES, Gabriel Costa Vieira. Et al. Análise e demonstração do teorema da assimetria matricial e do teorema da assimetria seletiva, dois resultados inéditos sobre o espaço vetorial das matrizes. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 08, Vol. 03, pp. 58-77. Agosto de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/teorema, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/teorema
RESUMO
O presente estudo relata dois teoremas inéditos sobre o espaço vetorial das matrizes, descobertos a partir da seguinte situação problema: duas matrizes retangulares A e B, onde o número de colunas da matriz A é igual ao número de linhas da matriz B, solicita-se a obtenção do produto matricial AxB e, posteriormente, o cálculo do determinante deste produto, denotado por det(AxB), sempre que isto for possível. Por conseguinte, notou-se que o resultado do determinante do produto matricial AxB, denotado por det(AxB), era invariavelmente nulo, em algumas condições. Levantou-se, então, a hipótese de que tal padrão poderia se manter para matrizes com ordens maiores, o que resultou no Teorema da Assimetria Matricial e no Teorema da Assimetria Seletiva. Desta forma, tem-se como objetivo analisar e demonstrar esses dois teoremas inéditos da Matemática sobre o espaço vetorial das matrizes, investigando os seus corolários e suas aplicações. Para isso, adotou-se o método dedutivo, através do levantamento de hipóteses, com a finalidade de demonstrar os teoremas desenvolvidos. Como resultados, apresenta-se o Teorema 1, denominado Teorema da Assimetria Matricial, onde, dadas duas matrizes retangulares A(mxn) e B(nxm) de ordens opostas, com m > n, tem-se det(AxB) = 0, independentemente de quais elementos estão dispostos nestas matrizes. A partir do Teorema 1, foram desvendados onze corolários de fundamental importância, reforçando a amplitude e a generalidade da sua proposição. Já o Teorema 2, denominado Teorema da Assimetria Seletiva, nos mostra que, considerando novamente duas matrizes retangulares A(mxn) e B(nxm) de ordens opostas, porém com m < n, não necessariamente se obtém det(AxB) = 0. Isto demonstra uma certa seletividade no núcleo do operador det(AxB), de acordo com as condições descritas, que se torna evidente a partir da comparação do caso onde m > n (Teorema 1) com o caso onde m < n (Teorema 2). Por fim, deixa-se, também, em aberto, uma hipótese, que, caso seja validada em estudos posteriores, certamente irá resultar em mais uma propriedade interessante do espaço vetorial das matrizes. Trata-se da Hipótese da Multiplicidade Algébrica.
Palavras-chave: Teorema da Assimetria Matricial, Teorema da Assimetria Seletiva, Matrizes.
INTRODUÇÃO
Durante o ano letivo de 2021, no instituto educacional Colégio JR, localizado na cidade de Goiânia/GO, o orientador Gabriel Arantes ministrava aulas da disciplina de Matemática para a turma da 2ª Série do Ensino Médio, cumprindo o conteúdo programático sobre matrizes. Juntamente com os demais autores, atentaram-se a um padrão matemático intrínseco ao espaço vetorial das matrizes.
Sendo assim, o levantamento das hipóteses se iniciou a partir do seguinte problema, aparentemente trivial: dadas duas matrizes retangulares A e B, onde o número de colunas da matriz A é igual ao número de linhas da matriz B, solicita-se a obtenção do produto matricial AxB e, posteriormente, o cálculo do determinante deste produto, denotado por det(AxB), sempre que isto for possível.
Durante as referidas aulas, o orientador caracterizou o problema proposto a partir de exemplos, empregando matrizes retangulares com ordens menores, a fim de explorar o problema desde os seus desafios mais simples.
Vale ressaltar que, ao longo deste artigo, a ordem de uma matriz será representada no formato A(mxn), onde “m” representa o número de linhas e “n” representa o número de colunas da matriz A (LIMA, 1996).
Nesse contexto, de acordo com a descrição do problema proposto, fica claro que somente é possível obter det(AxB) se o número de linhas da matriz A for igual ao número de colunas da matriz B (LANG, 1971).
Deste modo, o padrão matemático começou a se tornar evidente a partir do momento em que, durante a exemplificação do problema proposto, foram empregadas matrizes do tipo A(3×2) e B(2×3), com a condição de que o número de linhas da matriz A deveria ser maior do que o seu número de colunas, enquanto a ordem da matriz B deveria ser o contrário da ordem da matriz A. Por conseguinte, notou-se que o resultado do determinante do produto matricial AxB, denotado por det(AxB), era invariavelmente nulo, nas condições descritas anteriormente. Ademais, em todos os exemplos explorados, este resultado se mostrou independente dos elementos escolhidos nas linhas e colunas das matrizes A e B. Destarte, levantou-se a hipótese de que tal padrão poderia se manter para matrizes com ordens maiores. Obteve-se, então, uma hipótese generalizada, que, no presente artigo, é devidamente demonstrada, dando origem ao Teorema 1: sejam A(mxn) e B(nxm) matrizes retangulares tais que m > n, então tem-se det(AxB) = 0. Este teorema será denominado Teorema da Assimetria Matricial. O motivo desta denominação se tornará evidente ao longo do desenvolvimento deste artigo.
Desta forma, tem-se como objetivo analisar e demonstrar esses dois teoremas inéditos da Matemática sobre o espaço vetorial das matrizes, investigando os seus corolários e suas aplicações.
Para isso, foi utilizado o método dedutivo, através do levantamento de hipóteses, com a finalidade de demonstrar o Teorema da Assimetria Matricial (Teorema 1) como um resultado inédito, que foi fundamentado em um padrão matemático relacionado ao espaço vetorial das matrizes.
É de conhecimento geral, no meio científico, que todo teorema matemático possui limitações. No teorema em questão, deve-se atentar a apenas uma limitação, que diz respeito à relação entre as ordens das matrizes, fato que o torna um teorema forte, isto é, um teorema amplo, com poucas restrições.
Ademais, cumpre ressaltar que o estudo analítico do Teorema da Assimetria Matricial irá nos fornecer diversos corolários, que, por sua vez, são consequências diretas do resultado que será demonstrado neste teorema.
Unindo o Teorema da Assimetria Matricial com seus corolários, objetiva-se identificar diversas aplicações práticas, que deverão confirmar a aplicabilidade dos resultados teóricos obtidos, ao longo do desenvolvimento do artigo.
Um corolário é uma consequência direta de uma proposição mais ampla, que já foi demonstrada (LIMA, 1996). Isto posto, é notório que, a partir de um teorema, quanto mais corolários forem desvendados, mais forte este teorema será, tornando-o mais amplo e mais aplicável em diversos campos da Matemática (BOLDRINI et al., 1980).
O Teorema da Assimetria Matricial apresenta onze corolários distintos, no entanto, relacionados, pois derivam de uma mesma proposição. Ao final do desenvolvimento deste artigo, a fim de concretizar e aprofundar o significado holístico por trás do Teorema da Assimetria Matricial, demonstra-se um segundo teorema, igualmente importante e intrigante, denominado Teorema da Assimetria Seletiva (Teorema 2).
Ao final, os autores deixam, também, uma hipótese em aberto, que certamente produzirá frutos formidáveis com futuras demonstrações, devido ao grande impacto do seu enunciado. Trata-se da Hipótese da Multiplicidade Algébrica.
DESENVOLVIMENTO
Teorema 1 (Teorema da Assimetria Matricial): Sejam A(mxn) e B(nxm) duas matrizes retangulares quaisquer, tais que m > n. Deste modo, tem-se det(AxB) = 0.
Demonstração: Sejam A(mxn) e B(nxm) duas matrizes retangulares quaisquer, tais que m > n. De modo genérico, elas podem ser representadas da seguinte maneira:
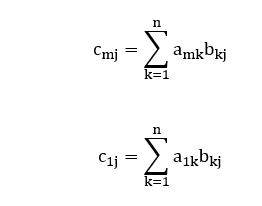
Isto posto, o produto AxB resultará em uma matriz quadrada C de ordem mxm tal que:
Agora, note que:
Sendo assim, a matriz C(mxm) = AxB pode ser representada, de modo geral, como:
1 ≤ i ≤ m e 1 ≤ j ≤ m representam, respectivamente, a linha e a coluna da matriz C(mxm) onde determinado elemento ![]() está localizado. Note que os índices dos somatórios foram omitidos, pois todos eles estão indexados de k = 1 até n ∈ ℕ.
está localizado. Note que os índices dos somatórios foram omitidos, pois todos eles estão indexados de k = 1 até n ∈ ℕ.
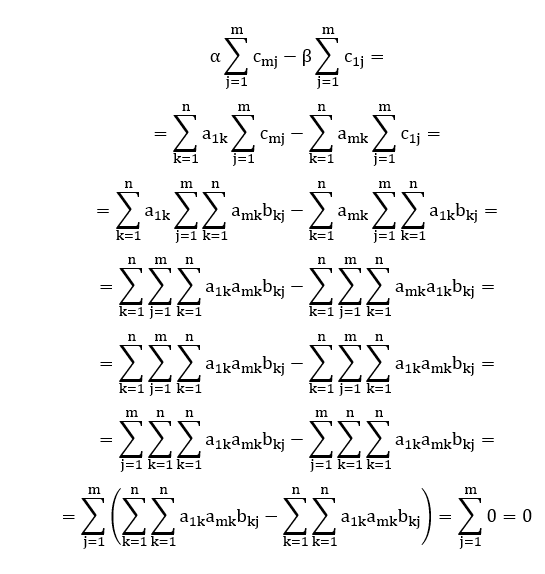
Agora, queremos provar que det(C) = det(AxB) = 0. Para isso, devemos mostrar que existem duas linhas da matriz C(mxm) que são linearmente dependentes entre si. Neste caso, utilizaremos a m-ésima linha e a primeira linha da matriz C(mxm) para tal finalidade. Em suma, basta mostrar que existe uma combinação linear nula entre o somatório dos elementos da m-ésima linha e o somatório dos elementos da primeira linha da matriz C(mxm). Algebricamente, isto significa que devem existir dois coeficientes reais α e β tais que:
Portanto, vamos às vias de fato. Primeiramente, note que:
Então, escolhendo os coeficientes reais adequados:
Obtemos a combinação linear nula desejada:
Portanto, tem-se de fato que det(C) = det(AxB) = 0. ∎
Corolário 1: Se uma matriz quadrada C(mxm) pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n, então a matriz C(mxm) não é inversível.
Demonstração: Pelo Teorema 1, se C(mxm) = AxB onde A(mxn) e B(nxm) são matrizes retangulares, com m > n, então det(AxB) = det(C) = 0. Por definição, se uma matriz quadrada C(mxm) possui determinante nulo, então ela não admite inversa. ∎
Corolário 2: Dados m e n naturais, seja![]() um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Definimos o funcional
um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Definimos o funcional
![]() . Então, o conjunto S definido a seguir é um subespaço vetorial do núcleo deste funcional, denotado por ker(Λ):
. Então, o conjunto S definido a seguir é um subespaço vetorial do núcleo deste funcional, denotado por ker(Λ):
Demonstração: Seja M o espaço vetorial das matrizes. Dados m, n ∈ ℕ, definimos o funcional
![]() é um subespaço vetorial de MxM. Por definição, o núcleo deste funcional é dado pelo conjunto:
é um subespaço vetorial de MxM. Por definição, o núcleo deste funcional é dado pelo conjunto:
Portanto, qualquer subconjunto de ker(Λ) cujos elementos são soluções da equação Λ(A,B) = 0 será um subespaço vetorial do mesmo. Deste modo, tem-se:
Λ(A,B) = 0
det(AxB) = 0
Pelo Teorema 1, sabemos que todos os pares de matrizes (A,B) ∈ ℳ tais que m > n constituem soluções da equação Λ(A,B) = det(AxB) = 0. Isto posto, podemos concluir que o conjunto S = {(A,B) ∈ ℳ | m > n} é um subespaço vetorial de ker(Λ). ∎
Corolário 3: Dados m e n naturais, seja![]() um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Então, o funcional
um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Então, o funcional
![]() não é bilinear.
não é bilinear.
Demonstração: Dados m e n naturais, seja ![]() um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Então, tomamos o funcional
um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Então, tomamos o funcional ![]() Dado
Dado ![]() , verifica-se facilmente que
, verifica-se facilmente que ![]() , pois AxB = C(mxm). Portanto, conclui-se que não ocorre
, pois AxB = C(mxm). Portanto, conclui-se que não ocorre ![]() para todo par (A,B) ∈ ℳ. Interpretando o resultado do Corolário 2, este fato se torna evidente, pois devem existir pares de matrizes
para todo par (A,B) ∈ ℳ. Interpretando o resultado do Corolário 2, este fato se torna evidente, pois devem existir pares de matrizes![]() tais que
tais que ![]() , o que implica em
, o que implica em ![]() , isto é,
, isto é, ![]() . Por conseguinte, tal constatação fere a definição de funcional bilinear. ∎
. Por conseguinte, tal constatação fere a definição de funcional bilinear. ∎
Corolário 4: Se uma matriz quadrada C(mxm) pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n, então a matriz C(mxm) pode admitir múltiplas decomposições do tipo LU.
Demonstração: Dados m, n ∈ ℕ, com m > n, escolhemos duas matrizes retangulares A(mxn) e B(nxm) tais que AxB = C(mxm) é uma matriz quadrada. Pelo Teorema 1, sabemos que det(C) = 0, nestas condições. Sabe-se que, se uma matriz quadrada possui determinante não-nulo, então ela admite uma única decomposição LU. De acordo com a contrapositiva desta afirmação, a matriz C(mxm) em questão pode admitir mais de uma decomposição do tipo LU. ∎
Corolário 5: Seja C(mxm) uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n. Seja C = LxU uma possível decomposição LU desta matriz C(mxm). Então, a matriz L(mxm) ou a matriz U(mxm) possuem linhas nulas.
Demonstração: Dados m, n ∈ ℕ, com m > n, escolhemos duas matrizes retangulares A(mxn) e B(nxm) tais que AxB = C(mxm) é uma matriz quadrada. Pelo Teorema 1, sabemos que det(C) = 0, nestas condições. Pelo Corolário 4, sabemos também que a matriz C(mxm) em questão admite pelo menos duas fatorações LU distintas. Em todas elas, tem-se C = LxU, onde L(mxm) é uma matriz triangular inferior e U(mxm) é uma matriz triangular superior. Pelo Teorema de Binet, se C = LxU, então det(C) = det(LxU) = det(L).det(U). Como det(C) = 0, tem-se det(L).det(U) = 0. Isto significa que det(L) = 0 ou det(U) = 0. Se det(L) = 0, então a matriz L(mxm) possui pelo menos uma linha nula. Se det(U) = 0, então a matriz U(mxm) possui pelo menos uma linha nula. ∎
Como exemplo ilustrativo deste Corolário 5, toma-se duas matrizes retangulares A(3×2) e B(2×3) em particular, apresentadas a seguir.
O produto AxB = C(3×3) resulta na seguinte matriz quadrada:
Note que o determinante desta matriz C(3×3) é nulo. Veja:
Este resultado já era esperado, de acordo com o que foi demonstrado no Teorema 1. Portanto, de acordo com o Corolário 5, na decomposição LU desta matriz C(3×3), certamente a matriz L(3×3) ou a matriz U(3×3) possuem pelo menos uma linha nula. De fato, observe uma possível decomposição LU da matriz C(3×3) a seguir.
Donde, nesta decomposição, temos as matrizes L(3×3) e U(3×3) a seguir:
Observe que, conforme esperado de acordo com o Corolário 5, a matriz U(3×3) possui uma linha nula, neste caso, a terceira linha.
Corolário 6: Seja C(mxm) uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n. Então, a matriz C(mxm) possui pelo menos um autovalor nulo λ = 0.
Demonstração: Dados m, n ∈ ℕ, com m > n, escolhemos duas matrizes retangulares A(mxn) e B(nxm) tais que AxB = C(mxm) é uma matriz quadrada. Pelo Teorema 1, sabemos que det(C) = 0, nestas condições. Isto significa que C(mxm) é uma matriz singular. Toda matriz singular possui pelo menos um autovalor nulo, λk = 0. Isto se deve ao fato de que o determinante de qualquer matriz quadrada C(mxm) de ordem m ∈ ℕ é igual ao produto dos seus m-autovalores, ou seja:![]() . Deste modo, se det(C) = 0, então
. Deste modo, se det(C) = 0, então ![]() , donde pelo menos um dos autovalores λk é nulo. ∎
, donde pelo menos um dos autovalores λk é nulo. ∎
Corolário 7: Seja C(mxm) uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n. Então, o sistema homogêneo CX = 0 é possível e indeterminado.
Demonstração: Dados m, n ∈ ℕ, com m > n, escolhemos duas matrizes retangulares A(mxn) e B(nxm) tais que AxB = C(mxm) é uma matriz quadrada. Pelo Teorema 1, sabemos que det(C) = 0, nestas condições. Seja ![]() uma matriz-coluna contendo m-variáveis reais
uma matriz-coluna contendo m-variáveis reais ![]() de tal modo que X possui ordem mx1, ou seja, X possui m linhas e uma coluna.
de tal modo que X possui ordem mx1, ou seja, X possui m linhas e uma coluna.
Seja 0 (mx1) a matriz-coluna nula de ordem m ∈ ℕ.
Definimos, então, o sistema homogêneo representado pela equação matricial:
Onde a matriz C(mxm) é a matriz dos coeficientes das m-variáveis reais ![]() da matriz X(mx1). Tendo em vista que det(C) = 0, existem duas possibilidades para o sistema homogêneo CX = 0, quais sejam: impossível (ausência de soluções) ou possível e indeterminado (infinitas soluções). Todo sistema homogêneo admite pelo menos a solução trivial nula, donde se tem
da matriz X(mx1). Tendo em vista que det(C) = 0, existem duas possibilidades para o sistema homogêneo CX = 0, quais sejam: impossível (ausência de soluções) ou possível e indeterminado (infinitas soluções). Todo sistema homogêneo admite pelo menos a solução trivial nula, donde se tem ![]() . Isto já descarta a possibilidade do sistema CX = 0 em questão ser impossível. Portanto, por exaustão das possibilidades, o sistema homogêneo CX = 0 é possível e indeterminado. ∎
. Isto já descarta a possibilidade do sistema CX = 0 em questão ser impossível. Portanto, por exaustão das possibilidades, o sistema homogêneo CX = 0 é possível e indeterminado. ∎
Corolário 8: Considere um sistema linear temporal de equações diferenciais ordinárias 2×2. Se a matriz quadrada dos coeficientes C(2×2) do sistema admitir uma decomposição do tipo C = AxB tal que A(2×1) e B(1×2) são matrizes retangulares, então o retrato de fase das soluções x = x(t) e y = y(t) do sistema apresenta uma reta de pontos de equilíbrio (caso degenerado).
Demonstração: Considere o sistema linear S(2×2) de equações diferenciais ordinárias a seguir, onde x = x(t) e y = y(t) são ambas funções dependentes do tempo.
Podemos transcrever este sistema na forma matricial da seguinte maneira:
Onde C(2×2) é a matriz quadrada dos coeficientes do sistema S(2×2). Suponha que esta matriz admita uma decomposição do tipo C = AxB onde A(2×1) e B(1×2) são matrizes retangulares. Pelo Teorema 1, temos então que det(AxB) = det(C) = 0. Consideremos agora o polinômio característico dessa matriz C(2×2) dado a seguir:
Como det(C) = 0 e tr(C) = a + d, segue que:
As raízes do polinômio característico da matriz C(2×2) são os seus autovalores:
Conforme esperado, de acordo com o resultado do Corolário 6, a matriz C(2×2) em questão possui pelo menos um autovalor nulo λ1 = 0. Vamos então analisar as possibilidades para o outro autovalor ![]()
![]() e então o retrato de fase formado pelas soluções x = x(t) e y = y(t) apresentará uma reta de pontos de equilíbrio repulsores.
e então o retrato de fase formado pelas soluções x = x(t) e y = y(t) apresentará uma reta de pontos de equilíbrio repulsores.
(II) Se ![]() e então o retrato de fase formado pelas soluções x = x(t) e y = y(t) apresentará uma reta de pontos de equilíbrio atratores.
e então o retrato de fase formado pelas soluções x = x(t) e y = y(t) apresentará uma reta de pontos de equilíbrio atratores.
(III) Se ![]() e então o sistema S(2×2) de EDO admite apenas as soluções triviais x(t) = 0 e y(t) = 0, um caso também degenerado. ∎
e então o sistema S(2×2) de EDO admite apenas as soluções triviais x(t) = 0 e y(t) = 0, um caso também degenerado. ∎
Corolário 9 (Dependência Linear): Seja C(mxm) uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) tais que m > n. Então, a matriz C(mxm) possui linhas linearmente dependentes.
Demonstração: Dados m, n ∈ ℕ, com m > n, escolhemos duas matrizes retangulares A(mxn) e B(nxm) quaisquer, de modo que AxB = C(mxm) é uma matriz quadrada. Pelo Teorema 1, sabemos que det(C) = 0, nestas condições. Na própria demonstração do Teorema 1, exibida anteriormente, este resultado deriva justamente do fato de que existe uma combinação linear nula entre a primeira linha e a m-ésima linha da matriz C(mxm), tornando-as linearmente dependentes. ∎
Corolário 10: Seja ![]() uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares
uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares ![]() donde se tem
donde se tem
![]() Então, o autovalor nulo λ = 0 da matriz C(2×2) possui multiplicidade algébrica igual a 1 se, e somente se, ocorrer
Então, o autovalor nulo λ = 0 da matriz C(2×2) possui multiplicidade algébrica igual a 1 se, e somente se, ocorrer ![]()
Demonstração: Sejam as matrizes retangulares genéricas A(2×1) e B(1×2) abaixo:
O produto matricial AxB resultará na matriz quadrada C(2×2) a seguir:
Note que det(C) = 0, conforme esperado, de acordo com o Teorema 1. Vamos agora determinar os autovalores da matriz C(2×2).
Desta equação, podemos deduzir que:
Donde podemos observar que ![]() se, e somente se, ocorrer
se, e somente se, ocorrer ![]() ∎
∎
Corolário 11 (Decomposição Assimétrica 2×2): Sejam ![]() . Tomemos uma matriz quadrada
. Tomemos uma matriz quadrada ![]() qualquer. A fim de verificar se existem decomposições do tipo
qualquer. A fim de verificar se existem decomposições do tipo ![]() são matrizes retangulares, basta averiguar se det(C) = 0. Em caso afirmativo, tem-se
são matrizes retangulares, basta averiguar se det(C) = 0. Em caso afirmativo, tem-se ![]() . Além disso, tem-se infinitas decomposições possíveis. Dentre elas, destaca-se a seguinte:
. Além disso, tem-se infinitas decomposições possíveis. Dentre elas, destaca-se a seguinte:
Demonstração: Sejam ![]() . Tomemos a matriz quadrada
. Tomemos a matriz quadrada ![]() genérica:
genérica:
Vamos partir da hipótese de que o determinante da matriz C(2×2) é nulo, ou seja:
De acordo com o Teorema da Assimetria Matricial, devem existir decomposições do tipo C = AxB onde ![]() são matrizes retangulares:
são matrizes retangulares:
A partir desta igualdade matricial, obtemos o seguinte sistema de equações lineares:
Analisando a matriz dos coeficientes do sistema linear obtido, verificamos que o seu determinante é nulo:
Neste caso, temos um sistema possível e indeterminado. Portanto, devem existir infinitas decomposições C = AxB possíveis. Dentre elas, vamos destacar aquela onde se fixa o valor ![]() , de tal modo que se obtém o seguinte resultado:
, de tal modo que se obtém o seguinte resultado:
Assim, fica demonstrado que, de fato:
É uma decomposição possível para toda matriz quadrada C(2×2) singular, isto é, cujo determinante é nulo. ∎
A título de exemplo ilustrativo do resultado que acabamos de demonstrar no Corolário 11, considere a seguinte matriz singular C(2×2) em particular:
Então, de acordo com o Algoritmo da Decomposição Assimétrica 2×2, segue que:
De tal modo que obtemos C = AxB da maneira como está explicitada abaixo:
Hipótese da Multiplicidade Algébrica: Seja C(mxm) uma matriz quadrada que pode ser decomposta como o produto de duas matrizes retangulares A(mxn) e B(nxm) donde se tem m > n. Então, o autovalor nulo λ = 0 da matriz C(mxm) possui multiplicidade algébrica maior ou igual à diferença entre m e n. Noutros termos, seja ![]() a multiplicidade algébrica do autovalor nulo λ = 0 da matriz C(mxm). Então, nas condições descritas anteriormente, devemos ter
a multiplicidade algébrica do autovalor nulo λ = 0 da matriz C(mxm). Então, nas condições descritas anteriormente, devemos ter![]()
Teorema 2 (Teorema da Assimetria Seletiva): Sejam A(mxn) e B(nxm) duas matrizes retangulares quaisquer, tais que m < n. Então, pode ocorrer ![]()
Demonstração: Dados m e n naturais, seja ![]() um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Definimos então o funcional
um subespaço vetorial de MxM, onde M é o espaço vetorial das matrizes. Definimos então o funcional ![]() um subconjunto de ℳ , cujos elementos são todos os pares de matrizes A(mxn) e B(nxm) tais que m > n. De acordo com o que foi demonstrado no Corolário 2 do Teorema da Assimetria Matricial, temos que S constitui um subespaço vetorial de ker(Λ), que, por sua vez, é o núcleo do funcional Λ. Em símbolos, mostramos que
um subconjunto de ℳ , cujos elementos são todos os pares de matrizes A(mxn) e B(nxm) tais que m > n. De acordo com o que foi demonstrado no Corolário 2 do Teorema da Assimetria Matricial, temos que S constitui um subespaço vetorial de ker(Λ), que, por sua vez, é o núcleo do funcional Λ. Em símbolos, mostramos que ![]() . Isto significa que
. Isto significa que
![]() . Agora, considere o conjunto definido por
. Agora, considere o conjunto definido por![]() , cujos elementos são todos os pares de matrizes A(mxn) e B(nxm) tais que m < n. Por conseguinte, tem-se
, cujos elementos são todos os pares de matrizes A(mxn) e B(nxm) tais que m < n. Por conseguinte, tem-se ![]() Pelo Teorema de Binet, sabemos que det(AxB) = det(A).det(B) = det(B).det(A) = det(BxA) se, e somente se, as matrizes A e B forem quadradas, ou seja, se elas possuírem a mesma quantidade de linhas e de colunas. Caso contrário, pode ocorrer
Pelo Teorema de Binet, sabemos que det(AxB) = det(A).det(B) = det(B).det(A) = det(BxA) se, e somente se, as matrizes A e B forem quadradas, ou seja, se elas possuírem a mesma quantidade de linhas e de colunas. Caso contrário, pode ocorrer ![]() . Portanto, dado o par de matrizes (A,B) ∈ S’ pode ocorrer
. Portanto, dado o par de matrizes (A,B) ∈ S’ pode ocorrer ![]() ∎
∎
Interpretando, em termos simples, o significado do Teorema da Assimetria Seletiva, em comparação com o resultado do Teorema da Assimetria Matricial, sejam A(mxn) e B(nxm) duas matrizes retangulares, tais que o produto AxB = C(mxm) de ambas constitui uma matriz quadrada. Se m > n, então obrigatoriamente ocorre det(C) = 0. Se m < n, então não necessariamente ocorre det(C) = 0. Tanto no caso onde m > n quanto no caso onde m < n, tem-se por hipótese uma decomposição assimétrica da matriz quadrada C(mxm) em duas matrizes retangulares A(mxn) e B(nxm). No entanto, tal assimetria é seletiva com relação ao funcional ![]() , pois todos os pares de matrizes retangulares
, pois todos os pares de matrizes retangulares ![]() tais que m > n pertencem ao núcleo do funcional Λ, denotado por ker(Λ), enquanto que nem todos os pares de matrizes retangulares
tais que m > n pertencem ao núcleo do funcional Λ, denotado por ker(Λ), enquanto que nem todos os pares de matrizes retangulares ![]() tais que m < n pertencem a ker(Λ).
tais que m < n pertencem a ker(Λ).
CONSIDERAÇÕES FINAIS
O Teorema da Assimetria Matricial (Teorema 1) é um resultado que pode ser amplamente aplicado em problemas que envolvem matrizes com ordens assimétricas, isto é, pares de matrizes retangulares do tipo A(mxn) e B(nxm), com a única condição de que se deve ter m > n.
Problemas envolvendo matrizes são geralmente associados à organização de dados, variáveis, informações, vetores, dentre outros elementos, dispostos em linhas e colunas, no formato de uma tabela, que comumente caracteriza uma matriz (HOFFMAN e KUNZE, 1979). Sendo assim, o Teorema 1 certamente pode contribuir para a resolução de problemas que envolvem a disposição assimétrica de dados, variáveis, informações ou vetores em matrizes retangulares.
Ademais, os autores sugerem, por exemplo, a investigação do problema da assimetria de bárions na Cosmologia, que visa examinar o motivo pelo qual a matéria bariônica prevaleceu sobre a antimatéria bariônica, no momento de origem do nosso Universo observável, durante um breve instante de tempo singular do Big Bang, onde ocorreu o desequilíbrio entre as quatro forças fundamentais da natureza, enquanto ainda estavam unificadas. Intuitivamente, os autores suspeitam que o resultado do Teorema da Assimetria Matricial, juntamente com os seus corolários, pode contribuir para a investigação do problema da assimetria de bárions na Cosmologia, que está em aberto no campo da Física Moderna por muitas décadas.
Além disso, agrega-se o resultado demonstrado no Teorema da Assimetria Seletiva (Teorema 2) a este contexto, a fim de assegurar a completude da interpretação matricial do problema da assimetria bariônica. Além do que foi proposto, seguramente os resultados dos teoremas e dos corolários demonstrados neste artigo podem contribuir para a resolução de diversos problemas intrínsecos à própria Matemática, em diferentes áreas e dimensões, tais como Álgebra Linear, Criptografia, Métodos Numéricos, Equações Diferenciais, Topologia, dentre outros campos que utilizam das ferramentas próprias do espaço vetorial das matrizes, conforme foi verificado ao longo do desenvolvimento deste estudo. Por fim, espera-se também que estudos futuros revelem a validade ou a não-validade da Hipótese da Multiplicidade Algébrica, através de uma demonstração rigorosa, pois, caso o enunciado desta hipótese seja validado, a comunidade científica terá mais uma ferramenta matemática poderosa ao seu dispor, capaz de ampliar as contribuições deste artigo.
Por fim, diante dos inúmeros resultados obtidos neste estudo, é importante destacar que o Teorema da Assimetria Matricial (Teorema 1) demonstra uma propriedade inédita sobre o espaço vetorial das matrizes, assim, expandindo os horizontes de diversas áreas da Matemática que utilizam as matrizes como elementos básicos de construção. Todos os onze corolários obtidos a partir do Teorema 1 reforçam a sua generalidade e a sua amplitude, provando o seu poder de aplicação. Além disso, o resultado demonstrado no Teorema da Assimetria Seletiva (Teorema 2) confere completude à interpretação holística do funcional ![]() definido por
definido por ![]() , tornando evidente a existência de uma seletividade, isto é, uma preferência, verificada no núcleo ker(Λ) deste funcional, onde predominam os pares de matrizes retangulares A(mxn) e B(nxm) onde m > n, em detrimento do caso onde m < n, produzindo uma assimetria no núcleo ker(Λ). A Hipótese da Multiplicidade Algébrica permanece sem demonstração, o que a torna objeto de estudo em artigos futuros.
, tornando evidente a existência de uma seletividade, isto é, uma preferência, verificada no núcleo ker(Λ) deste funcional, onde predominam os pares de matrizes retangulares A(mxn) e B(nxm) onde m > n, em detrimento do caso onde m < n, produzindo uma assimetria no núcleo ker(Λ). A Hipótese da Multiplicidade Algébrica permanece sem demonstração, o que a torna objeto de estudo em artigos futuros.
REFERÊNCIAS
BOLDRINI, José Luiz. et al. Álgebra Linear. São Paulo. Editora Harbra, 1980.
HOFFMAN, Kenneth; KUNZE, Ray. Álgebra Linear. Rio de Janeiro. Editora LTC, 1979.
LANG, Serge. Álgebra Linear. Editora Edgard Blücher. Rio de Janeiro, 1971.
LIMA, Elon Lages. Álgebra Linear. Projeto Euclides. IMPA. Rio de Janeiro, 1996.
[1] Especialista Lato Sensu (Pós-graduação) em Ensino de Estatística pela UFN, Licenciado em Física pela PUC Goiás, Licenciado em Química pela PUC Goiás. ORCID: 0000-0001-6298-1906.
[2] Estudante do Ensino Médio no Colégio JR de Goiânia.
[3] Estudante do Ensino Médio no Colégio JR de Goiânia.
[4] Estudante do Ensino Médio no Colégio JR de Goiânia.
[5] Estudante do Ensino Médio no Colégio JR de Goiânia.
[6] Estudante do Ensino Médio no Colégio JR de Goiânia.
[7] Estudante do Ensino Médio no Colégio JR de Goiânia.
Enviado: Novembro, 2021.
Aprovado: Agosto, 2022.
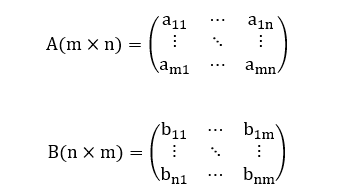
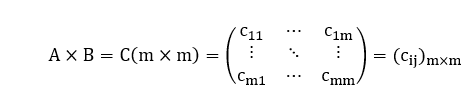
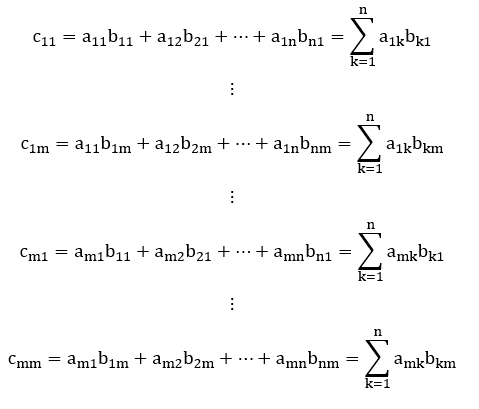
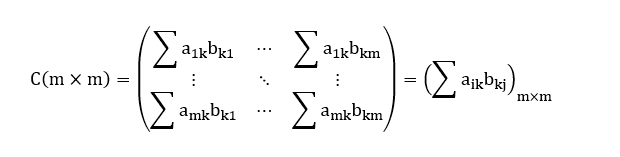
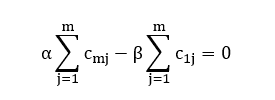
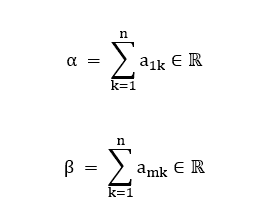
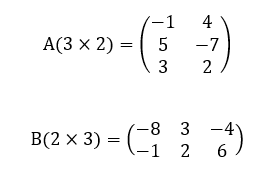
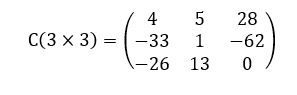
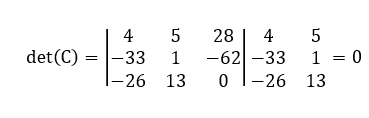
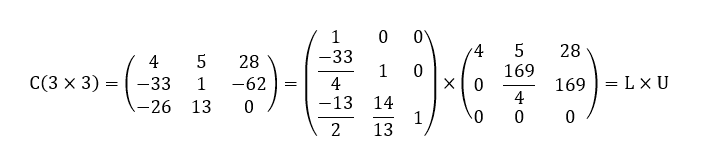
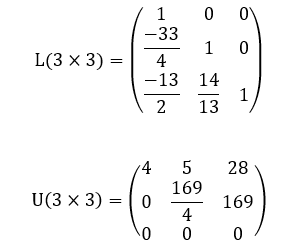
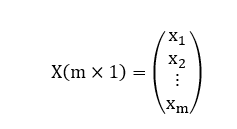
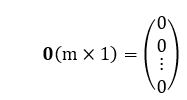
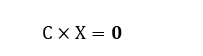
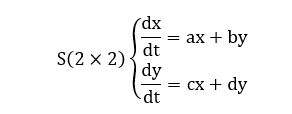
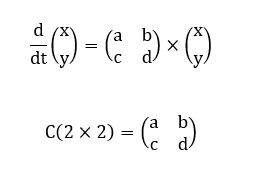
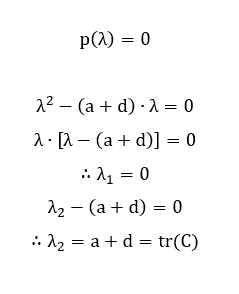
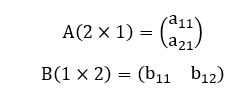
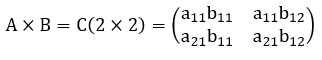
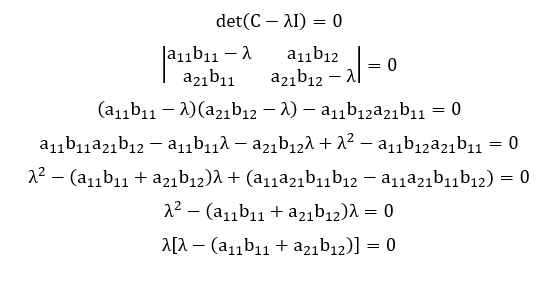
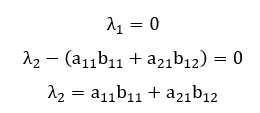
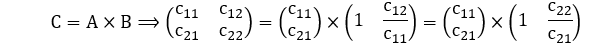
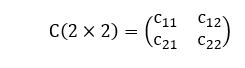
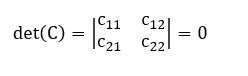
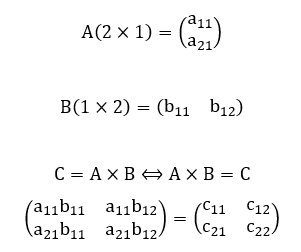
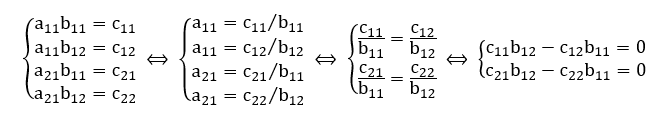
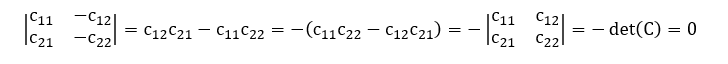
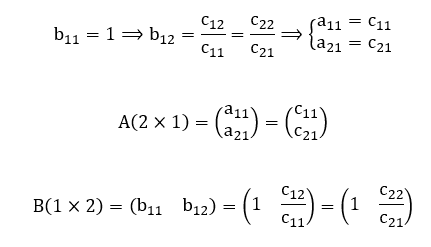
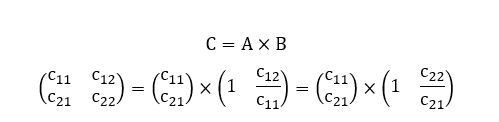
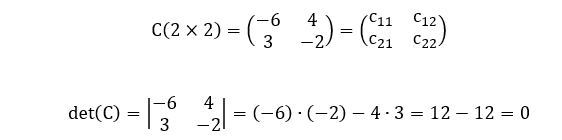
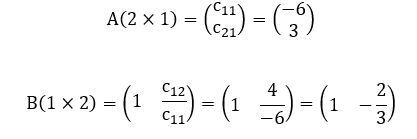
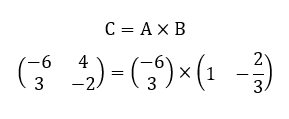

5 respostas
Artigo de muita importância e relevância para ciência e estudos matemáticos.
Parabens aos Alunos e Professores .
João Batista Elias de Sousa
Agradeço muito pelo seu elogio. Sempre avançando em prol da evolução da Matemática no Brasil!
Parabéns professor e alunos pelo empenho! Orgulhosa de vocês! Eu sempre gostei muito de matemática e me encantei com o teorema
Parabéns professor e alunos pelo empenho! Orgulhosa de vocês! Eu sempre gostei muito de matemática e me encantei com o teorema.
Simone Alves Barreto
Muito obrigado pelo seu elogio ao nosso artigo. Fico muito feliz pelo reconhecimento. A Matemática é de fato muito bela!