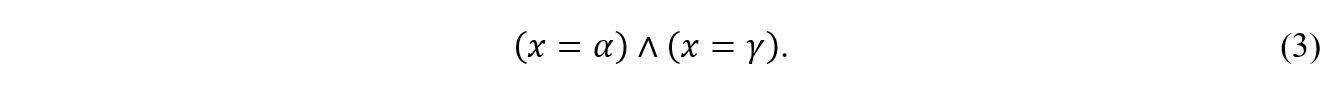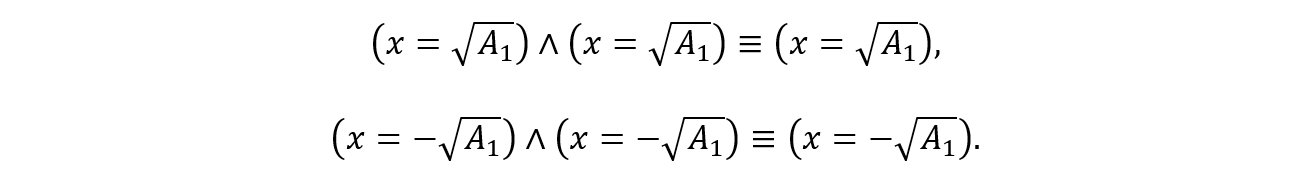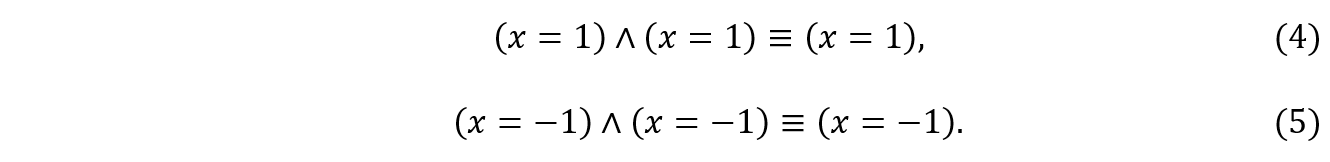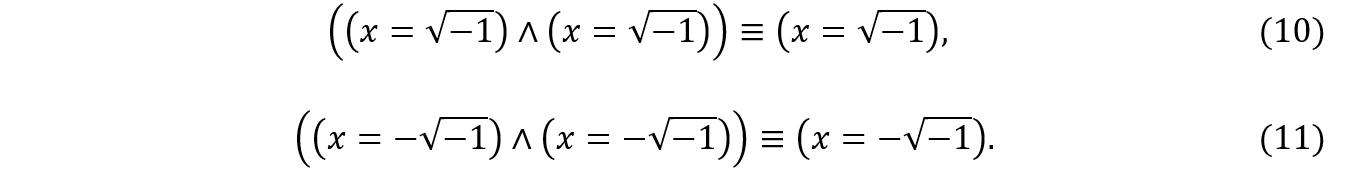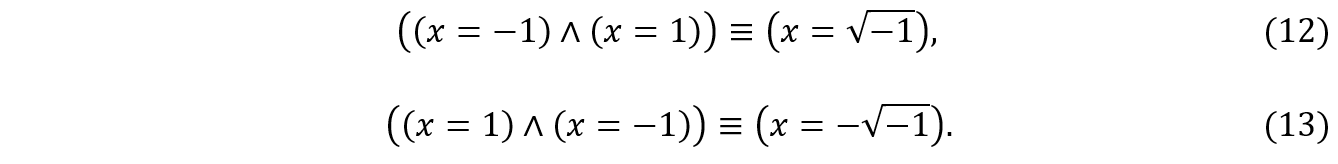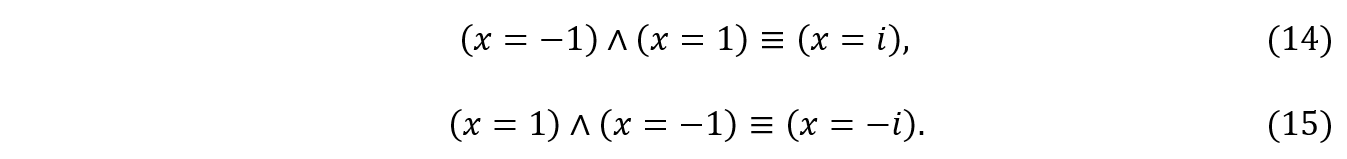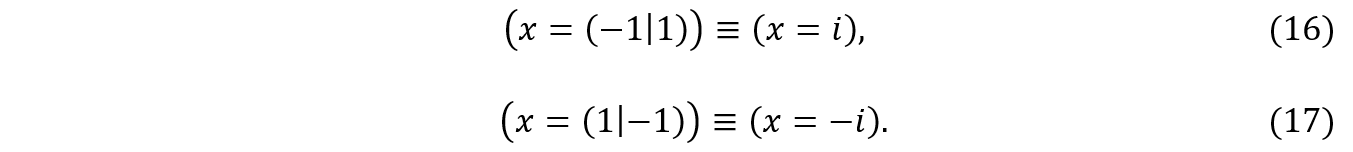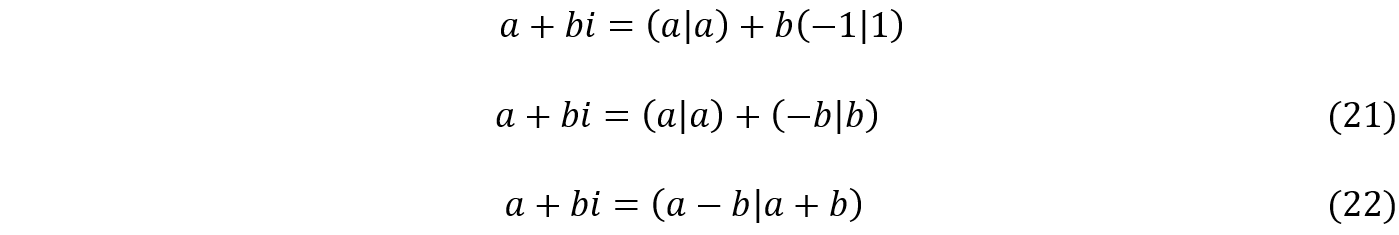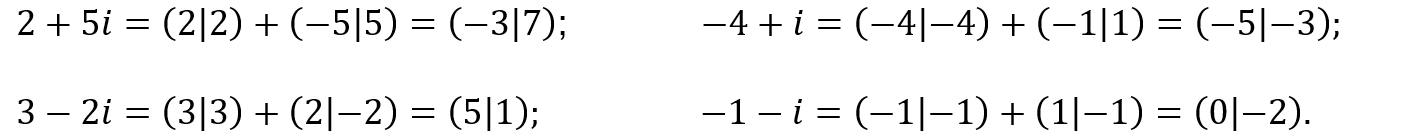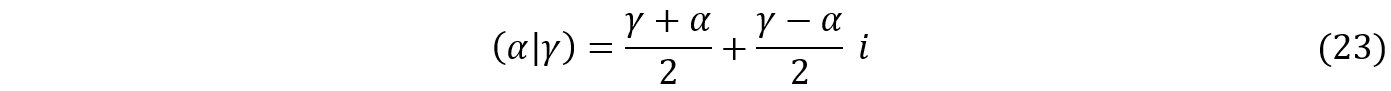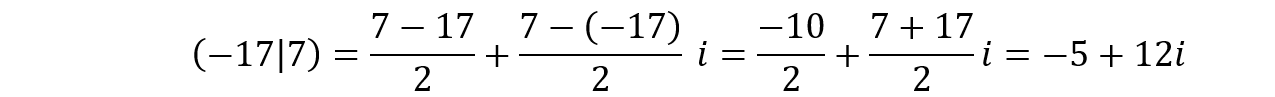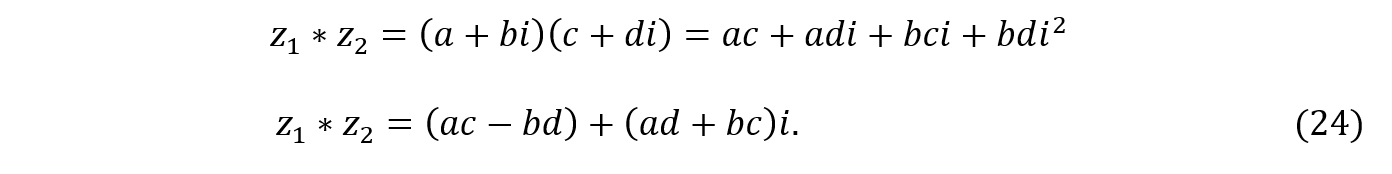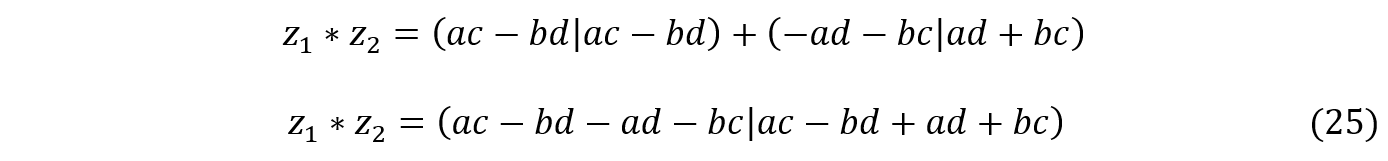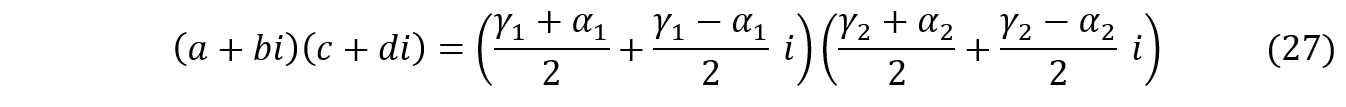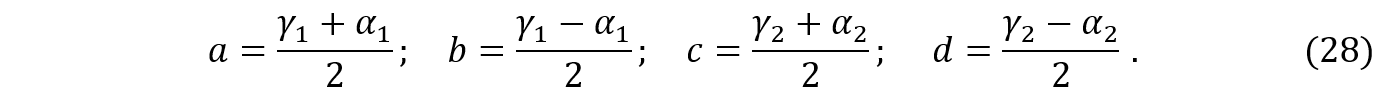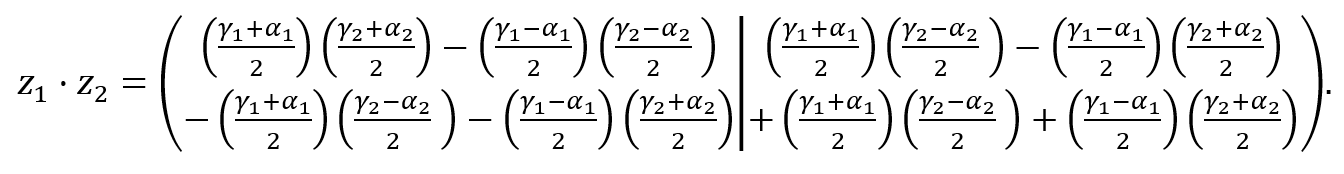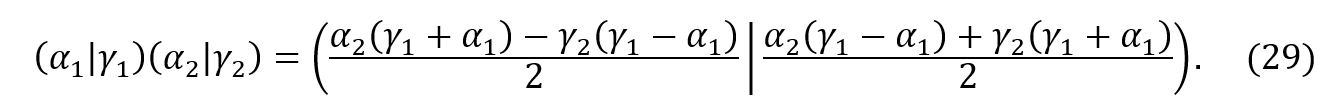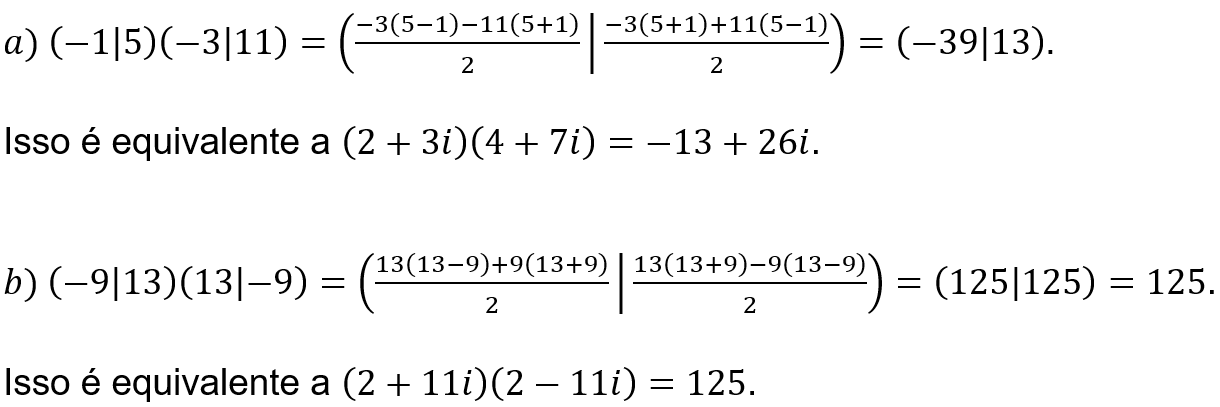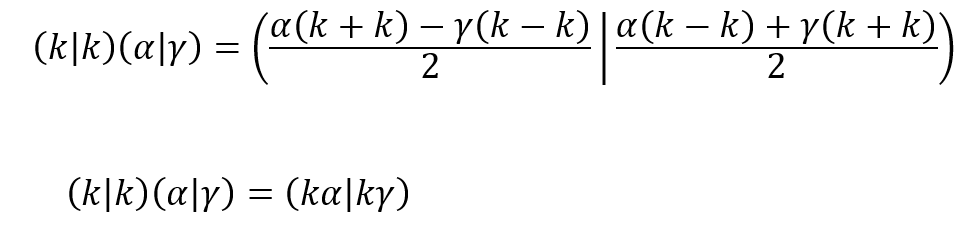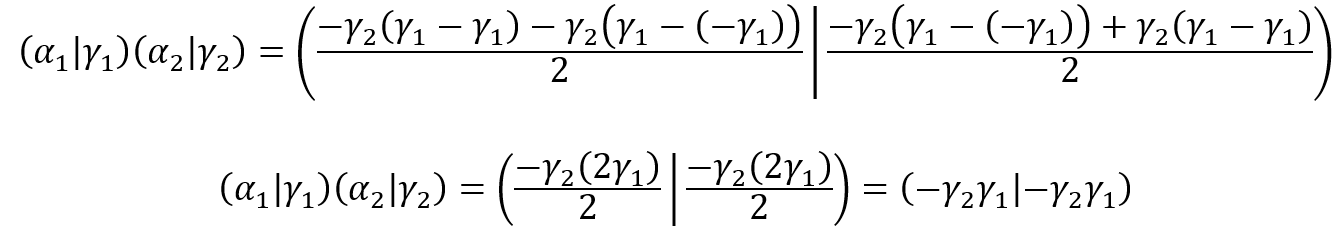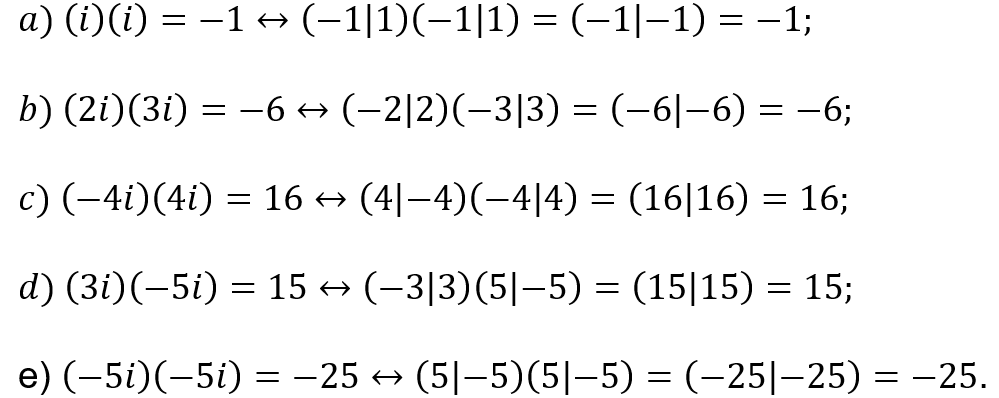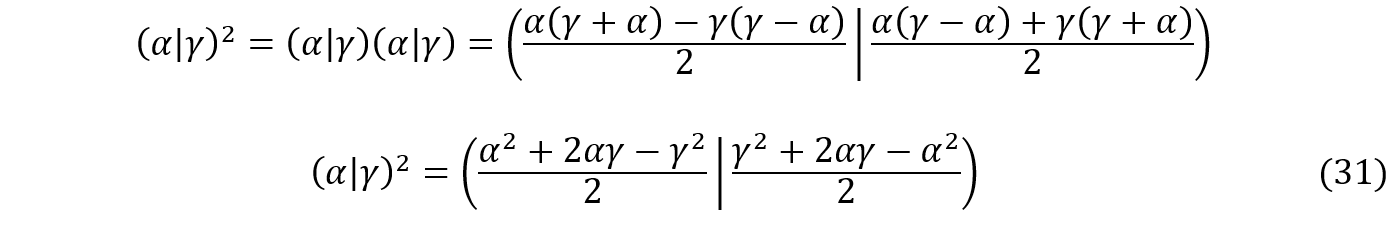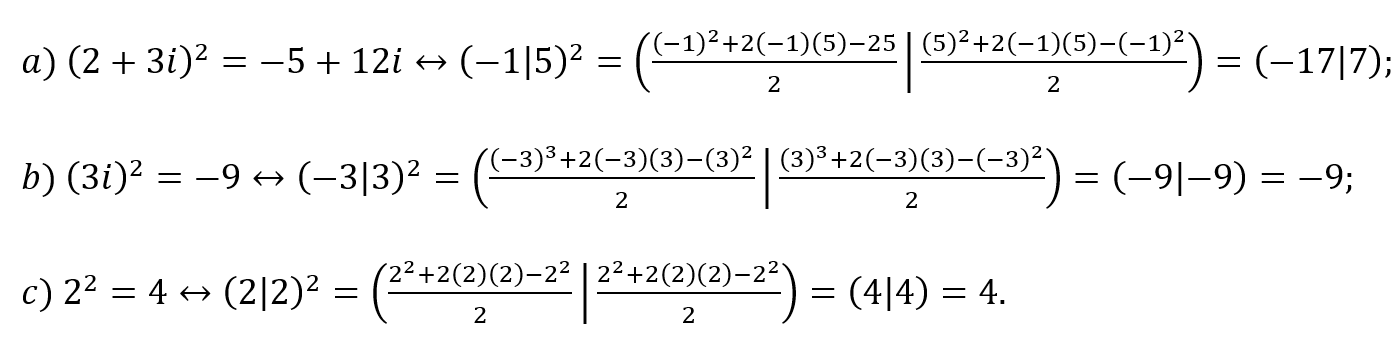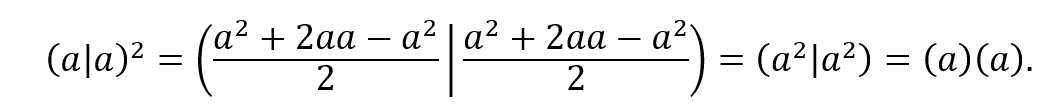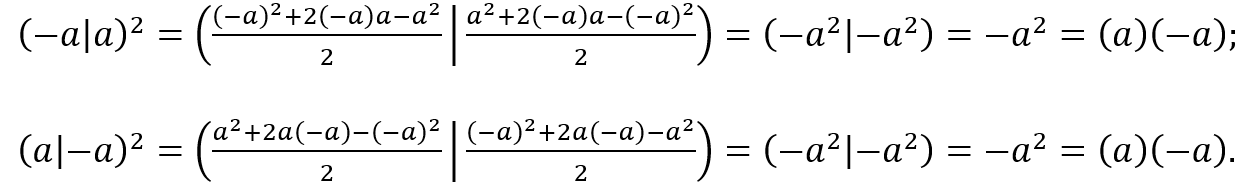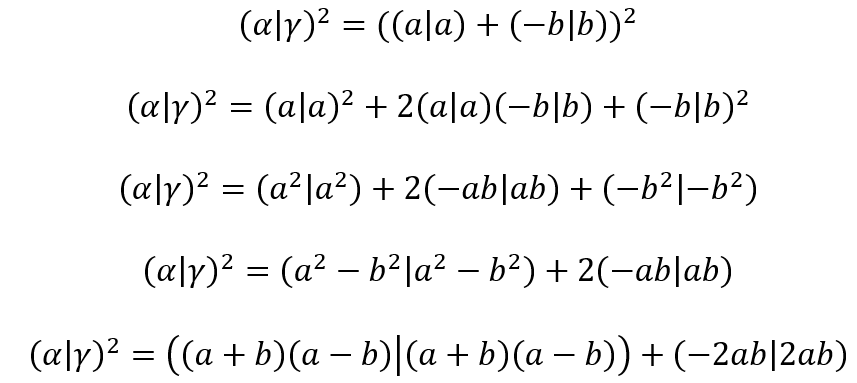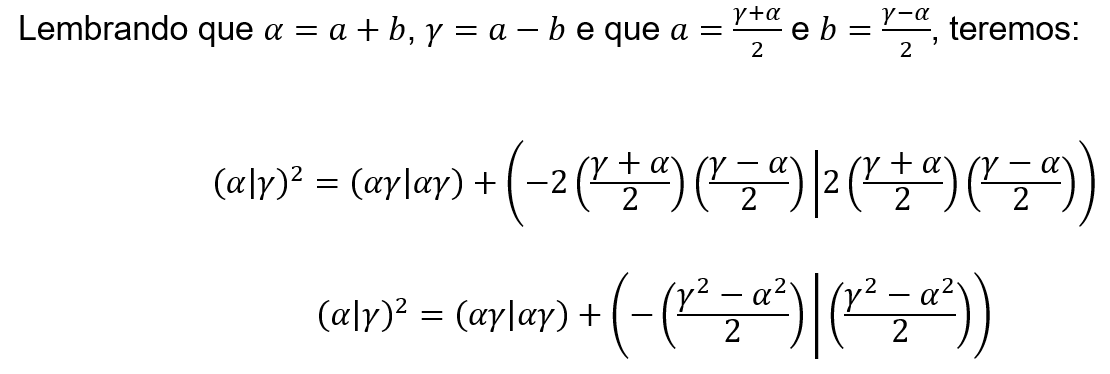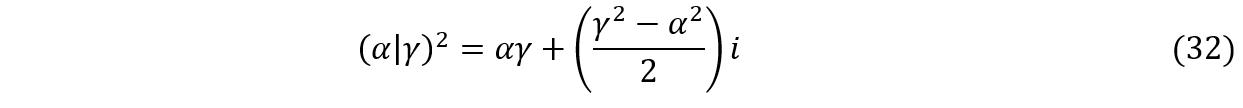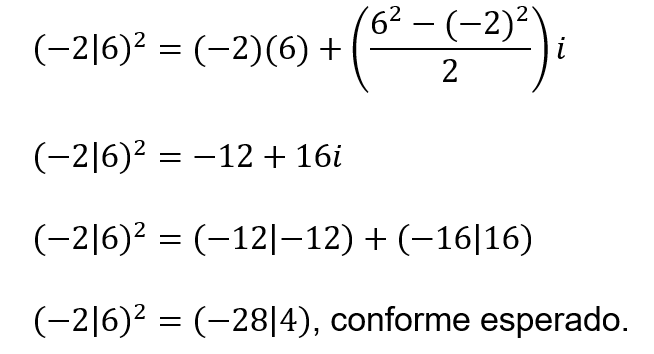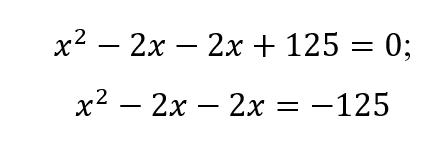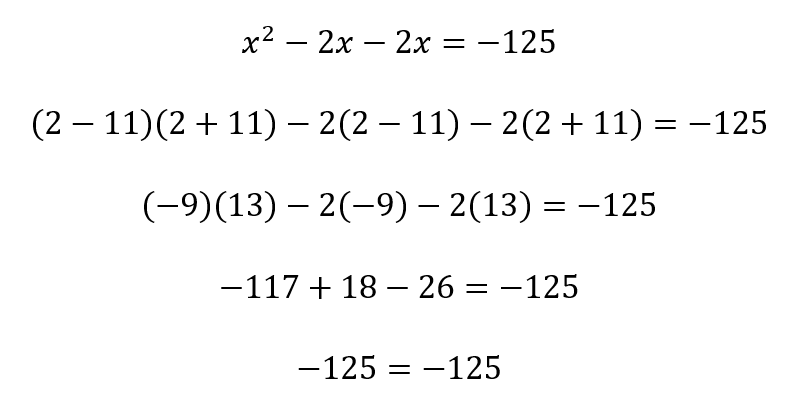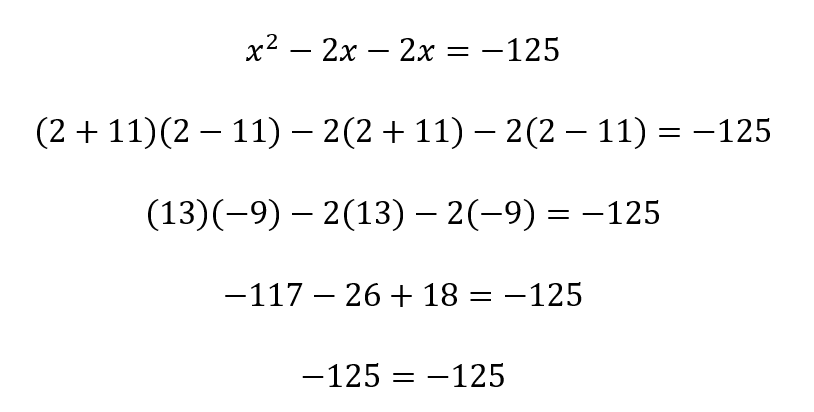ARTIGO ORIGINAL
MORAIS, Cláudio Marcelo [1]
MORAIS, Cláudio Marcelo. A unidade imaginária descrita como uma ambiguidade algébrica. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 09, Ed. 03, Vol. 01, pp. 05-28. Março de 2024. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/unidade-imaginaria, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/unidade-imaginaria
RESUMO
Um número complexo é formado por uma parte real e uma parte imaginária, sendo esta última composta por um número real multiplicado pela unidade imaginária “i“, definida como a raiz quadrada de![]() . Por essa razão os números imaginários não podem ser inseridos na reta dos números reais. A representação geométrica dos números complexos é feita no chamado plano complexo, composto de um eixo real e de um eixo imaginário, ortogonal à reta real. Entretanto, do ponto de vista filosófico, o fato do eixo imaginário não estar identificado com nenhum eixo no espaço euclidiano tridimensional, suscita questões ontológicas que transcendem o formalismo matemático bem estabelecido do conjunto dos números complexos: seriam os números imaginários apenas um sofisma, uma invenção arbitrária ou uma verdadeira descoberta matemática? Seriam os números imaginários o vislumbre de uma realidade paralela que está além da nossa percepção? Neste artigo, procuro demonstrar que a unidade imaginária pode ser interpretada como uma ambiguidade algébrica que surge ao se representar certos vetores do plano real como variáveis unidimensionais. Consequentemente, veremos como é possível expressar os números complexos a partir dos números reais.
. Por essa razão os números imaginários não podem ser inseridos na reta dos números reais. A representação geométrica dos números complexos é feita no chamado plano complexo, composto de um eixo real e de um eixo imaginário, ortogonal à reta real. Entretanto, do ponto de vista filosófico, o fato do eixo imaginário não estar identificado com nenhum eixo no espaço euclidiano tridimensional, suscita questões ontológicas que transcendem o formalismo matemático bem estabelecido do conjunto dos números complexos: seriam os números imaginários apenas um sofisma, uma invenção arbitrária ou uma verdadeira descoberta matemática? Seriam os números imaginários o vislumbre de uma realidade paralela que está além da nossa percepção? Neste artigo, procuro demonstrar que a unidade imaginária pode ser interpretada como uma ambiguidade algébrica que surge ao se representar certos vetores do plano real como variáveis unidimensionais. Consequentemente, veremos como é possível expressar os números complexos a partir dos números reais.
Palavras-chave: Números imaginários, Números complexos, Plano complexo, Funções polinomiais.
1. INTRODUÇÃO
Desde o seu surgimento na segunda metade do século XVI até hoje, os números complexos foram importantes não só para a matemática, mas também permitiu a cientistas e engenheiros (Cayemitte, 2000) inúmeras aplicações que ajudaram a impulsionar o desenvolvimento científico e tecnológico. Particularmente, em Física, estudos recentes, Renou et al. (2021) e Li et al. (2022), têm demonstrado que os números complexos são mesmo indispensáveis para expressar a teoria quântica padrão. Porém, antes do estabelecimento formal do sistema dos números complexos, os números imaginários eram vistos com certa desconfiança pelos matemáticos e foram inicialmente tratados apenas com um truque algébrico conveniente para solucionar equações cúbicas onde era necessário lidar com raízes quadradas de números negativos. A origem dos números complexos está ligada ao matemático italiano Rafael Bombelli (1526-1572), cujo trabalho (Bombelli, 1572) demonstrou que a manipulação de ![]() usando as regras comuns da aritmética levava a resultados corretos. O que se seguiu a partir daí foi uma longa história que envolveu várias gerações de matemáticos, indo desde nomes até então desconhecidos, como Gaspar Wessel e Jean-Robert Argand, até nomes consagrados, como Renè Descartes, John Wallis, Gauss e Hamilton. Para um panorama detalhado dessa fascinante história é recomendável a leitura do livro “An imaginary tale: the story of
usando as regras comuns da aritmética levava a resultados corretos. O que se seguiu a partir daí foi uma longa história que envolveu várias gerações de matemáticos, indo desde nomes até então desconhecidos, como Gaspar Wessel e Jean-Robert Argand, até nomes consagrados, como Renè Descartes, John Wallis, Gauss e Hamilton. Para um panorama detalhado dessa fascinante história é recomendável a leitura do livro “An imaginary tale: the story of ![]() ” (Nahin, 1998). Porém, longe de uma revisão histórica, o que se pretende aqui é apresentar uma interpretação completamente nova para a unidade imaginária que, caso venha a se mostrar correta, possa apontar para caminhos ainda inexplorados.
” (Nahin, 1998). Porém, longe de uma revisão histórica, o que se pretende aqui é apresentar uma interpretação completamente nova para a unidade imaginária que, caso venha a se mostrar correta, possa apontar para caminhos ainda inexplorados.
2. RETÂNGULOS ESCALARES E O PLANO ESCALAR
2.1 PRODUTO DAS COMPONENTES ESCALARES
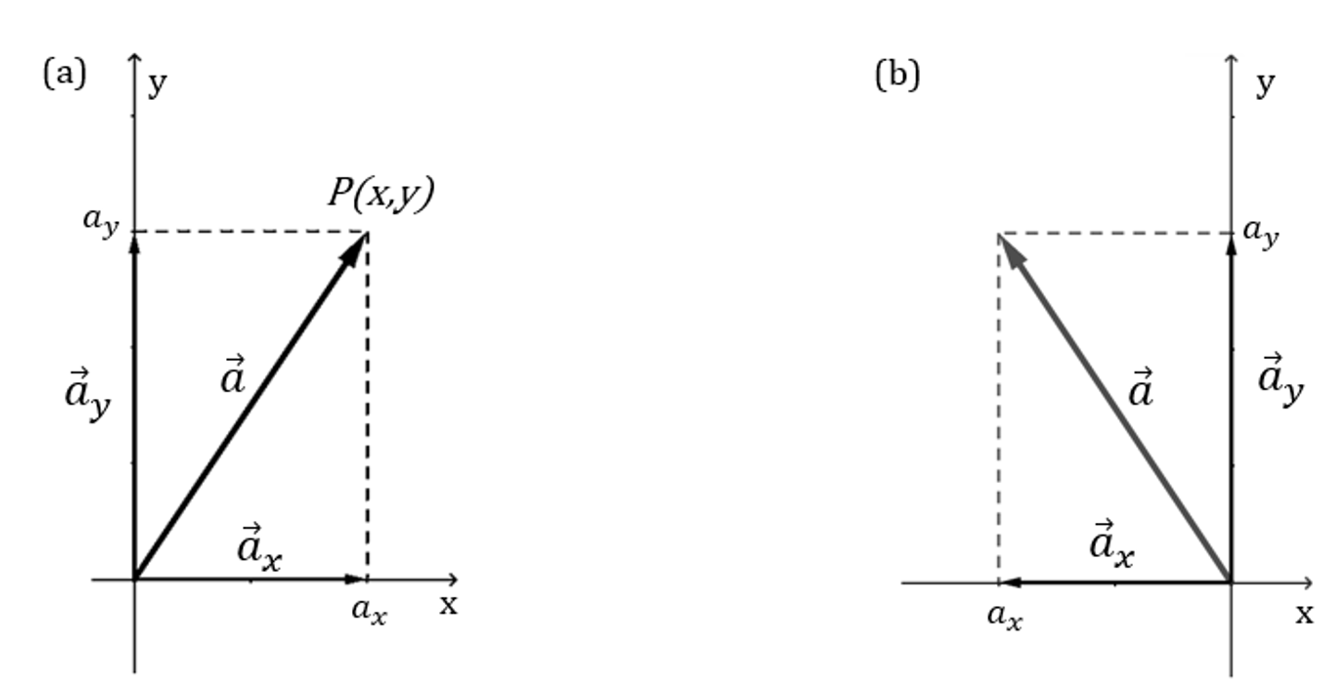
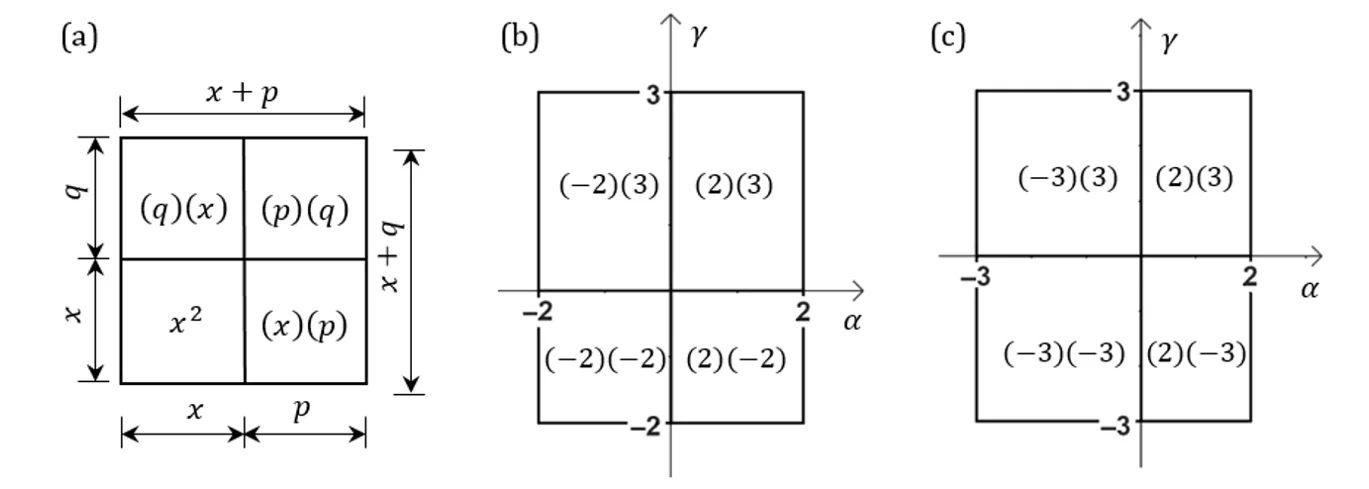
Dado um vetor ![]() , as quantidades
, as quantidades ![]() são chamadas de componentes vetoriais do vetor
são chamadas de componentes vetoriais do vetor ![]() , e as quantidades
, e as quantidades ![]() são chamadas de componentes escalares, ou simplesmente componentes (Halliday; Resnick, 1991). Fazendo a origem do vetor coincidir com a origem do sistema de coordenadas, podemos usar o ponto
são chamadas de componentes escalares, ou simplesmente componentes (Halliday; Resnick, 1991). Fazendo a origem do vetor coincidir com a origem do sistema de coordenadas, podemos usar o ponto ![]() na extremidade do vetor para defini-lo, conforme visto na figura 1a. Isso nos permite escrever o vetor na forma de par ordenado
na extremidade do vetor para defini-lo, conforme visto na figura 1a. Isso nos permite escrever o vetor na forma de par ordenado ![]() . Definiremos agora o produto das componentes escalares
. Definiremos agora o produto das componentes escalares ![]() de um dado vetor como:
de um dado vetor como:![]() Vemos que o vetor
Vemos que o vetor ![]() está diagonalmente inscrito num retângulo cujos lados, partindo da origem, são delimitados pelos escalares
está diagonalmente inscrito num retângulo cujos lados, partindo da origem, são delimitados pelos escalares ![]() . Por esse motivo chamaremos esse retângulo de ‘retângulo escalar’. Como consequência direta da definição (1), vetores nos quadrantes ímpares possuem produtos das componentes positivos, enquanto vetores nos quadrantes pares possuem produtos negativos, como visto na figura 1b. Podemos dizer que as componentes escalares
. Por esse motivo chamaremos esse retângulo de ‘retângulo escalar’. Como consequência direta da definição (1), vetores nos quadrantes ímpares possuem produtos das componentes positivos, enquanto vetores nos quadrantes pares possuem produtos negativos, como visto na figura 1b. Podemos dizer que as componentes escalares ![]() são complementares entre si, no sentido de que ambas determinam as componentes vetoriais que, quando somadas, nos permitem obter o vetor de interesse e, por consequência, o retângulo escalar a ele associado.
são complementares entre si, no sentido de que ambas determinam as componentes vetoriais que, quando somadas, nos permitem obter o vetor de interesse e, por consequência, o retângulo escalar a ele associado.
Fig. 1: (a) Vetor ![]() com suas componentes no primeiro quadrante; (b) Vetor
com suas componentes no primeiro quadrante; (b) Vetor ![]() e suas componentes no segundo quadrante: A negativo
e suas componentes no segundo quadrante: A negativo
2.2 O PLANO ESCALAR
Considere os planos xy e αγ no espaço euclidiano tridimensional. O plano xy será usado para traçarmos a curva de uma equação qualquer do segundo grau, enquanto o plano αγ, doravante denominado “plano escalar”, será usado para representarmos os termos dessa equação através de retângulos escalares e seus vetores associados. Para isso, vamos considerar a função polinomial quadrática ![]() e o seu desenvolvimento a seguir:
e o seu desenvolvimento a seguir: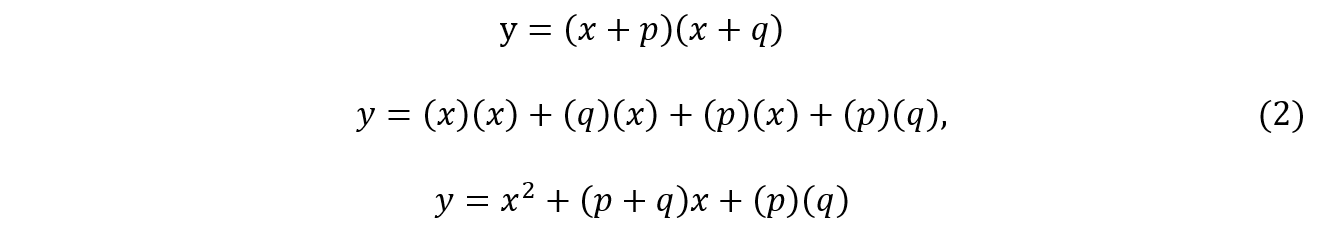
onde p e q são números reais. Fazendo ![]() , obtemos uma equação do segundo grau em que os valores
, obtemos uma equação do segundo grau em que os valores ![]() são as suas raízes. Se considerarmos cada um dos termos da função vista em (2) como o produto das componentes escalares de um vetor no plano αγ, veremos que a cada um desses produtos estará associado um retângulo escalar, o que nos permite obter o diagrama genérico visto na figura 2a. Observe nessa figura que no termo
são as suas raízes. Se considerarmos cada um dos termos da função vista em (2) como o produto das componentes escalares de um vetor no plano αγ, veremos que a cada um desses produtos estará associado um retângulo escalar, o que nos permite obter o diagrama genérico visto na figura 2a. Observe nessa figura que no termo ![]() a variável x forma os dois lados perpendiculares de um mesmo quadrado. Tomemos como exemplo a equação
a variável x forma os dois lados perpendiculares de um mesmo quadrado. Tomemos como exemplo a equação ![]() , cujas raízes são
, cujas raízes são ![]() . Ela pode ser escrita como
. Ela pode ser escrita como ![]() , o que nos permite obter a figura 2b para a raiz
, o que nos permite obter a figura 2b para a raiz ![]() e a figura 2c para
e a figura 2c para ![]() .
.
Fig. 2: (a) Diagrama para a função quadrática; (b) Representação da função ![]() para
para ![]() ; (c) A mesma representação para
; (c) A mesma representação para ![]()
3. AMBIGUIDADE E A NOTAÇÃO CONJUNTA
3.1 PLANO ESCALAR E A CONJUNÇÃO E
Na seção anterior vimos que a variável x origina os dois lados de um retângulo escalar quadrado, referente ao termo quadrático, quando representada no plano escalar. Portanto, nesse plano, x ocupa duas dimensões, a saber, uma no eixo α e outra no eixo γ. Assim, para qualquer x, temos ![]() no eixo horizontal e
no eixo horizontal e ![]() no eixo vertical, como no exemplo da figura 3a, onde temos um caso em que a raiz
no eixo vertical, como no exemplo da figura 3a, onde temos um caso em que a raiz ![]() é positiva e
é positiva e ![]() é negativa. Vamos, agora, proceder de modo contrário: em vez de obtermos um retângulo a partir do valor de x, vamos expressar essa variável partindo das componentes de um vetor
é negativa. Vamos, agora, proceder de modo contrário: em vez de obtermos um retângulo a partir do valor de x, vamos expressar essa variável partindo das componentes de um vetor ![]() e do retângulo escalar a ele associado. Isso pode ser feito com o auxílio da conjunção E, como segue:
e do retângulo escalar a ele associado. Isso pode ser feito com o auxílio da conjunção E, como segue:
Ainda que a variável x apresente valores numericamente iguais nesses dois eixos, ocorre uma ambiguidade à medida que ela representa simultaneamente as duas componentes complementares do mesmo vetor.
Fig. 3: (a) Caso em que há uma raiz em cada quadrante ímpar; (b) Cada quadrado tem lados com comprimento igual à raiz quadrada do produto das componentes; (c) As raízes de ![]() . O valor dentro de cada retângulo é o produto das componentes do vetor associado
. O valor dentro de cada retângulo é o produto das componentes do vetor associado
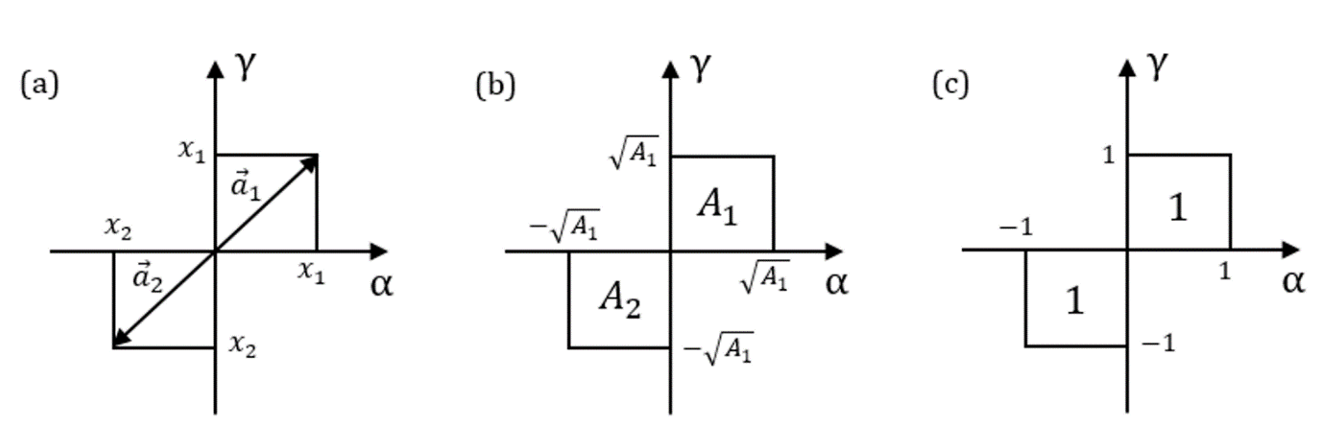
Vejamos agora como os valores complementares de x vistos no plano escalar correspondem ao valor único que essa variável apresenta no plano xy. Observe na figura 3b que cada lado do quadrado formado pela variável x tem comprimento igual a ![]() , onde
, onde ![]() é o produto das componentes do vetor associado a esse quadrado. Então, para
é o produto das componentes do vetor associado a esse quadrado. Então, para ![]() no primeiro quadrante, as componentes α e γ são iguais a
no primeiro quadrante, as componentes α e γ são iguais a ![]() , o que nos dá
, o que nos dá ![]() , conforme a notação vista em (3). No terceiro quadrante, teremos
, conforme a notação vista em (3). No terceiro quadrante, teremos ![]() , o que implicará em
, o que implicará em ![]() . Podemos agora aplicar a lei idempotente da conjunção (Lipschutz, 1972) para obtermos
. Podemos agora aplicar a lei idempotente da conjunção (Lipschutz, 1972) para obtermos
Como exemplo, vamos fazer o mesmo desenvolvimento para as raízes ![]() da equação
da equação ![]() , conforme ilustrado em 3c, obtendo
, conforme ilustrado em 3c, obtendo ![]() no primeiro quadrante e
no primeiro quadrante e ![]() no terceiro quadrante. Aplicando-se a lei da idempotência, teremos:
no terceiro quadrante. Aplicando-se a lei da idempotência, teremos:
Logo, a ambiguidade que a variável x exibe no primeiro e no terceiro quadrantes do plano escalar é redutível ao valor unívoco observado no plano xy.
3.2 NOTAÇÃO CONJUNTA
Antes de prosseguirmos, vamos fazer uma simplificação na notação vista em (3). Desse ponto em diante, vamos definir a seguinte notação:
Chamaremos essa forma de ‘notação conjunta’. As expressões (4) e (5), respectivamente, podem ser escritas nas seguintes formas conjuntas:
Igualando x nos dois lados de cada identidade em (8), temos:
Vamos considerar as posições relativas em que as componentes escalares aparecem em cada lado da equivalência vista em (7) como uma ordem canônica a ser seguida. Obviamente, para qualquer x real, haverá sempre a uma combinação de componentes ![]() no plano escalar. Vale ainda ressaltar que, sendo α e γ as duas coordenadas de um mesmo ponto no plano, a notação
no plano escalar. Vale ainda ressaltar que, sendo α e γ as duas coordenadas de um mesmo ponto no plano, a notação ![]() é equivalente à notação de par ordenado
é equivalente à notação de par ordenado ![]() e seu uso se justifica aqui apenas para diferenciá-la da notação
e seu uso se justifica aqui apenas para diferenciá-la da notação ![]() usada para representar números no plano complexo.
usada para representar números no plano complexo.
4. IMAGINÁRIOS E COMPLEXOS
4.1 A CONSTANTE IMAGINÁRIA
De acordo com o que foi visto até aqui, as raízes positivas das equações do segundo grau nos permitem formar retângulos no primeiro quadrante do plano escalar, enquanto as raízes negativas fazem o mesmo no terceiro quadrante. Entretanto, esses diagramas ainda não nos permitem representar raízes na forma de números complexos ou mesmo imaginários puros, uma vez que os eixos α e γ são reais. Daí, poderíamos nos indagar quanto aos segundo e quarto quadrantes desse plano: teriam eles alguma relação com os números complexos? Para respondermos a essa pergunta vamos partir das raízes de ![]() , que já foram vistas na figura 3c, e girar em torno da origem os vetores associados a essas raízes, fazendo um ângulo de 90°, como mostrado na figura 4a. Feito isso, podemos ver que cada vetor resultante agora possui uma componente unitária positiva e outra negativa, tanto no segundo quanto no quarto quadrantes. Vamos admitir que as mesmas propriedades válidas nos quadrante ímpares continuem valendo nos quadrantes pares após a rotação, i.e., o retângulo formado pela variável x continua sendo um quadrado com produto escalar
, que já foram vistas na figura 3c, e girar em torno da origem os vetores associados a essas raízes, fazendo um ângulo de 90°, como mostrado na figura 4a. Feito isso, podemos ver que cada vetor resultante agora possui uma componente unitária positiva e outra negativa, tanto no segundo quanto no quarto quadrantes. Vamos admitir que as mesmas propriedades válidas nos quadrante ímpares continuem valendo nos quadrantes pares após a rotação, i.e., o retângulo formado pela variável x continua sendo um quadrado com produto escalar ![]() , em que cada lado tem comprimento igual a
, em que cada lado tem comprimento igual a ![]() , vide figura 4b.
, vide figura 4b.
Fig. 4: (a)Mudança de quadrante girando os vetores em 90°; (b) As mesmas relações vistas para os quadrantes impares; (c) Retângulos escalares e suas raízes
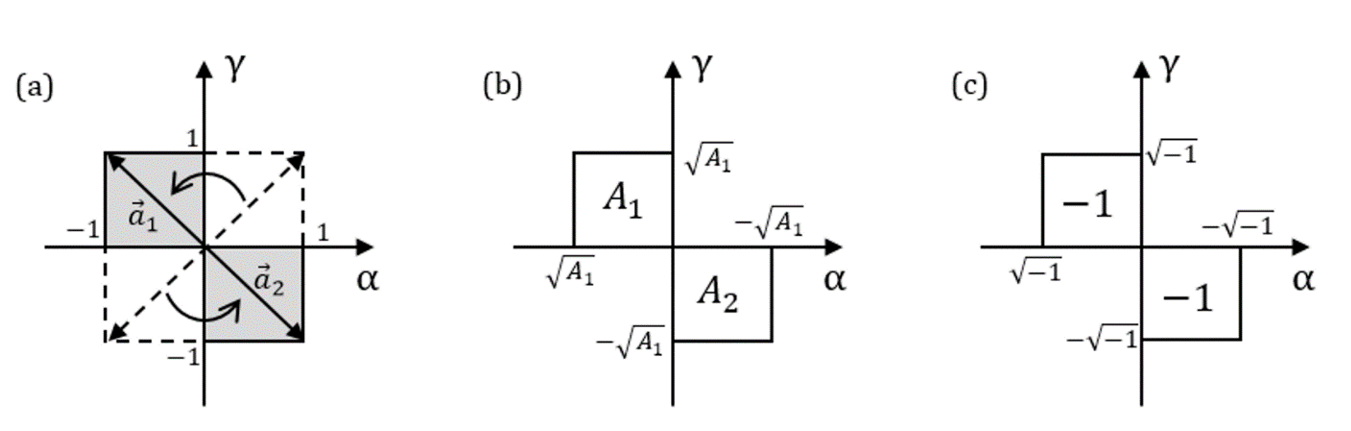
Então, caso a raiz da equação esteja no segundo quadrante do plano escalar, teremos α e γ iguais a ![]() , o que nos dá
, o que nos dá ![]() , conforme a notação vista em (3). No quarto quadrante, teremos
, conforme a notação vista em (3). No quarto quadrante, teremos ![]() , o que implica em
, o que implica em ![]() . Entretanto, como agora temos
. Entretanto, como agora temos ![]() , cada componente escalar vale
, cada componente escalar vale ![]() . Veja a figura 4c. Logo, temos
. Veja a figura 4c. Logo, temos ![]() no segundo quadrante e
no segundo quadrante e ![]() no quarto quadrante. Então, da mesma forma que fizemos para os quadrante ímpares, vamos aplicar a lei da idempotência da conjunção:
no quarto quadrante. Então, da mesma forma que fizemos para os quadrante ímpares, vamos aplicar a lei da idempotência da conjunção:
Para aplicarmos a (10) e a (11) a condição de ambiguidade do termo quadrático expressa por (3), vamos substituir os valores reais de α e γ vistos na figura 4a, obtendo:
Porém, diferentemente do que foi feito na seção 3.1, não é mais possível aplicar a lei idempotente da conjunção para atribuir um valor único à variável x, ou seja, nos quadrantes pares, as componentes escalares apresentam uma ambiguidade não redutível. Isso significa que existem combinações de componentes no plano escalar para as quais não está associando nenhum número real no plano xy. Todavia, sabemos que a solução ![]() também pode ser escrita como
também pode ser escrita como ![]() , onde i é a constante imaginária. Assim, substituindo
, onde i é a constante imaginária. Assim, substituindo ![]() por i em (12) e (13), obteremos:
por i em (12) e (13), obteremos:
Aplicando a notação conjunta a (14) e (15), teremos:
Finalmente, eliminando x em (16) e em (17) respectivamente, teremos:
Portanto, observe que a figura que obtivemos em 4a, ao girarmos em 90° as raízes de ![]() , corresponde às duas raízes da equação
, corresponde às duas raízes da equação ![]() no plano escalar, sendo elas
no plano escalar, sendo elas ![]() .
.
4.2 NÚMEROS IMAGINÁRIOS
A regra para multiplicar um número real pela unidade imaginária pode ser entendida como a multiplicação desse real por um vetor ![]() no plano escalar, ou seja, a multiplicação se dará componente a componente. Assim, sendo k uma constante real e
no plano escalar, ou seja, a multiplicação se dará componente a componente. Assim, sendo k uma constante real e ![]() , temos:
, temos:
Todavia, em notação conjunta, ![]() . Logo, podemos escrever:
. Logo, podemos escrever:
Fazendo k variar de ![]() , obtemos a sequência dos números imaginários no plano escalar. Eis alguns exemplos:
, obtemos a sequência dos números imaginários no plano escalar. Eis alguns exemplos:
4.3 NÚMEROS COMPLEXOS
A operação de somar dois reais, ![]() , consiste em somar dois vetores no plano escalar, o que é feito somando-se separadamente as componentes em cada eixo. Assim, sendo
, consiste em somar dois vetores no plano escalar, o que é feito somando-se separadamente as componentes em cada eixo. Assim, sendo ![]() , a soma é dada por:
, a soma é dada por:
Um número complexo pode ser descrito de maneira sucinta como um número real somado a um múltiplo da unidade imaginária. Assim, sendo a e b dois números reais e i a unidade imaginária, um número complexo pode ser representado algebricamente como ![]() . Da mesma forma que um número real, um número imaginário representa um vetor no plano escalar, como visto em (19). Portanto, a operação de somar um real com um imaginário se dará da mesma forma que se dá quando somamos dois reais. Assim, substituindo
. Da mesma forma que um número real, um número imaginário representa um vetor no plano escalar, como visto em (19). Portanto, a operação de somar um real com um imaginário se dará da mesma forma que se dá quando somamos dois reais. Assim, substituindo ![]() em (20) por a, e
em (20) por a, e ![]() por bi, temos:
por bi, temos:
Vejamos alguns exemplos:
Portanto, no plano escalar, um número complexo representa a soma de um vetor de um quadrante ímpar com um vetor de um quadrante par. Note também que temos duas maneiras para fazer a representação conjunta de um número complexo : a forma vista em (21) será chamada de forma conjunta analítica e a forma vista em (22) será chamada de forma conjunta sintética.
5. MUDANÇA DA FORMA CONJUNTA PARA A FORMA ALGÉBRICA
A mudança de um número escrito na forma algébrica ![]() para a forma conjunta sintética
para a forma conjunta sintética ![]() pode ser feita pela igualdade vista em (22). Para a mudança inversa, basta resolvermos o sistema composto por
pode ser feita pela igualdade vista em (22). Para a mudança inversa, basta resolvermos o sistema composto por ![]() , o que resulta em:
, o que resulta em:
Por exemplo, o complexo ![]() pode ser escrito como
pode ser escrito como ![]() na forma algébrica:
na forma algébrica:
6. MULTIPLICAÇÃO NA FORMA CONJUNTA
6.1 FÓRMULA GERAL
Vamos agora obter uma fórmula geral para multiplicar dois números quaisquer escritos na forma conjunta sintética. Primeiramente, dados dois números complexos na forma algébrica ![]() , podemos encontrar o produto entre ambos como segue:
, podemos encontrar o produto entre ambos como segue:
Usando a regra de transformação vista em (21), vamos passar apenas o lado direito da igualdade em (24) para a forma conjunta:
Na forma conjunta, o produto de dois complexos pode ser escrito como:
Substituindo ![]() por
por ![]() e passando o lado direto de (26) para a forma algébrica, conforme visto em (23), obtemos:
e passando o lado direto de (26) para a forma algébrica, conforme visto em (23), obtemos:
Assim, por comparação direta, obtemos:
Substituindo os valores de (28) em (25), obtemos:
Finalmente, desenvolvendo algebricamente as duas componentes da equação acima e substituindo ![]() por
por ![]() , chegamos à fórmula geral:
, chegamos à fórmula geral:
Exemplos:
6.2 MULTIPLICAÇÃO POR UM NÚMERO REAL
Para obtermos o produto entre um real e um complexo na forma conjunta, basta fazer ![]() , para obter a forma conjunta do número real e
, para obter a forma conjunta do número real e ![]() para um número complexo qualquer. Substituindo na equação (29), teremos:
para um número complexo qualquer. Substituindo na equação (29), teremos:
Esse resultado concorda com a equação (19) que foi utilizada para gerar um número imaginário qualquer a partir da unidade imaginária.
6.3 PRODUTO ENTRE DOIS IMAGINÁRIOS
Uma boa simplificação poderá ser obtida quando tivermos dois imaginários para serem multiplicados. Fazendo ![]() e na fórmula (29), obtemos:
e na fórmula (29), obtemos:
Opcionalmente, podemos eliminar as componentes negativas do resultado obtido fazendo ![]() , obtendo:
, obtendo:
Exemplos:
6.4 O QUADRADO DE UM COMPLEXO
Podemos simplificar um pouco a fórmula (29) ao multiplicarmos um complexo por ele mesmo. Fazendo ![]() , obtemos:
, obtemos:
Exemplos:
6.5 QUANDO O QUADRADO É IGUAL AO PRODUTO DAS COMPONENTES
O quadrado de um número real pode ser obtido de maneira simplificada fazendo ![]() na equação (31), como segue:
na equação (31), como segue:
De forma semelhante, podemos obter o quadrado de um número imaginário tanto na forma ![]() quanto na forma
quanto na forma ![]() como segue:
como segue:
Logo, tanto o quadrado de dois reais quanto o quadrado de dois imaginários podem ser obtidos pelo produto das componentes escalares.
6.6 QUANDO O QUADRADO DIFERE DO PRODUTO DAS COMPONENTES
Dado ![]() , com as componentes α e γ diferindo em módulo, se calcularmos
, com as componentes α e γ diferindo em módulo, se calcularmos ![]() pelo produto das componentes como fizemos em 2.2, obteremos um valor diferente daquele obtido pela fórmula (31). Por exemplo, sendo
pelo produto das componentes como fizemos em 2.2, obteremos um valor diferente daquele obtido pela fórmula (31). Por exemplo, sendo ![]() , se calcularmos
, se calcularmos ![]() como o produto das componentes, obtemos
como o produto das componentes, obtemos ![]() . Se calcularmos
. Se calcularmos ![]() como o quadrado de um complexo, encontramos
como o quadrado de um complexo, encontramos ![]() . Para entendermos por que isso ocorre, considere
. Para entendermos por que isso ocorre, considere ![]() . Elevando x ao quadrado na forma conjunta analítica, teremos:
. Elevando x ao quadrado na forma conjunta analítica, teremos:
Finalmente, escrevendo o resultado na forma algébrica, encontramos que:
Esse resultado nos mostra que quando elevamos um complexo ao quadrado, obtemos como resultado o produto das componentes escalares mais uma parcela imaginária, que pode ser descrita como a metade da diferença dos quadrados das componentes. Por isso, se ![]() for um número real
for um número real ![]() , ou se for um imaginário puro
, ou se for um imaginário puro ![]() , quando calcularmos o seu quadrado não haverá a parte imaginária e, portanto, o quadrado do complexo calculado pela fórmula (31) será igual ao produto das componentes.
, quando calcularmos o seu quadrado não haverá a parte imaginária e, portanto, o quadrado do complexo calculado pela fórmula (31) será igual ao produto das componentes.
Exemplo:
Sendo ![]() , o seu quadrado obtido por (31) é
, o seu quadrado obtido por (31) é ![]() . Este resultado pode ser obtido por (32):
. Este resultado pode ser obtido por (32):
7. VERIFICAÇÃO DA AMBIGUIDADE NAS EQUAÇÕES DO SEGUNDO GRAU
7.1 MÉTODO GEOMÉTRICO
Vamos agora verificar as soluções gráficas no plano real para as equações do segundo grau com raízes negativas. Para isso, vamos tomar como exemplo a equação ![]() , cujas raízes são
, cujas raízes são ![]() . Agora, escrevendo
. Agora, escrevendo ![]() na forma conjunta, obtemos:
na forma conjunta, obtemos:
O primeiro passo é escrever essa equação na forma de produtos escalares, semelhante ao que foi visto na seção 2.2 e, em seguida, separar o termo independente, como segue:
O termo independente nada mais é que o produto das duas raízes e seu cálculo já foi visto no exemplo b da seção 6.1. A parte à esquerda da igualdade nos permite obter o diagrama da figura 5a. No diagrama da figura 5b escrevemos ![]() na forma
na forma ![]() e dentro de cada retângulo está o produto das componentes escalares. Note que a base do retângulo assume o valor
e dentro de cada retângulo está o produto das componentes escalares. Note que a base do retângulo assume o valor ![]() por se referir ao eixo α, enquanto que o valor
por se referir ao eixo α, enquanto que o valor ![]() fica ao longo de sua altura por ser a componente do eixo γ. Tendo essa figura como referência e lembrando que
fica ao longo de sua altura por ser a componente do eixo γ. Tendo essa figura como referência e lembrando que ![]() é dado pelo produto das componentes, vejamos como o valor de
é dado pelo produto das componentes, vejamos como o valor de ![]() torna a equação verdadeira:
torna a equação verdadeira:
Fig.5: (a) Diagrama para ![]() ; (b) Diagrama para
; (b) Diagrama para ![]() ; (c) Os vetores no plano escalar para
; (c) Os vetores no plano escalar para ![]()
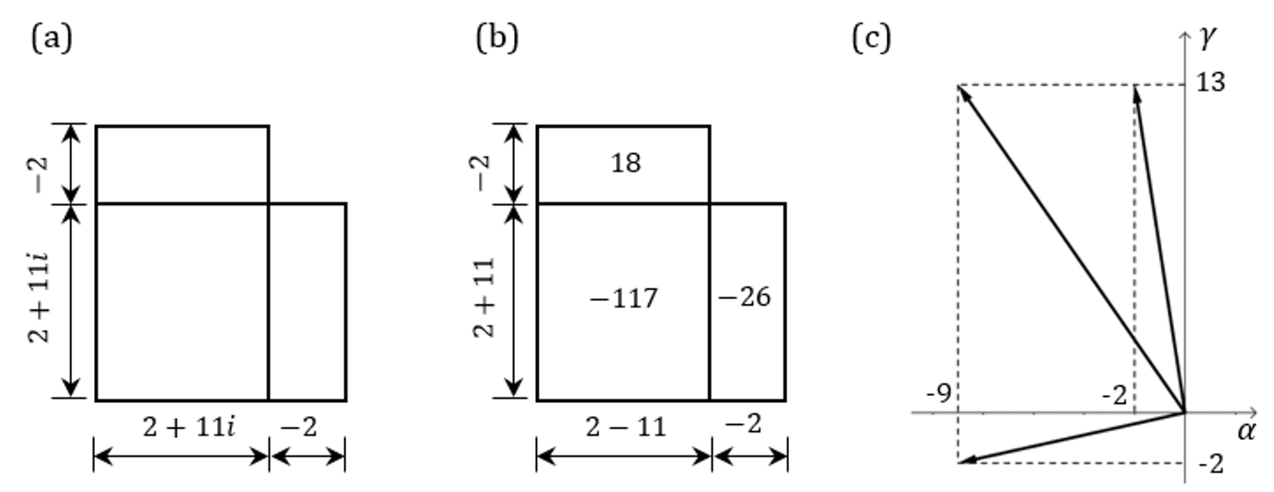
Na figura 5c podemos ver a combinação de vetores no plano escalar que representam a equação ![]() quando
quando ![]() . O mesmo procedimento pode ser aplicado à raiz
. O mesmo procedimento pode ser aplicado à raiz ![]() , como segue:
, como segue:
Substituindo ![]() na equação dada, temos:
na equação dada, temos:
Nas figuras 6a e 6b estão os diagramas escalares feitos a partir de ![]() e, na figura 6c, está a combinação de vetores que satisfazem a equação dada quando
e, na figura 6c, está a combinação de vetores que satisfazem a equação dada quando ![]() . Veja, portanto, que os complexos conjugados
. Veja, portanto, que os complexos conjugados ![]() nada mais são do que os dois retângulos que se obtém permutando-se a componentes α e γ, ambos correspondendo ao mesmo produto das componentes.
nada mais são do que os dois retângulos que se obtém permutando-se a componentes α e γ, ambos correspondendo ao mesmo produto das componentes.
Fig.6: (a) Diagrama para ![]() ; (b) Diagrama para
; (b) Diagrama para ![]() ; (c) Os vetores no plano escalar para
; (c) Os vetores no plano escalar para ![]()
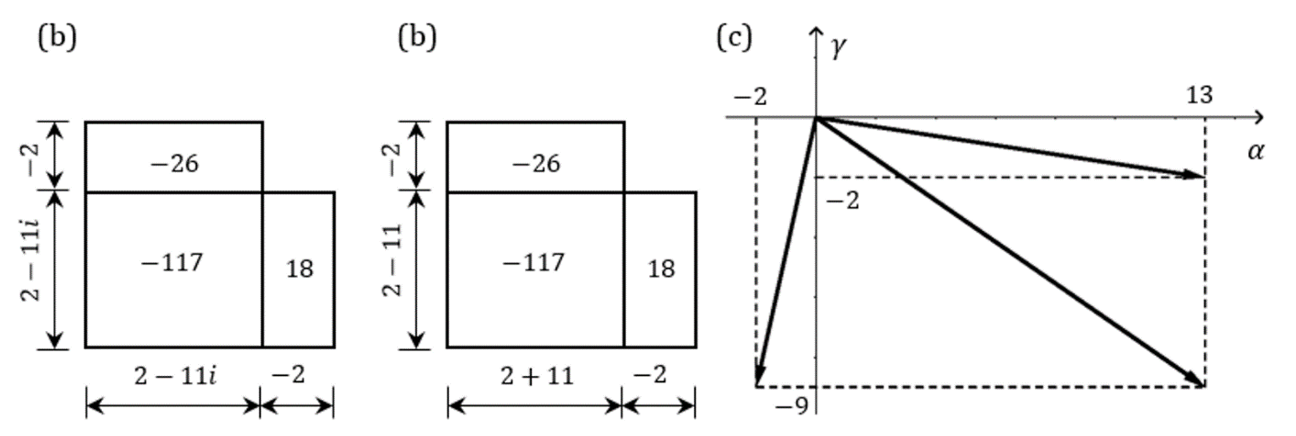
7.2 MÉTODO ALGÉBRICO
Uma segunda forma de verificarmos as raízes de uma equação do segundo grau sem fazer uso dos números imaginários é simplesmente trocar a forma algébrica pela forma conjunta. Voltando novamente à equação ![]() , suas raízes na forma conjunta são
, suas raízes na forma conjunta são ![]() . Substituindo a primeira raiz na equação dada, temos:
. Substituindo a primeira raiz na equação dada, temos:
Da mesma forma, substituindo a segunda raiz na equação dada, temos:
A diferença básica entre os dois métodos de verificação apresentados é que, no primeiro, embora a variável x assuma diferentes valores devido à sua natureza ambígua, cada ocorrência de x na equação corresponde a um valor real e unívoco, seguindo o diagrama usado como referência. Já no segundo método, a própria notação utilizada e as regras de manipulação algébrica apropriadas já trazem em si a natureza ambígua da variável, de modo que toda ocorrência de x sempre possa corresponder ao mesmo par de componentes escalares. Essa segunda forma de trabalhar com os números complexos, como vimos, é completamente equivalente à forma algébrica ![]() . Portanto, algebricamente, escrever
. Portanto, algebricamente, escrever ![]() , com
, com ![]() , em lugar de
, em lugar de ![]() , com
, com ![]() , nos permite trabalhar com objetos matemáticos bidimensionais de maneira semelhante com que se trabalha com números em uma única dimensão.
, nos permite trabalhar com objetos matemáticos bidimensionais de maneira semelhante com que se trabalha com números em uma única dimensão.
8. PLANO COMPLEXO VERSUS PLANOESCALAR
Os números complexos podem ser definidos como pares ordenados ![]() sobre os quais se realizam certas operações pré-definidas, de forma que, para cada ponto no plano ortogonal xy, exista um número complexo associado, veja figura 7a. “Logo, podemos representar os números complexos num plano coordenado da mesma maneira que fazemos ao marcar pontos no
sobre os quais se realizam certas operações pré-definidas, de forma que, para cada ponto no plano ortogonal xy, exista um número complexo associado, veja figura 7a. “Logo, podemos representar os números complexos num plano coordenado da mesma maneira que fazemos ao marcar pontos no ![]() , observando, naturalmente, o significado geométrico de tal marcação: que estão representando um número na forma
, observando, naturalmente, o significado geométrico de tal marcação: que estão representando um número na forma ![]() ” (Molter et al., 2020). Embora na notação
” (Molter et al., 2020). Embora na notação ![]() ambas as variáveis sejam números reais, a variável y funciona como um multiplicador da constante imaginária i, portanto, o plano complexo tem como eixo das abscissas a reta real e, como eixo das ordenadas, a reta imaginária, como mostrado na figura 7b. A notação de par ordenado apenas omite essa informação por ela ser inerente ao próprio contexto dos números complexos em que é utilizada. Note, portanto, que há uma diferença fundamental entre o plano complexo e o escalar: enquanto o plano complexo compreende um eixo real e outro imaginário, mesmo que isto não apareça de modo explícito na notação, o plano escalar possui eixos exclusivamente reais.
ambas as variáveis sejam números reais, a variável y funciona como um multiplicador da constante imaginária i, portanto, o plano complexo tem como eixo das abscissas a reta real e, como eixo das ordenadas, a reta imaginária, como mostrado na figura 7b. A notação de par ordenado apenas omite essa informação por ela ser inerente ao próprio contexto dos números complexos em que é utilizada. Note, portanto, que há uma diferença fundamental entre o plano complexo e o escalar: enquanto o plano complexo compreende um eixo real e outro imaginário, mesmo que isto não apareça de modo explícito na notação, o plano escalar possui eixos exclusivamente reais.
Fig.7: (a) Plano no ![]() associado ao conjunto dos complexos; (b) Eixo real e eixo imaginário no plano complexo
associado ao conjunto dos complexos; (b) Eixo real e eixo imaginário no plano complexo
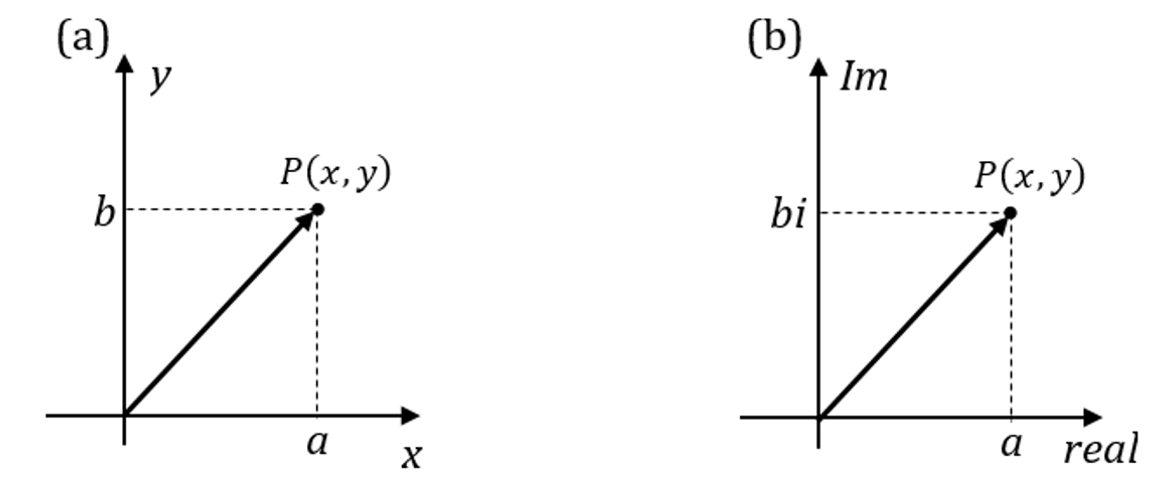
Assim, o uso do plano escalar para representar números complexos não é uma questão meramente formal, mas uma mudança de paradigma que nos permite compreender os números complexos como parte do plano real. Dessa forma, faz-se desnecessário estabelecer o conjunto dos números complexos ![]() , uma vez que qualquer elemento pertencente a
, uma vez que qualquer elemento pertencente a ![]() não é nada mais do que um elemento de
não é nada mais do que um elemento de ![]() e a unidade imaginária i não vai além de um recurso algébrico interessante que nos permite operar em apenas uma dimensão com os elementos pertencentes a
e a unidade imaginária i não vai além de um recurso algébrico interessante que nos permite operar em apenas uma dimensão com os elementos pertencentes a ![]() .
.
9. CONCLUSÃO
A constante imaginária, embora possa ser operada como número, não é um número propriamente dito, mas uma noção quantitativa ambígua que representa simultaneamente as duas componentes unitárias de um vetor localizado no segundo quadrante de um sistema de coordenadas reais, de forma que não podemos atribuir a i um valor unívoco: tudo o que podemos afirmar é que ![]() representa o produto das componentes desse vetor, ou seja,
representa o produto das componentes desse vetor, ou seja, ![]() . Os números complexos, por sua vez, são representações algébricas de retângulos escalares com lados desiguais. Cada um desses retângulos escalares resulta da soma de dois vetores, sendo um localizado em um quadrante ímpar e outro localizado em um quadrante par. O presente artigo constitui-se tão somente em uma proposta alternativa de interpretação dos números imaginários e, consequentemente, dos complexos. Claramente ainda faltam pontos a serem explorados como, por exemplo, a ambiguidade nas equações cúbicas e a forma trigonométrica da notação conjunta. Porém, essas questões fogem ao escopo do presente artigo e seria necessário muito mais espaço para tratá-las adequadamente. Devido à simplicidade e à eficácia do tratamento atual dado aos números complexos, acredito que qualquer esforço que se venha a fazer para o desenvolvimento da proposta aqui apresentada terá uma motivação primordialmente ontológica, ainda que, a partir desse novo enfoque, possam surgir resultados que venham a ser úteis não só para a matemática, mas também para todas as áreas do conhecimento que encontrem aplicações para os números complexos.
. Os números complexos, por sua vez, são representações algébricas de retângulos escalares com lados desiguais. Cada um desses retângulos escalares resulta da soma de dois vetores, sendo um localizado em um quadrante ímpar e outro localizado em um quadrante par. O presente artigo constitui-se tão somente em uma proposta alternativa de interpretação dos números imaginários e, consequentemente, dos complexos. Claramente ainda faltam pontos a serem explorados como, por exemplo, a ambiguidade nas equações cúbicas e a forma trigonométrica da notação conjunta. Porém, essas questões fogem ao escopo do presente artigo e seria necessário muito mais espaço para tratá-las adequadamente. Devido à simplicidade e à eficácia do tratamento atual dado aos números complexos, acredito que qualquer esforço que se venha a fazer para o desenvolvimento da proposta aqui apresentada terá uma motivação primordialmente ontológica, ainda que, a partir desse novo enfoque, possam surgir resultados que venham a ser úteis não só para a matemática, mas também para todas as áreas do conhecimento que encontrem aplicações para os números complexos.
REFERÊNCIAS
BOMBELLI, Rafael. L’algebra. Veneza: Giovanni Battista Pedrezani, 1572. 212 p.
CAYEMITTE, Fritz Isaac. Contribution of the theory of complex numbers to the field of electrical engineering education and practice. Columbia: Columbia University, 2000. 238 p.
HALLIDAY, David; RESNICK, Robert. Fundamentos de Física 1. Rio de Janeiro: LTC – Livros Técnicos e Científicos, 1991. 300 p. Tradução de Adir Moysés et al.
LI, Zheng-Da; MAO, Ya-Li; WEILENMANN, Mirjam; TAVAKOLI, Armin; CHEN, Hu; FENG, Lixin; YANG, Sheng-Jun; RENOU, Marc-Olivier; TRILLO, David; LE, Thinh P. Testing Real Quantum Theory in an Optical Quantum Network. Physical Review Letters, [S.L.], v. 128, n. 4, p. 4-28, 24 jan. 2022. American Physical Society (APS). http://dx.doi.org/10.1103/physrevlett.128.040402.
LIPSCHUTZ, Seymour. Teoria dos Conjuntos. São Paulo: McGraw-Hill do Brasil, 1972. 337 p. Tradução de Fernando Vilain Heusi da Silva.
MOLTER, Alexandre et al. Trigonometria e números complexos: com aplicações. São Paulo: Edgard Blücher Ltda, 2020. 312 p.
NAHIN, Paul J.. An imaginary tale: the story of [the square root of minus one]. Princeton: Princeton University Press, 1998. 297 p.
RENOU, Marc-Olivier; TRILLO, David; WEILENMANN, Mirjam; LE, Thinh P.; TAVAKOLI, Armin; GISIN, Nicolas; ACÍN, Antonio; NAVASCUÉS, Miguel. Quantum theory based on real numbers can be experimentally falsified. Nature, [S.L.], v. 600, n. 7890, p. 625-629, 15 dez. 2021. Springer Science and Business Media LLC. http://dx.doi.org/10.1038/s41586-021-04160-4.
[1] Especialização em Instrumentação e Controle de Processos pelo Serviço Nacional de Aprendizagem Industrial-SENAI; Habilitação profissional de Técnico em Eletrônica pelo Instituto Monitor S/C Ltda. Graduado em Física pela Universidade Federal de Minas Gerais. ORCID: 0009-0001- 4633-3914. Currículo Lattes: http://lattes.cnpq.br/9333737637565760.
Material recebido: 26 de dezembro de 2023.
Material aprovado pelos pares: 16 de janeiro de 2024.
Material editado aprovado pelos autores: 23 de fevereiro de 2024.