OLIVEIRA, Antônio Júnior de [1]
OLIVEIRA, Antônio Júnior de. Erros Matemáticos como um Ponto de Partida para a Aprendizagem: Um Relato de Experiência. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 04, Vol. 03, pp. 61-70, Abril de 2018. ISSN:2448-0959
RESUMO
Este relato descreve uma experiência no ensino de Matemática com um grupo de alunos do Ensino Médio do Instituto Federal do Triângulo Mineiro, no campus Patrocínio, no ano de 2017. Uma experiência focada em erros de Matemática básica como ponto de partida para a aprendizagem, tendo como objetivo a superação da defasagem de aprendizagem pelos alunos, para que eles pudessem aprender, com mais facilidade, novos conceitos matemáticos. Para isso, foi proposta uma atividade para os alunos na qual eles puderam identificar erros matemáticos em conceitos básicos do Ensino Fundamental, fizeram uma reflexão e uma pesquisa sobre os conteúdos nos quais cometeram erros e, por fim, socializaram os conhecimentos adquiridos com o grupo, momento no qual observou-se que os resultados da atividade foram positivos.
Palavras-Chave: Erros Matemáticos, Ensino, Aprendizagem.
1. CONSIDERAÇÕES INICIAIS
A ideia do presente estudo surgiu em uma discussão na sala dos professores na qual a aprendizagem matemática era abordada. Percebeu-se que, frequentemente, os alunos do Ensino Médio cometem erros de Matemática relacionados a conteúdos específicos do Ensino Fundamental. Então, pensando em desenvolver alguma atividade que pudesse contribuir para que os alunos superassem esta problemática, a pesquisa sobre como ensinar Matemática a partir dos erros cometidos pelos discentes impõe-se.
Ao fazer esta pesquisa, identificou-se que o assunto não é novo na educação e outros trabalhos com esta temática foram elencados, principalmente, em livros e dissertações. Destaca-se o livro da professora Helena Cury, o qual se coloca como motivação para desenvolver esta investigação.
O objetivo desta investigação foi levar os alunos da turma a refletirem sobre os erros matemáticos cometidos por eles e motivá-los a pesquisarem, buscando a compreensão e construção de conceitos matemáticos básicos.
A não consolidação de conceitos matemáticos básicos, neste contexto, pode-se dizer que, em muito, dificulta a aprendizagem de novos conceitos matemáticos, fato que se é observado nesta turma. Confirmando esta afirmação, Silva e Aumouloud (2008, p.76) dizem que “o aluno precisa dos conhecimentos iniciais bem fundamentados para ter sucesso na aprendizagem de novos conteúdos matemáticos”. Nota-se, então, que muitos alunos compreendiam a ideia do conceito novo, no entanto, ao resolver os exercícios, erravam operações básicas como operações com números inteiros, operações com números racionais, potenciação, radiciação, resolução de equações etc.
O trabalho foi dividido em quatro etapas. Na primeira, os alunos resolveram uma lista de exercícios com questões envolvendo apenas conteúdos básicos. Na segunda, foi corrigida a produção discente e feito um relatório para cada aluno no qual foram listadas as questões que eles não conseguiram resolver e os erros cometidos nas questões resolvidas. Na terceira, entregou-se o relatório para os alunos e eles pesquisaram sobre os conceitos matemáticos que eles erraram e relataram suas conclusões por escrito. Na quarta, os alunos socializaram, com os demais colegas, os conhecimentos adquiridos. Durante a realização das atividades pelos alunos, o processo foi mediado pelo professor, o qual fez as intervenções necessárias e deu suporte às tarefas realizadas.
2. ANÁLISE DE ERROS MATEMÁTICOS
Em Cury (2015), no livro – Análise de erros: o que podemos aprender com as respostas dos alunos – encontra-se o assunto de uma forma bastante abrangente. A leitura deste livro auxilia na fundamentação de atividades de ensino as quais valorizam as respostas dos alunos como ponto de partida para a compreensão e construção de conceitos matemáticos. Para a autora, a análise da produção dos discentes é uma metodologia de ensino. Considerando esta definição, analisar os erros matemáticos cometidos pelos discentes é uma atividade focada na relação entre o conhecimento matemático, o professor e o aluno.
Em síntese, Cury (2015) defende que é necessário discutir os erros detectados em avaliações com os alunos, embora não seja uma tarefa fácil. Ela acredita que analisar as produções dos alunos permite entender, de forma mais clara, como os estudantes apropriam-se do conhecimento. Sendo assim, o aluno não deve esconder o seu erro e nem o professor deve elaborar ciladas para que o aluno erre. O erro constitui ou deveria constituir um ponto de partida para a construção do conhecimento.
Para os professores de Matemática é comum encontrar vários erros ao corrigir uma avaliação. O que estes erros podem revelar? Várias as hipóteses. Por exemplo, uma falha no ensino, uma falha na aprendizagem, o que o aluno sabe, o que o aluno não sabe. Essas, dentre outras hipóteses, podem ser levantadas. No entanto, concordando com a autora supracitada, acredita-se que, no processo de ensino e aprendizagem, há uma forte tendência à valorização dos acertos, sendo descartados os erros.
Neste sentido, é preciso relacionar o erro à aprendizagem. Correia (2010) defende que o professor deve aproximar as hipóteses dos alunos com a veracidade da questão, promovendo, deste modo, o incentivo e a motivação para que o aluno possa descobrir caminhos para a construção do conhecimento. Nesta concepção, o erro não é considerado um indicador do fracasso do aluno, mas uma alternativa para que o aluno construa o saber.
Por este motivo, a análise de erros matemáticos, cada vez mais, ganha espaço entre os educadores. É comum a abordagem sobre o tema em dissertações, teses e em eventos destinados a professores de Matemática. O estudo sobre análise de erros pode auxiliar, em formação inicial ou continuada, professores da educação básica e professores da educação superior. A tarefa de analisar o que o aluno redigiu favorece o professor e o aluno na compreensão de como ocorre a aprendizagem, como o discente adquire o saber (CURY, 2015). Por outro lado, a não aprendizagem gera desmotivação e, consequentemente, reprovação ou evasão, as quais representam, indubitavelmente, perdas sociais e econômicas.
Face a esta situação, é importante ressaltar as causas pelas quais os alunos erram. Falta de atenção? Falta de conhecimento? Essas, dentre tantas outras, são causas que levam ao erro. Lorenzato (2006) apud Paias (2009, p. 28) aponta como possíveis causas para o erro: “falta de atenção, pressa, chute, falha de raciocínio, falta de estudo, mau uso ou má interpretação da linguagem oral ou escrita da matemática, deficiência de conhecimento da língua materna ou de conceitos matemáticos”. Para propor uma intervenção pedagógica coerente com as necessidades do discente, portanto, é preciso identificar, primeiramente, a causa do erro.
Mesmo assim, referir-se à intervenção pedagógica e à análise dos erros não significa que o professor é o responsável por todo este processo. A ação ativa do aluno é, sem dúvida, fator determinante em sua aprendizagem e o professor mediador é fundamental para aproximar aluno e conhecimento matemático.
Uma das maneiras de promover esta aproximação, ou seja, a aprendizagem é colocar o aluno em confronto com situações desafiadoras nas quais ele participa efetivamente e escolhe os seus próprios caminhos. (AZEVEDO, 2009)
Ainda considerando a participação ativa do discente, Feltes (2007) diz que o erro deve:
… ser encarado como uma etapa a ser vencida pelos alunos. Ele denuncia o percurso que o discente traçou, o caminho que ele percorreu até chegar a uma determinada resposta, e esses caminhos, esses percursos fazem parte de possibilidades na construção do seu conhecimento. (p. 31).
Assim, pode-se inferir que, se o aluno foi quem traçou o caminho para se chegar a uma determinada resposta, ele deverá rever este caminho com o apoio do professor, tomando o erro como um ponto de partida para a construção de conceitos matemáticos.
3. UMA PROPOSTA DE TRABALHO
Partindo de uma reflexão baseada na correção de avaliações dos alunos em que se constata vários erros matemáticos, percebe-se que a principal causa está relacionada à falta de domínio de conceitos básicos de Matemática. Nota-se que, frequentemente, os alunos cometem erros que envolvem as operações com números inteiros, as operações com números racionais, a potenciação, a radiciação, os produtos notáveis, a fatoração e a resolução de equações.
A partir desta problemática, na literatura, buscam-se maiores esclarecimentos sobre erros matemáticos cometidos pelos discentes e sobre a importância da consolidação de conteúdos básicos para a aprendizagem de novos conceitos matemáticos. Feito este estudo, foi proposto aos alunos um trabalho avaliativo no qual se detectou os principais erros matemáticos cometidos por cada um deles e feita uma intervenção na qual, mediados pelos docentes, os alunos investigaram os motivos que os levaram ao erro e socializaram suas conclusões com os demais colegas.
Para identificar os erros, os alunos fizeram uma lista de exercícios composta por atividades de cálculo envolvendo os tópicos básicos já mencionados. A lista foi corrigida e, para cada aluno, foi feito um levantamento dividido em duas partes. Na primeira, foram listadas as atividades que o aluno não fez e, na segunda, os erros que ele cometeu nas atividades resolvidas.
Estes levantamentos foram devolvidos aos alunos, juntamente com as listas que eles fizeram, e, neste momento, eles começaram a investigar conceitos matemáticos relacionados aos seus erros. Para esta investigação, eles puderam utilizar os recursos que acharam mais apropriados. A maioria dos alunos optou por buscar videoaulas na internet. Feita esta investigação, os alunos registraram suas conclusões evidenciando o erro, o motivo que o levou ao erro e a forma correta de resolução.
4. RESULTADOS
Em relação às operações com números inteiros, verificou-se que, nesta turma, a maioria dos alunos dominam este tópico. Mas, mesmo assim, alguns erros foram identificados. Conforme imagens abaixo:
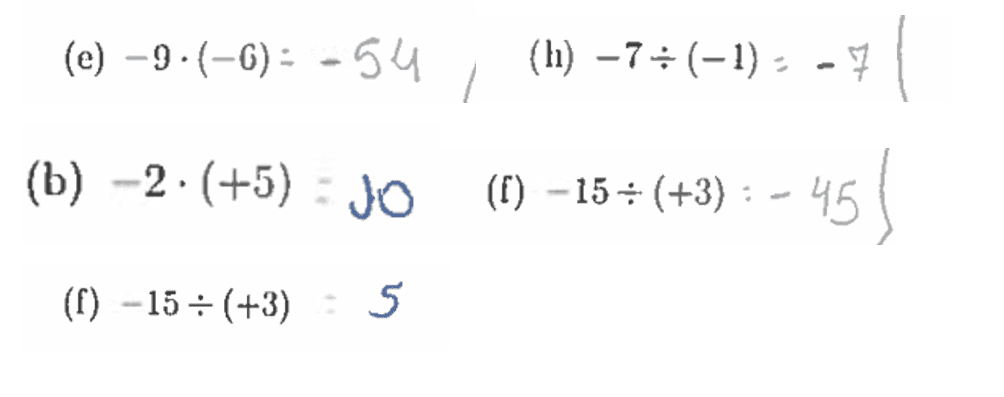
O principal motivo que os alunos alegaram no relatório foi a confusão entre a regra de sinais para a adição e subtração com a regra para a multiplicação e divisão. Outros declararam somente falta de atenção.
Em relação às operações com números racionais, notou-se uma grande deficiência quanto ao domínio deste conteúdo. Foi possível identificar também que muitos alunos têm dificuldades em relacionar a forma fracionária à forma decimal. Por exemplo, ao somar ½ + 1/2, colocam como resposta 2/4. Este erro teria uma probabilidade maior de ser evitado se o aluno identificasse que ½ + ½ = 0,5 + 0,5 = 1. Abaixo, seguem alguns erros:
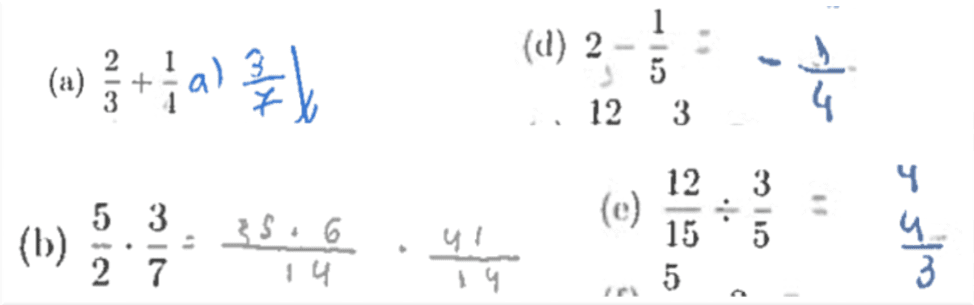
Em relação à adição e subtração de números fracionários, o maior motivo apontado pelos alunos foi não encontrar frações equivalentes com denominadores iguais para efetuar a soma. Quanto à multiplicação e divisão, o maior motivo apontado foi a confusão entre regras – adição e subtração, multiplicação e divisão.
Quanto ao tópico potenciação, nota-se, pelas produções dos alunos, que, para cada questão, a causa do erro foi quase unânime.
No cálculo de , a principal causa apontada, para o erro, foi formular um conceito matemático errado, “se o expoente é um número negativo, então, a potência será um número negativo”. O recorte abaixo ilustra este erro:
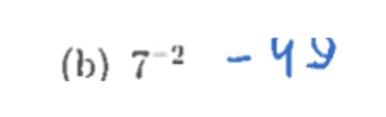
No cálculo de , a causa que se destacou para o erro foi não compreender a seguinte afirmação: “Todo número real elevado a dois é positivo”. O recorte abaixo ilustra esta situação:
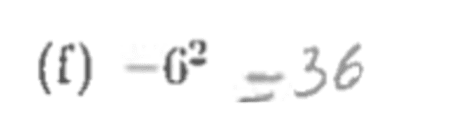
A confusão ocorreu por pensar que o número menos seis está elevado ao quadrado, enquanto que somente o número seis está elevado ao quadrado.
No cálculo de , a causa predominante foi inferir, erroneamente e de maneira intuitiva, que . Na figura abaixo, encontramos este erro:
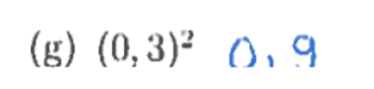
No cálculo de , o principal motivo para o erro foi aplicar de forma errada a propriedade: “Na multiplicação de potências de mesma base, conservamos a base e somamos os expoentes”. O recorte abaixo ilustra este erro:
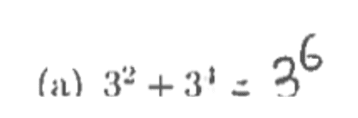
Destacam-se estes erros, pois apareceram com grande frequência.
Quanto à radiciação, foram propostas algumas questões cujo enunciado era “Simplifique”, nota-se que os erros não foram pontuais, foi verificada uma grande quantidade de erros distintos. Percebe-se que estes erros estão, fortemente, relacionados à falta de domínio de definições. Seguem alguns erros:
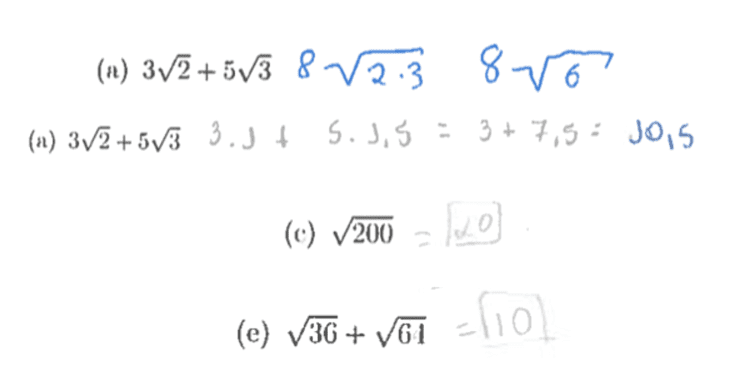
Quanto aos produtos notáveis, o erro mais evidente foi considerar, erroneamente, para todo , conforme recorte abaixo:
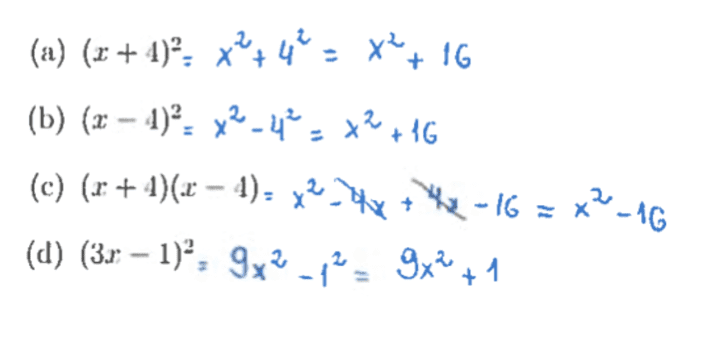
Quanto à fatoração, a maioria dos alunos declararam não dominar o conteúdo, portanto, deixaram as questões em branco. Algo esperado, vista a quantidade de erros nos tópicos anteriores.
Estes, dentre outros, foram erros detectados. Os alunos, frente ao problema, pesquisaram em diversos materiais (vídeos, livros, internet) e, auxiliados pelo professor, conseguiram, de forma significativa, compreender o erro e construir corretamente o conceito envolvido. Esta superação foi notada no momento em que os alunos socializaram os conhecimentos adquiridos com os demais colegas da turma e também em resultados positivos em avaliações posteriores à realização do trabalho.
CONSIDERAÇÕES FINAIS
A atividade desenvolvida, trabalhar com erros matemáticos na perspectiva de ponto de partida para o ensino e para a aprendizagem, possibilitou explorar a pesquisa, o trabalho em grupo, a participação efetiva do aluno e a socialização do conhecimento adquirido. O resultado deste processo foi percebido quando os alunos apresentaram seus trabalhos demonstrando que, realmente, conseguiram amenizar, significativamente, a defasagem em conceitos básicos de matemática.
Esta experiência positiva contribui para a realização de futuros trabalhos e pesquisas que objetivam diminuir os índices de evasão e repetência relacionados à disciplina de Matemática.
REFERÊNCIAS
AZEVEDO, Danielle Santos. Análise de Erros Matemáticos: interpretação das respostas dos alunos. Trabalho de conclusão de curso em Licenciatura em Matemática – Departamento de Matemática Pura e Aplicada, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2009.
CORREIA, Carlos Eduardo Felix. Matemática, análise de erro e formação continuada de professores polivalentes. São Paulo: Porto de Ideias, 2010.
CURY, Helena Noronha. Análise de erros: o que podemos aprender com as respostas
dos alunos. 2 ed. Belo Horizonte: Autêntica, 2015.
FELTES, Rejane Zeferino. Análise de erros em potenciação e radiciação: um
estudo com alunos de ensino fundamental e médio. Dissertação de Mestrado.
Porto Alegre: Pontifícia Universidade Católica do Rio Grande do Sul. 2007.
PAIAS, Ana Maria. Diagnóstico dos erros sobre a Operação Potenciação aplicado a alunos dos Ensinos Fundamental e Médio. Mestrado em Educação Matemática. São Paulo: PUC, 2009.
SILVA, Maria José Ferreira da.; ALMOULOUD, Saddo Ag. As Operações com Números
Racionais e seus Significados a partir da Concepção Parte-todo. Bolema: Mathematics
Education Bulletin = Bolema: Boletim de Educação Matemática, v. 21, n. 31,
2008.
[1] Professor de Matemática no Instituto Federal do Triângulo Mineiro (IFTM) / Campus Patrocínio. Mestre em Matemática pela Universidade Federal do Triângulo Mineiro (UFTM).

