ARTIGO DE REVISÃO
VICTORINO, Samuel Carlos [1]
VICTORINO, Samuel Carlos. Outra abordagem na elaboração de tabelas de frequência usando a teoria de distribuição normal de GAUSS. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 03, Vol. 07, pp. 139-154. Março de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/agronomia/tabelas-de-frequencia, DOI: 10.32749/nucleodoconhecimento.com.br/agronomia/tabelas-de-frequencia
RESUMO
A organização correta dos dados é de extrema importância para a análise no processo de inferência estatística, visando a elaboração de conclusões válidas e recomendações genéricas sobre determinado assunto em estudo. A literatura científica especializada descreve diversos procedimentos para a organização de dados em tabelas de distribuição de frequência. No entanto, não é sempre que imprecisões são feitas no uso de ferramentas de organização de dados. Essas imprecisões resultaram em análises distorcidas e conclusões incongruentes. Este artigo apresenta uma análise crítica dos métodos e procedimentos de organização de dados descritos na literatura, especificamente a distribuição de dados em tabelas de distribuição de frequência e propõe uma abordagem diferenciada na elaboração de tabelas de distribuição de frequência de classe. Para todas as variáveis com categorias predefinidas, esses e seus respectivos valores de referência servem como corpo da tabela. Para as variáveis que não possuem categorias pré-definidas, o uso da teoria da distribuição normal de Gauss como critério de categorização é proposto e justificado. As categorias geradas servem como corpo da tabela. Conclui-se que as tabelas de distribuição de frequência podem ser distinguidas em dois tipos, ou seja, tabelas de distribuição de frequência de classes ou categorias predefinidas e tabelas de distribuição de frequência de classes ou categorias a serem definidas, sugerindo sua adoção como conceito.
Palavras-chave: Distribuição normal, Tabela de distribuição de frequência simples, Tabela de distribuição de frequência das classes predefinidas, Tabela de distribuição de frequência das classes a definir.
1. INTRODUÇÃO
A estatística, como ciência, se resume em um conjunto de métodos e procedimentos que permitem a coleta, organização e apresentação de dados para sua análise, a fim de obter conclusões válidas e a elaboração de recomendações genéricas sobre uma dada população em estudo.
A estatística encontra aplicação nas mais diversas áreas do conhecimento como economia, psicologia, sociologia, agricultura e saúde, auxiliando no processo de tomada de decisão com base na análise de dados. Para que as estatísticas cumpram esta função, é imperativo que os métodos e procedimentos sejam aplicados de forma adequada. A coleta de dados envolve a correta aplicação de métodos de amostragem que culminam na seleção de amostras representativas e garantem a validade dos dados e, ao mesmo tempo, a validade dos estudos; a organização e apresentação dos dados visa a simplificação e compressão dos dados em tabelas de distribuição de frequência, sejam tabelas de frequência única ou tabelas de frequência de classe. Os dados resumidos em tabelas são geralmente, e quando apropriado, visualizados em gráficos, diagramas e outras ferramentas estatísticas. Sua correta organização é de extrema importância para a análise de dados no processo de inferência estatística.
A literatura científica especializada descreve uma ampla gama de procedimentos para organização de dados em tabelas de distribuição de frequência. Foi constatado que imprecisões no uso de ferramentas de organização de dados são frequentemente cometidas, resultando em interpretações distorcidas e conclusões incongruentes. Este artigo tem como objetivo apresentar uma análise crítica dos métodos e procedimentos de organização de dados descritos na literatura, especificamente a distribuição dos dados em tabelas de frequência e propõe uma abordagem diferenciada na elaboração de tabelas de distribuição de frequência.
2. REFERENCIAL TEÓRICO SOBRE TABELAS DE DISTRIBUIÇÃO DE FREQUÊNCIA
A estatística é dividida em dois grupos principais: estatística descritiva e estatística inferencial.
Estatística Descritiva é a parte que trata da descrição, classificação, organização e apresentação dos dados de uma variável. Permite resumir dados e ajudar a descrever os atributos de um determinado grupo de dados ou de uma população por meio do cálculo de medidas descritivas como a média e o desvio padrão. As técnicas descritivas tabulares e gráficas utilizadas com o apoio das capacidades gráficas dos computadores modernos e dos diversos softwares disponíveis tornam este tipo de resumo mais factível e compreensível.
Já a estatística inferencial é responsável pela análise dos dados para a obtenção de conclusões válidas e pela elaboração de recomendações genéricas sobre a população em estudo.
2.1 TÉCNICAS DESCRITIVAS TABULARES E GRÁFICAS
Os dados brutos de uma variável obtidos em um processo de amostragem não permitem a visualização de nenhuma característica da amostra e muito menos da população em estudo. Portanto, tabelas e gráficos são recursos estatísticos essenciais no processamento de dados.
As tabelas permitem resumir e compactar uma grande quantidade de informações proporcionando uma análise clara ao pesquisador. Os gráficos são complementos de tabelas que têm a função de transmitir uma ideia visual do comportamento dos dados. Existe uma grande variedade de gráficos, entre eles, gráficos de linhas, gráficos de barras, gráficos de área e gráficos de pizza como os mais comuns. Quanto às tabelas de distribuição de frequência, os seguintes tipos são fundamentalmente diferentes:
1 – Tabela de distribuição de frequência única
2 – Tabela de distribuição de frequência de classe
Uma única tabela de distribuição de frequência contém duas colunas principais. Na primeira coluna cada valor coletado é inserido sequencialmente, uma vez e em ordem crescente. Na segunda coluna da linha correspondente a cada valor observado é inserido o número de vezes que esses valores se repetem no conjunto de dados, que correspondem à respectiva frequência absoluta.
A tabela de distribuição de frequência das classes também contém duas colunas, a primeira para os intervalos das classes da variável e a segunda para o número de indivíduos pertencentes a cada classe, ou seja, a frequência absoluta da classe.
Tabelas de distribuição de frequência única apresentam a grande desvantagem de serem muito longas, devido ao fato de que todos os valores amostrados devem ser listados e, principalmente, não permitem a leitura das características dos dados. Esses tipos de tabelas são totalmente inadequados quando o objetivo é resumir grandes quantidades de dados. Para esses casos, as tabelas de distribuição de frequência de classe são mais adequadas, pois compactam grandes quantidades de dados em algumas classes e vinculam os atributos quantitativos da variável ao significado real das características da variável.
O aspecto fundamental na elaboração de tabelas de distribuição de frequências de aulas é a determinação do número de aulas, em que os dados serão enquadrados. Para o efeito, são descritos na literatura diversos critérios para a determinação do número de aulas, a maioria dos quais de base estritamente matemática.
Milton e Tsokos (1991) indicam o uso das seguintes fórmulas para determinar o número de classes:
1 – Número de classes = 5 x lg n onde n é o tamanho da amostra
2 – Número de aulas =![]()
Beiguelman (2002) indica que o número de aulas está entre 8 e 20, dependendo dos dados. Para Dawson e Trapp (2003) 6 e 14 classes são adequadas para fornecer informações suficientes sem detalhes excessivos. Triola e Triola (2006) recomendam que o número de turmas fique entre 5 e 20, enquanto Kuzma e Bohnenblust (2001) consideram que o número de turmas deve ser de 5 a 15. Reis (2005) afirma que o número de turmas deve ser entre 4 e 14 e sugere o uso de uma das seguintes soluções:
![]() 1 – Número de classes igual a 5 para amostras com tamanho menor que 25 e número de classes = para amostras com tamanho igual ou maior que 25.
1 – Número de classes igual a 5 para amostras com tamanho menor que 25 e número de classes = para amostras com tamanho igual ou maior que 25.
2 – Use a fórmula de Sturges: número de classes = 1 + 3,22 log n
O exposto acima mostra a variedade de critérios descritos na literatura para a construção de tabelas de distribuição de frequência. No entanto, esses critérios têm uma desvantagem comum que os torna inadequados como base para determinar o número de classes de dados para determinadas variáveis, como variáveis da área de biologia e ciências da saúde, economia, indústria, entre outras, que possuem pré- categorias definidas, ou seja, categorias padronizadas. Algumas dessas variáveis são descritas a seguir e os respectivos valores de referência das categorias predefinidas são indicados. No campo da biologia:
Exemplo 1: Valores de referência do colesterol total em humanos Tabela 1: Categorias e valores de referência do colesterol total em humanos.
| Colesterol total | Categoria |
| < 200 mg/dl | Desejável ou normal |
| 200 – 239 mg/dl | Média |
| ≥ 240 mg/dl | Alta |
Fonte: Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421
Exemplo 2: Valores de referência para índice de massa corporal (IMC).
O IMC ajuda a definir o grau de obesidade de uma pessoa de acordo com a Organização Mundial de Saúde. Ao calcular e interpretar o IMC é possível saber se uma pessoa está acima ou abaixo dos parâmetros de peso recomendados para sua estrutura física. Para o cálculo do IMC, o peso medido em kg é dividido pela altura ao quadrado (IMC = kg / m2).
Tabela 2: Categorias e valores de referência do Índice de Massa Corporal
| Categoria | IMC (kg/m2 ) |
| Abaixo do peso | < 18,5 |
| Normal (peso saudável) | 18,5 – 24,9 |
| Pré-obeso | 25,0 – 29,9 |
| Obesidade grau I | 30,0 – 34,9 |
| Obesidade grau II | 35,0 – 39,9 |
| Obesidade grau III | ≥ 40,0 |
Fonte: World Health Organization. Obesity (1998): Preventing and managing the global epidemic: report of a WHO Consultation on Obesity, Geneva, 3–5 June 1997. Geneva (CH): World Health Organization; 1998. http://whqlibdoc.who.int/hq/1998/WHO_NUT_NCD_98.1_(p1-158).pdf.
Exemplo 3 – Classificação da hipertensão arterial. Tabela 3: Classificação da hipertensão arterial
| Classificação da pressão arterial | Pressão arterial sistólica (mmHg) | Pressão sanguínea diastólica (mmHg) |
| Normal | < 120 | < 80 |
| Pré-hipertensão | 120 – 139 | 80 – 89 |
| Estágio 1 (grau I) hipertensão | 140 – 159 | 90 – 99 |
| Estágio 2 (grau II) hipertensão | ³ 160 | ³ 100 |
Fonte: The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Citado por PEDROSA e DRAGER (2010).
Exemplo 4: O ácido úrico resulta do metabolismo das purinas, os principais elementos estruturais do DNA e do RNA, muitos deles provenientes dos alimentos. O consumo excessivo de carne ou álcool pode aumentar os níveis de ácido úrico no sangue.
Os valores de referência são em geral 40 a 60 mg / L para homens, 30 a 50 mg / L para mulheres e 25 a 40 mg / L para crianças (CAQUET, 2011).
No campo da economia:
Exemplo 5: O Índice de Desenvolvimento Humano (IDH) é um dado estatístico criado pelo Programa das Nações Unidas para o Desenvolvimento (PNUD) para contrariar os dados puramente econômicos usados para medir a riqueza do país e para analisar o desenvolvimento incluindo outros fatores.
Para esta variável, as seguintes categorias são padronizadas sob as quais os países são divididos com base em seus respectivos IDH:
IDH Baixo: reúne todos os países com IDH abaixo de 0,500.
IDH médio: países com IDH entre 0,500 e 0,799.
IDH alto: países com IDH entre 0,800 e 0,899.
IDH muito alto: países cujo IDH é igual ou superior a 0,900.
Fonte: PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. acesso em Março, 25, 2020.
Os exemplos citados acima mostram que os critérios com base matemática não são adequados para todas as situações. Na definição das classes para a construção de uma tabela de frequências, as regras conhecidas na literatura e aqui apresentadas são meramente indicativas. A definição das classes, bem como do número de classes, deve primeiro basear-se no conhecimento do fenômeno em estudo e seus objetivos. Não existem fórmulas que se apliquem adequadamente a todas as situações. Mesmo quando o número de classes resultante do cálculo é igual ao número de classes predefinidas, os intervalos das classes não coincidem com os valores predefinidos. E é exatamente aí que reside o problema. Os intervalos de classe são atributos quantitativos que devem significar uma condição ou estado da variável. Por exemplo, uma pessoa com nível de colesterol de 260 mg / dl não é saudável, pois tem colesterol acima do normal. Da mesma forma, um país com Índice de Desenvolvimento Humano inferior a 0,5 é subdesenvolvido, pois é, sem dúvida, de baixo IDH. Assim, agrupar dados variáveis com categorias predefinidas sem respeitar essas mesmas categorias resulta na incapacidade de vincular o intervalo da classe ao seu respectivo significado dos valores do intervalo da classe. Essa falta de conexão entre o quantitativo (valores de intervalo de classe) e o qualitativo (categorias de variáveis) empobrece a interpretação dos dados e pode até deturpar a interpretação dos dados e levar a conclusões errôneas.
Portanto, para variáveis com categorias pré-definidas, o critério mais adequado para a construção da distribuição de frequência é a utilização dessas categorias e seus respectivos valores como corpo da tabela. Este critério associa os valores das categorias aos respectivos atributos qualitativos permitindo uma interpretação clara dos dados.
Quando as variáveis não possuem categorias predefinidas e se exaurem a busca por pistas ou indicadores que auxiliem na criação das categorias, sem ser por critério matemático, sugere-se aqui o uso da teoria da Distribuição Normal de Gauss para a categorização das variáveis. O objetivo é criar categorias que possibilitem vincular o quantitativo ao qualitativo e tornar a interpretação dos dados mais perceptível.
A teoria da distribuição normal de Gauss, amplamente referenciada na literatura (RICE e SCOTT, 2005), afirma que para um conjunto de dados normais (simétricos, unimodais), aproximadamente 68% dos dados estão localizados até uma unidade de desvio padrão do média, aproximadamente 95% dos dados estão localizados em até duas unidades de desvio padrão médio e 99% dos dados estão localizados em até três unidades de desvio padrão médio.
Tabela 4: Características da distribuição normal
| ± 1S | 68% dos dados |
| ± 2S | 95% dos dados |
| ± 3S | 99% dos dados |
Fonte: adaptado por Rice e Scott (2005)
Assim, estabelece-se como critério para a definição das categorias a partir da Teoria da Distribuição Normal, a utilização da faixa de variação de 68%, conforme segue: Tabela 5: Base para categorização das variáveis
| Nome da categoria ou classe | Valor da categoria ou grau |
| Acima da média | Acima ( + 1S) |
| Dentro da média | Entre( ± 1S) |
| Abaixo da média | Abaixo ( ˗ 1S) |
Fonte: autor.
Essa sugestão de categorização das variáveis baseia-se no cálculo de uma medida de tendência central, a média, e de uma medida de variabilidade, o desvio padrão. Valores que estão em um desvio padrão da média são considerados próximos da média, então a designação da categoria “dentro da média” ou “em torno da média” é sugerida. Valores fora desta faixa são considerados distantes da média e as designações “acima da média” e “abaixo da média” são sugeridas respectivamente. Desta forma, obtemos categorias que dão sentido aos valores da variável tornando mais clara a interpretação dos dados.
Porém, a metodologia proposta deve ser sempre aplicada, atendendo às condições específicas de cada caso. São sempre obtidas 3 classes, e se os dados forem de facto extraídos de uma população normal, a segunda classe terá uma frequência relativa em torno de 68% e as outras duas em torno de 16% cada, o que pode, em alguns casos, não ser desejável. Por outro lado, se houver algumas / muitas observações atípicas nos dados ou se a distribuição subjacente for enviesada, multimodal, o método em questão não produzirá os resultados desejados. De qualquer forma, é um critério que, bem considerada sua aplicação, pode ajudar a melhorar a interpretação dos dados e, assim, a compreensão de um determinado fenômeno.
2.2 DEMONSTRANDO A CONSTRUÇÃO DE TABELAS DE DISTRIBUIÇÃO DE FREQUÊNCIA
2.2.1 COLETA DE DADOS
Num processo de amostragem realizado durante o período de inscrição para exames de acesso à Faculdade de Ciências da Universidade Agostinho Neto de Luanda – Angola, nos anos letivos de 2008 e 2009, foram obtidos os dados, entre outras variáveis, da Idade (expressa em anos), do peso (expresso em quilogramas) e da altura (expressa em metros e centímetros) dos candidatos. O tamanho da amostra foi de 4.298 indivíduos em 2008 e 1.749 indivíduos em 2009, perfazendo uma amostra global de 6.047 indivíduos.
2.2.2 DISTRIBUIÇÃO DE FREQUÊNCIA SIMPLES
É representado a seguir uma tabela de distribuição simples construída a partir dos dados da idade.
Tabela 6: Distribuição de frequência simples das idades dos indivíduos amostrados.
| Indivíduos | ||
| Idade | 2008 | 2009 |
| 16 | 45 | 6 |
| 17 | 142 | 24 |
| 18 | 365 | 131 |
| 19 | 458 | 217 |
| 20 | 672 | 223 |
| 21 | 605 | 256 |
| 22 | 507 | 240 |
| 23 | 431 | 207 |
| 24 | 320 | 129 |
| 25 | 198 | 92 |
| 26 | 152 | 74 |
| 27 | 91 | 31 |
| 28 | 64 | 31 |
| 29 | 55 | 15 |
| 30 | 51 | 19 |
| 31 | 31 | 11 |
| 32 | 18 | 11 |
| 33 | 8 | 4 |
| 34 | 20 | 6 |
| 35 | 11 | 3 |
| 36 | 12 | 2 |
| 37 | 8 | 1 |
| 38 | 6 | 2 |
| … | … | … |
Fonte: autor
A Tabela 6, de distribuição de frequência simples, mostra sua inadequação para fins de sumarização de grandes quantidades de dados. A tabela é muito longa na vertical e, principalmente, não permite a leitura das características dos dados.
2.2.3 TABELA DE DISTRIBUIÇÃO DE FREQUÊNCIA DAS CLASSES A DEFINIR
A idade é uma variável que, para fins de análise demográfica, possui categorias pré-definidas. Porém, para outros fins, esta definição de categorias pode não ser adequada, como é o caso da análise de idade dos candidatos ao exame de acesso à Universidade. Neste caso particular, o objetivo é avaliar a variabilidade de idade do candidato, determinar o candidato com maior e menor idade, respectivamente, bem como analisar a variabilidade dos dados. É importante saber a que intervalos se distribuem as idades da maioria dos candidatos para tirar conclusões sobre o perfil dos alunos que concluem o ensino secundário e, portanto, são potenciais candidatos ao ensino superior.
Para fins de demonstração, uma sub amostra de 182 candidatos foi retirada aleatoriamente da amostra global para mostrar como a variável deve ser categorizada antes da construção da distribuição de frequência.
Tabela 7: Idade dos 182 candidatos inscritos nos exames da Faculdade de Ciências da Universidade Agostinho Neto, no ano letivo de 2009.
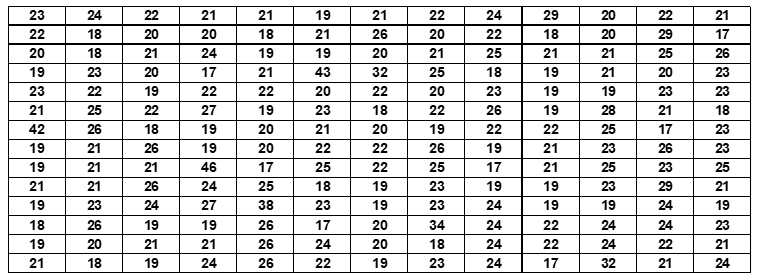
Para esses 182 dados, a média é de 22 anos e o desvio padrão é de 4 anos. O uso da teoria da distribuição normal de Gauss para a definição de categorias, conforme descrito na seção 2.1, resulta na seguinte categorização da variável e sua respectiva distribuição de frequência:
Tabela 8: Categorização da idade dos candidatos
| Nome da categoria ou grau | Valor da categoria ou classe |
| Acima da média | > 26 (22 + 4) |
| Dentro da média | 18 – 26 (22 ± 4) |
| Abaixo da média | < 18 (22 – 4) |
Fonte: Autor
Tabela 8: Categorização da idade dos candidatos
| Idade (em anos) | Número de candidatos | |
| Acima da média (> 26) | 13 | 7% |
| Dentro da média (18 – 26) | 162 | 89% |
| Abaixo da média (< 18) | 7 | 4% |
Fonte: Autor
Uma vez que a teoria de Gauss é aplicada e a tabela de distribuição de frequência construída, sua interpretação agora é fácil e clara de ser feita. A distribuição de frequência mostra que a maioria dos 182 candidatos, o que representa 89% deles, tem entre 18 e 26 anos e são considerados candidatos com idade dentro da média. A percentagem de candidatos acima e abaixo da média é comparativamente residual, sendo 7% e 4% respetivamente. Estas informações são de grande importância para a gestão da Universidade, que as poderá utilizar da melhor forma para o que julgar conveniente.
2.2.4 DISTRIBUIÇÃO DE FREQUÊNCIA USANDO CATEGORIAS PREDEFINIDAS
Os valores de referência e respectivas categorias, padronizados e certificados pela comunidade científica mundial por meio da Organização Mundial da Saúde (conforme já descrito na seção 2.1) são utilizados como corpo da tabela, resultando na seguinte distribuição de frequência do Índice de Massa Corporal dos candidatos ao exame de acesso nos anos letivos de 2008 e 2009:
Tabela 10: Distribuição do IMC dos indivíduos amostrados.
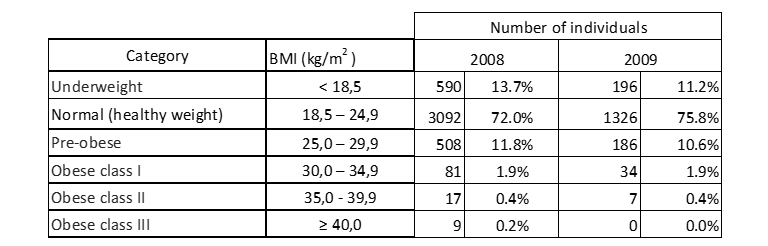
A Tabela 10 indica que a maioria dos candidatos, tanto em 2008 quanto em 2009, possui peso normal. Felizmente, o número de pessoas com obesidade grau III, e, portanto, com grande risco à saúde, é muito baixo em 2008 e inexistente no ano seguinte.
2.2.5 USO DE CATEGORIAS PRÉ-DEFINIDAS VERSUS CRITÉRIOS MATEMÁTICOS NA CONSTRUÇÃO DE TABELAS DE DISTRIBUIÇÃO DE FREQUÊNCIA DE CLASSE
Mostra-se a seguir a inadequação dos critérios matemáticos para a construção de tabelas de distribuição de frequência de classes para variáveis com categorias pré-definidas.
Considere os dados do Índice de Massa Corporal para o ano letivo de 2008, um total de 4.297 indivíduos. Observando os critérios descritos no ponto 2.1, aqueles que estabelecem 6 como número mínimo de categorias (DAWSON e TRAPP, 2003) são coincidentes com o número de categorias predefinidas para o IMC. Uma vez que o número de categorias é definido, o valor máximo e o valor mínimo devem ser identificados para calcular a amplitude total, que por sua vez será usada para calcular o intervalo de aula.
Tabela 11: Estatísticas de resumo dos dados amostrados
| Tamanho da amostra | 4297 |
| Valor máximo | 49 |
| Valor mínimo | 8 |
| Amplitude (máximo – mínimo) | 41 |
| Número de classes ou categorias | 6 |
| Faixa de classe (amplitude dividida pelo número de categorias) | 6.8 |
Fonte: Autor
Uma vez que a faixa de classe é determinada, os limites de cada uma das 6 categorias podem ser finalmente calculados. O limite inferior da 1ª categoria é o valor mínimo e o limite superior desta categoria é obtido somando o intervalo das classes. Isso é feito para as demais categorias e obtém-se o seguinte resultado:
Tabela 12: Categorias do IMC e seus valores calculados.
| Categoria | Valores do IMC | |
| 1 | 8,0 | 16,2 |
| 2 | 16,3 | 24,5 |
| 3 | 24,6 | 32,8 |
| 4 | 32,8 | 41,0 |
| 5 | 41,0 | 49,2 |
Fonte: Autor
A tabela abaixo mostra uma comparação entre os valores calculados e os valores predefinidos.
Tabela 13: Comparação dos valores pré-definidos com os valores calculados.
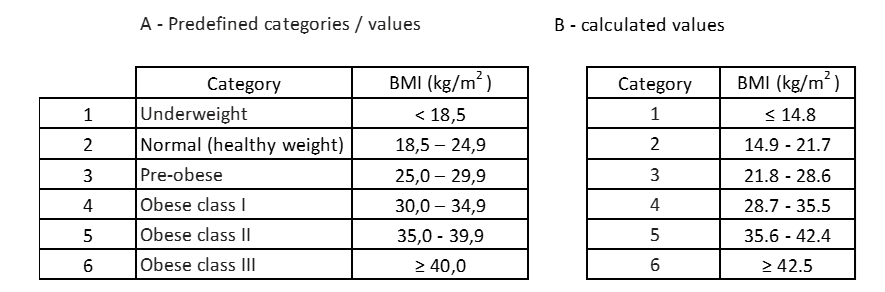
A primeira constatação é que as categorias calculadas não possuem designação própria, ou seja, não possuem atributos que qualificam a condição no indivíduo. A segunda constatação, apesar do mesmo número de categorias, os valores de cada categoria não são iguais. Pelas categorias calculadas, indivíduos com IMC entre 14,9 e 21,7 seriam confundidos com peso normal, quando na verdade alguns deles estão na condição de “baixo peso”.
3. CONSIDERAÇÕES FINAIS
As tabelas de distribuição de frequência são ferramentas muito úteis no processamento de dados. Sua construção deve, no entanto, obedecer a certos critérios cientificamente válidos. É fundamental garantir que, independentemente do critério adotado, a leitura interpretativa dos dados conduza a conclusões lógicas e compreensíveis sobre o comportamento da variável. Nesse sentido, a ligação entre atributos quantitativos e qualitativos é crucial. Assim, o critério sugerido, baseado na utilização da Teoria da Distribuição Normal de Gauss para a categorização das variáveis, é bastante viável.
Por tudo o que foi expresso, existe fundamento suficiente para introduzir a diferenciação das tabelas de distribuição de frequências das classes em dois tipos, ou seja, tabelas de frequências de classes ou categorias pré-definidas e tabelas de frequências de classes ou categorias a definir, sugerindo daí sua adoção como conceito.
REFERÊNCIAS
BEIGUELMAN, Bernardo. Curso prático de bioestatística. 5ª Edição Revisada. FUNPEC Editora, 1994.
CAQUET, René. 250 Exames de Laboratório – Prescrição e Interpretação, 10ª Edição. Rio de Janeiro: Livraria e Editora Revinter, 2011. ISBN 978-85-372-0338-5
DAWSON, Beth & TRAPP, Robert Greig. Bioestatística básica e clínica. 3ª edição. McGraw-Hill Interamericana do Brasil, 2003. ISBN 85-86804-32-0
GRUNDY, Scott M. Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421 https://ci.nii.ac.jp/naid/10030733296/
KEYS, A., FIDANZA, F., KARVONEN, M. J., KIMURA, N., & TAYLOR, H. L. (1972). Indices of relative weight and obesity. Journal of chronic diseases 25 (6-7), 329-343.
KUZMA, Jan W. & BOHNENBLUST Stephen E. Basic Statistics for the Health Sciences. (Fourth ed.). New York: McGraw-Hill Higher Education 2001. ISBN 0-7674-1752-6
MILTON, Janet Susan. & TSOKOS, Janice Oseth. (1991). Estadistica para biologia y ciencias de la salud. Madrid: Interamericana McGraw-Hill – Madrid.
PEDROSA, Rodrigo Pinto and DRAGER, Luciano Ferreira. “Diagnóstico e classificação da hipertensão arterial sistêmica.” MedicinaNET [https://scholar.google.com/scholar] (2017).
PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Available on: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. Retrieved on March 25, 2020.
REIS, Elisabeth. Estatística descritiva. Edições Sílabo, 2005. Lisboa. ISBN 972-618362-6
RICE, Kathryn and SCOTT Paul. Carl Friedrich Gauss. Australian Mathematics Teacher 61.4 (2005): 2-5.
The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Cited in Pedrosa and Drager (2010).
TRIOLA, Marc M. & TRIOLA, Mario F. Bioestatistics for the biological and health sciences. Boston: Pearson Education, 2006. ISBN 0-321-19436-5
WORLD HEALTH ORGANIZATION. “Obesity: preventing and managing the global epidemic.” (2000). Google Scholar
[1] Doutor em Ciências Agrárias (Dr Sc Agr), Engenheiro Agrônomo.
Enviado: Fevereiro de 2021.
Aprovado: Março de 2021.