ÜBERPRÜFUNG ARTIKEL
VICTORINO, Samuel Carlos [1]
VICTORINO, Samuel Carlos. Ein weiterer Ansatz bei der Erstellung von Häufigkeitstabellen unter Verwendung der GAUSS Normalverteilungstheorie. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 06, Ed. 03, Vol. 07, S. 139-154. März 2021. ISSN:2448-0959, Zugriffslink: https://www.nucleodoconhecimento.com.br/agronomie-de/haeufigkeitstabellen
ZUSAMMENFASSUNG
Die korrekte Organisation der Daten ist äußerst wichtig für die Analyse im Prozess der statistischen Inferenz, um gültige Schlussfolgerungen und allgemeine Empfehlungen zu einem bestimmten untersuchten Thema zu erarbeiten. Die wissenschaftliche Fachliteratur beschreibt verschiedene Verfahren zum Organisieren von Daten in Häufigkeitsverteilungstabellen. Bei der Verwendung von Datenorganisationstools treten jedoch nicht immer Ungenauigkeiten auf. Diese Ungenauigkeiten führten zu verzerrten Analysen und inkongruenten Schlussfolgerungen. Dieser Artikel enthält eine kritische Analyse der in der Literatur beschriebenen Datenorganisationsmethoden und -verfahren, insbesondere der Verteilung von Daten in Häufigkeitsverteilungstabellen, und schlägt einen anderen Ansatz bei der Erstellung von Klassenhäufigkeitsverteilungstabellen vor. Für alle Variablen mit vordefinierten Kategorien dienen diese und ihre jeweiligen Referenzwerte als Hauptteil der Tabelle. Für Variablen ohne vordefinierte Kategorien wird die Verwendung der Gauss-Normalverteilungstheorie als Kategorisierungskriterium vorgeschlagen und begründet. Die generierten Kategorien dienen als Hauptteil der Tabelle. Es wird der Schluss gezogen, dass die Häufigkeitsverteilungstabellen in zwei Typen unterschieden werden können, nämlich Häufigkeitsverteilungstabellen vordefinierter Klassen oder Kategorien und Häufigkeitsverteilungstabellen der zu definierenden Klassen oder Kategorien, was ihre Annahme als Konzept nahe legt.
Schlüsselwörter: Normalverteilung, einfache Frequenzverteilungstabelle, Frequenzverteilungstabelle der zu definierenden Klassen.
1. EINLEITUNG
Die Statistik als Wissenschaft wird in einer Reihe von Methoden und Verfahren zusammengefasst, die die Erhebung, Organisation und Darstellung von Daten für ihre Analyse ermöglichen, um gültige Schlussfolgerungen und die Ausarbeitung generischer Empfehlungen zu einer bestimmten Untersuchten Zulage zu erhalten.
Die Statistik findet Anwendung in den unterschiedlichsten Wissensbereichen wie Wirtschaft, Psychologie, Soziologie, Landwirtschaft und Gesundheit und unterstützt den Entscheidungsprozess auf der Grundlage von Datenanalysen. Damit Statistiken diese Funktion erfüllen können, müssen Methoden und Verfahren unbedingt ordnungsgemäß angewendet werden. Die Datenerfassung umfasst die korrekte Anwendung von Stichprobenverfahren, die in der Auswahl repräsentativer Stichproben gipfeln und die Gültigkeit der Daten und gleichzeitig die Gültigkeit der Studien gewährleisten. Die Organisation und Darstellung der Daten zielt darauf ab, die Daten zu vereinfachen und in Häufigkeitsverteilungstabellen zu komprimieren, unabhängig davon, ob es sich um einzelne Häufigkeitstabellen oder Klassenhäufigkeitstabellen handelt. Die in Tabellen zusammengefassten Daten werden normalerweise und gegebenenfalls in Grafiken, Diagrammen und anderen statistischen Tools visualisiert. Die korrekte Organisation ist äußerst wichtig für die Analyse von Daten im Prozess der statistischen Inferenz.
Die wissenschaftliche Fachliteratur beschreibt eine Vielzahl von Verfahren zur Organisation von Daten in Häufigkeitsverteilungstabellen. Es wurde festgestellt, dass Ungenauigkeiten bei der Verwendung von Datenorganisationstools häufig auftreten, was zu verzerrten Interpretationen und inkongruenten Schlussfolgerungen führt. Dieser Artikel zielt darauf ab, eine kritische Analyse der in der Literatur beschriebenen Methoden und Verfahren zum Organisieren von Daten zu präsentieren, insbesondere der Verteilung von Daten in Häufigkeitstabellen, und schlägt einen anderen Ansatz bei der Erstellung von Häufigkeitsverteilungstabellen vor.
2 . THEORETISCHER RAHMEN FÜR FREQUENZVERTEILUNGSTABELLEN
Die Statistik gliedert sich in zwei Hauptgruppen: beschreibende Statistiken und Inferentialstatistiken.
Deskriptive Statistiken sind der Teil, der sich mit der Beschreibung, Klassifizierung, Organisation und Darstellung der Daten einer Variablen befasst. Es ermöglicht die Zusammenfassung von Daten und hilft bei der Beschreibung der Attribute einer bestimmten Datengruppe oder einer Grundgesamtheit durch die Berechnung von beschreibenden Kennzahlen wie mittels Mittelwert und Standardabweichung. Die tabellarischen und grafischen Beschreibungstechniken, die mit Unterstützung der grafischen Fähigkeiten moderner Computer und der verschiedenen verfügbaren Software verwendet werden, um diese Art von Zusammenfassung machbarer und verständlicher zu machen.
Inferentialstatistiken sind hingegen für die Analyse der Daten verantwortlich, um valide Schlussfolgerungen zu erhalten, und für die Ausarbeitung allgemeiner Empfehlungen über die untersuchte Bevölkerung.
2.1 TABELLE UND GRAFISCHE BESCHREIBUNGSTECHNIKEN
Die Rohdaten einer Variablen, die bei einem Stichprobenverfahren ermittelt wurde, erlauben keine Visualisierung eines Merkmals der Stichprobe und viel weniger der untersuchten Population. Daher sind Tabellen und Grafiken wesentliche statistische Ressourcen in der Datenverarbeitung.
Tabellen ermöglichen es, eine große Menge an Informationen zusammenzufassen und zu verdichten, die dem Forscher eine klare Analyse bieten. Graphen sind Tabellenergänzungen, die die Funktion haben, eine visuelle Vorstellung vom Verhalten der Daten zu übertragen. Es gibt eine Vielzahl von Diagrammen, darunter Liniendiagramme, Balkendiagramme, Flächendiagramme und Kreisdiagramme als die häufigsten.Bei den Frequenzverteilungstabellen unterscheiden sich die folgenden Typen grundlegend:
1 – Einzelfrequenzverteilungstabelle
2 – Klassenfrequenzverteilungstabelle
Eine einzelne Frequenzverteilungstabelle enthält zwei Hauptspalten. In der ersten Spalte wird jeder gesammelte Wert sequenziell, einmal und in aufsteigender Reihenfolge eingefügt. In der zweiten Spalte in der Zeile, die jedem beobachteten Wert entspricht, wird die Anzahl der Wiederholungen dieser Werte im Datensatz eingefügt, was der jeweiligen absoluten Frequenz entspricht.
Die Häufigkeitsverteilungstabelle der Klassen enthält auch zwei Spalten, die erste für die Intervalle der Klassen der Variablen und die zweite für die Anzahl der zu jeder Klasse gehörenden Personen, dh die absolute Häufigkeit der Klasse.
Einzelne Frequenzverteilungstabellen haben den großen Nachteil, dass sie zu lang sind, da alle Stichprobenwerte aufgeführt werden müssen und vor allem das Lesen von Datenmerkmalen nicht erlaubt sind. Diese Art von Tabellen sind völlig ungeeignet, wenn der Zweck darin besteht, große Datenmengen zusammenzufassen. Für diese Fälle eignen sich Klassenfrequenzverteilungstabellen besser, da sie große Datenmengen in einige Klassen umteilen und die quantitativen Attribute der Variablen mit der aktuellen Bedeutung der Merkmale der Variablen verknüpfen.
Der grundlegende Aspekt bei der Ausarbeitung von Verteilungstabellen von Klassenfrequenzen ist die Bestimmung der Anzahl der Klassen, in denen die Daten eingerahmt werden. Zu diesem Zweck werden in der Literatur mehrere Kriterien zur Bestimmung der Anzahl der Klassen beschrieben, von denen die meisten rein mathematisch begründet sind.
Milton und Tsokos (1991) geben die Verwendung der folgenden Formeln an, um die Anzahl der Klassen zu bestimmen:
1 – Anzahl der Klassen = 5 x lg n wobei n die Stichprobengröße ist
Beiguelman (2002) gibt an, dass die Anzahl der Klassen zwischen 8 und 20 liegt, abhängig von den Daten. Für Dawson und Trapp (2003) sind 6 und 14 Klassen ausreichend, um ausreichende Informationen ohne übermäßige Details zur Verfügung zu stellen. Triola und Triola (2006) empfehlen, dass die Anzahl der Klassen zwischen 5 und 20 liegen sollte, während Kuzma und Bohnenblust (2001) der Meinung sind, dass die Anzahl der Klassen 5 bis 15 betragen sollte. Reis (2005) erklärt, dass die Anzahl der Klassen zwischen 4 und 14 liegen sollte, und schlägt auch die Verwendung einer der folgenden Lösungen vor:
![]()
1 – Anzahl der gleichen Klassen 5 für Stichproben mit einer Größe kleiner als 25 und Anzahl der Klassen = für Stichproben mit einer Größe von gleich oder größer als 25.
2 – Verwenden Sie die Sturges-Formel: Anzahl der Klassen = 1 + 3,22 n log
Das vorgenannte zeigt die Vielfalt der in der Literatur beschriebenen Kriterien für die Erstellung von Frequenzverteilungstabellen. Diese Kriterien haben jedoch einen gemeinsamen Nachteil, der sie als Grundlage für die Bestimmung der Anzahl der Datenklassen für bestimmte Variablen ungeeignet macht, wie z. B. Variablen im Bereich der Biologie und Gesundheitswissenschaften, der Wirtschaft, der Industrie, unter anderem, die vordefinierte Kategorien haben, d. h. standardisierte Kategorien. Einige dieser Variablen sind unten beschrieben und die jeweiligen Referenzwerte der vordefinierten Kategorien sind angegeben.Im Bereich der Biologie:
Beispiel1: Referenzwerte des Gesamtcholesterins beim Menschen Tabelle 1: Kategorien und Referenzwerte des Gesamtcholesterins beim Menschen.
| Total Cholesterin | Kategorie |
| < 200 mg/dl | Wünschenswert oder Normal |
| 200 – 239 mg/dl | Grenze |
| ≥ 240 mg/dl | Hoch |
Quelle: Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421
Beispiel 2: Referenzwerte für den Body-Mass-Index (BMI).
Das BMI hilft, den Adipositas-Grad einer Person nach Angaben der Weltgesundheitsorganisation zu definieren. Durch die Berechnung und Interpretation des BMI ist es möglich zu wissen, ob eine Person über oder unter den Gewichtsparametern liegt, die für ihre physikalische Struktur empfohlen werden. Zur Berechnung des BMI wird das in kg gemessene Gewicht durch die quadratisch gequadratte Höhe (BMI = kg / m2) dividiert.
Tabelle 2: Kategorien und Referenzwerte des Body Mass Index
| Kategorie | BMI (kg/m2 ) |
| Untergewicht | < 18,5 |
| Normal (gesundes Gewicht) | 18,5 – 24,9 |
| Präfettadipische | 25,0 – 29,9 |
| Fettleibige Klasse I | 30,0 – 34,9 |
| Fettleibige Klasse II | 35,0 – 39,9 |
| Fettleibige Klasse III | ≥ 40,0 |
Quelle: World Health Organization. Obesity (1998): Preventing and managing the global epidemic: report of a WHO Consultation on Obesity, Geneva, 3–5 June 1997. Geneva (CH): World Health Organization; 1998. http://whqlibdoc.who.int/hq/1998/WHO_NUT_NCD_98.1_(p1-158).pdf.
Beispiel 3 – Klassifizierung der arteriellen Hypertonie. Tabelle 3: Klassifizierung arterieller Hypertonie
| Klassifizierung des Blutdrucks | Sistolischer Blutdruck (mmHg) | Diastolischer Blutdruck (mmHg) |
| Normalen | < 120 | < 80 |
| Prähypertonie | 120 – 139 | 80 – 89 |
| Stufe 1 (Grad I) Bluthochdruck | 140 – 159 | 90 – 99 |
| Stufe 2 (Grad II) Hypertonie | ³ 160 | ³ 100 |
Quelle: The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Zitiert von PEDROSA und DRAGER (2010).
Beispiel 4: Harnsäure entsteht aus dem Stoffwechsel von Purinen, wichtigen Strukturelementen von DNA und RNA, ein Großteil davon aus DerNahrung. Übermäßiger Verzehr von Fleisch oder Alkohol kann harnsäurehaltige Werte im Blut erhöhen.
Die Referenzwerte liegen im Allgemeinen bei Männern bei 40 bis 60 mg/L, bei Frauen bei 30 bis 50 mg/L und bei Kindern bei 25 bis 40 mg/L (CAQUET, 2011).
Im Bereich der Wirtschaft:
Beispiel 5: Der Human Development Index (HDI) sind statistische Daten, die vom Entwicklungsprogramm der Vereinten Nationen (UNDP) erstellt wurden, um den rein wirtschaftlichen Daten entgegenzuwirken, die zur Messung des Wohlstands des Landes und zur Analyse der Entwicklung einschließlich anderer Faktoren verwendet werden.
Für diese Variable werden die folgenden Kategorien standardisiert, unter welchen Ländern auf der Grundlage ihrer jeweiligen HDI aufgeteilt werden:
Low HDI: vereint alle Länder mit HDI unter 0,500.
Durchschnittlicher HDI: Länder mit HDI zwischen 0.500 und 0.799.
High HDI: Länder mit HDI zwischen 0,800 und 0,899.
Sehr hohe HDI: Länder, deren HDI gleich oder über 0,900 ist.
Quelle: PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. März 2020.
Die oben angeführten Beispiele zeigen, dass die Kriterien mit mathematischer Grundlage nicht für alle Situationen geeignet sind. Bei der Definition von Klassen zum Erstellen einer Frequenztabelle sind die Regeln, die in der Literatur bekannt sind und hier vorgestellt werden, lediglich indikativ. Die Definition der Klassen sowie die Anzahl der Klassen müssen zunächst auf der Kenntnis des untersuchten Phänomens und seiner Ziele beruhen. Es gibt keine Formeln, die für alle Situationen richtig gelten. Selbst wenn die Anzahl der Klassen, die sich aus der Berechnung ergeben, der Anzahl vordefinierter Klassen entspricht, stimmen die Klassenintervalle nicht mit den vordefinierten Werten überein. Und genau hier liegt das Problem. Klassenintervalle sind quantitative Attribute, die eine Bedingung oder einen Zustand der Variablen bedeuten müssen. Zum Beispiel, eine Person mit einem Cholesterinspiegel von 260 mg/dl ist ungesund, weil er Cholesterin über normal hat. Ebenso ist ein Land mit einem Index für menschliche Entwicklung, der unter 0,5 bewertet wird, unterentwickelt, da es zweifellos von niedrigem HDI ist. Das Gruppieren von Variablendaten mit vordefinierten Kategorien ohne Berücksichtigung derselben Kategorien führt daher dazu, dass der Klassenbereich nicht an die jeweilige Bedeutung der Klassenbereichswerte gebunden werden kann. Dieser Mangel an Verbindung zwischen den quantitativen (Klassenintervallwerten) und den qualitativen (variablen Kategorien) verarmt die Interpretation von Daten und kann sogar die Interpretation von Daten falsch darstellen und zu falschen Schlussfolgerungen führen.
Daher ist für Variablen mit vordefinierten Kategorien das am besten geeignete Kriterium für die Konstruktion der Frequenzverteilung die Verwendung dieser Kategorien und ihrer jeweiligen Werte als Text der Tabelle. Dieses Kriterium ordnet die Werte von Kategorien den jeweiligen qualitativen Attributen zu, die eine klare Dateninterpretation ermöglichen.
Wenn die Variablen keine vordefinierten Kategorien haben und die Suche nach Hinweisen oder Indikatoren erschöpft haben, die helfen, die Kategorien zu erstellen, ohne dass dies nach mathematischen Kriterien geschieht, wird hier die Verwendung der Theorie der Normalverteilung von Gauss für die Variable Kategorisierung vorgeschlagen. Damit sollen Kategorien geschaffen werden, die es ermöglichen, das Quantitative mit dem Qualitativen zu verknüpfen und die Dateninterpretation spürbarer zu machen.
Die Gauss-Normalverteilungstheorie, die in der Literatur weithin erwähnt wird (RICE und SCOTT, 2005), besagt, dass sich bei einer Reihe normaler (symmetrischer, unimodaler) Daten etwa 68 % der Daten bis zu einer Einheit der Standardabweichung des Mittelwerts befinden, etwa 95 % der Daten bis zu zwei Einheiten mittlerer Standardabweichung und 99 % der Daten bis zu drei Einheiten mittlerer Standardabweichung befinden.
Tabelle 4: Characterik als normale Distribuition
| ± 1S | 68% der Daten |
| ± 2S | 95% der Daten |
| ± 3S | 99% der Daten |
Quelle: adaptiert von Rice und Scott (2005)
So wird es als Kriterium für die Definition von Kategorien aus der Theorie der Normalverteilung, die Verwendung des Variationsbereichs von 68% festgelegt, wie folgt: Tabelle 5: Grundlage für die variable Kategorisierung
| Kategorie- oder Klassenname | Kategorie- oder Klassenwert |
| Über dem Mittelwert | Oben ( + 1S) |
| Innerhalb des Mittelwerts | Zwischen (± 1S) |
| Unterhalb des Mittelwerts | Unten ( 1S ) |
Quelle: Autor.
Dieser Vorschlag der Variablenkategorisierung basiert auf der Berechnung eines Messwerts der zentralen Tendenz, des Mittelwerts und eines Maßs der Variabilität, der Standardabweichung. Werte, die sich bei einer Standardabweichung des Mittelwerts befinden, werden als nahe am Mittelwert betrachtet, so dass die Bezeichnung der Kategorie “innerhalb des Mittelwerts” oder “um den Mittelwert” vorgeschlagen wird. Werte, die außerhalb dieses Bereichs liegen, werden als weit entfernt vom Mittelwert betrachtet, und die Bezeichnungen “über dem Mittelwert” bzw. “unterhalb des Mittelwerts” werden vorgeschlagen. Auf diese Weise erhalten wir Kategorien, die den Werten der Variablen einen Sinn verleihen, wodurch die Dateninterpretation klarer wird.
Die vorgeschlagene Methodik muss jedoch stets angewandt werden, wobei die spezifischen Bedingungen des einzelfalls zu berücksichtigen sind. 3 Klassen werden immer erhalten, und wenn die Daten tatsächlich aus einer normalen Population extrahiert werden, wird die zweite Klasse eine relative Häufigkeit um 68% und die anderen beiden um jeweils 16% haben, was in einigen Fällen nicht wünschenswert sein kann. Andererseits führt die betreffende Methode nicht zu den gewünschten Ergebnissen, wenn sich einige atypische Beobachtungen in den Daten befinden oder wenn die zugrunde liegende Verteilung voreingenommen und multimodal ist. Jedenfalls ist es ein Kriterium, das, wohl über seine Anwendung, dazu beitragen kann, die Interpretation der Daten und damit das Verständnis eines bestimmten Phänomens zu verbessern.
2.2 DEMONSTRATION DER ERSTELLUNG VON FREQUENZVERTEILUNGSTABELLEN
2.2.1 DATENERFASSUNG
In einem Probenahmeverfahren, das während der Einschreibungsphase für Zugangsprüfungen an der Fakultät für Wissenschaften der Agostinho Neto Universität in Luanda – Angola durchgeführt wurde, wurden in den akademischen Jahren 2008 und 2009 Daten unter anderem aus dem Alter (ausgedrückt in Jahren), aus dem Gewicht (ausgedrückt in Kilogramm) und der Höhe (ausgedrückt in Metern und Zentimetern) der Kandidaten gewonnen. Der Stichprobenumfang betrug 4298 Probanden im Jahr 2008 und 1749 Probanden im Jahr 2009, was eine globale Stichprobe von 6047 Personen.
2.2.2 EINFACHE FREQUENZVERTEILUNG
Es handelt sich um die unten abgebildete einfache Verteilungstabelle, die anhand der Altersdaten erstellt wird.
Tabelle 6: Einfache Häufigkeit Verteilung des Alters der untersuchten Personen.
| Einzelpersonen | ||
| Rechtsakte | 2008 | 2009 |
| 16 | 45 | 6 |
| 17 | 142 | 24 |
| 18 | 365 | 131 |
| 19 | 458 | 217 |
| 20 | 672 | 223 |
| 21 | 605 | 256 |
| 22 | 507 | 240 |
| 23 | 431 | 207 |
| 24 | 320 | 129 |
| 25 | 198 | 92 |
| 26 | 152 | 74 |
| 27 | 91 | 31 |
| 28 | 64 | 31 |
| 29 | 55 | 15 |
| 30 | 51 | 19 |
| 31 | 31 | 11 |
| 32 | 18 | 11 |
| 33 | 8 | 4 |
| 34 | 20 | 6 |
| 35 | 11 | 3 |
| 36 | 12 | 2 |
| 37 | 8 | 1 |
| 38 | 6 | 2 |
| … | … | … |
Quelle: Autor
Tabelle 6 der einfachen Frequenzverteilung zeigt ihre Unzulänglichkeit für die Zusammenfassung großer Datenmengen. Die Tabelle ist zu lang in der vertikalen und vor allem, es erlaubt nicht das Lesen der Datenmerkmale.
2.2.3 FREQUENZVERTEILUNGSTABELLE DER ZU DEFINIERENDEN KLASSEN
Das Alter ist eine Variable, die für die Zwecke der demografischen Analyse vordefinierte Kategorien enthält. Für andere Zwecke ist diese Definition von Kategorien jedoch möglicherweise nicht ausreichend, wie dies bei der Altersanalyse der Bewerber für die Zugangsprüfung für die Universität der Fall ist. In diesem speziellen Fall geht es darum, die Altersvariabilität des Kandidaten zu bewerten, den Kandidaten mit dem höchsten bzw. niedrigsten Alter zu bestimmen und die Datenvariabilität zu analysieren. Es ist wichtig zu wissen, in welchen Intervallen das Alter der meisten Kandidaten verteilt wird, um Rückschlüsse auf das Profil der Schüler zu ziehen, die die Sekundarschule abschließen und daher potenzielle Kandidaten für eine höhere Bildung sind.
Zu Demonstrationszwecken wurde eine Teilstichprobe von 182 Kandidaten nach dem Zufallsprinzip aus der globalen Stichprobe zurückgezogen, um zu zeigen, wie die Variable vor der Erstellung der Frequenzverteilung kategorisiert werden muss.
Tabelle 7: Alter von 182 Bewerbern, die sich für die Prüfungen an der Fakultät für Wissenschaften der Agostinho Neto Universität im akademischen Jahr 2009 eingeschrieben haben.
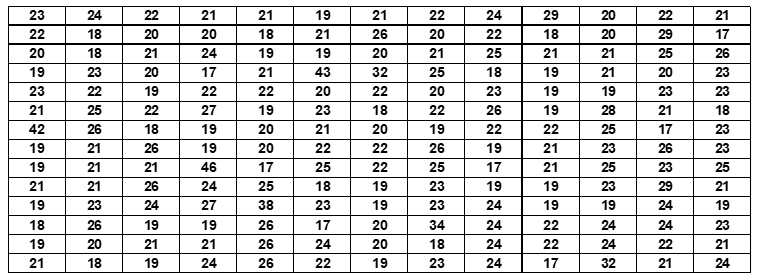
Für diese 182 Daten beträgt der Mittelwert 22 Jahre und die Standardabweichung 4 Jahre. Die Verwendung der Gauss-Normalverteilungstheorie für die Definition von Kategorien, wie in Abschnitt 2.1 beschrieben, führt zu folgender Kategorisierung der Variablen und ihrer jeweiligen Frequenzverteilung:
Tabelle 8: Kategorisierung des Alters der Kandidaten
| Name der Kategorie oder Grad | Kategorie- oder Klassenwert |
| Über dem Mittelwert | > 26 (22 + 4) |
| Innerhalb des Mittelwerts | 18 – 26 (22 ± 4) |
| Unterhalb des Mittelwerts | < 18 (22 – 4) |
Sorce: Autor
Tabelle 9: Häufigkeitsverteilung des Alters von 182 Jahren Zugang zu Prüfungskandidaten.
| Alter (in Jahren) | Anzahl der Kandidaten | |
| Über dem Mittelwert (> 26) | 13 | 7% |
| Innerhalb des Mittelwerts (18 – 26) | 162 | 89% |
| Unterhalb des Mittelwerts (< 18) | 7 | 4% |
Quelle: Autor
Sobald die Gauss-Theorie angewendet und die Frequenzverteilungstabelle erstellt ist, ist ihre Interpretation nun einfach und klar zu tun. Die Frequenzverteilung zeigt, dass die Mehrheit der 182 Kandidaten, die 89 % von ihnen repräsentieren, 18 bis 26 Jahre alt sind und als Kandidaten mit einem Alter innerhalb des Mittelwerts betrachtet werden. Der Anteil der Bewerber, die über und unter dem Durchschnitt liegen, liegt vergleichsweise gering und beträgt 7 % bzw. 4 %. Diese Informationen sind von großer Bedeutung für das Management der Universität, die sie für das, was sie für bequem hält, optimal nutzen kann.
2.2.4 FREQUENZVERTEILUNG UNTER VERWENDUNG VORDEFINIERTER KATEGORIEN
Die Referenzwerte und die jeweiligen Kategorien, die von der weltweiten wissenschaftlichen Gemeinschaft über die Weltgesundheitsorganisation (wie bereits in Abschnitt 2.1 beschrieben) standardisiert und zertifiziert wurden, werden als Text der Tabelle verwendet, was zu der folgenden Häufigkeitsverteilung des Body Mass Index der Kandidaten zur Zugangsprüfung in den akademischen Jahren 2008 und 2009 führt:
Tabelle 10: BMI-Verteilung der in die Stichprobe einbezogenen Personen.
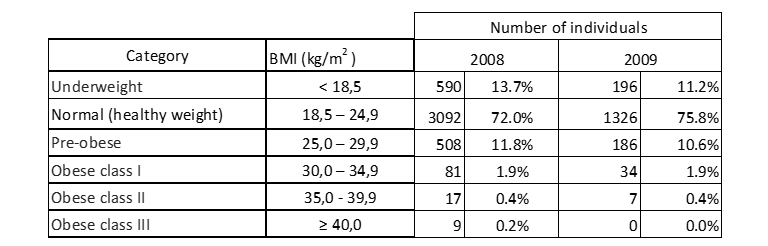
Tabelle 10 zeigt, dass die meisten Kandidaten sowohl in den Jahren 2008 als auch 2009 ein normales Gewicht haben. Glücklicherweise ist die Zahl der Menschen mit Adipositas der Klasse III und damit mit großem Gesundheitsrisiko im Jahr 2008 sehr gering und im darauffolgenden Jahr nicht vorhanden.
2.2.5 VERWENDUNG VORDEFINIERTER KATEGORIEN GEGEN MATHEMATISCHE KRITERIEN BEI DER KONSTRUKTION VON KLASSENFREQUENZVERTEILUNGSTABELLEN
Es wird unten die Unzulänglichkeit der mathematischen Kriterien für die Erstellung von Frequenzverteilungstabellen von Klassen für Variablen mit vordefinierten Kategorien gezeigt.
Man denke an die Body Mass Index Daten für das akademische Jahr 2008, insgesamt 4297 Personen. Betrachtet man die in Punkt 2.1 beschriebenen Kriterien, so sind diejenigen, die 6 als Mindestanzahl von Kategorien festlegen (DAWSON und TRAPP, 2003), mit der Anzahl der vordefinierten Kategorien für den BMI deckungsgleich. Sobald die Anzahl der Kategorien definiert ist, müssen der Maximalwert und der Mindestwert identifiziert werden, um die Gesamtamplitude zu berechnen, die wiederum zur Berechnung des Klassenintervalls verwendet wird.
Tabelle 11: Zusammenfassung der Stichprobendaten
| Stichprobengröße | 4297 |
| Maximaler Wert | 49 |
| Mindestwert | 8 |
| Amplitude (maximal – minimum) | 41 |
| Anzahl der Klassen oder Kategorien | 6 |
| Klassenbereich (Amplitude dividiert durch die Anzahl der Kategorien) | 6.8 |
Quelle: Autor
Sobald der Klassenbereich bestimmt ist, können die Grenzen jeder der 6 Kategorien endgültig berechnet werden. Die untere Grenze der ersten Kategorie ist der Mindestwert, und die obere Grenze dieser Kategorie wird durch Hinzufügen des Klassenbereichs erreicht. Dasselbe gilt für die anderen Kategorien, und das folgende Ergebnis wird erzielt:
Tabelle 12: Kategorien des BMI und deren berechnete Werte.
| Kategorie | BMI-Werte | |
| 1 | 8,0 | 16,2 |
| 2 | 16,3 | 24,5 |
| 3 | 24,6 | 32,8 |
| 4 | 32,8 | 41,0 |
| 5 | 41,0 | 49,2 |
Quelle: Autor
Die folgende Tabelle zeigt einen Vergleich zwischen den berechneten Werten und den vordefinierten Werten.
Tabelle 13: Vergleich der vordefinierten Werte mit den berechneten Werten.
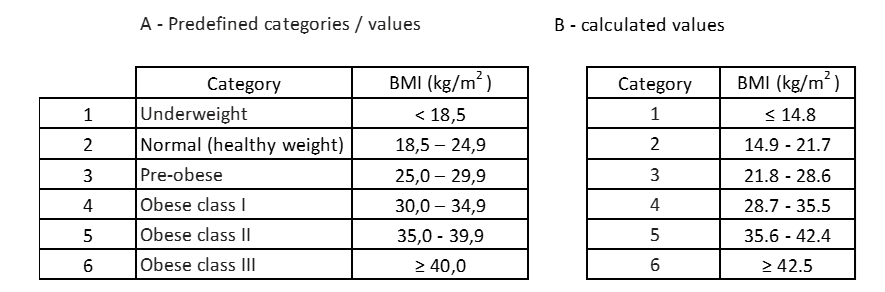
Die erste Erkenntnis ist, dass die berechneten Kategorien keine eigene Bezeichnung haben, das heißt, sie haben keine Attribute, die die Bedingung in der Person qualifizieren. Der zweite Befund ist, dass trotz der gleichen Anzahl von Kategorien die Werte jeder Kategorie nicht gleich sind. Nach den berechneten Kategorien würden Personen mit einem BMI zwischen 14,9 und 21,7 für normales Gewicht gehalten, obwohl einige von ihnen tatsächlich im Zustand “geringes Gewicht” sind.
3. SCHLUSSBEMERKUNGEN
Frequenzverteilungstabellen sind sehr nützliche Werkzeuge in der Datenverarbeitung. Ihre Konstruktion muss jedoch bestimmten wissenschaftlich gültigen Kriterien entsprechen. Es muss unbedingt sichergestellt werden, dass das interpretative Lesen der Daten unabhängig vom angenommenen Kriterium zu logischen und Schlussfolgerungen führt, die über das Verhalten der Variablen verständlich sind. In dieser Hinsicht ist die Verbindung zwischen quantitativen und qualitativen Merkmalen von entscheidender Bedeutung. Somit ist das vorgeschlagene Kriterium, das auf der Verwendung von Gauss Normalverteilungstheorie für die Kategorisierung von Variablen basiert, durchaus machbar.
Für alles, was ausgedrückt wurde, gibt es genügend Gründe, die Unterscheidung von Häufigkeitsverteilungstabellen für Klassen in zwei Typen einzuführen, dh Häufigkeitstabellen für vordefinierte Klassen oder Kategorien und Häufigkeitstabellen für zu definierende Klassen oder Kategorien, was nahe legt seine Annahme als Konzept.
VERWEISE
BEIGUELMAN, Bernardo. Curso prático de bioestatística. 5ª Edição Revisada. FUNPEC Editora, 1994.
CAQUET, René. 250 Exames de Laboratório – Prescrição e Interpretação, 10ª Edição. Rio de Janeiro: Livraria e Editora Revinter, 2011. ISBN 978-85-372-0338-5
DAWSON, Beth & TRAPP, Robert Greig. Bioestatística básica e clínica. 3ª edição. McGraw-Hill Interamericana do Brasil, 2003. ISBN 85-86804-32-0
GRUNDY, Scott M. Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421 https://ci.nii.ac.jp/naid/10030733296/
KEYS, A., FIDANZA, F., KARVONEN, M. J., KIMURA, N., & TAYLOR, H. L. (1972). Indices of relative weight and obesity. Journal of chronic diseases 25 (6-7), 329-343.
KUZMA, Jan W. & BOHNENBLUST Stephen E. Basic Statistics for the Health Sciences. (Fourth ed.). New York: McGraw-Hill Higher Education 2001. ISBN 0-7674-1752-6
MILTON, Janet Susan. & TSOKOS, Janice Oseth. (1991). Estadistica para biologia y ciencias de la salud. Madrid: Interamericana McGraw-Hill – Madrid.
PEDROSA, Rodrigo Pinto and DRAGER, Luciano Ferreira. “Diagnóstico e classificação da hipertensão arterial sistêmica.” MedicinaNET [https://scholar.google.com/scholar] (2017).
PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Available on: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. Retrieved on March 25, 2020.
REIS, Elisabeth. Estatística descritiva. Edições Sílabo, 2005. Lisboa. ISBN 972-618362-6
RICE, Kathryn and SCOTT Paul. Carl Friedrich Gauss. Australian Mathematics Teacher 61.4 (2005): 2-5.
The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Cited in Pedrosa and Drager (2010).
TRIOLA, Marc M. & TRIOLA, Mario F. Bioestatistics for the biological and health sciences. Boston: Pearson Education, 2006. ISBN 0-321-19436-5
WORLD HEALTH ORGANIZATION. “Obesity: preventing and managing the global epidemic.” (2000). Google Scholar
[1] Promotion in Agrarwissenschaften (Dr. Sc Ag), Agronom.
Eingereicht: Februar 2021.
Genehmigt: März 2021.


