ARTICLE DE RÉVISION
VICTORINO, Samuel Carlos [1]
VICTORINO, Samuel Carlos. Une autre approche dans l’élaboration de tableaux de fréquences utilisant la théorie de la distribution normale de GAUSS. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 06, Ed. 03, Vol. 07, p. 139-154. mars 2021. ISSN:2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/agronomie-fr/tableaux-de-frequences
RÉSUMÉ
L’organisation correcte des données est d’une extrême importance pour l’analyse dans le processus d’inférence statistique, visant à élaborer des conclusions valides et des recommandations génériques sur un certain sujet à l’étude. La littérature scientifique spécialisée décrit plusieurs procédures d’organisation des données dans les tableaux de distribution des fréquences. Cependant, il n’est pas souvent que des inexactitudes sont faites dans l’utilisation d’outils d’organisation de données. Ces inexactitudes ont donné lieu à des analyses déformées et à des conclusions incongrues. Cet article présente une analyse critique des méthodes et procédures de l’organisation des données décrites dans la littérature, en particulier la distribution des données dans les tableaux de distribution des fréquences et propose une approche différente dans l’élaboration des tableaux de distribution des fréquences des classes. Pour toutes les variables avec des catégories prédéfinis, celles-ci et leurs valeurs de référence respectives servent de corps au tableau. Pour les variables qui n’ont pas de catégories prédéfines, l’utilisation de la théorie normale de la distribution de Gauss comme critère de catégorisation est proposée et justifiée. Les catégories générées servent de corps de table. On conclut que les tableaux de distribution des fréquences peuvent être distingués en deux types, c’est-à-dire les tableaux de distribution des fréquences des classes ou catégories prédéfinis et les tableaux de répartition des fréquences des classes ou des catégories à définir, suggérant ainsi leur adoption comme concept.
Mots-clés: Distribution normale, Table de distribution de fréquences simples, Table de distribution des fréquences des classes à définir.
1. INTRODUCTION
Les statistiques, en tant que science, sont résumées dans un ensemble de méthodes et de procédures qui permettent la collecte, l’organisation et la présentation des données pour leur analyse, afin d’obtenir des conclusions valides et l’élaboration de recommandations génériques sur une population donnée étudiée.
Les statistiques trouvent l’application dans les domaines les plus divers de la connaissance tels que l’économie, la psychologie, la sociologie, l’agriculture et la santé, aidant dans le processus de prise de décision basé sur l’analyse des données. Pour que les statistiques remplissent ce rôle, il est impératif que les méthodes et les procédures soient correctement appliquées. La collecte de données implique l’application correcte de méthodes d’échantillonnage qui aboutissent à la sélection d’échantillons représentatifs et assurent la validité des données et, en même temps, la validité des études; l’organisation et la présentation des données visent la simplification et la compression des données dans les tableaux de distribution de fréquences, qu’il s’agisse de tables à fréquence unique ou de tables de fréquences de classe. Les données résumées dans les tableaux sont généralement et, le cas échéant, visualisées dans des graphiques, des diagrammes et d’autres outils statistiques. Leur organisation correcte est d’une extrême importance pour l’analyse des données dans le processus d’inférence statistique.
La littérature scientifique spécialisée décrit un large éventail de procédures d’organisation des données dans les tableaux de distribution des fréquences. Il a été constaté que des inexactitudes dans l’utilisation des outils d’organisation des données sont souvent commises, ce qui entraîne une interprétation déformée et des conclusions incongrues. Cet article vise à présenter une analyse critique des méthodes et procédures de l’organisation des données décrites dans la littérature, en particulier la distribution des données dans les tableaux de fréquences et propose une approche différente dans l’élaboration des tableaux de distribution des fréquences.
2. CADRE THÉORIQUE DES TABLEAUX DE DISTRIBUTION DE FRÉQUENCE
La statistique est divisée en deux groupes principaux : les statistiques descriptives et les statistiques inférentielles.
Les statistiques descriptives sont la partie qui traite de la description, de la classification, de l’organisation et de la présentation des données d’une variable. Il permet de résumer les données et aide à décrire les attributs d’un groupe de données donné ou d’une population au moyen du calcul de mesures descriptives telles que la moyenne et l’écart type. Les techniques descriptives tabulaires et graphiques utilisées avec le soutien des capacités graphiques des ordinateurs modernes et des différents logiciels disponibles pour rendre ce type de résumé plus faisable et plus compréhensible.
En revanche, les statistiques inférentielles sont chargées d’analyser les données afin d’obtenir des conclusions valables et d’élaborer des recommandations génériques sur la population à l’étude.
2.1 TECHNIQUES DESCRIPTIVES TABULAIRES ET GRAPHIQUES
Les données brutes d’une variable obtenue dans le cadre d’un processus d’échantillonnage ne permettent pas la visualisation d’une caractéristique quelconque de l’échantillon et encore moins de la population à l’étude. Par conséquent, les tableaux et les graphiques sont des ressources statistiques essentielles dans le traitement des données.
Les tableaux permettent de résumer et de compacter une grande quantité d’information fournissant une analyse claire au chercheur. Les graphiques sont le complément du tableau qui ont pour fonction de transmettre une idée visuelle du comportement des données. Il existe une grande variété de graphiques, parmi eux, des graphiques linéaires, des graphiques à barres, des graphiques de zone et des diagrammes à secteurs comme les plus communs.En ce qui concerne les tableaux de distribution des fréquences, les types suivants sont fondamentalement différents :
1 – Table de distribution à fréquence unique
2 – Table de distribution des fréquences de classe
Une table de distribution à fréquence unique contient deux colonnes principales. Dans la première colonne, chaque valeur collectée est insérée séquentiellement, une fois et dans l’ordre ascendant. Dans la deuxième colonne de la ligne correspondant à chaque valeur observée est inséré le nombre de fois que ces valeurs sont répétées dans l’ensemble de données, qui correspond à la fréquence absolue respective.
Le tableau de distribution des fréquences de classe contient également deux colonnes, la première pour les intervalles de classe de la variable et la seconde pour le nombre d’individus appartenant à chaque classe, c’est-à-dire la fréquence absolue de la classe.
Les tableaux de distribution à fréquence unique ont l’inconvénient majeur d’être trop longs, en raison du fait que toutes les valeurs échantillonnées doivent être répertoriées et, surtout, ne permettent pas la lecture des caractéristiques des données. Ce type de tableaux est totalement inapproprié lorsque le but est de résumer de grandes quantités de données. Dans ces cas, les tableaux de distribution des fréquences de classe sont plus appropriés, car ils compactent de grandes quantités de données en quelques classes et relient les attributs quantitatifs de la variable à la signification actuelle des caractéristiques de la variable.
L’aspect fondamental de l’élaboration des tableaux de distribution des fréquences de classe est la détermination du nombre de classes, dans lesquelles les données seront encadrées. À cette fin, plusieurs critères pour déterminer le nombre de classes sont décrits dans la littérature, dont la plupart sont strictement mathématiques.
Milton et Tsokos (1991) indiquent l’utilisation des formules suivantes pour déterminer le nombre de classes :
1 – Nombre de classes = 5 x lg n où n est la taille de l’échantillon
2 – Nombre de classes =
Beiguelman (2002) indique que le nombre de classes se situe entre 8 et 20, selon les données. Pour Dawson et Trapp (2003), les classes 6 et 14 sont suffisantes pour fournir suffisamment d’information sans trop de détails. Triola et Triola (2006) recommandent que le nombre de classes se situe entre 5 et 20, tandis que Kuzma et Bohnenblust (2001) considèrent que le nombre de classes devrait être de 5 à 15. Reis (2005) déclare que le nombre de classes devrait se situer entre 4 et 14 et suggère également l’utilisation de l’une des solutions suivantes :
![]()
1 – Nombre de classes égales 5 pour les échantillons de taille inférieure à 25 et nombre de classes = pour les échantillons d’une taille égale ou supérieure à 25.
2 – Utilisez la formule Sturges : nombre de classes = 1 + 3,22 n journal
Ce qui précède montre la variété des critères décrits dans la littérature pour la construction de tableaux de distribution de fréquences. Toutefois, ces critères ont un désavantage commun qui les rend inadaptés comme base pour déterminer le nombre de classes de données pour certaines variables, telles que les variables dans le domaine de la biologie et des sciences de la santé, l’économie, l’industrie, entre autres, qui ont des catégories prédéfinis, c’est-à-dire des catégories normalisées. Certaines de ces variables sont décrites ci-dessous et les valeurs de référence respectives des catégories prédéfinises sont indiquées.Dans le domaine de la biologie :
Exemple1 : Valeurs de référence du cholestérol total chez l’homme Tableau 1 : Catégories et valeurs de référence du cholestérol total chez l’homme.
| Cholestérol total | catégorie |
| < 200 mg/dl | Souhaitable ou normal |
| 200 – 239 mg/dl | frontière |
| ≥ 240 mg/dl | haut |
Source : Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421
Exemple 2 : Valeurs de référence pour l’indice de masse corporelle (IMC).
L’IMC aide à définir le degré d’obésité d’une personne selon l’Organisation mondiale de la santé. En calculant et en interprétant l’IMC, il est possible de savoir si une personne est au-dessus ou en dessous des paramètres de poids recommandés pour sa structure physique. Pour calculer l’IMC, le poids mesuré en kg est divisé par la hauteur au carré (IMC = kg / m2).
Tableau 2 : Catégories et valeurs de référence de l’indice de masse corporelle
| catégorie | IMC (kg/m2) |
| Insuffisance pondérale | < 18,5 |
| Normal (poids santé) | 18,5 – 24,9 |
| Pré-obèses | 25,0 – 29,9 |
| Degré d’obésité I | 30,0 – 34,9 |
| Degré d’obésité II | 35,0 – 39,9 |
| Degré d’obésité III | ≥ 40,0 |
Source : World Health Organization. Obesity (1998): Preventing and managing the global epidemic: report of a WHO Consultation on Obesity, Geneva, 3–5 June 1997. Geneva (CH): World Health Organization; 1998. http://whqlibdoc.who.int/hq/1998/WHO_NUT_NCD_98.1_(p1-158).pdf.
Exemple 3 – Classification de l’hypertension artérielle.Tableau 3 : Classification de l’hypertension artérielle
| Classification de la pression artérielle | Pression artérielle sistolic (mmHg) | Pression artérielle diastolique (mmHg) |
| normal | < 120 | < 80 |
| Pré-hypertension | 120 – 139 | 80 – 89 |
| Hypertension de stade 1 (degré I) | 140 – 159 | 90 – 99 |
| Hypertension de stade 2 (degré II) | ³ 160 | ³ 100 |
Source : The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Cité par PEDROSA et DRAGER (2010).
Exemple 4 : L’acide urique résulte du métabolisme des purines, des principaux éléments structurels de l’ADN et de l’ARN, en grande partie à partir de nourriture. Une consommation excessive de viande ou d’alcool peut augmenter les niveaux d’acide urique dans le sang.
Les valeurs de référence sont en général de 40 à 60 mg/L pour les hommes, de 30 à 50 mg/L pour les femmes et de 25 à 40 mg/L pour les enfants (CAQUET, 2011).
Dans le domaine de l’économie :
Exemple 5 : L’Indice de développement humain (IDH) est une donnée statistique créée par le Programme des Nations Unies pour le développement (PNUD) pour contrer les données purement économiques utilisées pour mesurer la richesse des pays et analyser le développement en incluant d’autres facteurs.
Pour cette variable, les catégories suivantes sont normalisées en fonction de laquelle les pays sont divisés en fonction de leur IDH respectif :
Faible IDH : regroupe tous les pays dont l’IDH est inférieur à 0.500.
IDH moyen : pays dont l’IDH se situe entre 0.500 et 0.799.
IDH élevé : pays dont l’IDH se situe entre 0.800 et 0.899.
IDH très élevé : pays dont l’IDH est égal ou supérieur à 0.900.
Source: PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Disponible sur: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. acesso em Março, 25, 2020.
Les exemples cités ci-dessus montrent que les critères à base mathématique ne conviennent pas à toutes les situations. Dans la définition des classes pour construire une table de fréquences, les règles qui sont connues dans la littérature et présentées ici ne sont qu’indicatives. La définition des classes, ainsi que le nombre de classes, doivent d’abord être basées sur la connaissance du phénomène à l’étude et de ses objectifs. Il n’existe pas de formules qui s’appliquent correctement à toutes les situations. Même lorsque le nombre de classes résultant du calcul est égal au nombre de classes prédéfinis, les intervalles de classe ne correspondent pas aux valeurs prédéfinis. Et c’est exactement là que réside le problème. Les intervalles de classe sont des attributs quantitatifs qui doivent signifier une condition ou un état de la variable. Par exemple, une personne avec un taux de cholestérol de 260 mg/dl est malsaine, parce qu’elle a du cholestérol au-dessus de la normale. De même, un pays dont l’indice de développement humain est évalué en dessous de 0,5 est sous-développé, car il est sans aucun doute à faible IDH. Ainsi, le regroupement de données variables avec des catégories prédéfinises sans respecter ces mêmes catégories entraîne l’incapacité de lier la plage de classe à sa signification respective des valeurs de plage de classe. Ce manque de connexion entre le quantitatif (valeurs d’intervalle de classe) et le qualitatif (catégories variables) appauvrit l’interprétation des données et peut même déformer l’interprétation des données et conduire à des conclusions erronées.
Par conséquent, pour les variables ayant des catégories prédéfinis, le critère le plus approprié pour la construction de la distribution des fréquences est l’utilisation de ces catégories et de leurs valeurs respectives comme corps du tableau. Ce critère associe les valeurs des catégories aux attributs qualitatifs respectifs permettant une interprétation claire des données.
Lorsque les variables n’ont pas de catégories prédéfinis et épuisé la recherche d’indices ou d’indicateurs qui aident à créer les catégories, sans être par critère mathématique, il est suggéré ici l’utilisation de la théorie de la distribution normale de Gauss pour la catégorisation variable. Il s’agit de créer des catégories qui rendent plus perceptible le lien entre le quantitatif et le qualitatif et rendent l’interprétation des données plus perceptible.
La théorie de la distribution normale de Gauss, largement référencée dans la littérature (RICE et SCOTT, 2005), indique que pour un ensemble de données normales (symétriques, nonimodales), environ 68 % des données sont situées jusqu’à une unité d’écart type de la moyenne, environ 95 % des données sont situées jusqu’à deux unités d’écart type moyen et 99 % des données sont situées jusqu’à trois unités d’écart type moyen.
Tableau 4: Characterístics comme la distribuition normale
| ± 1S | 68% des données |
| ± 2S | 95% des données |
| ± 3S | 99% des données |
Source: adapté par Rice et Scott (2005)
Ainsi, il est établi comme critère pour la définition des catégories à partir de la théorie de la distribution normale, l’utilisation de la fourchette de variation de 68%, comme suit: Tableau 5: Base pour la catégorisation variable
| Nom de catégorie ou de classe | Valeur de catégorie ou de classe |
| Au-dessus de la moyenne | Ci-dessus ( + 1S) |
| Dans la moyenne | Entre (± 1S) |
| En dessous de la moyenne | Ci-dessous ( 1S ) |
Source: l’auteur.
Cette suggestion de catégorisation des variables est basée sur le calcul d’une mesure de la tendance centrale, de la moyenne et d’une mesure de la variabilité, l’écart type. Les valeurs qui sont à un écart type de la moyenne sont considérées comme proches de la moyenne, de sorte que la désignation de la catégorie « dans la moyenne » ou « autour de la moyenne » est suggérée. Les valeurs qui sont en dehors de cette fourchette sont considérées comme éloignées de la moyenne et les désignations « au-dessus de la moyenne » et « inférieures à la moyenne » sont suggérées respectivement. De cette façon, nous obtenons des catégories qui donnent un sens aux valeurs de la variable rendant l’interprétation des données plus claire.
Toutefois, la méthodologie proposée doit toujours être appliquée, en prenant soin des conditions spécifiques de chaque cas. 3 classes sont toujours obtenues, et si les données sont effectivement extraites d’une population normale, la deuxième classe aura une fréquence relative autour de 68% et les deux autres autour de 16% chacune, ce qui peut, dans certains cas, ne pas être souhaitable. D’autre part, s’il y a quelques/beaucoup d’observations atypiques dans les données ou si la distribution sous-jacente est biaisée, multimodale, la méthode en question ne produira pas les résultats souhaités. Quoi qu’il en soit, c’est un critère qui, bien considéré comme son application, peut contribuer à améliorer l’interprétation des données et donc la compréhension d’un certain phénomène.
2.2 DÉMONSTRATION DE LA CONSTRUCTION DE TABLES DE DISTRIBUTION DE FRÉQUENCES
2.2.1 COLLECTE DE DONNÉES
Dans le cadre d’un processus d’échantillonnage effectué pendant la période d’inscription aux examens d’accès à la Faculté des sciences de l’Université Agostinho Neto de Luanda – Angola, dans les années académiques 2008 et 2009, des données ont été obtenues, entre autres variables, de l’âge (exprimé en années), du poids (exprimé en kilogrammes) et de la hauteur (exprimée en mètres et centimètres) des candidats. La taille de l’échantillon était de 4298 sujets en 2008 et de 1749 sujets en 2009, soit un échantillon global de 6047 individus.
2.2.2 DISTRIBUTION SIMPLE DE FRÉQUENCES
Il s’agit de la représentation ci-dessous une table de distribution simple construite en utilisant les données de l’âge.
Tableau 6 : Répartition simple des fréquences des âges des personnes échantillonnées.
| Individus | ||
| agit | 2008 | 2009 |
| 16 | 45 | 6 |
| 17 | 142 | 24 |
| 18 | 365 | 131 |
| 19 | 458 | 217 |
| 20 | 672 | 223 |
| 21 | 605 | 256 |
| 22 | 507 | 240 |
| 23 | 431 | 207 |
| 24 | 320 | 129 |
| 25 | 198 | 92 |
| 26 | 152 | 74 |
| 27 | 91 | 31 |
| 28 | 64 | 31 |
| 29 | 55 | 15 |
| 30 | 51 | 19 |
| 31 | 31 | 11 |
| 32 | 18 | 11 |
| 33 | 8 | 4 |
| 34 | 20 | 6 |
| 35 | 11 | 3 |
| 36 | 12 | 2 |
| 37 | 8 | 1 |
| 38 | 6 | 2 |
| … | … | … |
Source: l’auteur
Le tableau 6, de la distribution simple des fréquences, montre son insuffisance aux fins de la synthèse de grandes quantités de données. La table est trop longue dans la verticale et surtout, elle ne permet pas la lecture des caractéristiques des données.
2.2.3 TABLEAU DE RÉPARTITION DES FRÉQUENCES DES CLASSES À DÉFINIR
L’âge est une variable qui, aux fins de l’analyse démographique, a des catégories prédéfines. Toutefois, à d’autres fins, cette définition des catégories peut ne pas être adéquate, comme c’est le cas pour l’analyse de l’âge des candidats à l’examen d’accès à l’Université. Dans ce cas particulier, l’objectif est d’évaluer la variabilité de l’âge du candidat, de déterminer le candidat ayant l’âge le plus élevé et le plus bas, respectivement, ainsi que d’analyser la variabilité des données. Il est important de savoir à quels intervalles l’âge de la plupart des candidats sont répartis afin de tirer des conclusions sur le profil des élèves qui terminent leurs études secondaires et qui sont donc des candidats potentiels à l’enseignement supérieur.
Aux fins de la démonstration, un sous-échantillon de 182 candidats a été retiré au hasard de l’échantillon global pour montrer comment la variable doit être catégorisée avant la construction de la distribution des fréquences.
Tableau 7 : Âge de 182 candidats inscrits aux examens à la Faculté des sciences de l’Université Agostinho Neto, au cours de l’année universitaire 2009.
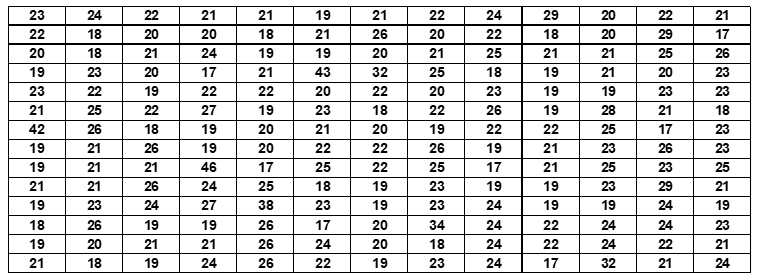
Pour ces 182 données, la moyenne est de 22 ans et l’écart type est de 4 ans. L’utilisation de la théorie normale de la distribution de Gauss pour la définition des catégories décrite à la section 2.1 entraîne la catégorisation suivante de la variable et de sa répartition respective des fréquences :
Tableau 8 : Categorizatio de l’âge des candidats
| Nom de catégorie ou de classe | Valeur de catégorie ou de classe |
| Au-dessus de la moyenne | > 26 (22 + 4) |
| Dans la moyenne | 18 – 26 (22 ± 4) |
| En dessous de la moyenne | < 18 (22 – 4) |
Sorcière: Auteur
Tableau 9 : Répartition des fréquences de l’âge de 182 candidats à l’examen d’accès.
| Âge (en années) | Nombre de candidats | |
| Au-dessus de la moyenne (> 26) | 13 | 7% |
| Dans la moyenne (18 – 26) | 162 | 89% |
| En dessous de la moyenne (< 18) | 7 | 4% |
Source: Auteur
Une fois que la théorie de Gauss est appliquée et que la table de distribution des fréquences est construite, son interprétation est maintenant facile et claire à faire. La répartition des fréquences montre que la majorité des 182 candidats, soit 89 % d’entre eux, sont âgés de 18 à 26 ans et sont considérés comme des candidats ayant un âge dans la moyenne. Le pourcentage de candidats au-dessus et en dessous de la moyenne est relativement résiduel, soit 7 % et 4 % respectivement. Cette information est d’une grande importance pour la direction de l’Université qui peut en tirer le meilleur parti pour ce qu’elle juge pratique.
2.2.4 DISTRIBUTION DE FRÉQUENCES EN UTILISANT DES CATÉGORIES PRÉDÉFINIS
Les valeurs de référence et les catégories respectives, normalisées et certifiées par la communauté scientifique mondiale par l’intermédiaire de l’Organisation mondiale de la santé (comme déjà décrit à la section 2.1) sont utilisées comme corps du tableau, ce qui entraîne la distribution de fréquences suivantes de l’indice de masse corporelle des candidats à l’examen d’accès dans les années scolaires de 2008 et 2009 :
Tableau 10 : Répartition de l’IMC des personnes échantillonnées.
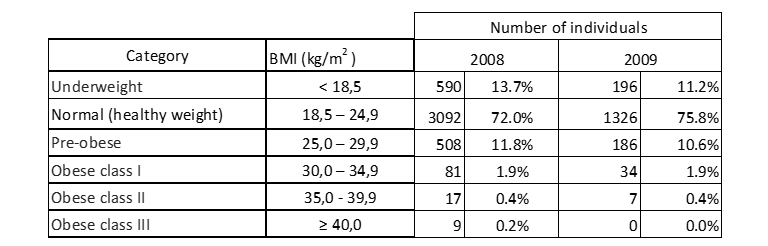
Le tableau 10 indique que la plupart des candidats, tant en 2008 qu’en 2009, ont un poids normal. Heureusement, le nombre de personnes atteintes d’obésité de degré III, et donc avec un grand risque pour la santé, est très faible en 2008 et inexistant l’année suivante.
2.2.5 UTILISATION DE CATÉGORIES PRÉDÉFINIES PAR RAPPORT À DES CRITÈRES MATHÉMATIQUES DANS LA CONSTRUCTION DES TABLEAUX DE RÉPARTITION DES FRÉQUENCES DE CLASSE
Il est montré ci-dessous l’insuffisance des critères mathématiques pour la construction de tableaux de distribution des fréquences des classes pour les variables avec des catégories prédéfinie.
Prenons les données de l’indice de masse corporelle pour l’année scolaire 2008, soit un total de 4 297 personnes. Si l’on examine les critères décrits au point 2.1, ceux qui établissent 6 comme nombre minimum de catégories (DAWSON et TRAPP, 2003) coïncident avec le nombre de catégories prédéfinis pour l’IMC. Une fois que le nombre de catégories est défini, la valeur maximale et la valeur minimale doivent être identifiées pour calculer l’amplitude totale, qui à son tour sera utilisée pour calculer l’intervalle de classe.
Tableau 11 : Statistiques sommaires des données échantillonnées
| Taille de l’échantillon | 4297 |
| Valeur maximale | 49 |
| Valeur minimale | 8 |
| Amplitude (maximum – minimum) | 41 |
| Nombre de classes ou de catégories | 6 |
| Plage de classe (Amplitude divisée par le nombre de catégories) | 6.8 |
Source: Auteur
Une fois la plage de classe déterminée, les limites de chacune des 6 catégories peuvent être finalement calculées. La limite inférieure de la 1ère catégorie est la valeur minimale et la limite supérieure de cette catégorie est obtenue en ajoutant la plage de classe. Il en va de même pour les autres catégories et le résultat suivant est obtenu :
Tableau 12 : Catégories de l’IMC et valeurs calculées.
| catégorie | Valeurs de l’IMC | |
| 1 | 8,0 | 16,2 |
| 2 | 16,3 | 24,5 |
| 3 | 24,6 | 32,8 |
| 4 | 32,8 | 41,0 |
| 5 | 41,0 | 49,2 |
Source: Auteur
Le tableau ci-dessous montre une comparaison entre les valeurs calculées et les valeurs prédéfinis.
Tableau 13 : Comparaison des valeurs prédéfinises avec les valeurs calculées.
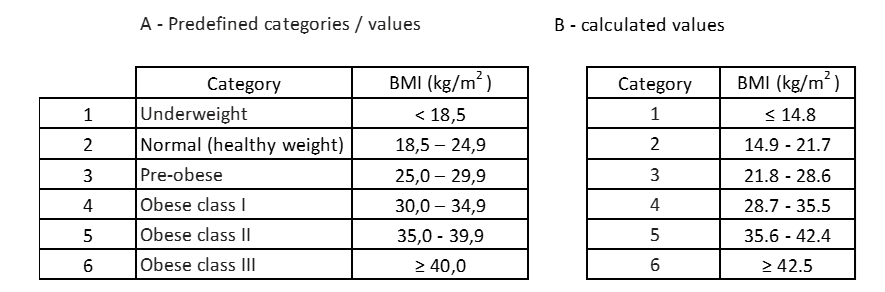
La première conclusion est que les catégories calculées n’ont pas leur propre désignation, c’est-à-dire qu’elles n’ont pas d’attributs qui qualifient la condition chez l’individu. La deuxième constatation, malgré le même nombre de catégories, les valeurs de catégorie chacune ne sont pas égales. Selon les catégories calculées, les personnes dont l’IMC se situe entre 14,9 et 21,7 seraient confondues avec un poids normal, alors qu’en fait certaines d’entre elles sont dans un état d’« insuffisance pondérale ».
3. CONSIDÉRATIONS FINALES
Les tableaux de distribution de fréquences sont des outils très utiles dans le traitement des données. Leur construction doit toutefois se conformer à certains critères scientifiquement valides. Il est essentiel de s’assurer que, quel que soit le critère adopté, la lecture interprétative des données conduit à des compréhensibles logiques et de conclusion sur le comportement de la variable. À cet égard, le lien entre les attributs quantitatifs et qualitatifs est crucial. Ainsi, le critère suggéré, basé sur l’utilisation de la théorie de la distribution normale de Gauss pour la catégorisation des variables, est tout à fait faisable.
Pour tout ce qui a été exprimé, il y a suffisamment de terrain pour introduire la différenciation des tableaux de distribution des fréquences de classe en deux types, c’est-à-dire des tableaux de fréquences de classes ou de catégories prédéfinies et des tableaux de fréquences de classes ou de catégories à définir, suggérant ainsi son adoption en tant que concept.
RÉFÉRENCES
BEIGUELMAN, Bernardo. Curso prático de bioestatística. 5ª Edição Revisada. FUNPEC Editora, 1994.
CAQUET, René. 250 Exames de Laboratório – Prescrição e Interpretação, 10ª Edição. Rio de Janeiro: Livraria e Editora Revinter, 2011. ISBN 978-85-372-0338-5
DAWSON, Beth & TRAPP, Robert Greig. Bioestatística básica e clínica. 3ª edição. McGraw-Hill Interamericana do Brasil, 2003. ISBN 85-86804-32-0
GRUNDY, Scott M. Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421 https://ci.nii.ac.jp/naid/10030733296/
KEYS, A., FIDANZA, F., KARVONEN, M. J., KIMURA, N., & TAYLOR, H. L. (1972). Indices of relative weight and obesity. Journal of chronic diseases 25 (6-7), 329-343.
KUZMA, Jan W. & BOHNENBLUST Stephen E. Basic Statistics for the Health Sciences. (Fourth ed.). New York: McGraw-Hill Higher Education 2001. ISBN 0-7674-1752-6
MILTON, Janet Susan. & TSOKOS, Janice Oseth. (1991). Estadistica para biologia y ciencias de la salud. Madrid: Interamericana McGraw-Hill – Madrid.
PEDROSA, Rodrigo Pinto and DRAGER, Luciano Ferreira. “Diagnóstico e classificação da hipertensão arterial sistêmica.” MedicinaNET [https://scholar.google.com/scholar] (2017).
PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Available on: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. Retrieved on March 25, 2020.
REIS, Elisabeth. Estatística descritiva. Edições Sílabo, 2005. Lisboa. ISBN 972-618362-6
RICE, Kathryn and SCOTT Paul. Carl Friedrich Gauss. Australian Mathematics Teacher 61.4 (2005): 2-5.
The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Cited in Pedrosa and Drager (2010).
TRIOLA, Marc M. & TRIOLA, Mario F. Bioestatistics for the biological and health sciences. Boston: Pearson Education, 2006. ISBN 0-321-19436-5
WORLD HEALTH ORGANIZATION. “Obesity: preventing and managing the global epidemic.” (2000). Google Scholar
[1] Docteur en sciences agricoles (Dr Sc Agr), agronome.
Soumis : Février 2021.
Approuvé : Mars 2021.


