ARTICOLO DI REVISIONE
VICTORINO, Samuel Carlos [1]
VICTORINO, Samuel Carlos. Un altro approccio nell’elaborazione di tabelle di frequenza utilizzando la teoria della distribuzione normale di GAUSS. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 06, Ed. 03, Vol. 07, pp. 139-154. marzo 2021. ISSN:2448-0959, collegamento di Access: https://www.nucleodoconhecimento.com.br/agronomia-it/tabelle-di-frequenza
ASTRATTO
La corretta organizzazione dei dati è di estrema importanza per l’analisi nel processo di inferenza statistica, finalizzata all’elaborazione di conclusioni valide e raccomandazioni generiche su un determinato argomento in esame. La letteratura scientifica specializzata descrive diverse procedure per l’organizzazione dei dati nelle tabelle di distribuzione delle frequenze. Tuttavia, non è spesso che si vengono fatte imprecisioni nell’uso degli strumenti di organizzazione dei dati. Queste imprecisioni hanno portato ad analisi distorte e conclusioni incongrue. Questo documento presenta un’analisi critica dei metodi e delle procedure dell’organizzazione dei dati descritti in letteratura, in particolare la distribuzione dei dati nelle tabelle di distribuzione delle frequenze e propone un approccio diverso nell’elaborazione delle tabelle di distribuzione delle frequenze delle classi. Per tutte le variabili con categorie predefinite, questi e i rispettivi valori di riferimento fungono da corpo della tabella. Per le variabili che non hanno categorie predefiniti, l’uso della teoria della distribuzione normale di Gauss come criterio per la categorizzazione è proposto e giustificato. Le categorie generate servono come corpo del tavolo. Si conclude che le tabelle di distribuzione delle frequenze possono essere distinte in due tipi, vale a dire tabelle di distribuzione delle frequenze di classi o categorie predefinite e tabelle di distribuzione delle frequenze di classi o categorie da definire, suggerendone così l’adozione come concetto.
Parole chiave: distribuzione normale, tabella di distribuzione della frequenza semplice, tabella di distribuzione della frequenza delle classi da definire.
1. INTRODUZIONE
Le statistiche, come scienza, sono riassunte in una serie di metodi e procedure che consentono la raccolta, l’organizzazione e la presentazione dei dati per la loro analisi, al fine di ottenere conclusioni valide e l’elaborazione di raccomandazioni generiche su una data popolazione studiata.
Le statistiche trovano applicazione nelle più diverse aree della conoscenza come economia, psicologia, sociologia, agricoltura e salute, aiutando nel processo decisionale basato sull’analisi dei dati. Affinché le statistiche adempiano a questo ruolo, è imperativo che i metodi e le procedure siano applicati correttamente. La raccolta dei dati comporta la corretta applicazione di metodi di campionamento che culminano nella selezione di campioni rappresentativi e garantiscono la validità dei dati e, allo stesso tempo, la validità degli studi; l’organizzazione e la presentazione dei dati mira alla semplificazione e compressione dei dati in tabelle di distribuzione delle frequenze, che si tratti di tabelle a frequenza singola o di tabelle di frequenza di classe. I dati riassunti nelle tabelle sono generalmente e, se del caso, visualizzati in grafici, diagrammi e altri strumenti statistici. La loro corretta organizzazione è di estrema importanza per l’analisi dei dati nel processo di inferenza statistica.
La letteratura scientifica specializzata descrive un’ampia gamma di procedure per l’organizzazione dei dati nelle tabelle di distribuzione delle frequenze. Si è riscontrato che spesso si impegnano imprecisioni nell’uso degli strumenti di organizzazione dei dati, con conseguente interpretazione distorta e conclusioni incongruenti. Questo articolo si propone di presentare un’analisi critica dei metodi e delle procedure dell’organizzazione dei dati descritti in letteratura, in particolare la distribuzione dei dati nelle tabelle di frequenza e propone un approccio diverso nell’elaborazione delle tabelle di distribuzione delle frequenze.
2 . QUADRO TEORICO DELLE TABELLE DI DISTRIBUZIONE DELLE FREQUENZE
La statistica è divisa in due gruppi principali: statistiche descrittive e statistiche inferenziali.
Statistiche descrittive è la parte che si occupa della descrizione, classificazione, organizzazione e presentazione dei dati di una variabile. Consente di riassumere i dati e aiuta a descrivere gli attributi di un dato gruppo di dati o di una popolazione attraverso il calcolo di misure descrittive come la media e la deviazione standard. Le tecniche descrittive tabulari e grafiche utilizzate con il supporto delle capacità grafiche dei moderni computer e dei vari software disponibili per rendere questo tipo di riassunto più fattibile e più comprensibile.
Le statistiche inferenziali, d’altra parte, sono responsabili dell’analisi dei dati al fine di ottenere conclusioni valide e l’elaborazione di raccomandazioni generiche sulla popolazione studiata.
2.1 TECNICHE DESCRITTIVE TABULARI E GRAFICHE
I dati grezzi di una variabile ottenuta in un processo di campionamento non consentono la visualizzazione di alcuna caratteristica del campione e molto meno della popolazione in esame. Pertanto, le tabelle e i grafici sono risorse statistiche essenziali nell’elaborazione dei dati.
Le tabelle consentono di riassumere e compattare una grande quantità di informazioni fornendo un’analisi chiara al ricercatore. I grafici sono il complemento della tabella che ha la funzione di trasmettere un’idea visiva del comportamento dei dati. C’è un’ampia varietà di grafici, tra cui grafici a linee, grafici a barre, grafici ad area e grafici a torta come i più comuni.Per quanto riguarda le tabelle di distribuzione delle frequenze, i seguenti tipi sono fondamentalmente diversi:
1 – Tabella di distribuzione a frequenza singola
2 – Tabella di distribuzione delle frequenze di classe
Una singola tabella di distribuzione delle frequenze contiene due colonne principali. Nella prima colonna ogni valore raccolto viene inserito in sequenza, una volta e in ordine crescente. Nella seconda colonna della riga corrispondente a ogni valore osservato viene inserito il numero di volte in cui questi valori vengono ripetuti nel set di dati, che corrisponde alla rispettiva frequenza assoluta.
La tabella di distribuzione della frequenza delle classi contiene anche due colonne, la prima per gli intervalli di classe della variabile e la seconda per il numero di individui appartenenti a ciascuna classe, o cioè la frequenza assoluta della classe.
Le tabelle di distribuzione a frequenza singola hanno il grave svantaggio di essere troppo lunghe, a causa del fatto che tutti i valori campionati devono essere elencati e, soprattutto, non consentono la lettura delle caratteristiche dei dati. Questo tipo di tabelle è del tutto inappropriato quando lo scopo è quello di riassumere grandi quantità di dati. Per questi casi, le tabelle di distribuzione della frequenza delle classi sono più adatte, in quanto compattano grandi quantità di dati in poche classi e collegano gli attributi quantitativi della variabile al significato corrente delle caratteristiche della variabile.
L’aspetto fondamentale nell’elaborazione delle tabelle di distribuzione delle frequenze di classe è la determinazione del numero di classi, in cui i dati saranno inquadrati. A questo scopo, diversi criteri per determinare il numero di classi sono descritti nella letteratura, la maggior parte dei quali sono strettamente matematici.
Milton e Tsokos (1991) indicano l’uso delle seguenti formule per determinare il numero di classi:
1 – Numero di classi = 5 x lg n dove n è la dimensione del campione
2 – Numero di classi =
Beiguelman (2002) indica che il numero di classi è compreso tra 8 e 20, a seconda dei dati. Per Dawson e Trapp (2003) 6 e 14 classi sono adeguate a fornire informazioni sufficienti senza dettagli eccessivi. Triola e Triola (2006) raccomandano che il numero di classi sia compreso tra 5 e 20, mentre Kuzma e Bohnenblust (2001) ritengono che il numero di classi dovrebbe essere compreso tra 5 e 15. Reis (2005) afferma che il numero di classi dovrebbe essere compreso tra 4 e 14 e suggerisce anche l’uso di una delle seguenti soluzioni:
1 – Numero di classi uguali 5 per campioni con dimensioni inferiori a 25 e numero di classi = per campioni con una dimensione uguale o superiore a 25.
2 – Utilizzare la formula Sturges: numero di classi = 1 + 3,22 n log
Quanto sopra mostra la varietà di criteri descritti nella letteratura per la costruzione di tabelle di distribuzione delle frequenze. Tuttavia, questi criteri hanno uno svantaggio comune che li rende inadatti come base per determinare il numero di classi di dati per determinate variabili, come variabili nel campo della biologia e delle scienze della salute, economia, industria, tra gli altri, che hanno categorie predefiniti, cioè categorie standardizzate. Alcune di queste variabili sono descritte di seguito e sono indicati i rispettivi valori di riferimento delle categorie predefiniti.Nel campo della biologia:
Esempio1: Valori di riferimento del colesterolo totale nell’uomo Tabella 1: Categorie e valori di riferimento del colesterolo totale nell’uomo.
| Colesterolo totale | categoria |
| < 200 mg/dl | Desiderabile o normale |
| 200 – 239 mg/dl | confine |
| ≥ 240 mg/dl | alto |
Fonte: Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421
Esempio 2: Valori di riferimento per l’indice di massa corporea (IMC).
L’IMC aiuta a definire il grado di obesità di una persona secondo l’Organizzazione Mondiale della Sanità. Calcolando e interpretando l’IMC è possibile sapere se una persona è al di sopra o al di sotto dei parametri di peso raccomandati per la propria struttura fisica. Per calcolare l’IMC, il peso misurato in kg è diviso per l’altezza al quadrato (BMI = kg / m2).
Tabella 2: Categorie e valori di riferimento dell’indice di massa corporea
| categoria | IMC (kg/m2) |
| sottopeso | < 18,5 |
| Normale (peso sano) | 18,5 – 24,9 |
| Pre-obesi | 25,0 – 29,9 |
| Classe Obesa I | 30,0 – 34,9 |
| Classe Obese II | 35,0 – 39,9 |
| Classe Obesa III | ≥ 40,0 |
Fonte: World Health Organization. Obesity (1998): Preventing and managing the global epidemic: report of a WHO Consultation on Obesity, Geneva, 3–5 June 1997. Geneva (CH): World Health Organization; 1998. http://whqlibdoc.who.int/hq/1998/WHO_NUT_NCD_98.1_(p1-158).pdf.
Esempio 3 – Classificazione dell’ipertensione arteriosa. Tabella 3: Classificazione dell’ipertensione arteriosa
| Classificazione della pressione sanguigna | Pressione sanguigna sistolica (mmHg) | Pressione sanguigna diastolica (mmHg) |
| normale | < 120 | < 80 |
| Pre-ipertensione | 120 – 139 | 80 – 89 |
| Fase 1 (grado I) ipertensione | 140 – 159 | 90 – 99 |
| Fase 2 (ii grado) ipertensione | ³ 160 | ³ 100 |
Fonte: The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Citato da PEDROSA e DRAGER (2010).
Esempio 4: L’acido urico è il risultato del metabolismo delle purine, dei principali elementi strutturali del DNA e dell’RNA, in gran parte dal cibo. Il consumo eccessivo di carne o alcol può aumentare i livelli di acido urico nel sangue.
I valori di riferimento sono in generale da 40 a 60 mg/L per gli uomini, da 30 a 50 mg/L per le donne e da 25 a 40 mg/L per i bambini (CAQUET, 2011).
Nel campo dell’economia:
Esempio 5: L’indice di sviluppo umano (ISU) è un dato statistico creato dal Programma delle Nazioni Unite per lo sviluppo (PNUS) per contrastare i dati puramente economici utilizzati per misurare la ricchezza del paese e analizzare lo sviluppo includendo altri fattori.
Per questa variabile sono standardizzate le seguenti categorie in base alle quali i paesi sono divisi in base al rispettivo ISU:
ISU basso: riunisce tutti i paesi con ISU inferiore a 0,500.
ISU medio: paesi con ISU compreso tra 0,500 e 0,799.
ISU alto: paesi con ISU compreso tra 0,800 e 0,899.
ISU molto alto: paesi il cui ISU è uguale o superiore a 0,900.
Fonte: PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. Recuperato il 25 marzo 2020.
Gli esempi sopra citati mostrano che i criteri con base matematica non sono adatti a tutte le situazioni. Nella definizione delle classi per costruire una tabella di frequenza, le regole che sono conosciute nella letteratura e presentate qui sono puramente indicative. La definizione delle classi, così come il numero di classi, devono prima basarsi sulla conoscenza del fenomeno in esame e dei suoi obiettivi. Non ci sono formule che si applicano correttamente a tutte le situazioni. Anche quando il numero di classi risultanti dal calcolo è uguale al numero di classi predefinite, gli intervalli di classi non corrisponderanno ai valori predefiniti. Ed è esattamente qui che risiede il problema. Gli intervalli di classi sono attributi quantitativi che devono significare una condizione o uno stato della variabile. Ad esempio, una persona con un livello di colesterolo di 260 mg / dl non è sana, perché ha colesterolo sopra il normale. Allo stesso modo, un paese con un indice di sviluppo umano valutato sotto 0,5 è sottosviluppato, in quanto è senza dubbio di basso ISU. Pertanto, il raggruppamento di dati variabili con categorie predefiniti senza rispettare queste stesse categorie comporta l’impossibilità di associare l’intervallo di classi al rispettivo significato dei valori dell’intervallo di classi. Questa mancanza di connessione tra i valori quantitativi (valori dell’intervallo di classe) e quelli qualitativi (categorie variabili) impoverisce l’interpretazione dei dati e può persino travisare l’interpretazione dei dati e portare a conclusioni errate.
Pertanto, per le variabili con categorie predefinite, il criterio più adatto per la costruzione della distribuzione delle frequenze è l’uso di queste categorie e dei rispettivi valori come corpo della tabella. Questo criterio associa i valori delle categorie ai rispettivi attributi qualitativi consentendo una chiara interpretazione dei dati.
Quando le variabili non hanno categorie predefinite ed esauriscono la ricerca di indizi o indicatori che aiutano a creare le categorie, senza essere per criterio matematico, si suggerisce qui l’uso della teoria della distribuzione normale di Gauss per la categorizzazione variabile. L’obiettivo è quello di creare categorie che perivolino di collegare il quantitativo al qualitativo e rendere più percettibile l’interpretazione dei dati.
La teoria della distribuzione normale di Gauss, ampiamente menzionata in letteratura (RICE e SCOTT, 2005), afferma che per un insieme di dati normali (simmetrici, unimodali), circa il 68% dei dati si trova fino a un’unità di deviazione standard della media, circa il 95% dei dati si trova fino a due unità di deviazione standard media e il 99% dei dati si trova fino a tre unità di deviazione standard media.
Tabella 4: La caratterizzazione come distribuzione normale
| ± 1S | 68% dei dati |
| ± 2S | 95% dei dati |
| ± 3S | 99% dei dati |
Fonte: adattato da Rice e Scott (2005)
Pertanto, è stabilito come criterio per la definizione di categorie dalla teoria della distribuzione normale, l’uso dell’intervallo di variazione del 68%, come segue: Tabella 5: Base per la categorizzazione variabile
| Nome categoria o grado | Valore di categoria o grado |
| Al di sopra della media | Sopra ( + 1S) |
| All’interno della media | Tra (± 1S) |
| Al di sotto della media | Di seguito ( 1S ) |
Fonte: l’autore.
Questo suggerimento di categorizzazione delle variabili si basa sul calcolo di una misura della tendenza centrale, della media e di una misura della variabilità, della deviazione standard. I valori che si trovano a una deviazione standard della media sono considerati vicini alla media, quindi viene suggerita la designazione della categoria “all’interno della media” o “intorno alla media”. I valori che non rientrano in questo intervallo sono considerati distanti dalla media e vengono suggerite rispettivamente le designazioni “sopra la media” e “al di sotto della media”. In questo modo otteniamo categorie che danno senso ai valori della variabile rendendo più chiara l’interpretazione dei dati.
Tuttavia, la metodologia proposta deve sempre essere applicata, curando le condizioni specifiche di ciascun caso. 3 classi sono sempre ottenute, e se i dati vengono effettivamente estratti da una popolazione normale, la seconda classe avrà una frequenza relativa intorno al 68% e le altre due circa il 16% ciascuna, il che potrebbe, in alcuni casi, non essere desiderabile. D’altra parte, se ci sono alcune / molte osservazioni atipiche nei dati o se la distribuzione sottostante è distorta, multimodale, il metodo in questione non produrrà i risultati desiderati. Ad ogni modo, è un criterio che, ben ponderato la sua applicazione, può contribuire a migliorare l’interpretazione dei dati e quindi la comprensione di un certo fenomeno.
2.2 CHE DIMOSTRA LA COSTRUZIONE DI TABELLE DI DISTRIBUZIONE DELLE FREQUENZE
2.2.1 RACCOLTA DATI
In un processo di campionamento svolto durante il periodo di iscrizione agli esami di accesso alla Facoltà di Scienze dell’Università Agostinho Neto di Luanda – Angola, negli anni accademici 2008 e 2009, sono stati ottenuti dati, tra le altre variabili, dall’Età (espressa in anni), dal peso (espresso in chilogrammi) e dall’altezza (espressa in metri e centimetri) dei candidati. La dimensione del campione è stata di 4298 soggetti nel 2008 e 1749 soggetti nel 2009 che hanno fatto un campione globale di 6047 individui.
2.2.2 DISTRIBUZIONE SEMPLICE DELLA FREQUENZA
È raffigurato sotto una semplice tabella di distribuzione costruita utilizzando i dati dell’età.
Tabella 6: Frequenza semplice Distribuzione dell’età degli individui campionati.
| Individui | ||
| Atti | 2008 | 2009 |
| 16 | 45 | 6 |
| 17 | 142 | 24 |
| 18 | 365 | 131 |
| 19 | 458 | 217 |
| 20 | 672 | 223 |
| 21 | 605 | 256 |
| 22 | 507 | 240 |
| 23 | 431 | 207 |
| 24 | 320 | 129 |
| 25 | 198 | 92 |
| 26 | 152 | 74 |
| 27 | 91 | 31 |
| 28 | 64 | 31 |
| 29 | 55 | 15 |
| 30 | 51 | 19 |
| 31 | 31 | 11 |
| 32 | 18 | 11 |
| 33 | 8 | 4 |
| 34 | 20 | 6 |
| 35 | 11 | 3 |
| 36 | 12 | 2 |
| 37 | 8 | 1 |
| 38 | 6 | 2 |
| … | … | … |
Fonte: l’autore
La tabella 6, della semplice distribuzione delle frequenze, mostra la sua inadeguatezza per riassumere grandi quantità di dati. La tabella è troppo lunga in verticale e, soprattutto, non consente la lettura delle caratteristiche dei dati.
2.2.3 TABELLA DI DISTRIBUZIONE DELLE FREQUENZE DELLE CLASSI DA DEFINIRE
L’età è una variabile che, ai fini dell’analisi demografica, ha categorie predefiniti. Tuttavia, per altri scopi, questa definizione di categorie potrebbe non essere adeguata, come nel caso dell’analisi dell’età dei candidati all’esame di accesso per l’Università. In questo caso particolare, l’obiettivo è valutare la variabilità dell’età del candidato, determinare il candidato con l’età più alta e più bassa, rispettivamente, nonché analizzare la variabilità dei dati. È importante sapere a quali intervalli viene distribuita l’età della maggior parte dei candidati al fine di trarre conclusioni sul profilo degli studenti che terminano la scuola secondaria e quindi sono potenziali candidati all’istruzione superiore.
A scopo dimostrativo, un sottocampo di 182 candidati è stato ritirato casualmente dal campione globale per mostrare come la variabile deve essere classificata prima della costruzione della distribuzione delle frequenze.
Tabella 7: Età di 182 candidati iscritti agli esami presso la Facoltà di Scienze dell’Università Agostinho Neto, nell’anno accademico 2009.
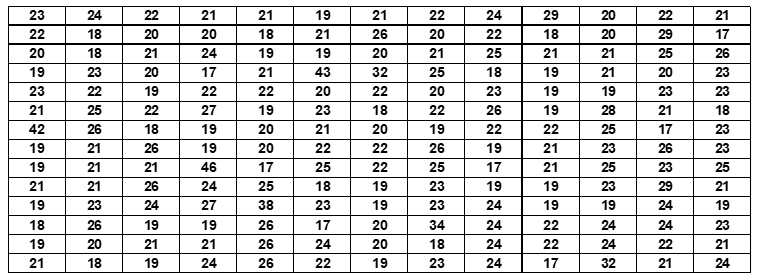
Per questi 182 dati la media è di 22 anni e la deviazione standard è di 4 anni. L’uso della teoria della distribuzione normale di Gauss per la definizione delle categorie come descritto nella sezione 2.1 si traduce nella seguente categorizzazione della variabile e della sua rispettiva distribuzione di frequenza:
Tabella 8: Categorizatio dell’età dei candidati
| Nome categoria o classe | Valore di categoria o classe |
| Al di sopra della media | > 26 (22 + 4) |
| All’interno della media | 18 – 26 (22 ± 4) |
| Al di sotto della media | < 18 (22 – 4) |
Sorce: Autore
Tabella 9: Distribuzione in frequenza dei candidati all’esame di accesso di età superiore ai 182 anni.
| Età (in anni) | Numero di candidati | |
| Sopra la media (> 26) | 13 | 7% |
| All’interno della media (18 – 26) | 162 | 89% |
| Al di sotto della media (< 18) | 7 | 4% |
Fonte: Autore
Una volta applicata la teoria di Gauss e costruita la tabella di distribuzione delle frequenze, la sua interpretazione è ora facile e chiara da fare. La distribuzione delle frequenze mostra che la maggior parte dei 182 candidati, che rappresentano l’89% di essi, hanno dai 18 ai 26 anni e sono considerati candidati con un’età all’interno della media. La percentuale di candidati superiori e inferiori alla media è relativamente residuale, rispettivamente del 7% e del 4%. Queste informazioni sono di grande importanza per la gestione dell’Università che può sfruttarla al meglio per ciò che ritiene conveniente.
2.2.4 DISTRIBUZIONE DELLE FREQUENZE MEDIANTE CATEGORIE PREDEFINITE
I valori di riferimento e le rispettive categorie, standardizzati e certificati dalla comunità scientifica mondiale attraverso l’Organizzazione Mondiale della Sanità (come già descritto nella sezione 2.1) sono utilizzati come corpo della tabella, risultando nella seguente distribuzione di frequenza dell’Indice di Massa Corporea dei candidati all’esame di accesso negli anni accademici 2008 e 2009:
Tabella 10: Distribuzione dell’IMC degli individui campionati.
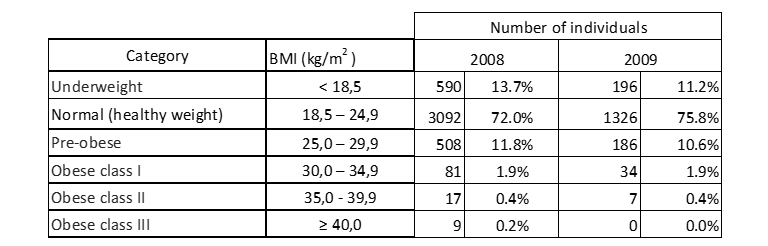
La tabella 10 indica che la maggior parte dei candidati, sia nel 2008 che nel 2009, ha un peso normale. Fortunatamente, il numero di persone con obesità di classe III, e quindi con un grande rischio per la salute, è molto basso nel 2008 e inesistente nell’anno successivo.
2.2.5 USO DI CATEGORIE PREDEFINITI RISPETTO A CRITERI MATEMATICI NELLA COSTRUZIONE DI TABELLE DI DISTRIBUZIONE DELLE FREQUENZE DI CLASSE
Si mostra qui di seguito l’inadeguatezza dei criteri matematici per la costruzione di tabelle di distribuzione delle frequenze di classi per variabili con categorie predefinite.
Si consideri i dati dell’indice di massa corporea per l’anno accademico 2008, per un totale di 4297 individui. Esaminando i criteri descritti al punto 2.1, quelli che stabiliscono 6 come numero minimo di categorie (DAWSON e TRAPP, 2003) coincidono con il numero di categorie predefinite per l’IMC. Una volta definito il numero di categorie, è necessario identificare il valore massimo e il valore minimo per calcolare l’ampiezza totale, che a sua volta verrà utilizzata per calcolare l’intervallo di classe.
Tabella 11: Statistiche sommarie dei dati campionati
| Dimensione del campione | 4297 |
| Valore massimo | 49 |
| Valore minimo | 8 |
| Ampiezza (massimo – minimo) | 41 |
| Numero di classi o categorie | 6 |
| Intervallo di classi (ampiezza divisa per il numero di categorie) | 6.8 |
Fonte: Autore
Una volta determinato l’intervallo di classi, i limiti di ciascuna delle 6 categorie possono essere infine calcolati. Il limite inferiore della prima categoria è il valore minimo e il limite superiore di questa categoria si ottiene aggiungendo l’intervallo di classi. Lo stesso vale per le altre categorie e si ottiene il seguente risultato:
Tabella 12: Categorie dell’IMC e loro valori calcolati.
| categoria | Valori BMI | |
| 1 | 8,0 | 16,2 |
| 2 | 16,3 | 24,5 |
| 3 | 24,6 | 32,8 |
| 4 | 32,8 | 41,0 |
| 5 | 41,0 | 49,2 |
Fonte: Autore
La tabella seguente mostra un confronto tra i valori calcolati e i valori predefiniti.
Tabella 13: Confronto dei valori predefiniti con i valori calcolati.
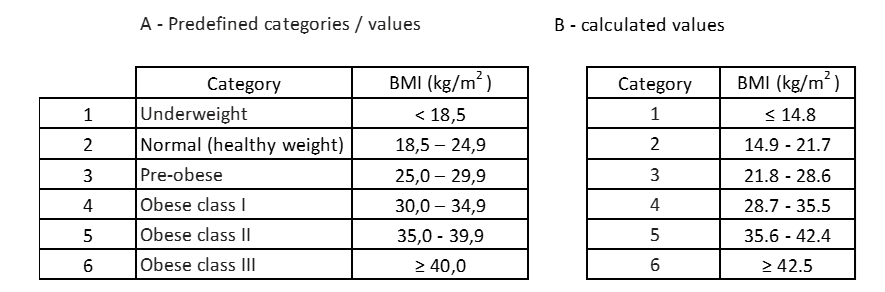
La prima constatazione è che le categorie calcolate non hanno una propria designazione, cioè non hanno attributi che qualificano la condizione nell’individuo. La seconda constatazione, nonostante lo stesso numero di categorie, i valori della categoria ciascuno non sono uguali. Per le categorie calcolate, gli individui con un IMC compreso tra 14,9 e 21,7 sarebbero scambiati per avere un peso normale, quando in realtà alcuni di loro sono in condizioni di “sottopeso”.
3. CONSIDERAZIONI FINALI
Le tabelle di distribuzione delle frequenze sono strumenti molto utili nell’elaborazione dei dati. La loro costruzione deve tuttavia rispettare determinati criteri scientificamente validi. È essenziale garantire che, indipendentemente dal criterio adottato, la lettura interpretativa dei dati porti a comprensibili logiche e conclusioni sul comportamento della variabile. A questo proposito, il legame tra attributi quantitativi e qualitativi è cruciale. Quindi, il criterio suggerito, basato sull’uso della teoria della distribuzione normale di Gauss per la categorizzazione delle variabili, è abbastanza fattibile.
Per tutto ciò che è stato espresso, c’è abbastanza terreno per introdurre la differenziazione delle tabelle di distribuzione delle frequenze delle classi in due tipi, cioè tabelle di frequenze di classi o categorie predefiniti e tabelle di frequenze di classi o categorie da definire, suggerendo così la sua adozione come concetto.
RIFERIMENTI
BEIGUELMAN, Bernardo. Curso prático de bioestatística. 5ª Edição Revisada. FUNPEC Editora, 1994.
CAQUET, René. 250 Exames de Laboratório – Prescrição e Interpretação, 10ª Edição. Rio de Janeiro: Livraria e Editora Revinter, 2011. ISBN 978-85-372-0338-5
DAWSON, Beth & TRAPP, Robert Greig. Bioestatística básica e clínica. 3ª edição. McGraw-Hill Interamericana do Brasil, 2003. ISBN 85-86804-32-0
GRUNDY, Scott M. Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Final report. Circulation, 2002, 106:3143–3421 https://ci.nii.ac.jp/naid/10030733296/
KEYS, A., FIDANZA, F., KARVONEN, M. J., KIMURA, N., & TAYLOR, H. L. (1972). Indices of relative weight and obesity. Journal of chronic diseases 25 (6-7), 329-343.
KUZMA, Jan W. & BOHNENBLUST Stephen E. Basic Statistics for the Health Sciences. (Fourth ed.). New York: McGraw-Hill Higher Education 2001. ISBN 0-7674-1752-6
MILTON, Janet Susan. & TSOKOS, Janice Oseth. (1991). Estadistica para biologia y ciencias de la salud. Madrid: Interamericana McGraw-Hill – Madrid.
PEDROSA, Rodrigo Pinto and DRAGER, Luciano Ferreira. “Diagnóstico e classificação da hipertensão arterial sistêmica.” MedicinaNET [https://scholar.google.com/scholar] (2017).
PENA, Rodolfo F. Alves. “Como é feito o cálculo do IDH?”; Brasil Escola. Available on: https://brasilescola.uol.com.br/geografia/desenvolvimento-humano.htm. Retrieved on March 25, 2020.
REIS, Elisabeth. Estatística descritiva. Edições Sílabo, 2005. Lisboa. ISBN 972-618362-6
RICE, Kathryn and SCOTT Paul. Carl Friedrich Gauss. Australian Mathematics Teacher 61.4 (2005): 2-5.
The seventh report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. JAMA 2003; 289: 2560-72. Cited in Pedrosa and Drager (2010).
TRIOLA, Marc M. & TRIOLA, Mario F. Bioestatistics for the biological and health sciences. Boston: Pearson Education, 2006. ISBN 0-321-19436-5
WORLD HEALTH ORGANIZATION. “Obesity: preventing and managing the global epidemic.” (2000). Google Scholar
[1] Dottorato in Scienze Agrarie (Dr Sc Ag), Agronomo.
Inviato: Febbraio 2021.
Approvato: Marzo 2021.