Aplicação do método de bound contraction para problemas de programação não linear inteira mista contendo bilinearidade

ARTIGO ORIGINAL

PEDROZA, Ivone Cristina Barros ^[1], CARVALHO, Esdras Penêdo de ^[2], RAVAGNANI, Mauro Antônio da Silva Sá ^[3]

PEDROZA, Ivone Cristina Barros. CARVALHO, Esdras Penêdo de. RAVAGNANI, Mauro Antônio da Silva Sá. Aplicação do método de bound contraction para problemas de programação não linear inteira mista contendo bilinearidade. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 05, Vol. 12, pp. 56-75. Maio de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/metodo-de-bound, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/metodo-de-bound

RESUMO

Neste trabalho aplicou-se o método de bound contraction para problemas com formulação MINLP (mixed integer nonlinear programming). Os problemas a serem abordados são aqueles que contêm termos bilineares. A maioria dos solucionadores de otimização global, usam como recurso reduzir o espaço de busca através do limite das variáveis. A metodologia de particionamento utilizada neste trabalho tem por finalidade gerar modelos, que garantem limites cada vez menores do problema. Os resultados obtidos foram satisfatórios, pois, o método utilizado reduziu a distância entre o limite inferior e o limite superior e gerou solução para o ótimo global para cada caso analisado.

Palavras-chave: bound contraction, termo bilinear, otimização.

1. INTRODUÇÃO

Programação matemática é uma área caracterizada pelo uso de modelos matemáticos, em especial os modelos de otimização. A otimização refere-se ao estudo de problemas em que se busca encontrar os máximos ou mínimos de uma função através da escolha de valores reais, ou inteiros dentro de um conjunto viável. A otimização utiliza técnicas e algoritmos para solucionar problemas modelados matematicamente.

O campo da programação matemática é amplo e suas técnicas consagraram-se em face a sua grande utilidade na solução de problemas de otimização (GOLDBARG e LUNA, 2005). A otimização tem várias aplicações nas mais diversas áreas como, por exemplo, na pesquisa operacional, na engenharia de processos, no controle de processos, no controle ótimo ou adaptativo, na regressão ou na solução de sistemas lineares, em redes de distribuição de água ou redes de distribuição de gás em cidades, entre outras aplicações.
Alguns modelos matemáticos apresentam restrições como, por exemplo, o produto de duas variáveis. Esse produto forma termos bilineares que são não convexos e de difícil resolução, apresentando várias soluções locais.

Os termos bilineares aparecem em sistemas de energia hidrelétrica, em descarga e armazenamento de água Garcia et. al. (2007); Catalão (2011), nos problemas de escalonamento dos sistemas de eletricidade Kolodziej et. al. (2013), no planejamento do sistema de tratamento de águas poluídas (MEYER; FLOUDAS, 2006) entre outras.
A finalidade de um problema de otimização, contendo bilinearidade é encontrar soluções ótimas globais. Existem vários métodos de calcular a solução ótima global para um determinado modelo matemático como, por exemplo, o método denominado de Bound Contraction. A ideia principal desse método é contrair os limites de uma variável por vez com o intuito de diminuir a distância entre o limite inferior e o limite superior. Neste trabalho apresenta-se a técnica de otimização global que tem por base o método de Bound Contraction proposto por Faria e Bagajewicz (2011a), para problemas MINLP contendo bilinearidade.

Zamora e Grossmann (1999), apresentaram um algoritmo para problemas contendo termos bilineares e fracionários bem como funções côncavas e univariadas. Aplicaram o método de bound contraction nas variáveis, uma de cada vez em cada nó. Para o modelo de limite inferior usaram subestimadores do tipo McCormick (1976), para os termos bilineares e fracionários, e subestimadores lineares para as funções côncavas. A solução do limite superior é encontrada maximizando ou minimizando cada um dos valores sujeitos à linearização.

O algoritmo de otimização global para problemas MINLP com termos bilineares, côncavos e univariados, proposto por Faria e Bagajewicz (2011b), foi aplicado a problemas de gerenciamento de água. O particionamento das variáveis com termos bilineares foi baseado no método de bound contraction. Os resultados foram comparados com os resultados de outros métodos de otimização global como discretização direta e McCormick (1976). Geralmente, o desempenho do bound contraction foi superior aos demais métodos.

Faria e Bagajewicz (2012), apresentam uma abordagem para problemas MINLP contendo termos bilineares. A metodologia utilizada para o particionamento das variáveis do termo bilinear foi o bound contraction baseado na discretização da variável, para construir os estimadores do limite inferior. Com base nessa informação, utiliza-se o valor do limite inferior para executar o problema MINLP original. Sendo assim, o processo será repetido com novos limites até que os limites não possam mais ser contraídos. Constatou-se que, em todos os casos testados identificou-se o ótimo global.

O objetivo principal deste trabalho é aplicar o método de bound contraction para problemas com formulação MINLP (mixed integer nonlinear programming) para obtenção do ótimo global, assim como, reduzir a distância entre o limite inferior e o limite superior.

Os problemas a serem abordados são aqueles que contêm termos bilineares na restrição. Aplicou-se o método para três problemas de minimização. Cada problema contendo uma função objetivo, duas restrições de desigualdade e limites para as variáveis de decisão. As restrições de desigualdades serão representadas da seguinte forma: a primeira delas será uma função linear e a segunda será representada por uma função bilinear.

O artigo está organizado da seguinte forma: inicialmente apresentamos a metodologia de relaxação, o algoritmo de bound contraction, em seguida a definição do problema e por fim os estudos de caso.

2. DESENVOLVIMENTO

2.1 METODOLOGIA

A metodologia de relaxação que iremos apresentar baseia-se em gerar modelos que garantem limites cada vez menores do problema, ou seja, permite gerar modelos com uma distância cada vez menor entre o limite superior e o limite inferior do problema. A metodologia aqui apresentada foi proposta por Faria e Bagajewicz (2011a), baseada na contração do limite para as restrições bilineares. Ao contrário de alguns métodos baseados em particionamento da variável, esse procedimento de bound contraction que iremos apresentar não introduz novos inteiros ou intervalos.

Considerar, z_ij, como sendo o produto de duas variáveis contínuas, sendo x_i e y_j:

z_ij = x_iy_j, ∀i = 1, 2, …, n; ∀j = 1, 2, …, m      (1)

em que: x_i e y_j estão sujeitos a certos limites:

A equação (1) será substituída pelas duas desigualdades seguintes:

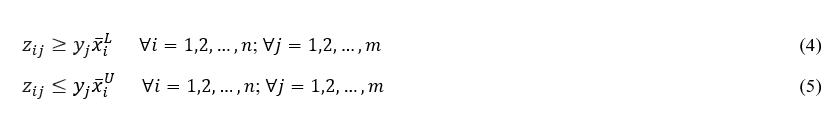
Considere:os limites inferior e superior atualizados para o problema relaxado.

A equação (1) é substituída pela relaxação das equações (4) e (5), com isso, o problema proposto é LP (ou MILP caso haja variáveis inteiras ou binárias). Seja, os resultados do limite inferior e superior do problema relaxado e o valor de z_ij. Em seguida, definir os valores de referência, da seguinte maneira:

Assumir que, é uma estimativa melhor de x_i do que . Ainda na metodologia de relaxação é introduzida a noção de distância inferior e superior para os limites da seguinte forma:

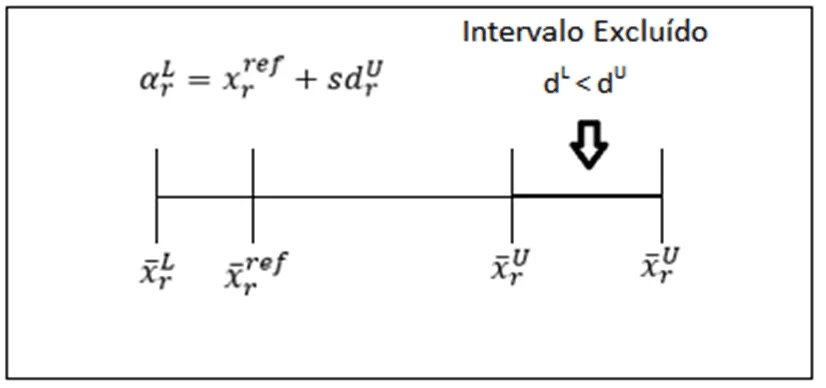
Os valores do x de referência, são calculados depois que o limite inferior é obtido usando o modelo relaxado. A Figura 1, mostra o intervalo excluído do bound contraction, quando , os valores de referência estão mais próximos do limite inferior, então a contração ocorre no limite superior. Quando isso acontece calcula-se o valor de

Figura 1: Intervalo excluído para bound contraction quando

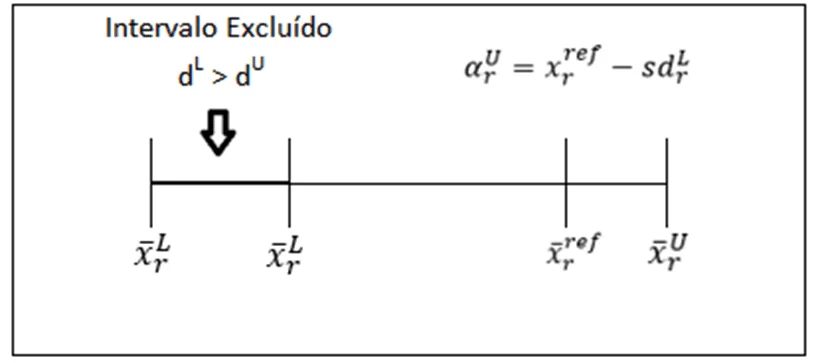
O caso contrário está representado na Figura 2, mostra o intervalo excluído do bound contraction, quando , os valores de referência estão mais próximos do limite superior, a contração ocorre no limite inferior. Então, calcula-se .

Figura 2: Intervalo excluído para bound contraction quando

2.2 ALGORITMO DE OTIMIZAÇÃO GLOBAL – BOUND CONTRACTION

O método de bound contraction consiste em contrair os limites de uma variável por vez permitindo, assim, reduzir a distância entre o limite inferior e o limite superior. A seguir apresentaremos o algoritmo de bound contraction, baseado em Faria e Bagajewicz (2011a):

1. Supor:

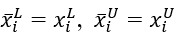
Sabendo que: = limite inferior atualizado

= limite superior atualizado
Definir ϵ=0,2;

2. Executar o modelo de limite inferior relaxado LB (do inglês Lower Bound) relaxando os termos bilineares, conforme a metodologia de relaxação apresentada anteriormente. O modelo LB é executado obtendo valores para as variáveis, , valor da função objetivo S(x, y) e o valor de referência ;

3. Executar o modelo de limite superior UB (do inglês Upper Bound) utilizando como estimativa inicial os valores de, , calculados no passo anterior, para o problema MINLP. Caso a resposta seja inviável podemos testar algum problema específico para o limite superior, como por exemplo, usar o limite superior da iteração anterior;

4. Calcular as distâncias d_i^L e d_i^U. Determinar o índice r = i. Se ir para o passo “5”. Caso contrário ir para o passo “6”;

5. Executar o modelo linear auxiliar inferior ALB_r^L para diferentes valores de s(∆s), até que o problema seja inviável ou a função objetivo seja maior do que o incumbente[4]. Atualizar o limite superior para, . Ir para o passo 7;

6. Executar o modelo linear auxiliar superior ALB_r^U para diferentes valores de s(∆s), até que o problema seja inviável ou a função objetivo seja maior do que o incumbente. Atualiza-se o limite inferior para, . Ir para o passo 7;

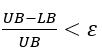7. Se (tolerância) ∀ i∈I ou (tolerância) FIM. Caso contrário, ir para o passo 8;

8. Se nenhuma resposta viável for encontrada no passo anterior dividir o problema em subproblemas e repetir os passos de 1 até 7 para cada subproblema.

2.3 DEFINIÇÃO DO PROBLEMA

O algoritmo de bound contraction foi implementado no software computacional Matlab versão R2018b e no software Gams (General Algebraic Modeling System) versão 31.2. Ambos foram implementados em um computador com processador Intel(R), CORE(TM) i7, de 3.6GHz de 8GB de memória RAM. O software matlab e o gams é um ambiente de programação de alto nível, especializado e otimizado para cálculos científicos e de engenharia. Para a implementação desse algoritmo no matlab foram utilizados os solvers linprog, resolve problemas de programação linear e fmincon, resolve problemas de programação não linear. No Gams foi usado o otimizador GAMS/CONOPT.

O exemplo que apresentaremos trata-se da minimização de uma função objetivo cujas variáveis de decisão estão sujeitas a certas restrições, que podem ser de igualdade ou desigualdade, no nosso caso, uma dessas desigualdades irá conter um termo bilinear.

O procedimento de bound contraction pode ser implementado para ambas as variáveis da bilinearidade, para este trabalho vamos considerar a contração apenas na variável x do termo bilinear.

Aplicaremos o método de bound contraction para um problema de minimização contendo uma função objetivo, duas restrições de desigualdades e limites para as variáveis de decisão x e y. As restrições de desigualdades serão representadas da seguinte forma: a primeira delas será uma função linear do tipo Ax + By ≤ k, ∀k ∈ R o gráfico é uma reta que passa pela origem; a segunda restrição será representada pelo termo bilinear do tipo g(x) y ≤ k, ∀k ∈ R o gráfico é estritamente decrescente em (0,+∞) e em (-∞,0) e não é definida para g(x) = 0. Observe que um termo bilinear pode ser reescrito como uma função recíproca, ou seja, y = k/g(x), ∀k ∈ R, ∀g (x) ≠ 0.

O método será analisado para três casos, considerando que, cada caso será representado por um termo bilinear distinto em uma das restrições de desigualdade, porém a função objetivo e umas das restrições de desigualdade foram as mesmas para os três casos.

2.3.1 FORMULAÇÃO MATEMÁTICA DO PROBLEMA

Nesta seção será apresentada a formulação matemática do problema de minimização. Na formulação apresentada abaixo, S (x, y) é a função objetivo, x e y são as variáveis de decisão, g(x) y representa o termo bilinear, x^L e x^U são os limites inferior e superior da variável x e y^L e y^U são os limites inferior e superior da variável y.

min⁡ S(x,y)

sujeito a:

Considera-se a função objetivo S(x, y) = -4x – y, uma restrição de desigualdade 0,64x – y ≤ 0 e os seguintes termos bilineares correspondentes aos casos de 1 a 3: (e^x) y ≤ 4, (lnx) y ≤ 4 e (x²) y ≤ 4.

3. RESULTADOS E DISCURSÕES

3.1 ESTUDO DE CASOS

O objetivo desse estudo é encontrar o ótimo global, para cada caso usando o método de bound contraction. Seja uma função, F: X ⊆ Rⁿ → R. Diz-se que, x^* é considerado um mínimo global de F, se F (x^*) ≤ F(x) ∀x ∈ X e x^* é um mínimo local de F se existe ϵ > 0, tal que F (x^*) ≤ F(x) ∀x ∈ X tal que ‖x-x^*‖ < ϵ. De modo geral, uma função pode ter muitos mínimos locais e um mínimo global.

A ideia principal é encontrar uma variável, x^* ∈ Rⁿ que minimize a função objetivo S(x, y), e que atenda as restrições de desigualdade apresentadas pelo problema.

Os casos, a seguir, foram baseados no exemplo proposto por Faria e Bagajewicz (2011a), o exemplo consiste em um problema de minimização. Os resultados obtidos foram: ótimo global para o problema original x = 2,5 e y = 1,6 função objetivo S(x, y) = -11,6 gerados na segunda iteração tendo com estimativa inicial x = 3,2 e y = 8, o ótimo local x = 0,5 e y = 8 função objetivo S(x, y) = -10 gerados na primeira iteração. Ao final de cada iteração o limite superior é atualizado, até que o critério de parada seja satisfeito. Na terceira iteração acha-se que nenhuma contração para o limite superior foi possível, então tentou-se contrair o limite inferior resolvendo o Modelo Linear Auxiliar Superior ALB^U, dessa forma, atualiza-se o limite inferior para x^{– L}_r = 0,51. O processo continuou por mais algumas iterações até que a diferença entre o limite superior e o limite inferior foi menor que a tolerância. Conclui-se que o método de bound contraction diminuiu a distância entre o limite inferior e o limite superior e apresentou solução para ótimo global.

3.1.1 CASO 1

O primeiro caso estudado está representado pelo seguinte problema de minimização:
Solução do modelo

Inicialmente aplica-se a metodologia de relaxação, detalhada anteriormente, então temos o modelo de limite inferior LB:

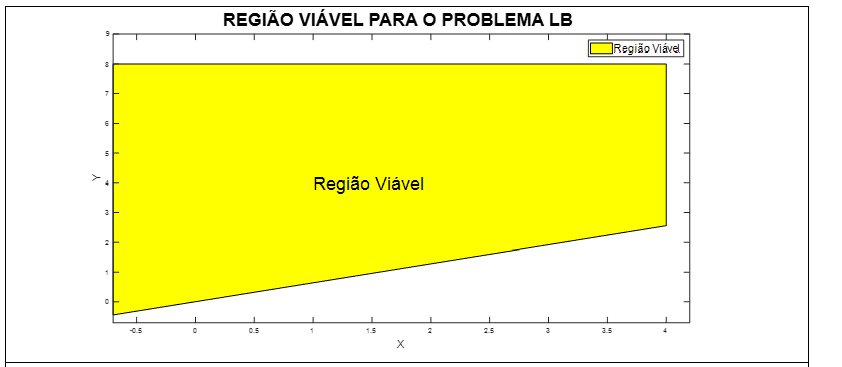
A Figura 3, representa a região viável do problema LB para a 1a iteração. A solução encontrada foi: (x, y) = (4, 8), função objetivo S(x, y) = -24 e z = 0,49. Utilizam-se esses valores como estimativa inicial para o cálculo do limite superior UB. Obtém-se o mínimo local em x = -0,69 e y = 8, função objetivo S(x, y) = -5,23.

Figura 3: Região viável do problema LB para 1a iteração

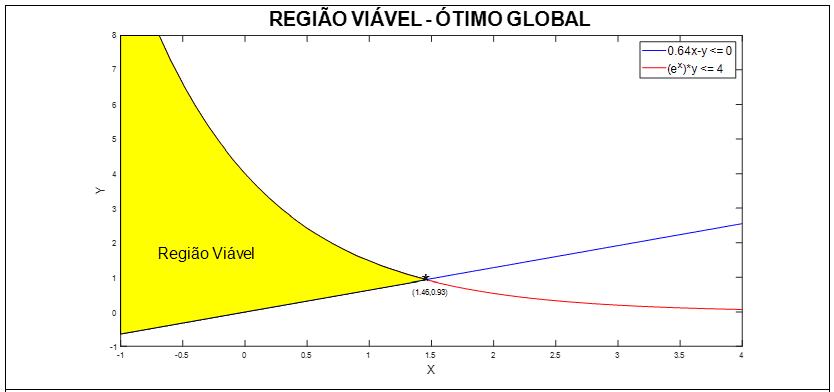
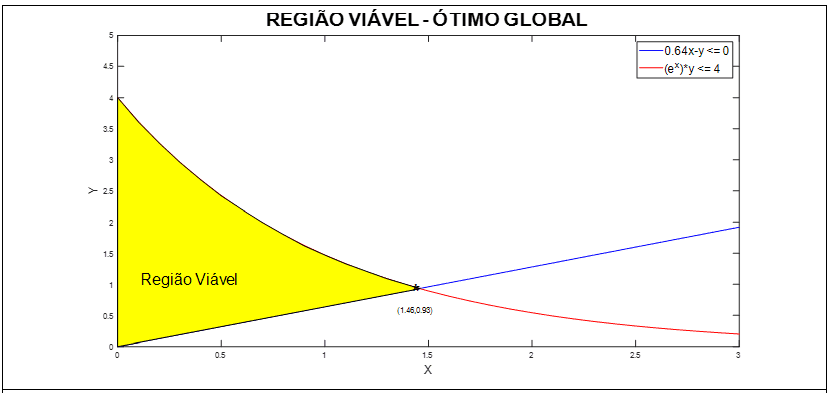
A região viável e ponto de ótimo global para o problema MINLP está representado na Figura 4, em x = 1,46 e y = 0,93 com o valor da função objetivo S(x, y) = -6,76. O ótimo global foi encontrado tendo como estimativa inicial os valores de x = 3,2 e y = 8.

Figura 4: Região viável – ótimo global do problema original

Em seguida, calculam-se os valores de referência, e as distâncias . Observa-se, que , quando isso acontece o está mais perto do , então calcula-se o Modelo Linear Auxiliar Inferior ALB^L, caso contrário calcularíamos o Modelo Linear Auxiliar Superior ALB^U. Define-se que s pode variar de 0 até 1 com ∆s = 0,2, calcula-se o valor de . O modelo ALB^L pode ser escrito da seguinte forma:

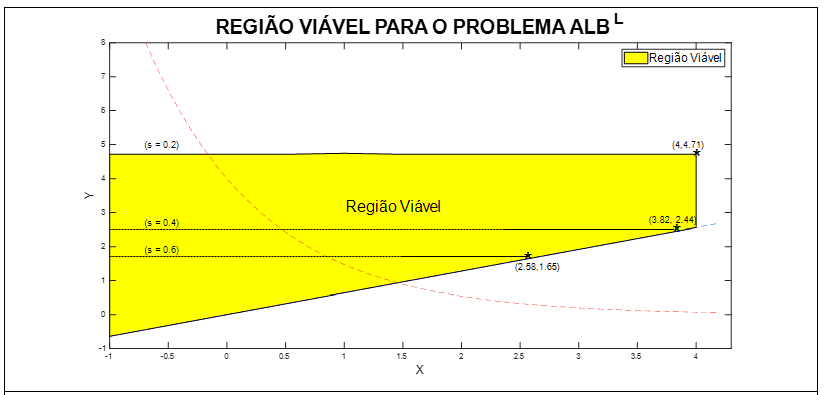
A Figura 5, ilustra a região viável para o problema ALB^L. Foram obtidos os seguintes valores para as variáveis de decisão: s = 0,2 corresponde a, x = 4 e y = 4,71, para s = 0,4 temos, x = 3,82 e y = 2,44, e finalmente para s = 0,6 os valores apresentados foram x = 2,58 e y = 1,65, com seus respectivos valores para a função objetivo S(x, y) = -20, 71, -17, 72 e -11,96. Para s = 0,8 nenhum ponto viável foi encontrado.

Figura 5: Região viável do problema ALB^L para 1^a iteração

Como a tolerância proposta, ϵ = 0,2, não é satisfeita, recorre-se a calcular um novo LB. A solução encontrada para o modelo de limite inferior LB para a 2^a iteração foi x = 3,2 e y = 8 para as variáveis, valor da função objetivo S(x, y) = -20,85 e o valor z = 0,49. Mais uma vez, com os resultados acima calcula-se o x de referência , e as distâncias d_i^L = 0,76 e d_i^U = 3,15, como  está mais perto do calcula-se o Modelo Linear Auxiliar Inferior ALB^L.

A região viável para o problema ALB^L para a 2^a iteração está representada na Figura 6, os valores para as variáveis são: x = 3,2 e y = 5,78 para o s = 0,2 a função objetivo corresponde S(x, y) = -18,63; para s = 0,4 temos, x = 3,2 e y = 3,03 correspondendo ao seguinte valor da função objetivo S(x, y) = -15,88 e para o s = 0,6, temos x = 3,2 e y = 2,05 e S(x, y) = -14,86. Para s = 0,8 o problema é inviável.

Figura 6: Região viável do problema ALB^L para 2^a iteração

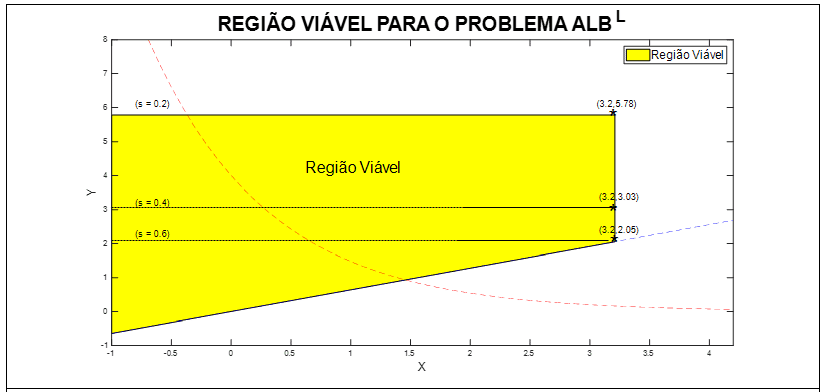
Foram realizadas mais duas iterações, os resultados estão representados na Tabela 1. Na quinta iteração acha-se que nenhuma contração para o limite superior é possível, então tentamos contrair o limite inferior resolvendo o Modelo Linear Auxiliar Superior ALB^U dessa forma atualiza-se o limite inferior para .

Tabela 1: Resultados numéricos para o caso 1, obtidos pelo método de bound contraction

O processo continua por mais algumas iterações até que a diferença entre o limite superior e o limite inferior seja menor que a tolerância. A partir da segunda iteração os limites começam a ser contraídos, pois, a cada passagem pelo passo 5 ou 6, proposto no algoritmo, os limites são atualizados gerando novos limites para a próxima iteração.
Para o caso 1, foi analisado também o seguinte intervalo, x ∈ [0, 3] e y ∈ [0, 5]. A Figura 7, ilustra a região viável e ponto de ótimo global para o problema original em x = 1,46 e y = 0,93 com o valor da função objetivo S(x, y) = -6,76. Para este intervalo não foi encontrado o ponto de ótimo local.

Figura 7: Região viável – ótimo global do problema original

Observe que um dos componentes do termo bilinear é uma função exponencial de base e. Veja que o gráfico interceptou o eixo y no ponto de ordenada y = 4, a curva representativa está acima do eixo dos x, pois y = e^x > 0, são alguns aspectos da função exponencial. As soluções apresentadas foram as mesmas tanto o software matlab como para o gams.

3.1.2 CASO 2

Para o segundo caso, utilizou-se o seguinte termo bilinear (lnx) y ≤ 4. O termo bilinear é composto pelo logaritmo de x na base e, também chamado de logaritmo natural de x ou logaritmo neperiano. O problema de minimização foi analisado com o seguinte intervalo x ∈ [0, 6] e y ∈ [0, 7].

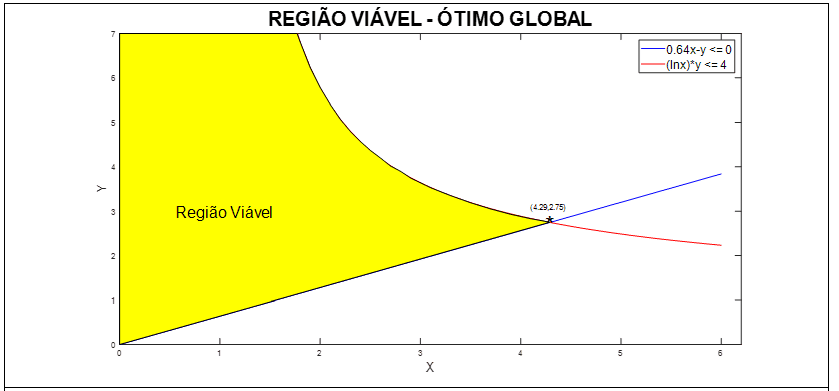
A solução do problema LB para a 1a iteração foi (x, y) = (6, 7), função objetivo S(x, y) = -31 e z = 0, esses valores foram utilizados como estimativa inicial para o cálculo do ponto de ótimo global. A Figura 8, ilustra a região viável e ótimo global para o problema original cujo valores são: x = 4,29 e y = 2,75 com o valor da função objetivo S(x, y) = -19,91. A solução para o ótimo local foi x = 1,77 e y = 7 função objetivo S(x, y) = -14,08.

Figura 8: Região viável – ponto de ótimo global do problema original

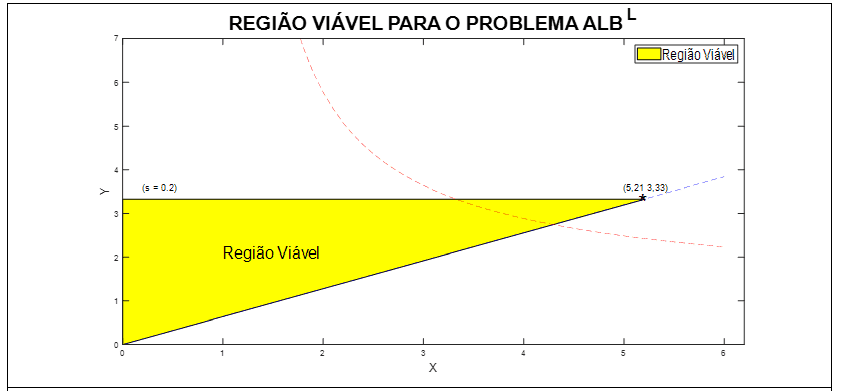
Observa-se claramente que o valor do x de referência é igual a zero e que a distância inferior é menor que a distância superior, então calcula-se o Modelo Linear Auxiliar Inferior ALB^L. A Figura 9, mostra a região viável para o problema ALB^L. Foram obtidos os seguintes valores para s = 0,2 corresponde a, x = 5,21 e y = 3,33, função objetivo S(x, y) = -24,17 para s = 0,4, 0,6 e 0,8 nenhum ponto viável foi encontrado. Ao final da primeira iteração o limite superior foi atualizado para .

Figura 9: Região viável do problema ALB^L para 1^a iteração

O algoritmo realizou apenas uma iteração, a partir da segunda iteração acha-se que nenhuma contração é mais possível para o limite superior, com isso, tentamos contrair o limite inferior resolvendo o Modelo Linear Auxiliar Superior ALB^U atualiza-se o limite inferior para . O processo continua por mais sete iterações até que a diferença entre o limite superior e o limite inferior seja menor que a tolerância.

Analisou-se também, para este caso, o seguinte intervalo x ∈ [0, 4] e y ∈ [0, 7], a solução encontrada foi o mínimo local (1,77, 7) função objetivo S(x, y) = -14,08 na segunda iteração tendo como estimativa inicial x = 2,4 e y = 7, porém não foi apresentado uma solução para o ótimo global. Os resultados foram os mesmos para ambos os softwares utilizados.

3.1.3 CASO 3

O termo bilinear para o terceiro caso, foi (x²) y ≤ 4. O procedimento utilizado para calcular o ótimo global foi o mesmo utilizado para os casos anteriores. Os intervalos analisados para este problema de minimização foram x ∈ [0, 3,5] e y ∈ [0, 6].

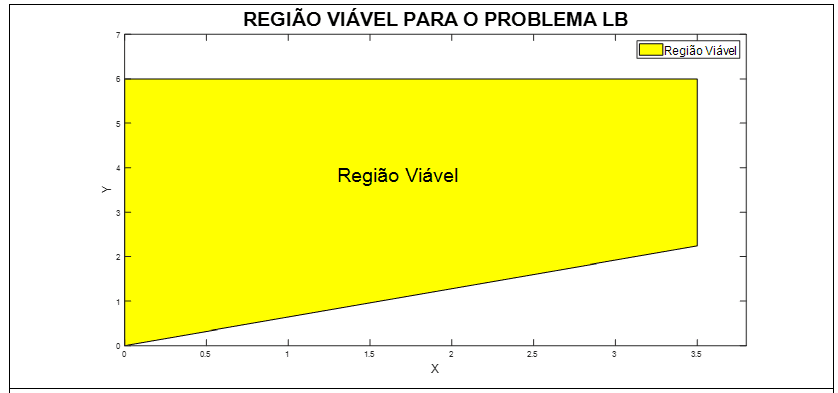
A Figura 10, mostra a região viável do problema LB para a primeira iteração. A solução apresentada foi: x = 3,5 e y = 6, função objetivo S(x, y) = -21. Esses valores foram utilizados como estimativa inicial para o cálculo do modelo de limite superior UB, e obtém-se o mínimo local em x = 0,82 e y = 6 para as variáveis de decisão e a função objetivo
S(x, y) = -9,27.

Figura 10: Região viável – problema LB para a 1^a iteração

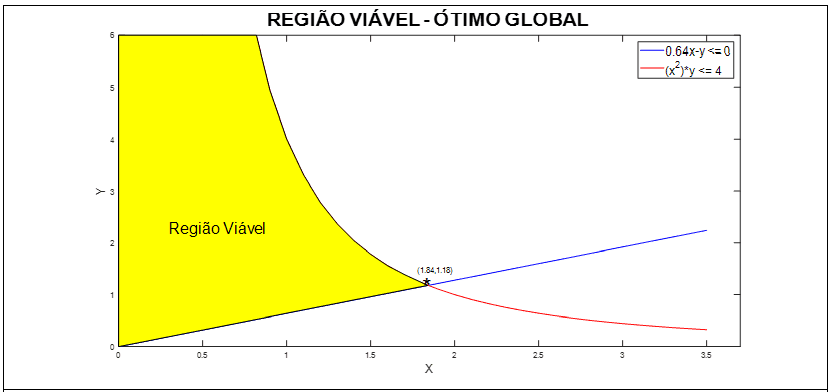
O ótimo global foi encontrado na segunda iteração. A Figura 11, mostra a região viável e ótimo global para o problema original cujo valores são x = 1,84 e y = 1,18 com o valor da função objetivo S(x, y) = -8,55.

Figura 11: Região viável – problema LB para a 1^a iteração

Os valores do x de referência será o mesmo para todas as iterações, ou seja, 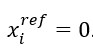. Foram realizadas duas iterações, os resultados para o modelo de limite inferior e para o modelo linear auxiliar inferior estão representados na Tabela 2. Observe que ao final da primeira iteração o limite superior foi atualizado para  e na segunda iteração para . Na terceira iteração acha-se que o limite superior não pode mais ser contraído, então tentou-se contrair o limite inferior resolvendo o Modelo Linear Auxiliar Superior ALB^U, atualiza-se o limite inferior para .

Tabela 2: Resultados numéricos para o caso 3, obtidos pelo método de bound contraction

O processo atingiu um total de quatorze iterações até que diferença entre o limite superior e o limite inferior foi menor que tolerância. Na décima quarta iteração, o critério de parada foi satisfeito sendo 0,09 a diferença entre o limite superior e o limite inferior. Os resultados foram os mesmo para ambos os softwares utilizados.

4. CONCLUSÃO

Neste trabalho, foi proposto a resolução de problemas MINLP contendo termos bilineares na restrição. Como esses problemas são não linear e de difícil resolução, optamos por utilizar o método de bound contraction para a obtenção do ótimo global e reduzir a distância entre o limite inferior e o limite superior. Neste caso, em particular, o que torna esses problemas de difícil solução é a bilinearidade apresentada na restrição. Assim, os estudos de casos propostos, foram implementados nos softwares computacionais Matlab versão R2018b e o Gams versão 31.2, foram utilizados os solvers comerciais linprog e fmincon, e o otimizador GAMS/CONOPT respectivamente.

Conclui-se que o método de bound contraction, aplicado para problemas contendo termo bilinear na restrição, obteve resultados satisfatórios, pois apresentou solução para o ótimo global. Em todos os casos analisados o algoritmo gerou modelos com uma distância cada vez menor entre o limite inferior e o limite superior, com isso, garantindo limites cada vez menores para o problema.

REFERÊNCIAS

CATALÃO, J. P. S., POUSINHO, H. M. I. and MENDES, V. M. F. Hydro energy systems management in Portugal: Profit-based evaluation of a mixed-integer nonlinear approach. Energy, v. 36, p. 500-507, 2011.

FARIA, D. C., BAGAJEWICZ, M. J. Novel bound contraction procedure for global optimization of bilinear MINLP problems with applications to water mangement problems. Computers and Chemical Engineering, v. 35, p. 446-455, 2011a.

FARIA, D. C., BAGAJEWICZ, M. J. Global optimization of water manegement problems using linear relaxation and bound contraction methods. Industrial e Engineering Chemistry Research, v. 50, p. 3738-3753, 2011b.

FARIA, D. C. and BAGAJEWICZ, M. J. A new approach for global optimization of a class of minlp problems with applications to water management and pooling problems. AIChE J. v. 58, 8a ed., p. 2320–2335, 2012.

GARCÍA-GONZÁLEZ, J., PARRILLA, E and, MATEO, A. Risk-averse profit-based optimal scheduling of a hydro-chain in the day-ahead electricity market. European Journal of Operational Research, v. 18, p. 1354-1369 2007.

GOLDBARG, M. C.; LUNA, H. P. L. Otimização combinatória e programação linear modelos e algoritmos. 2a ed. Rio de Janeiro: Elsevier, 2005.

KOLODZIEJ, S. P., GROSSMANN, I. E, FURMAN, K. C. and SAWAYA, N. W. A Discretization based Approach for the Optimization of the Multiperiod Blend Scheduling Problem. Computers and Chemical Engineering, v. 53, p. 122-142, 2013.

MCCORMICK, G. P. Computability of global solutions to factorable nonconvex programs. Part I. Convex underestimating problems. Mathematical Programming, v. 10, p. 147-175, 1976.

MEYER, C. A.; FLOUDAS, C. A. Global optimization of a combinatorially complex generalized pooling problem. AIChE American Institute of Chemical Engineers, Washington, v. 52, n. 3, p. 1027-1037, 2006.

ZAMORA, J. M. and GROSSMANN, I. E. A branch and contract algorithm for problems with concave univariate, bilinear and linear fractional terms. Journal Global Optimizzation. v. 14; p. 217–249, 1999.

APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ

4. Incumbente é a melhor solução até, então encontrada.

^[1] Doutoranda em Engenharia Química, Mestre em Matemática aplicada a Meteorologia, Especialista em Ensino de Matemática Básica, Graduada em Matemática.

^[2] Doutor em Engenharia Elétrica, Mestre em Ciências da Computação e Matemática, Especialista em Estatística Aplicada e Graduado em Engenharia Química.

^[3] Orientador. Doutor em Engenharia Química, Mestre em Engenharia Química e Graduado em Engenharia Química.

Enviado: Março, 2021.

Aproado: Maio, 2021.