61ARTIGO ORIGINAL
SAMPAIO JUNIOR, Cloves Rocha [1]
SAMPAIO JUNIOR, Cloves Rocha. Metodologia do círculo trigonométrico isométrico polar cartesiano no software GeoGebra demonstrando a racionalidade da constante π. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 08, Ed. 08, Vol. 05, pp. 61-109. Agosto de 2023. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/circulo-trigonometrico, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/circulo-trigonometrico
RESUMO
O artigo apresentará modelos matemáticos demonstrando cálculos das relações e proporções do círculo trigonométrico do círculo periódico infinito, utilizando o software GeoGebra no plano cartesiano, isométrico e polar, e considerando o primeiro quadrante do ciclo trigonométrico para os cálculos das funções das identidades trigonométricas, e os mesmos cálculos de raciocínio para os outros quadrantes. As relações e proporções infinitamente entre os perímetros das circunferências e seus diâmetros, os ângulos (arcos radianos) das circunferências, raízes quadradas. A mais antiga constante universal da matemática, envolvida em simetrias circulares, caminhos circulares de estrelas e planetas, na propagação de campos eletromagnéticos, círculos e esferas e suas relações e proporções são todas aproximadas. Seu relacionamento pode ser conhecido exatamente ou devemos limitar-nos apenas às aproximações dos cálculos do número π. Esse procedimento pode ser calculado com a ajuda da computação, e tentar obter seu valor racional e periódico com régua e compasso, só levará à frustração. A demonstração realizada no software GeoGebra, por meio de modelos matemáticos no plano cartesiano, isométrico e polar, demonstram aos cálculos interligados e teoremas das relações e proporções com valores racionais e periódicos das somas infinitas dos cálculos racionais periódicos do número π(pi) (BECKMANN, 1971).
Palavras-chave: Número π(pi), Círculo trigonométrico, Ângulos radianos, Polígonos.
1. INTRODUÇÃO
Estudo da matemática responsável pela relação e proporção existente entre os lados e ângulos de um triângulo retângulo, eles têm valores fracionários conhecidos representados para as relações de seno, cosseno, tangente, cotangente, cossecante, secante. Do século 15 para a modernidade dos cálculos e a criação de situações teóricas relacionadas aos estudos dos ângulos das funções dos cálculos diferencial e integral, pelos cientistas Isaac Newton e Leibniz, com métodos definitivos no cenário da matemática, sendo constantemente empregados em outras ciências, Medicina, Engenharia, Física, Química, Geografia, Astronomia, Biologia, Cartografia, Navegação.
2. DESENVOLVIMENTO
2.1 CIRCUNFERÊNCIA TRIGONOMÉTRICA NO PLANO CARTESIANO
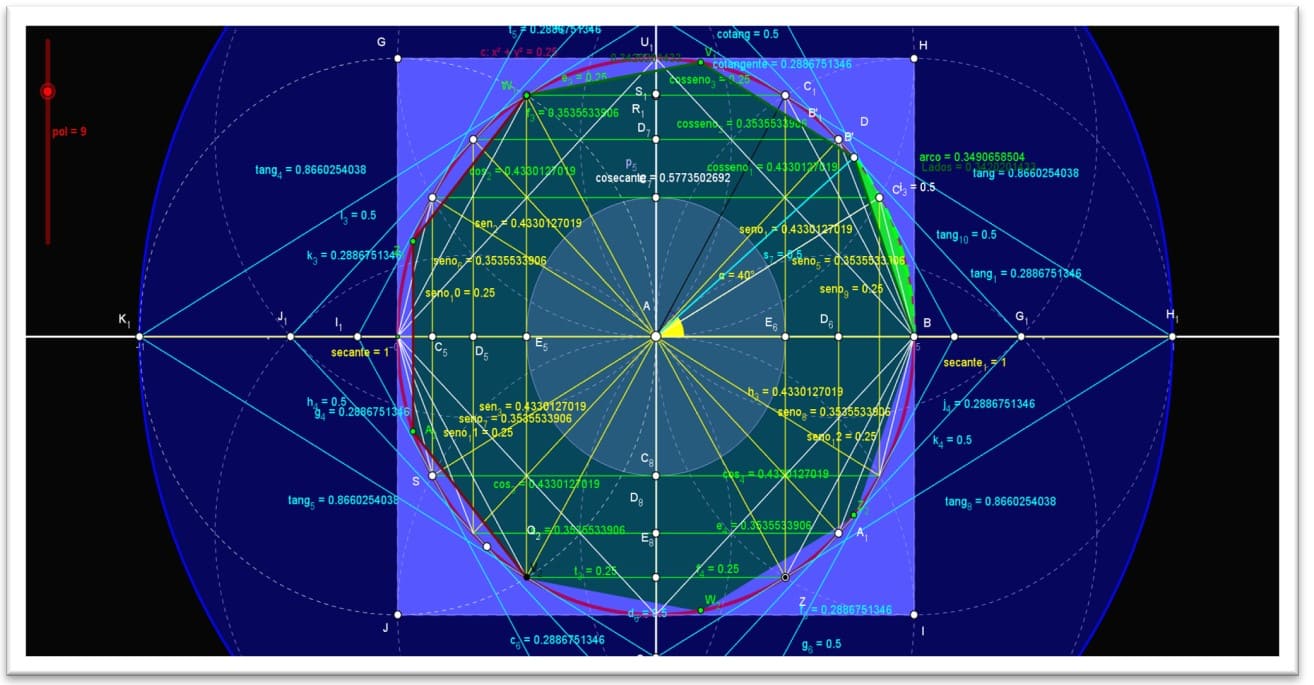
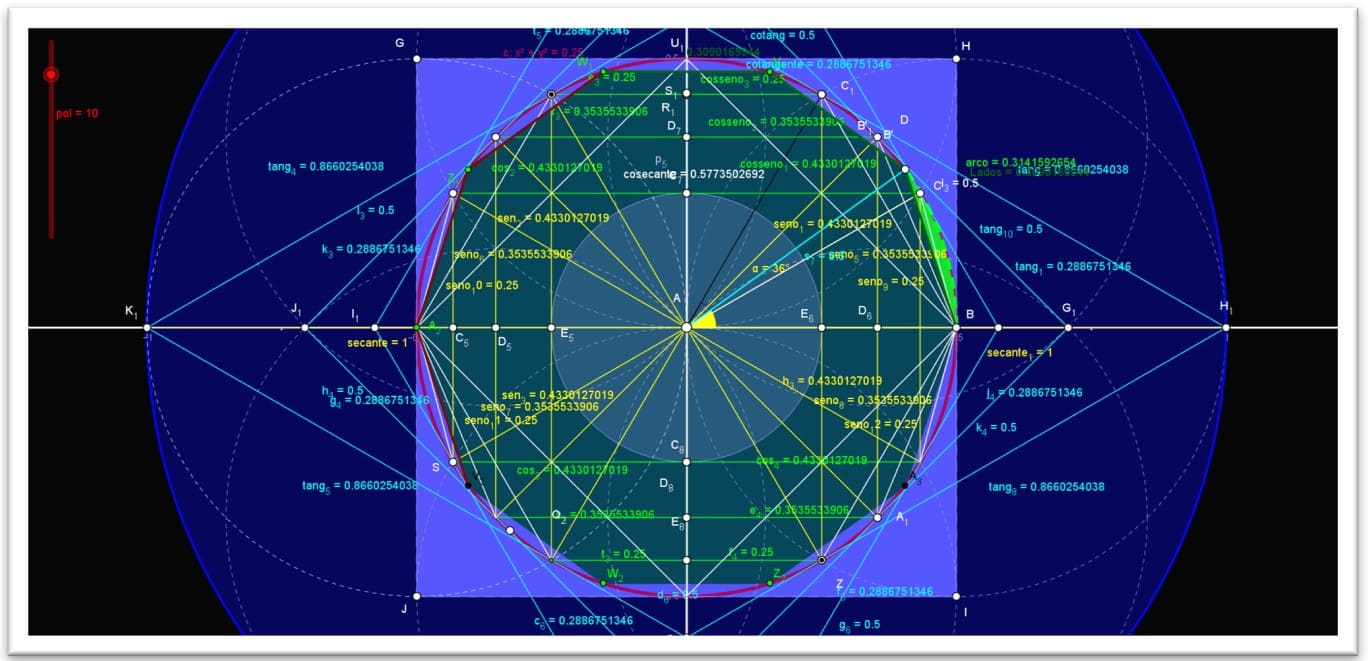
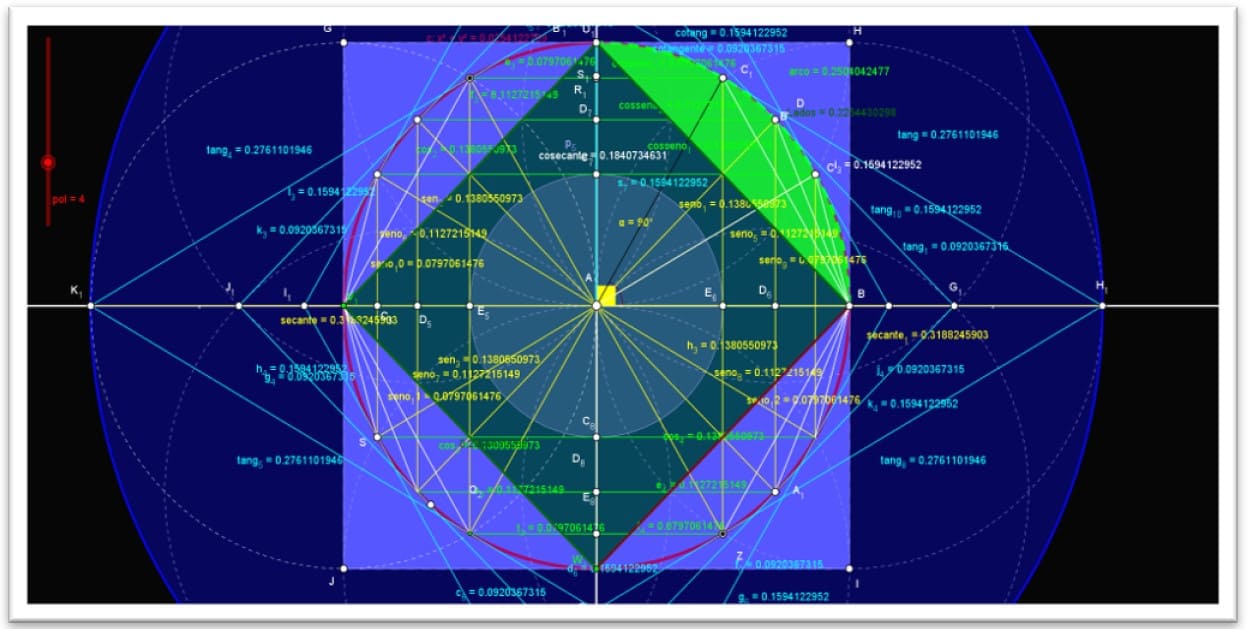
O sistema cartesiano ortogonal, consideremos o ponto A (0,1) do eixo A(x), de abscissa igual a 1. Construímos então, com centro na origem O (0,0) do sistema, uma circunferência que passa por A, de raio unitário. Vamos convencionar que o ponto A, será a origem dos arcos orientados dessa circunferência, isto é, que para percorrer estes arcos, o ponto A, será sempre o ponto de partida. Assim, dado um plano α, um ponto O (0,0), é uma distância Raio (r), temos: C: x 2 + y2 =IR (reais).
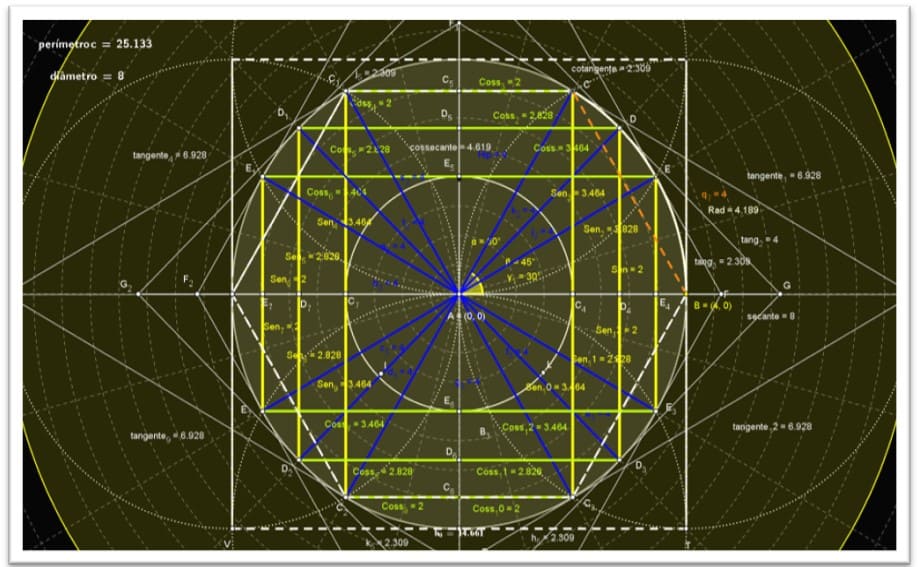
Figura 1. Demonstração do círculo trigonométrico no plano cartesiano raio=1
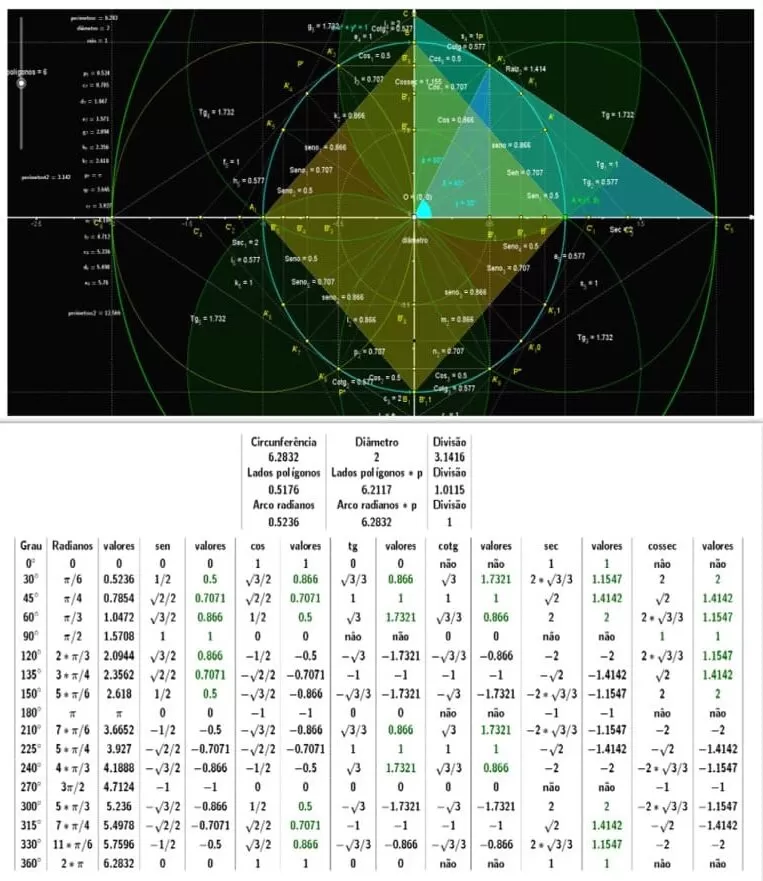
Figura 2. Demonstração do círculo trigonométrico no plano cartesiano raio=0,5
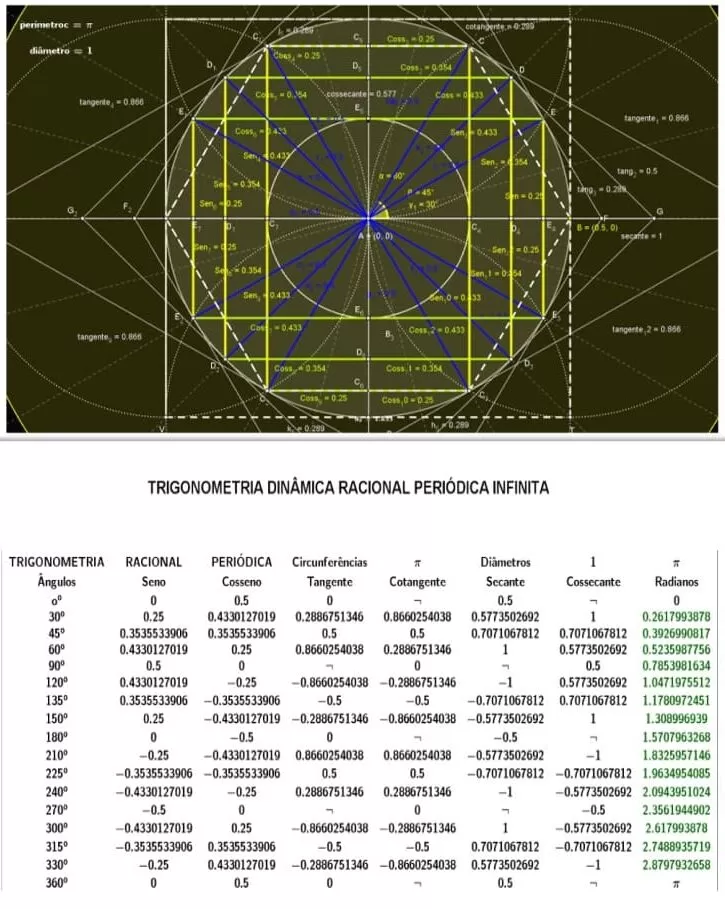
Figura 3. Demonstração do círculo trigonométrico no plano cartesiano raio=1.5
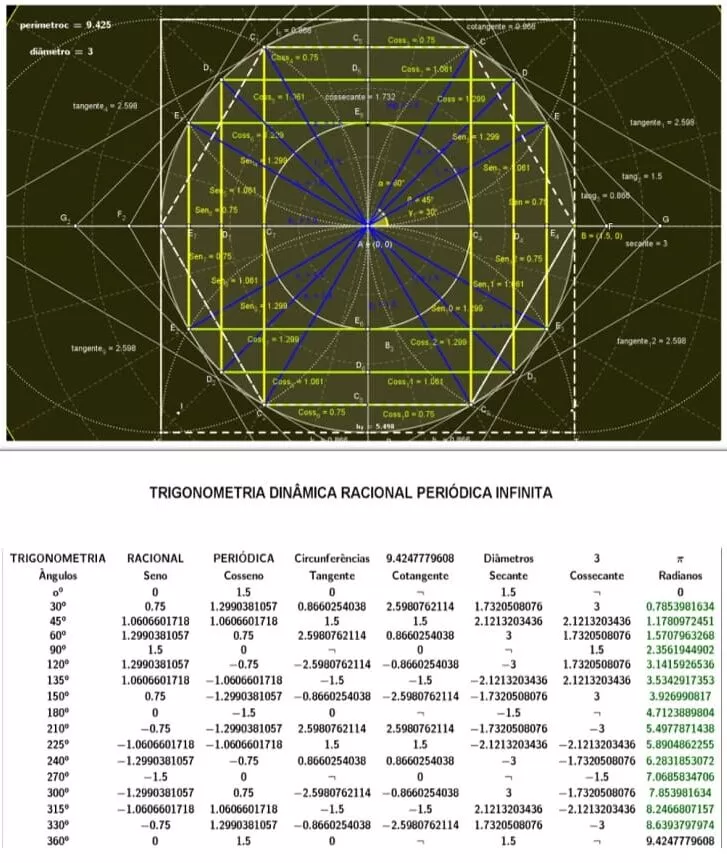
Figura 4. Demonstração do círculo trigonométrico no plano cartesiano raio=2
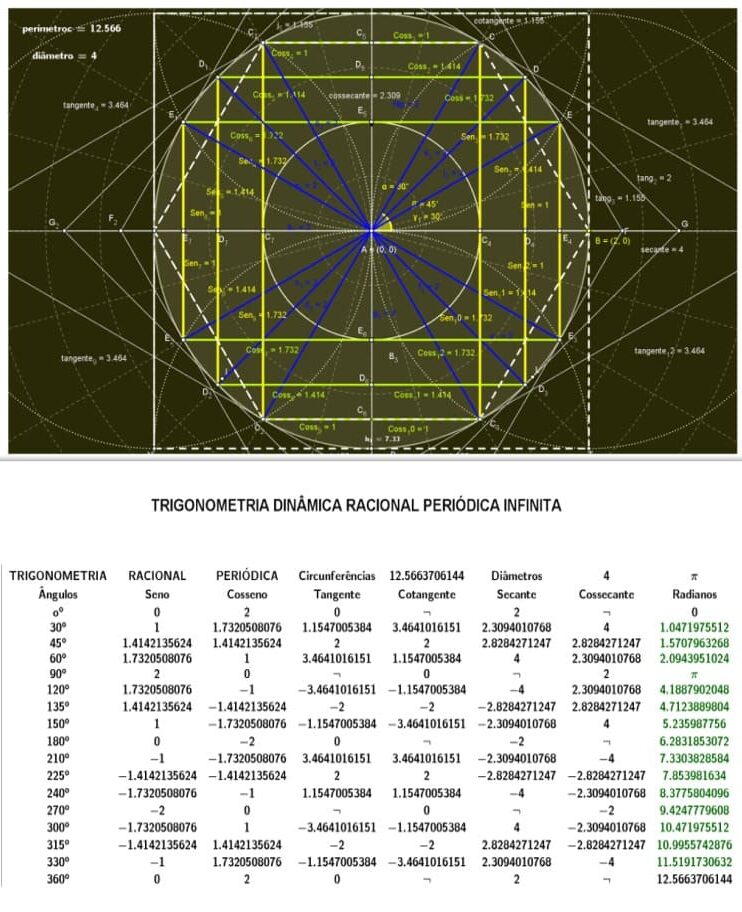
Figura 5. Demonstração do círculo trigonométrico no plano cartesiano raio=2.5
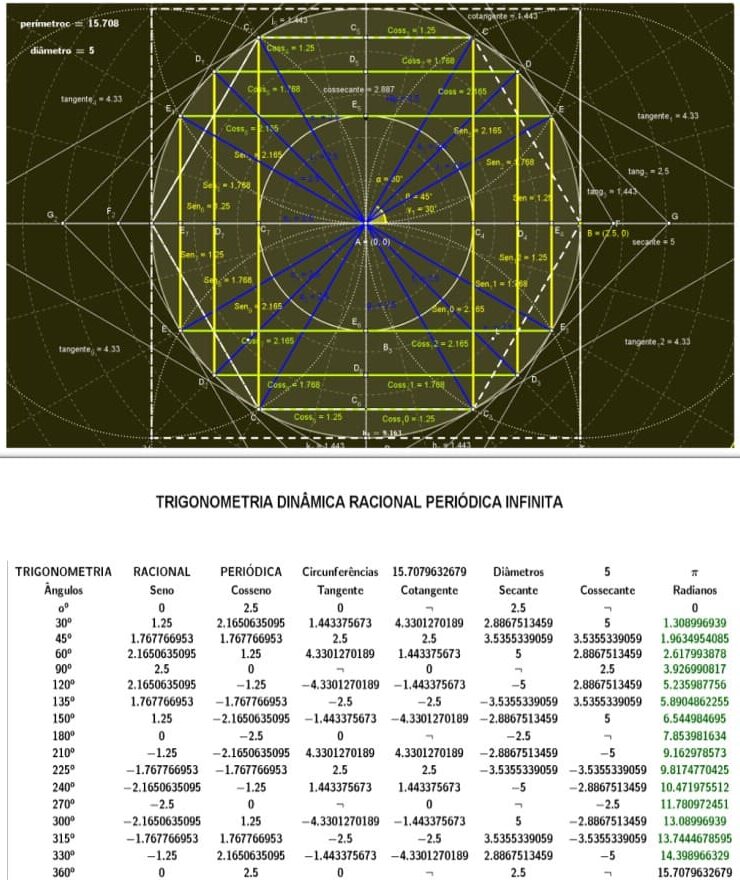
Figura 6. Demonstração do círculo trigonométrico no plano cartesiano raio=3
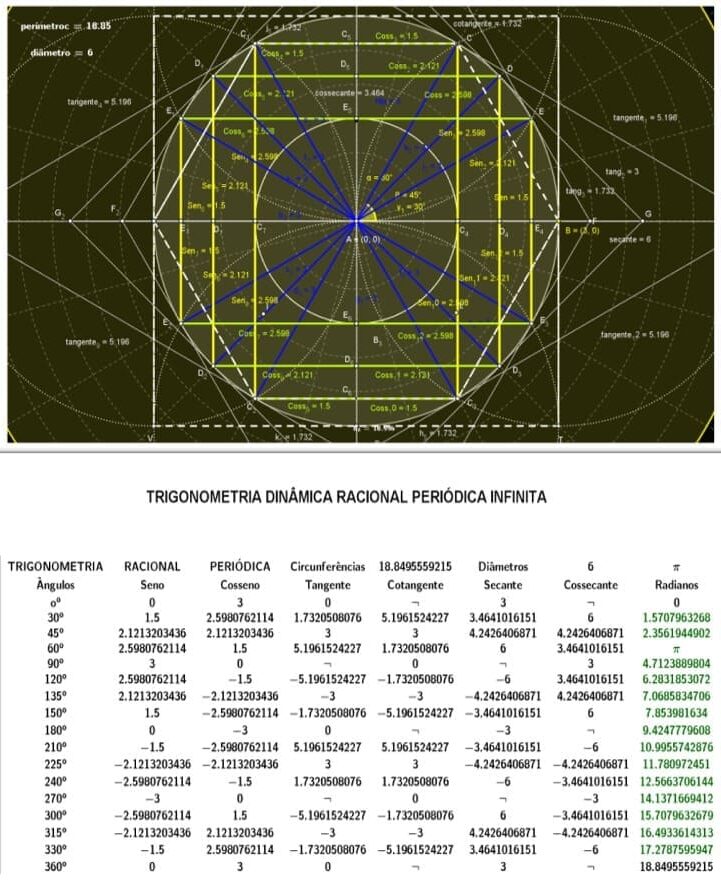
Figura 7. Demonstração do círculo trigonométrico no plano cartesiano raio=3.5
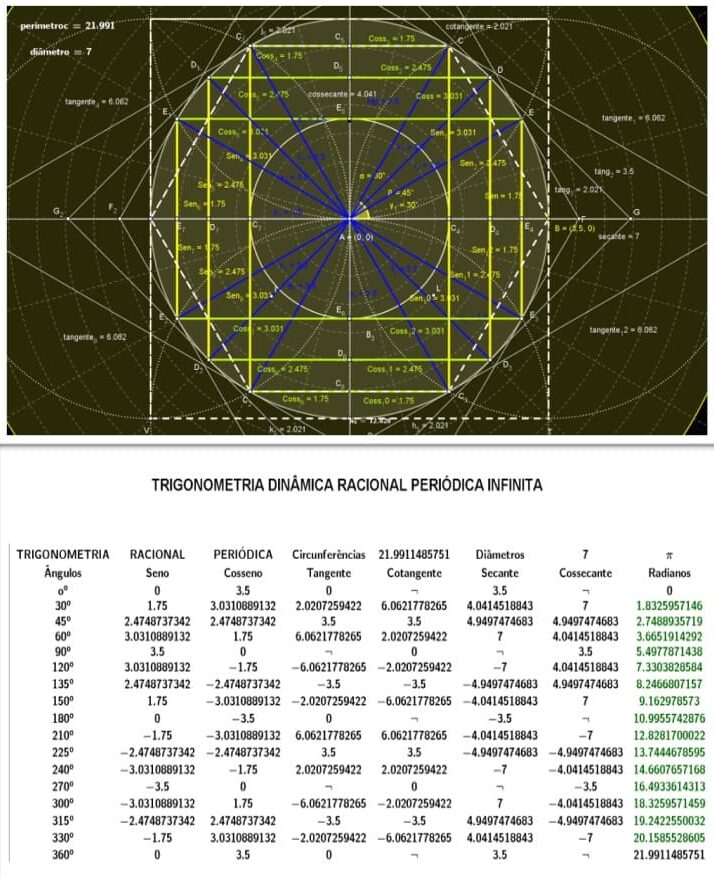
Figura 8. Demonstração do círculo trigonométrico no plano cartesiano raio=4

Figura 9. Demonstração do círculo trigonométrico no plano cartesiano raio=4.5
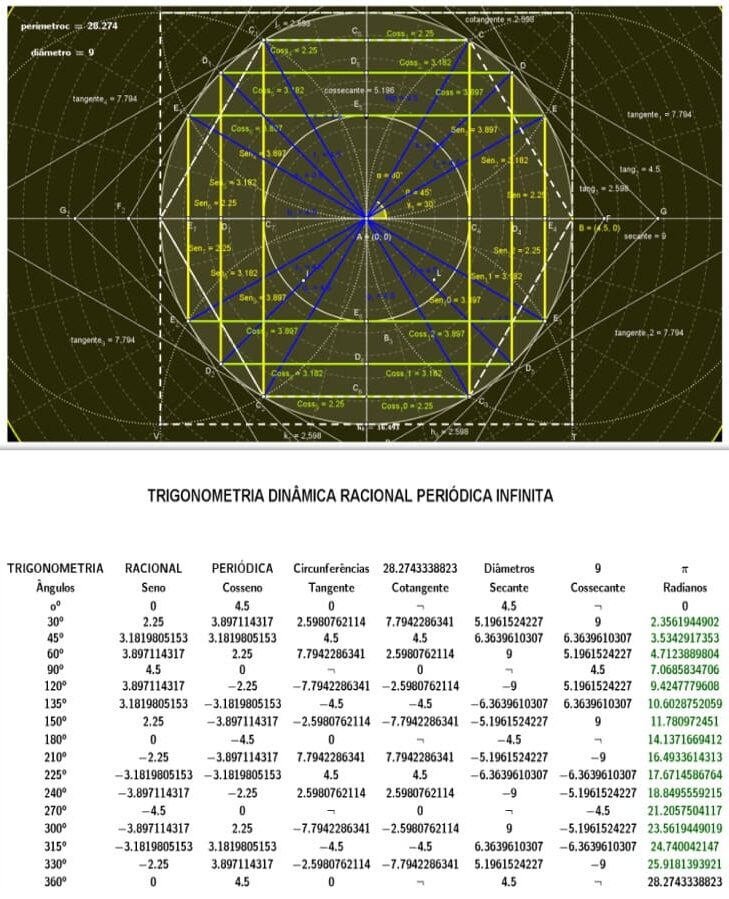
Figura 10. Demonstração do círculo trigonométrico no plano cartesiano raio=5
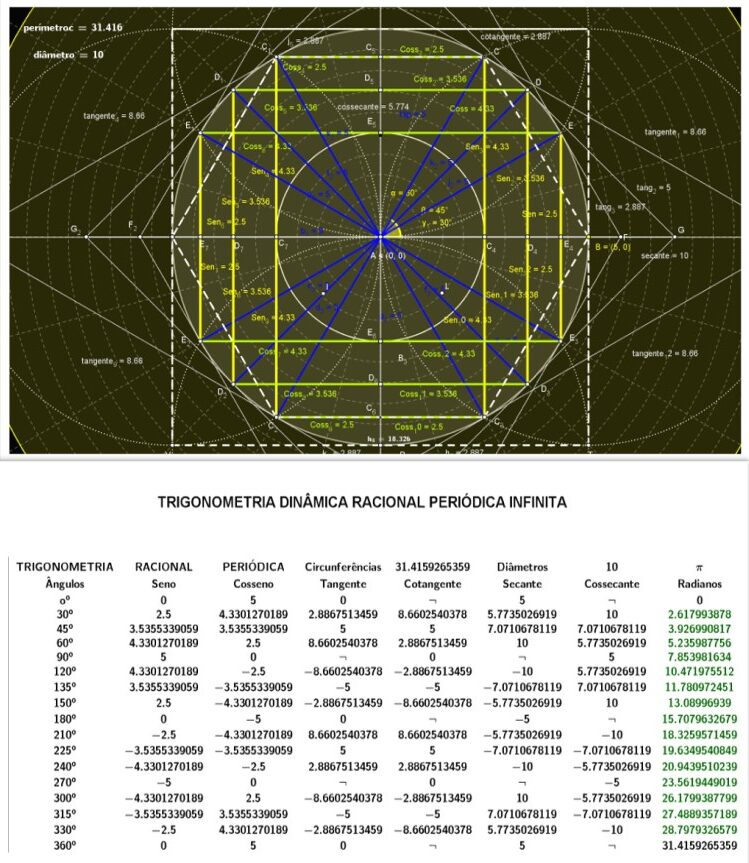
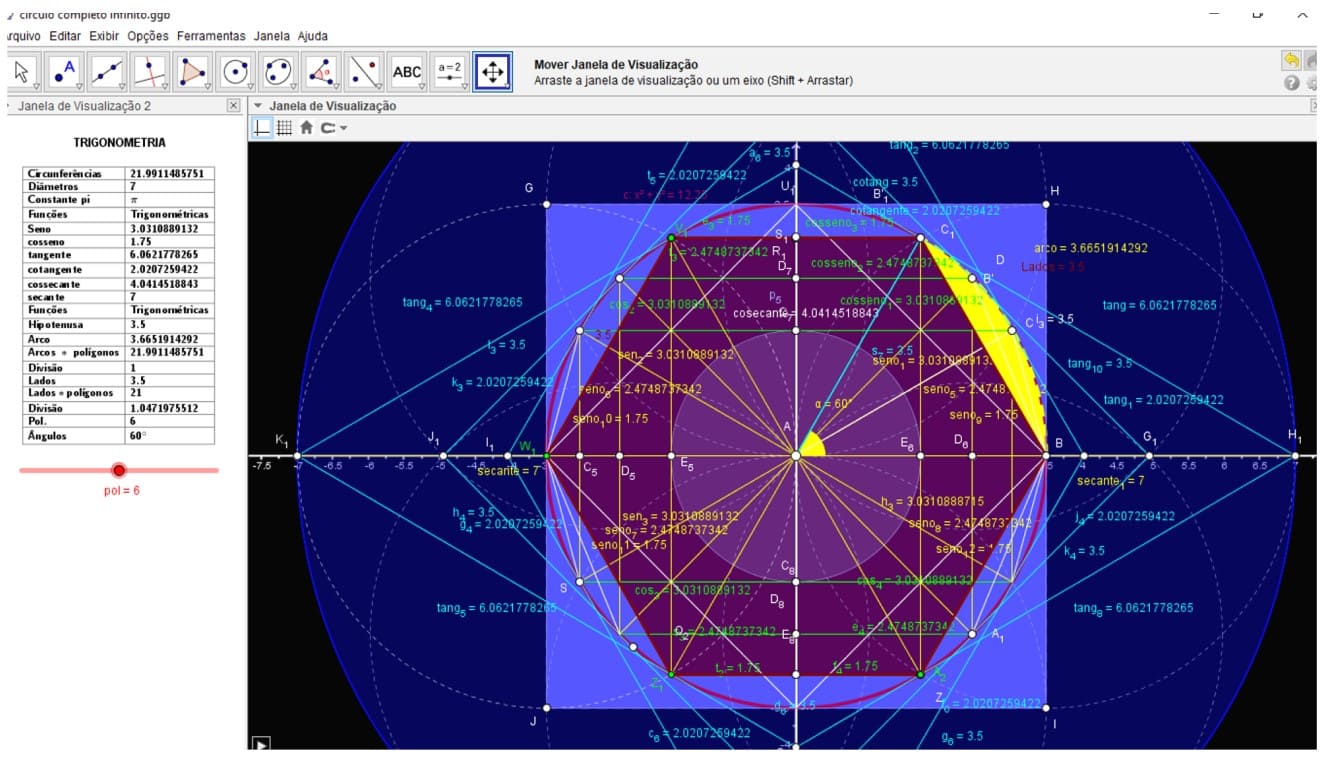
2.2 CIRCUNFERÊNCIA TRIGONOMÉTRICA NO PLANO ISOMÉTRICO
A circunferência é um conjunto de pontos em um plano cuja distância a um determinado ponto desse plano é igual a uma distância. O ponto dado é o centro, e a distância dada é o raio (r) da circunferência. Assim, dado um plano α, um ponto O (0,0), é uma distância Raio (r) temos: C: x2 + y2 = IR (reais)
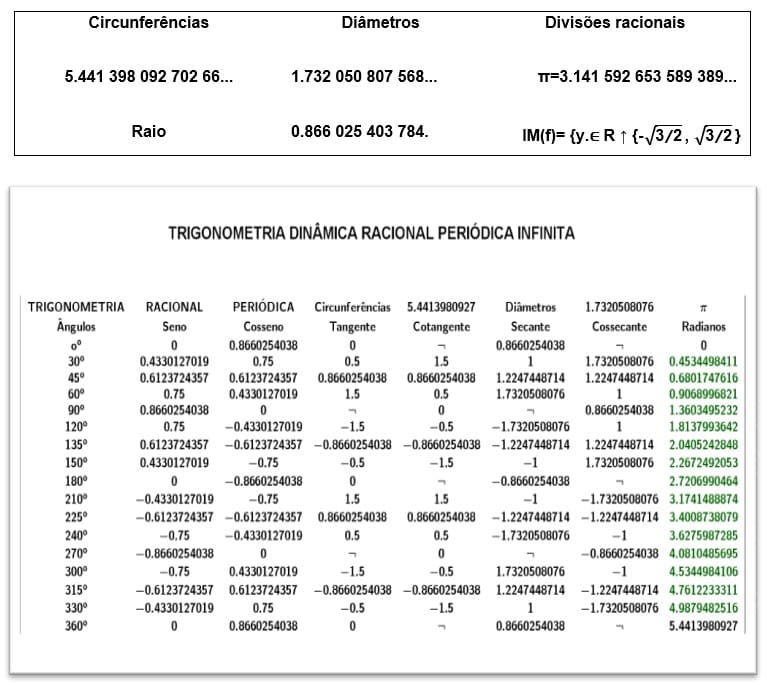
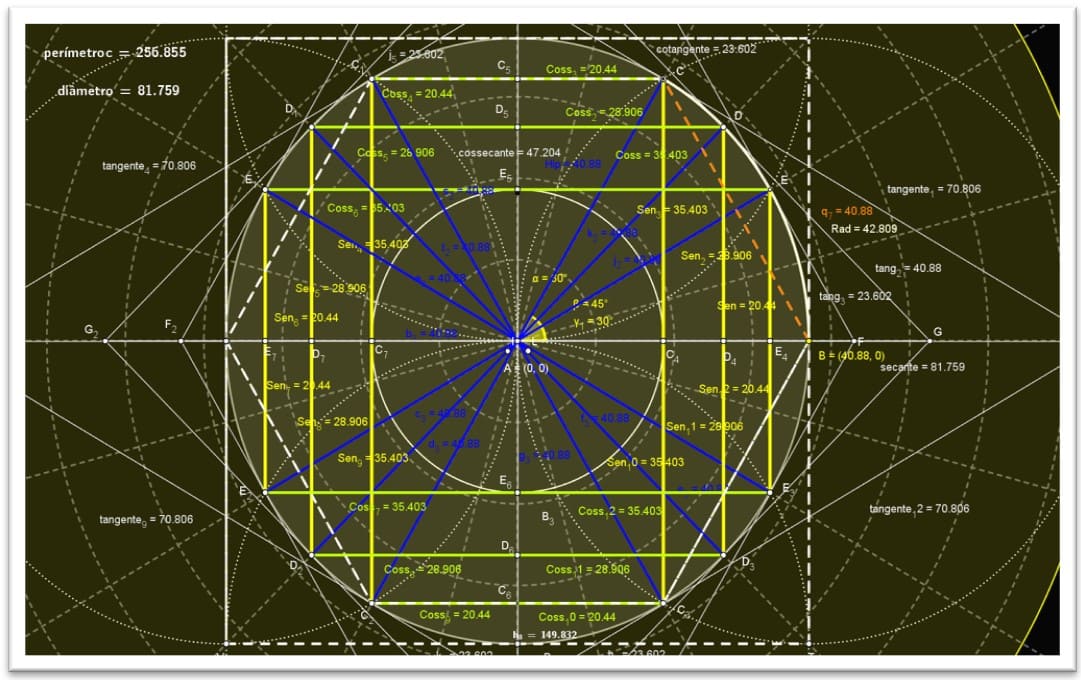
Figura 11. Círculo trigonométrico no plano isométrico diâmetro= ![]()
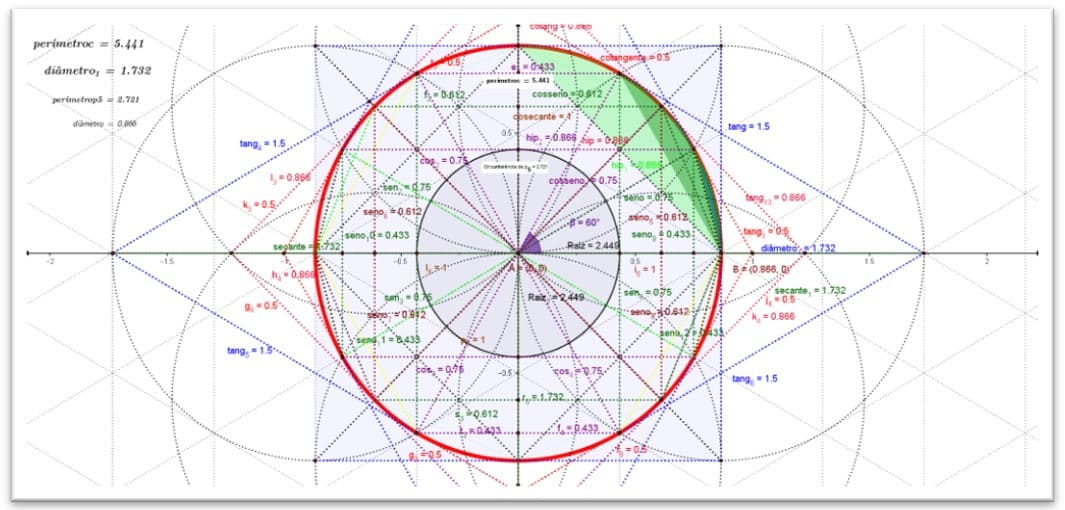
Tabela 1. Demonstração no plano isométrico racional periódico infinito fig. 11
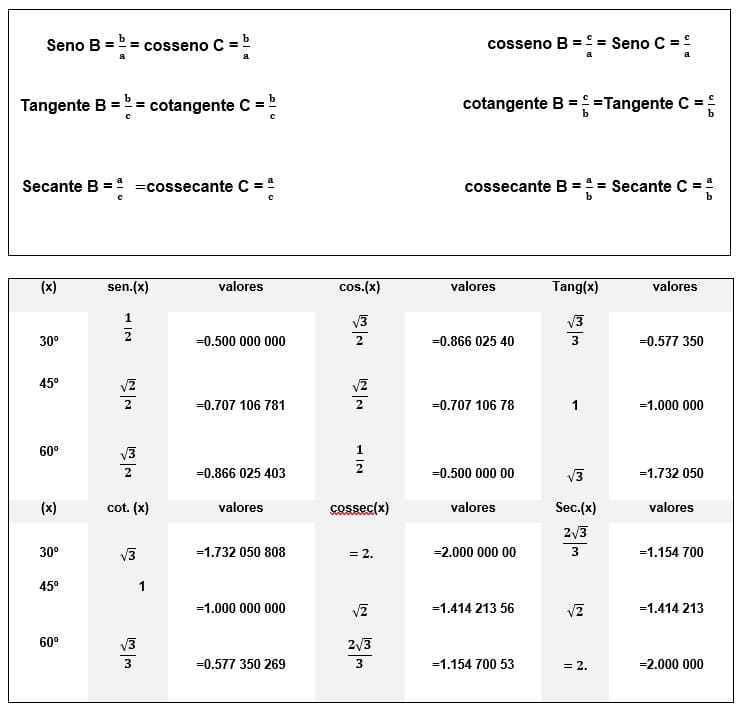
2.3 VALORES NOTÁVEIS
A partir de convenientes triângulos retangulares, as definições de seno, cosseno, tangente, cotangente, cossecante e (secante), permitem a seguinte tabela de infinitos valores racionais periódicos notáveis (IEZZI, 1993).
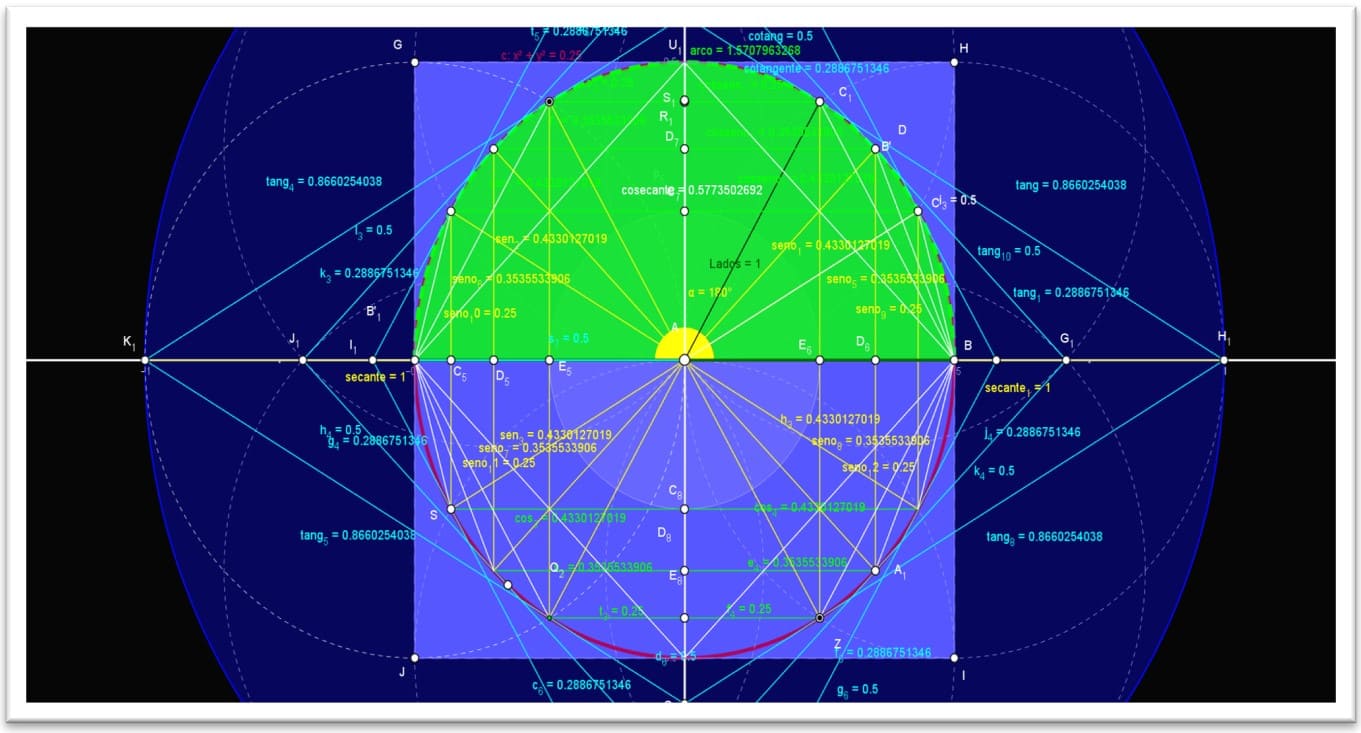
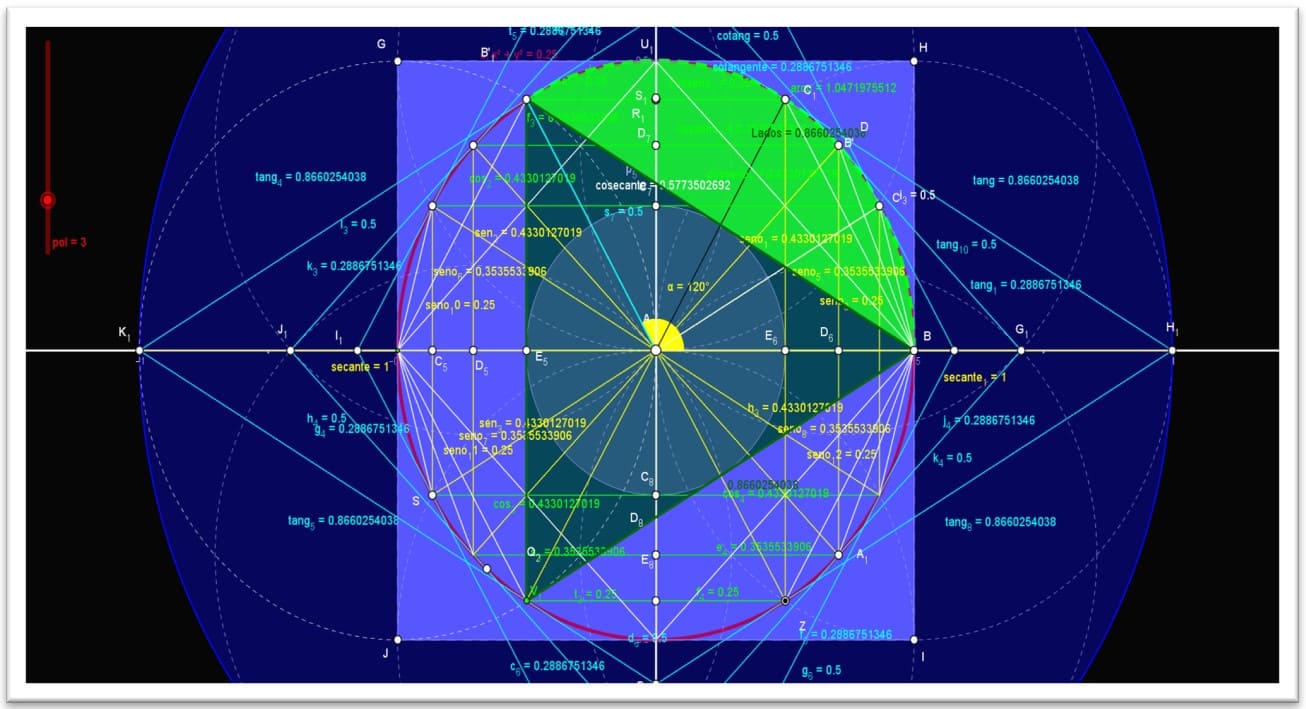
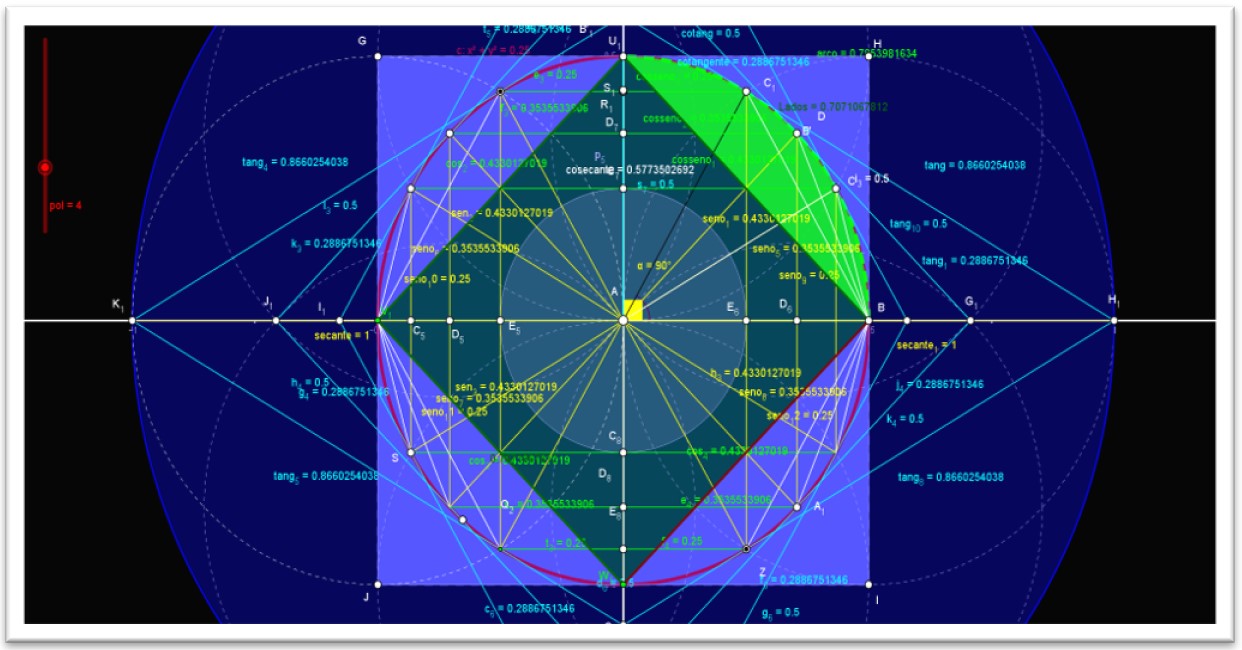
2.4 FUNÇÕES TRIGONOMÉTRICAS
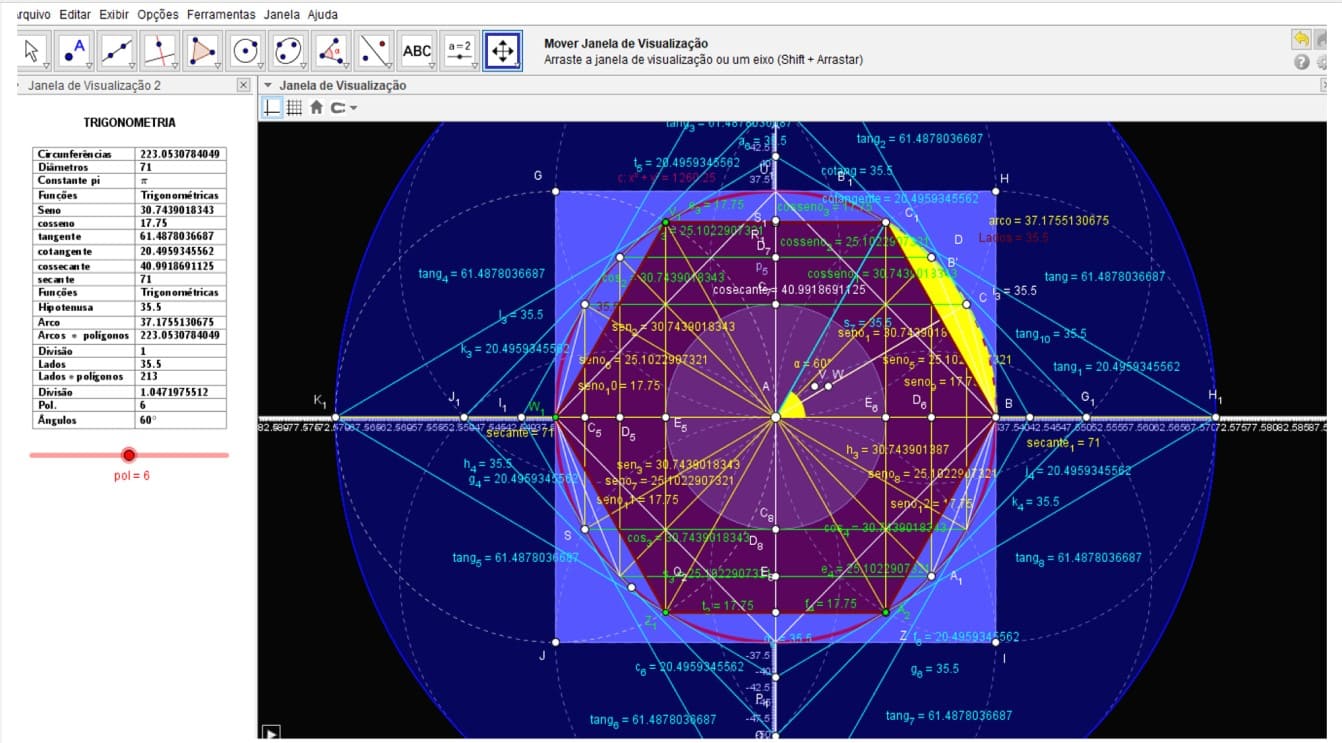
As funções trigonométricas no círculo trigonométrico estão associadas aos quatros eixos, nos quais serão definidas as funções trigonométricas seno, cosseno, tangente, cotangente, secante e cossecante no plano cartesiano.
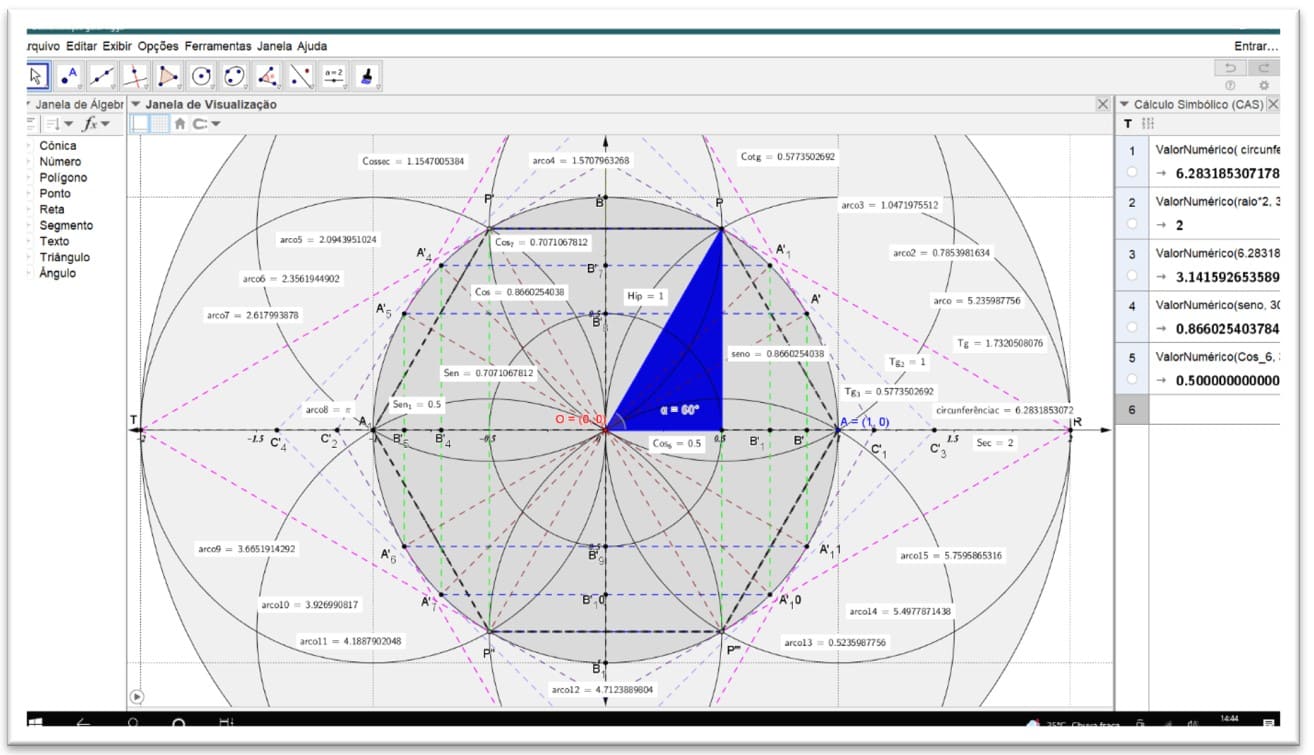
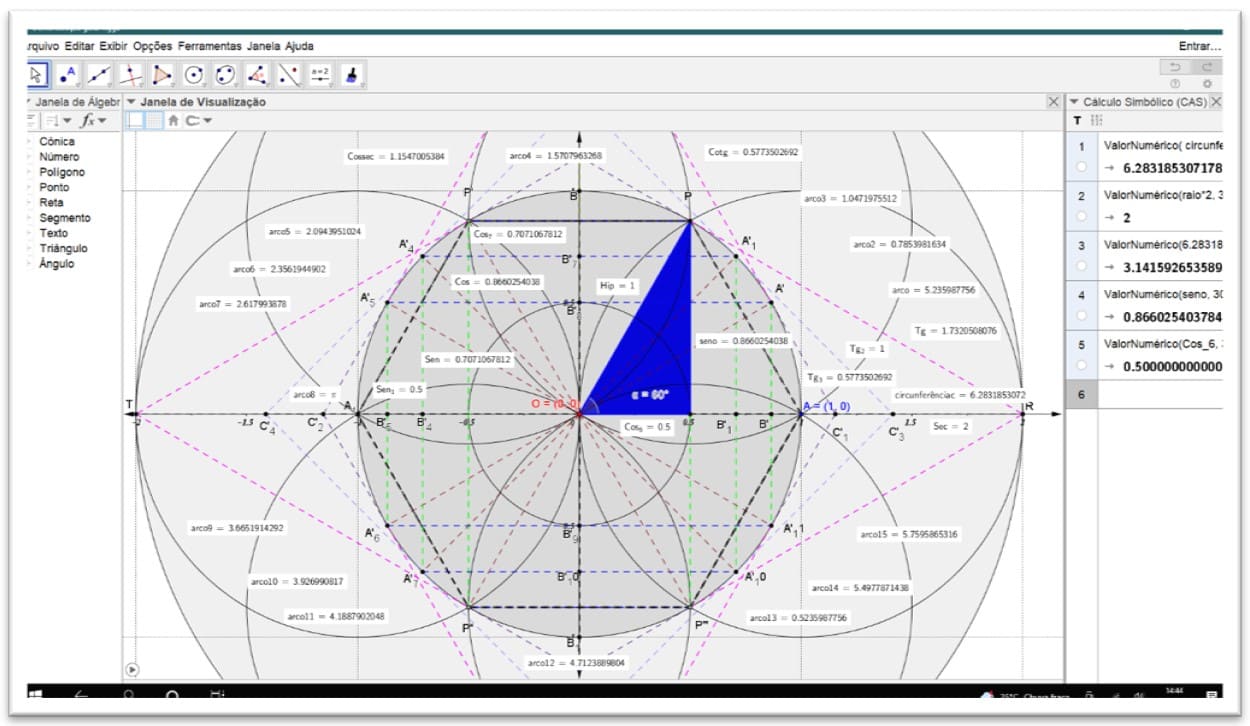
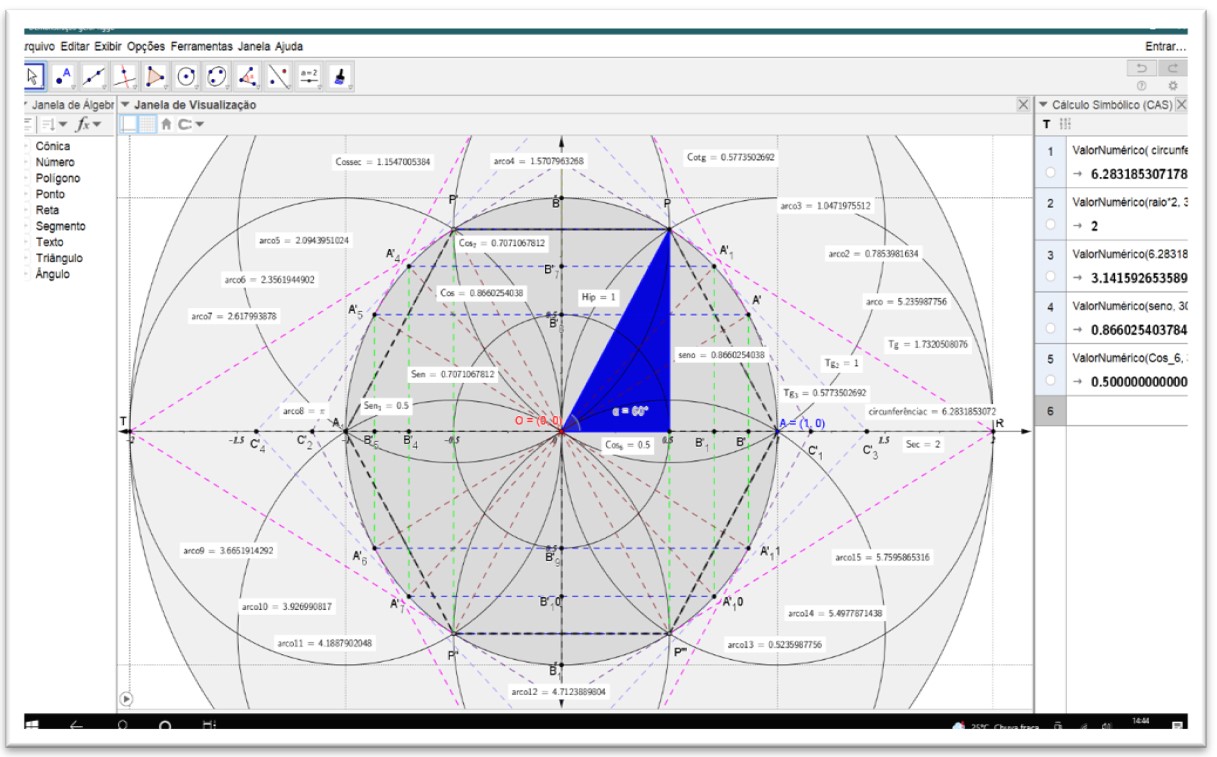
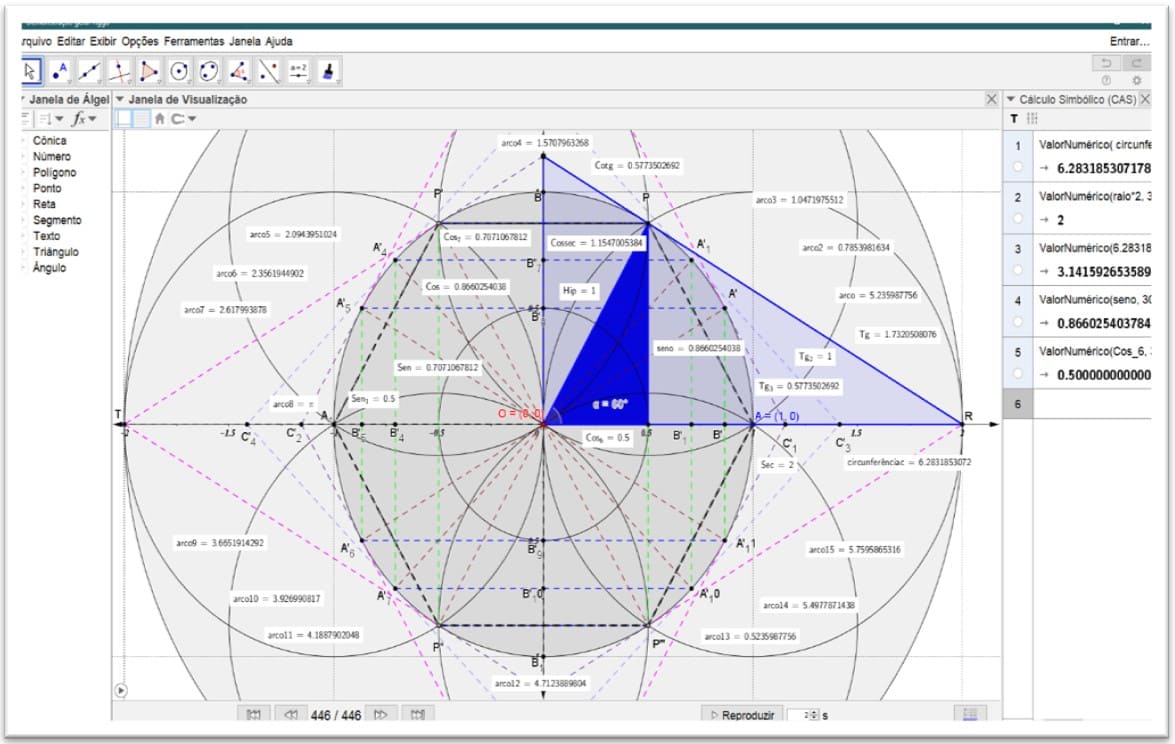
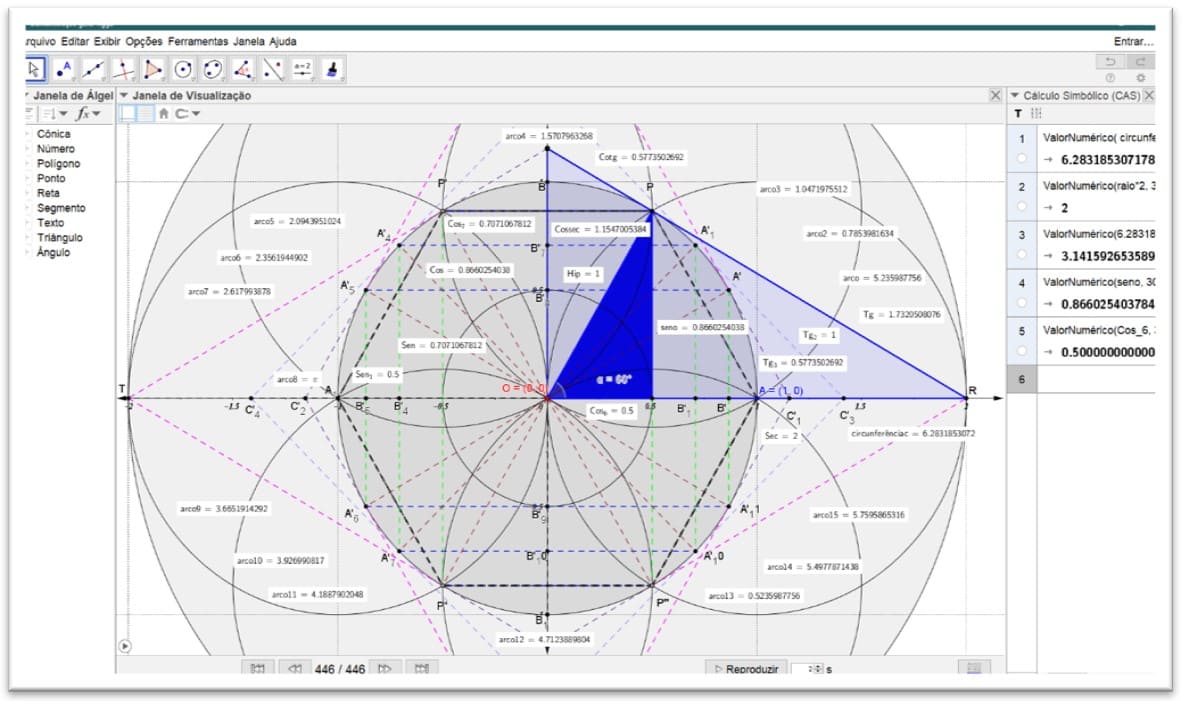
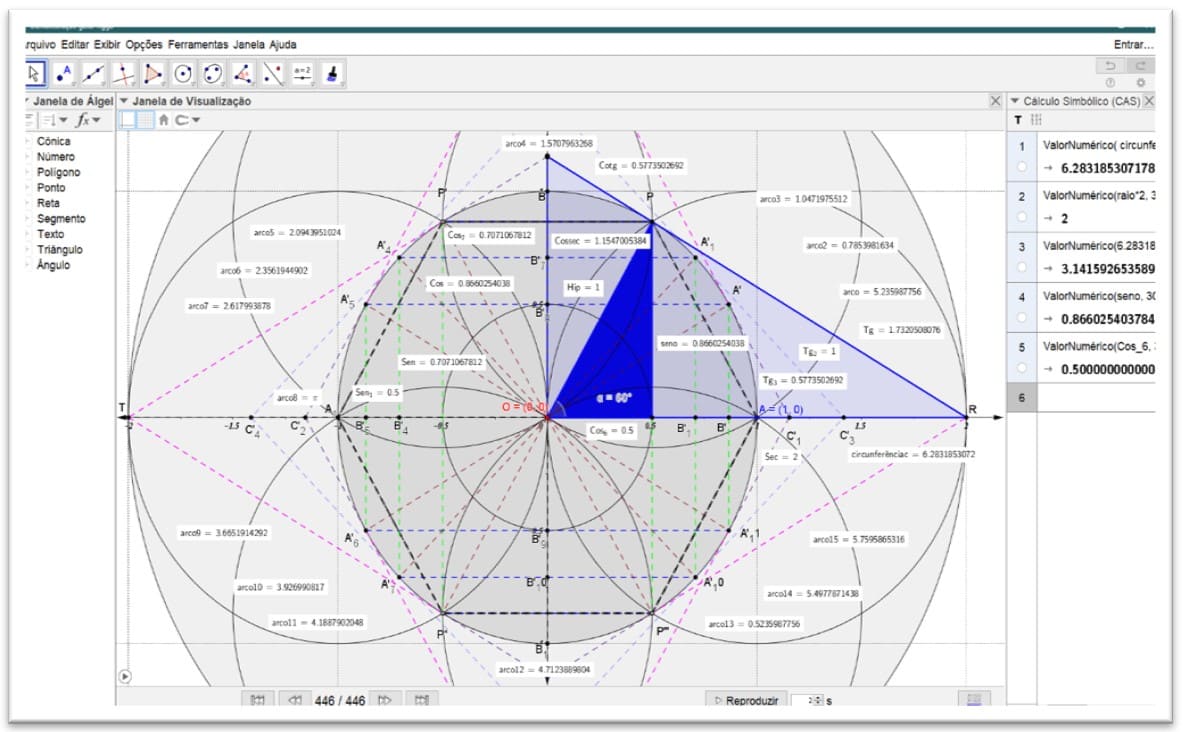
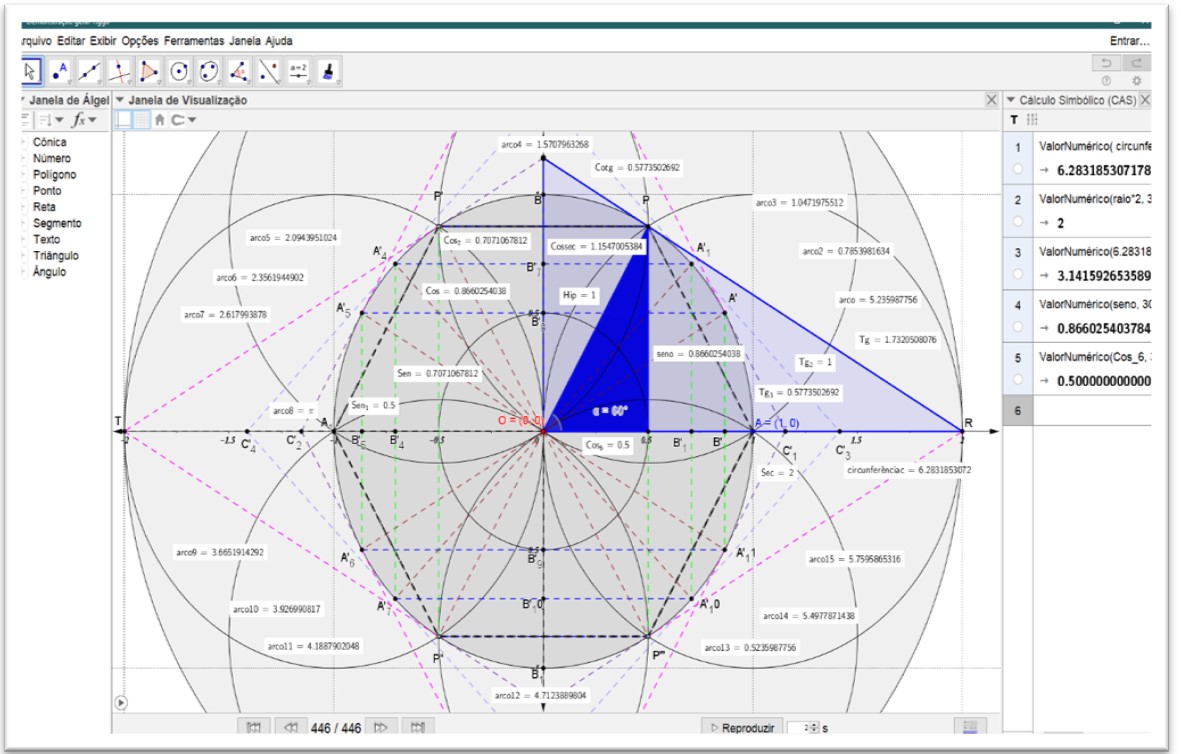
Figura 12. Os quatro eixos das funções trigonométricas completas. C: x 2 + y2 = 1

2.4.1 SENO
Definição do seno α, como sendo razão e proporção entre o cateto oposto a α, e a hipotenusa do triângulo retângulo. Pode-se, portanto, definir uma função de R em R, tal que a cada x associa em y= seno α.
Da definição da função y=f(x)= seno x, decorre que o Domínio: D(F)=R; imagem: ![]()
Figura 13. As funções trigonométricas completas seno α 60º C: x 2 + y2 = 1

2.4.2 COSSENO
Definição do cosseno α, como sendo razão e proporção entre o cateto adjacente a (α), e a hipotenusa do triângulo retângulo. Pode-se, portanto, definir uma função de R em R, tal que a cada x associa em y= cos α.
Da definição da função y=f(x)=cos x, decorre que o Domínio: D(F)=R; imagem: ![]()
Figura 14. Demonstração dos quatro eixos das funções trigonométricas completas. Cosseno (α=60º) C: x 2 + y2 = 1

2.4.3 TANGENTE
Definição da α tangente, como sendo razão e proporção entre o cateto oposto (α) e cateto adjacente (α), e a hipotenusa do triângulo retângulo.
Figura 15. Demonstração dos quatro eixos das funções trigonométricas completas. Tangente (α=60º) C: x 2 + y2 = 1

2.4.4 COTANGENTE
Definição da cotangente (α) é o inverso da tangente, sendo a razão e proporção entre o cateto adjacente (α), e o cateto oposto (α), e a hipotenusa do triângulo retângulo.
Figura 16. Demonstração dos quatro eixos das funções trigonométricas completas. Cotangente (α=60º) C: x 2 + y2 = 1

2.4.5 COSSECANTE
Definição de cossecante (α) é o inverso do senso, sendo a razão e proporção entre (α), a hipotenusa e o cateto oposto (α).
Figura 17. Demonstração dos quatro eixos das funções trigonométricas. Cossecante: C: x 2 + y2 = 1

2.4.6 SECANTE
Definição da secante (α), como a recíproca do cosseno, corresponde à razão e proporção da hipotenusa pelo cateto adjacente.
Figura 18. Demonstração dos quatro eixos das funções trigonométricas. Secante: C: x 2 + y2 = 1

2.5 NÚMERO IRRACIONAL Π
Sua representação, pela letra grega π (pi), deve-se à palavra grega perímetro (πρειµετρoς), e foi introduzida em 1706, por William Jones (1676-1749), e popularizada por Leonhard Euler (1707-1783). Matemáticos de várias épocas têm tentado buscar uma racionalidade para a constante π. A prova de que a constante π é um número irracional foi feita por Johann Lambert em 1761 e Legendre em 1794.O número π é um número transcendente, que foi provado por Ferdinand Lindemann em 1882.
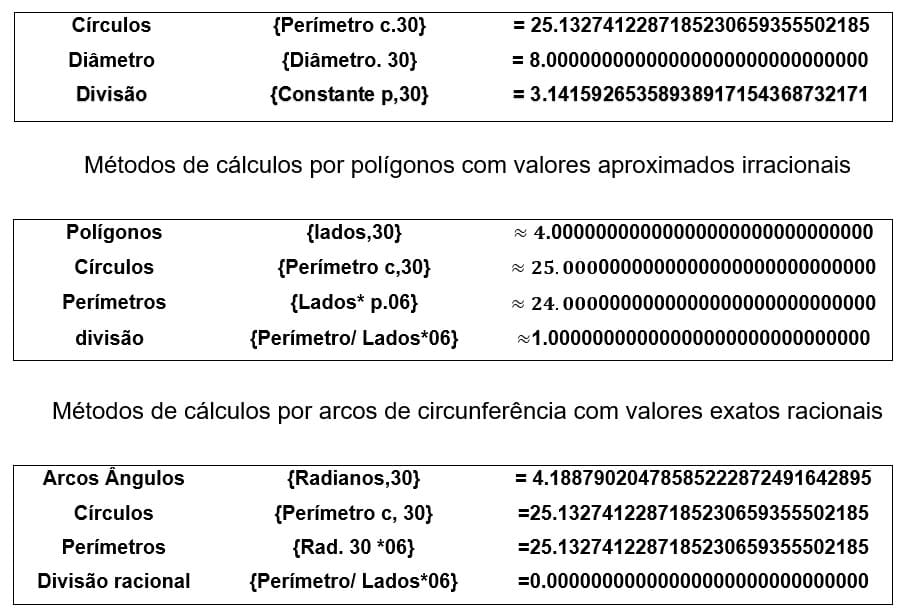
2.5.1 PERÍMETRO DA CIRCUNFERÊNCIA
A extensão da circunferência, isto é, seu perímetro c, pode ser calculada através da equação. C=π*d 2*π*r.
constanteπ(pi)=3.141 592 653 589 389 171 543 687 321 706 908 213…
2.5.2 RACIONALIDADE CONSTANTE Π
O círculo é a área interna (α), delimitada na circunferência, que pode ser calculada usando a equação. Área(a)=π*r2.
Área (2*π) =6.283 185 307 178 778 343 087 374 643 413 816 427 962…
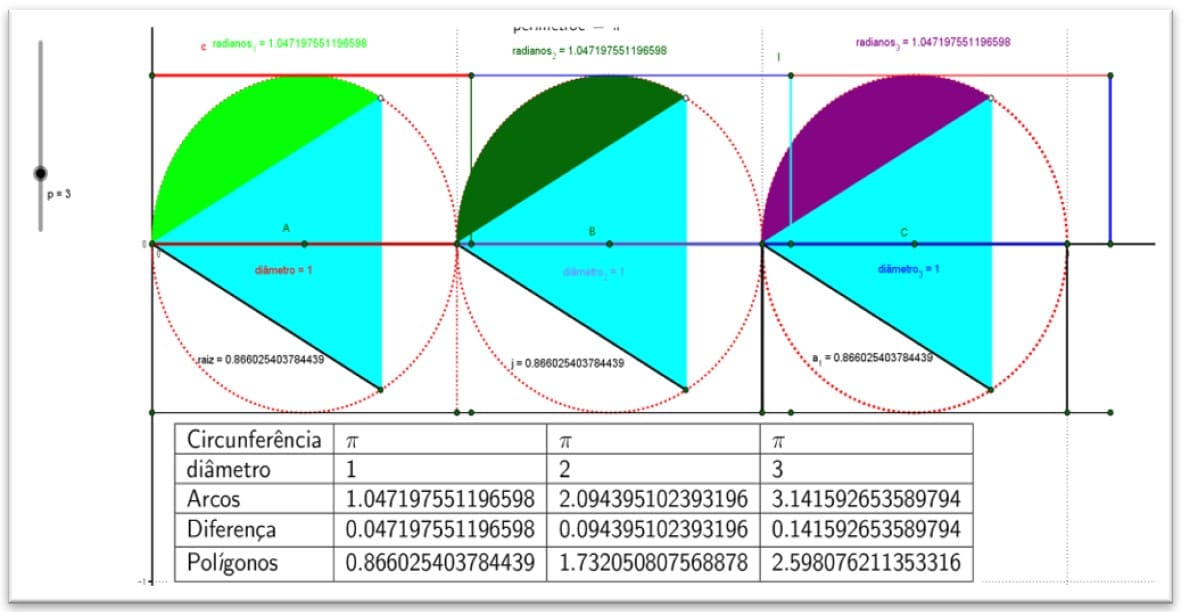
Figura 19. Demonstração e comparações da trissecção dos perímetros das circunferências
A busca pela racionalidade do π, algumas abordagens históricas
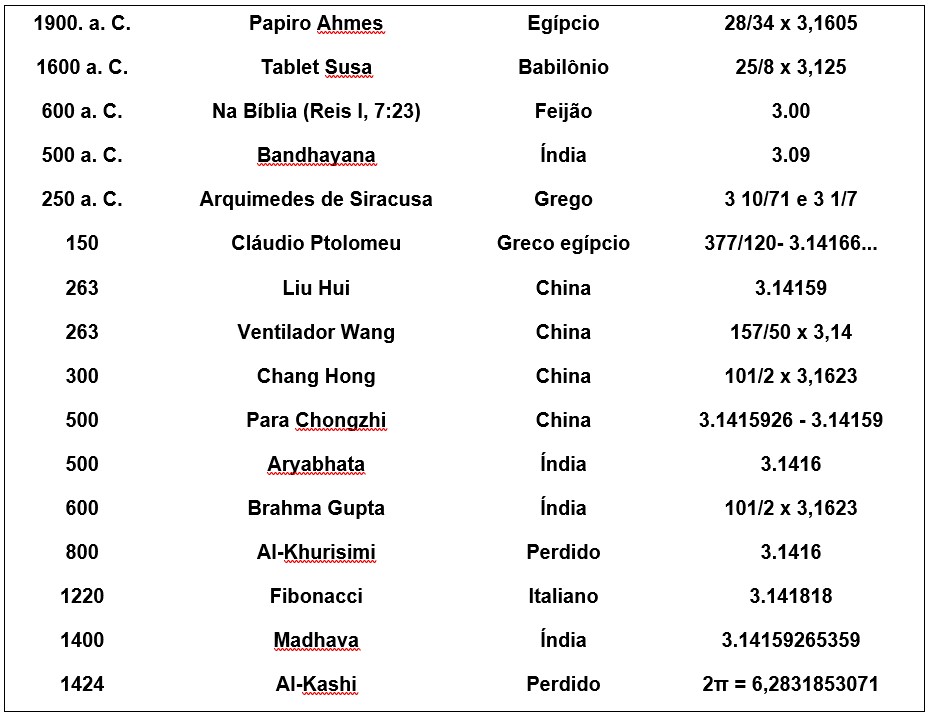
2.5.3 MÉTODOS CLÁSSICOS DA BABILÔNIA (2000 B. C)
Os arqueólogos têm trabalhado na Mesopotâmia sistematicamente desde antes de meados do século 19 e desenterraram mais de meio milhão de tábuas de argila, das quais quatrocentas foram identificadas como estritamente matemáticas. Os museus de Paris, Berlim e Londres e algumas universidades como Yale, Columbia e Pensilvânia têm excelentes coleções dessas praças, que são variáveis em tamanho e de aproximadamente um centímetro e meio de espessura. Eles são muitas vezes de formas arredondadas, com escritos cuneiformes em apenas um de seus rostos, e às vezes em ambos.
O número de frações contínuas π habitar aproximadamente
O número da fração contínua π, racional periódico infinito
Figura 20. Demonstração da divisão do método clássico da Babilônia da circunferência
2.5.4 MÉTODOS CLÁSSICOS DO PAPIRO DE RHIND AHMES (1650 A.C.)
O escriba egípcio autor Ahmes, 2.000 anos a.C. A maioria desses problemas vem de fórmulas de medição necessárias para calcular áreas de terra e volumes de celeiro. Um desses registros afirma que a área de um círculo é igual a um quadrado cujo lado é do diâmetro. ![]() A fração contínua do π habita aproximadamente:
A fração contínua do π habita aproximadamente:
Figura 21. Os métodos clássicos do papiro de Rhind com valores racionais

2.5.5 ARQUIMEDES DE SIRACUSA (250 A.C.)
O matemático grego Arquimedes de Siracusa (287-212 a.C.) descobriu um método muito eficiente para obter sequências de aproximações da constante π. Em seu trabalho as medidas do círculo, ele desenvolveu um método de aproximações sucessivas para o cálculo do comprimento de uma circunferência.
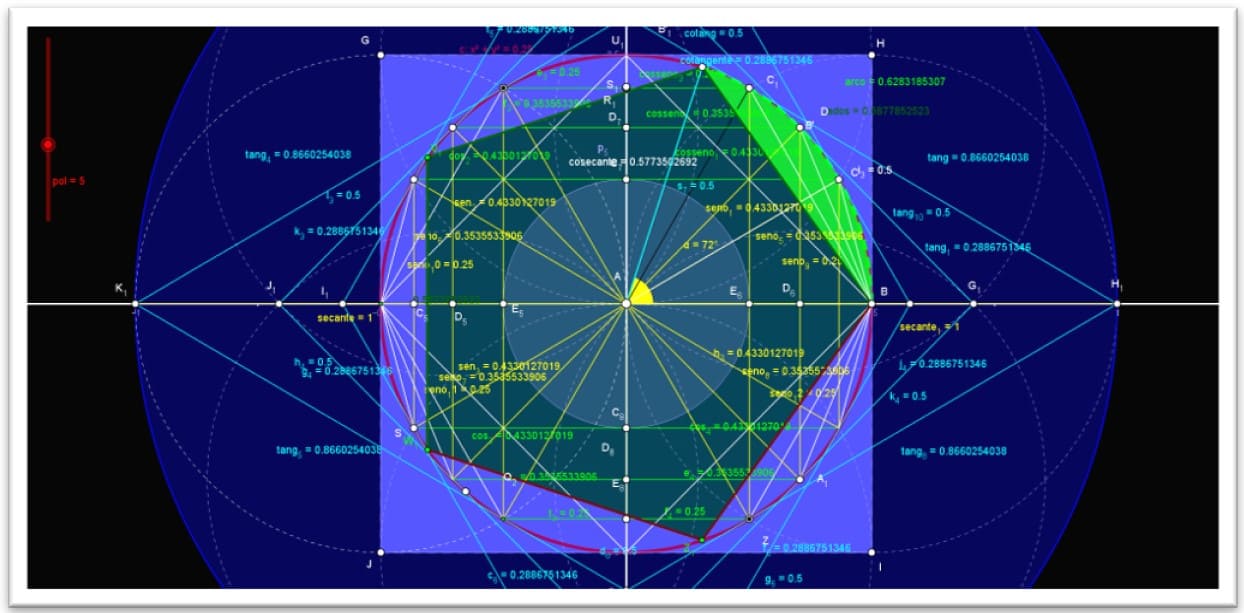
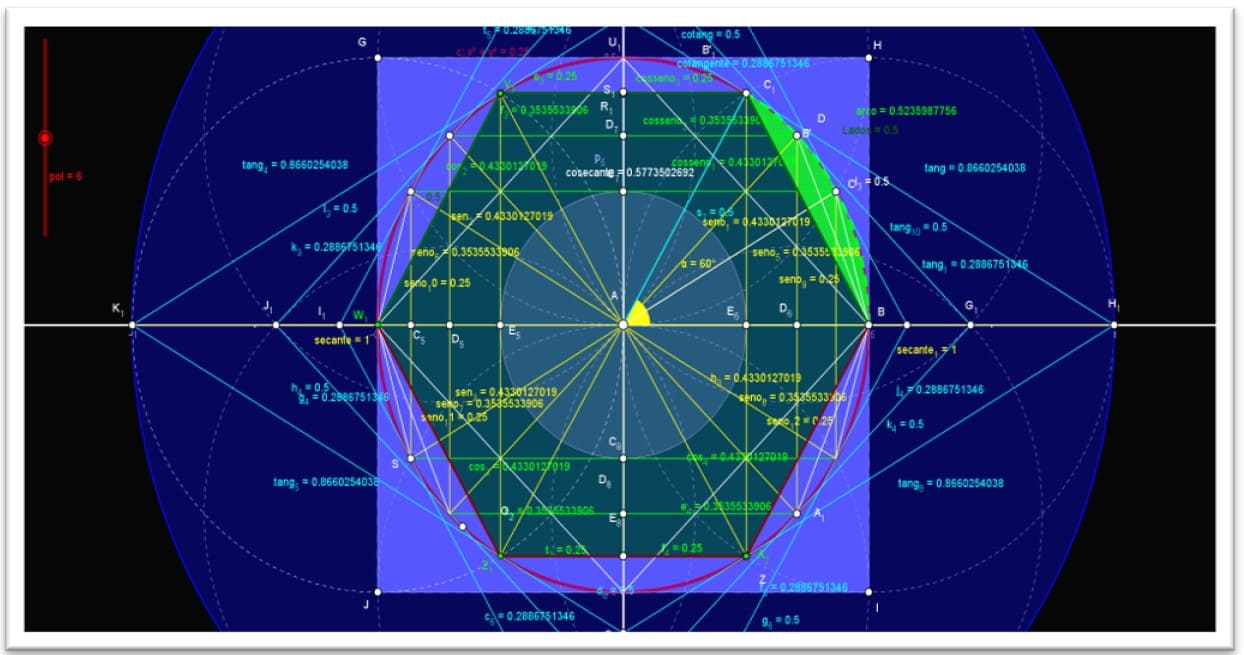
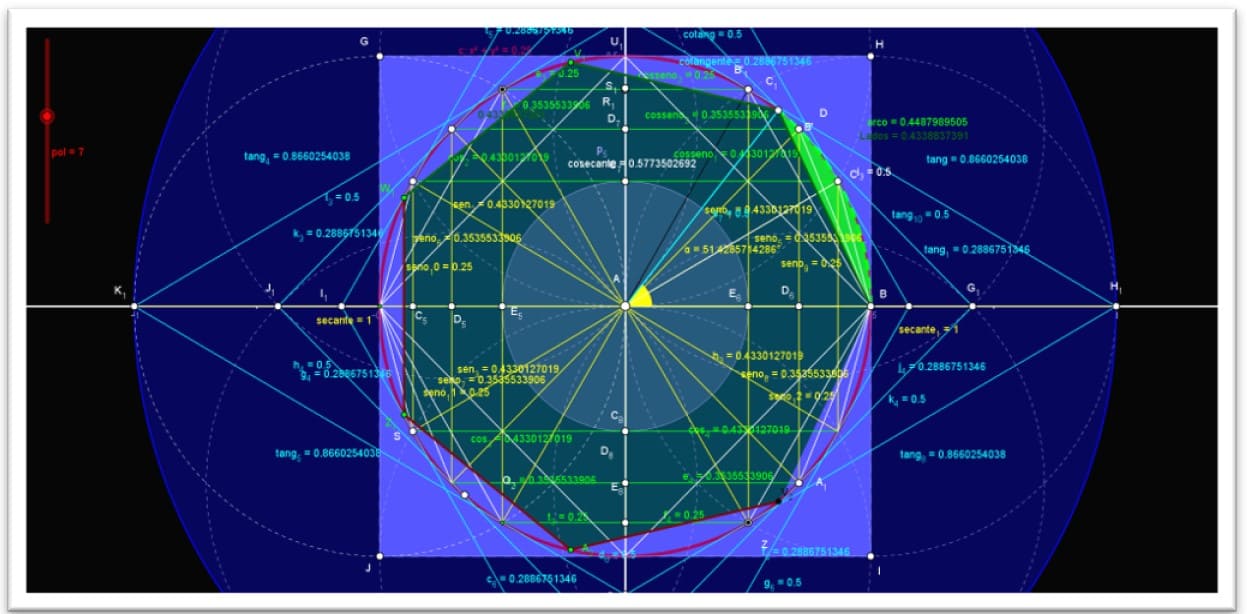
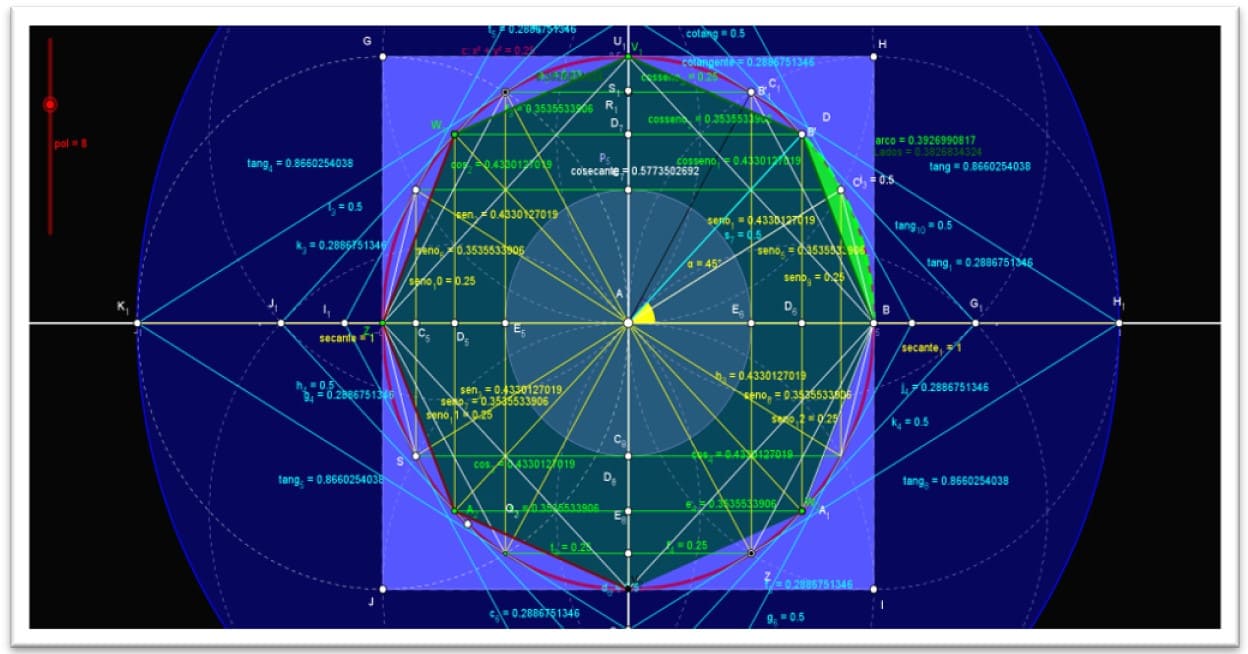
Ele construiu polígonos regulares inscritos e circunscritos e dividiu o perímetro de cada um pelo diâmetro da circunferência, seus estudos com hexágonos regulares e dobrando o número de lados desses polígonos até atingir um polígono de 96 lados.
Figura 22. Demonstração dos métodos clássicos de Arquimedes
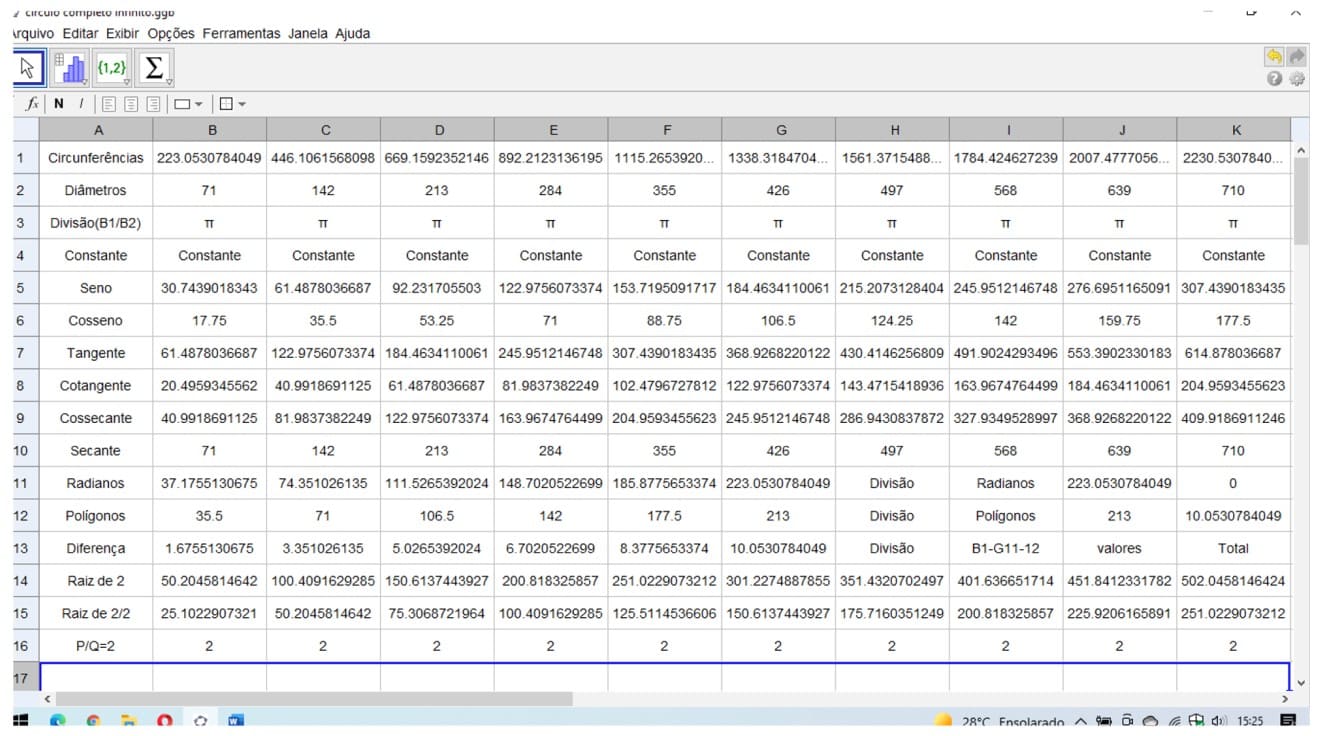
Figura 23. Os métodos clássicos de Arquimedes com valores racionais
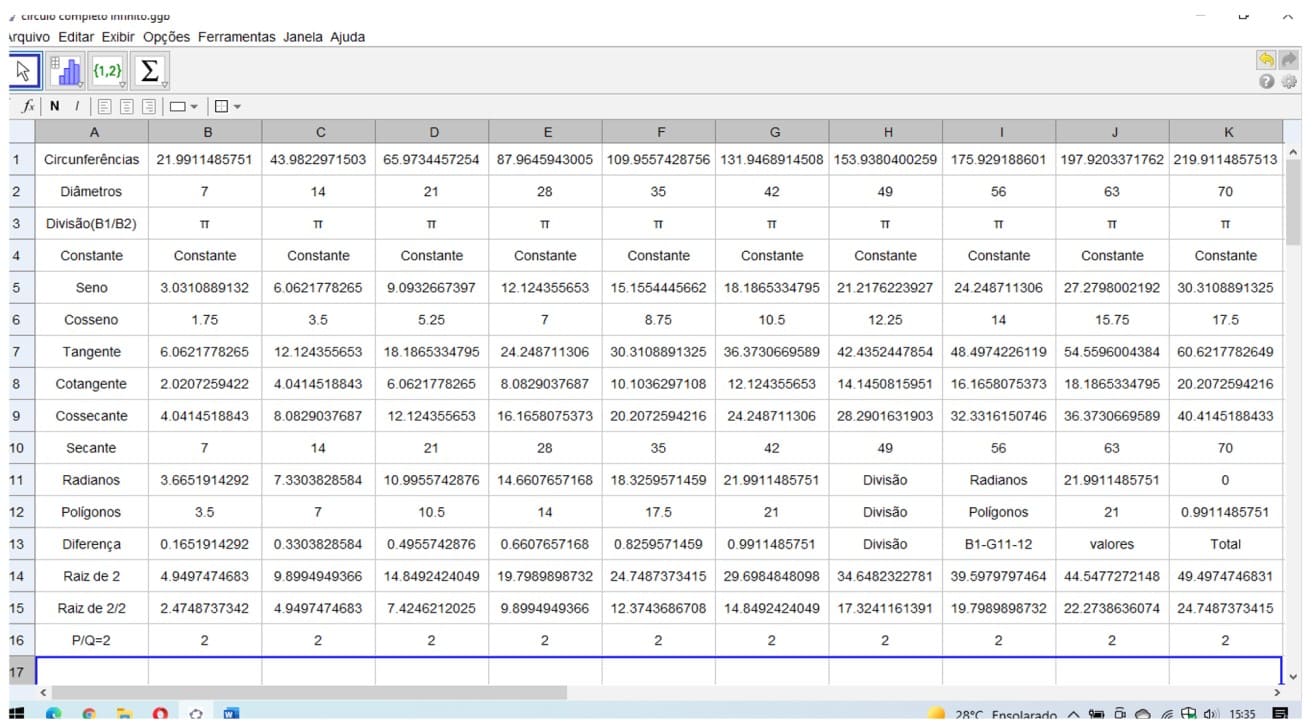
2.6 ARCOS E ÂNGULOS DE CIRCUNFERÊNCIA (GRAU E RADIANOS)
A circunferência em que são tomados dois pontos A e B. A circunferência ficará dividida em duas partes chamadas arcos. Os pontos A e B são as extremidades desses arcos. Quando A e B coincidem, um desses arcos é chamado nulo e o outro, arco de uma volta, diremos que o arco nulo tem por medida 0º e o arco de uma volta tem por medida 360º. Dessa forma:![]() do arco de uma volta. Como submúltiplos do grau, temos: 1 minuto
do arco de uma volta. Como submúltiplos do grau, temos: 1 minuto ![]() , do grau, ou 60 minutos = 1 grau (60’=1º), e 1 segundo
, do grau, ou 60 minutos = 1 grau (60’=1º), e 1 segundo ![]() do minuto ou 60 segundos = 1 minuto (60” =1’).
do minuto ou 60 segundos = 1 minuto (60” =1’).
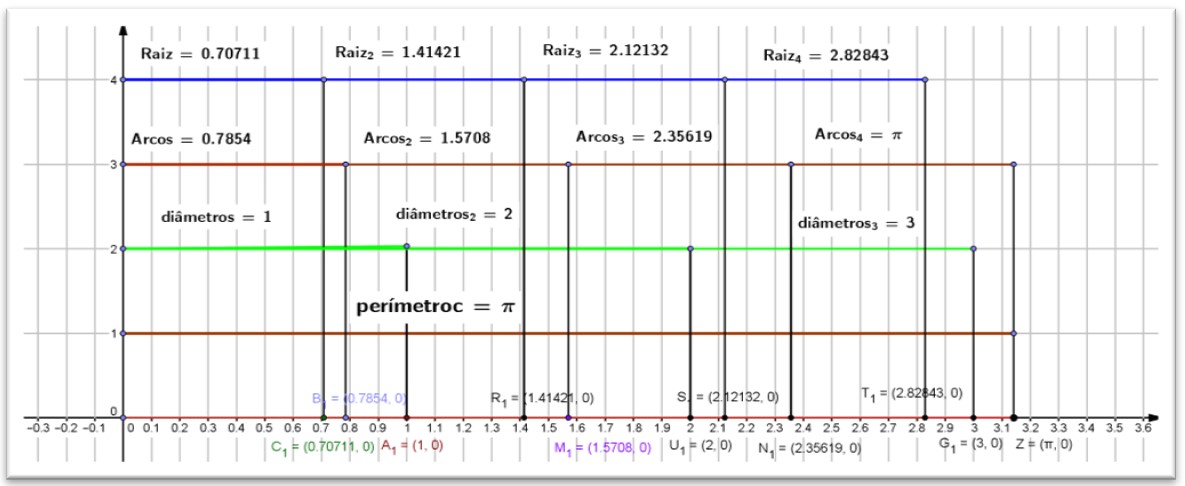
Radiano é a medida de um arco que corresponde ao mesmo comprimento do raio(r) da circunferência em relação ao ângulo central.
Arco de um radiano (1rad) é aquele cujo comprimento é igual ao raio da circunferência. C = 2*π*r – 360º – 2 π radianos (NETO, 1978).
Figura 24. Demonstração do círculo trigonométrico dinâmico racionais infinitos
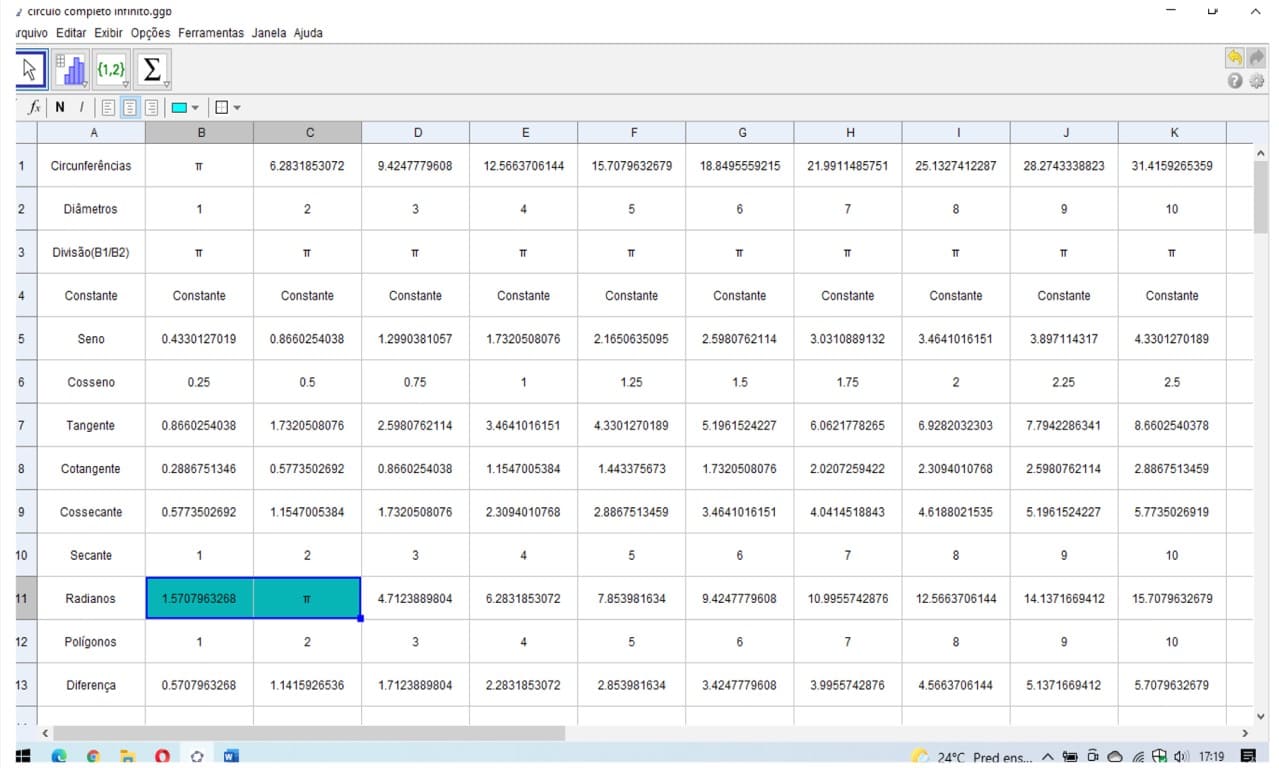
Figura 25. Demonstração entre circunferências e seus diâmetros valores racionais
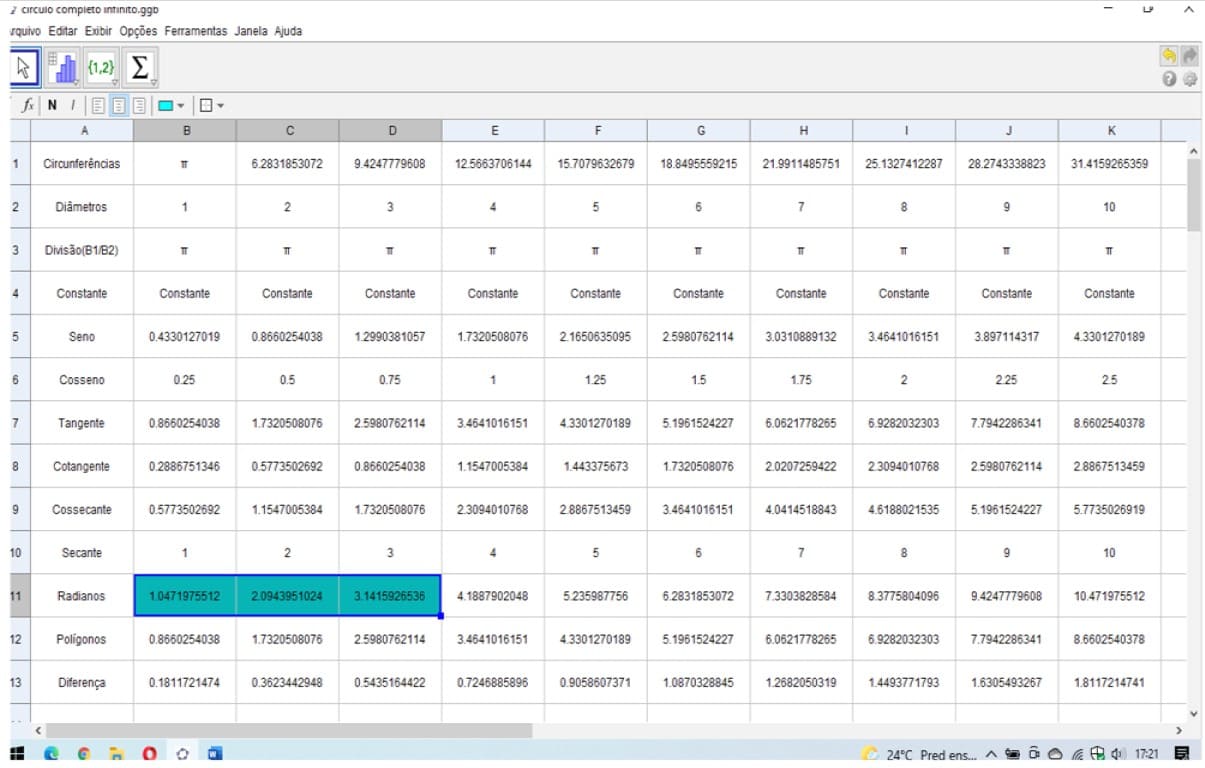
Figura 26. Demonstração entre circunferências e seus diâmetros valores racionais
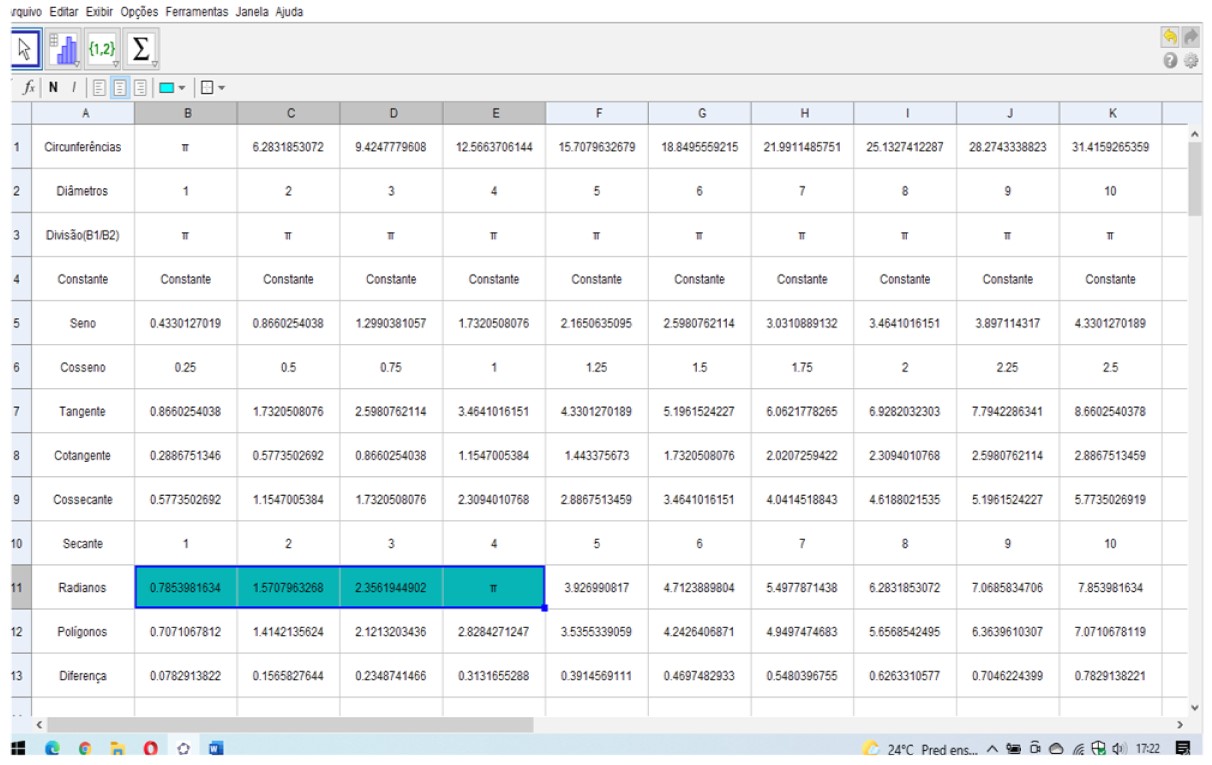
Figura 27. Demonstração entre circunferências e seus diâmetros valores racionais
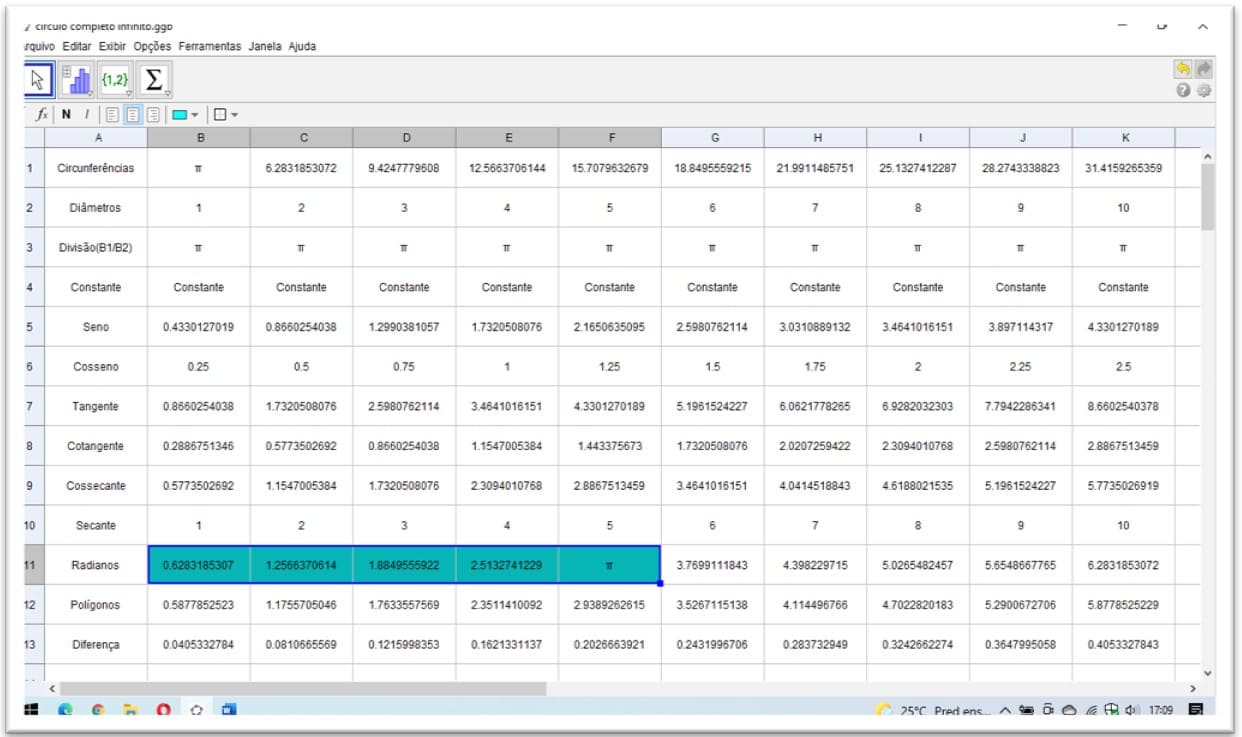
Figura 28. Demonstração entre circunferências e seus diâmetros valores racionais
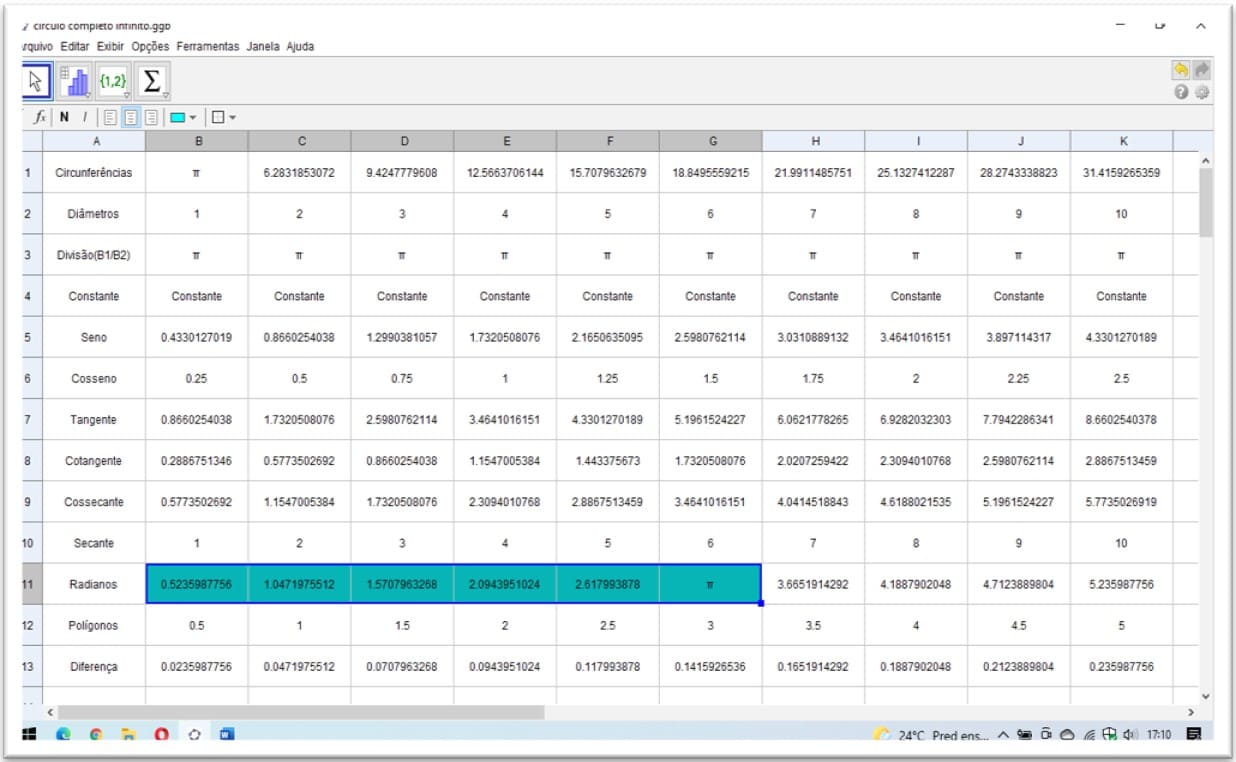
Figura 29. Demonstração entre circunferências e seus diâmetros valores racionais
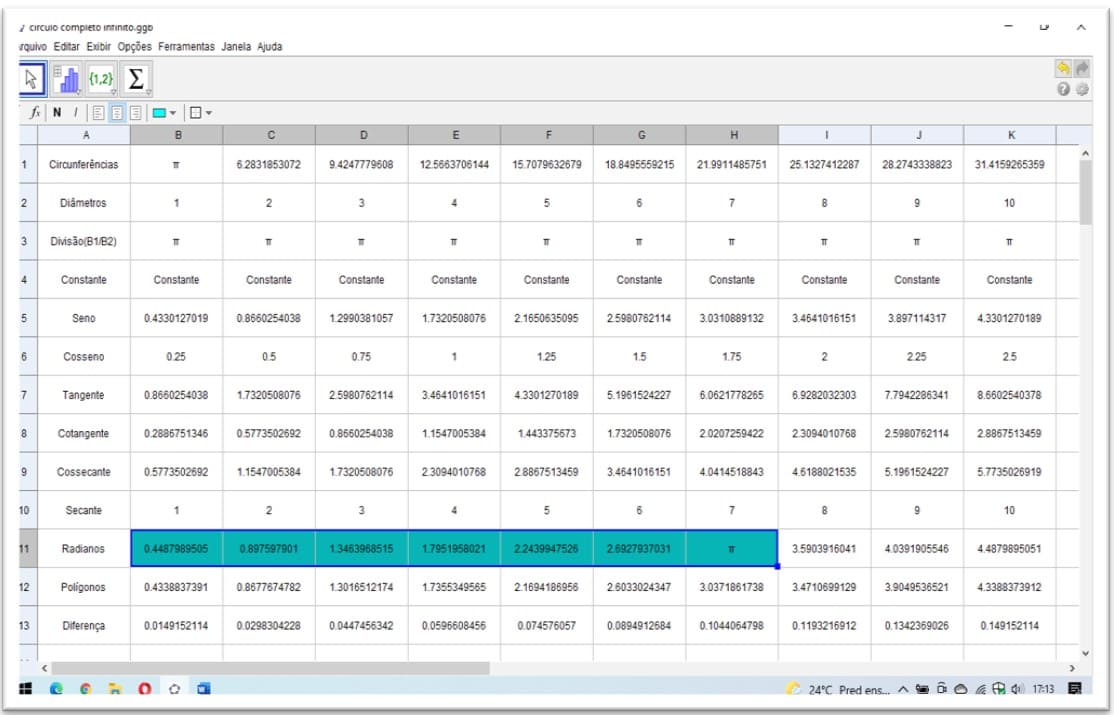
Figura 30. Demonstração entre circunferências e seus diâmetros valores racionais
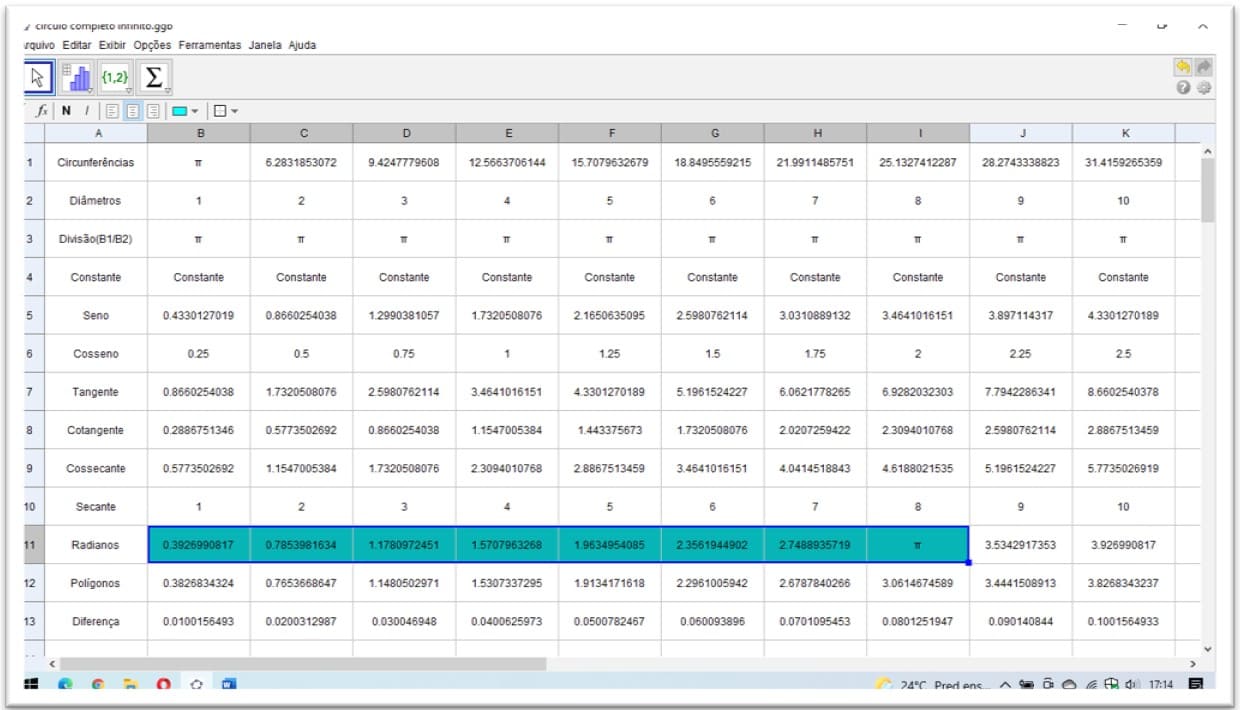
Figura 31. Demonstração entre circunferências e seus diâmetros valores racionais
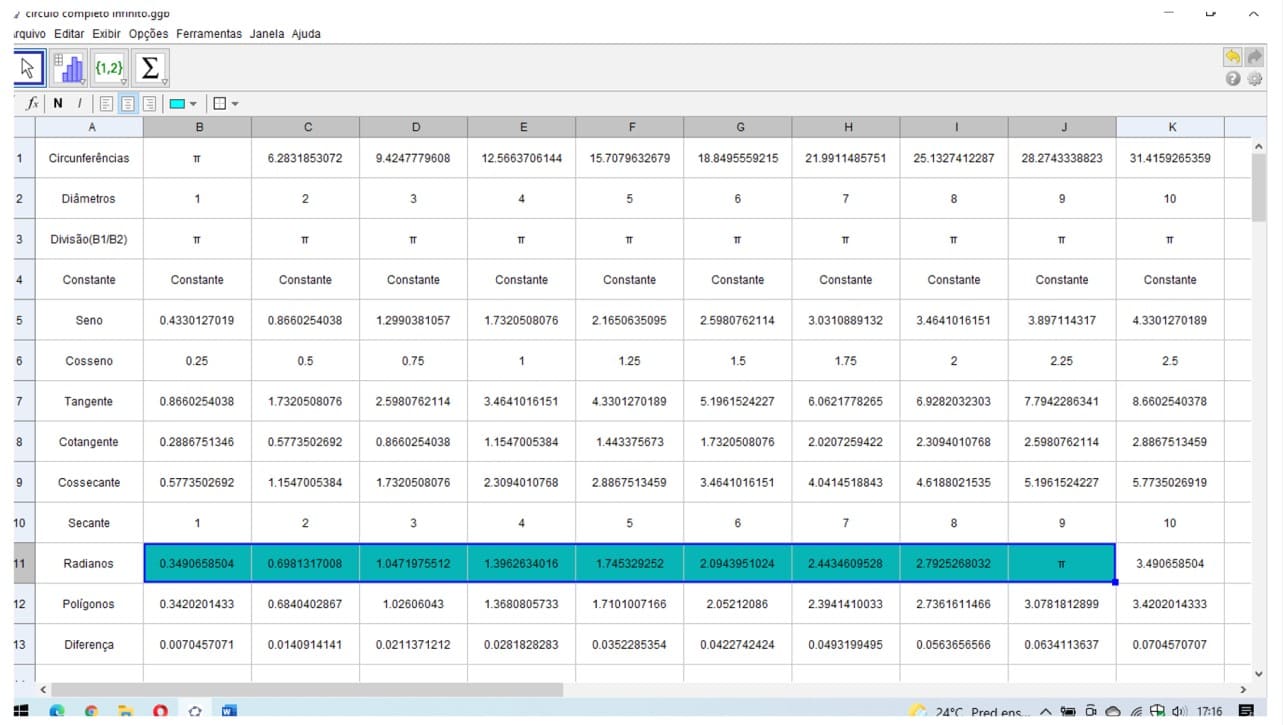
Figura 32. Demonstração entre circunferências e seus diâmetros valores racionais
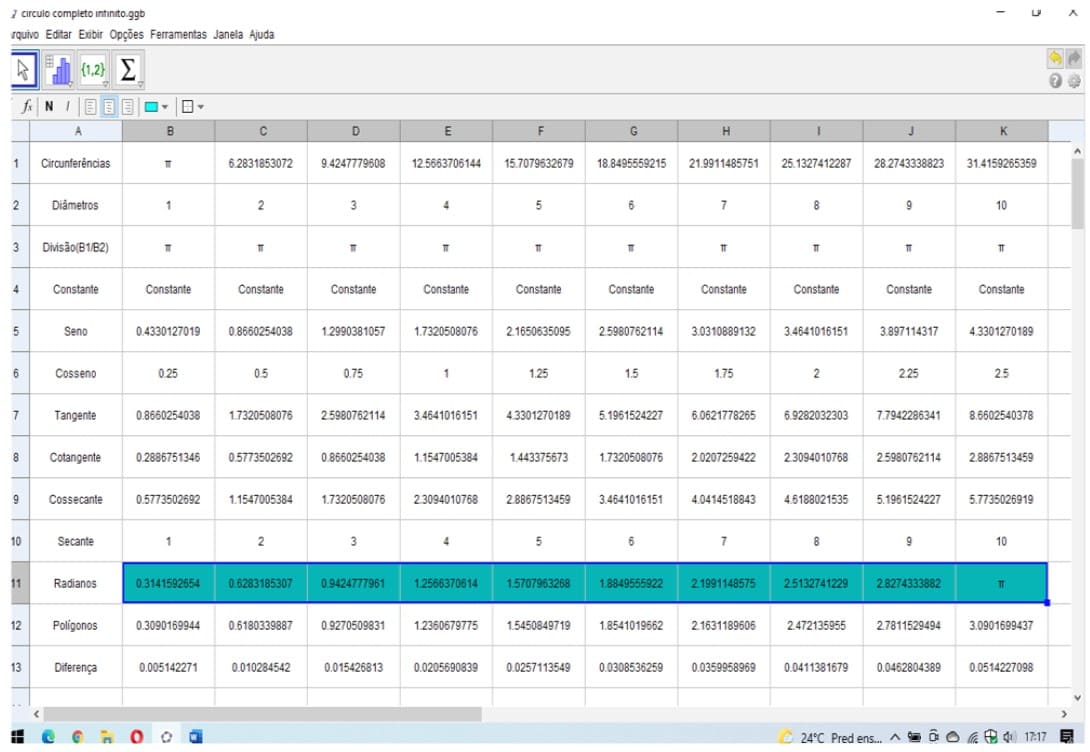
Figura 33. Demonstração da divisão racional provando com cálculos (0,9999…≠1)
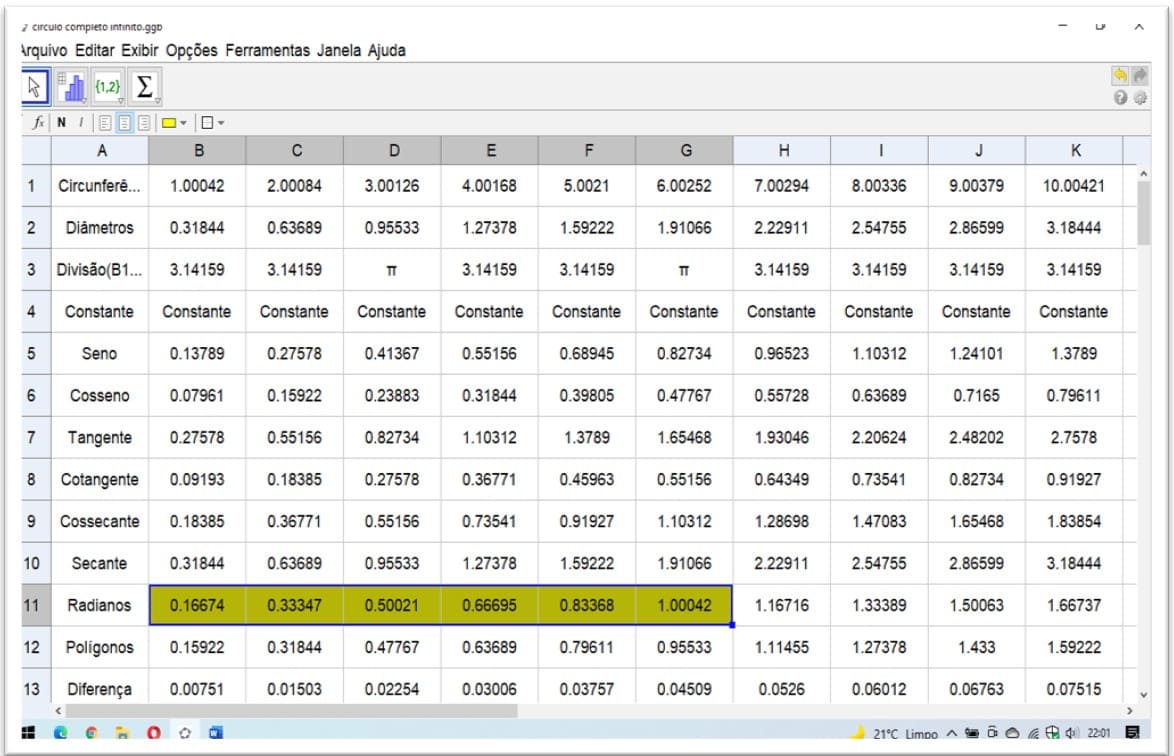
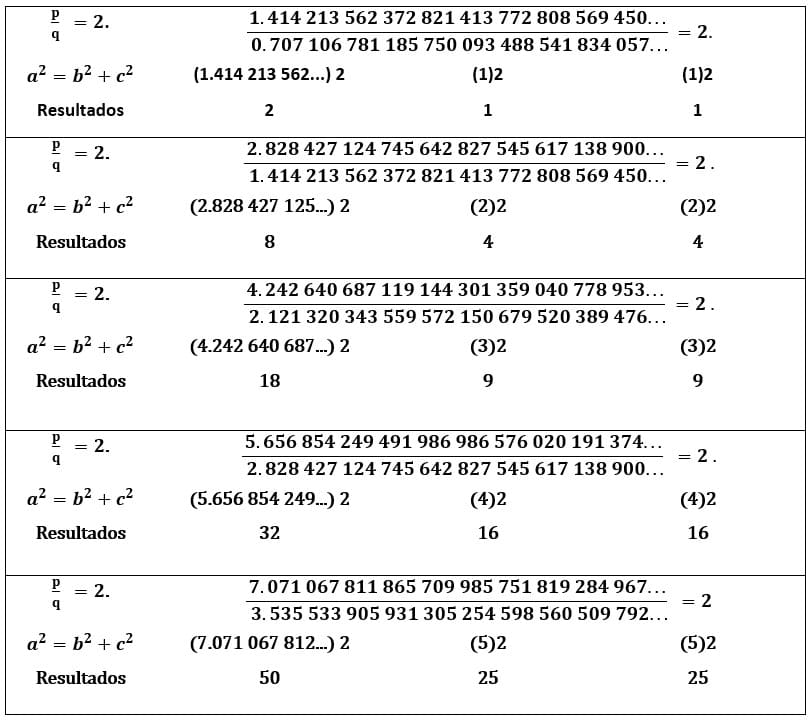
2.7 DEMONSTRAÇÕES DO TEOREMA DE PITÁGORAS E DA RAIZ QUADRADA RACIONAL 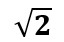
O teorema de Pitágoras leva o nome do Grego Pitágoras (570 a.C-495 a.C.). A definição do teorema é uma relação matemática entre os comprimentos dos lados do triângulo retângulo. A área do quadrado cujo lado é a hipotenusa é a soma das áreas dos quadrados cujos lados são os catetos ![]()
2.8 A DIAGONAL (D) DO QUADRADO
Pitágoras sabia na época, entretanto, que seu teorema tinha uma falha. Quando os catetos do triângulo eram iguais, seu teorema não funcionava, pois não haveria uma medida irracional para a hipotenusa![]() Matemáticos que o sucederam desde aquela época tentavam compreender o porquê da incomensurabilidade, os lados do triângulo não tinham medida em comum, não podiam ser medidos de forma exata através de uma unidade comum a ambos.
Matemáticos que o sucederam desde aquela época tentavam compreender o porquê da incomensurabilidade, os lados do triângulo não tinham medida em comum, não podiam ser medidos de forma exata através de uma unidade comum a ambos.
Com efeito, suponha que seja a hipotenusa (p), os catetos sejam iguais e representados pela letra (q). Sabe-se que p / q é uma fração irredutível, restando um numerador par e um denominador ímpar, ou vice-versa. Da aplicação do teorema resulta (p² = 2q²). Obviamente (p²) é par, pois é o dobro de (q²), ou seja, vem de um produto de um número multiplicado por 2. Se p² é par, implica que p é par (o quadrado de um número par é sempre número par e o quadrado de um número ímpar é sempre número ímpar), logo (q) obrigatoriamente deve ser ímpar, senão a fração dada acima não seria irredutível. Fazendo agora (p = 2k), pois p é par, reescrevemos: (2k) ² = (2q²), simplificando resulta (4k²=2q²) que resulta (2k²=q²).
Vamos calcular a diagonal (d) do quadrado em função do lado L. O problema pode também ser formulado assim: dado o lado L, calcule a diagonal (d). Aplicando o teorema de Pitágoras, podemos calcular a hipotenusa a partir dos quadrados dos catetos ![]()
Figura 34. Demonstrações dos resultados do teorema de Pitágoras racional
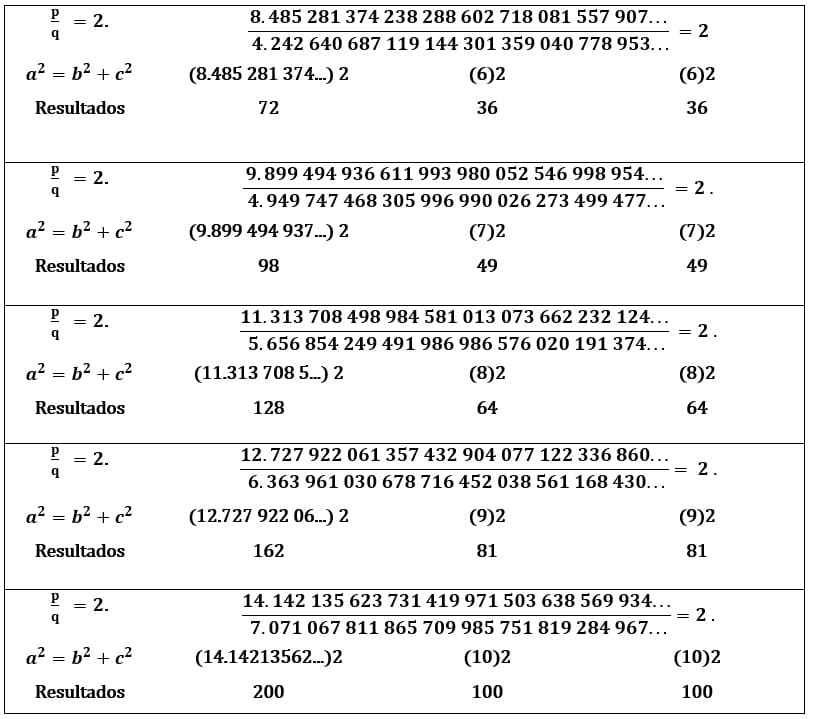
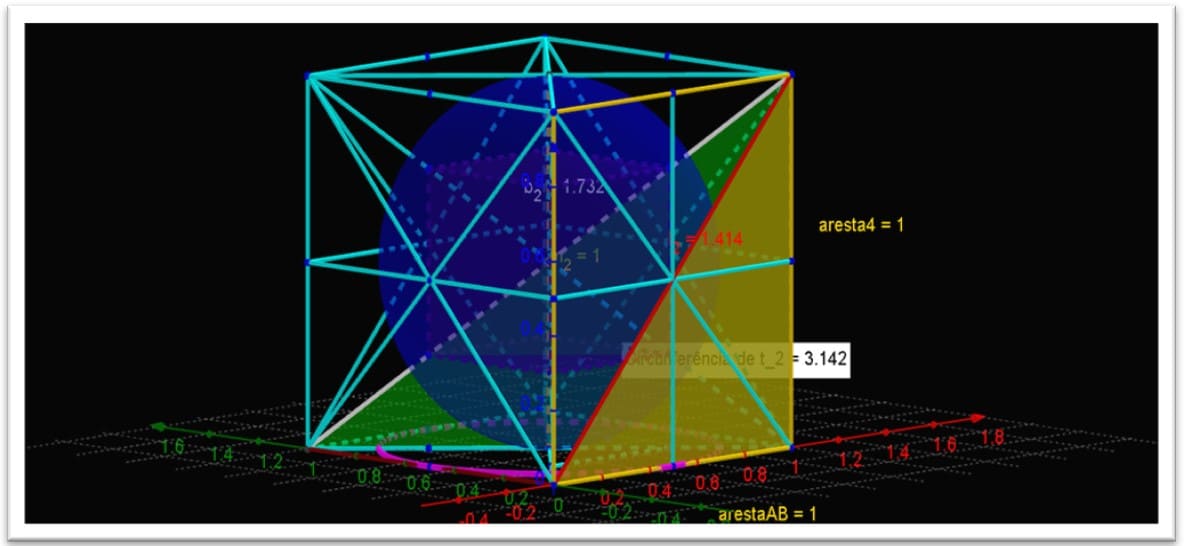
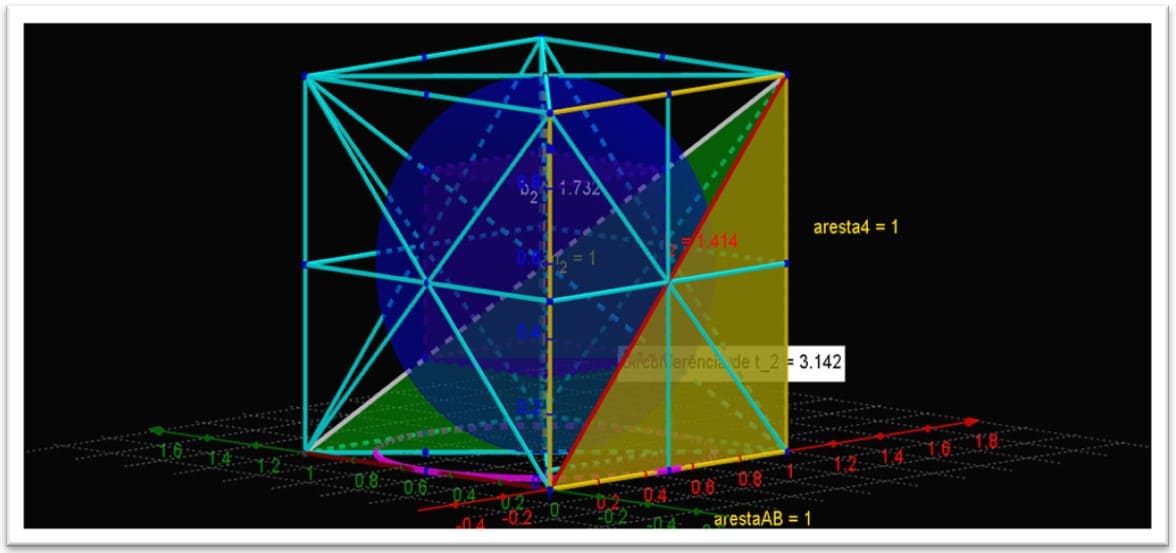
2.9 A DIAGONAL (D) DO CUBO
Vamos calcular a diagonal (D) do cubo em função do lado L. Aplicando o Teorema de Pitágoras no triângulo, temos ![]()
Figura 35. Demonstrações dos resultados do teorema de Pitágoras: (p² = 2q²)
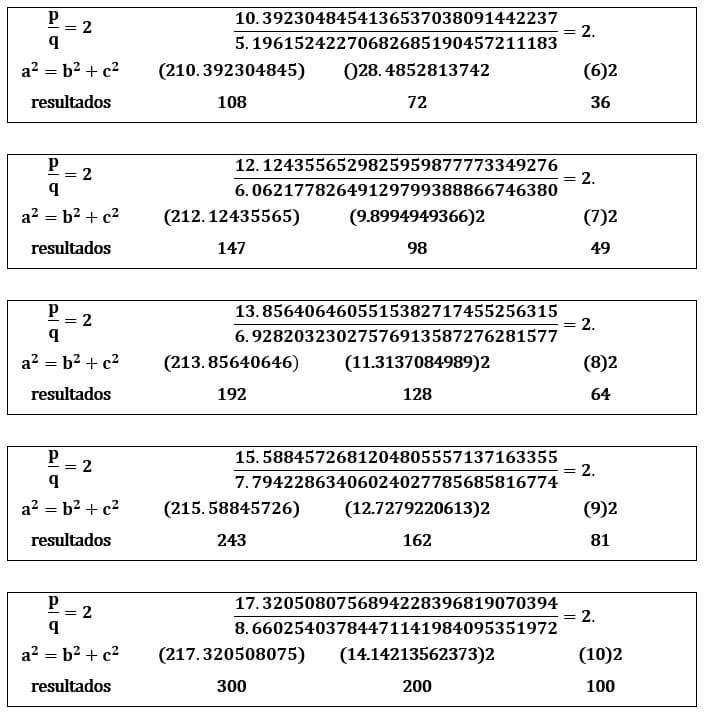
Figura36. Círculo trigonométrico em (3 d) de valores racionais atômicos
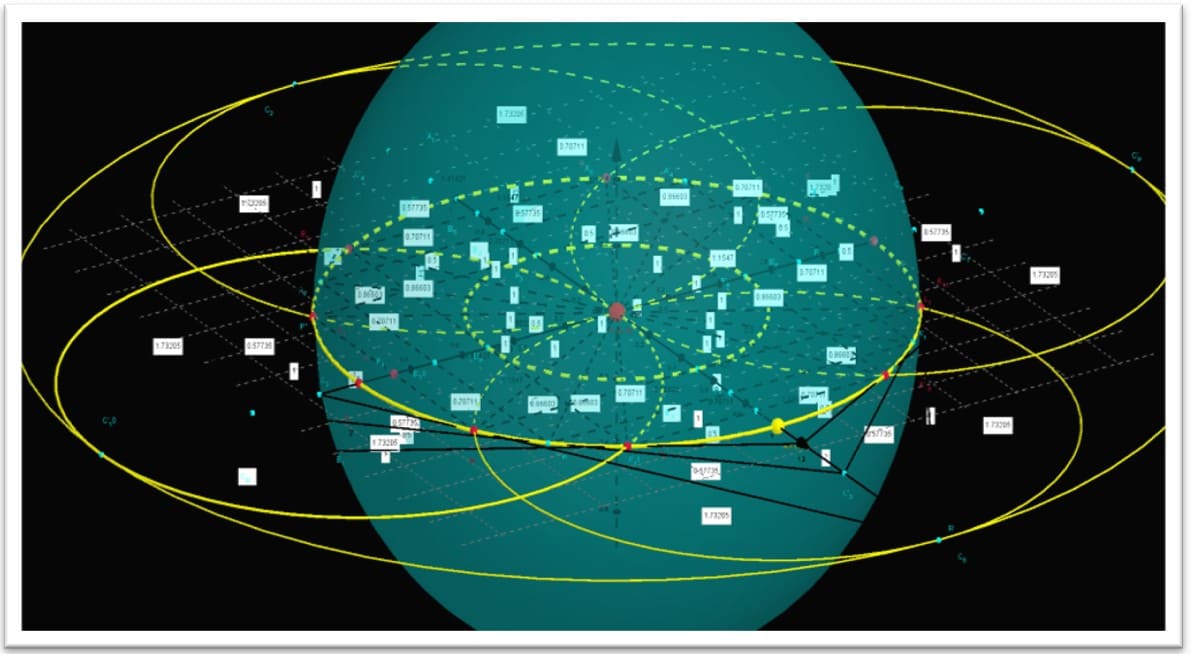
Figura 37. Demonstração de círculo trigonométrico em (3 d) de valores racionais
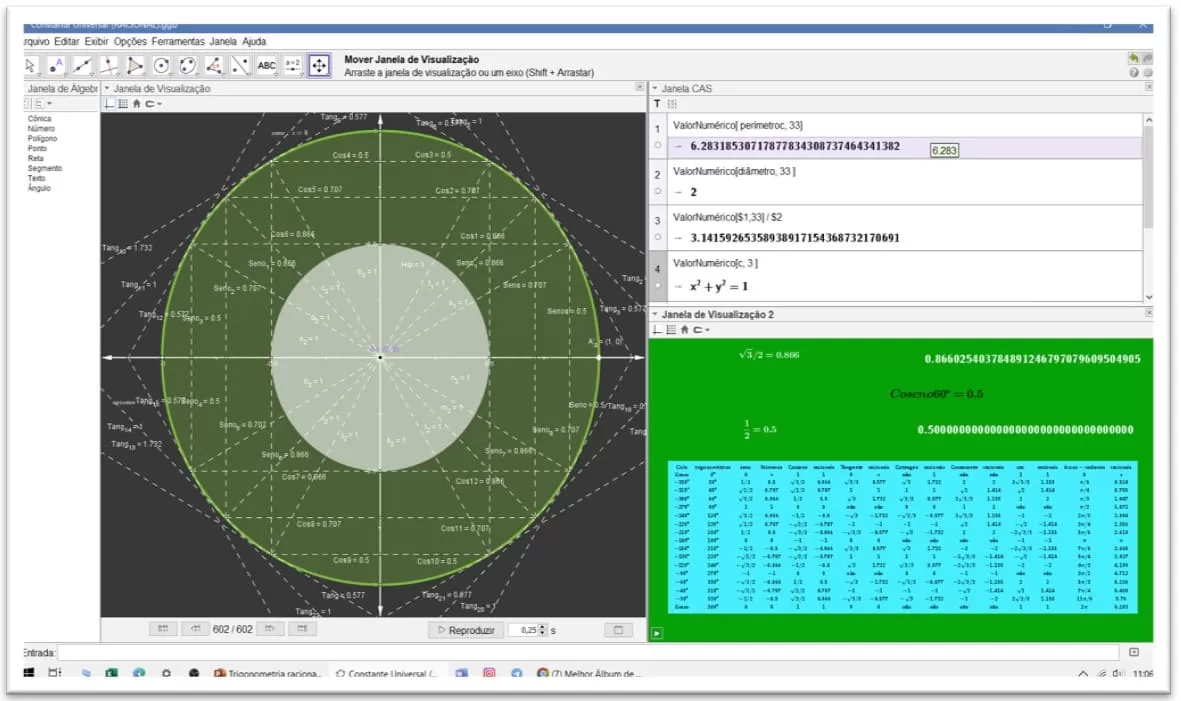
3. CONSIDERAÇÕES FINAIS
Matemáticos de vários tempos procuraram buscar uma racionalidade da constante π. No entanto, eles chegaram a uma descoberta incrível para a época da existência de números irracionais. A prova de que a constante π é irracional foi feita por Johann Lambert em 1761 e Legendre em 1794. Além de irracional, π é um número transcendente, o que foi provado por Ferdinand Lindemann em 1882. Isso significa que não há polinômio com coeficientes inteiros ou racionais. A representação decimal não tem previsibilidade.
Os resultados das demonstrações dos modelos matemáticos cartesiano, isométrico e polar, com cálculos racionais periódicos infinitos, podem ser aplicados em todas as ciências, geometrias de corpos circulares e esféricos, da física e astronomia.
REFERÊNCIAS
BECKMANN. P. A History of (pi)π. Citação Archimedes of Syracuse cap. 6; pg.63. Citação Leonhard Euler cap.14; pag. 149, Electrical Engineering Department University of Colorado. Ed. Barnes & Noble Books. United States of America, 1971.
IEZZI. G. Trigonometria. Matemática; 2º grau. Versão azul; (et al.). São Paulo: Atual, 1993.
NETO. A. A. Trigonometria Noções de Matemática. 2º grau;(et al.). São Paulo: Ed. Moderna, 1978.
WIKIPÉDIA. O papiro de Rhind. A enciclopédia livre, 2022.
[1] Ensino médio completo. ORCID: 0009-0001-1467-1150.
Enviado: 5 de junho, 2023.
Aprovado: 12 de julho, 2023.
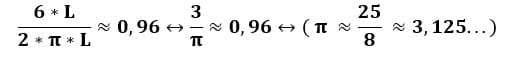





10 respostas
Sensacional, muito bem elaborado, muito bem explicado, parabéns Clovis Sampaio por esse rico e valioso artigo
Parabéns pelo artigo.
Impressionante! Parabéns pelas conclusões.
Eu nao entendo muito, mas saber que existem mentes tão podetosas ,, avançadas e comprometidas com o estudo, conhecimento e brasileiro, isso me enche de orgulho, parabéns!
Estudo louvável! Parabéns!
Parabéns pela publicação! Um artigo sensacional que traz luz ao grande mistério que a constante pi.
Parabéns Clóvis!! Arrasou!! Realmente Deus te presenteou com uma inteligência singular!! Amante da matemática que sou, admiro e aplaudo de pé este seu trabalho! Show!! Que seja o primeiro de muitos!! Parabéns!!
Parabéns Clóvis! Arrasou! Realmente Deus te presenteou com uma inteligência singular! Amante da matemática que sou, admiro e aplaudo de pé este seu trabalho! Que seja o primeiro de muitos!! Show! Parabéns!!
As aplicações da racionalidade do Pi mudam tudo que conhecemos. A tão procurada exatidão dessa constante faz com que nossos cálculos celulares e astronômicos sejam mais exatos e completos como nunca antes.
O problema da modernidade não está nas equações ou nas descobertas mas em como usar e aplicar as descobertas nos nossos sistemas já pré estabelecidos.
Muito legal seu trabalho ,no meio de tanta Tecnologia saber mais um pouco sobre a matemática e os cálculos fazer bem para nós 👏👏👏 parabéns mesmo pelo seu trabalho e talento