Considerações sobre a reta real à luz da incomensurabilidade entre racionais e irracionais

ARTIGO ORIGINAL

PEREIRA, Olavo de Carvalho ^[1]

PEREIRA, Olavo de Carvalho. Considerações sobre a reta real à luz da incomensurabilidade entre racionais e irracionais. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 01, Vol. 01, pp. 46-52. Janeiro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/reta-real

RESUMO

O artigo mostra a inconsistência de se ter, na mesma reta, irracionais e racionais, partindo do fato da incomensurabilidade de um sistema de medidas em relação ao outro.

Palavras-Chave: Reta real.

1. INTRODUÇÃO

O presente artigo tem o objetivo de rever a afirmação de que, na mesma reta, podemos ter inteiros, racionais e irracionais, isto é, rever a afirmação de que existe a reta real.

Isto será feito à luz do que se conhece da teoria de conjuntos numéricos.

1.1 A RETA REAL: NÚMEROS RACIONAIS E IRRACIONAIS NA MESMA RETA

Alguns autores, por exemplo, Iezzi e Murakami (1991), em Fundamentos da Matemática Elementar, e Bianchini (1996), afirmam que os inteiros e racionais são insuficientes para preencher a reta, necessitando, por isso, dos números irracionais para preenchê-la completamente. Outros, embora não explicitem tal afirmação, como, por exemplo, Lima (1978) e Silveira e Marques (1996), desenvolvem esse tópico baseando-se em tal afirmação.

No presente artigo, mostraremos a impossibilidade de termos racionais (inteiros e racionais) e irracionais na mesma reta.

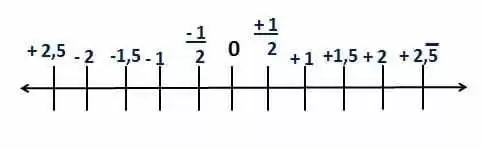
Sabemos que números racionais são frações de números inteiros. Isto significa que qualquer parte de um inteiro é um número racional. Se olharmos a reta numerada, por exemplo, onde números são identificados com segmentos e pontos com extremidade de segmentos, podemos afirmar que qualquer ponto entre zero e um, sendo uma divisão do inteiro um, constitui um número racional; qualquer ponto da divisão de um inteiro contido na reta numerada corresponde a um número racional.

Sabemos, também, que um número irracional é aquele que não pode ser escrito na forma de fração, isto é, um número irracional não corresponde a um número racional, não pode ser expresso como a relação entre dois inteiros.

Sabemos que, também pelo que foi dito acima, não existe um padrão de medida que seja comum aos números racionais e irracionais, isto é, um submúltiplo que consiga medir um número racional e um número irracional.

Com base no exposto, e lembrando que medir um segmento com a reta numerada significa localizar na reta um ponto que corresponda ao ponto que é extremidade do segmento, podemos concluir que não é possível situar os números racionais e irracionais na mesma reta, pois, fazendo isso, estaríamos admitindo que existe um mesmo padrão de medida para ambos e que, sendo assim, seria possível  medir números irracionais com a reta numerada com inteiros e racionais (que sabemos não ser possível).

Com isso queremos dizer, por exemplo, que não existe número irracional entre zero e um, ou entre zero e dois, etc.

O que existe entre zero e um inteiro qualquer é uma subdivisão, uma fração, daquele inteiro e, portanto, um número racional.

Se disséssemos, por exemplo, que raiz quadrada de dois (cujo valor pode ser aproximado por um racional localizado  entre um e dois) está localizada entre um e dois, nós teríamos que afirmar que ela é um número racional, pois, seria uma fração de dois (enfatizando: identificando números como segmentos de reta e pontos de extremidades desses segmentos, todos os pontos entre zero e um número inteiro qualquer são frações daquele inteiro, isto é, são números racionais).

Sabemos que todo número irracional pode ser aproximado, tanto quanto quisermos, por um número racional. Então, quando dizemos que a raiz quadrada de dois tem um valor entre um e dois, queremos dizer que esse valor é aproximado, isto é, que temos números racionais entre um e dois cujo valor se aproxima do valor da raiz quadrada de dois, mas nunca teremos, nesse intervalo, o valor exato da raiz quadrada de dois, pois ela não é um número racional.

O número raiz quadrada de dois não é um número de uma dimensão, ele é um número de duas dimensões, isto é, de duas coordenadas, pois só ocorre no plano (é o número correspondente às coordenadas (1,1), de um eixo de coordenadas X0Y).

Se usássemos um sistema de medidas cuja unidade padrão fosse raiz quadrada de dois, com esse sistema não conseguiríamos medir com exatidão os números inteiros e os racionais (simplesmente porque suas extremidades não estariam nele) e, da mesma forma, se usássemos um sistema de medidas cuja unidade padrão fosse um inteiro, como na reta numerada, com ele não conseguiríamos medir, com exatidão, a raiz quadrada de dois (simplesmente porque sua extremidade não estaria lá). Se optamos por um dos sistemas, perdemos o outro.

Um exemplo ilustrativo do exposto acima é o fato da diagonal de um quadrado ser incomensurável com a medida de seu lado, isto é, se criarmos um sistema de medidas utilizando-se a medida do lado de um quadrado como unidade padrão desse sistema, não conseguiremos medir sua diagonal com esse sistema de medidas.

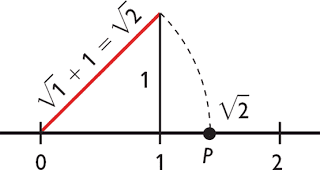
Alguns argumentam que, com um compasso, podemos projetar com exatidão, o segmento de medida correspondente a √2 na reta numerada com os inteiros e racionais (gráfico abaixo).

Isso não é verdade, pois, com essa mesma abertura do compasso, que corresponde ao sistema de medidas com padrão de unidade igual a raiz quadrada de dois, não conseguimos medir, com exatidão, nenhum número inteiro nem racional, e se conseguíssemos medi-los eles seriam números irracionais, uma vez que uma fração de um número irracional, isto é, um irracional dividido por um número inteiro, é sempre um número irracional.

Assim, o 1 (um), se estivesse localizado entre zero e √2 , seria uma fração de √2  e, portanto, um número irracional.

Explicando melhor: para numerarmos a reta com os números 1, 2, 3, etc. utilizamos um compasso com uma abertura que convencionamos chamar de  unidade padrão, equivalente ao segmento de valor unitário 1 (um); com centro em zero, marcamos o 1, com centro em 1, marcamos o número 2, com centro em 2, marcamos o número 3, e assim sucessivamente fomos numerando a reta com os inteiros; obtida a √2 no eixo coordenado X0Y, para medi-la, isto é, para medir o segmento correspondente a ela, tivemos que alterar a abertura do compasso que foi utilizada para numerar a reta com os inteiros aumentando-a até atingir a extremidade do segmento correspondente a √2 ; ao fazermos isso, mudamos de padrão, isto é, saímos do padrão unitário 1, utilizado para numerar a reta com inteiros, e fomos para o padrão √2, isto é, com essa nova abertura do compasso poderíamos numerar uma reta com √2 , 2√2 , 3√2 etc (a cada abertura do compasso corresponde uma unidade de medida, isto é, um padrão de medida); sabemos que, com a reta numerada, isto é, com o padrão de medida utilizado para numerar a reta com inteiros e, claro, com racionais, não conseguimos medir o segmento correspondente a √2  e, reciprocamente, com uma reta numerada com o padrão √2 , não conseguimos medir os números 1, 2, 3, etc, nem suas frações, isto é, esses dois padrões de medida são incomensuráveis, um não consegue medir o outro, um não pode ser convertido no outro; sendo assim, não podem coexistir na mesma reta. Então, neste exemplo específico, ou temos na reta os números inteiros e suas frações, ou os irracionais com padrão √2  e suas frações, que são, também, irracionais, mas nunca os dois. Dessa forma, quando projetamos o segmento √2  na reta “aparentemente” numerada com os inteiros e os racionais, isto é, quando mudamos do padrão unitário (um) para o padrão √2,  os segmentos de medidas 1, 2, 3, etc. e suas frações, que ainda parecem estar na reta, simplesmente desapareceram dessa reta, não estão mais na reta, pois não conseguimos medi-los com este novo padrão irracional; se conseguíssemos medi-los, eles seriam frações de √2 , 2√2 , etc, todos números irracionais e, portanto, seriam números irracionais.

Se usamos um sistema de medidas com padrão de unidade de medida um número irracional, com o mesmo sistema não conseguimos medir números inteiros nem racionais.

Não podemos ter na mesma reta segmentos que são incomensuráveis, um em relação ao outro, isto é, dois sistemas de medidas, um para número racional e outro para número irracional (se utilizamos um sistema, perdemos o outro).

Resumindo: os números irracionais representam medidas de segmentos que são incomensuráveis com segmentos de medida correspondente a números racionais.

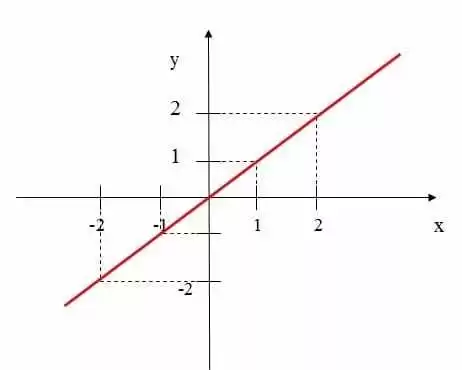
Usando a nomenclatura decorrente da explicação acima, somente a título de exemplo, a função de Q em Q, definida por y=x, fornece a reta com padrão raiz quadrada de dois, isto é, à coordenada (1,1) corresponde a raiz quadrada de dois (√2 ); à coordenada (2,2) corresponde a dois raiz quadrada de dois (2√2) e assim por diante, na mesma  reta (gráfico abaixo):

A análise que fizemos acima se utilizou de apenas um número irracional, isto é,  o número irracional √2 , mas podemos generalizar o que foi dito para todo e qualquer número irracional, uma vez que nenhum deles pode ser expresso como razão entre dois inteiros e, portanto, não podem figurar na reta numerada com inteiros e racionais.

Concluímos, então, que todos os números irracionais estão fora da reta numerada com inteiros e racionais.

Logo não existe a reta real (constituída de números racionais e irracionais, na mesma reta), isto é, na reta numerada só existem os inteiros e os racionais.

Ressaltamos que não se está questionando nada sobre a existência dos números reais (resultado da união dos racionais (incluindo os inteiros) com os irracionais), mas apenas afirmando a impossibilidade de sua representação na reta numerada (irracionais não podem estar junto com racionais na mesma reta).

2. CONCLUSÃO

No exposto mostramos a impossibilidade de existência da reta real.

A tese se baseou na própria teoria já estabelecida, não se tendo utilizado de nada de estranho à mesma para justificá-la.

Relatamos esta observação na intenção de corrigir tópico tão fundamental na matemática.

Os resultados decorrentes da presente conclusão devem ser reavaliados.

3. REFERÊNCIAS

BIANCHINI, Edwaldo. Matemática 7ª Série, 4ª Edição, 1996.

IEZZI, Gelson e MURAKAMI, Carlos. Fundamentos de Matemática Elementar, vol. 1, 1991.

LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.

SILVEIRA, Ênio e MARQUES, Cláudio. Matemática 7ª Série, 1ª Edição, 1996.

^[1] Graduação – Bacharelado em Matemática pela Universidade de Brasília.

Enviado: Novembro, 2019.

Aprovado: Janeiro, 2020.